Квазилинейный метод анализа автогенераторов. Нелинейное уравнение автогенератора

1.

Тема:
КВАЗИЛИНЕЙНЫЙ МЕТОД АНАЛИЗА
АВТОГЕНЕРАТОРОВ.
НЕЛИНЕЙНОЕ УРАВНЕНИЕ
АВТОГЕНЕРАТОРА
1

2.

1. Квазилинейный метод анализа стационарного
режима работы автогенератора
1.1. Средняя крутизна
Средняя крутизна − отношение комплексной амплитуды первой гармоники тока в цепи коллектора к комплексной амплитуде напряжения на базе транзистора, т.е.
1
I
S ср
.
U б
Другие составляющие спектра коллекторного тока не
представляют интереса, так как они отфильтровываются
контуром.
В общем случае средняя крутизна является комплексной величиной, т.е. S S ei s .
ср
ср
2

3.

1.2. Баланс амплитуд и баланс фаз
Учитывая частотно-избирательные свойства колебательного контура в цепи коллектора, в силу которых в формировании выходного напряжения будет участвовать только первая гармоника тока, комплексные амплитуды напряжений на выходе генератора и на входе усилителя
(на базе транзистора) будут иметь вид:
U I 1Z I 1Z 0e
j к
;
j
j к
U б U I1Z 0e e .
С другой стороны I 1 U б S ср U б Scp e j s .
Тогда
Scpe
j s
j
j s
j к
U б U б Scpe Z 0e e ;
Z 0e
j к
e
j
1;
K у e
j ( s к )
1.
3

4.

Получены два условия, обеспечивающие устойчивую работу генератора по формированию гармонического колебания с постоянной амплитудой:
1.
S cp Z 0 K у 1
− баланс амплитуд.
2.
s к z 2 n
− баланс фаз.
Последние рассуждения позволяют данный метод назвать квазилинейным, так как создается иллюзия, что система работает с единственным гармоническим колебанием без каких либо искажений, т.е. работает как линейное устройство.
4

5.

2. Определение амплитуды колебаний в
стационарном режиме
Рассматривают два режима работы автогенератора:
– мягкий режим, при котором рабочая точка расположена на участке ВАХ с максимальной крутизной (на
линейном участке характеристики);
– жесткий режим, при котором рабочая точка расположена на нижнем сгибе ВАХ.
5

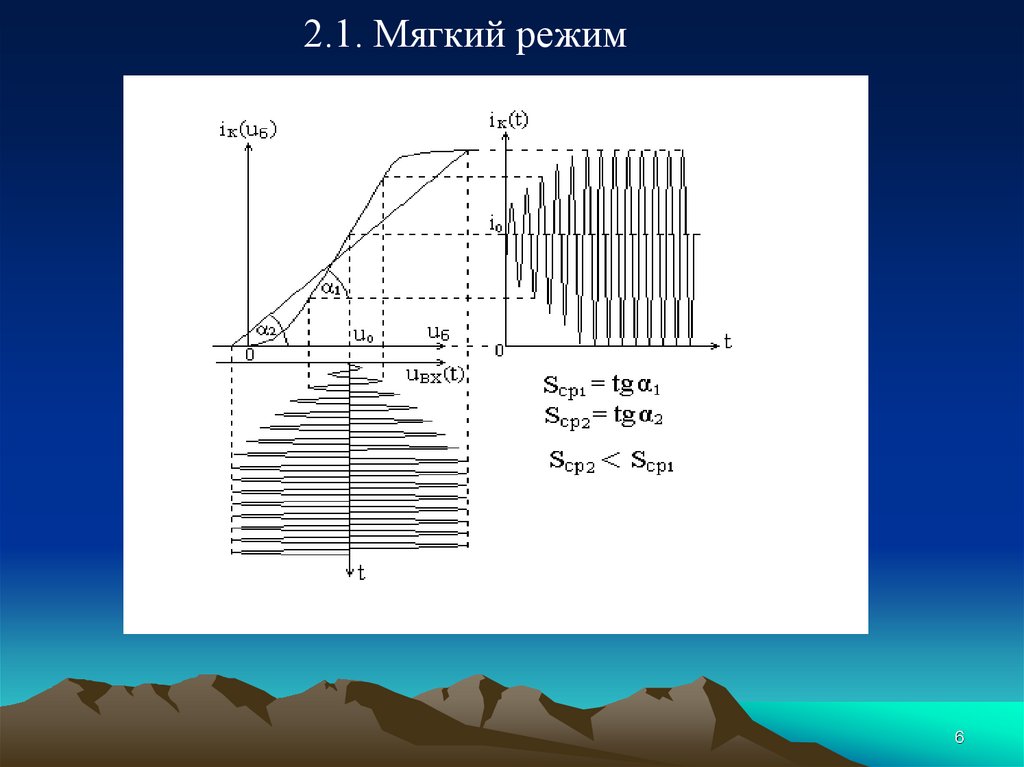
6.

2.1. Мягкий режим
6

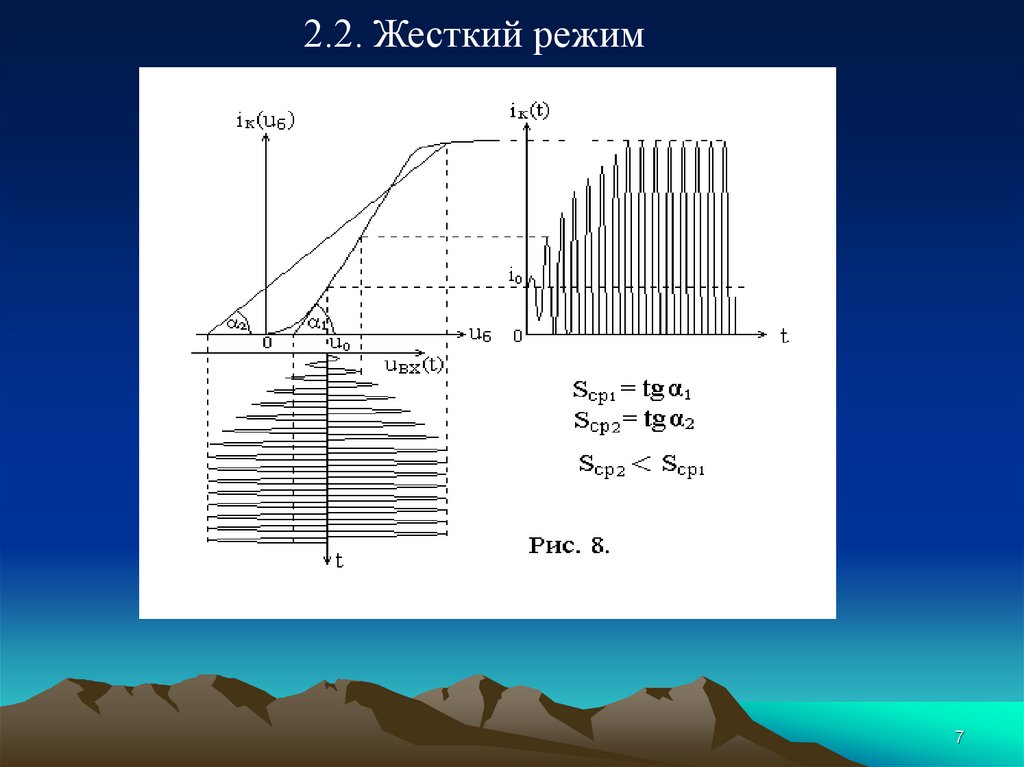
7.

2.2. Жесткий режим
7

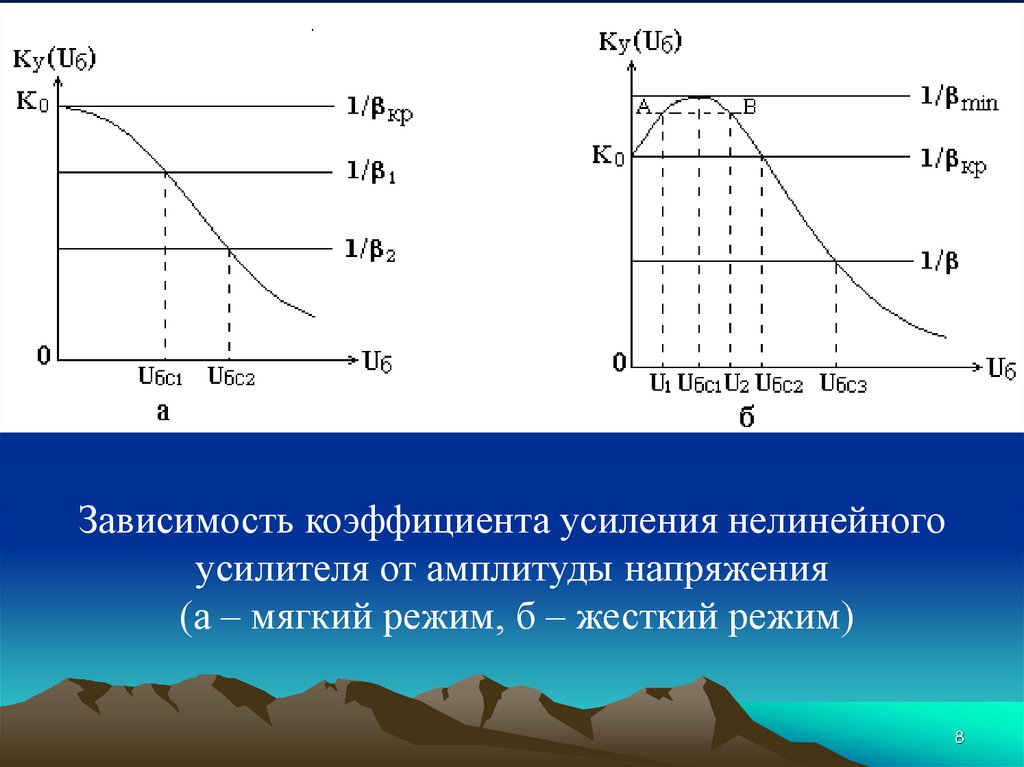
8.

Зависимость коэффициента усиления нелинейного
усилителя от амплитуды напряжения
(а – мягкий режим, б – жесткий режим)
8

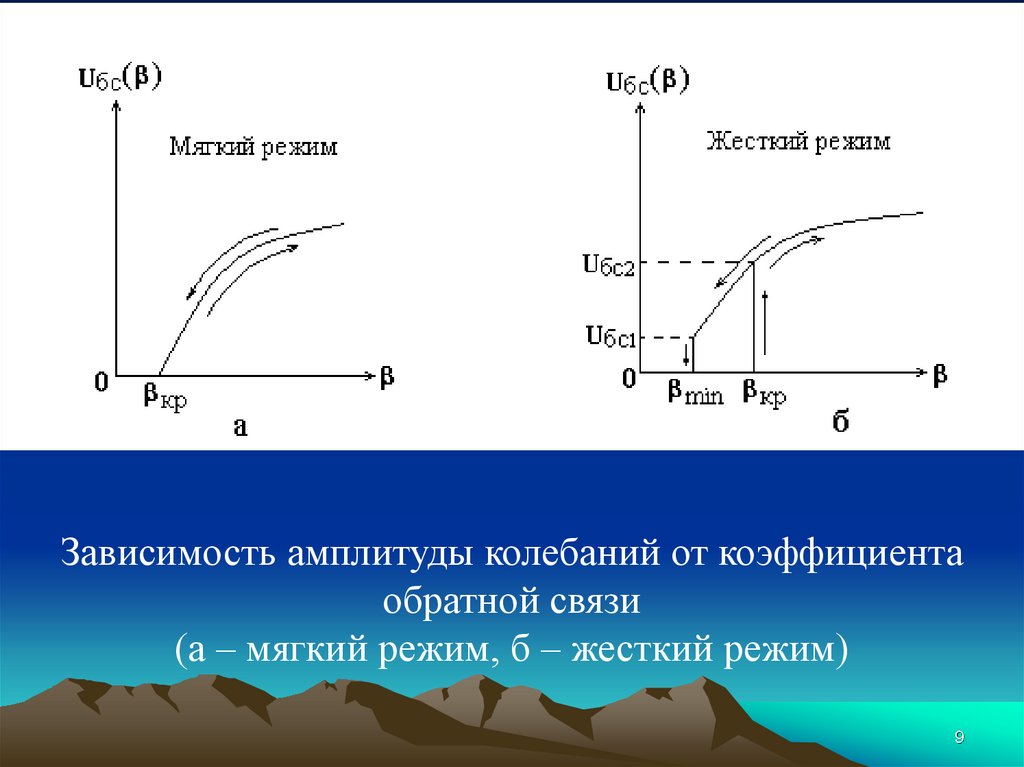
9.

Зависимость амплитуды колебаний от коэффициента
обратной связи
(а – мягкий режим, б – жесткий режим)
9

10.

3. Определение частоты генерируемых колебаний
Частоту генерируемых колебаний можно определить,
s к 2 n.
исходя из условия баланса фаз
Комплексное входное сопротивление контура в составе генератора определяется формулой:
R0
R0
R0
Z ( j )
.
2
1 j 1 jQ 1 jQ
R
p
2
2
arctgQ
;
Следовательно, к
arctgQ
2 n s z ;
p
p
1
1
tg ( s )]
tg ( s ); 0 p [1
p 2Q
2Q
Таким образом, частота генерируемых колебаний в основном определяется резонансной частотой контура.
10

11.

4. Нелинейное уравнение автогенератора
Для описания работы автогенератора в переходном и
стационарном режимах необходимо отказаться от усло-вия
независимости средней крутизны от напряжения. При
этом получим нелинейное дифференциальное уравнение
автогенератора
d 2u 1 1 S (u ) M du
2
pu 0.
2
С R
L dt
dt
В результате преобразований получаем уравнение,
которое называется уравнением Ван-дер-Поля.
2
d u
2 du
1 u
u 0.
2
d
d
11

12.

При симметричной ВАХ и положении рабочей точки,
соответствующей мягкому режиму работы автогенератора, аппроксимируем функцию S(u) с использованием полинома вида ik=a0+a1u-a3u3, где коэффициент a1 является
крутизной S0 линейной части ВАХ. При этом получаем
Подставим полученное выражение в дифференциальное
уравнение и выполним некоторые преобразования.
d 2u 1 1 S0 M 3a3Mu 2 du
2
0 u 0.
2
L
LC dt
dt
С R
d 2u
2 du
2
2
u
0 u 0.
2
dt
dt
12

13.

Здесь 2 1 1 S0 M ,
С R
L
2
3a3 0 M .
M RC,
,
L
1
2 1 K 0 .
Учитывая, что K 0 S0 R,
можно записать
Перейдем к безразмерному напряжению, осуществив
замену
u u
.
2
2
2
Разделим на 0 . Введем параметр
.
0
2
1 d u 1
2 du
1 u
u 0.
2
2
0
dt
0 dt
13

14.

Приведем полученное
времени 0t .
уравнение
к
безразмерному
d 2u
2 du
Получаем
1 u
u 0.
2
d
d
Уравнение можно использовать для полного анализа поведения автогенератора на всех стадиях процесса установ2
ления колебаний. При малых напряжениях, когда u 1 ,
полученное уравнение становится линейным. При увеличении напряжения проявляется нелинейность, обусловленная составляющей u 2 .
Нет методов, позволяющих получить точное решение
уравнения Ван-дер-Поля. Существуют приближенные методы, среди которых достаточные для практики результаты дает метод фазовой плоскости и метод медленно меняющихся амплитуд.
14

15.

Выражение для огибающей
U (t )
U ст
2 t
2
2
1 (U ст U 0 1) e
U ст U 0 1 , огибающая равна
При запуске, когда
U (t )
U ст
2
1 (U ст
.
2 t
2
U 0 1) e
U ст
(U ст U 0 ) e
U0 e
t
t
.
Выходное напряжение
u (t ) U 0 e
t
cos( 0t 0 ).
15

16.

При
t
U (t )
U ст
2
1 U ст
U 02 1
U ст
u (t ) U ст cos( 0 t 0 )
16