Похожие презентации:
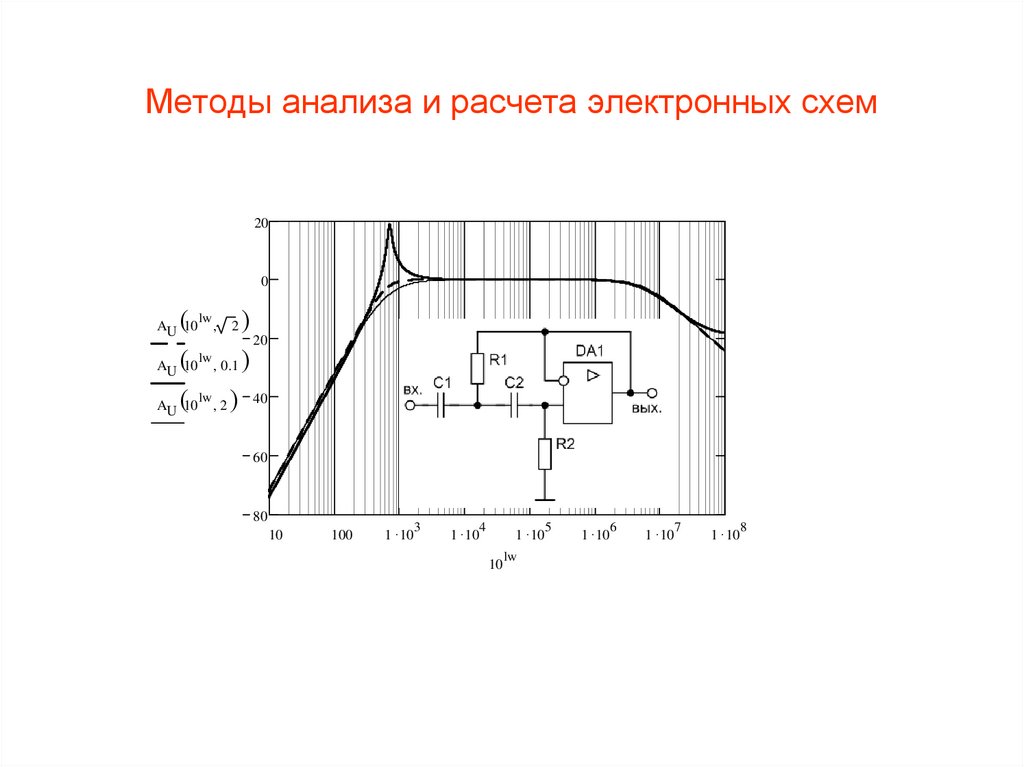
Методы анализа и расчета электронных схем
1. Методы анализа и расчета электронных схем
200
lw
lw
0.1
lw
2
AU 10
AU 10
AU 10
2
20
40
60
80
10
100
1 10
3
1 10
1 10
4
10
lw
5
1 10
6
1 10
7
1 10
8
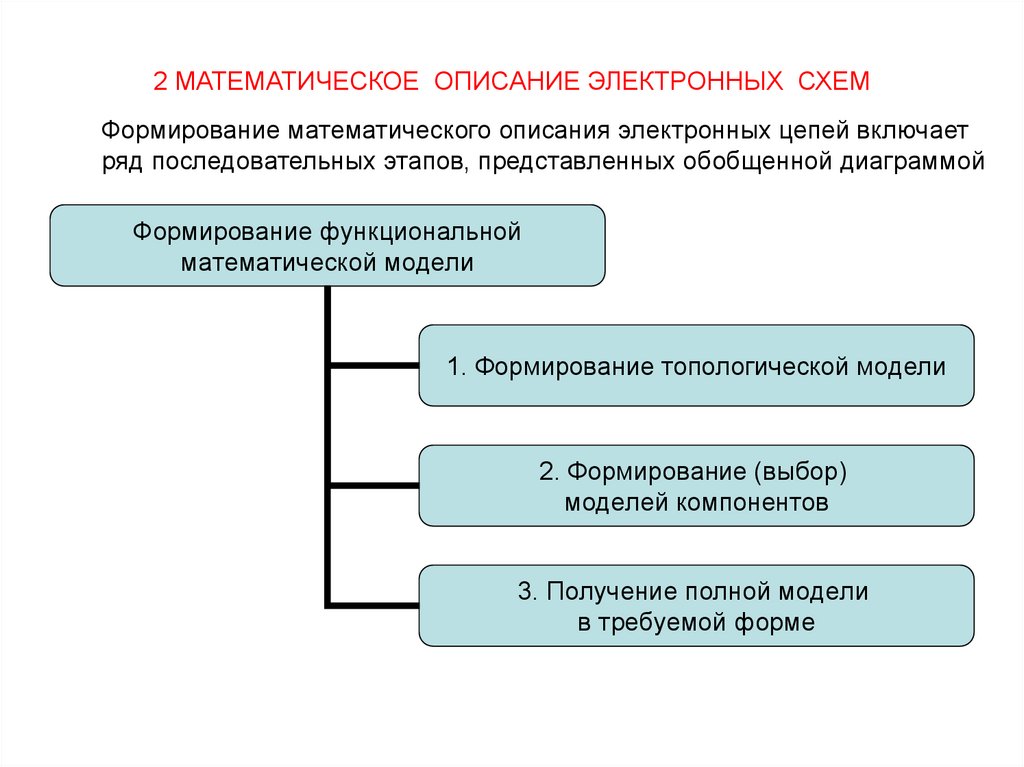
2.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМФормирование математического описания электронных цепей включает
ряд последовательных этапов, представленных обобщенной диаграммой
Формирование функциональной
математической модели
1. Формирование топологической модели
2. Формирование (выбор)
моделей компонентов
3. Получение полной модели
в требуемой форме
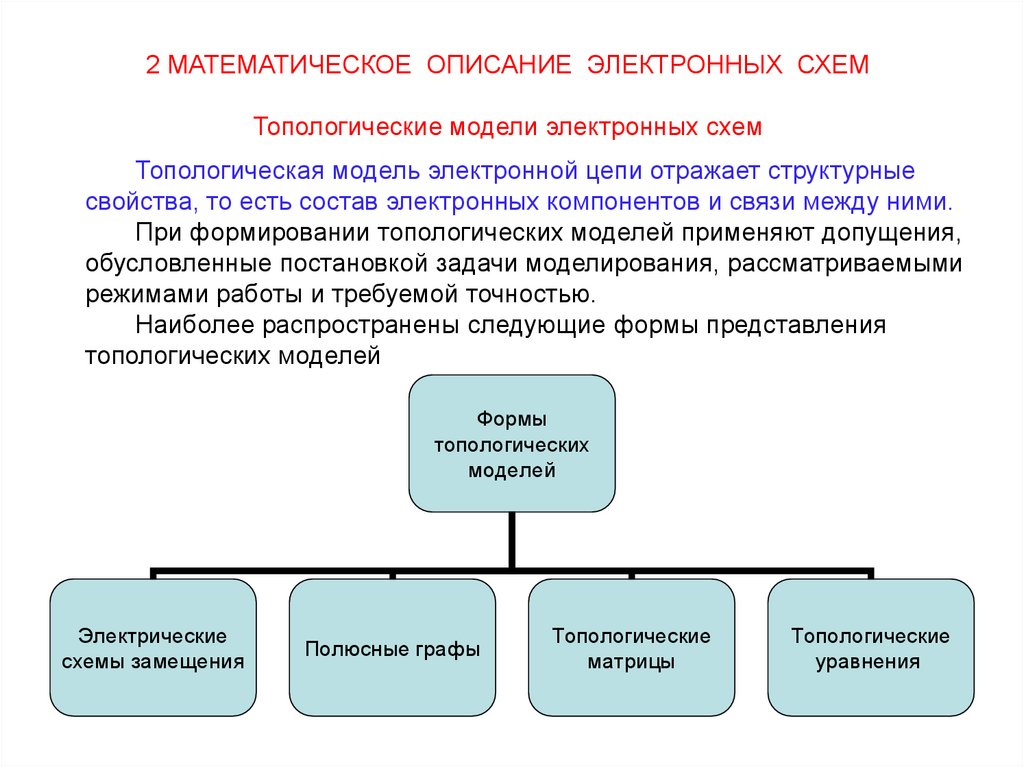
3.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМТопологические модели электронных схем
Топологическая модель электронной цепи отражает структурные
свойства, то есть состав электронных компонентов и связи между ними.
При формировании топологических моделей применяют допущения,
обусловленные постановкой задачи моделирования, рассматриваемыми
режимами работы и требуемой точностью.
Наиболее распространены следующие формы представления
топологических моделей
Формы
топологических
моделей
Электрические
схемы замещения
Полюсные графы
Топологические
матрицы
Топологические
уравнения
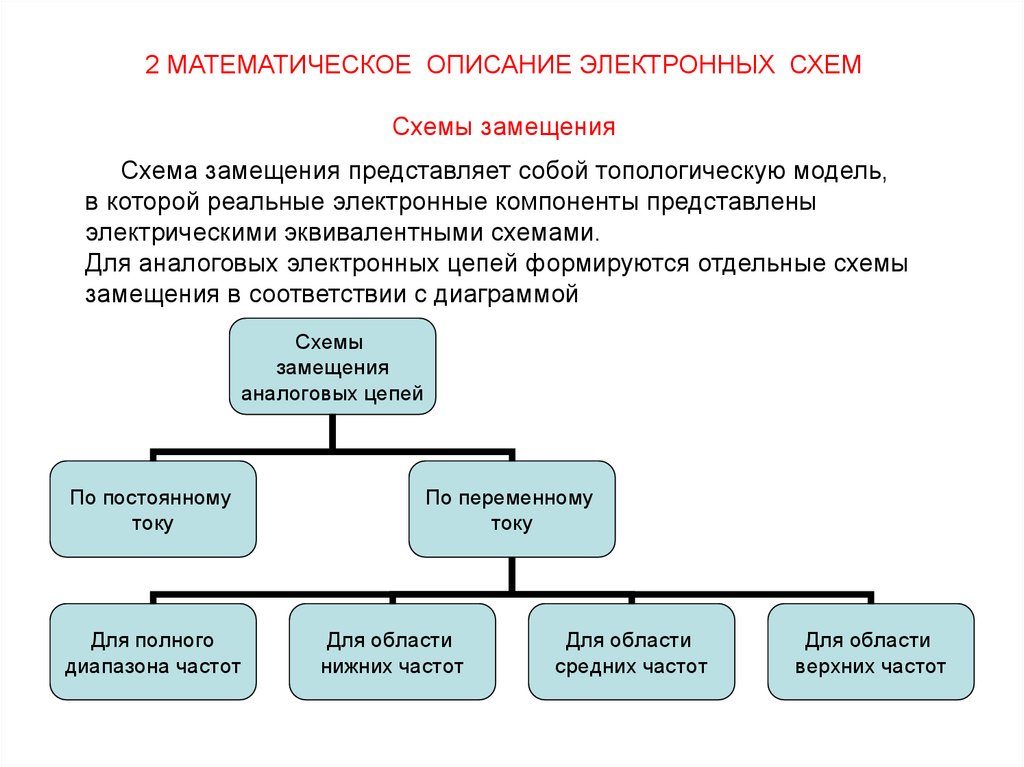
4.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМСхемы замещения
Схема замещения представляет собой топологическую модель,
в которой реальные электронные компоненты представлены
электрическими эквивалентными схемами.
Для аналоговых электронных цепей формируются отдельные схемы
замещения в соответствии с диаграммой
Схемы
замещения
аналоговых цепей
По постоянному
току
Для полного
диапазона частот
По переменному
току
Для области
нижних частот
Для области
средних частот
Для области
верхних частот
5.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМСхемы замещения по переменному току
При исследовании аналоговых электронных схем наибольшее значение
имеют схемы замещения по переменному току.
Применение схем замещения
по переменному току
Анализ в частотной области
Исследование переходных процессов
Анализ чувствительности выходных
параметров
Исследование на устойчивость
6.
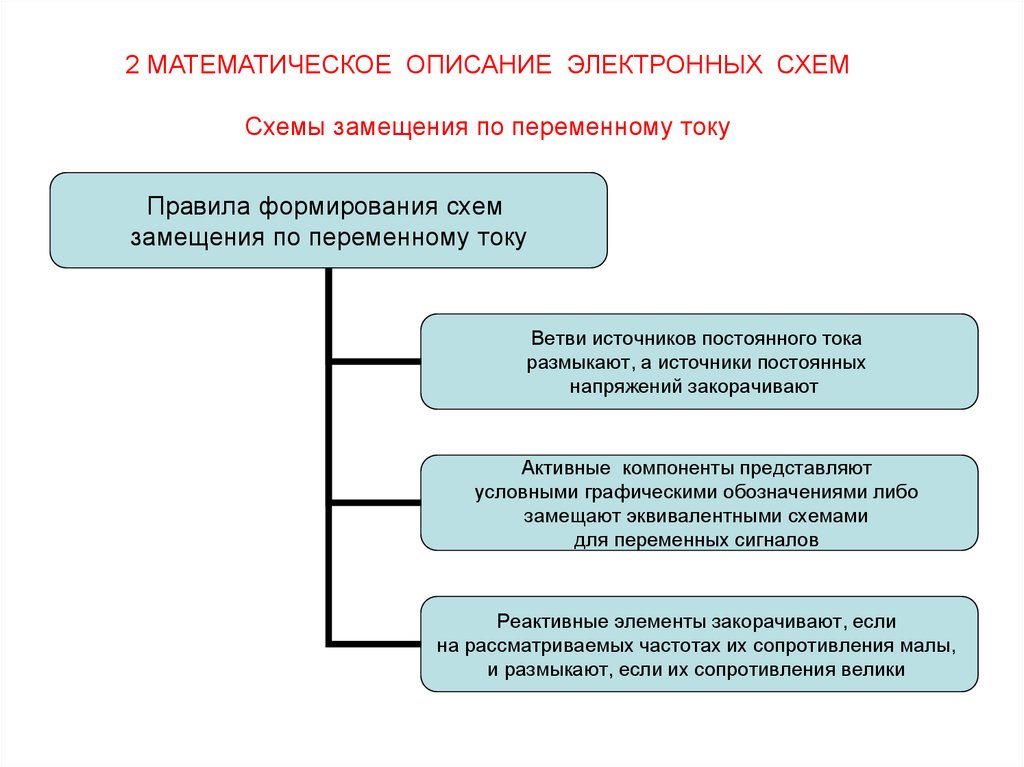
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМСхемы замещения по переменному току
Правила формирования схем
замещения по переменному току
Ветви источников постоянного тока
размыкают, а источники постоянных
напряжений закорачивают
Активные компоненты представляют
условными графическими обозначениями либо
замещают эквивалентными схемами
для переменных сигналов
Реактивные элементы закорачивают, если
на рассматриваемых частотах их сопротивления малы,
и размыкают, если их сопротивления велики
7.
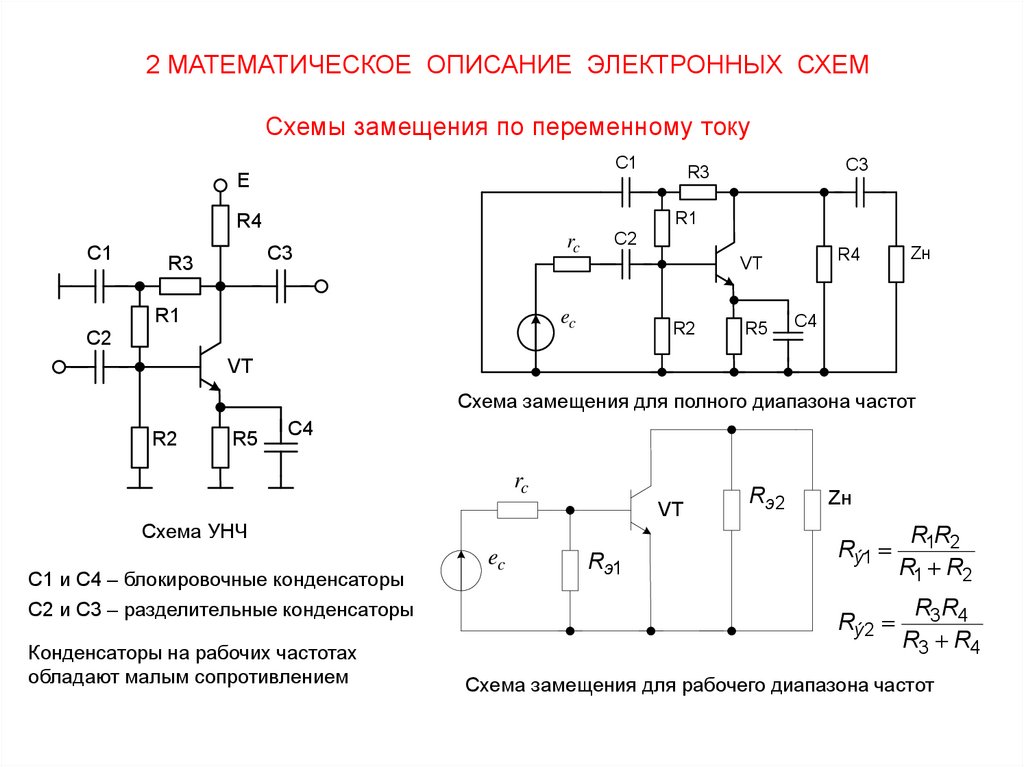
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМСхемы замещения по переменному току
C1
R1
R4
C1
rc
C3
R3
C3
R3
E
C2
R4
VT
R1
ec
C2
R2
R5
Zн
C4
VT
Схема замещения для полного диапазона частот
R2
R5
C4
rc
VT
Схема УНЧ
С1 и С4 – блокировочные конденсаторы
С2 и С3 – разделительные конденсаторы
Конденсаторы на рабочих частотах
обладают малым сопротивлением
ec
Rэ1
Rэ 2
Zн
Rý1
R1R2
R1 R2
Rý2
R3R4
R3 R4
Схема замещения для рабочего диапазона частот
8.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Наиболее компактно структура электронной цепи отображается с помощью
полюсных графов электронных схем.
Граф G(Х,А,Г) представляет собой совокупность непустого множества вершин X
(X≠Ø), не пересекающегося с ним множества ребер
A (A∩X≠Ø) и закона Г,
устанавливающего взаимосвязь между элементами множества вершин с помощью
элементов множества ребер. Аналитически закон Г
описывается логическим
высказыванием следующего вида
1, вершины xi и x j связаны ребром ak
Γ xi , ak , x j
0, вершины xi и x j не связаны ребром ak
9.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Геометрически граф принято изображать совокупностью точек, взаимно
однозначно соответствующих вершинам, и связывающих их линий
произвольной кривизны, взаимно однозначно соответствующих ребрам графа.
При необходимости учета направлений связей между вершинами графа
соответствующим ребрам приписываются направления, отмечаемые
стрелками, а сами ребра называют дугами. Графы, содержащие только
ненаправленные ребра, называют ненаправленными графами. Графы,
включающие только направленные ребра (дуги), называют направленными
или ориентированными графами, а также орграфами. Графы, содержащие
как направленные, так и ненаправленные ребра, носят название смешанных.
10.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Полюсный граф электронной схемы представляет собой граф, вершины
которого соответствуют узлам схемы, ребра – ветвям схемы, а в качестве
закона Г выступает порядок связей ветвей схемы между собой. Ребрам
полюсного
графа
приписывают
направления,
совпадающие
с
положительными направлениями токов соответствующих ветвей. При этом в
ветви, содержащей источник э.д.с. положительное направление тока следует
выбирать противоположным направлению э.д.с. Последовательно и
параллельно включенные ветви схемы в полюсном графе могут быть
объединены в эквивалентные дуги.
11.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Формирование полюсного графа электронной схемы
III
R1
L
1
R2 IV 3
II 2
V
C
E
III
1
J
R3
II
IV
2
I
V
3
VI
I
0
0
VI
Источник тока J и сопротивление R3 представлены одной эквивалентной дугой,
направление которой совпадает с направлением задающего тока J.
12.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Ребро графа и его граничная вершина называются инцидентными друг
другу: вершина инцидентна ребру, ребро инцидентно вершине. В орграфах
различают положительную инцидентность (дуга исходит из вершины) и
отрицательную инцидентность (дуга заходит в вершину). Число ребер,
инцидентных i-ой вершине, называют степенью вершины tii, при этом петля
учитывается дважды. Вершина со степенью, равной 1, называется концевой
или висячей.
Граничные вершины какого-либо ребра называют смежными.
Количество ребер, соединяющих смежные вершины i и j, называют взаимной
степенью tij этих вершин.
13.
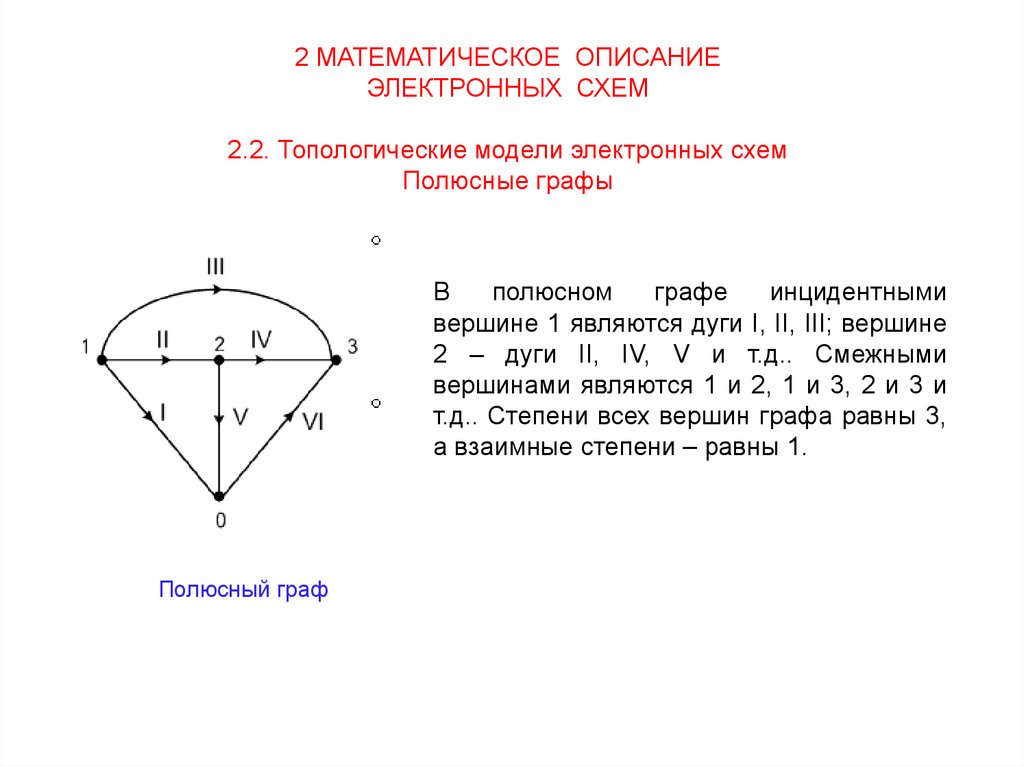
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.2. Топологические модели электронных схем
Полюсные графы
В
полюсном
графе
инцидентными
вершине 1 являются дуги I, II, III; вершине
2 – дуги II, IV, V и т.д.. Смежными
вершинами являются 1 и 2, 1 и 3, 2 и 3 и
т.д.. Степени всех вершин графа равны 3,
а взаимные степени – равны 1.
Полюсный граф
14.
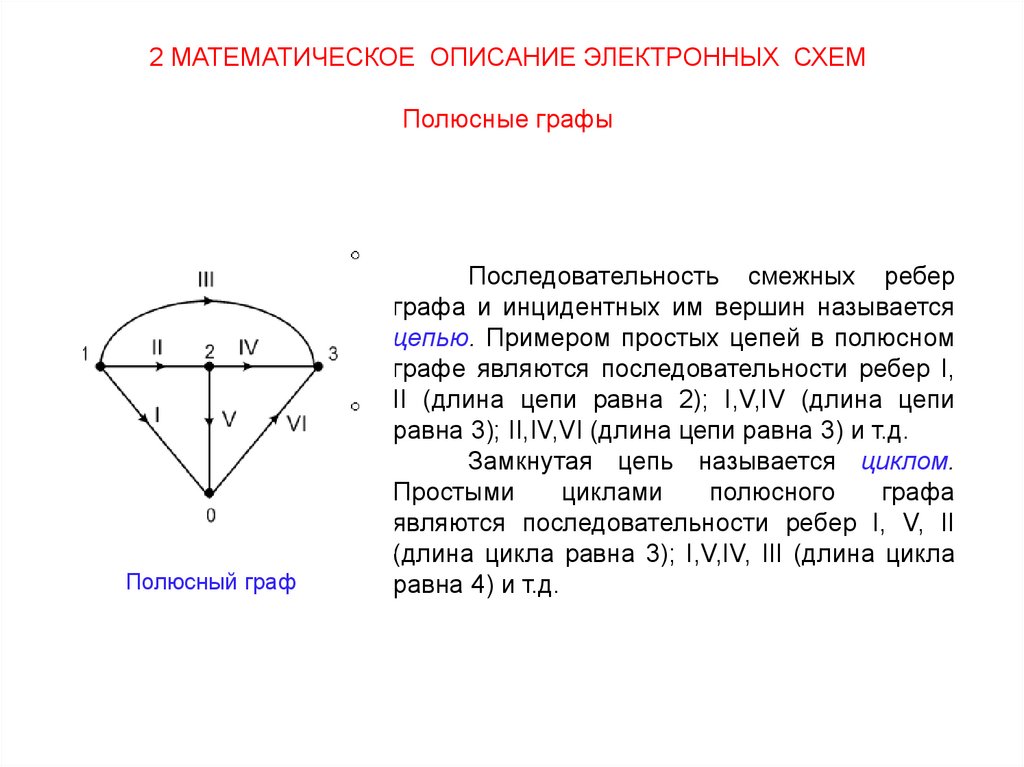
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Полюсный граф
Последовательность смежных ребер
графа и инцидентных им вершин называется
цепью. Примером простых цепей в полюсном
графе являются последовательности ребер I,
II (длина цепи равна 2); I,V,IV (длина цепи
равна 3); II,IV,VI (длина цепи равна 3) и т.д.
Замкнутая цепь называется циклом.
Простыми
циклами
полюсного
графа
являются последовательности ребер I, V, II
(длина цикла равна 3); I,V,IV, III (длина цикла
равна 4) и т.д.
15.
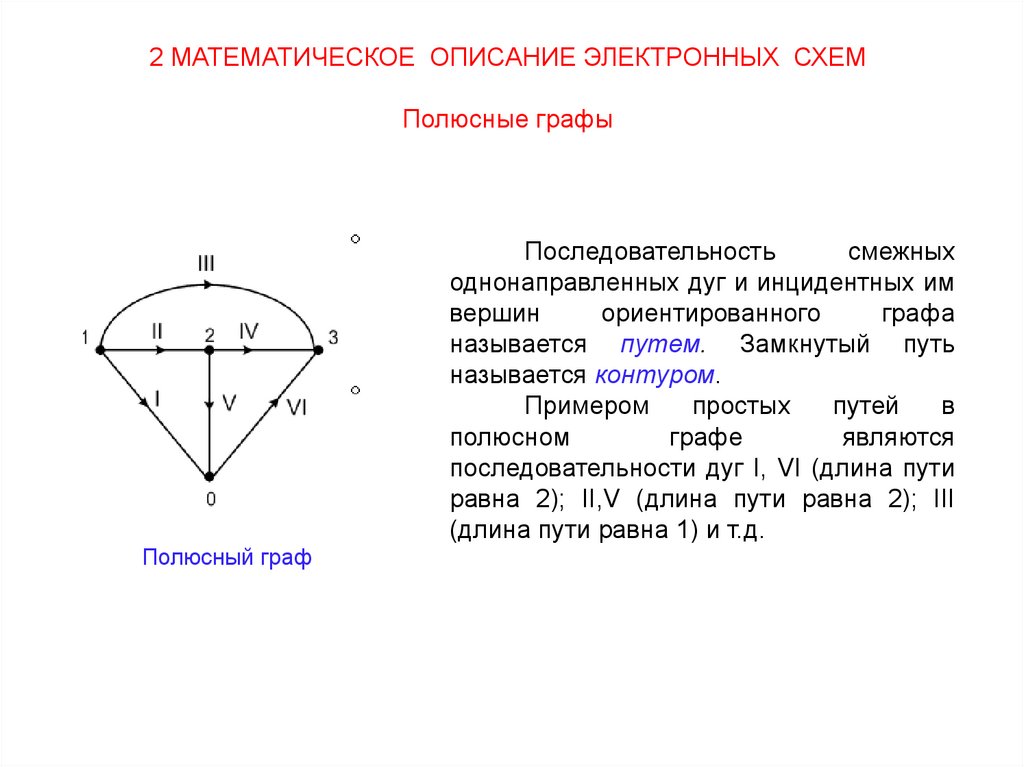
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Последовательность
смежных
однонаправленных дуг и инцидентных им
вершин
ориентированного
графа
называется путем. Замкнутый путь
называется контуром.
Примером
простых
путей
в
полюсном
графе
являются
последовательности дуг I, VI (длина пути
равна 2); II,V (длина пути равна 2); III
(длина пути равна 1) и т.д.
Полюсный граф
16.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.2. Топологические модели электронных схем
Полюсные графы
Часть графа, содержащая некоторое подмножество ребер и все
вершины исходного графа, называется суграфом.
III
1
II
IV
2
V
0
Исходный граф
Суграф
3
VI
17.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Две вершины графа называются связанными, если между ними
существует цепь. Граф, любая пара вершин которого связана, называют
связным графом. В противном случае граф называется несвязным.
Несвязный граф представляет собой совокупность отдельных частей
(подграфов), называемых компонентами. Любая связная совокупность
ребер графа, не содержащая контуров, вместе с инцидентными им
вершинами образует дерево графа. Если такое дерево является
суграфом, то оно называется покрывающим деревом или остовом. Ребра
дерева называют ветвями. Ребра графа, не входящие в покрывающее
дерево (остов), образуют дополнение дерева и называются хордами.
Дерево, содержащее все вершины исходного графа, называют
фундаментальным
деревом
этого
графа.
При
этом
ребра
фундаментального дерева в общем случае не совпадают с ребрами
исходного графа. Частным случаем фундаментального дерева является
покрывающее дерево графа.
18.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМПолюсные графы
Исходный граф
Покрывающее дерево
Дополнение дерева
19.
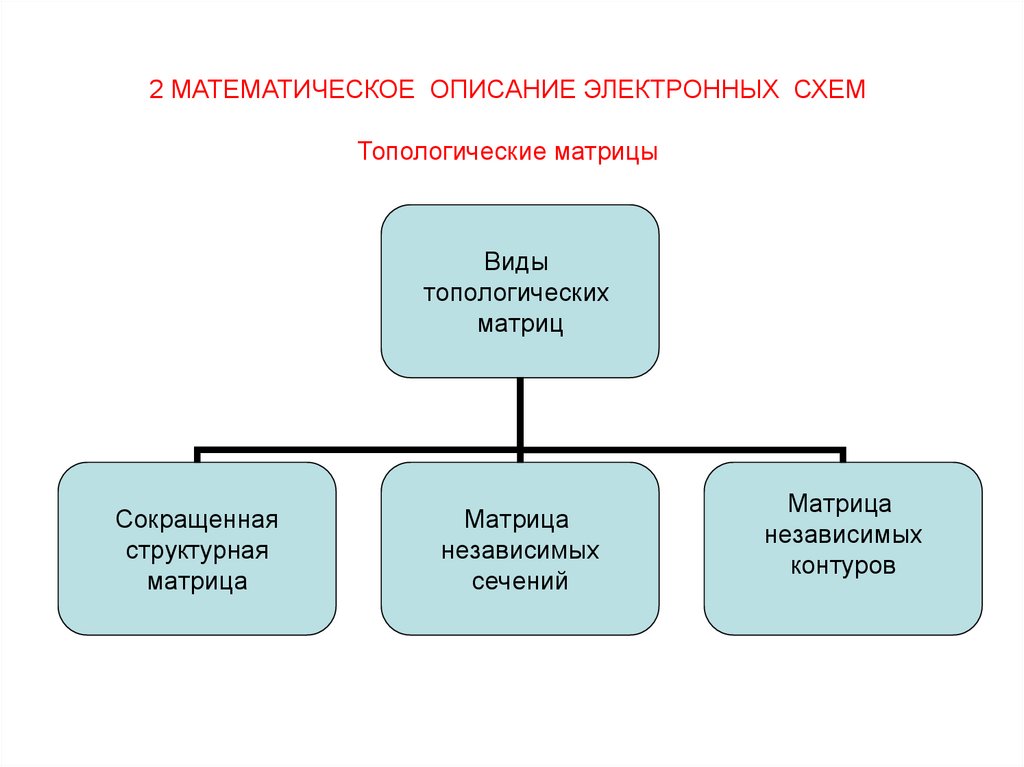
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМТопологические матрицы
Виды
топологических
матриц
Сокращенная
структурная
матрица
Матрица
независимых
сечений
Матрица
независимых
контуров
20.
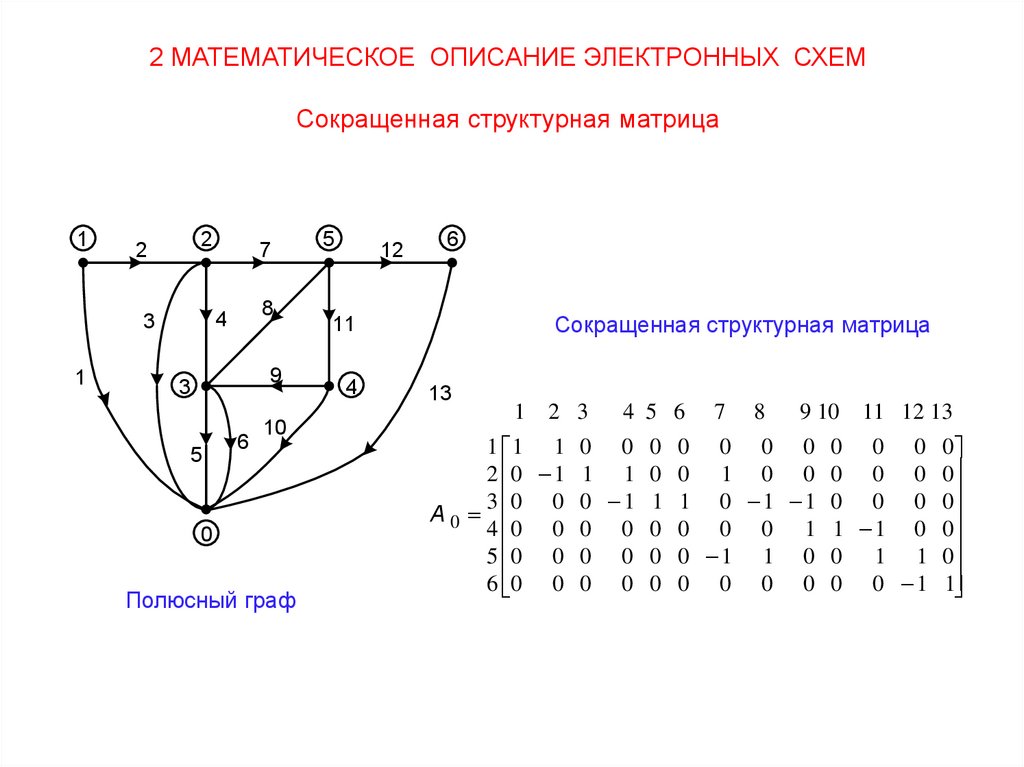
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМСокращенная структурная матрица
1
2
2
8
4
3
1
7
9
3
5
6
10
0
Полюсный граф
5
12
6
Сокращенная структурная матрица
11
4
13
1
2 3
4 5 6
7
8
9 10 11 12 13
1 1 1 0 0 0 0 0 0 0 0 0 0
2 0 1 1 1 0 0 1 0 0 0 0 0
3 0 0 0 1 1 1 0 1 1 0 0 0
A0
4 0 0 0 0 0 0 0 0 1 1 1 0
5 0 0 0 0 0 0 1 1 0 0 1 1
6 0 0 0 0 0 0 0 0 0 0 0 1
0
0
0
0
0
1
21.
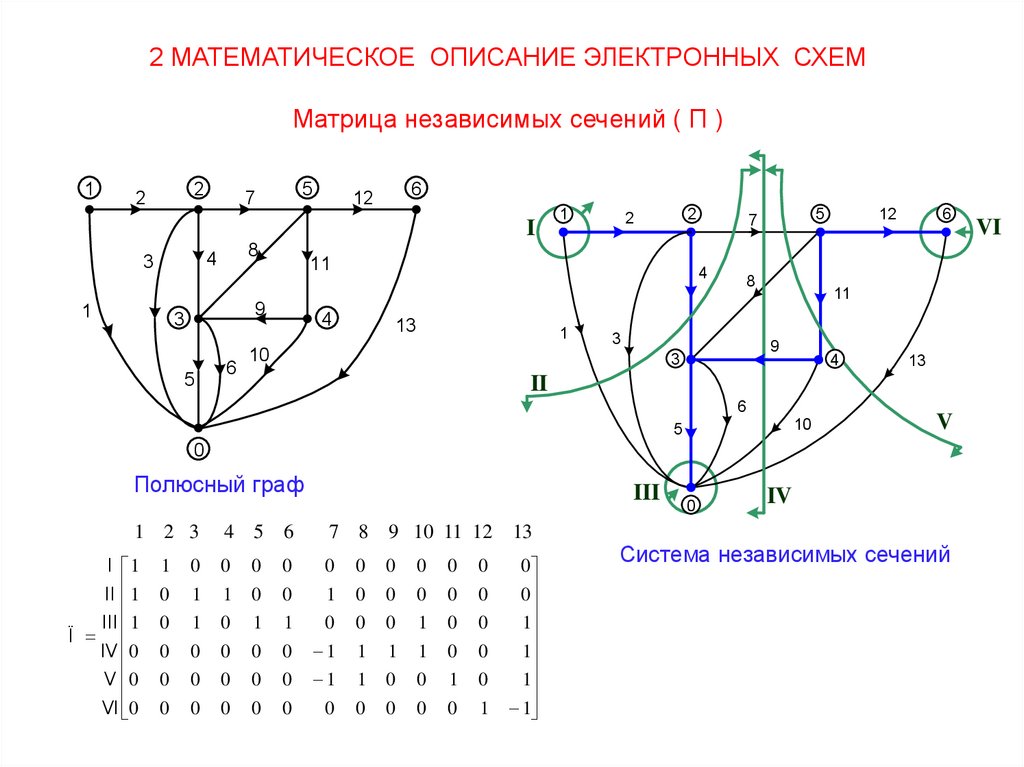
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕММатрица независимых сечений ( П )
1
2
2
5
7
6
12
I
8
4
3
1
5
6
2
2
11
9
3
1
4
4
13
1
8
3
10
5
7
6
11
9
3
12
4
13
II
6
10
5
V
0
Полюсный граф
1 2 3
I 1
II 1
III 1
Ï
IV 0
V 0
VI 0
III
4 5 6
7 8 9 10 11 12 13
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
0
0
1
0
1
1
0
0
0
1
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
1
1
1
0
IV
Система независимых сечений
VI
22.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕММатрица независимых контуров ( Р )
1
2
2
5
8
4
3
1
7
5
6
1
2
2
III 8
I
4
1
13
3
6
12
11
VII
IV
II
9
3
10
5
7
4
11
9
3
6
12
V
5
6
4
13
VI
10
0
Полюсный граф
1
2 3
4
5 6
I 1 1 0 1 1 0
II 0
0 1 1 1 0
III 0
0 0 1 0 0
P IV 0
0 0
0
0 0
V 0
0 0
0 1 1
VI 0
0 0
0 1 0
VII 0
0 0
0 1 0
0
7 8
0
0
1
0
0
0
0
9 10
11 12 13
0
0 0
0 0
0
0 0
0 0
0
1 0
1 0
1 1 0 1 0
0
0 0
0 0
0 1 1 0 0
0 1 0 1 1
0
0
0
0
0
0
1
Система независимых контуров
23.
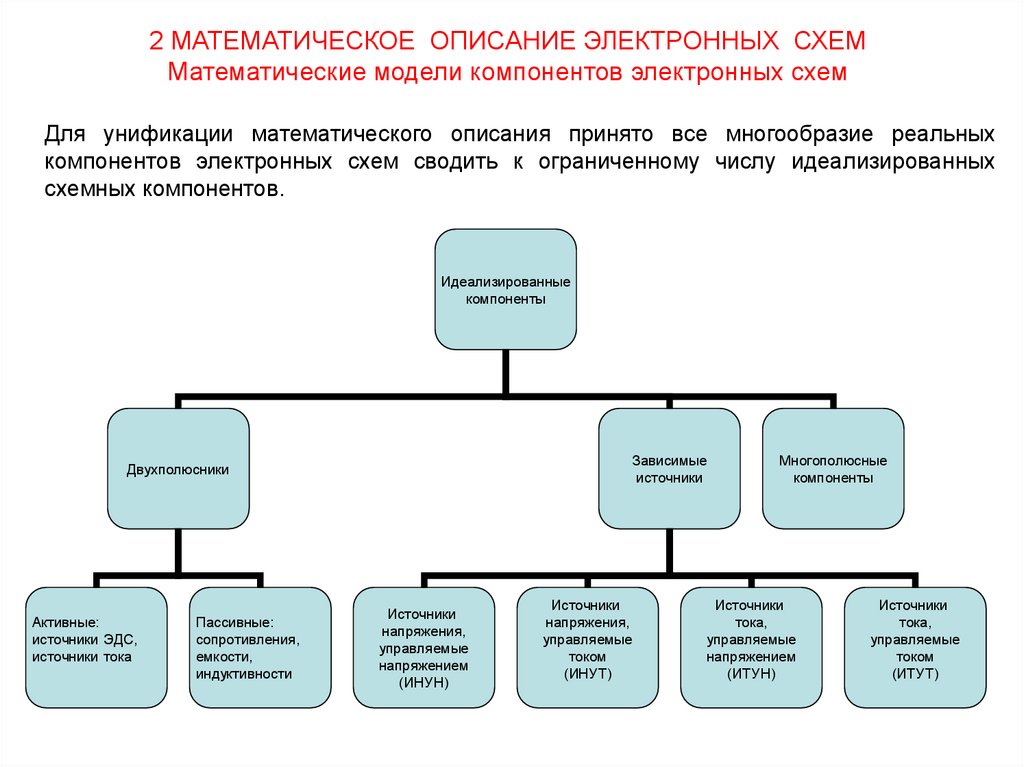
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕММатематические модели компонентов электронных схем
Для унификации математического описания принято все многообразие реальных
компонентов электронных схем сводить к ограниченному числу идеализированных
схемных компонентов.
Идеализированные
компоненты
Зависимые
источники
Двухполюсники
Активные:
источники ЭДС,
источники тока
Пассивные:
сопротивления,
емкости,
индуктивности
Источники
напряжения,
управляемые
напряжением
(ИНУН)
Источники
напряжения,
управляемые
током
(ИНУТ)
Многополюсные
компоненты
Источники
тока,
управляемые
напряжением
(ИТУН)
Источники
тока,
управляемые
током
(ИТУТ)
24.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Электронные компоненты цепей (транзисторы, диоды, тиристоры,
резисторы, конденсаторы и т.п.) могут быть представлены эквивалентными
схемами, состоящими из идеальных схемных компонентов. В зависимости от
режима работы электронной схемы и задачи исследования, эквивалентные
схемы можно подразделить на следующие группы:
• низкочастотные линейные малосигнальные для квазилинейного режима
на низких частотах;
• нелинейные постоянного тока для статического режима и больших
низкочастотных сигналов;
• высокочастотные линейные малосигнальные для квазилинейного
режима на высоких частотах;
• нелинейные универсальные для переходных режимов при больших
сигналах.
25.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Применение той или иной эквивалентной схемы чаще всего является
результатом выбора наилучшего компромисса между двумя противоречивыми
требованиями: достаточно высокой степенью точности отображения реальных
процессов и предельной простоты модели. Использование при анализе
электронных схем универсальных эквивалентных схем, снимает этот вопрос,
но при этом решение сравнительно простых задач неоправданно
усложняется. Поэтому представление электронных компонентов их
эквивалентными схемами различных уровней является оправданным.
26.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы пассивных двухполюсников
Эквивалентные схемы пассивных двухполюсных электронных компонентов,
как правило, содержат идеальные схемные компоненты, отражающие основные
физические параметры (для резистора – сопротивление, для конденсатора –
емкость, для катушки индуктивности - индуктивность) и, при необходимости,
паразитные параметры (индуктивности выводов, межвитковые емкости, омическое
сопротивление обмотки катушки индуктивности, сопротивление утечки и т.д.).
27.
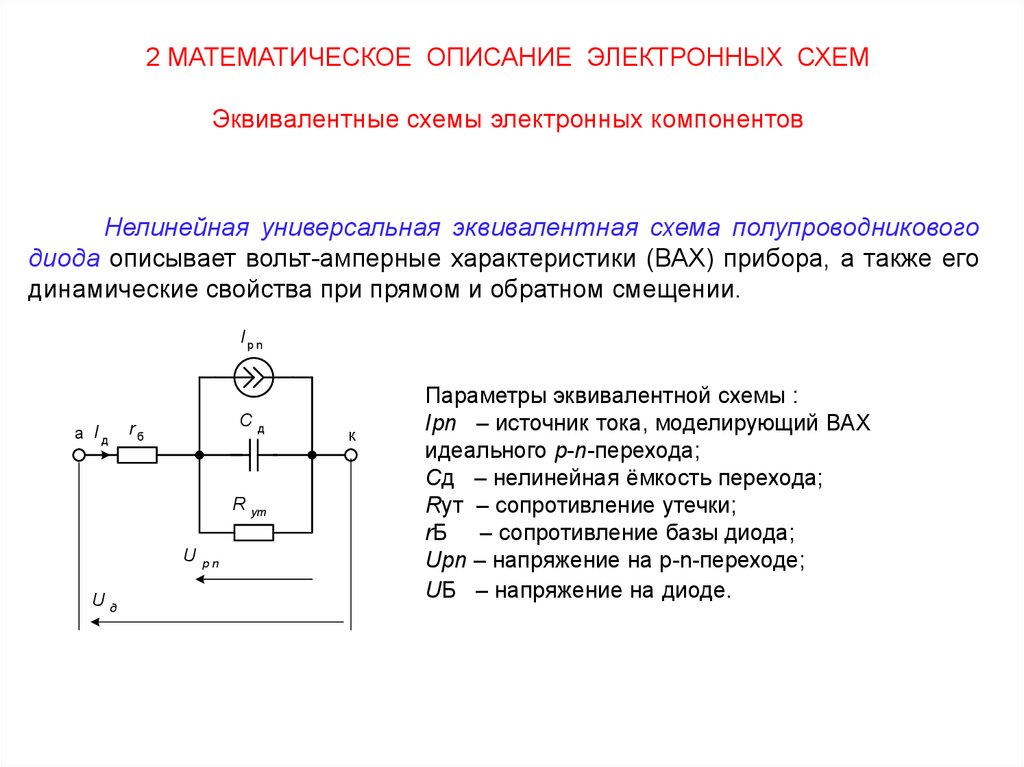
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Нелинейная универсальная эквивалентная схема полупроводникового
диода описывает вольт-амперные характеристики (ВАХ) прибора, а также его
динамические свойства при прямом и обратном смещении.
Ipn
Cд
rб
а Iд
R ут
U
U
д
pn
к
Параметры эквивалентной схемы :
Ipn – источник тока, моделирующий ВАХ
идеального p-n-перехода;
Сд – нелинейная ёмкость перехода;
Rут – сопротивление утечки;
rБ – сопротивление базы диода;
Upn – напряжение на p-n-переходе;
UБ – напряжение на диоде.
28.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Нелинейной универсальной эквивалентной схеме полупроводникового диода
соответствуют уравнения :
I д I pn
U pn
Rу т
Cд
dU pn
dt
I pn
U ä ráI ä U pn ráI ä T ln
1
I0
к
Cб Cб0
U
pn
к
U pn
I pn I0 exp
T
1
Cд Cб Cдифф.
m
Cдифф.
(I pn I0 )
T
29.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
В уравнениях нелинейной универсальной эквивалентной схемы
полупроводникового диода :
I0 – обратный тепловой ток перехода (тепловой ток);
φT – фактическое значение температурного потенциала;
CБ и Cдифф – барьерная и диффузионная емкости p-n-перехода;
СБ0 – барьерная емкость при Upn=0;
φк – контактная разность потенциалов;
m – параметр аппроксимации вольт-фарадной характеристики
барьерной емкости;
τ – эффективное время жизни неосновных носителей в базе диода.
Эффективное время жизни τ в полупроводниковых диодах обычно
составляет (0,1÷0,2)мкс, но в ряде случаев может быть на порядок больше
или меньше этих значений. Значение контактной разности потенциалов у
кремниевых полупроводниковых диодов при температуре T0=300K достигает
(0,7÷0,8)В.
30.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Нелинейная универсальная эквивалентная схема стабилитрона
Источник тока Iст моделирует вольт-амперную характеристику
Iст
Cб
а
Iст
E ст
к
I с т .m in
C д и ф ф.
U ст
U ст
31.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Ток источника тока Iст является кусочно-непрерывной функцией от
напряжения на стабилитроне. В зависимости от соотношения между
напряжением стабилизации Eст и падением напряжения на стабилитроне Uст
ВАХ стабилитрона разбивается на три области:
• область прямого смещения (Uст ≥ 0);
• предпробойная область (–Eст ≤ Uст < 0);
• область пробоя (–Uст ≤ –Eст).
I cm
U cm
1 ,
I
exp
0
T
U E cm
B
A U cm E cm cm
I cm. min ,
R
проб
U cm E cm
I cm. min ,
R
проб
U cm 0,
E cm U cm 0 ,
U cm E cm ,
32.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
В эквивалентной схеме стабилитрона :
I0
φT
Rпроб = tgα
Iст.min
AиВ
– обратный тепловой ток перехода (тепловой ток);
– тепературный потенциал
– дифференциальное сопротивление в области пробоя
– минимальный ток стабилизации стабилитрона
– коэффициенты аппроксимации.
I0
E
Iст.min ст
Rпроб
A
;
B
Eст
0
Cб Cб0
0 Uст
B
Т
Iст.min
Eст
m
Сдиф
1
Rпроб
;
1
Rпроб
Iст I0 .
Т
Параметры Сдифф, Сб, Сб0, φк, m, τ имеют такой же смысл, что и для модели диода.
33.
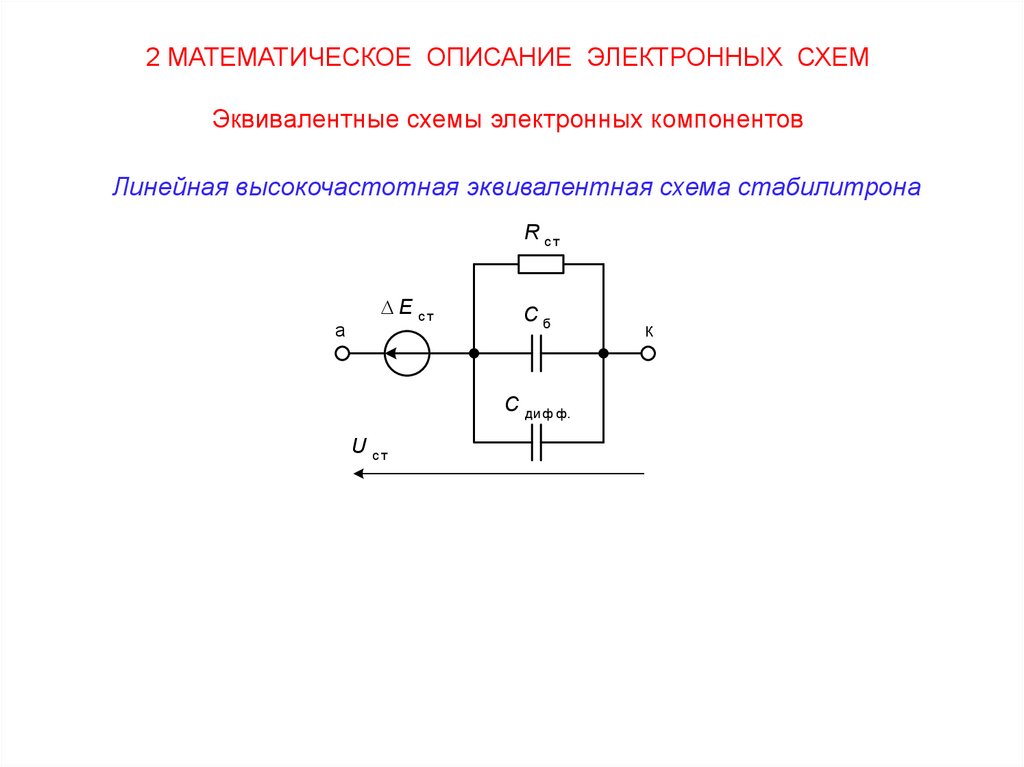
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Линейная высокочастотная эквивалентная схема стабилитрона
R ст
а
E ст
Cб
C ди ф ф.
U ст
к
34.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
В эквивалентной схеме стабилитрона :
Rст
– дифференциальное сопротивление p-n-перехода стабилитрона;
ΔEст – автономный источник напряжения, который моделирует
температурное изменение напряжения на стабилитроне.
Rcm
T
,
U cm
I0 exp
T
1
1
B 1
AB U cm Ecm
,
R
проб
Rпроб ,
m
U cm 0,
Ecm U cm 0 ,
U cm Ecm.
0
;
Cб Cб0
0 U ст
Сдифф
Eст
Rст
.
U ст
T ТКН T ,
T
35.
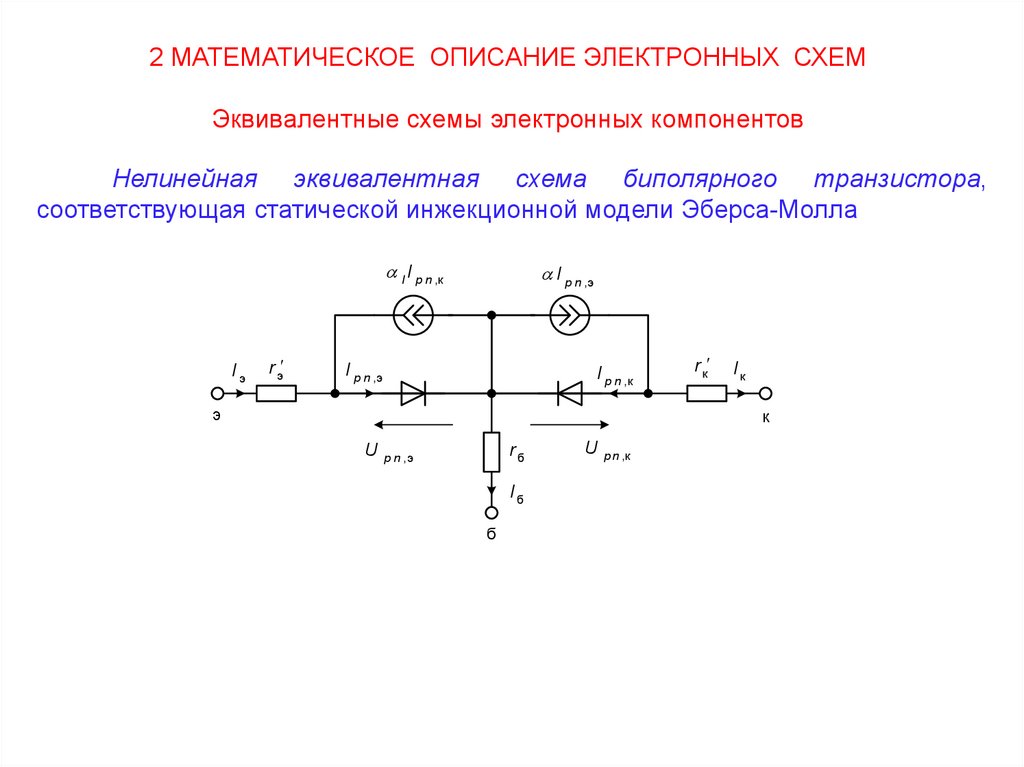
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Нелинейная эквивалентная схема биполярного транзистора,
соответствующая статической инжекционной модели Эберса-Молла
I I p n ,к
Iэ
r э
I p n ,э
I p n ,э
I p n ,к
э
r к
Iк
к
U
rб
p n ,э
Iб
б
U
p n ,к
36.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
В нелинейной эквивалентной схеме биполярного транзистора :
диоды отражают эмиттерный и коллекторный переходы;
Ipn,э - это ток при заданном напряжении Upn,э протекающий через эмиттерный
переход при закороченном коллекторном переходе;
Ipn,к - это ток при заданном напряжении Upn,к, протекающий через
коллекторный переход при закороченном эмиттерном переходе;
связь переходов через область базы показана с помощью зависимых
источников тока αIpn,э и αIIpn,э управляемых токами Ipn,э и Ipn,к соответственно;
α - это интегральный коэффициент передачи тока эмиттера для большого
сигнала при нормальном включении транзистора;
αI - это интегральный коэффициент передачи тока коллектора для большого
сигнала при инверсном включении транзистора;
сопротивления rБ, rк′, rэ′ представляют собой объемные и контактные
сопротивления областей базы, коллектора и эмиттера.
37.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
В нелинейной эквивалентной схеме биполярного транзистора :
I pn,э
U pn,э
1
Iэбк exp
mэ T
I pn ,к
U pn ,к
1
Iкбк exp
mк T
Iэбк, Iкбк - начальные токи эмиттерного и коллекторного переходов;
mэ, mк - эмпирические коэффициенты, характеризующие отклонение граничных условий от
условий Шокли при высоких уровнях инжекции и учитывающие влияние токов утечки, канальных
токов и токов рекомбинации-генерации.
Для кремниевых транзисторов наиболее вероятные значения mэ и mк лежат в пределах 1,2 2,
для германиевых транзисторов – в пределах 1,2 1,5.
38.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Полагая в первом приближении, что mэ=mк=m, и пренебрегая
объемными сопротивлениями областей транзистора, модель Эберса-Молла
можно представить системой уравнений:
U
Iэ Iэбк exp бэ
m T
U
1 I Iкбк exp бк 1
m T
U
Iк Iэбк exp бэ
m T
U
1 Iкбк exp бк 1
m T
U
U
Iб Iэ Iк Iэбк 1 exp бэ 1 Iкбк 1 I exp бк 1
m T
m T
39.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Для удобства определения параметров модели уравнения ЭберсаМолла целесообразно представить через обратные токи переходов
транзистора:
Iэ
U бэ
Iэб0
I
1 I кб0
exp
1 I
1 I
m T
Iк
Iэб0
1 I
Iб Iэб0
exp U бэ 1 Iкб0
m 1
T
I
1
1 I
Iэб0 I Iкб0
exp U бк 1
m
T
U бк
1
exp
m
T
Uбэ
1 I
1 Iкб0
exp
1 I
m T
exp Uбк 1
m
T
40.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
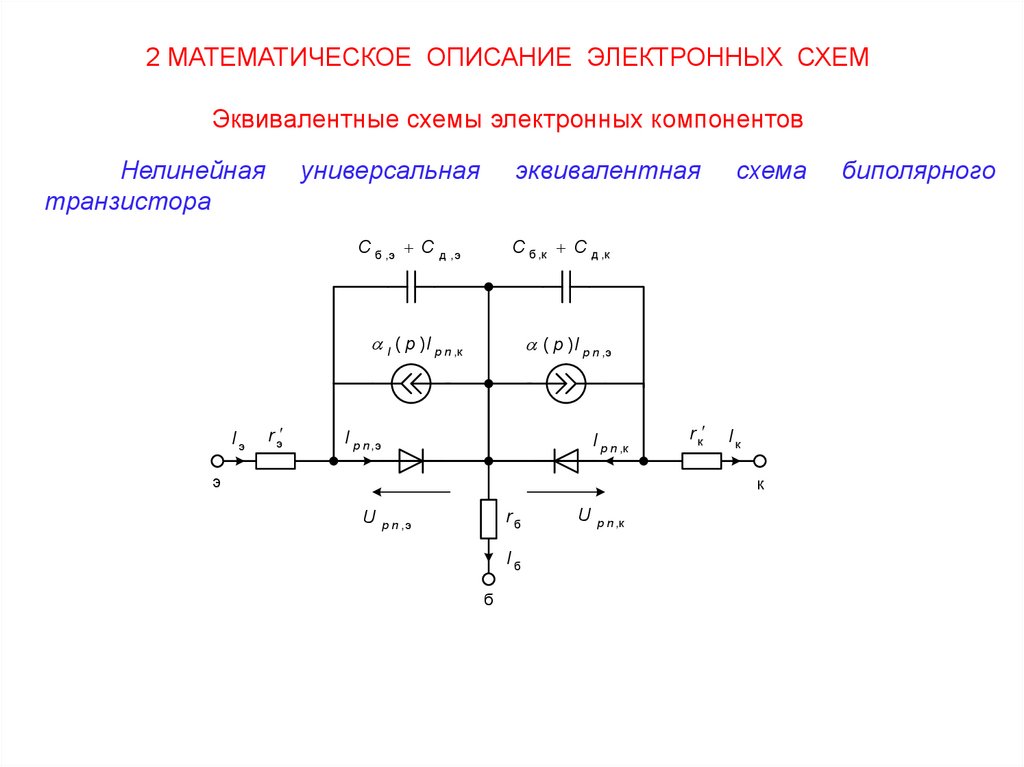
Нелинейная
транзистора
Iэ
универсальная
r э
эквивалентная
C б ,э C д ,э
C б ,к C д ,к
I ( p ) I p n ,к
( p ) I p n ,э
I p n ,э
I p n ,к
э
r к
схема
Iк
к
U
rб
p n ,э
Iб
б
U
p n ,к
биполярного
41.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Барьерные емкости биполярного транзистора :
Cб,э
к,э
Cб0,э
к,э U pn,э
n
Cб,к
к,к
Cб0,к
к,к U pn,к
Сб0,э
– барьерные емкости эмиттерного и коллекторного переходов
при Upn,э=0 и Upn,к=0 соответственно
φк,э и φк,к – контактные разности потенциалов эмиттерного и коллекторного
переходов;
n
– параметр аппроксимации вольт-фарадной характеристики
барьерной емкости.
Диффузионные емкости биполярного транзистора :
Cд,э
Iэбк I
U
exp pn,э
T
T
Cд,к
Iкбк N
T
U
exp pn,к
T
λ
- поправочный коэффициент;
τN и τI - эффективное время полета неосновных носителей через область базы
при нормальном и инверсном включении транзистора соответственно.
n
42.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Для учета конечного времени пролета носителей заряда через базу и через
область объемного заряда коллекторного перехода в эквивалентной схеме ЭберсаМолла используются динамические коэффициенты передачи токов эмиттера и
коллектора, представленные операторными изображениями α(p), αI(p).
Наиболее простая аппроксимация коэффициента передачи тока эмиттера имеет
вид:
( p)
1 p
f
arctg
f
( ) arctg
где
f
1
2
( )
1
2
f
1
f
t
(t ) 1 exp
- предельная частота коэффициента передачи тока эмиттера
2
43.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
Высокочастотная линейная малосигнальная эквивалентная схема
биполярного транзистора
Cк
Cэ
rэ
iэ
э
U кб
rк
i p n ,э
iк
i p n ,к
к
U кб
rб
iб
б
i p n ,э
44.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕКТРОННЫХ СХЕМЭквивалентные схемы электронных компонентов
В малосигнальной эквивалентной схеме биполярного транзистора :
• – дифференциальный коэффициент передачи тока эмиттера для малого сигнала;
• rэ – дифференциальное сопротивление эмиттерного перехода;
• rк – дифференциальное сопротивление коллекторного перехода;
• rб – объемное сопротивление области базы;
• μ – коэффициент внутренней обратной связи по напряжению;
• Cэ, Cк – дифференциальные емкости эмиттерного и коллекторного переходов
Эти параметры рассчитываются и достаточно точно контролируются в процессе
изготовления транзистора. Емкость Cэ эмиттерного перехода обычно не учитывается.
rэ
Т
Iэ
26
Ом
Iэ мА
2qeNб L2б Uк.б.обр.
rк
0 w
Iэ
rэ
2 rк 1
где
W
Lб
Nб
γ
– толщина базы;
– диффузионная длина неосновных носителей заряда в базе;
– концентрация примесей в базе;
– коэффициент инженкции
Емкости переходов составляют десятки и даже сотни пФ и обычно приводятся в справочниках.
45.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
На рис. 2.22 приведена упрощенная линейная эквивалентная схема,
соответствующая включению транзистора с общим эмиттером.
*
Cк
iб
*
rб
rк
б
iк
к
rэ
iб
iэ
э
Рис. 2.22. Линейная эквивалентная схема биполярного транзистора,
включенного с общим эмиттером
46.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Параметры эквивалентной схемы рис. 2.22 определяются соотношениями
1
*
rк
,
r к 1
rк
1
,C
*
к
Cк
1
C к 1 .
47.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Для коэффициента передачи
операторное изображение вида
( p)
тока
базы
чаще
всего
используют
1 p
где
β – статический коэффициент передачи тока базы
1 – постоянная времени коэффициента передачи тока
1
базы.
48.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Амплитудно-частотная, фазо-частотная и переходная характеристики,
соответствующие операторному изображению (2.35), имеют вид:
( )
1
2
( ) arctg
f
1
f
2
arctg f
f
t
(t ) 1 exp
49.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
где
f
1
2
1 f
f
1
- предельная частота коэффициента
передачи тока базы, на которой амплитуда
гармонического тока коллектора в раз
меньше, чем амплитуда гармонического
тока базы, а отставание по фазе тока
коллектора от тока базы составляет 45 эл.
град
Из выражений для fβ и τβ следует, что коэффициент передачи тока базы
обладает худшими частотными и переходными характеристиками, чем
коэффициент передачи тока эмиттера.
50.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Для анализа работы биполярных транзисторов в режиме малого сигнала
широко используются линейные эквивалентные схемы биполярного
транзистора как линейного проходного четырехполюсника в системах z-, y- и
h-параметров. Параметры таких эквивалентных схем получают на основании
измерения напряжений и токов на внешних полюсах транзистора, не
рассматривая при этом внутренние физические процессы.
51.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
В системе z-параметров основными величинами являются приращения
входного и выходного токов, а второстепенными – приращения входного и
выходного напряжений, связанные уравнениями
dU вх z11 z12 dIвх
dU z
вых 21 z22 dIвых
где
z11
Uвх dUвх
Iвх
dIвх
dIвых 0
Uвых dUвых
z21
Iвх
dIвх
dIвых 0
z12
z22
Uвх dUвх
Iвых dIвых
dIвх 0
Uвых dUвых
Iвых
dIвых
dIвх 0
52.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Параметры z11, z21 представляет собой входное сопротивление и
сопротивление прямой передачи транзистора, определяемые при условии
постоянства выходного тока. Параметры z12, z22 представляет собой
сопротивление обратной связи и выходное сопротивление транзистора,
определяемые при постоянстве входного тока. Постоянство тока в ветви
является режимом холостого хода для переменных сигналов, так как
эквивалентно разрыву ветви для переменной составляющей тока.
Система z-параметров удобна для анализа и расчета электронных схем.
Кроме того, зависимость z-параметров транзистора от режима работы и
температуры просто выражается аналитически. Недостатком системы zпараметров является трудность определения параметров z11 и z21,
обусловленная сложностью обеспечения режима холостого хода по
переменному току на выходе вследствие большого выходного сопротивления
транзистора.
53.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Эквивалентная схема биполярного транзистора как проходного
четырехполюсника с короткозамкнутой стороной в системе z-параметров
представлена на рис. 2.23
I1
z22 I
2
z 11
z 12 I 2
U1
z 21 I1
U
2
Рис. 2.23. Эквивалентная схема биполярного транзистора как проходного
четырехполюсника с короткозамкнутой стороной в системе z-параметров
54.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
В системе y-параметров основными величинами являются приращения
входного и выходного напряжений, а второстепенными – приращения
входного и выходного токов, связанные уравнениями
dIвх y11 y12 dU вх
dI y
dU
y
вых 21
22
вых
где
Iвх
dIвх
y11
Uвх dUвх
I
dI
y 21 вых вых
Uвх dUвх
dUвых 0
dUвых 0
Iвх
dIвх
Uвых dUвых
dUвх 0
Iвых
dIвых
Uвых dUвых
dUвх 0
y12
y 22
55.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Параметры y11, y21 представляют собой входную проводимость и
проводимость прямой передачи транзистора, определяемые при постоянном
выходном напряжении. Параметры у12, у22 представляет собой проводимость
обратной связи транзистора и выходную проводимость, определяемые при
постоянстве входного напряжения. Постоянство напряжения является
режимом короткого замыкания для переменных сигналов, так как
эквивалентно закорачиванию соответствующего участка цепи.
Недостатком системы y-параметров является малая точность измерения
параметров y12 и y22, что объясняется трудностью обеспечения режима
короткого замыкания по переменному току на входе из-за малого входного
сопротивления транзистора. Кроме того,
y-параметры имеют сложную
зависимость от температуры, режима и частоты.
56.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Эквивалентная схема биполярного транзистора как проходного
четырехполюсника с короткозамкнутой стороной в системе y-параметров
представлена на рис. 2.24.
I1
I2
y 11
U1
y 12 U
2
y 21 U 1
y 22
U
2
Рис. 2.24. Эквивалентная схема биполярного транзистора как проходного
четырехполюсника с короткозамкнутой стороной в системе y-параметров
57.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
В системе h-параметров основными величинами являются приращения
входного тока и выходного напряжения, а второстепенными – приращения
входного напряжения и выходного тока, связанные уравнениями
dU вх h11 h12 dIвх
dI h
вых 21 h22 dU вых
где
h11
Uвх dUвх
Iвх
dIвх
h21
Iвых dIвых
Iвх
dIвх
dUвых 0
h12
Uвх
dUвх
Uвых dUвых
dIвх 0
dUвых 0
h22
Iвых
dI
вых
Uвых dUвых
dIвх 0
58.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Система h-параметров является смешанной (гибридной), так как hпараметры имеют разную размерность:
имеет размерность h11
сопротивления, h22 - размерность проводимости, а параметры h12 и h21
являются безразмерными.
Параметр h11 представляет собой входное сопротивление транзистора, а
h21 - коэффициент передачи тока, определяемые при условии постоянства
выходного напряжения. Параметр h12 представляет собой коэффициент
обратной связи по напряжению, а h22 - выходную проводимость транзистора,
определяемые при постоянном входном токе.
Основным достоинством системы h-параметров является точность
измерения, так как необходимые для измерения параметров режимы
холостого хода на входе и короткого замыкания на выходе легко
осуществимы. По этой причине система h-параметров нашла широкое
практическое применение. Вместе с тем система h-параметров обладает
недостатком, связанным со сложностью расчетных соотношений.
59.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
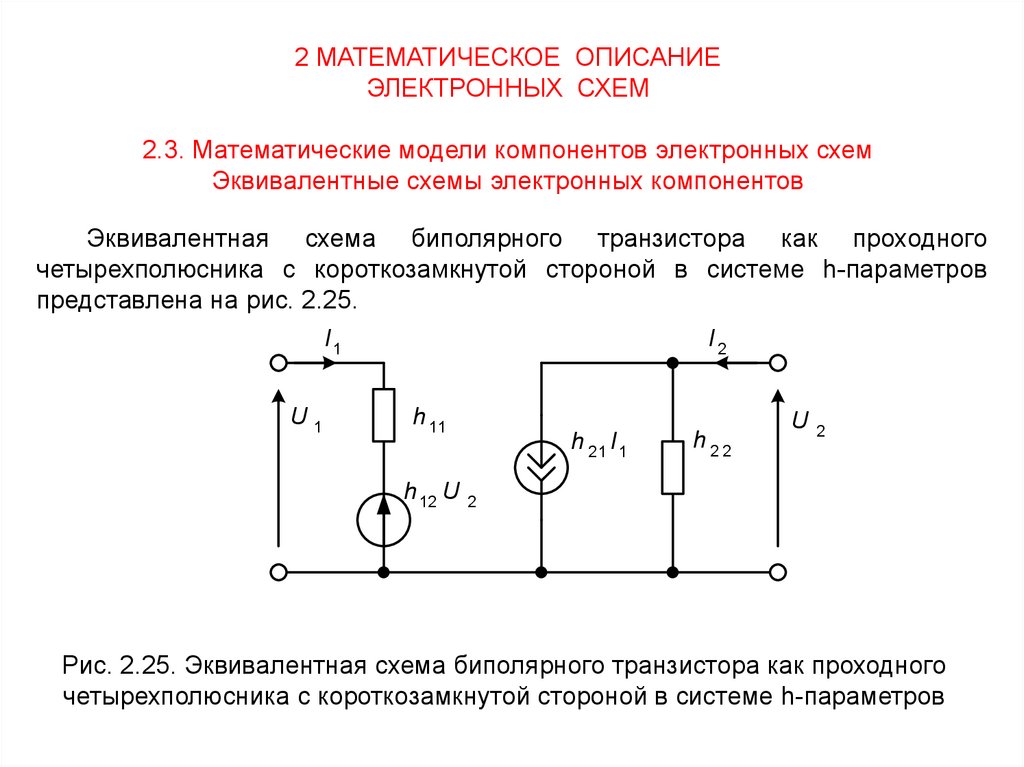
Эквивалентная схема биполярного транзистора как проходного
четырехполюсника с короткозамкнутой стороной в системе h-параметров
представлена на рис. 2.25.
I1
U1
I2
h 11
h 12 U
h 21 I 1
h22
U
2
2
Рис. 2.25. Эквивалентная схема биполярного транзистора как проходного
четырехполюсника с короткозамкнутой стороной в системе h-параметров
60.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Каждая из систем параметров однозначно определяет электрические
свойства транзисторов в режиме малого сигнала и является одной из форм
записи зависимостей между переменными составляющими токов и
напряжений. Переход от одной систем параметров к другой достаточно прост.
Для этого необходимо уравнения исходной системы решить относительно
переменных, являющихся второстепенными в системе, к которой
осуществляется переход. Полученные коэффициенты при токах и
напряжениях определяют формулы пересчета (таблица 2.1).
61.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Таблица 2.1 – Взаимосвязь параметров проходного четырехполюсника
Вычисляемая величина
Исходный
параметр
h
y
z
h
h11 h12
h
21 h22
1 1 y12
y11 y 21 y
1 z z12
z22 z21 1
y
1 1 h12
h11 h21 h
y11 y12
y
21 y 22
1 z22 z12
z z21 z11
z
1 h h12
h22 h21 1
z z11z22 z12z21
1
y
y 22 y12
y
21 y11
y y11y 22 y12 y 21
z11 z12
z
21 z22
h h11h22 h12h21
62.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Значения параметров транзистора, представленного в виде проходного
четырехполюсника, зависят от схемы его включения, поэтому в обозначениях
параметров цифровые индексы дополняют буквами, которые обозначают
вывод
транзистора,
соответствующий
короткозамкнутой
стороне
четырехполюсника: “э” для схемы включения с общим эмиттером, “б” для
схемы включения с общей базой, “к” для схемы включения с общим
коллектором. Для перехода от параметров одной схемы включения
транзистора, к параметрам другой схемы включения следует переменные
исходной схемы включения выразить через переменные, которые для
искомой схемы включения являются входными и выходными. Например,
соотношения, связывающие h-параметры транзистора, включенного с общей
базой, с h-параметрами транзистора, включенного с общим эмиттером,
приведены в таблице 2.2.
63.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Таблица 2.2 – Связь h-параметров схем с общей базой и общим эмиттером
h-параметры
схемы ОЭ
h11э
h12э
h21э
h22э
Через
h-параметры
схемы ОБ
h11б
1 h21б
h11бh22б
h12б
1 h21б
h
21б
1 h21б
h22б
1 h21б
h-параметры
схемы ОБ
h11б
h12б
h21б
h22б
Через
h-параметры
схемы ОЭ
h11э
1 h21э
h11эh22э
h12э
1 h21э
h
21э
1 h21э
h22э
1 h21э
64.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Параметры транзистора как проходного четырехполюсника можно
выразить через дифференциальные параметры
физических линейных
эквивалентных схем. Соответствующие формулы пересчета приведены в
таблице 2.3.
65.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Таблица 2.3 – Связь параметров транзистора с элементами низкочастотной
эквивалентной схемы
Параметр
h11
h12
Схема с общим
эмиттером
rб
rэrк
rэ rк (1 )
Схема с общей
базой
rэ
rэ
rэ rк (1 )
rк rэ
h21
rэ rк (1 )
h22
1
rэ rк (1 )
(1 )rбrк
rб rк
rб
rб rк
rб rк
rб rк
1
rб rк
Схема с общим
коллектором
rб
rэrк
rэ rк (1 )
rк (1 )
rэ rк (1 )
rк
rэ rк (1 )
1
rэ rк (1 )
66.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Эквивалентная схема полевого транзистора с управляющим p-nпереходом и каналом n-типа, наиболее полно отражающая физические
процессы в полевом транзисторе, представлена на рис. 2.26.
67.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
с
з
VD1
rc
~
C зс
Iк ан
~
C зи
VD2
rи
и
Рис. 2.26. Нелинейная универсальная эквивалентная схема полевого
транзистора с управляющим p-n-переходом
68.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Эквивалентная схема содержит:
• нелинейный источник тока Iкан., который описывает статические вольтамперные характеристики транзистора;
• сопротивления rс и rи между рабочей областью транзистора и выводами
стока и истока;
• диоды VD1, VD2, соответствующие участкам управляющего перехода
затвор-сток и затвор-исток;
~
~
• нелинейные емкости Cзи между затвором и истоком и Cзс между затвором и
стоком.
69.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
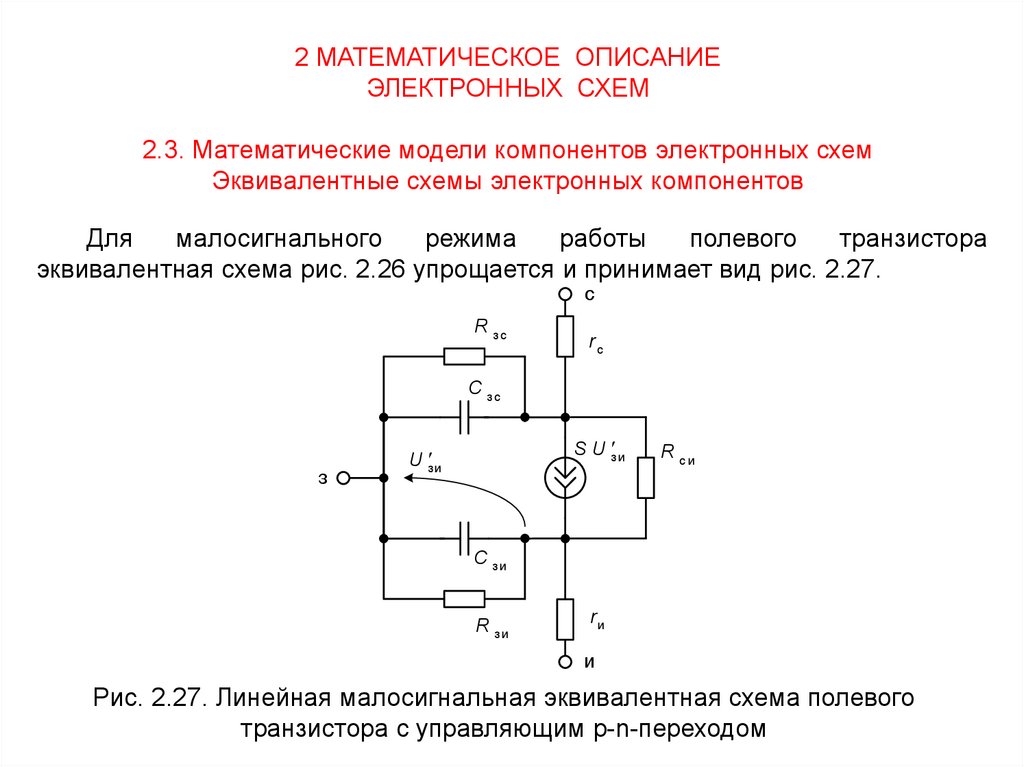
Для
малосигнального
режима
работы
полевого
транзистора
эквивалентная схема рис. 2.26 упрощается и принимает вид рис. 2.27.
с
R зс
rc
C зс
з
S U з и
U з и
R си
C зи
R зи
rи
и
Рис. 2.27. Линейная малосигнальная эквивалентная схема полевого
транзистора с управляющим p-n-переходом
70.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Поскольку при работе транзистора управляющий переход смещен в
обратном направлении, диоды VD1 и VD2 представлены сопротивлениями
Rзи, Rзс соответствующих участков закрытого управляющего перехода.
Источник тока Iкан. для малых приращений токов и напряжений
представлен линейным зависимым источником тока SU'зи с параллельным
внутренним сопротивлением Rси. Крутизна S передаточной характеристики и
внутреннее сопротивление Rси канала определяются выражениями:
71.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
U зи
S Sнач 1
U зи.отс.
Rcи
L0
U Ucи.нас.
1 cи
Iс
2 0
Ucи Ucи.нас.
qeN Д
Где
Sнач
2Iс.нач.
– начальная крутизна;
U зи.отс.
L0 – технологическая длина канала;
Nд– концентрация донорной примеси в канале
72.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
~ ~
Нелинейные емкости Cзи,Cзс заменены соответствующими постоянными
усредненными емкостями Cзи и Cзс.
Так как сопротивления Rзи, Rзс в кремниевых полевых транзисторах
велики (десятки – сотни МОм), их в большинстве случаев можно не учитывать.
Сопротивления rи и rс могут иметь значительную величину (до ста Ом и
более) и оказывают существенное влияние на параметры транзистора.
Наличие сопротивления rи уменьшает крутизну, сужает полосу рабочих частот,
увеличивает напряжение насыщения и тепловые потери. Влияние
сопротивления rс проявляется в увеличении напряжения насыщения и
тепловых потерь. Тем не менее, сопротивления rи, rс могут быть исключены
из эквивалентной схемы, а их влияние отражено введением эффективной
крутизны S* и эффективного дифференциального сопротивления канала R*си.
73.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
В первом приближении без учета сопротивлений Rзи, Rзс и емкостей Cзи, Cзи
при Uси=const можно записать:
dIс
Rси
Rси
SdUзи
S dU зи rиdIс
Rси rи rc
Rси rи rc
(2.6)
а при Uзи=const
dUси Rси rи rc dIс
(2.7)
74.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Из (2.6) следует
S*
dIс
dU зи
Uси const
Rси
S
Rси rи rc 1 Srи
а из (2.7):
*
Rси
dU си
dIс
U зи const
Rси rи rc
75.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
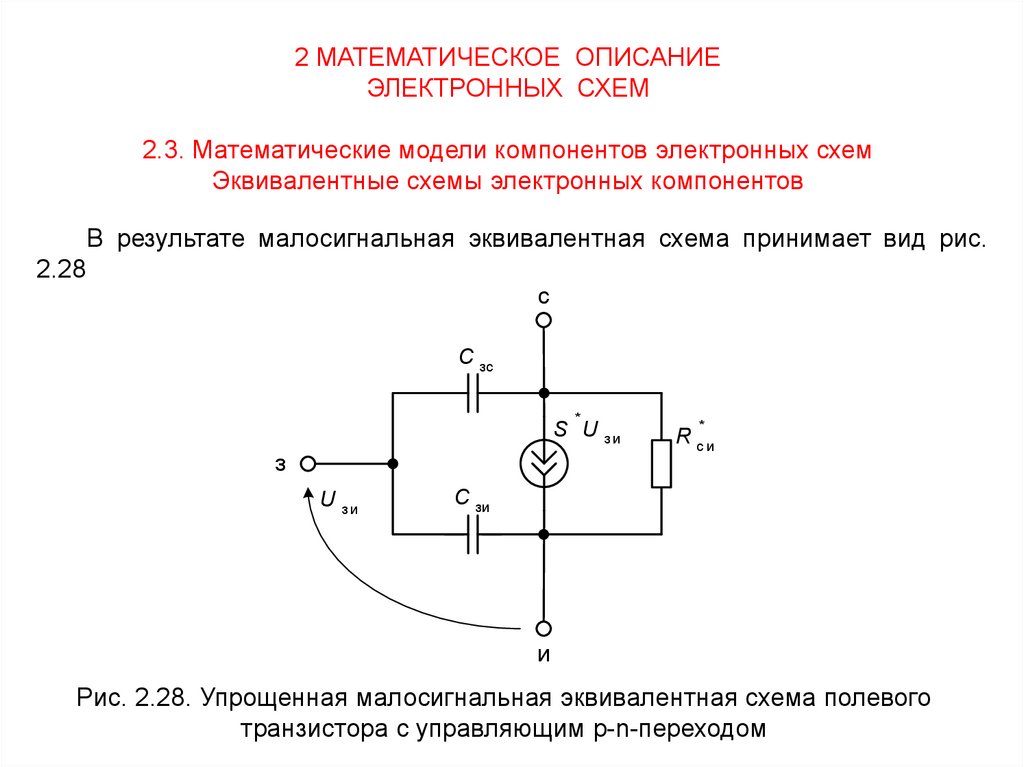
В результате малосигнальная эквивалентная схема принимает вид рис.
2.28
с
C зс
*
S U
з
U
зи
зи
*
R си
C зи
и
Рис. 2.28. Упрощенная малосигнальная эквивалентная схема полевого
транзистора с управляющим p-n-переходом
76.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
При анализе и расчете электронных схем, содержащих МДП-транзисторы
можно использовать эквивалентные схемы МДП-транзисторов, аналогичные
рассмотренным
эквивалентным
схемам
полевых
транзисторов
с
управляющим p-n-переходом.
В практике анализа и расчета электронных схем, как правило, применяют
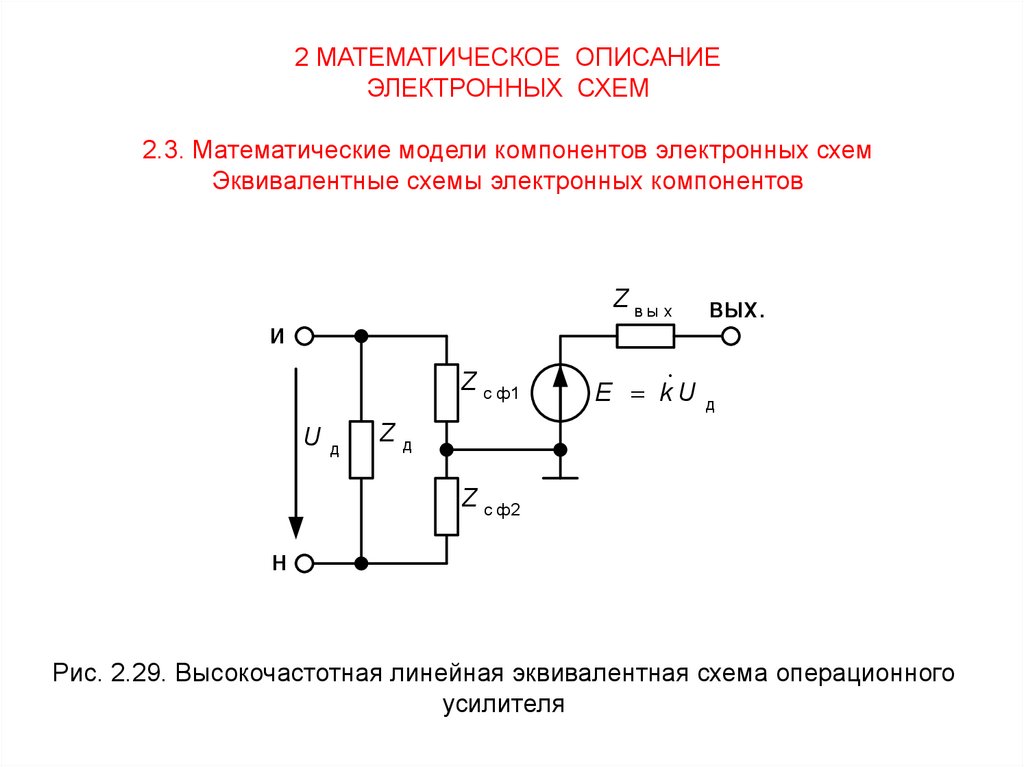
макромодели операционных усилителей. Высокочастотная эквивалентная
схема операционного усилителя, соответствующая работе операционного
усилителя в линейном режиме, представлена на рис. 2.29.
77.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Z вы х
и
Z с ф1
U
д
E k U
вых.
д
Zд
Z с ф2
н
Рис. 2.29. Высокочастотная линейная эквивалентная схема операционного
усилителя
78.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
Параметры высокочастотной эквивалентной
усилителя определяются выражениями:
Zд
Rд
RдCд p 1
Zсф.1
Rсф.1
Rсф.1Cсф.1p 1
Zсф.2 Rсф.2 ZCсф.2
Zвых Rвых ZCвых
Rсф.2
Rсф.2Cсф.2 p 1
Rвых
RвыхCвых p 1
схемы
операционного
79.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Эквивалентные схемы электронных компонентов
где
k - коэффициент усиления операционного усилителя;
τОУ - постоянная времени операционного усилителя;
Rд - входное сопротивление для входного дифференциального сигнала;
Rсф.1, Rсф.2 - входные сопротивления для входных синфазных сигналов;
Rвых - выходное сопротивление;
Cд, Cсф.1, Cсф.2, Cвых - паразитные емкости операционного усилителя.
Полагая в эквивалентной схемы рис. 2.29 и не учитывая паразитные
емкости, можно получить низкочастотную линейную эквивалентную схему
операционного усилителя.
80.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
В зависимости от характера компонентов схемы ребра ее графа можно
разделить на следующие типы:
• Ребра
пассивных
двухполюсников
(сопротивлений,
емкостей,
индуктивностей);
• Ребра полюсных графов многополюсных компонентов;
• Ребра независимых источников (напряжения и тока);
• Ребра зависимых источников (напряжения и тока);
• Управляющие ребра (по напряжению и току) зависимых источников;
• Ребра искомых токов и напряжений.
81.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Каждому из ребер соответствует уравнение двухполюсного или
многополюсного компонента (компонентное уравнение). В зависимости от
вида компонентных уравнений ребра разбивают на два подмножества: yребра (уравнения выражают токи) и z-ребра (уравнения выражают
напряжения). Ребра, которые допускают выражения как для токов, так и для
напряжений, называют взаимно определенными. Отнесение ребра к одному
из двух подмножеств зависит от его характера, связи с другими ребрами и
процедуры формирования уравнений схемы. В общем случае токи y-ребер и
напряжения z-ребер могут зависеть от токов и напряжений любых ребер
графа, а также от задающих токов и напряжений.
82.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Поэтому компонентные уравнения ребер графа электронной схемы можно
записать в виде:
I y YвU y NIz N I y G Uz Jв ,
Uz MU y ZвIz R I y M Uz Eв ,
где
I y , I z - векторы токов y-ребер и z-ребер;
U y , U z - векторы напряжений y-ребер и z-ребер;
Jв - вектор задающих токов;
Eв- вектор задающих э.д.с..
(2.8)
83.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Уравнения (2.8) можно объединить в одно обобщенное компонентное
уравнение:
X VX V X F
или
(2.9)
1 V X VX F
где X' и X'' выражаются через векторы токов и напряжений y- и z-ребер:
I y
U y
X X
U z
I z
(2.10)
84.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Обобщенные компонентные матрицы V, V' и задающий вектор F имеют
вид:
Yв
V
M
N
Zв
N G
V
R
M
Jв
F
Eв
(2.11)
85.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Элементами компонентных матриц являются параметры компонентов
схемы. При этом в Yв входят проводимости y-двухполюсников и управляющие
проводимости зависимых источников тока, управляемых напряжениями yребер, а в Zв – сопротивления z-двухполюсников и управляющие
сопротивления зависимых источников напряжения, управляемых токами zребер. Элементами остальных субматриц являются соответствующие
управляющие параметры зависимых источников.
86.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Обобщенное компонентное уравнение (2.9) можно упростить, если
предположить, что y-ребра могут быть управляющими только по напряжению,
а z-ребра – управляющими только по току. Тогда и (2.9) приводится к виду
X VX F
(2.12)
87.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Это уравнение можно распространить и на общий случай, вводя при
необходимости дополнительные управляющие ребра. Последовательно с
управляющими по току y-ребрами вводят короткозамкнутые управляющие по
току z-ребра, а параллельно с управляющими по напряжению z-ребрами –
разомкнутые управляющие по напряжению y-ребра. Условные изображения
управляющих ребер представлены на рис. 2.30.
а)
б)
Рис. 2.30. Условные изображения разомкнутого (а) и короткозамкнутого (б)
ребер полюсных графов
88.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Компонентные уравнения управляющих ребер имеют вид:
Uz 0
Iy 0
(2.13)
Специальные управляющие ребра вводят и в тех случаях, если
управляющий ток или напряжение не совпадают с током или напряжением
какого-либо ребра графа или если целесообразно исключить из числа
управляющих какой-либо класс ребер (например, ребра реактивных
двухполюсников или независимых источников).
89.
2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕЭЛЕКТРОННЫХ СХЕМ
2.3. Математические модели компонентов электронных схем
Компонентные уравнения
Если искомые токи и напряжения не совпадают с токами и напряжениями
каких-либо ветвей схемы, вводят специальные ребра искомых величин –
короткозамкнутые для токов и разомкнутые для напряжений. Их уравнения
совпадают с (2.13).
Следует отметить, что выражения (2.8) могут применяться для описания
нелинейных компонентных уравнений
I y f (U y , Iz , I y ,U z , Jв );
U z (U y , Iz , I y ,U z , Eв ).
(2.14)
их линеаризацией, при этом элементы компонентных матриц V, V'
определяются частными производными выражений (2.14) и являются
переменными величинами.




































































 Электроника
Электроника








