Похожие презентации:
Контрольная работа по математическим моделям в экономике и управлении. Решение задачи № 1
1. Решение задачи № 1
Контрольная работапо математическим
моделям в экономике и
управлении
Решение задачи № 1
2. Использование функций MS Excel
Функция СРЗНАЧ вычисляет среднее арифметическое изнескольких массивов (аргументов) чисел.
Функция МЕДИАНА позволяет получать медиану заданной
выборки. Медиана - это элемент выборки, число элементов
выборки со значениями больше которого и меньше которого равно.
Функция МОДА вычисляет наиболее часто встречающееся
значение в выборке.
Функция ДИСП позволяет оценить дисперсию по выборочным
данным.
Функция СТАНДОТКЛОН вычисляет стандартное отклонение.
Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным
данным.
Функция СКОС позволяет оценить асимметрию выборочного
распределения.
Функция КВАРТИЛЬ вычисляет квартили распределения. Функция
имеет формат КВАРТИЛЬ(массив, значение), где массив –
интервал ячеек, содержащих значения СВ; значение определяет
какая квартиль должна быть найдена (0 – минимальное значение,
1 – нижняя квартиль, 2 – медиана, 3 – верхняя квартиль, 4 –
максимальное значение распределения).
2
3. Определение числа интервалов
1) Объем каждой выборки равен N = 100.Найдем
максимальное,
минимальное
значение и размах для каждой выборки:
Max (X) = 120
Min (X) = 90
L (X) = Max - Min = 30
2) Разобьем отрезок
Max (Y)= 156
Min (Y) = 80
L (Y)=Max - Min =76
L
L
Min
;
Max
20
20
на 10 (т.к.
) равных
по 10длине интервалов
N 100
3
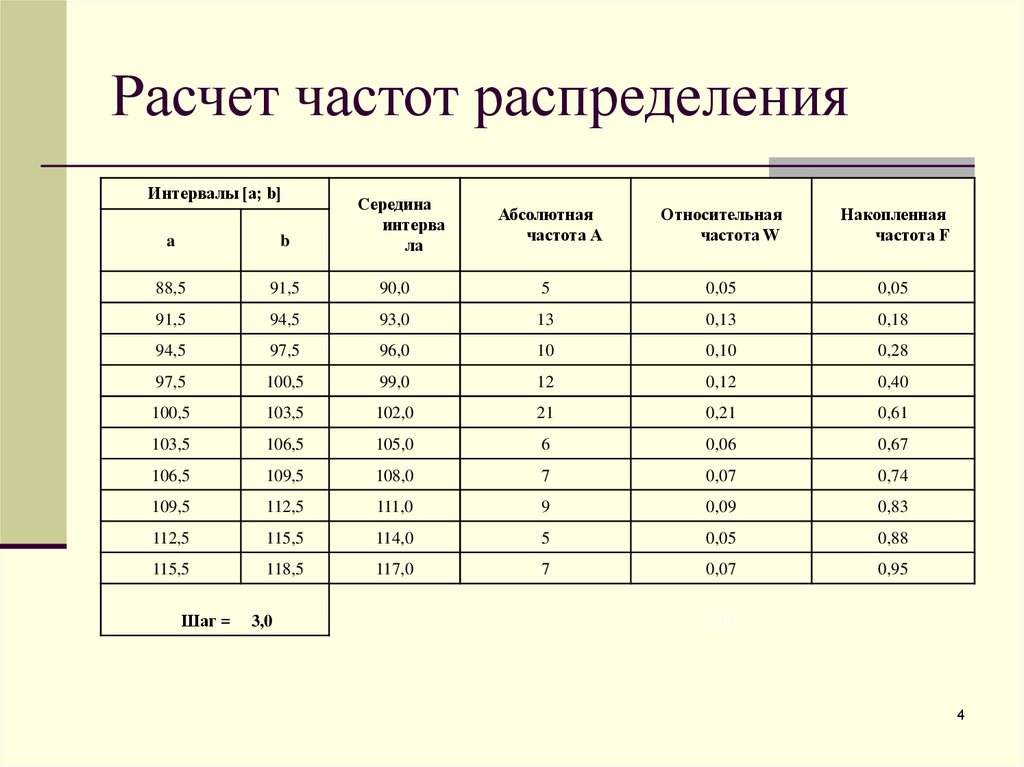
4. Расчет частот распределения
Интервалы [a; b]a
b
Середина
интерва
ла
88,5
91,5
90,0
5
0,05
0,05
91,5
94,5
93,0
13
0,13
0,18
94,5
97,5
96,0
10
0,10
0,28
97,5
100,5
99,0
12
0,12
0,40
100,5
103,5
102,0
21
0,21
0,61
103,5
106,5
105,0
6
0,06
0,67
106,5
109,5
108,0
7
0,07
0,74
109,5
112,5
111,0
9
0,09
0,83
112,5
115,5
114,0
5
0,05
0,88
115,5
118,5
117,0
7
0,07
0,95
Шаг =
3,0
Абсолютная
частота А
Относительная
частота W
Накопленная
частота F
1,00
4
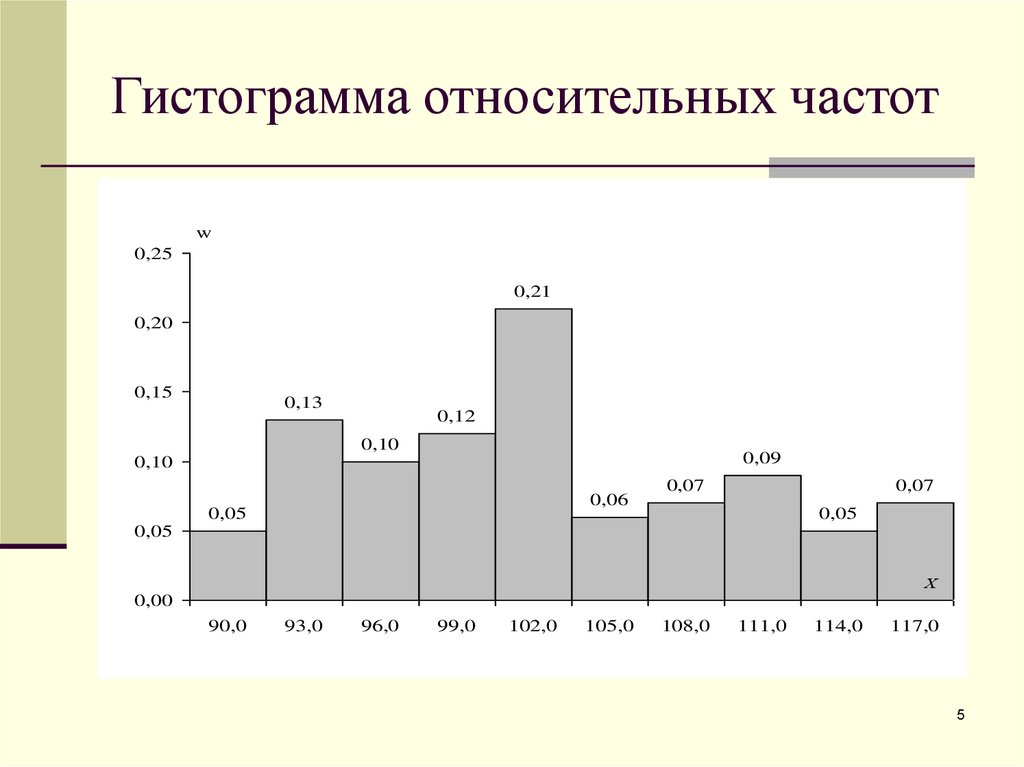
5. Гистограмма относительных частот
w0,25
0,21
0,20
0,15
0,13
0,12
0,10
0,09
0,10
0,06
0,05
0,07
0,07
0,05
0,05
Х
0,00
90,0
93,0
96,0
99,0
102,0
105,0
108,0
111,0
114,0
117,0
5
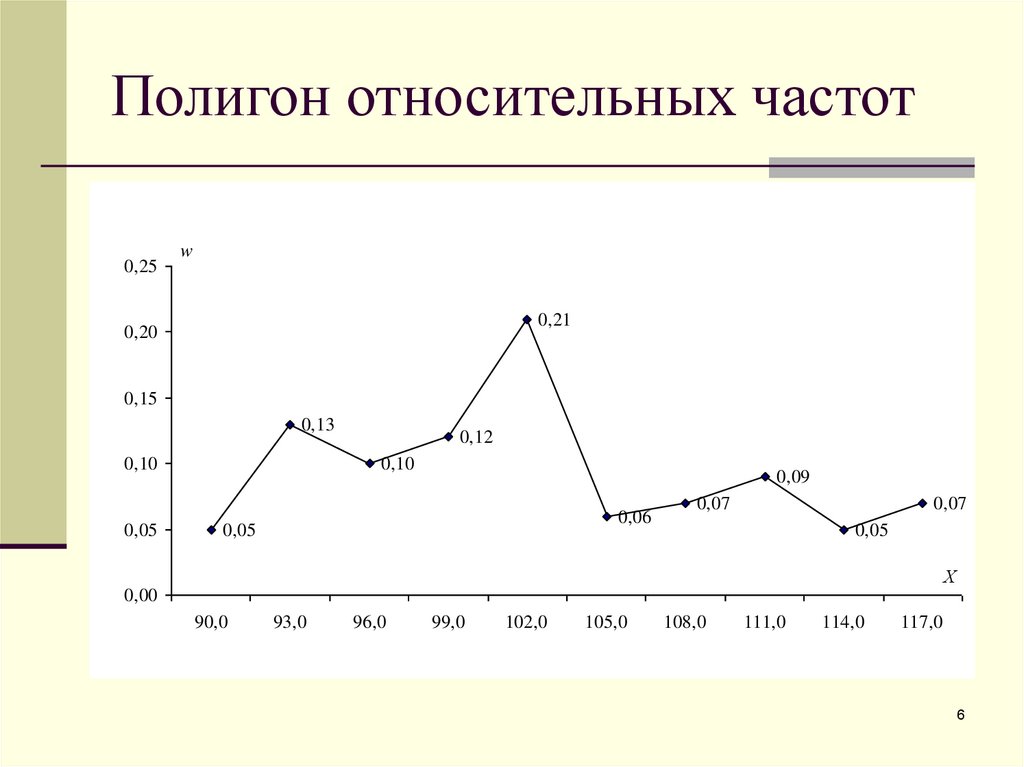
6. Полигон относительных частот
0,25w
0,21
0,20
0,15
0,13
0,10
0,05
0,12
0,10
0,09
0,06
0,05
0,07
0,07
0,05
Х
0,00
90,0
93,0
96,0
99,0
102,0
105,0
108,0
111,0
114,0
117,0
6
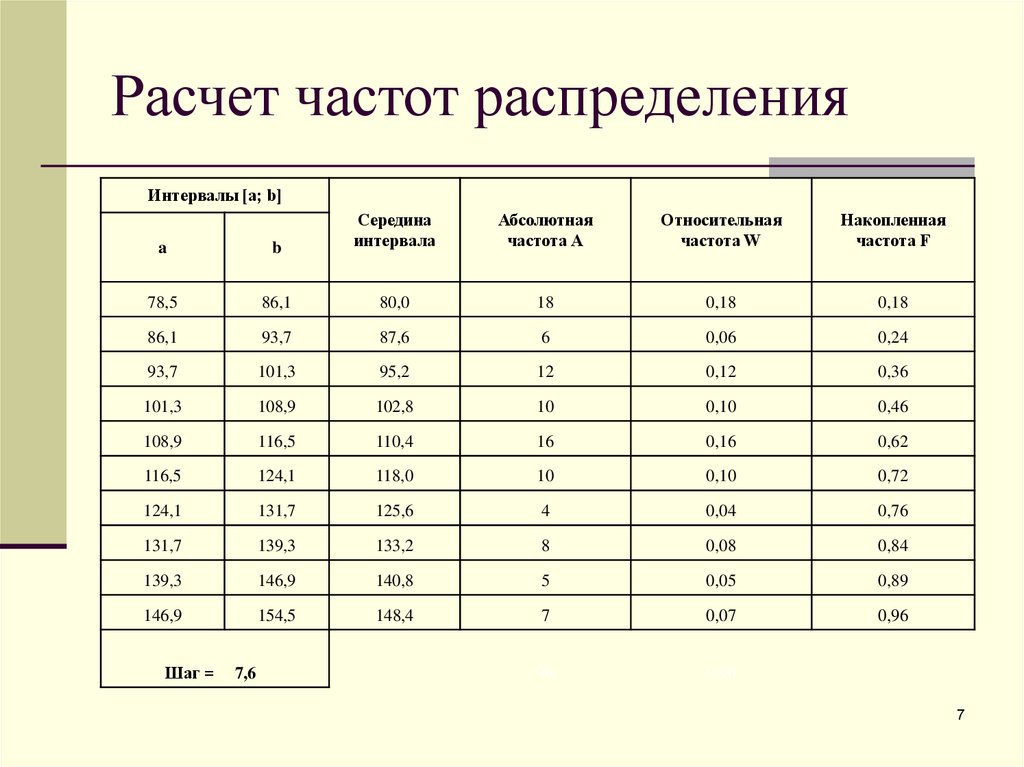
7. Расчет частот распределения
Интервалы [a; b]a
b
Середина
интервала
78,5
86,1
80,0
18
0,18
0,18
86,1
93,7
87,6
6
0,06
0,24
93,7
101,3
95,2
12
0,12
0,36
101,3
108,9
102,8
10
0,10
0,46
108,9
116,5
110,4
16
0,16
0,62
116,5
124,1
118,0
10
0,10
0,72
124,1
131,7
125,6
4
0,04
0,76
131,7
139,3
133,2
8
0,08
0,84
139,3
146,9
140,8
5
0,05
0,89
146,9
154,5
148,4
7
0,07
0,96
96
0,96
Шаг =
7,6
Абсолютная
частота А
Относительная
частота W
Накопленная
частота F
7
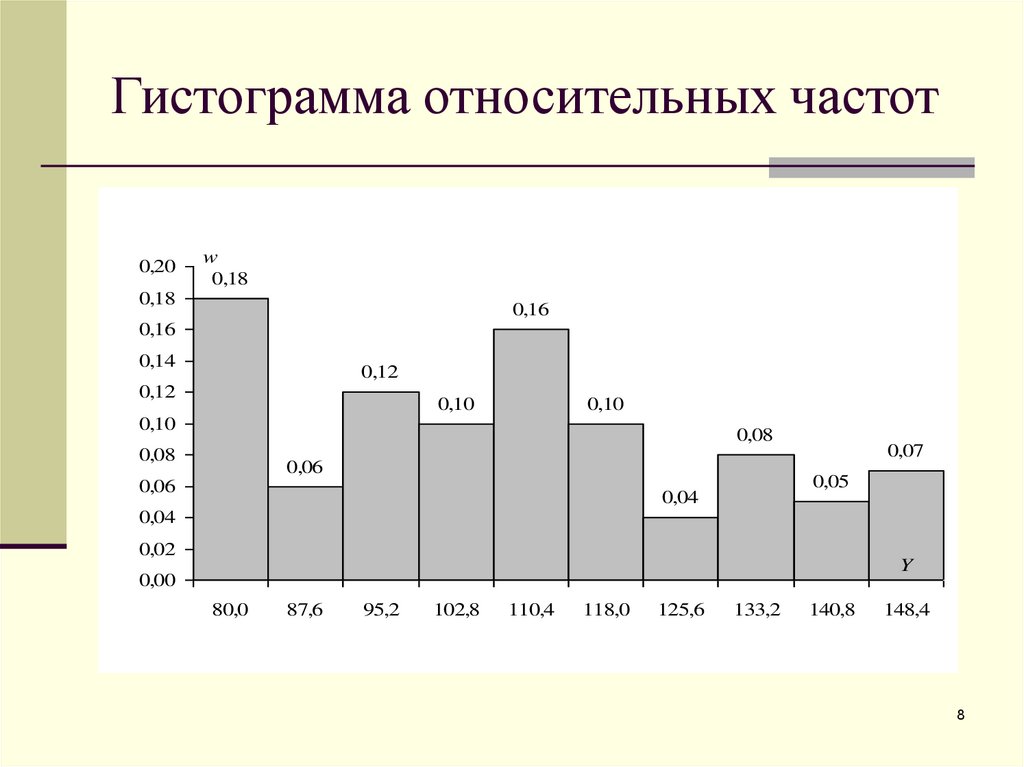
8. Гистограмма относительных частот
0,20w
0,18
0,18
0,16
0,16
0,14
0,12
0,12
0,10
0,10
0,10
0,08
0,08
0,06
0,06
0,07
0,05
0,04
0,04
0,02
Y
0,00
80,0
87,6
95,2
102,8
110,4
118,0
125,6
133,2
140,8
148,4
8
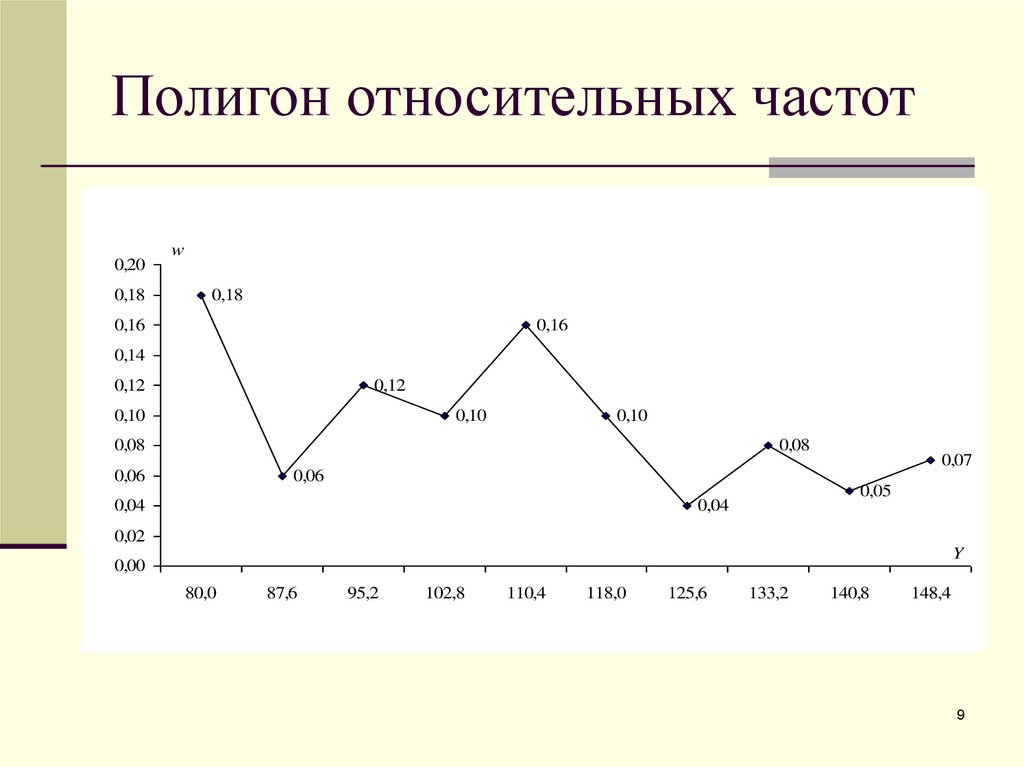
9. Полигон относительных частот
0,200,18
w
0,18
0,16
0,16
0,14
0,12
0,12
0,10
0,10
0,10
0,08
0,08
0,06
0,06
0,05
0,04
0,04
0,07
0,02
Y
0,00
80,0
87,6
95,2
102,8
110,4
118,0
125,6
133,2
140,8
148,4
9
10. Выборочное среднее
Выборочное среднее вычисляется по формулеn
xi
x i
n
где x i измеренная величина, n - количество измеренных
значений.
Пусть в результате эксперимента получена выборка
значений: 3, 2, 1, 0, 3, 2, 3.
Рассчитаем ее выборочное среднее
3 2 1 0 3 2 3 14
x
2.
7
2
10
11. Расчет средних и дисперсий
Выборочное среднее характеризует среднее значение экспериментального показателя в выборке наблюдений, т.е. Х хi wi , где xi – середины интервалов, wi –i
относительные частоты. Таким образом, Х 103,1. Аналогично, Y 112,6.
Выборочная дисперсия характеризует меру рассеяния случайной величины
относительно выборочного среднего значения и вычисляется по формуле:
х Х
2
D( Х )
i
i
xi Х wi .
2
N
i
Следовательно, D(X ) 70,9, аналогично D(Y ) 504,0.
11
12. Расчет исправленных дисперсий и среднеквадратичного отклонения
Выборочное среднеквадратическое отклонение вычисляется как положительноезначение квадратного корня из дисперсии: ( Х ) D( Х ) 8,4. Аналогично
(Y ) D(Y ) 22,5.
Тогда исправленная выборочная дисперсия равна:
N
100
S2(Х )
D( Х )
D( Х ) 72,
S 2 (Y ) 509.
N 1
100 1
И исправленное выборочное среднеквадратическое отклонение равно
S ( Х ) S 2 ( Х ) 8,5,
S (Y ) 22,6.
12
13. Проверка нормальности распределения
Из гистограмм выборки можно предположить о нормальности распределения.Найдем асимметрию А и эксцесс Е выборки:
X X
3
A( X )
i
i
= 0,4,
N 3
X X
4
E( X )
i
i
N 4
3 = -0,9.
Для проверки нормальности распределения по значениям асимметрии и эксцесса
найдем для них критические значения по формулам:
6( N 1)
D( A)
0,06;
A 3 D( A) 0,7;
( N 1)( N 3)
24( N 2)( N 3) N
D( E )
0,22;
E 5 D( E ) 2,32.
( N 1) 2 ( N 3)( N 5)
Таким образом, т.к. найденные значения асимметрии и эксцесса не превышаю
по модулю своих критических значений, то распределение можно считать нормальным.
13
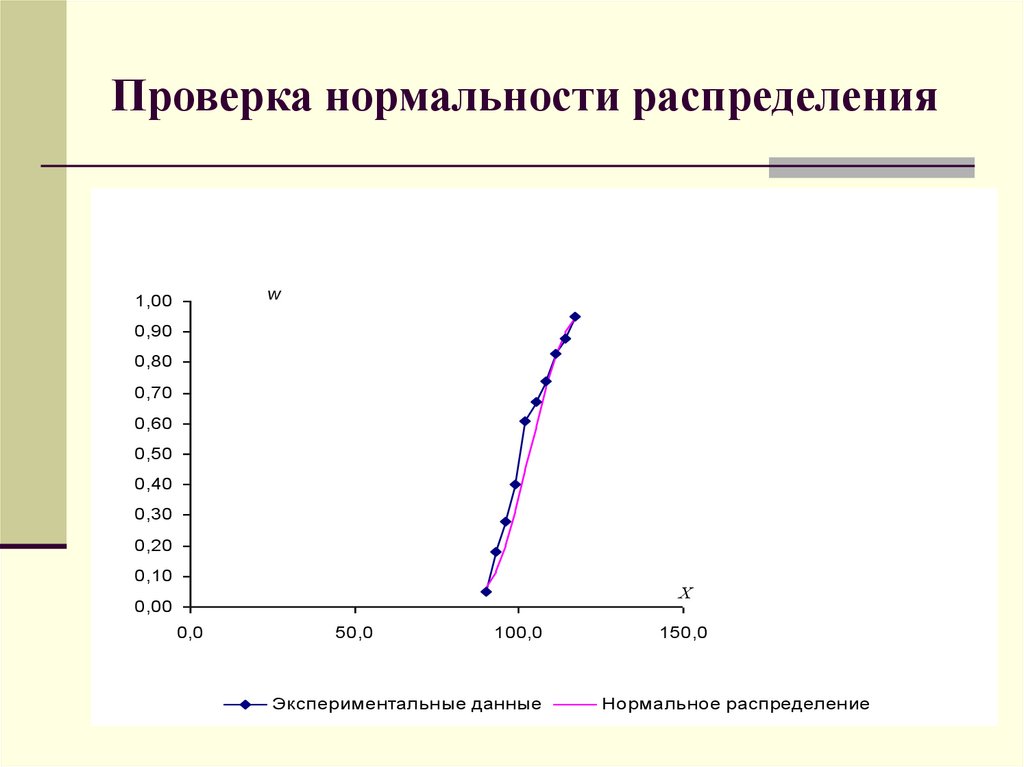
14. Проверка нормальности распределения
Проверим с помощью критерия Колмогорова-Смирнова гипотезу о том, чтоэмпирические данные, представленные в таблице 1, подчиняются нормальному
распределению при уровне значимости =0,1.
Статистика Колмогорова для проверки гипотезы H0 против двусторонней
альтернативы определяется как максимум модуля отклонения эмпирической функции
распределения F’(x) от гипотетической F(x).
Dn max F ' ( x) F ( x)
x
Из таблицы распределения Колмогорова-Смирнова при =0,1 найдем =1,22.
1,22
0,385 . Поскольку величина
Для N = 10 критическое значение d Крит (0,1)
10
max F ' ( x) F ( x) = 0,13 сильно меньше критического значения 0,385, то гипотеза о
x
принадлежности выборки нормальному закону не отвергается.
14
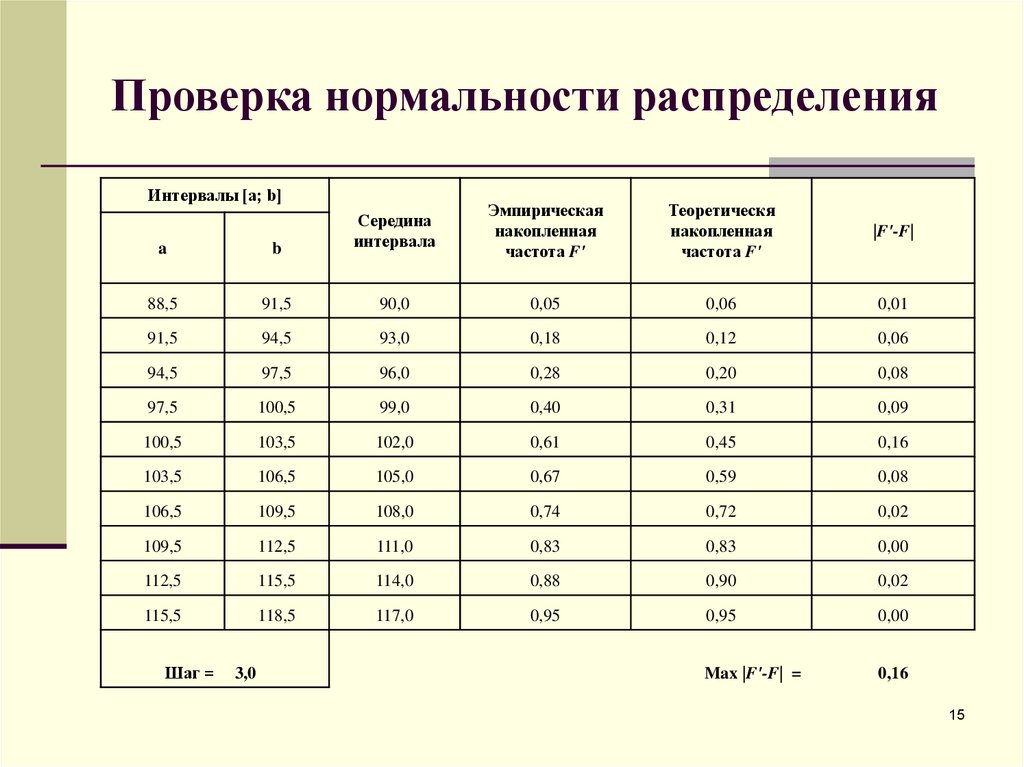
15. Проверка нормальности распределения
Интервалы [a; b]Эмпирическая
накопленная
частота F'
Теоретическя
накопленная
частота F'
|F'-F|
a
b
Середина
интервала
88,5
91,5
90,0
0,05
0,06
0,01
91,5
94,5
93,0
0,18
0,12
0,06
94,5
97,5
96,0
0,28
0,20
0,08
97,5
100,5
99,0
0,40
0,31
0,09
100,5
103,5
102,0
0,61
0,45
0,16
103,5
106,5
105,0
0,67
0,59
0,08
106,5
109,5
108,0
0,74
0,72
0,02
109,5
112,5
111,0
0,83
0,83
0,00
112,5
115,5
114,0
0,88
0,90
0,02
115,5
118,5
117,0
0,95
0,95
0,00
Max |F'-F| =
0,16
Шаг =
3,0
15
16. Проверка нормальности распределения
w1,00
0,90
0,80
0,70
0,60
0,50
0,40
0,30
0,20
0,10
Х
0,00
0,0
50,0
100,0
Экспериментальные данные
150,0
Нормальное распределение
16








 Математика
Математика








