Задачи экометрии

1.

ЗАДАЧИ ЭКОМЕТРИИ
1 задача: Указать способы сбора и группировки стат.
сведений, полученных в результате наблюдений или
некоторых поставленных экспериментов в области
экологии и природопользования
2 задача: Разработать методы анализа стат.данных в
зависимости от целей исследования:
а).оценка неизвестной вероятности события; оценка
неизвестной функции распределения; оценка
параметров распределения; оценка зависимости
случайной величины от других случайных величин
б).проверка стат.гипотез о виде неизвестного
распределения

2.

Гл.1 Случайные величины
§1. Основные понятия
Случайная величина
Дискретная (ДСВ)
Непрерывная (НСВ)
ДСВ обозначаем: X,Y,Z…, а их значения x,y,z…
ДСВ имеет конечное число значений,
НСВ- имеет бесконечное число значений.

3.

§2. ВЫБОРОЧНЫЙ МЕТОД
п.1.Генеральная и выборочная совокупность
СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
(ОБЪЕМ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ)
ВЫБОРКА
ПОВТОРНЫЕ
(ОБЪЕМ ВЫБОРКИ)
БЕСПОВТОРНЫЕ
РЕПРЕЗЕНТАТИВНАЯ

4.

п.2. Статистическое распределение выборки.
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
Значение х1 наблюдалось п1 раз; х2-п2 раза;…;
хk- nk раз.
k
п1 п2 ... пk пi
i 1
х1;х2;…хk-варианты
n1;n2;…nk – частоты
пi
п1
1 ;... i
п
n
относительные частоты

5.

§2. ВЫБОРОЧНЫЙ МЕТОД
Задано распределение частот
выборки объема п=20
Написать распределение
относительных частот
ПРИМЕР
хi
2
6
12
ni
3
10
7
3
1
0,15
20
10
2
0,5
20
7
3
0,35
20
хi
i
2
0,15
пi 20
6
0,5
12
0,35
Проверка: 0,15+0,5+0,35=1

6.

п.3. Полигон и гистограмма
§2. ВЫБОРОЧНЫЙ МЕТОД
Графическое изображение статистического
распределения
Полигон частот: ломаная ( х1 ; п1 )...( хk ; nk )
Полигон относительных частот: ( х1; 1 )...( хk ; k )
Графическое изображение непрерывного
распределения
Гистограмма- ступенчатая фигура, состоящая из
прямоугольников, основаниями которых служат
частичные интервалы длиной h, а высоты равны
отношению пi -плотности частот
h

7.

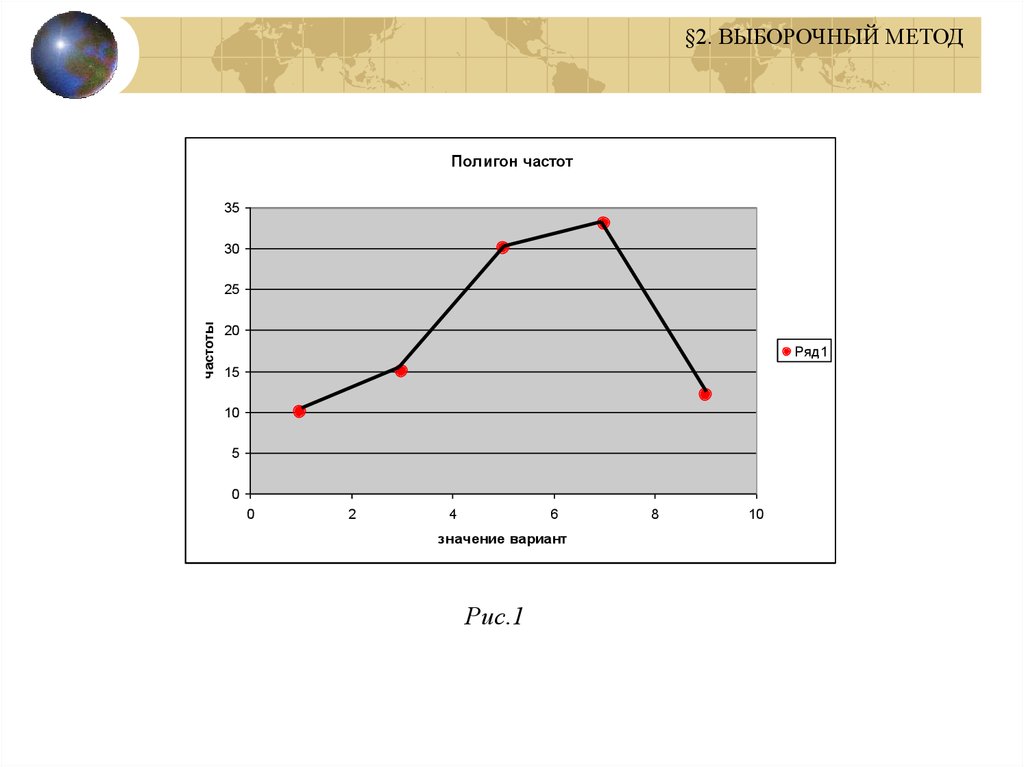
1).Построить полигоны частот и
относительных частот распределения.
§2. ВЫБОРОЧНЫЙ МЕТОД
пi 100
Пример 1.
(Рис.1.)
хi
1
3
5
7
9
ni
10
15
30
33
12
хi
1
i
0,1
3
0,15
5
0,3
i 1
7
9
0,33
0,12
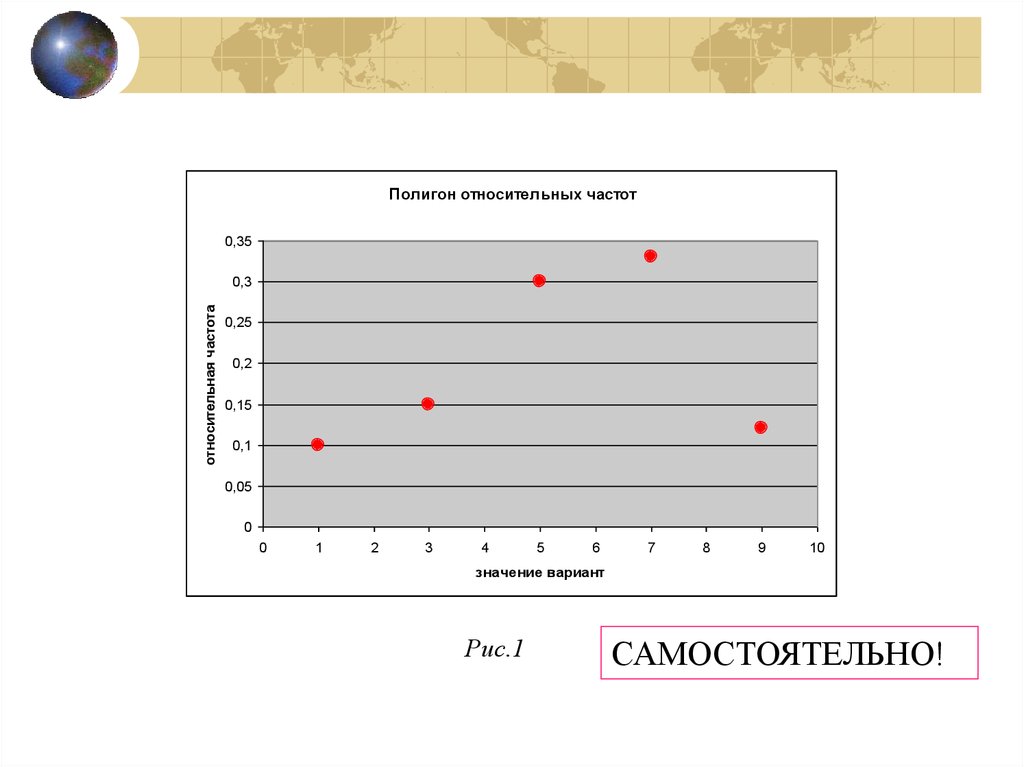
(Рис.2.)

8.

§2. ВЫБОРОЧНЫЙ МЕТОД
Полигон частот
35
30
частоты
25
20
Ряд1
15
10
5
0
0
2
4
6
значение вариант
Рис.1
8
10

9.

Полигон относительных частот
0,35
относительная частота
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
6
7
8
9
10
значение вариант
Рис.1
САМОСТОЯТЕЛЬНО!

10.

§2. ВЫБОРОЧНЫЙ МЕТОД
2). Построить гистограмму частот и
относительных частот распределения.
Частичный
интервал
Сумма частот
вариант
2-5
5-8
8-11
11-14
9
10
25
6
Плотность
частот
9/3=3
10/3=3,3(3)
25/3=8,3(3)
6/3=2
Длина частичного интервала равна 3
пi
Найдем плотность частоты
h
ni 50

11.

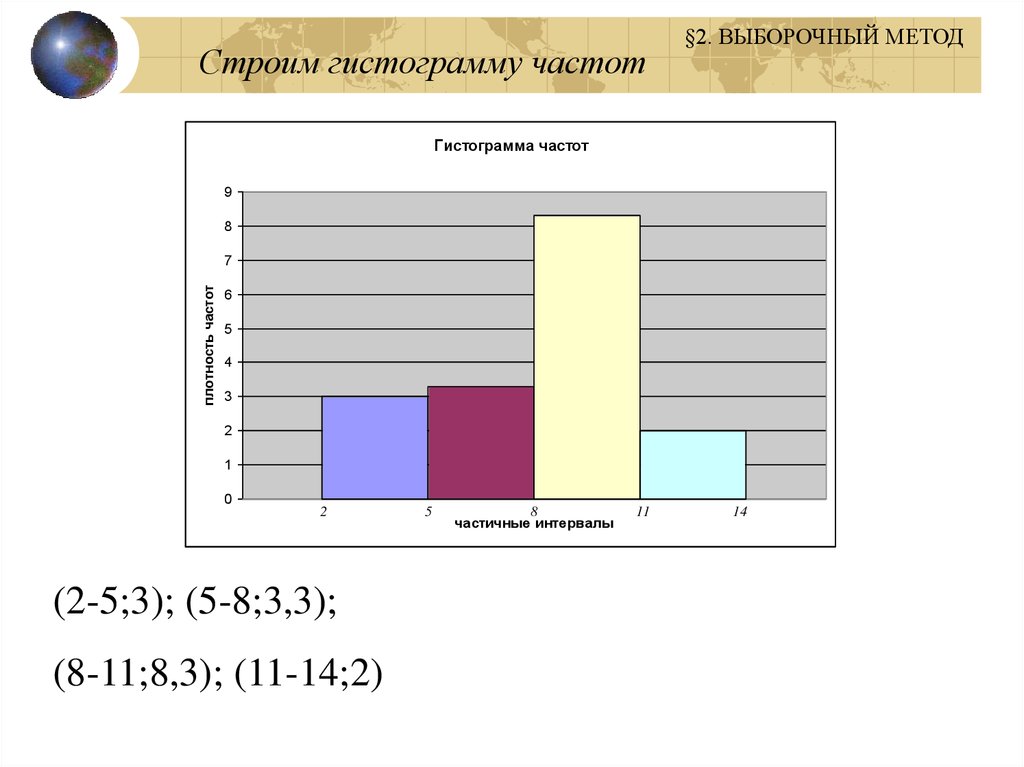
Строим гистограмму частот
§2. ВЫБОРОЧНЫЙ МЕТОД
Гистограмма частот
9
8
плотность частот
7
6
5
4
3
2
1
0
2
(2-5;3); (5-8;3,3);
(8-11;8,3); (11-14;2)
5
8
частичные интервалы
11
14

12.

§2. ВЫБОРОЧНЫЙ МЕТОД
Частичный
интервал
2-5
5-8
8-11
11-14
пi
i
n
9/50 =0,18
10/50=0,2
25/50 =0,5
6/50=0,12
Плотность отн. wi
частоты
h
0,18/3=0,06
0,2/3=0,08
0,5/3=0,16
0,12/3=0,04
Построить гистограмму

13.

§2. ВЫБОРОЧНЫЙ МЕТОД
Гистограмма относительных частот
плотность относительных частот
0,18
0,16
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
2
5
8
11
частичные интервалы
14

14.

§2. ВЫБОРОЧНЫЙ МЕТОД
П. 4. Эмпирическая функция
распределения.
Пусть пх- число наблюдений
п- объем выборки
пх
- относительная частота
п
пх
п
- функция,
зависящая от х
эмпирическая - установленная опытным
путем

15.

ОПРЕДЕЛЕНИЕ
n x функция распределения
F ( x)
n выборки
*
пх-число вариант, меньших х
п-объем выборки
* Функцию распределения генеральной
совокупности называют теоретической
функцией распределения F(x)

16.

•Теоретическая функция F(x) определяет
вероятность события Х<х, а эмпирическая
функция F*(x) определяет относительную
частоту этого же события .
•Если объем выборки п число большое,
то функции F(x) и F*(x) мало
отличаются друг от друга, т.е.
lim P( F ( x) F ( x) ) 1
*
n
(ε>0)
Это равенство (теорема Чебышева)
является теоретической основой
выборочного метода.

17.

ПРИМЕР:
Дано распределение выборки
х-варианты
1
5
9
п-частоты
6
12
22
п=40объем
выборки
Построить эмпирическую функцию.
1). Наименьшая варианта равна 1, по свойству
функции распределения F*(x)=0 при х 1
2). Значение X<5 наблюдалось 6 раз,т.е.
6
F ( x)
40
*
1 x 5

18.

3). Значение X<9 наблюдалось 6+12=18
раз,т.е.
18
*
F ( x)
40
5 x 9
4) Наибольшая варианта х=9, тогда
F*(x)=1 при x>9
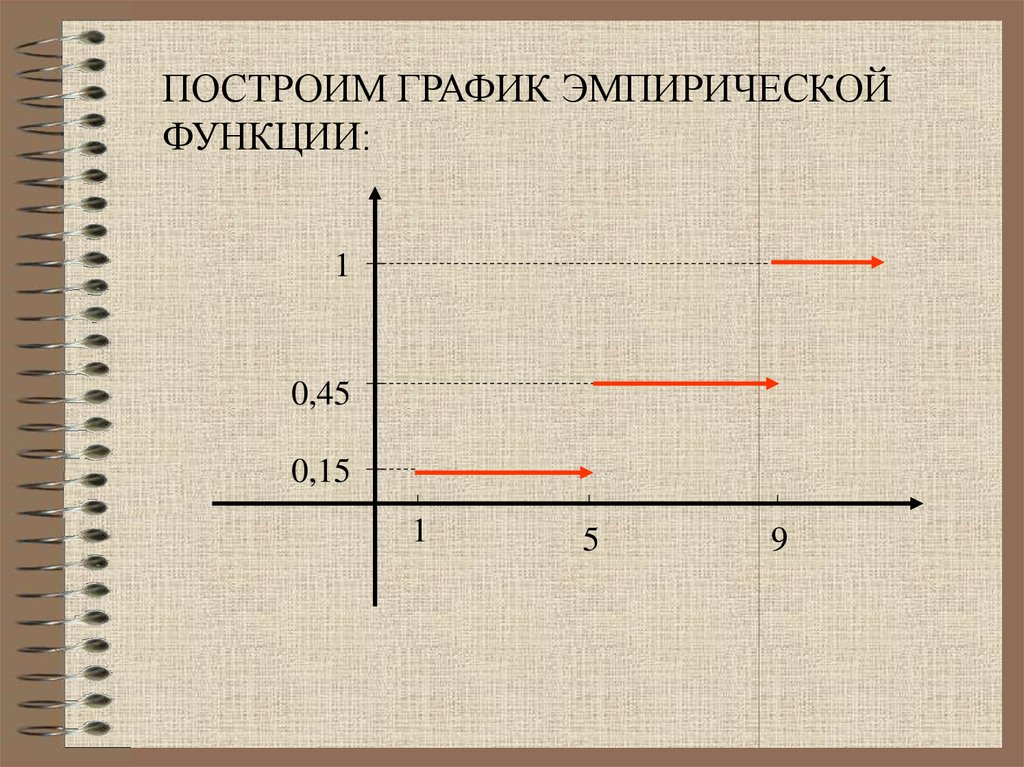
0; x 1
0,15;1 x 5
*
F ( x)
0,45;5 x 9
1; x 9

19.

ПОСТРОИМ ГРАФИК ЭМПИРИЧЕСКОЙ
ФУНКЦИИ:
1
0,45
0,15
1
5
9

20.

§3. Оценки параметров генеральной
совокупности по ее выборке.
П.1. Х-количественный признак, х-значения
этого признака.
Х-случайная величина, х-одно из
возможных ее значений
х1;х2;…хп- значения количественного
признака, полученные в результате пнезависимых испытаний

21.

Найти оценку неизвестного параметразначит найти функцию от наблюдаемых
СВ Х1;Х2;…Хп , которая дает
приближенное значение оцениваемого
параметра
П.2.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ
СРЕДНИЕ
Пусть изучается дискретная генеральная
совокупность объема N относительно
количественного признака Х

22.

ОПРЕДЕЛЕНИЕ
Генеральной средней х Г называется среднее
арифметическое значений признака
генеральной совокупности, т.е.
х1 х2 ... х N
хГ
N
Если значения х1;х2;…хk имеют соответственно
частоты N1;N2;…;Nk, причем N1+N2+…+Nk=N
х1 N1 х2 N 2 ... хk N k 1 k
хГ
xi N i
N
N i 1

23.

Так как каждый объект может быть
извлечен с одной и той же вероятностью
1/N, то тогда генеральная средняя
хГ M ( X )
ОПРЕДЕЛЕНИЕ
Выборочной средней называется среднее
арифметическое значений признака выборочной
совокупности.
Если все значения х1;х2;…;хп признака
выборки объема п различны, то средняя
х1 х2 ... хп
выборочная равна
хВ
п

24.

Если же значения х1;х2;…хk имеют
частоты n1;n2;…nk, причем
k
1
n1+n2+…+nk=п, то х x п
В
i i
п i 1
Выборочная средняя для различных выборок
того же объема из той же генеральной
совокупности может получаться различной.
Всевозможные, получающиеся выборочные
средние есть возможные значения случайной
величины, которая называется выборочной
средней СВ
Х
-выборочная средняя

25.

Если варианты хi –большие числа, то
для облегчения вычисления выборочной
средней применяют, так называемый,
«ложный нуль»
n
n
Пусть С-const, т.к. xi ( xi C ) nC
i 1
i 1
тогда выборочная средняя вычисляется по
формуле
1 n
1 n
1 n
х В xi ( ( xi C ) nC ) С ( xi C )
п i 1
п i 1
п i 1
С-const-«ложный нуль», постоянную берут
такой, чтобы хi C были небольшими и
С по возможности было числом круглым

26.

пример
х1=71,88
х2=71,93
х3=72,05
Имеется выборка
х4=72,07
х5=71,90
х6=72,02
х7=71,93
х8=71,77
х9=72,71
х10=71,96
С=72, найдем разность хi-С=αi
α1= - 0,12
α4=0,07
α7= - 0,07 α10= - 0,04
α2= - 0,07
α5= - 0,1
α8=-0,23
α3=0,05
α6=0,02
α9=0,71
Их сумма равна 0,22
i 0,02 среднее арифметическое
10

27.

Тогда выборочная средняя равна
72+0,02=72,02
П.3.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ
ДИСПЕРСИЯ
ОПРЕДЕЛЕНИЕ
Генеральной дисперсией DГ называют среднее
арифметическое квадратов отклонений
значений признака Х генеральной
совокупности от генеральной средней х Г

28.

n
1
D Г ( xi x Г )
N i 1
2
Генеральным средним квадратическим
отклонением (стандартом) называется
Г DГ
( Х ) - средняя квадратическая ошибка

29.

ОПРЕДЕЛЕНИЕ
Выборочной дисперсией называется среднее
арифметическое квадратов отклонений
наблюдаемых значений признака Х от
выборочной средней
n
1
D В ( xi x В )
п i 1
Выборочный стандарт
2
В DВ

30.

Выборочную дисперсию, рассматриваемую
как случайную величину, будем обозначать
~2 1 n
S ( X i X )2
n i 1
X
-выборочная средняя случайная величина
n 1
~2
М (S )
DГ
n
ТЕОРЕМА
•Если варианты – большие числа,то для
вычисления используем «ложный нуль» С
n
2
1
2
D В ( xi С ) ( х В С )
п i 1

31. §4.Точность оценки, доверительная вероятность(надежность), доверительный интервал

• Точечной называют
оценку, которая
определяется одним
числом
• При выборке малого
объема точечная оценка
значительно отличается
от оцениваемого
параметра
• Интервальной называют
оценку, которая
определяется двумя
числами, концами
интервала
• Интервальные оценки
позволяют установить
точность и надежность
оценки

32. Интервальные оценки

• Статистическая характеристика θ*, найденная
по данным выборки, служит оценкой
неизвестного параметра θ
• Пусть θ –постоянное число или случайная
величина
• Чем меньше модуль разности * , тем
точнее θ * определяет θ
• Пусть * ,при δ>0. Чем меньше δ, тем
оценка точнее, т.е. δ характеризует точность
оценки

33. Интервальные оценки

• Доверительной
• (θ *-δ; θ *+δ)
вероятностью или
интервал
надежностью оценки
доверительный
θ по θ * называют
• Он покрывает
вероятность γ, с
неизвестный
которой
параметр с заданной
осуществляется
надежностью γ
неравенство
*

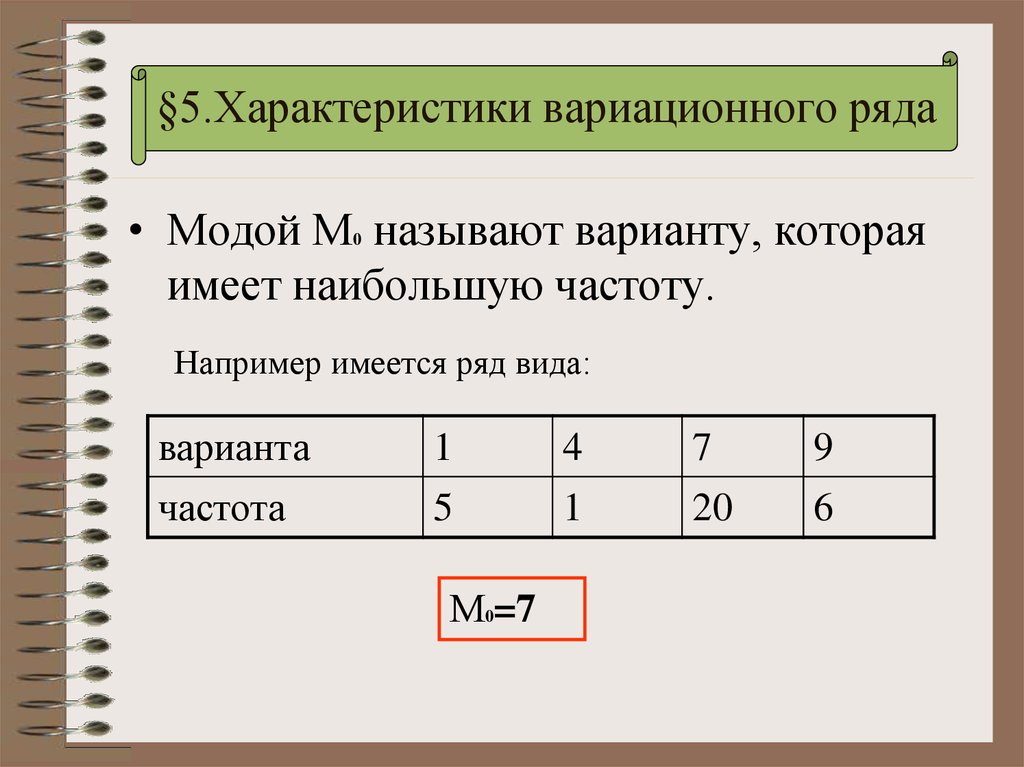
34. §5.Характеристики вариационного ряда

• Модой М называют варианту, которая
имеет наибольшую частоту.
0
Например имеется ряд вида:
варианта
1
4
7
9
частота
5
1
20
6
М0=7

35. Характеристики вариационного ряда

• Медианой те называют варианту, которая
делит вариационный ряд на две части ,
равные по числу вариант. Если число вариант
нечетно, т.е. n=2k+1, то те=xk+1, при четном
n=2k медиана
x k x k 1
me
2
• Размахом варьирования R называют разность
между наибольшей и наименьшей вариантами
R=xmax-xmin.
Размах является простейшей
характеристикой вариационного ряда.

36. Характеристики вариационного ряда

• Средним абсолютным отклонением
θ (тэта) называют среднее арифметическое
абсолютных отклонений
n x x
n
i
i
в
i
Среднее абсолютное отклонение служит
для характеристики рассеяния вариационного
ряда

37. Пусть дан вариационный ряд

xi
ni
1
4
3
10
6
5
16
1
4 1 10 3 5 6 1 16 80
xi
4
4 10 5 1
20
4 1 4 10 3 4 5 6 4 1 16 4
2,2
4 10 5 1
Среднее абсолютное отклонение

38. Характеристики вариационного ряда

• Коэффициентом вариации V называют выраженное в процентах
отношение выборочного среднего квадратического отношения
к выборочной средней
V
в
xв
100%
Коэффициент вариации служит для сравнения величин
рассеяния по отношению к выборочной средней двух
вариационных рядов: тот из рядов имеет большее рассеяние по
отношению к выборочной средней, у которого коэффициент
вариации больше.
• Коэффициент вариации- безразмерная величина, поэтому он
пригоден для сравнения рассеяний вариационных рядов,
варианты которых имеют различную размерность, например,
если варианты одного ряда выражены в сантиметрах, а другогов граммах.

39.

• Если вариационный ряд составлен по
данным выборки, то все описанные
характеристики называют
выборочными.
• Если вариационный ряд составлен по
данным генеральной совокупности, то
характеристики называют
генеральными

40. §6.Методы расчета сводных характеристик выборки

ui
xi C
h
§6.Методы расчета сводных характеристик
выборки
П.1. Условные варианты
Пусть варианты выборки расположены в
возрастающем порядке, т.е. в виде вариационного
ряда.
Равноотстоящими называют варианты, которые
образуют арифметическую прогрессию с разность h
Условными называют варианты, определяемые
равенством
xi C
ui
h
где С- ложный нуль, h- шаг, т.е. разность между любыми двумя
соседними первоначальными вариантами.

41.

• Упрощенные методы расчета сводных характеристик
выборки основаны на замене первоначальных
вариант условными.
• Если вариационный ряд состоит из равноотстоящих
вариант с h- шагом, то условные варианты есть
целые числа
• Выберем в качестве ложного нуля произвольную
варианту, например хт, тогда условная варианта
xi xm x1 (i 1)h x1 (m 1)h
ui
i m
h
h
• т.к. i и m целые числа, то и их разность есть целое
число

42.

Замечание 1. В качестве ложного нуля можно взять
любую варианту. Максимальная простота
вычислений достигается, если в качестве ложного
нуля выбрать варианту, которая расположена
приблизительно в середине вариационного ряда
(часто такая варианта имеет наибольшую частоту)
Замечание 2. Варианте, которая принята в качестве
ложного нуля, соответствует условная варианта
равная нулю.

43. П.2.Обычные начальные и центральные эмпирические моменты

• Обычным эмпирическим моментом порядка k
называют среднее значение k-х степеней
разностей xi-C
M k*
k
n
(
x
C
)
i i
n
хi-наблюдаемая варианта, С- ложный нуль, пi-частота
варианты, п- объем выборки

44.

• Начальным
эмпирическим
моментом порядка k
называется обычный
момент порядка k при
С=0
• Начальный
эмпирический момент
первого порядка равен
выборочной средней
Mk
M1
k
n
(
x
)
i i
n
nx
i i
n
xв

45.

• Центральным эмпирическим
k
n
(
x
x
)
моментом порядка k
i i в
mk
называется обычный момент
n
порядка k при С= xв
2
• Центральный эмпирический
n
(
x
x
)
i i в D
момент второго порядка равен m2
в
n
выборочной дисперсии
• Выразим центральные
*
* 2
m
M
(M
2
2
1)
моменты через обычные
m3 M 3* 3M 2* M 1* 2( M 1* ) 3
m4 M 4* 4 M 3* M 1* 6 M 2* ( M 1* ) 2 3( M 1* ) 4

46. П.3. Условные эмпирические моменты. Отыскание центральных моментов по условным

• Для упрощения расчетов первоначальные варианты
заменяем условными
• Условным эмпирическим моментом порядка k
называется начальный момент порядка k,
вычисленный для условных вариант
xi C
n
i
h
M k*
n
k
при k =1
xi C
n
i
1 ni xi
h
*
M1
C
n
h n
n 1 x
i
n
h
в
С

47. Для того, чтобы найти выборочную среднюю, необходимо условный момент первого порядка умножить на шаги к результату прибавить ложный нуль

xв M h C
*
1
Найдя таким образом обычные моменты можно
получить центральные, в итоге получаем удобные для
вычислений формулы, выражающие центральные
моменты через условные
m2 (M 2* (M1* ) 2 )h 2
m3 ( M 3* 3M 2* M 1* 2( M 1* )3 )h 3
m4 ( M 4* 4M 3* M 1* 6M 2* ( M 1* ) 2 3( M 1* ) 4 )h 4

48.

• В соответствии с
предыдущими
формулами получим
формулу для
вычисления
*
* 2
2
D
M
(
M
)
h
в
2
1
выборочной
дисперсии по
условным моментам
первого и второго
порядков

49. Метод произведений для вычисления выборочной средней и выборочной дисперсии

П. 4
• Метод произведений –это удобный способ для вычисления
условных моментов вариационного ряда с равноотстоящими
вариантами. Зная условные моменты, найдем начальные и
центральные моменты и соответственно выборочную среднюю
и выборочную дисперсию
• Этот метод удобнее оформлять в таблицу
Выборочн
ые
варианты в
возрастаю
щем
порядке
Частоты
вариант
…
…
Условные
варианты
ui
ni n
…
xi C
h
Частоты
умножают
на
варианты
ni ui
2
ni (ui 1) 2
ni ui
…
niui
…
n u
i i
2
…
n (u 1)
i
i
2

50.

Заполняя третий столбец,
варианту с большей частотой
или варианту, находящуюся
примерно в середине
вариационного ряда берут за
0, в клетках над ним берут -1,2,-3…, под ним 1,2,3…и т.д.
После заполнения расчетной
таблицы вычисляются
условные моменты и затем выборочные средние и
выборочная дисперсия:
4
1
M1
nx
i i
n
2
M
*
2
nx
2
i i
n
*
x
M
3 в
1h C
Dв M 2* ( M 1* ) 2 h 2

51.

П.5.
Построение нормальной кривой по
опытным данным
• Находим xв ; в , например по методу
произведений
• Находим ординаты (выравнивающие частоты)
теоретической кривой по формуле
nh
где п- сумма наблюдаемых
yi
(ui )
в
частот, h- разность между двумя соседними
вариантами, значения выборочных средних равны
ui
xi х в
в
(u )
1
е
2
и2
2

52.

• Строим точки с координатами (хi;уi) в
прямоугольной системе координат и
соединяем их плавной кривой
• Близость выравнивающих частот к
наблюдаемым подтверждает правильность
допущения о том, что обследуемый признак
распределен нормально

53.

Построить нормальную кривую по данному распределения
хi
15
20
25
30
40
45
50
55
пi
6
13
38
74 106 85
30
10
4
35
Пользуясь методом произведений получим
в 7.38
Найдем выравнивающие частоты
xв 34.7

54.

хi
15
20
25
30
35
40
45
50
55
пi
6
13
38
74
106
85
30
10
4
366
xi х в
nh
xi xв ui
y
(ui )
(ui ) i
в
в
-19.7
-14.7
-9.7
-4.7
0.3
5.3
10.3
15.3
20.3
-2.67
-1.99
-1.31
-0.63
0.05
0.73
1.41
2.09
2.77
0.0113
0.0551
0.1691
0.3271
0.3984
0.3056
0.1476
0.0449
0.0086
3
14
42
82
99
76
37
11
2
366

55.

нормальная кривая и полигон частот
120
100
80
Ряд1
60
Ряд2
40
20
0
15
20
25
30
35
40
45
50
55
Для того, чтобы более уверенно считать, что данные
наблюдений свидетельствуют о нормальном
распределении признака, пользуются специальными
правилами – критериями согласия (рассмотреть
самостоятельно!)