СÑ‚аÑ‚истическая проверка стаÑ‚истических гипоÑ‚ез

1. Математическая статистика

2. Статистическая проверка статистических гипотез

3. Статистическая гипотеза

Статистической гипотезой называется гипотеза о
виде неизвестного распределения или о параметрах
известных распределений.
Например, статистическими будут гипотезы:
1) генеральная совокупность распределена по закону
Пуассона;
2) дисперсии двух нормальных совокупностей равны
между собой.
В первой гипотезе сделано предположение о виде
неизвестного распределения, во второй – о параметрах
двух известных распределений.

4.

Наряду с выдвинутой гипотезой рассматривают и
противоречащую ей гипотезу. Если выдвинутая
гипотеза будет отвергнута, то имеет место
противоречащая гипотеза.
Нулевой (основной) называется выдвинутая гипотеза
Н0. Конкурирующей (альтернативной) называется
гипотеза Н1, которая противоречит нулевой.
Если гипотеза содержит только одно предположение,
то она называется простой. Если гипотеза содержит
несколько предположений, то есть состоит из конечного
или бесконечного числа простых гипотез, то она
называется случайной.

5.

Выдвинутая гипотеза может быть как правильной, так
и неправильной. Поэтому возникает необходимость ее
проверить.
Поскольку проверку производят статистическими
методами, то ее называют статистической проверкой
статистических гипотез. В итоге статистической
проверки гипотезы в двух случаях может быть принято
неправильное решение:
Ошибка I рода состоит в том, что будет отвергнута
правильная гипотеза;
Ошибка II рода состоит в том, что будет принята
неправильная гипотеза.

6.

Последствия этих ошибок могут быть различными.
Например, если отвергнуто правильное решение
«продолжать строительство жилого дома», то эта
ошибка I рода повлечет материальный ущерб.
Если же принято неправильное решение «продолжать
строительство», несмотря на опасность обвала стройки,
то эта ошибка II рода может повлечь гибель людей.
Иногда ошибка I рода влечет более тяжелые
последствия, чем ошибка II рода.

7.

Замечание 1. Правильное решение может быть
принято также в двух случаях:
– гипотеза принимается, причем и в действительности
она правильная;
– гипотеза отвергается, причем и в действительности
она неправильная;
Замечание 2. Вероятность совершить ошибку первого
рода принято обозначать через α, ее называют уровнем
значимости. Наиболее часто уровень значимости
принимают равным 0.05 или 0.01.
Если принят уровень значимости равный 0.05, то в
пяти случаях из ста мы рискуем допустить ошибку I
рода (отвергнуть правильную гипотезу).

8. Статистический критерий проверки нулевой гипотезы

9.

Для проверки нулевой гипотезы Н0 используют
специально подобранную случайную величину, точное
или приближенное распределение которой известно.
Статистическим критерием называется случайная
величина К, которая используется для проверки нулевой
гипотезы.
Для проверки гипотезы по данным выборки
вычисляют частные значения входящих в критерий
величин, и получают наблюдаемое (частное) значение
критерия Кнабл.

10.

Для проверки гипотезы множество всех значений
критерия К разбивается на два непересекающихся
множества:
– критическую область, включающую в себя
значения критерия К, при которых нулевая гипотеза не
выполняется;
– область принятия гипотезы (область допустимых
значений), включающая в себя значения критерия К, при
которых гипотеза принимается.

11.

Принцип проверки статистической гипотезы: если
наблюдаемое значение критерия Кнабл принадлежит
критической области, гипотеза отвергается, а если
области
допустимых
значений,
то
гипотеза
принимается.
Поскольку критерий К – одномерная случайная
величина, то все ее возможные значения принадлежат
некоторому интервалу. Поэтому критическая область и
область
принятия
гипотезы
также
являются
интервалами и, следовательно, существуют точки,
которые их разделяют.

12.

Критическими точками (границами) kкр называют
точки, отделяющие критическую область от области
принятия гипотезы (рис. 1).
Kкр
K
Рис. 1
Различают одностороннюю (левостороннюю или
правостороннюю) и двухстороннюю критические
области.

13.

Правосторонней называется критическая область,
определяемая неравенством K>kкр, где kкр>0 (рис. 2).
Левосторонней называется критическая область,
определяемая неравенством K<kкр, где kкр<0 (рис. 3).
0 Kкр
Рис. 2
Kкр 0
Рис. 3
Двусторонней называется критическая область,
определяемая неравенствами K<k1, K>k2, где k2>k1.

14.

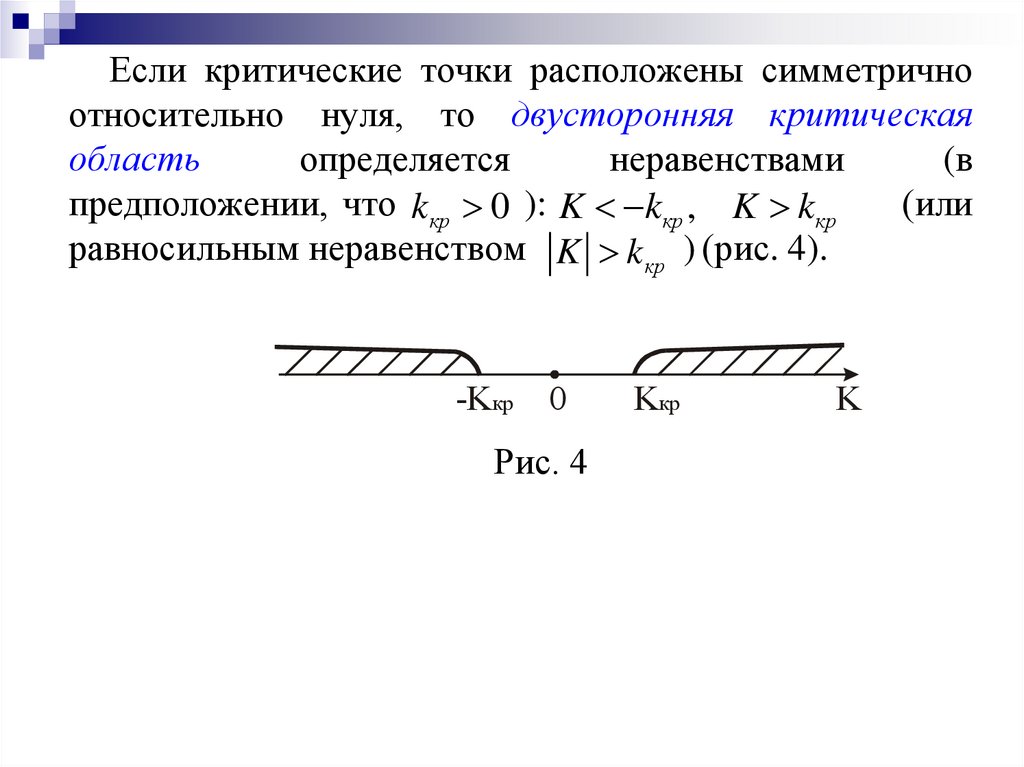
Если критические точки расположены симметрично
относительно нуля, то двусторонняя критическая
область
определяется
неравенствами
(в
предположении, что kкр 0 ): K kкр , K kкр
(или
равносильным неравенством K kкр ) (рис. 4).
-Kкр
0
Рис. 4
Kкр
K

15.

Для
отыскания
правосторонней
критической
области необходимо найти критическую точку.
С этой целью задаются достаточно малой
вероятностью – уровнем значимости . Затем ищут
критическую точку kкр , чтобы при условии
справедливости нулевой гипотезы, вероятность была
равна принятому уровню значимости:
P( K kкр ) , kкр 0.
Замечание: Когда критическая точка найдена,
вычисляют по данным выборок наблюдаемое значение
K набл kкр , то нулевую гипотезу
критерия и, если
отвергают, если K набл kкр
, то нет оснований, чтобы
отвергнуть нулевую гипотезу.

16.

Левосторонняя критическая область определяется
аналогично:
P( K kкр ) , kкр 0.
Критические точки для двусторонней критической
области определяются из условия, что
P( K k1 ) P ( K k2 ) .
Если области симметричны относительно нуля, то
P( K kкр ) P( K kкр ).
Для двусторонней критической области справедливо
P( K kкр )
.
2
Для каждого критерия имеются специальные таблицы,
по которым определяется kкр.

17. Проверка гипотезы о нормальности распределения

18.

Критерии проверки гипотезы о предполагаемом
законе
неизвестного
распределения
называются
критериями
согласия.
Существуют
различные
приближенные и точные критерии оценки нормальности
распределения. Для проверки гипотезы используется
статистический ряд: x1, x2, …, xn.
Требуется проверить выполнение нулевой гипотезы
Н0: случайная величина (генеральная совокупность)
распределена
по
нормальному
закону
при
альтернативной гипотезе Н1: случайная величина не
распределена по нормальному закону распределения.

19. Проверка нормальности распределения по критерию моментов

Этот критерий является приближенным и связан с
оценкой центральных моментов 3-го и 4-го порядков.
Для нормального распределения центральный момент
третьего порядка
3
3 M X M ( X ) 0,
а момент четвертого порядка
4
4 M X M ( X ) 3 ( x).
Если для изучаемого распределения моменты 3-го и
4-го порядков несущественно отличаются от значений
определяемых выражениями, то распределение можно
считать нормальным.

20.

Для оценки нормальности распределения
критерию моментов вводятся две характеристики:
Асимметрия теоретического распределения
3
3
AX 3 , где 3 M X M ( X ) ,
X
по
которая характеризует асимметричность нормального
распределения.
Если
кривая
нормального
распределения
симметрична, то АХ=0.
Если длинная часть кривой слева, то АХ<0, если
длинная часть кривой справа, то АХ>0.
Выборочная асимметрия определяется по формуле:
1 n
3
AB
x x ni .
3 i
n X i 1

21.

Эксцесс теоретического распределения
4
4
E X 4 3, где 4 M X M ( X ) 3 ( x),
X
который характеризует крутость кривой нормального
распределения.
Для кривой нормального распределения ЕХ=0.
Если кривая имеет острую вершину (вытянута), то
ЕХ>0, а если кривая пологая, то есть имеет плоскую
вершину, то ЕХ<0.
Выборочный эксцесс определяется по формуле:
1 n
4
EB
x x ni 3.
4 i
n B i 1

22.

Для
оценки
нормальности
распределения
вычисляется:
6( n 1)
Дисперсия асимметрии DА
.
(n 1)( n 3)
24n(n 2)(n 3)
.
Дисперсия эксцесса DE
2
(n 1) (n 3)(n 6)
Случайная
величина
имеет
нормальное
распределение (выполняется нулевая гипотеза), если
выполняются одновременно неравенства:
AB 3 DA ,
EB 5 DE .
Если хотя бы одно из неравенств не выполняется, то
гипотеза о нормальности распределения отвергается.

23. Проверка нормальности распределения по критерию χ2-Пирсона

В
качестве
проверки
нулевой
гипотезы
рассматривается случайная величина
2
ni ni
k
2
,
i 1
ni
где k – число интервалов; ni – эмпирические частоты;
ni'- теоретические частоты.
Величина 2 показывает, что чем меньше отличаются
между собой эмпирические и теоретические частоты,
тем меньше эта величина. Возведение в квадрат разности
частот устраняет возможность взаимного погашения
положительных и отрицательных разностей.

24.

Величина 2 распределена по закону 2 –Пирсона,
который при n→ стремится к нормальному закону.
Случайная величина распределена по нормальному
закону, если
2
набл
kp2 , ,
2
где kp , – критическое значение распределения
2–Пирсона, определяемое по таблице критических
точек распределения 2 при заданном уровне
значимости и числу степеней свободы k 3.

25.

Применение
критерия
2–Пирсона
требует
представления
исходной
выборки
в
виде
последовательности
интервалов
с
определением
эмпирической частоты ni и нормированных границ
интервалов:
xi x
zi
.
B
При этом теоретические частоты определяются по
выражению
ni npi ,
где pi – вероятность попадания случайной величины Х
в интервал (xi, xi+1), определяемая формулой:
pi ( zi 1 ) ( zi ),
Ф(z) – функция Лапласа.

26.

Пример. Проверить гипотезу о нормальности
распределения случайной величины Х с эмпирическим
распределением выборки объема n=200 по критерию
моментов и по критерию 2– Пирсона.
xi
0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
ni
6
9
26
25
30
26
21
24
20
8
5
Решение:
1. По критерию моментов:
Определим число интервалов: k n 11.
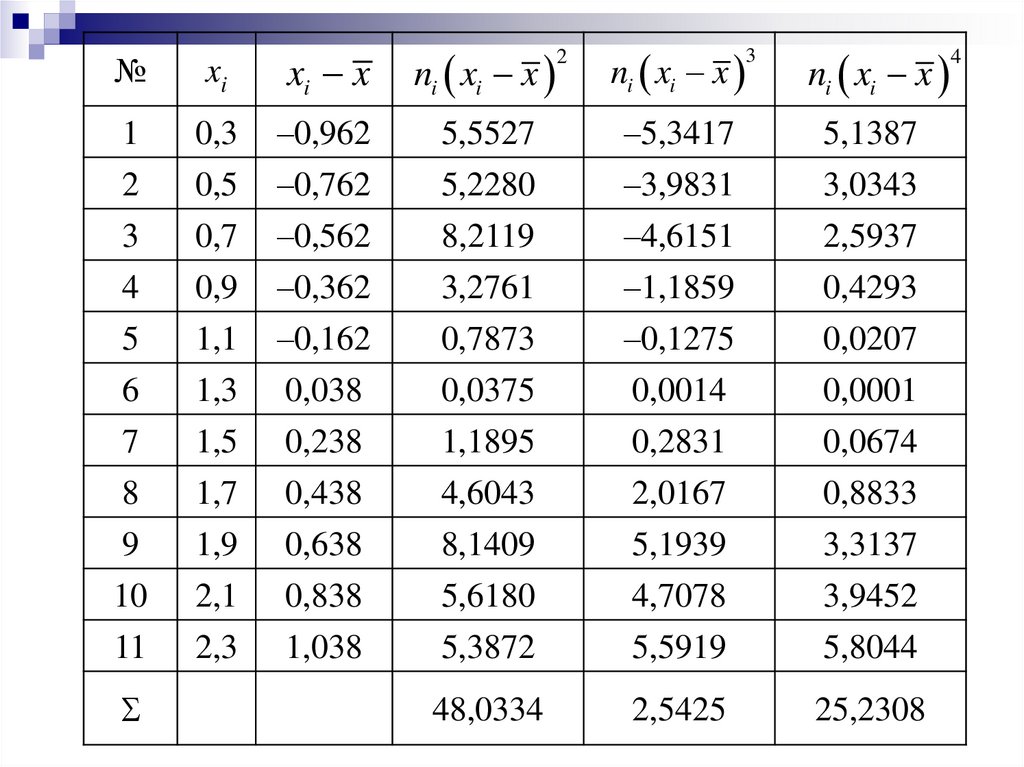
Для расчета асимметрии и эксцесса составим
вспомогательную таблицу, предварительного вычислив
x 1.262.

27.

№
xi
xi x
ni xi x
1
2
0,3
0,5
–0,962
–0,762
5,5527
5,2280
–5,3417
–3,9831
5,1387
3,0343
3
4
5
0,7
0,9
1,1
–0,562
–0,362
–0,162
8,2119
3,2761
0,7873
–4,6151
–1,1859
–0,1275
2,5937
0,4293
0,0207
6
1,3
0,038
0,0375
0,0014
0,0001
7
8
1,5
1,7
0,238
0,438
1,1895
4,6043
0,2831
2,0167
0,0674
0,8833
9
10
11
1,9
2,1
2,3
0,638
0,838
1,038
8,1409
5,6180
5,3872
5,1939
4,7078
5,5919
3,3137
3,9452
5,8044
48,0334
2,5425
25,2308
2
ni xi x
3
ni xi x
4

28.

1 k
48.0334
2
DB ni ( xi x )
0.24017,
n i 1
200
B 0.24017 0.49.
Определим асимметрию:
1 n
2.5425
3
AB
x x ni
0.1081.
3 i
3
n B i 1
200 (0.49)
Определим эксцесс:
1 k
4
EB
x x ni 3
4 i
n B i 1
1
25.2308 3 0.8117.
4
200 (0.49)

29.

Вычислим дисперсию асимметрии и эксцесса:
6(n 1)
6 199
DА
0.02926,
(n 1)(n 3) 201 203
24n(n 2)(n 3)
24 200 198 197
DE
0.1108.
2
2
(n 1) ( n 3)( n 6) (201) 203 206
Проверим условия выполнения нулевой гипотезы
AB 0.1081 3 DA 3 0.02926 3 0.171 0.513,
EB 0.8117 5 DE 5 0.1108 5 0.3329 1.6645.
Оба условия выполнены, следовательно, выборка
распределена по нормальному закону распределения.

30.

2. По критерию 2 – Пирсона.
Если считать xi в данной задаче серединными
значениями, то имеем следующее статистическое
распределение:
xi
ni
0,2-0,4 0,4–0,6 0,6–0,8 0,8–1 1–1,2 1,2–1,4 1,4–1,6 1,6–1,8 1,8–2 2–2,2 2,2–2,4
6
9
26
25
Используя формулу
30
zi
26
xi x
B
21
24
20
8
получим значения
нормированных значений границ интервалов:
0.2 1.262
0.4 1.262
z1
2.17, z2
1.76,
0.49
0.49
0.6 1.262
z3
1.35 и так далее.
0.49
5

31.

Определим pi:
p1 ( z2 ) ( z1 ) ( 1.76) ( 2.17)
(1.76) (2.17) 0.4608 0.485 0.0242;
p2 ( z3 ) ( z2 ) ( 1.35) ( 1.76)
(1.35) (1.76) 0.4115 0.4608 0.0493;
Теоретические значения частот ni' определяем по
формуле ni npi
n1 np1 200 0.0242 4.84,
n2 np2 200 0.0493 9.86, и так далее.
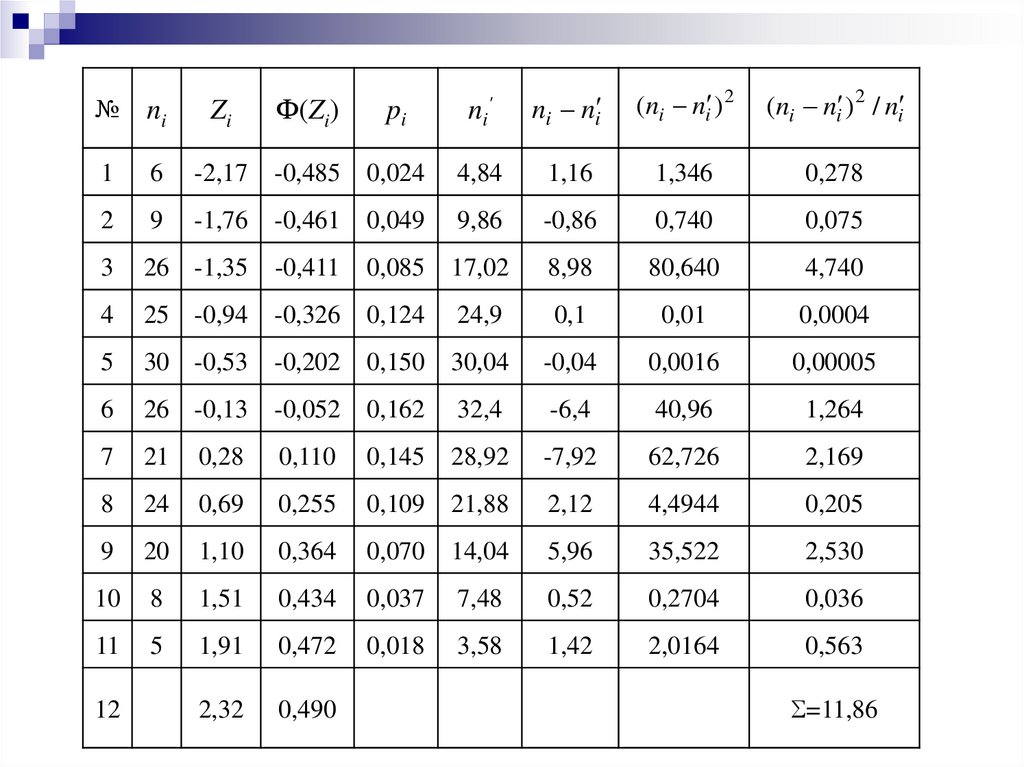
Результаты расчетов заносим в таблицу.

32.

№
ni
Zi
Ф(Zi)
pi
n i'
ni ni
(ni ni ) 2
(ni ni ) 2 / ni
1
6
-2,17
-0,485
0,024
4,84
1,16
1,346
0,278
2
9
-1,76
-0,461
0,049
9,86
-0,86
0,740
0,075
3
26 -1,35
-0,411
0,085
17,02
8,98
80,640
4,740
4
25 -0,94
-0,326
0,124
24,9
0,1
0,01
0,0004
5
30 -0,53
-0,202
0,150
30,04
-0,04
0,0016
0,00005
6
26 -0,13
-0,052
0,162
32,4
-6,4
40,96
1,264
7
21
0,28
0,110
0,145
28,92
-7,92
62,726
2,169
8
24
0,69
0,255
0,109
21,88
2,12
4,4944
0,205
9
20
1,10
0,364
0,070
14,04
5,96
35,522
2,530
10
8
1,51
0,434
0,037
7,48
0,52
0,2704
0,036
11
5
1,91
0,472
0,018
3,58
1,42
2,0164
0,563
2,32
0,490
12
=11,86

33.

n n
По формуле
определим как
2
k
2
i
i
2
ni
2
сумму последнего столбца таблицы набл 11.86.
i 1
Определим
по
таблице
критических
точек
распределения 2 – Пирсона критическое значение
kp2 kp2 , ,
где =0.05, =11–3=8.
Для =8
kp2 15.5
2
набл
kp2 11.86 15.5,
Так как
распределена по нормальному закону.
то выборка