Похожие презентации:
Проверка статистических гипотез
1. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
12. ОСНОВНЫЕ ПОНЯТИЯ
Определение: Статистической гипотезой называется любое предположение о видеили параметрах неизвестного закона распределения генеральной совокупности
Определение: Подлежащую проверке гипотезу будем называть основной или нулевой
и обозначать Н0.
Определение: Конкурирующей (альтернативной) гипотезой (Н1) будем называть
гипотезу противоположную нулевой.
Определение: Гипотеза называется простой, если она однозначно характеризует
параметр или свойство генеральной совокупности, например Н0: 0 ; или Н0:
N (m , 2 ) - генеральная совокупность распределена по нормальному закону). В
противном случае гипотеза называется сложной. Например Н0: 0 1 или Н0:
N (m , 2 ) закон распределения СВ отличен от нормального
Определение: Статистические гипотезы относительно неизвестного истинного
значения параметра распределения называют параметрическими гипотезами.
Определение: Статистические гипотезы о характере распределения генеральной
совокупности называются непараметрическими гипотезами.
Определение: Критерием, или статистическим критерием, проверки гипотез
называют однозначно определенное правило, по которому по данным апостериорной
выборки принимается решение о справедливости Н0 или Н1 гипотез (т.е. проверяемую
гипотезу Н0 следует либо принять, либо отклонить)
2
3.
ВЫБОРОЧНОЕ ПРОСТРАНСТВООпределение:
вектора 1,n .
Выборочное пространство – это множество всех возможных значений
W W - выборочное пространство;
W - критическая область (область отклонения гипотезы Н0);
W - область принятия гипотезы Н0.
Если выборка x1,n W , то - гипотеза Н0 отвергается и принимается гипотеза Н1.
Если выборка x1,n W , то- гипотеза Н1 отвергается и принимается гипотеза Н0.
3
4. КРИТИЧЕКИЕ ТОЧКИ
Пусть из генеральной совокупности значений СВ извлечена выборка объемом n ивычислена статистика ˆ( 1,n ) , точное или приближенное распределение которой известно,
как правило определяет меру расхождения выборочных данных с высказанной гипотезой
Н0.
Затем по этому выборочному распределению определяется критическое значение кр ,
которое все множество возможных значений статистики n* будем разбивать на два
непересекающихся подмножества (области): критическую область W (область отклонения
гипотезы) и область принятия решений W (гипотезы).
W
кр
W
Точки, разделяющие критическую область и область принятия решения, будем
называть критическими.
Наша задача, научиться находить критические точки.
4
5. КРИТИЧЕСКАЯ ОБЛАСТЬ
Зададимся достаточно малой величиной " ", называемой уровнем значимостикритерия и определим критическую область (обозначим W ), как множество таких
значений ˆ( 1,n ) , вероятность попадания которых в W равнялась бы " ", то есть
P( ˆ( 1,n ) W )
если, полученное по данным выборки, значения статистики критерия попадают в
критическую область ˆ( 1,n ) W , то гипотезу Н0 отвергают
если наблюденные значения статистики критерия не попадают в критическую
область ˆ( 1,n ) W , т.е. ˆ( 1,n ) W то гипотезу Н0 не отвергают (принимают).
5
6. ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА
Определение: Уровнем значимости 1 называютсовершить ошибку первого рода P( ˆ ( 1,n W / H 0 ) min
вероятность
Определение: Мощностью статистического критерия называют величину
1 , равную вероятности отклонить основную гипотезу H 0 , когда она
неверна (т.е. вероятность не совершить ошибку второго рода)
P( ˆ ( 1,n W / H1 ) 1 max
6
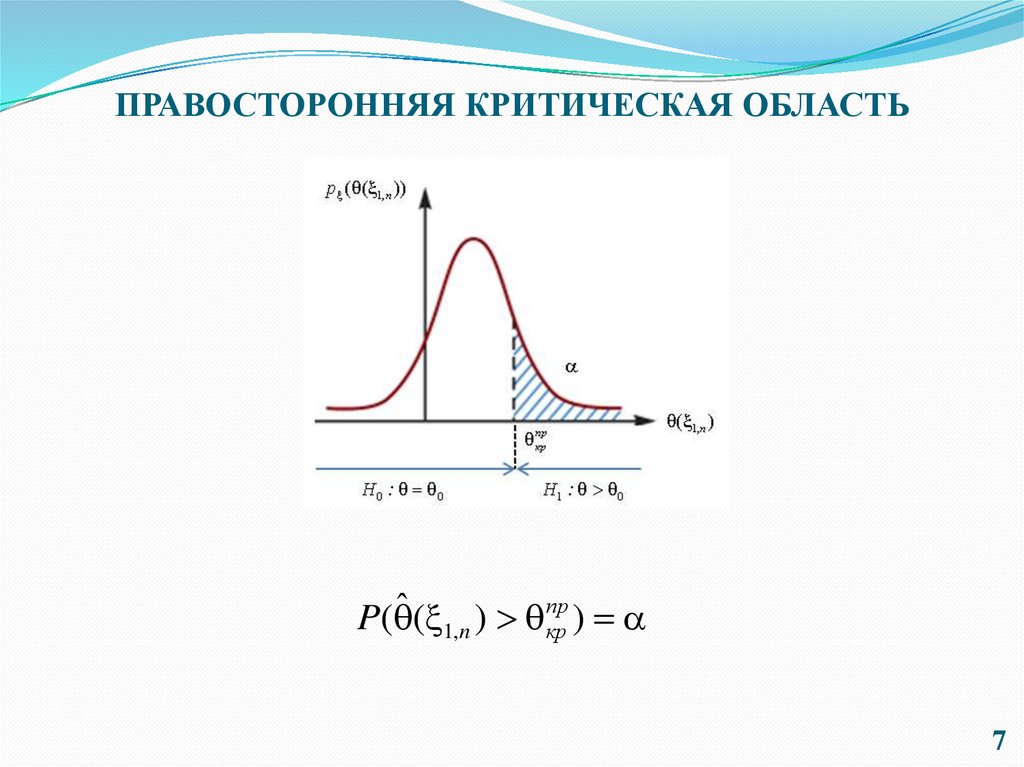
7. ПРАВОСТОРОННЯЯ КРИТИЧЕСКАЯ ОБЛАСТЬ
P( ˆ ( 1,n ) пркр )
7
8.
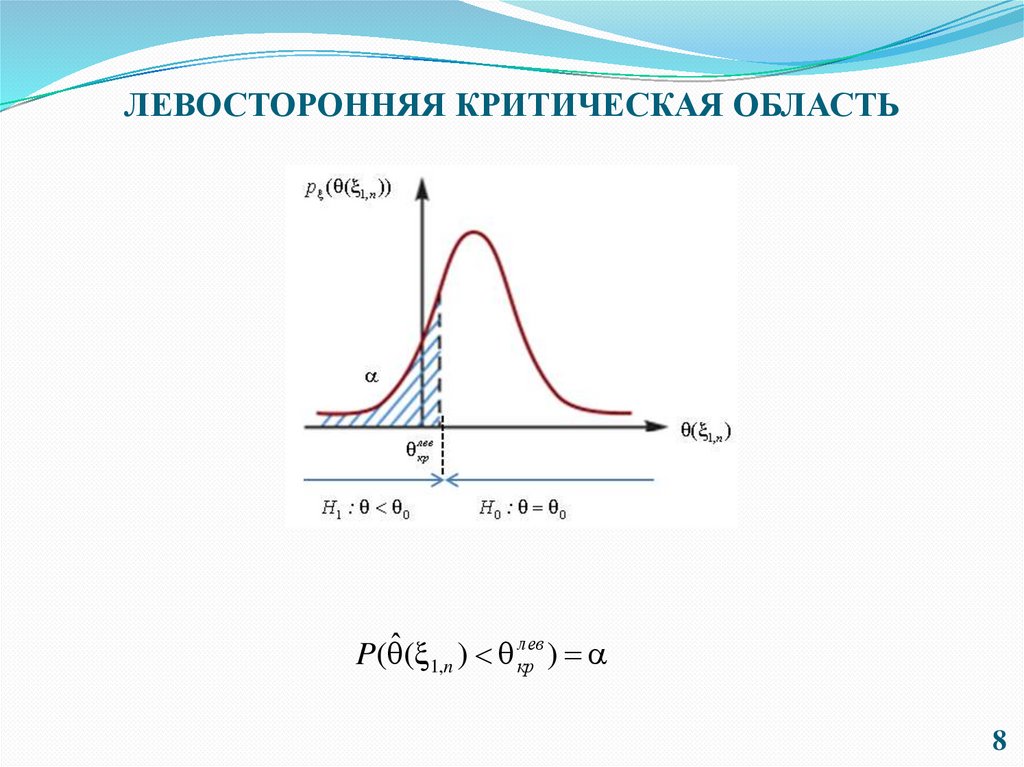
ЛЕВОСТОРОННЯЯ КРИТИЧЕСКАЯ ОБЛАСТЬлев
P( ˆ ( 1,n ) кр
)
8
9. ДВУСТОРОННЯЯ КРИТИЧЕСКАЯ ОБЛАСТЬ
P( ˆ ( 1,n ) kp1 )2
P( ˆ ( 1,n ) kp 2 )
2
9
10. ПРОВЕРКА НЕПАРАМЕТРИЧЕСКИХ ГИПОТЕЗ
1011. Постановка задачи
Пусть - СВ (дискретная или непрерывная) с неизвестным законом распределения вформе функции распределения F (x) или плотности распределения p (x) ;
1,n ( 1 , 2 ,... n ) - априорная случайная повторная выборка с взаимно независимыми и
одинаково распределенными компонентами;
х1,n ( x1 , x2 ,..xn ) - реализация случайной выборки 1, n
эмпирические Fˆn ( x) и/или pˆ n ( x);
на основе, которой получены
F0 ( x) - предполагаемая функция распределения генеральной совокупности;
p0 ( x) - предполагаемая плотность распределения генеральной совокупности.
Требуется выяснить, согласуется ли гипотеза H 0 : F0 ( x) или H 0 : p0 ( x) с полученными
экспериментальными данными x1,n или не согласуется.
11
12. НЕПАРАМЕТРИЧЕСКИЕ ГИПОТЕЗЫ: ОБЩИЙ СЛУЧАЙ
На основе гистограммы или полигонараспределения генеральной совокупности:
H 0 : F0 ( x)
H 1 : F0 ( x)
или
выдвигается
гипотеза
о
характере
H 0 : p 0 ( x)
H 1 : p 0 ( x)
12
13. НЕПАРАМЕТРИЧЕСКИЕ ГИПОТЕЗЫ: ЧАСТНЫЕ СЛУЧАИ
H 0 : Распределение СВ не отличается от нормального H 0 : N (m, 2 )H 1 : Распределение СВ отличается от нормального H1 : N (m, 2 )
H 0 : Закон распределения не отличается от экспоненциального F (x) или p (x) ,
H 1 : Закон распределения отличается от экспоненциального F (x) или p (x) ,
1 e x , x 0
где F ( x)
0,
x 0
e x , x 0
p ( x )
x 0
0,
H 0 : Закон распределения не отличается от равномерного F (x) или p (x) ,
H 1 : Закон распределения отличается от равномерного F (x) или p (x) ,
x a
0,
x a
где F ( x)
, a x b
b a
x b
1,
1
, x [ a, b]
p ( x ) b a
0, x [a, b]
13
14. КРИТЕРИЙ СОГЛАСИЯ
Для статистической проверки гипотез о теоретическом (модельном) виде законараспределения вероятностей исследуемой случайной величины используют критерии
согласия.
Критериями согласия называют статистические критерии, предназначенные для
обнаружения
расхождения
между
гипотетической
статистической
моделью
(теоретическим распределением) и реальными данными, которые эта модель призвана
описать.
Пусть статистика T ( 1,n ), являющаяся случайной величиной, характеризующей меру
отклонения эмпирического закона распределения от гипотетического (статистический
критерий);
t - критическое значение, отделяющее область принятия гипотезы H 0 от
критической области, и определяемое из условия:
Р(T ( 1,n ) t )
где - уровень значимости нулевой гипотезы ( 0,01; 0,05; 0,001; 0,005 )
Если
испытаний
если
испытаний
значение статистики
T ( х1,n ) t , то гипотеза
значение статистики
T ( х1,n ) t , то гипотеза
критерия, найденной по результатам проведенных
H 0 отвергается;
критерия, найденной по результатам проведенных
H 0 принимается.
14
15. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
(niЭ niТ ) 2 k (niЭ np0i ) 22 (k r 1)
Строится статистика: ( 1,n )
Т
np0i
ni
i 1
i 1
k
2
где niЭ – эмпирическая частота - частота варианты хi дискретного вариационного ряда
или число вариант, которые находятся в i ом интервале интервального вариационного
ряда;
k - число возможных вариант дискретного вариационного ряда или число
интервалов интервального вариационного ряда;
niТ или np 0i – теоретическая частота.
p 0i - вероятность наблюдения варианты xi или вероятность попадания исследуемой
случайной величины в i ый интервал интервального вариационного ряда
k
p
i 1
i
1
В случае проверки гипотезы о нормальном характере распределения вычисляются
по интегральной теореме Лапласа
V xB
V xB
р0i P(Vi 1 Vi ) i 1
i
S
S
В случае равномерного закона распределения
р0i P(Vi 1 x Vi )
Vi Vi 1
, где a V0 , b Vk , все вероятности должны
b a
иметь одинаковые значения
В случае экспоненциального закона распределения
р0i P(Vi 1 x Vi ) e Vi 1 e Vi
15
16. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА: ПРОДОЛЖЕНИЕ
r - число параметров предполагаемого теоретического законаВ случае нормального закона распределения r 2 ( m , 2 )
В случае равномерного закона распределения r 2 ( a, b )
В случае показательного закона распределения r 1 ( )
Для проверки гипотезы H 0 строим двухстороннюю критическую
область, критические точки определяются из уравнений:
, откуда 2kp 2 Pi 1 ( )
2
2
P( 2 2kp1 ) , откуда 2kp1 Pi 1 (1 )
2
2
P ( 2 2kp 2 )
Если
x kp2 1 (1
, k r 1) 2набл 2kp 2 ( , k r 1) ,
2
2
то
гипотеза
H0
принимается и делается вывод в пользу проверяемого закона распределения,
в противном случае гипотезу Н0 следует отклонить.
16
17. ПРОВЕРКА НЕПАРАМЕТРИЧЕСКОЙ ГИПОТЕЗЫ: ПРИМЕР
Имеются сгруппированные данные о дневной выручке в магазинеэлектротоваров.
Сумма
продаж
190-200
200-210
210-220
220-230
230-240
240-250
Число
продаж
10
26
56
64
30
14
70
60
50
40
30
20
10
0
190-200 200-210 210-220 220-230 230-240 240-250
Требуется проверить гипотезу о характере распределения СВ - сумма
продаж ( 0,05 )
По виду гистограммы можно предположить, что СВ распределена по
нормальному закону. Проверим данное предположение.
H 0 : Распределение СВ не отличается от нормального
H1 : Распределение СВ отличается от нормального
17
18. ПРОВЕРКА НЕПАРАМЕТРИЧЕСКОЙ ГИПОТЕЗЫ: ПРИМЕР продолжение
Для проверки гипотезы воспользуемся статистикой Пирсона :(niЭ niТ ) 2 k (niЭ np 0i ) 2
( 1,n )
Т
np 0i
n
i 1
i 1
i
распределена по закону 2 -распределение с числом степеней свободы
k r 1
Vi x B
Vi 1 x B
где р0i P(Vi 1 Vi )
S
S
k
2
Предварительно были определены выборочная средняя и выборочная
дисперсия x 221, S 2 152 , S 12,3
18
19. ПРОВЕРКА НЕПАРАМЕТРИЧЕСКОЙ ГИПОТЕЗЫ: ПРИМЕР продолжение
k(niЭ niТ ) 2
i 1
niТ
Для расчета 2 ( 1, n )
составим таблицу
н2 2,999
x kp2 1 (1
2
, k r 1) Pi 1 (1
2
, k r 1) Pi 1 (0,975,3) 0,22
200 221
190 221
р01 P(190 x 200)
12.3
12.3
( 1.71) ( 2.52) 0.4565 0.4941 0.0376
210 221
200 221
р02 P(200 x 210)
12.3
12.3
( 0.89) ( 1.71) 0.3133 0.4565 0.1432
220 221
210 221
р03 P(210 x 220)
12.3
12.3
( 0,08) ( 0,89) 0,0319 0,3133 0,2814
230 221
220 221
р04 P(220 x 230)
12.3
12.3
(0,73) ( 0,08) 0,2673 0,0319 0,2992
240 221
230 221
р05 P(230 x 240)
12.3
12.3
(1,54) (0,73) 0,4382 0,2673 0,1709
250 221
240 221
р06 P(240 x 250)
12.3
12.3
(2,36) (1,54) 0,4909 0,4382 0,0527
x kp2 2 ( , k r 1) Pi ( , k r 1) Pi (0,025,3) 9,35
2
2
2
2
2
Т.к. x kp
1 x набл x kp2 , гипотеза о нормальном характере распределения
принимается.
19
20.
ПРОВЕРКА ПАРАМЕТРИЧЕСКИХГИПОТЕЗ
ПРОВЕРКА ГИПОТЕЗ О ПАРАМЕТРАХ
НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ
ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
20
21. ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ: ПОСТАНОВКА ЗАДАЧИ
Пусть 1, n - случайная выборка из генеральной совокупности N (m; 2 ) ,где математическое ожидание m неизвестно.
1 n
Точечной оценкой m является выборочное среднее x( 1, n ) i ,
n i 1
1 n
известно значение выборочного среднего x xi .
n i 1
Ставится задача на уровне значимости проверить гипотезу H 0 : m m0 .
21
22.
ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИ МАТЕМАТИЧЕСКОГООЖИДАНИЯ: СЛУЧАЙ 1
Дисперсия 2 известна
Тогда при условии справедливости гипотезы H 0 статистика u ( 1,n )
Пусть H1 : m m0 .
Строим правостороннюю критическую область:
x 1,n m0
P u( 1, n ) uкр.прав ,
n N (0;1) .
1
u кр.прав Ф 1 ( )
2
-
1
u кр.л ев Ф 1 ( )
2
-
определяется по таблице Лапласса. Правосторонняя критическая область имеет вид: (uкр.прав; ) .
Пусть H1 : m m0 .
Строим
левостороннюю
критическую
область:
P u ( 1, n ) uкр.лев ,
определяется по таблице Лапласса. Левосторонняя критическая область имеет вид: ( ; uкр.лев ) .
Пусть H1 : m m0 .
Строим двустороннюю критическую область:
P u ( 1,n ) uкр1 / 2 , P u ( 1,n ) uкр2 / 2 ;
1
1
u кр1 Ф( ) , u кр2 Ф( ) - определяются по таблице Лапласса.
2 2
2 2
Двусторонняя критическая область имеет вид: ( ; uкр1 ) (uкр2 ; ) .
Если uнабл
x m0
n принадлежит критической области, то гипотеза H 0 отвергается с вероятностью
совершить ошибку первого рода .
22
23.
ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИ МАТЕМАТИЧЕСКОГООЖИДАНИЯ: СЛУЧАЙ 2
Дисперсия 2 неизвестна
Тогда
S ( 1,n )
при
условии
справедливости
гипотезы
H0
статистика
t ( 1,n )
x 1,n m0
S 1,n
n 1 ,
где
1 n
2
( i x( 1,n )) имеет распределение Стьюдента с n 1 степенями свободы.
n i 1
Пусть H1 : m m0 . Строим правостороннюю критическую область:
P t ( 1, n ) t кр.прав ; t кр.прав St 1 (2 , n 1) - определяется по таблице Стьюдента с числом степеней свободы
n 1.
Критическая область имеет вид: (tкр.прав; ) .
Пусть H1 : m m0 . Строим левостороннюю критическую область:
P t ( 1, n ) t кр.лев ; t кр.лев St 1 (2 , n 1) - определяется по таблице Стьюдента с числом степеней свободы
n 1.
Левосторонняя критическая область имеет вид: ( ; t кр.лев ) .
Пусть H1 : m m0 . Строим двустороннюю критическую область:
P t ( 1, n ) t кр1 / 2 , P t ( 1, n ) t кр2 / 2 ;
t кр1 St 1 ( , n 1) , t кр2 St 1 ( , n 1) - определяются по таблице Стьюдента с числом степеней свободы n 1 .
Двусторонняя критическая область имеет вид: ( ; t кр1 ) (t кр2 ; ) .
x m0
Если tнабл
S
1 n
2
( xi x ) , принадлежит критической области, то гипотеза H 0 отвергается с
n i 1
23
вероятностью совершить ошибку первого рода .
n 1 , где S
24.
ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИМАТЕМАТИЧЕСКОГО ОЖИДАНИЯ: ПРИМЕР 1
Автоматическая линия фасует пакеты с мукой весом в 1 кг. (1000 грамм). Производитель
утверждает, что точность наладки линии достаточно высока и средний вес наполненных
пакетов в точности равен 1 кг. Покупатель же партии фасованной муки сомневается в
точности веса и выдвигает предположение, что вес пакета меньше одного кг. Проведена
случайная выборка 100 пакетов с мукой. Повторное их взвешивание показало, что
средний выборочный вес пакета x 995 грамм. Предполагается, что известна и равна
10 граммам. На 5%-ом уровне значимости, проверить, прав производитель или
покупатель.
Решение:
Выдвигаем гипотезу H 0 : m 1000
и альтернативную ей H1 : m 1000
x m0
995 1000
n
100 5
10
как m m0 , строится левосторонняя
u набл
Так
критическая область
1
u кр.лев Ф 1 ( ) 1,645
2
Так как u набл u кр.лев Н 0 отвергается m 1000 (прав покупатель, вес пакета с мукой меньше
1 кг)
24
25.
ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИМАТЕМАТИЧЕСКОГО ОЖИДАНИЯ: ПРИМЕР 2
25
26. ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИ ГЕНЕРАЛЬНОЙ ДИСПЕРСИИ: ПОСТАНОВКА ЗАДАЧИ
Пусть 1, n - случайная выборка из генеральной совокупности N (m; 2 ) , снеизвестными параметрами m и 2 .
Точечной оценкой m является выборочное среднее
1 n
x( 1,n ) i , значение
n i 1
1 n
выборочного среднего x xi .
n i 1
2
1 n
Точечной оценкой является выборочная дисперсия S ( 1,n ) i x( 1,n ) ,
n i 1
1 n
2
значение выборочной дисперсии S xi x 2 .
n i 1
2
2
Ставится задача на уровне значимости проверить гипотезу H 0 : 2 02 .
26
27.
ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИ ГЕНЕРАЛЬНОЙДИСПЕРСИИ
Для проверки нулевой гипотезы H 0 используется статистика ( 1,n )
2
nS 2 ( 1,n )
02
которая имеет распределение 2 - Пирсона с числом степеней свободы n 1 .
1 n
, где S ( 1,n ) ( i x( 1,n )) 2 ,
n i 1
2
Пусть H1 : 2 02 . Строим правостороннюю критическую область:
P 2 ( 1,n ) 2 кр.прав ; 2 кр.прав Pi 1 ( , n 1) - определяется по таблице Пирсона с числом степеней свободы
n 1.
Критическая область имеет вид: ( 2 кр.прав ; ) .
Пусть H1 : 2 02 . Строим левостороннюю критическую область:
P 2 ( 1,n ) 2 кр.лев ; 2 кр.лев Pi 1 (1 , n 1) - определяется по таблице Пирсона с числом степеней свободы
n 1.
Левосторонняя критическая область имеет вид: (0; 2 кр.лев ) .
Пусть H1 : 2 02 . Строим двустороннюю критическую область:
P 2 ( 1,n ) 2 кр1 / 2 , P 2 ( 1,n ) 2 кр2 / 2 ;
2 кр1 Pi 1 (1
n 1.
, n 1) , 2 кр2 Pi 1 ( , n 1) - определяются по таблице Пирсона с числом степеней свободы
2
2
Двусторонняя критическая область имеет вид: (0; 2 кр1 ) ( 2 кр2 ; ) .
Если
2
набл
1 n
nS 2
2
2 , где S ( xi x) 2 , принадлежит критической области, то гипотеза H 0 отвергается с
n i 1
0
вероятностью совершить ошибку первого рода .
27
28. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ МАТЕМАТИЧЕСКМХ ОЖИДАНИЙ: ПОСТАНОВКА ЗАДАЧИ
Пусть N (m , 2 ), N (m , 2 ) – нормально распределенные генеральные совокупности сизвестными дисперсиями
( 1 , 2 ,... n )
и
( 1 , 2 ,... n )
2
и 2 и неизвестными математическими ожиданиями
- две случайные выборки из генеральных совокупностей
m
и
m .
и .
– реализация случайной выборки 1,n .
y1,n ( y1 , y2 ,.. yn ) – реализация случайной выборки 1,n .
x1,n ( x1 , x2 ,..xn )
По выборкам (объема n и n ) найдены выборочные оценки: X ( 1,n ) и Y ( 1,n )
Требуется проверить гипотезу: Н0: m m
при одной из альтернативных гипотез
Н1: m m
Н1: m m
Н1: m m .
28
29.
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ МАТЕМАТИЧЕСКМХОЖИДАНИЙ: СЛУЧАЙ 1
Дисперсии 2 и 2 известны
Тогда при условии справедливости гипотезы H 0 статистика u ( 1,n , 1,n )
X ( 1,n ) Y ( 1,n )
2
n
Пусть
H1 : m m .
Строим
правостороннюю
критическую
2
n
область:
N (0,1) .
P u( 1, n ) uкр.прав ,
1
u кр.прав Ф 1 ( ) - определяется по таблице Лапласа. Правосторонняя критическая область имеет вид:
2
(uкр.прав; ) .
Пусть H1 : m m . Строим левостороннюю критическую область: P u ( 1, n ) uкр.лев , uкр.л ев Ф 1 ( )
- определяется по таблице Лапласа. Левосторонняя критическая область имеет вид: ( ; uкр.лев ) .
1
2
Пусть H1 : m m . Строим двустороннюю критическую область:
P u( 1, n ) uкр1 / 2 , P u ( 1, n ) uкр2 / 2 ;
1
1
u кр1 Ф 1 ( ) , u кр2 Ф 1 ( ) - определяются по таблице Лапласа.
2 2
2 2
Двусторонняя критическая область имеет вид: ( ; uкр1 ) (uкр2 ; ) .
Если u набл
X Y
2
n
2
принадлежит критической области, то гипотеза H 0 отвергается с вероятностью
n
совершить ошибку первого рода .
29
30.
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ МАТЕМАТИЧЕСКМХОЖИДАНИЙ: СЛУЧАЙ 2
Дисперсии 2 и 2 неизвестны.
Тогда
при
условии
справедливости
гипотезы
H0
статистика
T
X ( 1,n ) Y ( 1,n )
n S 2 ( 1,n ) n S 2 ( 1,n )
n n
n n
,
где
n n 2
S 2 ( 1,n )
1 n
1 n
( i x( 1,n )) 2 , S 2 ( 1,n ) ( i y ( 1,n )) 2 , имеет распределение Стьюдента с n n 2 степенями свободы.
n i 1
n i 1
Пусть H 1 : m m . Строим правостороннюю критическую область:
P t ( 1, n ) t кр.прав ; tкр.прав St 1 (2 , n n 2) - определяется по таблице Стьюдента с числом степеней свободы
n n 2 .
Критическая область имеет вид: (tкр.прав; ) .
Пусть H1 : m m . Строим левостороннюю критическую область:
P t ( 1, n ) t кр.лев ; tкр.лев St 1 (2 , n n 2) - определяется по таблице Стьюдента с числом степеней свободы
n n 2 .
Левосторонняя критическая область имеет вид: ( ; t кр.лев ) .
Пусть H 1 : m m . Строим двустороннюю критическую область:
P t ( 1, n ) t кр1 / 2 , P t ( 1, n ) t кр2 / 2 ;
tкр1 St 1 ( , n n 2) , t кр2 St 1 ( , n n 2) - определяются по таблице Стьюдента с числом степеней свободы
n n 2 .
Двусторонняя критическая область имеет вид: ( ; t кр1 ) (t кр2 ; ) .
Если t набл
X Y
n S X2 n SY2
n n
n n
, , где S X2
1 n
1 n
( xi x ) 2 , S Y2 ( y i y ) 2 принадлежит критической области, то гипотеза
n i 1
n i 1
n n 2
H 0 отвергается с вероятностью совершить ошибку первого рода .
30
31. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ ДИСПЕРСИЙ: ПОСТАНОВКА ЗАДАЧИ
ПустьN (m , ), N (m , )
генеральные совокупности.
и ( 1 , 2 ,... n ) совокупностей и
( 1 , 2 ,... n )
-
нормально
распределенные
две случайные выборки из генеральных
– реализация случайной выборки 1,n .
y1,n ( y1 , y2 ,.. yn ) – реализация случайной выборки 1,n .
x1,n ( x1 , x2 ,..xn )
По выборкам (объема n и n ) найдены выборочные оценки:
Sˆ 2 ( 1,n ), Sˆ 2 ( 1,n ), (Sˆ 2 ( 1,n ) Sˆ 2 ( 1,n ))
Требуется проверить гипотезу Н0: 2 2
Н1: 2 2 .
31
32. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ ДИСПЕРСИЙ
Строится статистика:Sˆ 2 ( 1,n )
,
F ( 1,n , 1,n ) 2
Sˆ ( ),
которая при справедливости нулевой
1, n
гипотезы распределена по закону Фишера-Снедекора (F-распределение) с
1 n 1 и 2 n 1 степенями свободы.
Для проверки гипотезы строится правосторонняя критическая область из
уравнения: P( F ( x1,n ) Fkp.прав ) , Fkp.прав F 1 ( , nx 1, ny 1) , определяется по таблице
Фишера-Снедекора
Если
Fнабл Fkp.прав ,
то
H0
принимается, если
Fнабл Fkp.прав H 0
отвергается.
32
































 Математика
Математика








