Основы термодинамики. Лекция 04

1.

ОСНОВЫ ТЕРМОДИНАМИКИ
Лекция 04 (18.03.22)
Термодинамика - раздел физики, изучающий закономерности превращения энергии
из одного вида в другой. В основе термодинамики лежат три закона. Они
называются началами и являются обобщением человеческого опыта.
I - ое начало термодинамики выражает закон сохранения и превращения энергии
для тепловых процессов;
II – ое начало связано с необратимостью тепловых процессов;
III - е начало - это тепловая теорема Нернста, из нее следует недостижимость
абсолютного нуля температуры.
После их формулировки стало ясно - вечный двигатель ни I-ого, ни II-ого рода невозможен.
1. Внутренняя энергия U
Внутренняя энергия U - это энергия хаотического (теплового) движения микрочастиц
системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих
частиц.
Внутренняя энергия -однозначная функция термодинамического состояния системы в каждом состоянии система обладает вполне определенной внутренней энергией.
При переходе системы из одного состояния в другое изменение внутренней энергии
определяется только разностью значений внутренней энергии этих состояний и не
зависит от пути перехода.
К внутренней энергии не относятся кинетическая энергия движения системы как
целого и потенциальная энергия системы во внешних полях.
1

2.

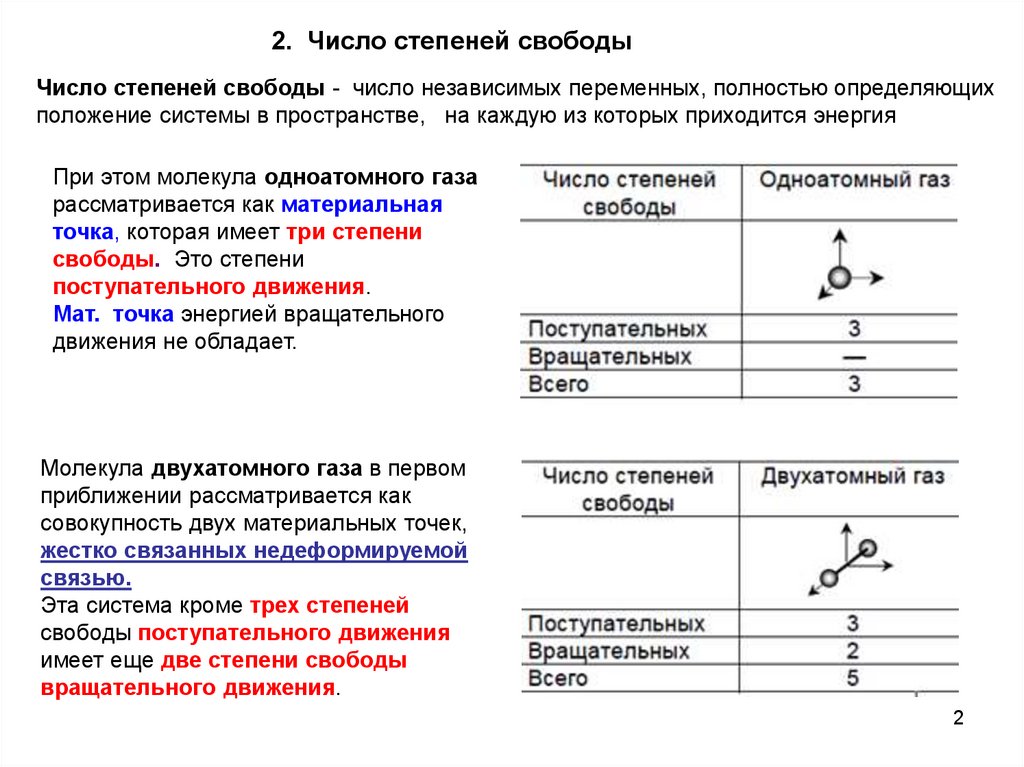
2. Число степеней свободы
Число степеней свободы - число независимых переменных, полностью определяющих
положение системы в пространстве, на каждую из которых приходится энергия
При этом молекула одноатомного газа
рассматривается как материальная
точка, которая имеет три степени
свободы. Это степени
поступательного движения.
Мат. точка энергией вращательного
движения не обладает.
Молекула двухатомного газа в первом
приближении рассматривается как
совокупность двух материальных точек,
жестко связанных недеформируемой
связью.
Эта система кроме трех степеней
свободы поступательного движения
имеет еще две степени свободы
вращательного движения.
2

3.

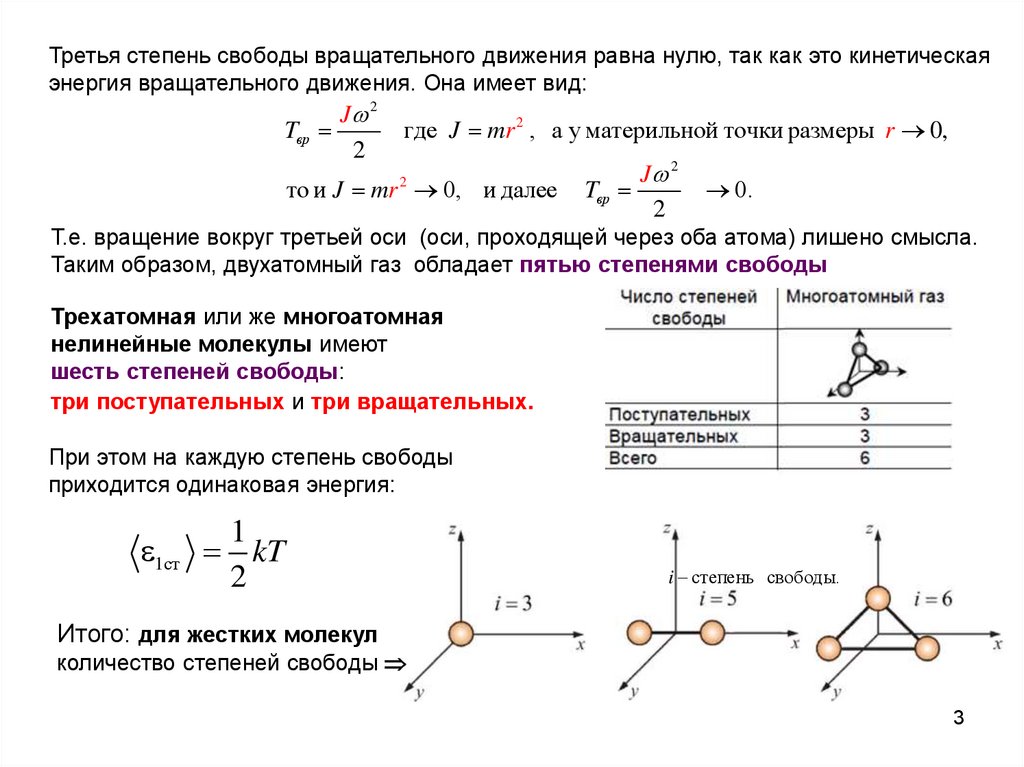
Третья степень свободы вращательного движения равна нулю, так как это кинетическая
энергия вращательного движения. Она имеет вид:
J 2
Tвр
2
где J mr 2 , а у материльной точки размеры r 0,
то и J mr 0, и далее
2
J 2
Tвр
2
0.
Т.е. вращение вокруг третьей оси (оси, проходящей через оба атома) лишено смысла.
Таким образом, двухатомный газ обладает пятью степенями свободы
Трехатомная или же многоатомная
нелинейные молекулы имеют
шесть степеней свободы:
три поступательных и три вращательных.
При этом на каждую степень свободы
приходится одинаковая энергия:
1
1ст kT
2
i степень свободы.
Итого: для жестких молекул
количество степеней свободы
3

4.

В действительности связь между атомами в молекуле упругая.
Жесткой связи между атомами не существует.
Поэтому для реальных молекул (связь между атомами в которых упругая)
необходимо учесть еще и степени свободы колебательного движения. Для
многоатомных
молекул
количество
колебательных
степеней
свободы
определяется количеством нежестких связей в молекуле.
При этом энергия колебательного движения приходится на две степени свободы,
отвечающие за потенциальную и кинетическую энергии, и на каждую из них приходится
та же энергия.
Тогда полная внутренняя энергия одной молекулы, состоящей из 2-ух упруго связанных
атомов равна :
колебат
внутрен.
энергия
пост вращ колеб 3 2
поступ
вращ
кин
потен
7
kT
3
1
Почему решили, что на одну степень свободы приходится энергия: kT
2
Вспомним: согласно основному уравнению молекулярно-кинетической
3
kT
теории газов, средняя кинетическая энергия одной частицы газа равна:
2
При этом, очевидно, что частица имеет три степени свободы и все они поступательные.
Ни одна из поступательных степеней свободы не имеет преимущества перед другими,
поэтому очевидно, что на каждую из них приходится одинаковая энергия, равная одной
трети полной энергии поступательного (кинетического) движения частицы.
Более того, это положение было доказано и обосновано Больцманом.
4

5.

3. Закон Больцмана о равномерном распределении
энергии по степеням свободы молекул
В классической статистической физике выводится закон Больцмана о равномерном
распределении энергии по степеням свободы молекул: для статистической
системы, находящейся в состоянии термодинамического равновесия, на каждую
поступательную и вращательную степени свободы приходится в среднем
кинетическая энергия, равная
kT/2 , а на каждую колебательную степень свободы -
в среднем энергия, равная: kT
Колебательная степень "обладает" вдвое большей энергией потому, что на нее
приходится не только кинетическая энергия (как в случае поступательного и
вращательного движений), но и потенциальная, причем средние значения
кинетической и потенциальной энергий одинаковы.
Таким образом, средняя
энергия молекул :
i
kT
2
i - сумма числа поступательных, числа
где - вращательных и удвоенного числа
колебательныхстепеней свободы молекул
i iпост iвращ 2iколеб
В классической теории рассматривают молекулы с жесткой связью между атомами;
для них i совпадает с числом степеней свободы молекулы.
5

6.

Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю
(молекулы между собой не взаимодействуют), то внутренняя энергия, отнесенная к
одному молю газа, будет равна сумме кинетических энергий
i
i
U N A kTN A RT
2
2
NA молекул
mi
i
Для произвольной
Um
RT RT
массы газа m
2
2
6

7.

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики - это закон сохранения и превращения энергии в
термодинамических процессах.
Изменить внутреннюю энергию системы можно:
совершая над системой работу (например, сжимая газ в цилиндре);
сообщая системе теплоту (например, нагревая газ ).
В термодинамике при переходе замкнутой системы из одного энергетического
состояния 1 в другое состояние 2, механическая энергия не изменяется, а изменяется
лишь ее внутренняя энергия.
Внутреннюю энергию системы можно изменить (результаты наблюдений) в
результате некоторых процессов, например, совершения над системой работы
или сообщения ей теплоты.
1) При вдвигании поршня в цилиндр, в котором находится газ, газ сжимается, в
результате чего его температура повышается, т.е. тем самым изменяется
(увеличивается) внутренняя энергия газа.
2) Температуру газа и его внутреннюю энергию можно увеличить за счет сообщения
газу некоторого количества теплоты - энергии, переданной системе внешними телами
путем теплообмена (процесс обмена внутренними энергиями при контакте тел с
разными температурами).
7

8.

Т.Е. говорим о двух формах передачи энергии от одних тел к другим: работе и
теплоте. Энергия механического движения может превращаться в энергию
теплового движения, и наоборот. При этих превращениях соблюдается закон
сохранения и превращения энергии.
Этим законом и является первое начало термодинамики, установленное в
результате обобщения многовековых опытных данных.
Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем),
обладая внутренней энергией U 1 , получила количество теплоты Q и, перейдя в
новое состояние, характеризующееся внутренней энергией U 2 , совершила работу
A над внешней средой, т.е. против внешних сил.
Количество теплоты считается положительным, когда оно подводится к системе,
а работа - положительной, когда система совершает ее против внешних сил.
Опыт показывает, что в соответствии с законом сохранения энергии при любом способе
перехода системы из первого состояния во второе изменение внутренней энергии:
U U 2 U1
будет одинаковым и равным разности между количеством теплоты, полученным
системой, и работой, совершенной системой против внешних сил:
Q U A
8

9.

Это уравнение выражает первое начало термодинамики: теплота, сообщаемая
системе, расходуется на изменение ее внутренней энергии и на совершение
ею работы против внешних сил. Вид уравнения в дифференциальный форме:
d ' Q dU d ' A или Q dU A
где dU - бесконечно малое изменение внутренней энергии
системы (полный дифференциал) Дж ; A элементарная работа Дж ;
Q бесконечно малая добавка к системе Дж . Дж
Таким
образом
Если система периодически возвращается в первоначальное состояние,
то его внутренняя энергия не изменяется: dU 0
.
Тогда, согласно этому первому началу термодинамики A Q
Вывод. Вечный двигатель первого рода - периодически действующий двигатель,
который совершал бы большую работу, чем сообщенная ему извне энергия, невозможен.
9

10.

Внутренняя энергия системы является однозначной функцией состояния системы,
теплота и работа являются функциями процесса.
РАБОТА ГАЗА ПРИ ЕГО РАСШИРЕНИИ.
10

11.

11

12.

Теплоемкость идеального газа
Экспериментальный факт - внутренняя энергия U
идеального газа зависит только от температуры Т:
U
T
Коэффициент пропорциональности (теплоемкость) зависит от рода газа.
Теплоемкость С тела (газа) - количество тепла, которое
нужно сообщить телу, чтобы повысить температуру на
один кельвин:
Q
CТела
dT
Теплоемкость - функция процесса.
Q
Дж
Молярная теплоемкость : C
; единица моль К
dT
C
m Q
Дж
Удельная теплоемкость : с
; ед - ца кг К
mdT
молярная масса; m масса
12

13.

Молярная теплоемкость при постоянном объеме.
т.е. dU CV dT
13

14.

Молярная теплоемкость при постоянном давлении. Уравнение Майера
14

15.

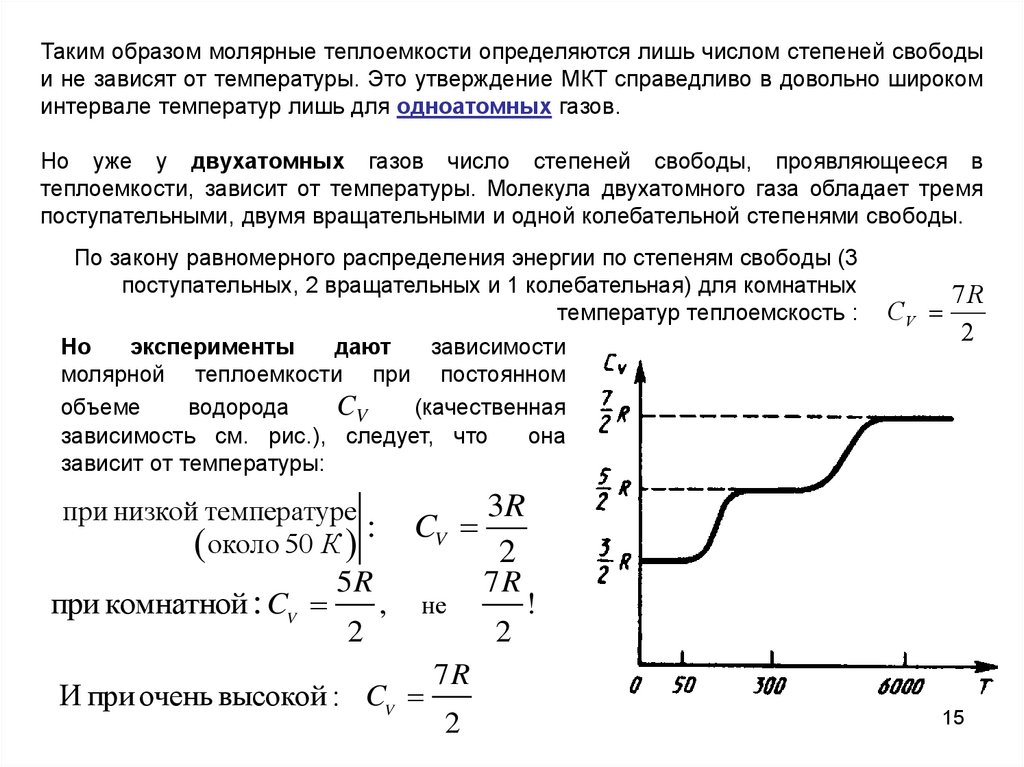
Таким образом молярные теплоемкости определяются лишь числом степеней свободы
и не зависят от температуры. Это утверждение МКТ справедливо в довольно широком
интервале температур лишь для одноатомных газов.
Но уже у двухатомных газов число степеней свободы, проявляющееся в
теплоемкости, зависит от температуры. Молекула двухатомного газа обладает тремя
поступательными, двумя вращательными и одной колебательной степенями свободы.
По закону равномерного распределения энергии по степеням свободы (3
поступательных, 2 вращательных и 1 колебательная) для комнатных
температур теплоемскость :
Но
эксперименты
дают
зависимости
молярной теплоемкости при постоянном
объеме
водорода
CV
(качественная
зависимость см. рис.), следует, что
она
зависит от температуры:
при низкой температуре
около 50 К :
3R
CV
2
5R
7R
при комнатной : CV
,
не
2
И при очень высокой : CV
CV
7R
2
!
2
7R
2
15

16.

Это можно объяснить, предположив, что при температурах:
низких наблюдается только поступательное движение молекул;
комнатных - добавляется их вращение,
высоких - к этим двум видам движения добавляются еще и колебания молекул.
Объяснение
расхождения
теории
и
эксперимента.
При
вычислении
теплоемкости надо учитывать квантование энергии вращения и колебаний
молекул (т.е. возможны не любые вращательные и колебательные энергии, а
лишь определенный дискретный ряд значений энергий). Если энергия теплового
движения недостаточна, например, для возбуждения колебаний, то эти колебания
не вносят своего вклада в теплоемкость
(соответствующая степень свободы
"замораживается" - к ней не применим закон равнораспределения энергии). Этим
объясняется, что теплоемкость моля двухатомного газа – водорода - при
комнатной температуре равна
5R / 2 вместо 7R / 2
.
Аналогично можно объяснить уменьшение теплоемкости при низкой температуре
("замораживаются" вращательные степени свободы) и увеличение при высокой
("возбуждаются" колебательные степени свободы).
16

17.

Среди равновесных процессов, происходящих с
термодинамическими системами, выделяют изопроцессы, при
которых один из основных параметров состояния системы
сохраняется постоянным.
Применим первое начало термодинамики к изопроцессам
ИЗОПРОЦЕССЫ.
Установим, какие параметры I-го начала термодинамики претерпевают
изменения в том или ином изопроцессе.
Изохорный процесс (V = const).
17

18.

Изобарный процесс (р = const)
В изобарном процессе при сообщении газу массой m количества теплоты
Q
m
C p dT его внутренняя энергия возрастает на величину dU
и совершает работу, определяемую выражением dA
m R
m
CV dT
dT
18

19.

Изотермический процесс (T = const)
При этом dU
m
CV dT 0
Следовательно, для того чтобы при расширении газа температура не понижалась, к
газу в течение изотермического процесса необходимо подводить количество
теплоты, эквивалентное внешней работе расширения.
Рассмотренные изопроцессы вытекают из экспериментальных законов ГейЛюссака и Бойля – Мариотта, но формулирование еще одного закона – первого
19
закона термодинамики привело к пониманию, что есть еще изопроцессы…

20.

Адиабатический процесс ( Q =0)
Это процесс, при котором отсутствует
теплообмен между системой и окружающей средой.
Адиабатические процессы - это все быстропротекающие процессы (теплообмен не
успевает совершиться).
Например, распространение звука в среде, так как скорость распространения звуковой
волны настолько велика, что обмен энергией между волной и средой произойти не
успевает. К адиабатическим процессам относятся и циклы расширения и сжатия в
двигателях внутреннего сгорания, в холодильных установках и т. д.
Тогда первое начало термодинамики : Q dU A примет вид 0 dU A или
A dU , а с учетом явного вида работы A pdV и внутренней энергии dU СV dT
СV dT pdV для любого количества газа :
pdV
m
CV dT
т.е. в этом процессе внешняя работа газа (взаимодействие газа со внешней
средой) совершается за счет изменения внутренней энергии системы.
Продифференцировав уравнение состояния идеального газа
pdV Vdp
m
p dV
RdT , а из dT
m CV
pV
m
RT
pdV Vdp
получим :
m p dV
R
m CV 20

21.

и далее
C p CV
pdV Vdp
R
;
p dV
CV
CV
R
pdV Vdp
p dV ;
CV
СP
Vdp;
1
1. Разделим переменные
p dV
CV
Учитывая, что
Cp
CV
dp dV СP
.
p
V CV
dp
dV
.
p
V
получим
это дифференциальное уравнение в пределах от
Интегрируя
p1 до
p2 , и
p2
V2
соответственно от V1 до V2 , получим : ln
ln
p1
V1
а затем потенциря и перегруппировывая придем к выражению :
p2 V1
p1 V2
или
p1V1 p2V2
Полученное выражение -уравнение адиабатического процесса,
или уравнение Пуассона
21

22.

22