Физическая кинетика (лекция 16)

1.

Физическая кинетика
Парфентьева Наталия Андреевна

2.

При нарушении равновесного состояния возникают потоки молекул, теплоты и т.д.
т.к. система снова стремится к нему вернуться.
Энтропия системы возрастает.
Термодинамический поток — поток вещества, энергии, импульса, заряда и
пр. из одной части среды, находящейся в неравновесном состоянии, в
другую часть среды с установлением равновесного состояния. При наличии
в среде различной концентрации какой-либо примеси возникают
диффузионные потоки, в случае
разной температуры — тепловые потоки, при различной скорости
течения — поток импульса.
Три явления переноса – диффузия, теплопроводность и внутреннее трение.
Молекулы, двигаясь хаотически, переносят соответствующую им кинетическую
энергию, массу и импульс направленного движения.
Явления переноса наблюдаются тогда, когда в пространстве есть неравномерное
распределение температуры, концентрации или скорости направленного движения
слоев газа или жидкости.

3.

Феноменологическая теория явлений переноса
1. Теплопроводность
dT
q = kT
dx
1 dQ
q=
ΔS dt
q kT gradT – закон Фурье

4.

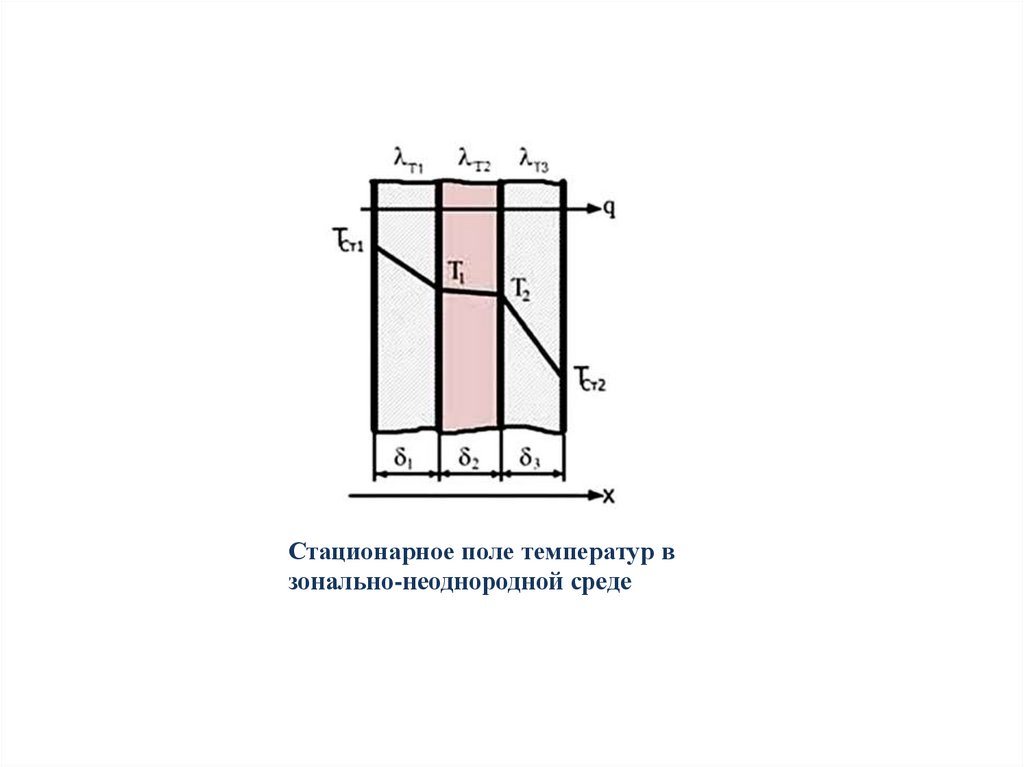
Стационарное поле температур в
зонально-неоднородной среде

5.

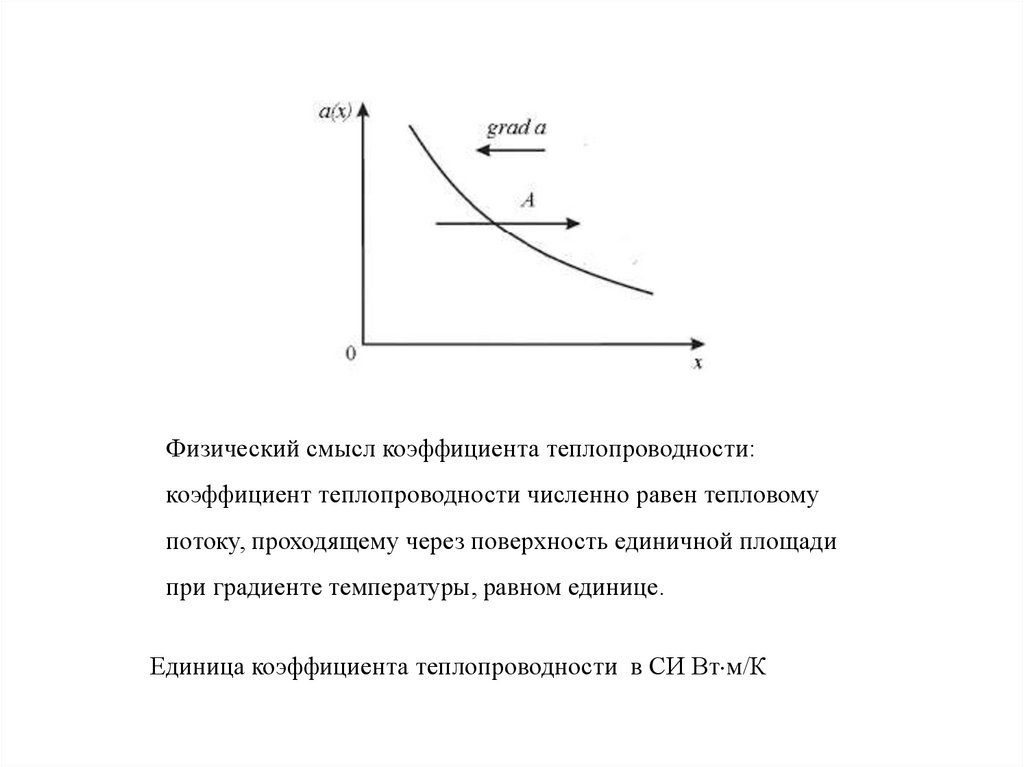
Физический смысл коэффициента теплопроводности:
коэффициент теплопроводности численно равен тепловому
потоку, проходящему через поверхность единичной площади
при градиенте температуры, равном единице.
Единица коэффициента теплопроводности в СИ Вт м/К

6.

2. Диффузия
Поток молекул примеси, переходящий через поверхность единичной
площади за единицу времени, прямо пропорционален градиенту
концентрации:
Закон Фика : j Dgradn
где D – коэффициент диффузии.
Физический смысл коэффициента диффузии – коэффициент диффузии
численно равен потоку частиц, проходящих через поверхность
единичной площади за единицу времени при градиенте концентрации
равном единице.
Единица коэффициента диффузии в СИ м2/с.

7.

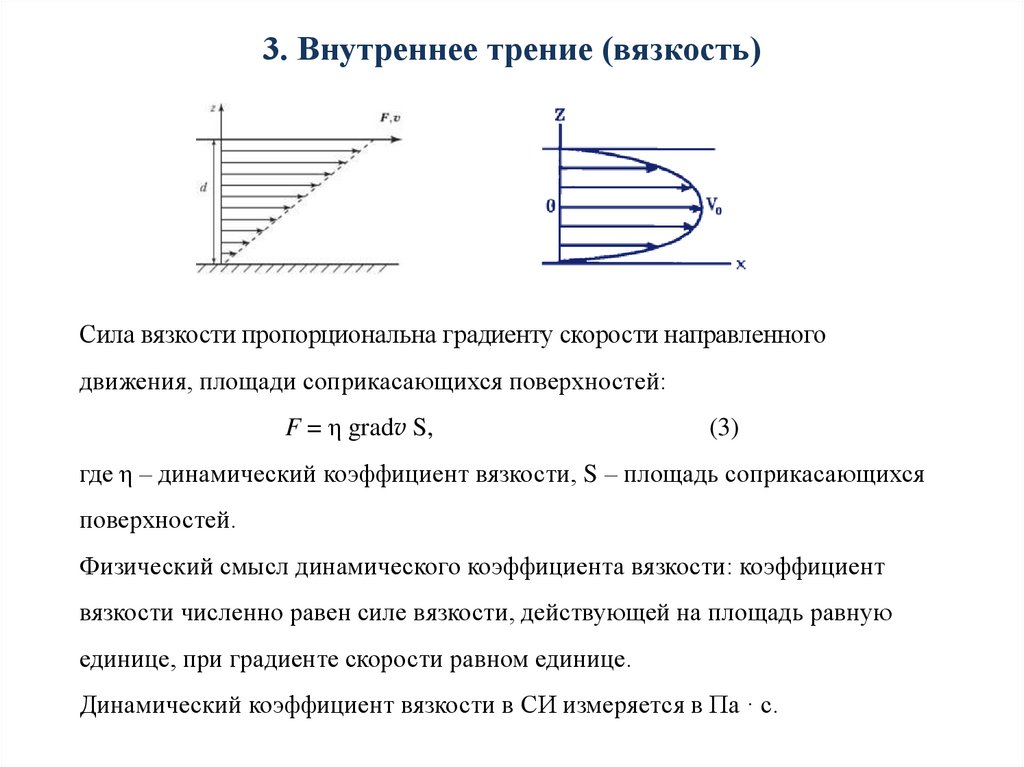
3. Внутреннее трение (вязкость)
Сила вязкости пропорциональна градиенту скорости направленного
движения, площади соприкасающихся поверхностей:
F = η gradv S,
(3)
где η – динамический коэффициент вязкости, S – площадь соприкасающихся
поверхностей.
Физический смысл динамического коэффициента вязкости: коэффициент
вязкости численно равен силе вязкости, действующей на площадь равную
единице, при градиенте скорости равном единице.
Динамический коэффициент вязкости в СИ измеряется в Па · с.

8.

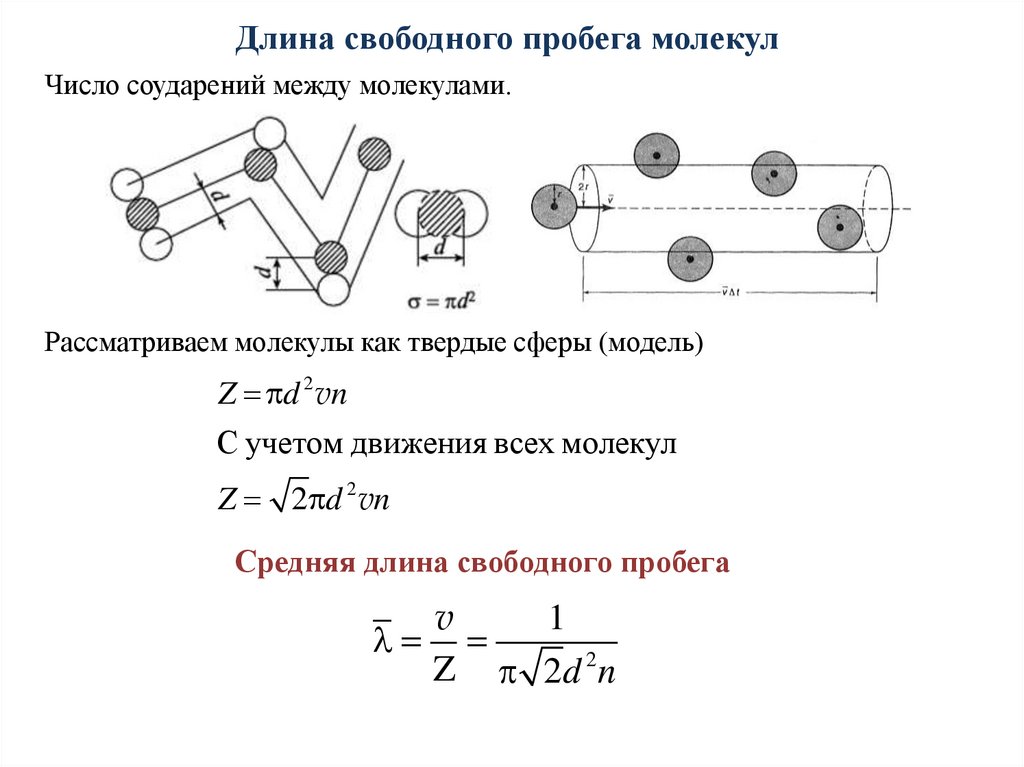
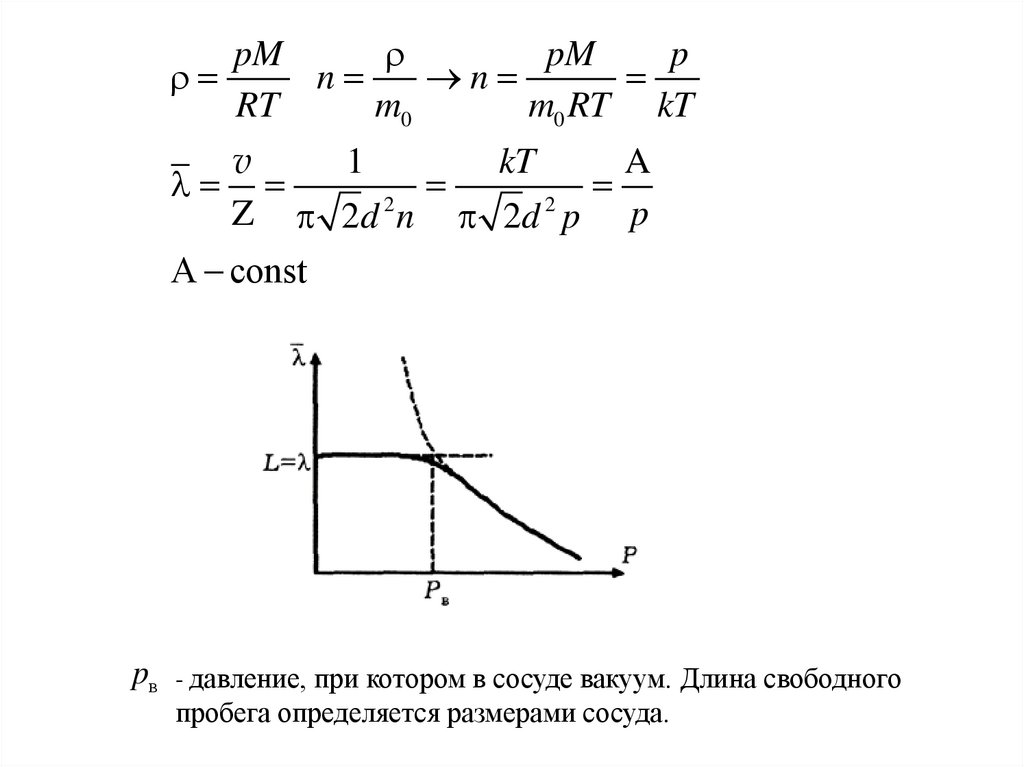
Длина свободного пробега молекул
Число соударений между молекулами.
Рассматриваем молекулы как твердые сферы (модель)
Z d 2 vn
С учетом движения всех молекул
Z 2 d 2 vn
Средняя длина свободного пробега
v
1
Z 2d 2 n

9.

pM
pM
p
n
n
RT
m0
m0 RT kT
v
1
kT
A
2
2
Z 2d n 2d p p
А const
pв - давление, при котором в сосуде вакуум. Длина свободного
пробега определяется размерами сосуда.

10.

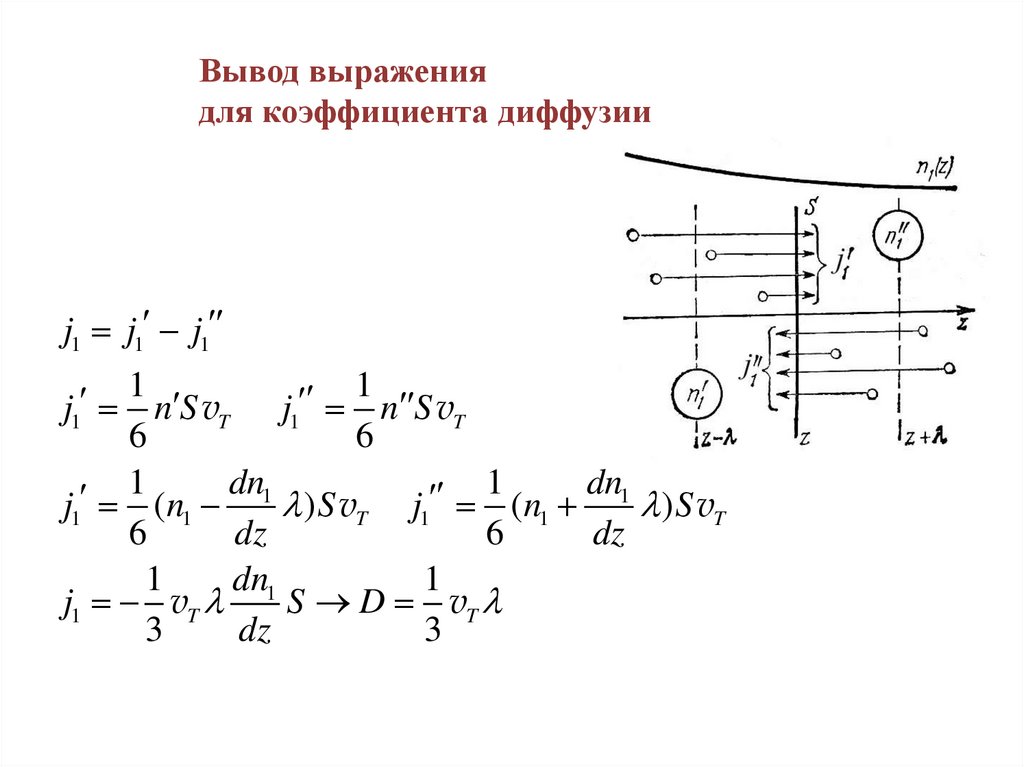
Вывод выражения
для коэффициента диффузии
j1 j1 j1
1
1
j1 n S vT j1 n S vT
6
6
dn1
dn1
1
1
j1 (n1
) S vT j1 (n1
) S vT
6
dz
6
dz
dn1
1
1
j1 vT
S D vT
3
dz
3

11.

Коэффициент диффузии
1
D vT
3
1
1.
n
n
2. vT
p D
1
p
T
3.Самодиффузия (вещество внутри самого вещества)
При разных веществах разные давления - течение газа.
Взаимная диффузия - разные газы.

12.

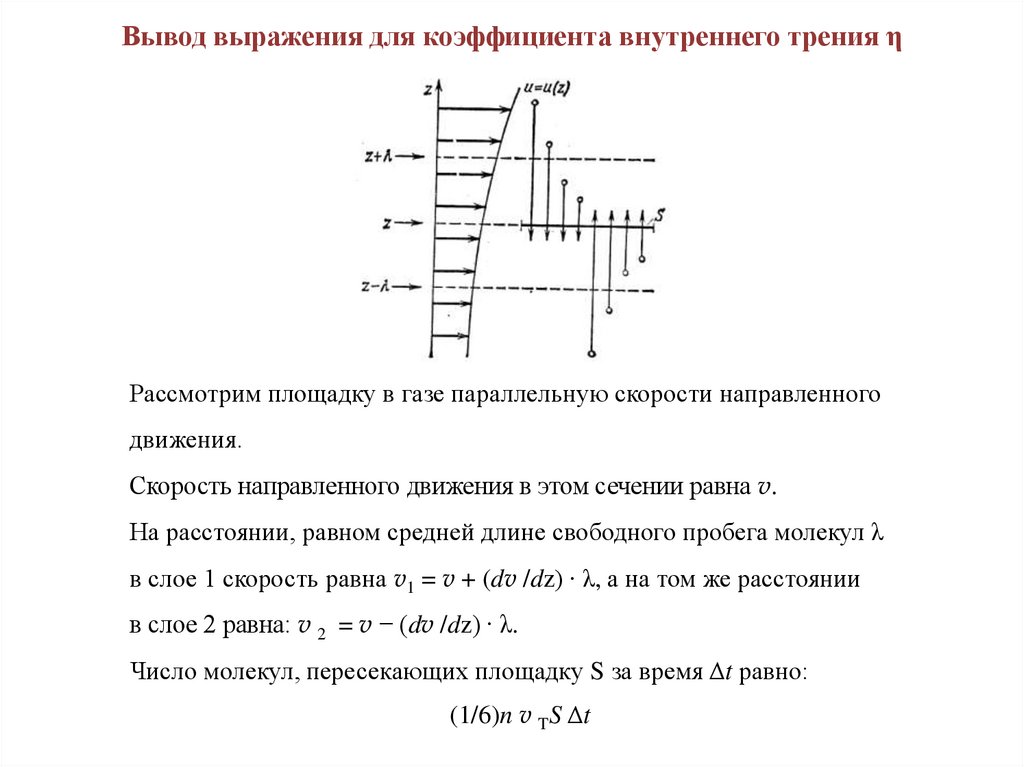
Вывод выражения для коэффициента внутреннего трения η
Рассмотрим площадку в газе параллельную скорости направленного
движения.
Скорость направленного движения в этом сечении равна v.
На расстоянии, равном средней длине свободного пробега молекул λ
в слое 1 скорость равна v1 = v + (dv /dz) ∙ λ, а на том же расстоянии
в слое 2 равна: v 2 = v − (dv /dz) ∙ λ.
Число молекул, пересекающих площадку S за время Δt равно:
(1/6)n v TS Δt

13.

Изменение импульса выделенного слоя равно:
(1/6) m0nvT S Δt(v + (dv/dz) ∙ λ − v + (dv/dz) ∙ λ) =
m0(1/6) nvT S Δ t · 2 (dv/dz)∙ λ = m0nvT S Δ t · (dv/dz) ∙ λ
Согласно 2-му Ньютона
F Δ t = (1/3) m0nvTS Δ t · (dv/dz) ∙ λ
F = η(dv/dz)∙ S
η = (1/3) m0nvT λ = (1/3)ρvT λ

14.

Динамический коэффициент вязкости
1
3
vT
1.
1
n
n
T
2. vT
p f p
p
T
3.Возможно измерить
Способы : затухание колебаний, капиллярный вискозиметр
R4
8vl
p

15.

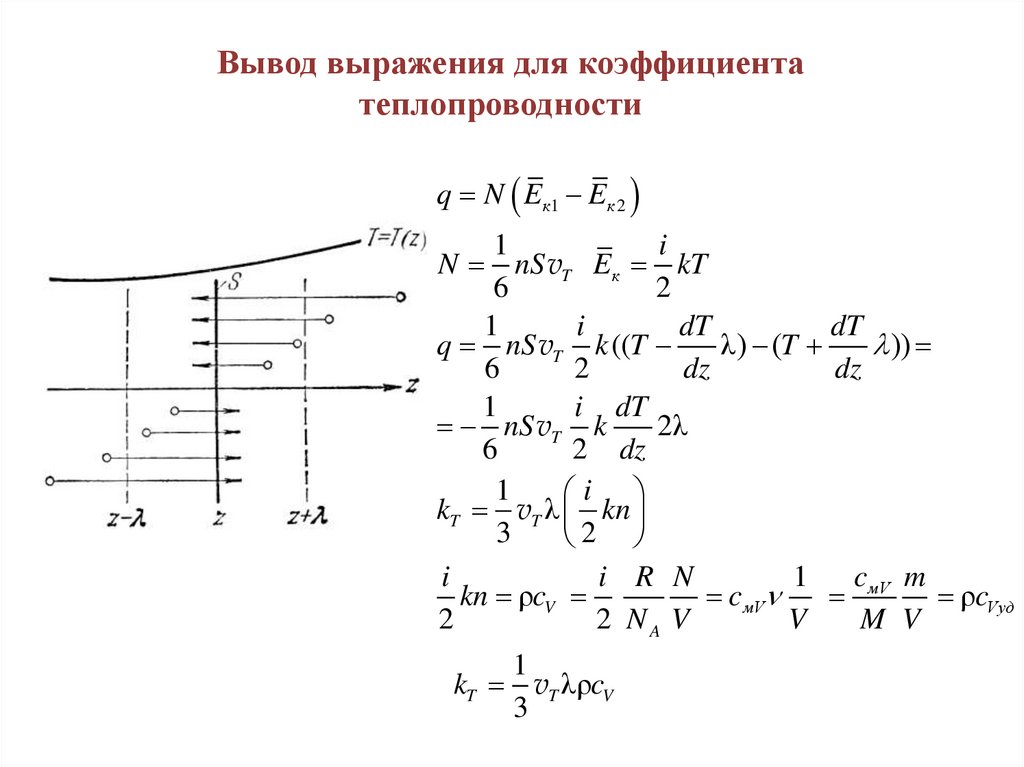
Вывод выражения для коэффициента
теплопроводности
q N Eк 1 E к 2
1
i
N nS vT Eк kT
6
2
1
i
dT
dT
q nS vT k ((T
λ) (T
))
6
2
dz
dz
1
i dT
nS vT k
2λ
6
2 dz
1
i
kT vT λ kn
3
2
cмV m
i
i R N
1
kn ρcV
cмV
ρcVуд
2
2 NA V
V
M V
1
kT vT λρcV
3

16.

Коэффициент теплопроводности
1
kT vT cVуд
3
1 kT f p
2. vT
T kT
T
3. зависит от массы молекул

17.

Коэффициенты переноса
1
1
D vT λ η 1/ 3 ρvT λ kT vT λρcVуд
3
3
η
η
D диффузия скорости
D
кинематический коэффициент вязкости
vd
(число Рейнольдса Re =
)
kT
a D диффузия температуры
ρcVуд
a коэффициент температуропроводности,
определяет нестационарное поле температур

18.

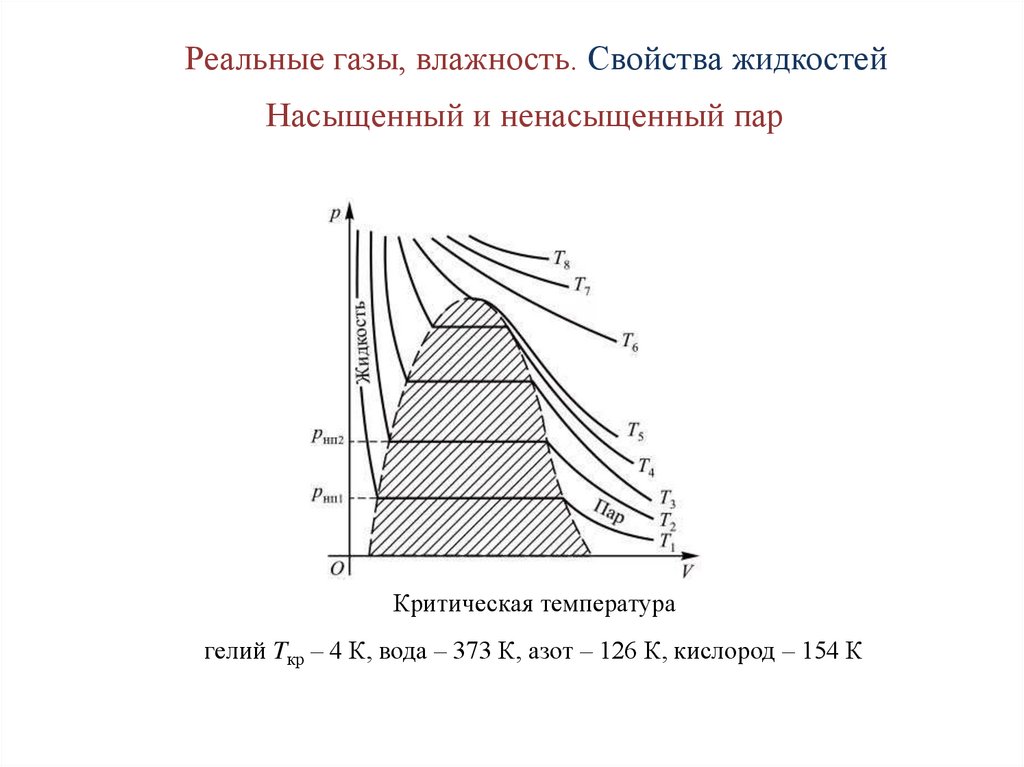
Реальные газы, влажность. Свойства жидкостей
Насыщенный и ненасыщенный пар
T1 < T2 < T3 < T4 < … < Tn
Критическая температура
гелий Tкр – 4 К, вода – 373 К, азот – 126 К, кислород – 154 К

19.

Свойства насыщенного пара
1. Насыщенный пар находится в динамическом
равновесии с жидкостью.
2. Насыщенный пар не подчиняется газовым законам.
pн
н
M
RT
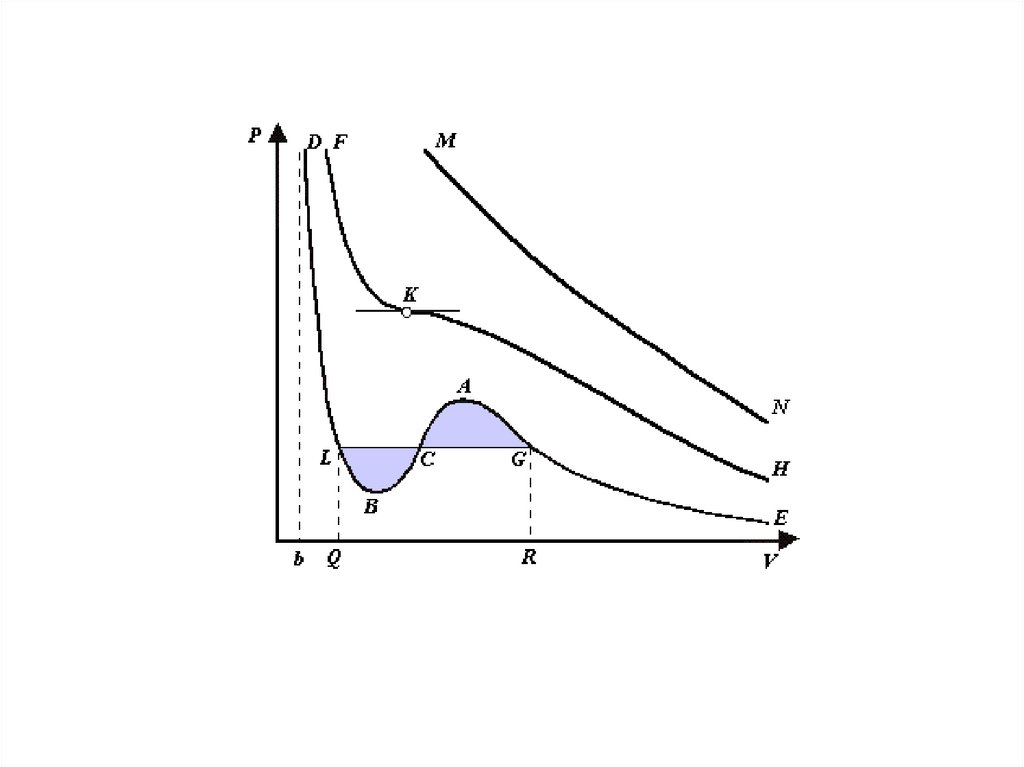
Уравнение Ван-дер Ваальса
a m2
m m
p
V
b
RT
2
2
V M
M M
8a
a
Tкр
pкр
Vкр 3b
2
27 Rb
27b
i
a 2
U cV T
2
V

20.

21.

Влажность
Давление воздуха
pатм pс.в. pп.
Абсолютная влажность определяется количеством паров воды в
воздухе (плотностью п).
Относительная влажность определяется отношением
плотности пара к плотности насыщенного пара нп при
той же температуре, или отношением парциального
давления пара к давлению насыщенного пара рнп при той
же температуре:
pп
100%
pн.п