Похожие презентации:
Тригонометрические уравнения и неравенства
1.
2.
3.
4.
1.2.
3.
4.
5.
Тригонометрические уравнения и неравенства
Все формулы тригонометрии
Знать определение и свойства обратных тригонометрических функции. Включая их графики
Свойства изученных элементарных функций, их графики, обратные функции, композицию функций
Элементы комбинаторики и теории вероятностей. Элементы математической статистики: законы
распределения, дисперсия
6. Последовательности, формула n-го члена. Арифметическая, геометрическая (в т. ч. бесконечно убывающая)
прогрессии
7. Пределы, правила раскрытия неопределенностей, нахождение асимптот графиков функций
8. Производная, правила, производные основных элементарных функций. Производная сложной функции
9. Геометрический и физический смысл производной. Уравнение касательной и нормали к графику функции
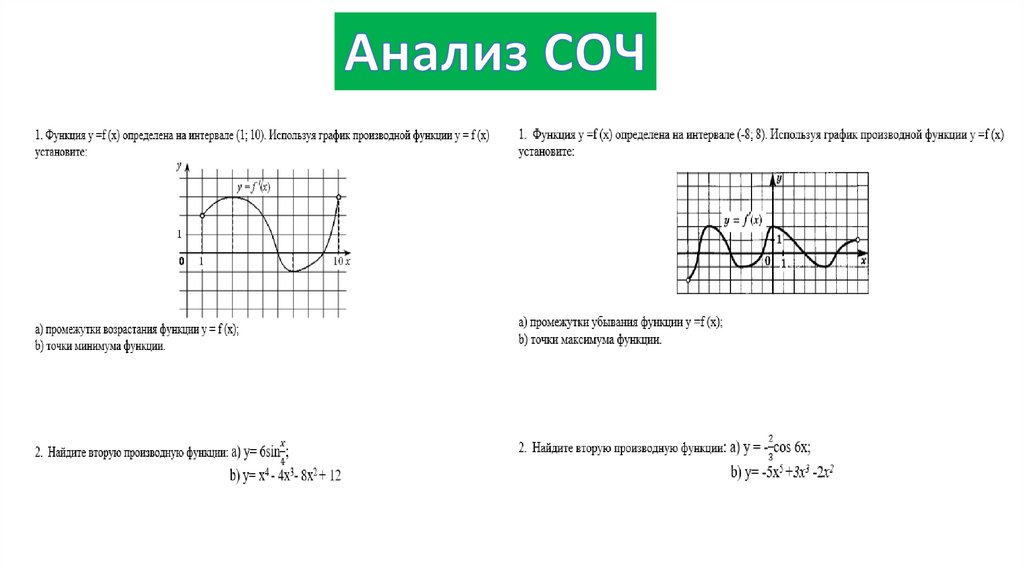
10. Применение производной: критические, стационарные точки, точки экстремума и экстремумы функции,
промежутки монотонности функции, вторая производная, точки перегиба, промежутки выпуклости
(вогнутости), нахождение наибольшего и наименьшего значения функции на отрезке, задачи на оптимизацию
11. Решение уравнений высших степеней. Теорема о рациональном корне многочлена. Теорема Безу. Схема
Горнера. Разложение многочлена на множители. Метод неопределенных коэффициентов
5.
1. Понятие о первообразной и неопределенном интеграле. Правила интегрирования. Интегралы от основныхэлементарных функций. Геометрический смысл интеграла
2. Определенный интеграл. Формула Ньютона-Лейбница. Нахождение площади криволинейной трапеции, площади
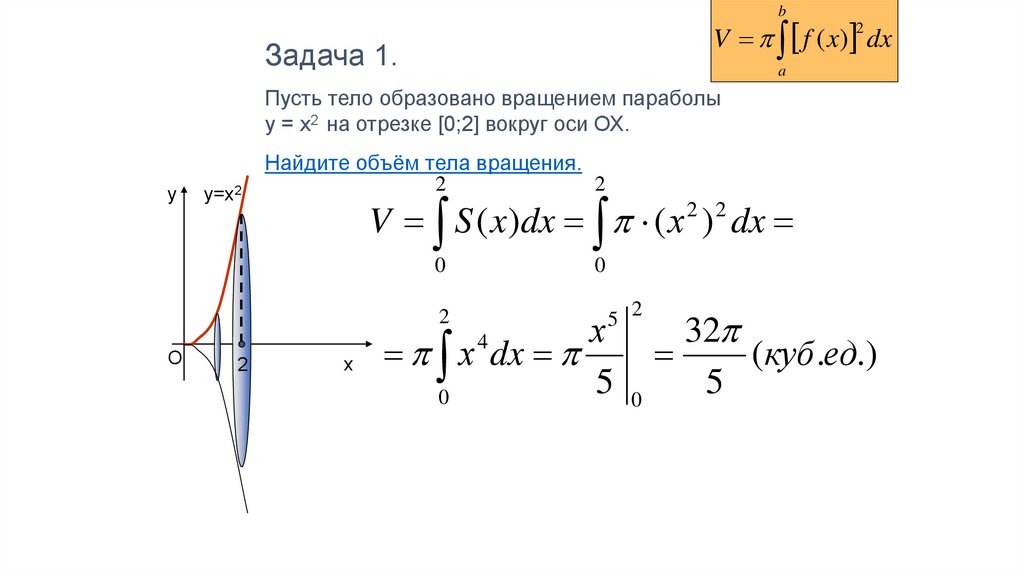
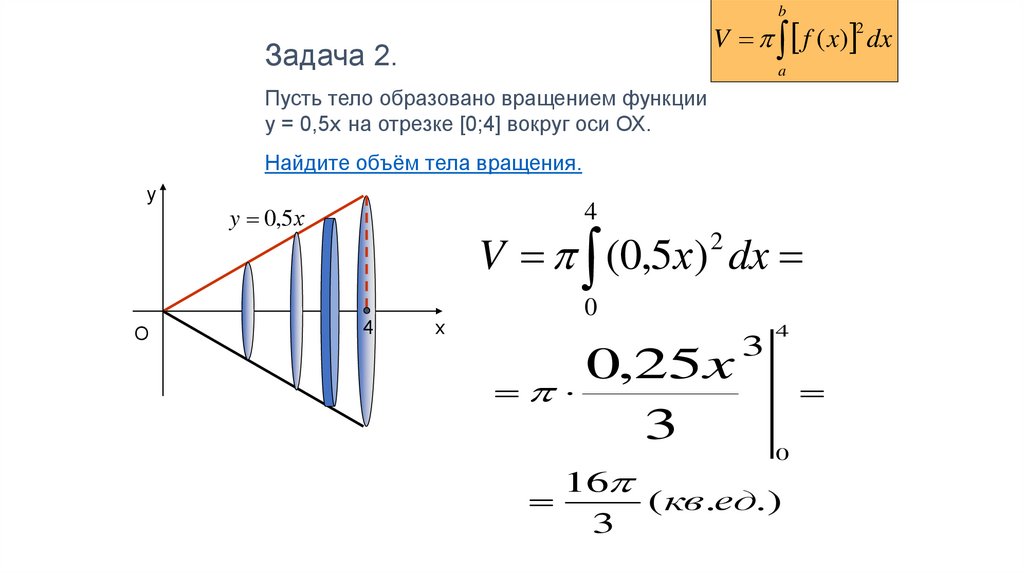
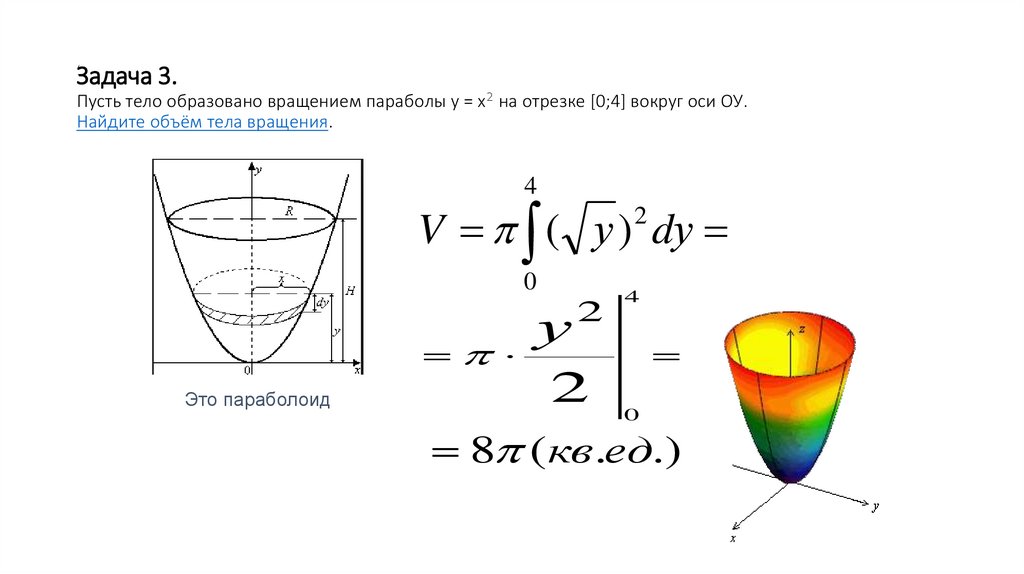
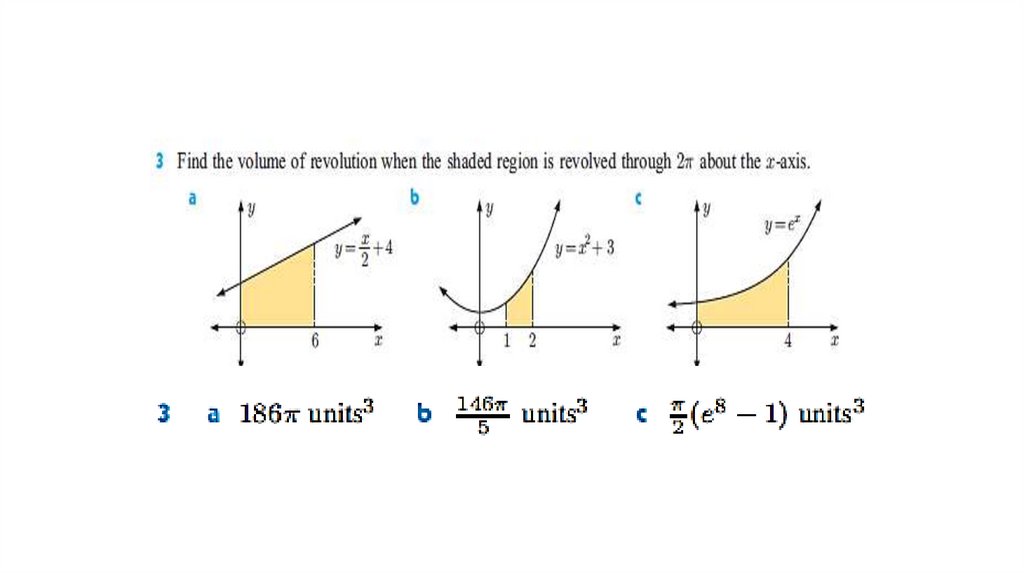
фигуры, ограниченной линиями, нахождение объема тела вращения, нахождение длины арки кривой
3. Физический смысл интеграла
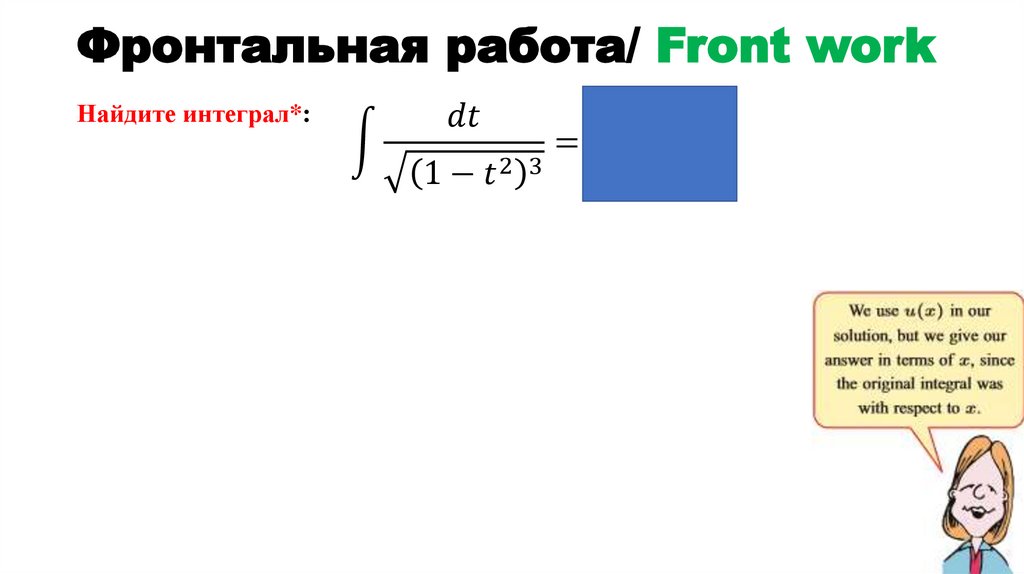
4. Методы интегрирования: по частям, заменой переменной
5. Свойства и график степенной функции. Свойства корней n-степени и степени с рациональным показателем
6. Методы решения иррациональных уравнений и иррациональных неравенств
7. Понятие о комплексных числах: модуль, аргумент, изображение на диаграмме Аргана.
8. Все действия с комплексными числами
9. Решение уравнений с комплексными числами
10. Теорема Муавра. Тригонометрическая форма записи комплексного числа
11. Определение логарифма числа. Свойства логарифмов.
12. Показательная и логарифмическая функции, их свойства и графики. Производная и интеграл этих функций. Второй
замечательный предел
13. Методы решения показательных и логарифмических уравнений, неравенств и их систем
14. Понятие о дифференциальных уравнениях. Общий интеграл ДУ. ДУ первого порядка, решаемые методом замены,
через уравнение Бернулли, через интегрирующий множитель, ДУ с разделяющимися переменными. Задача КОШИ.
Уравнения второго порядка. Уравнение гармонических колебаний
15. Решение физических задач с помощью дифференциальных уравнений
6.
Экзаменационный уголокРешите уравнение:
















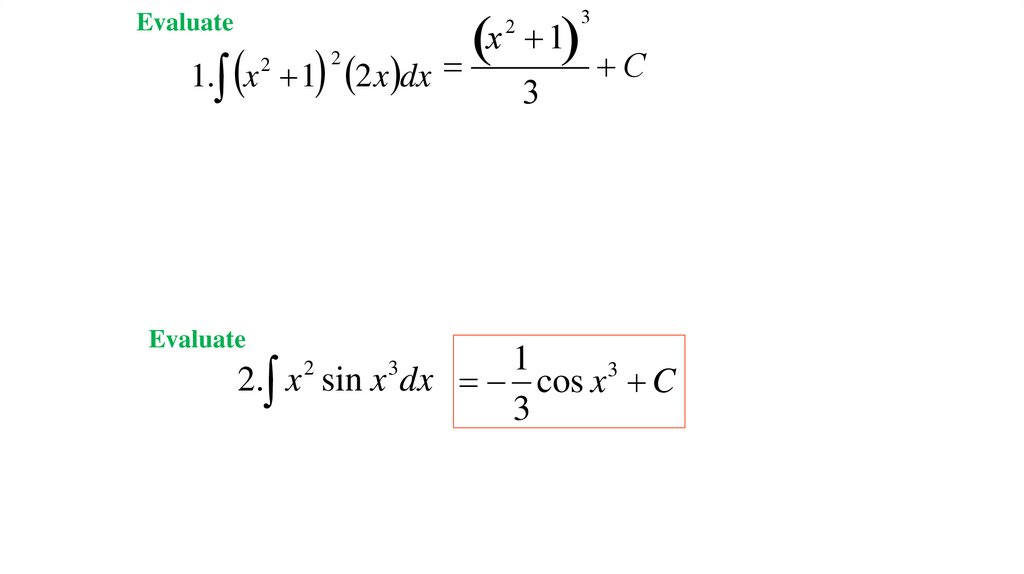










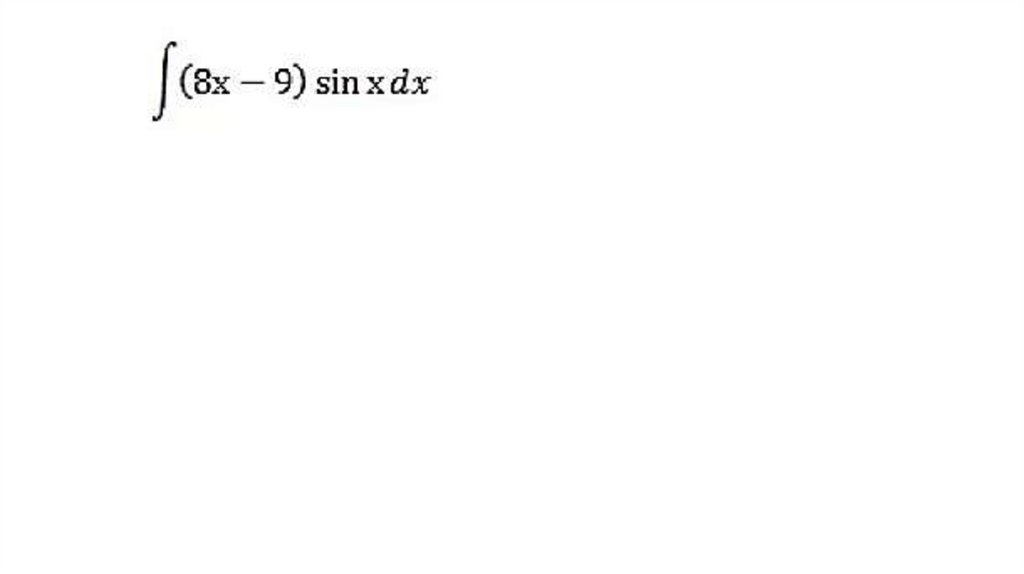
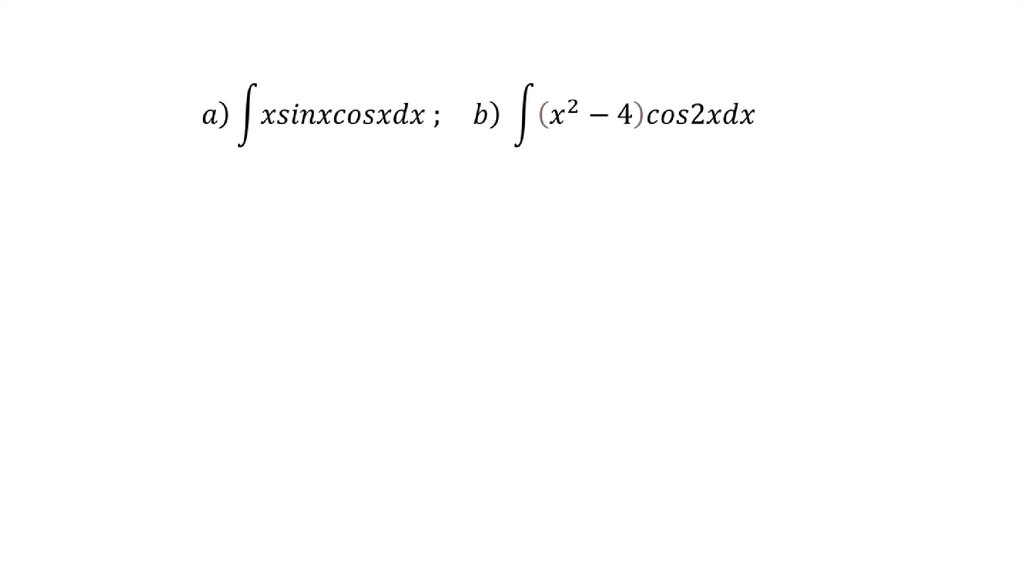
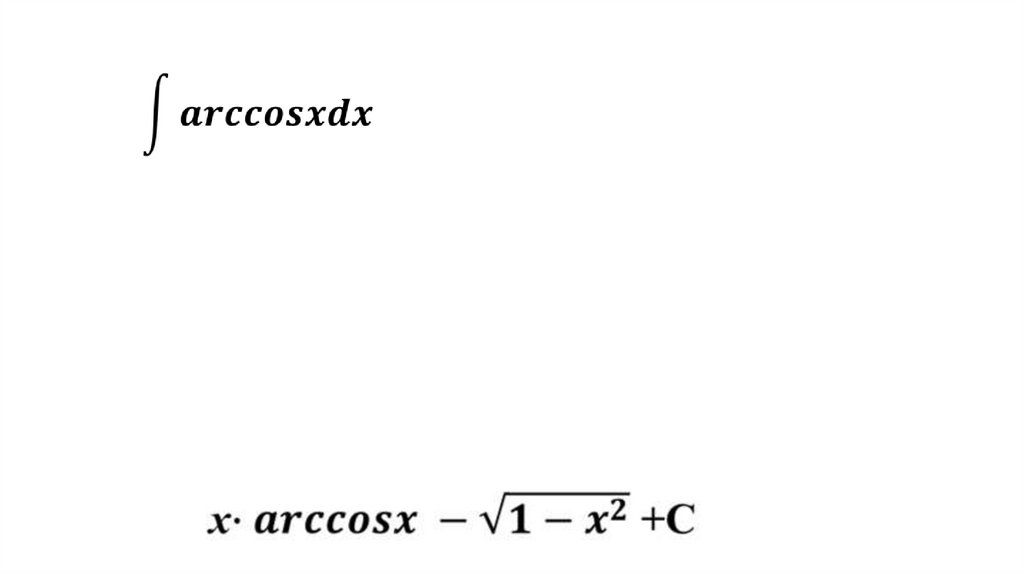





 Математика
Математика








