Похожие презентации:
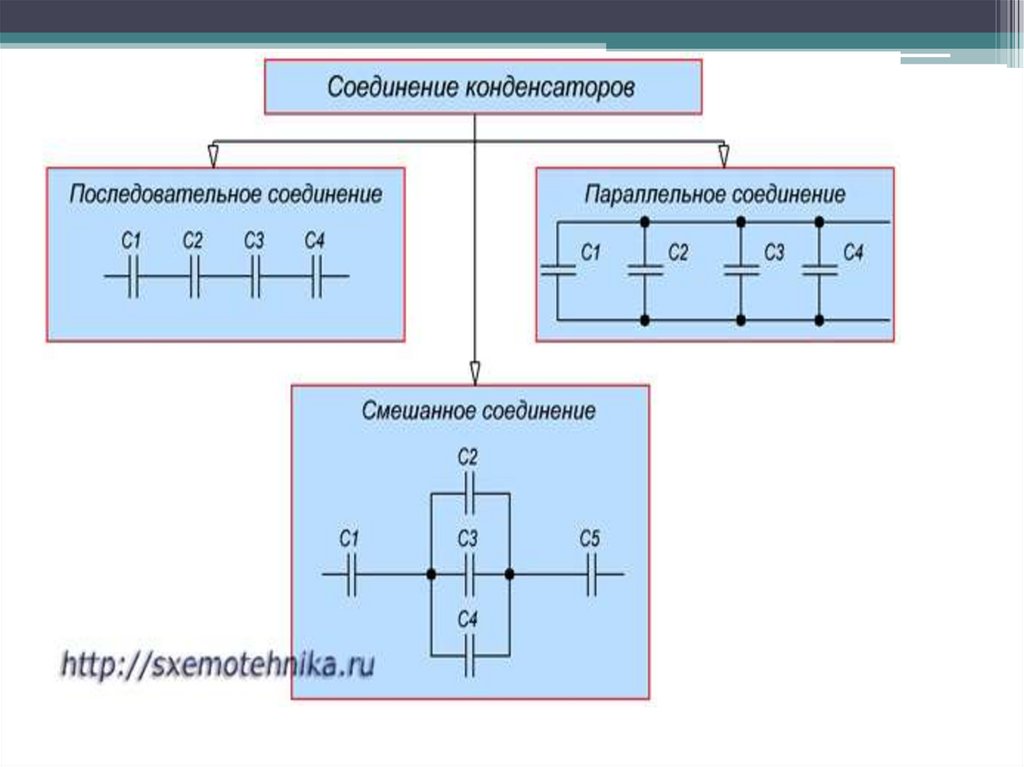
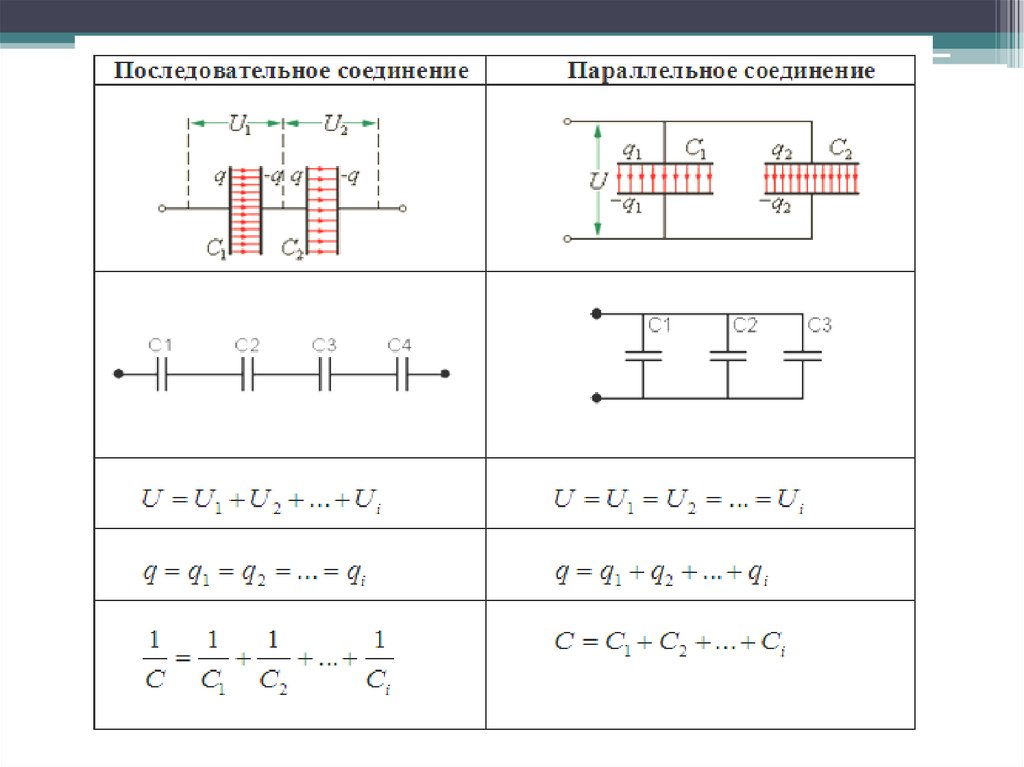
Соединения конденсаторов
1. «Соединения конденсаторов»
Физика2.
3.
4.
Примеры решения задачСоединение конденсаторов
Алгоритм решения задач
1) Делаем рисунок.
2) Определяем последовательно и параллельно соединенные
конденсаторы. Напоминаем, что признаком последовательного
соединения является равенство заряда, а параллельного одинаковая
разность потенциалов.
3) Если соединения неочевидны, то находим точки схемы, потенциалы
которых равны.
4) Соединяем эти точки или не учитываем наличие конденсатора,
присоединенного к этим точкам, т.к. он не накапливает электрический
заряд.
5) Рисуем эквивалентную схему, которую используем для расчета Сэкв.
5.
Задача 1. Четыре конденсатора электроемкостями С1 = 1 мкФ,С2 = 1 мкФ, С3 = 3 мкФ, С4 = 2 мкФ соединены, как показано
на рисунке. К точкам А и В подводится напряжение U = 140 В.
Найдите заряд и напряжение на каждом из конденсаторов.
Решение.
С2,3 С2 С3
1
1
1
1
Cэкв С1 С2,3 С4
q1 q2,3 q4 CэквU
1
1
1 1
7 1
6
6
6
Cэкв 1 10
1 3 10 2 10 Ф 4 10 6 Ф
Сэкв 4 / 7 10 6 Ф
1
q1 q2,3 q4 4 / 5 10 6 140 Кл 8 10 5 Кл
6.
q1 8 10 5U1
В 80 В
6
C1 1 10
q4 8 10 5
q4 8 10 Кл, U 4
В = 40 В
6
C4 2 10
5
8 10 5
U 2 U3
В = 20В
6
C2,3 4 10
q2,3
q2 C2U 2 1 10 6 20Кл 2 10 5 Кл
q3 C3U 3 3 10 6 20 Кл 6 10 5 Кл
7.
Задача 2. Определите эквивалентную электрическую емкостьв цепи, изображенной на рисунке. Электроемкости всех
конденсаторов одинаковы и равны С.
Решение.
1
1
1
Cэкв 2C1 2C2
Cэкв
C1C2
C
C2 C2 2
Сэкв
2C1C2
C
C2 C2
Сэкв 2Cэкв
2C1C2
C2 C2
8.
Задача 4. Определите емкость системы, изображенной нарисунке, если C1 = С2 = С3 = С4 = С5 = С6 = С7 = С.
Решение.
С6,7 2 С
1
1
1
1
1
3
2
С5,6,7 С
C5,6,7 C6,7 C 2С С 2С
3
С4 – С7 :
С
5
С4,5,6,7 2 С С
3
3
Сэкв 13 / 21 С
9.
Задача 5. Конденсатор электроемкостью С1 = 1 мкФ,заряженный до разности потенциалов U1 = 100 В и отключенный
от источника, соединили параллельно с конденсатором
электроемкостью С2 = 3 мкФ, заряженным до разности
потенциалов U2 = 60 В. Определите заряд каждого
из конденсаторов и разность потенциалов между обкладками
после их соединения, если
1) соединяются обкладки, имеющие одноименные заряды;
2) соединяются обкладки, имеющие разноименные заряды.
Решение.
1) Сэкв С1 С2 , q q1 q2 C1U1 C2U 2
U 0
С1U1 C2U 2
q
70 В
Cэкв
Cэкв
q1 С1U '0 7 10 5 Кл
q2 С2U '0 21 10 5 Кл
10.
q q1 – q2 C1U1 – C2U 2C1U1 C2U 2
U 0
20В
C1 C2
5
q1 С1U 0 2 10 Кл
5
q2 C2U 0 6 10 Кл
11.
Задача 6. Энергия плоского воздушного конденсатораW1 = 2 10-7 Дж. Определите энергию конденсатора после
заполнения его диэлектриком с диэлектрической
проницаемостью = 2, если:
1) конденсатор отключен от источника питания;
2) конденсатор подключен к источнику питания.
Решение.
q02
1) W2
2C2
ε 0 εS
0 S
C2 =
C1 C1
d
d
q02
W
W2
10 7 Дж
2 C1
C2U 02
2) W2
С2 С1
2
C1U 02
W2
W1 4 10 7 Дж
2
12.
Задача 7. Пластины плоского конденсатора подключенык источнику U = 2 В. Определите изменение емкости и энергии
электрического поля конденсатора, если конденсатор
наполовину заполнен диэлектриком с диэлектрической
проницаемостью = 2. Расстояние между пластинами d = 1 см,
площадь пластин S = 50 см2.
Решение.
ε0 S ε0 S
εε S
C1 =
=
C2 = 0
d
2d
2d
ε S
C = C1 +C2 = 0 ( ε + 1 )
2d
S
S S
С С – С0 0 1 0 0 1 2, 21 10 12 Ф
2d
d
2d
CU 2 C0U 2 ΔCU 2
W =
2
2
2
S 1 U
W 0
8,85 10 12 Дж
2d
2
2
2
13.
Задача 8. В плоский воздушный конденсатор вставляется металлическаяпластина толщиной d0. Заряд на обкладках конденсатора q. Конденсатор
отключен от источника. Расстояние между пластинами d, площадь
пластин S. Определите изменение электроемкости конденсатора и
энергии его электрического поля, если конденсатор не подключен к
источнику.
Решение.
0 S
0 S
C1
, С2
l1
l2
l
l
l l
1
1
1
1 2 1 2
Cэкв С1 С2 ε 0 S ε 0 S
ε0 S
S
l1 l2 d – d 0 , Cэкв 0
d d0
ε S
ε S
ε 0 Sd 0
С Сэкв – С0 0 0
0
d d0
d
d d0 d
q2
q2
q 2 d d0
d q 2 d 0
W
0
2Cэкв 2C0 2 0 S
0 S 2 0 S
14.
Задача 9. Определите изменение заряда проводящей сферырадиуса 10 см, первоначально заряженной до потенциала 104 В,
если с течением времени она частично потеряла заряд и ее энергия
уменьшилась на 1,5 10-4 Дж.
Решение.
C 2
Wэ
С 4πε 0 εr
2
C
ΔWэ = Wэ2 – Wэ1 = ( φ 22 – φ12 )
2
2 Wэ
Wэ
2
2
1
φ12
C
2πε 0 εr
Wэ
2
q C ( 2 1 ) 4 0 r
1 1 1, 67 10 8 Кл
2πε 0 r












 Физика
Физика








