Признаки равенства треугольников. Урок по геометрии. 7 класс

1.

Урок по геометрии.
7 класс.
Учитель математики Спицына Татьяна Дмитриевна. Школа №1, п. Таксимо

2.

Треугольники вокруг нас
Треугольник
–
самая
простая
замкнутая
прямолинейная фигура, одна из первых, свойства
которых человек узнал еще в глубокой древности, т.
к. эта фигура всегда имела широкое применение в
практической жизни.
Платон утверждал, что
вообще вся
“Поверхность состоит
из треугольников”.

3.

Изображения треугольников и
задачи на треугольники
встречаются во многих
папирусах Древней Греции и
Древнего Египта. Еще в
древности стали вводить
некоторые знаки для обозначения
геометрических фигур.
Древнегреческий
ученый Герон (I век)
Впервые применил
знак вместо слова
треугольник.

4.

5.

Прямоугольный треугольник применялся
тысячелетия назад строителями египетских пирамид.

6.

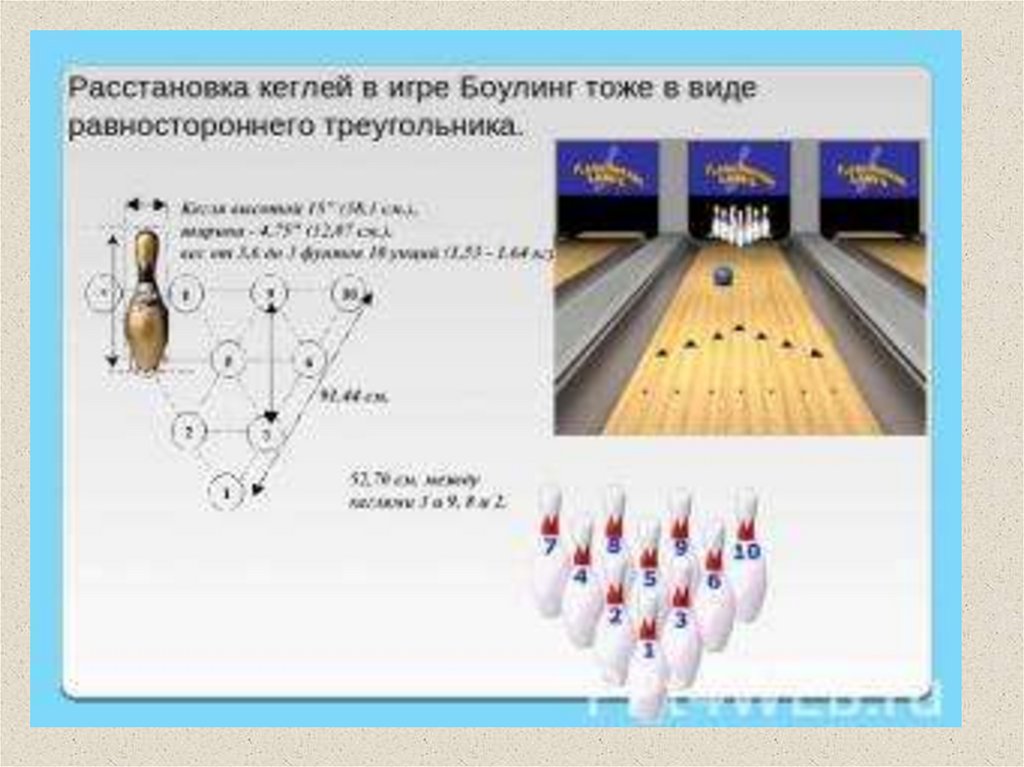
Уже со времён палеолита и неолита в древнем
искусстве очень широко распространяются
изображения равностороннего треугольника.
Вожди племен
североамериканских индейцев
носили на груди символ власти:
равносторонний треугольник.
В Африке женщины украшали себя
большими пластинами из
равносторонних треугольников.

7.

8.

В оригами используются треугольники

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

Треугольник –
геометрическая фигура,
состоящая из трех точек,
не лежащих на одной
прямой, последовательно
соединенных отрезками

20.

Треугольником также называется часть
плоскости ограниченная отрезками АВ,
ВС, АС.
• А, В, С – вершины.
• АВ, ВС, СА-стороны.
• <АВС, <ВСА, <САВ-углы
треугольника,(<А,< В, <С
или α, β, γ ).
А
С
В

21.

Виды
треугольников:
• остроугольные
• Тупоугольные
• прямоугольные

22.

Если два треугольника
равны, то элементы одного
треугольника соответственно
равны элементам другого
треугольника.
В равных треугольниках против
соответственно равных сторон
лежат равные углы, и обратно:
против соответственно равных
углов лежат равные стороны.

23.

24.

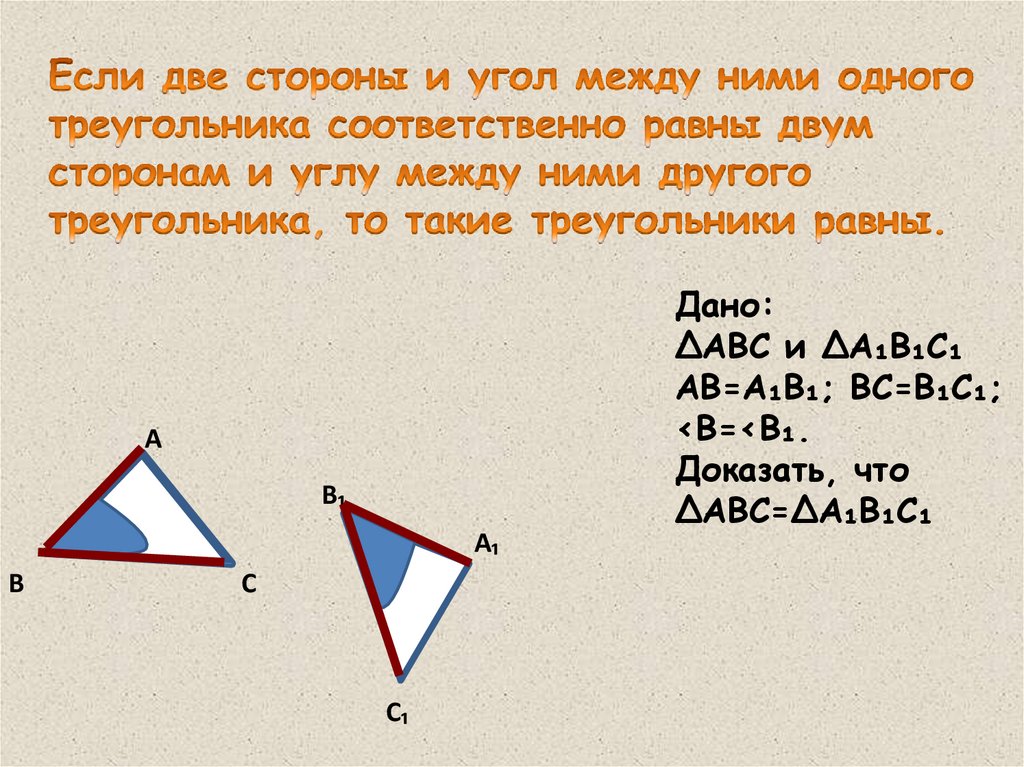
Первый признак равенства
треугольников:
• Если две стороны и угол
между ними одного
треугольника соответственно
равны двум сторонам и углу
между ними другого
треугольника, то такие
треугольники равны.

25.

А
В₁
А₁
В
С
С₁
Дано:
∆АВС и ∆А₁В₁С₁
АВ=А₁В₁; ВС=В₁С₁;
<В=<В₁.
Доказать, что
∆АВС=∆А₁В₁С₁

26.

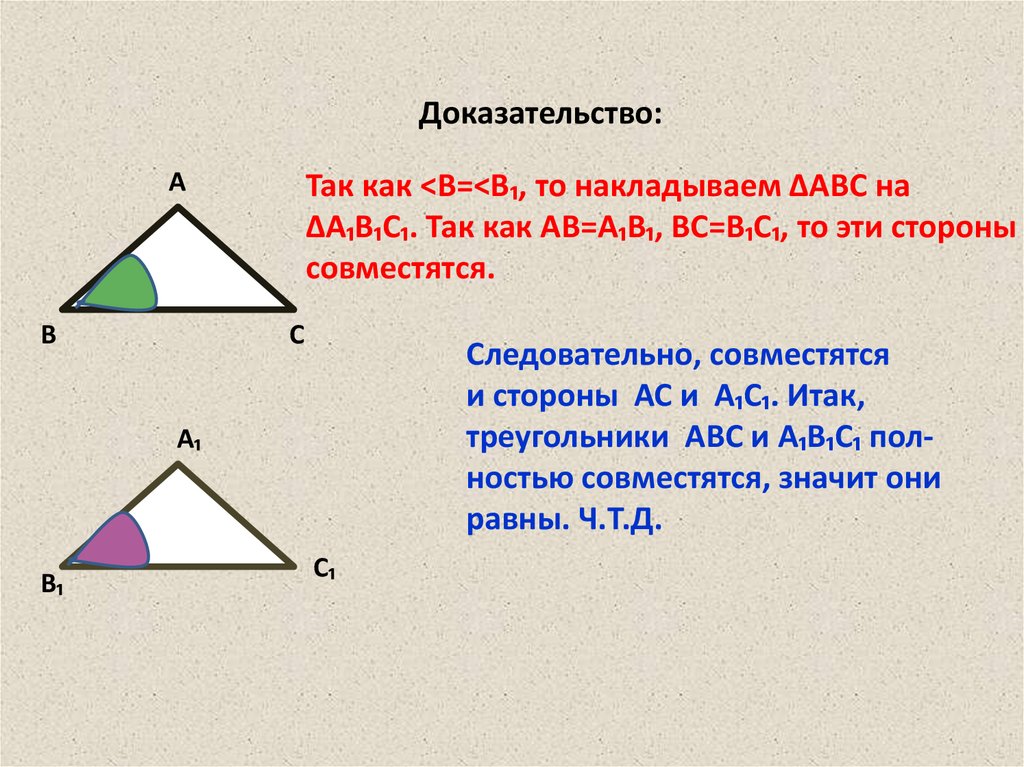
Доказательство:
А
В
Так как <В=<В₁, то накладываем ∆АВС на
∆А₁В₁С₁. Так как АВ=А₁В₁, ВС=В₁С₁, то эти стороны
совместятся.
С
Следовательно, совместятся
и стороны АС и А₁С₁. Итак,
треугольники АВС и А₁В₁С₁ полностью совместятся, значит они
равны. Ч.Т.Д.
А₁
В₁
С₁

27.

28.

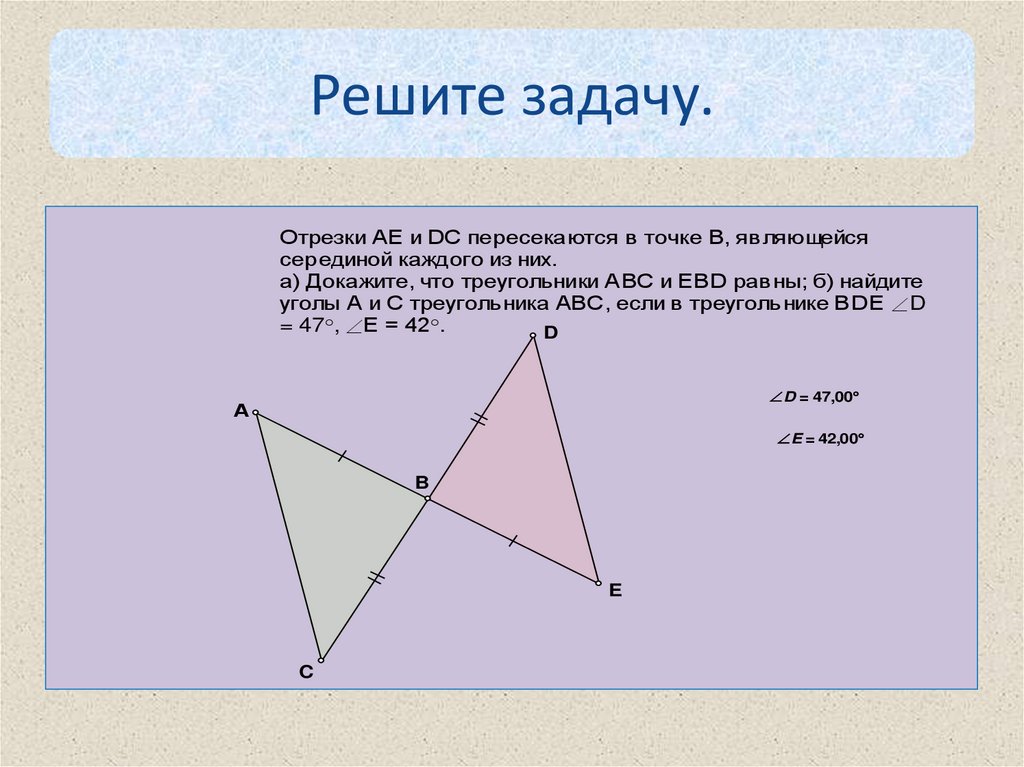
Решите задачу.
Отрезки АЕ и DC пересекаются в точке В, являющейся
серединой каждого из них.
а) Докажите, что треугольники АВС и EBD равны; б) найдите
уголы А и С треуголь ника АВС, если в треуголь нике BDE D
= 47 , Е = 42 .
D
D = 47,00
А
E = 42,00
B
E
C

29.

30.

31.

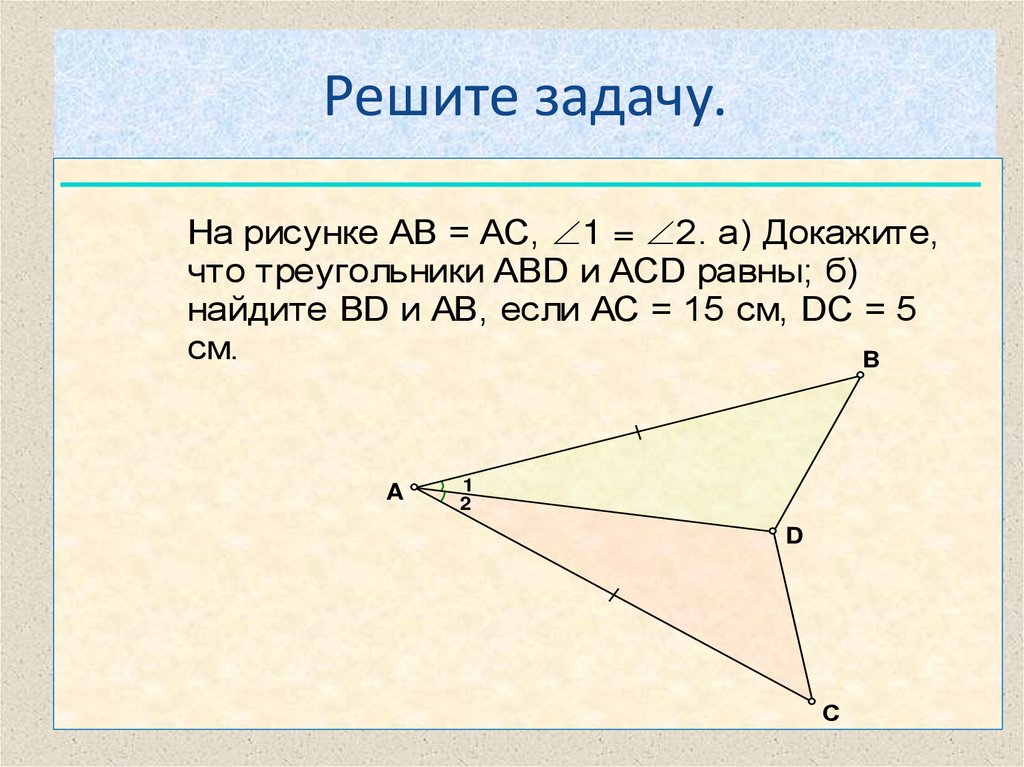
Решите задачу.
На рисунке АВ = АС, 1 = 2. а) Докажите,
что треугольники АВD и ACD равны; б)
найдите BD и АВ, если АС = 15 см, DC = 5
см.
B
A
1
2
D
С

32.

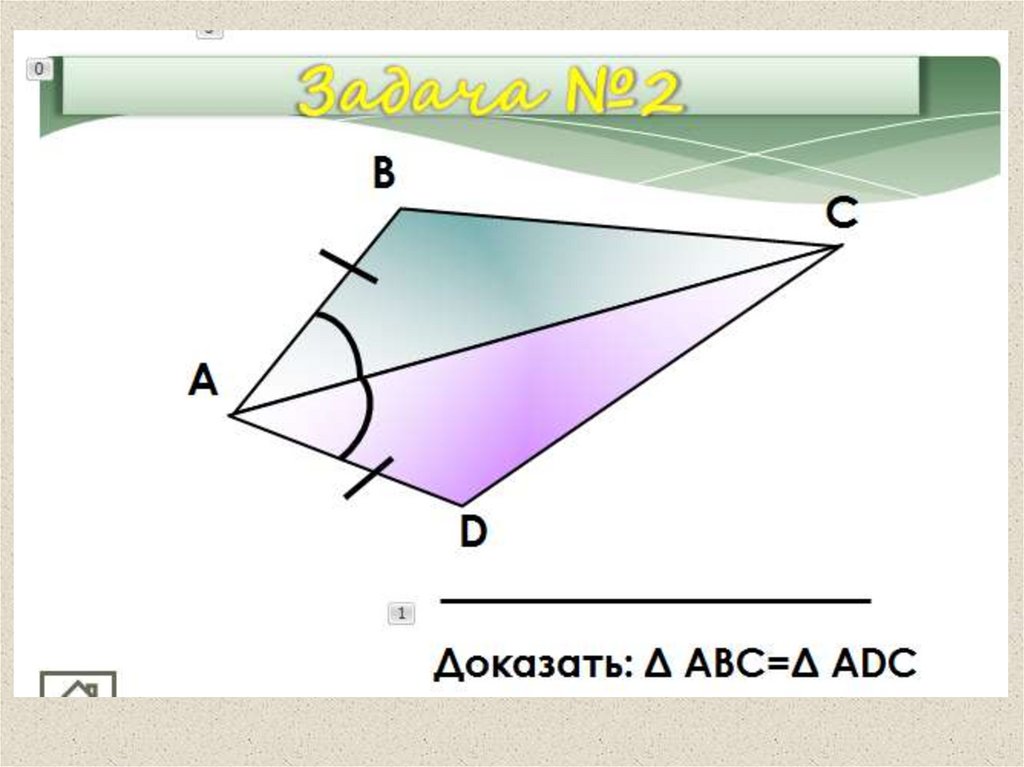
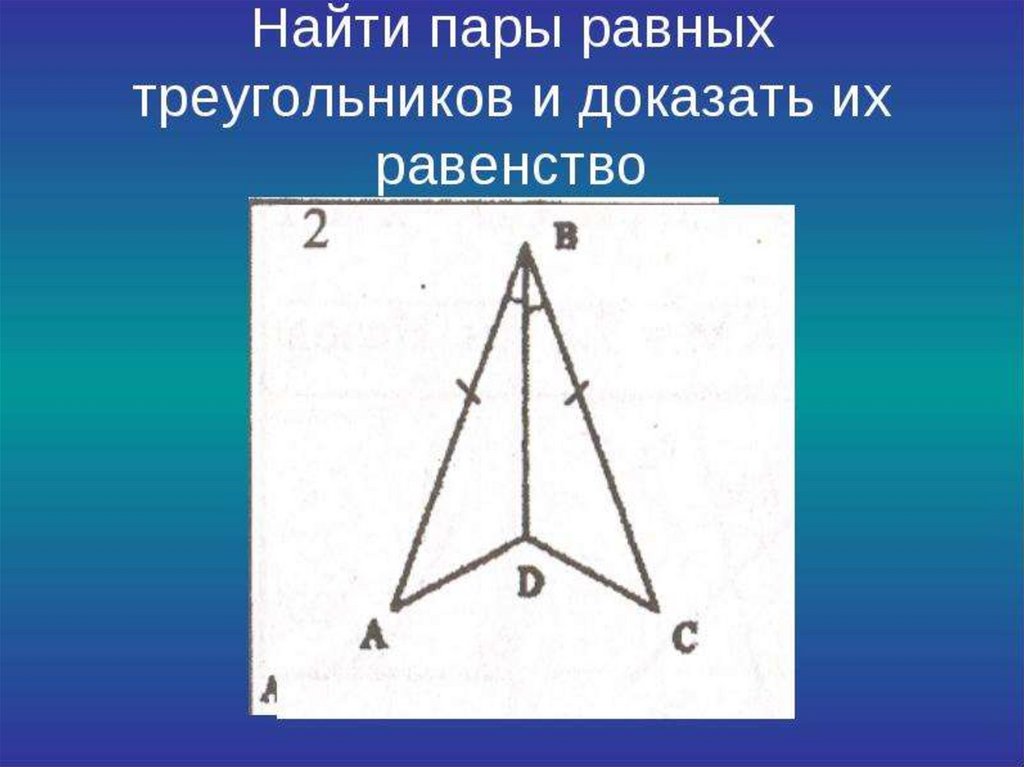
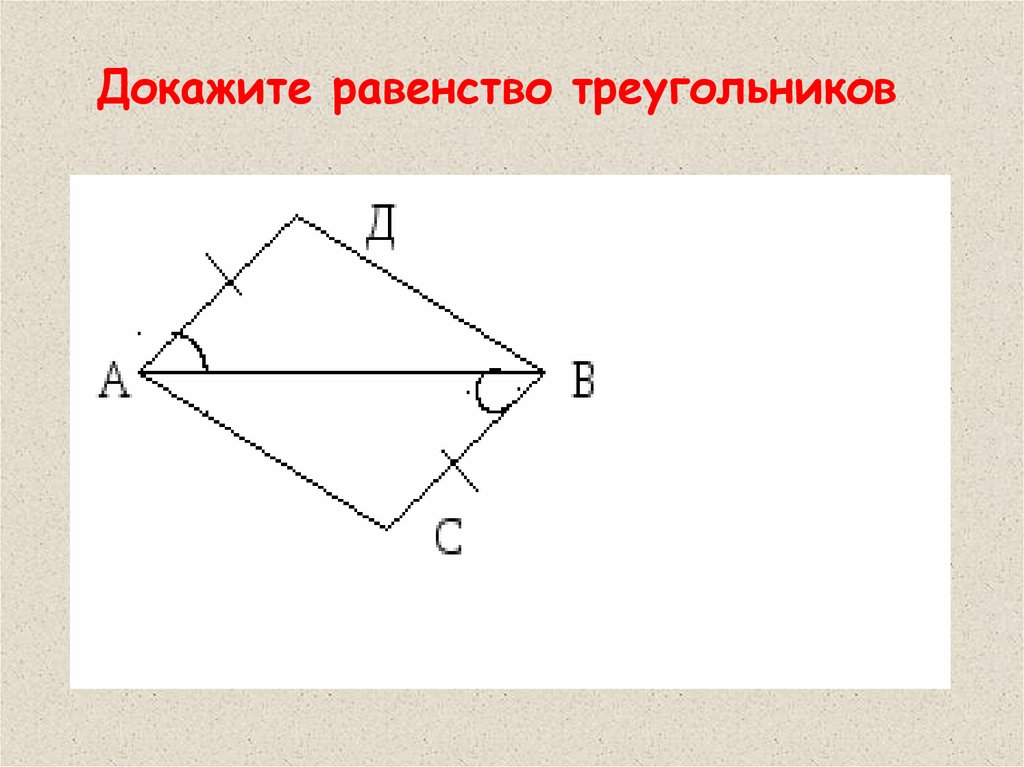
Докажите равенство треугольников

33.

Решите задачу.
На рисунке ВС = AD, 1 = 2. а) Докажите,
что треугольники АВС и CDA равны; б)
найдите АВ и ВС, если AD = 17 см, DC = 14
см.
C
1
B
A
2
D

34.

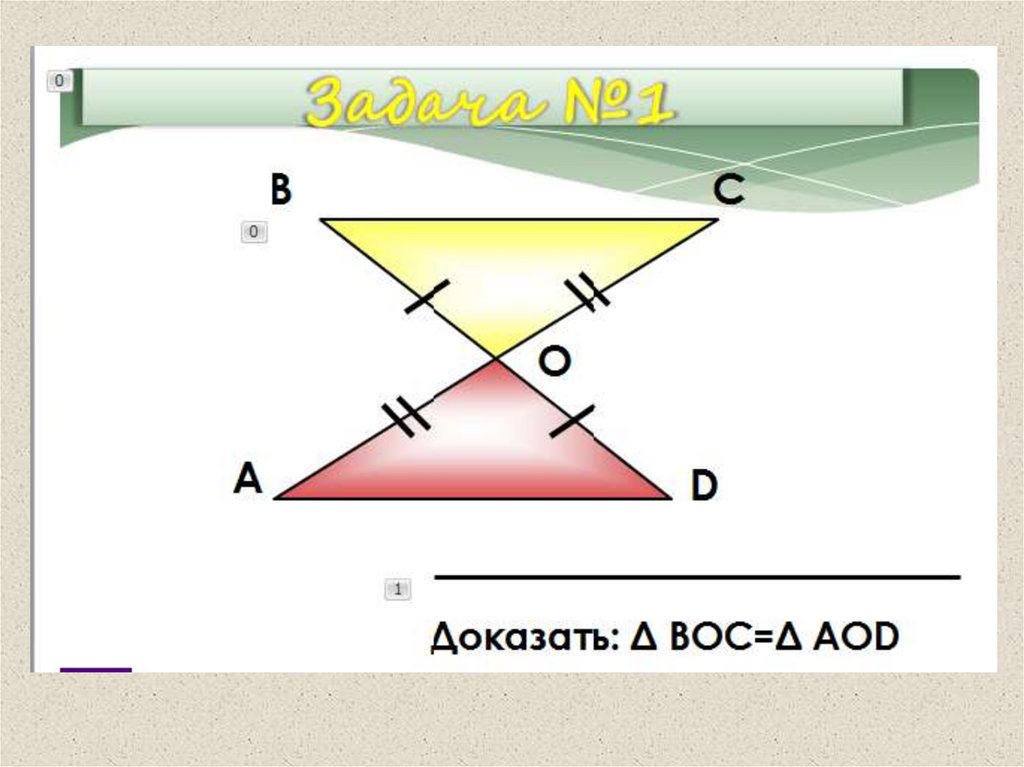
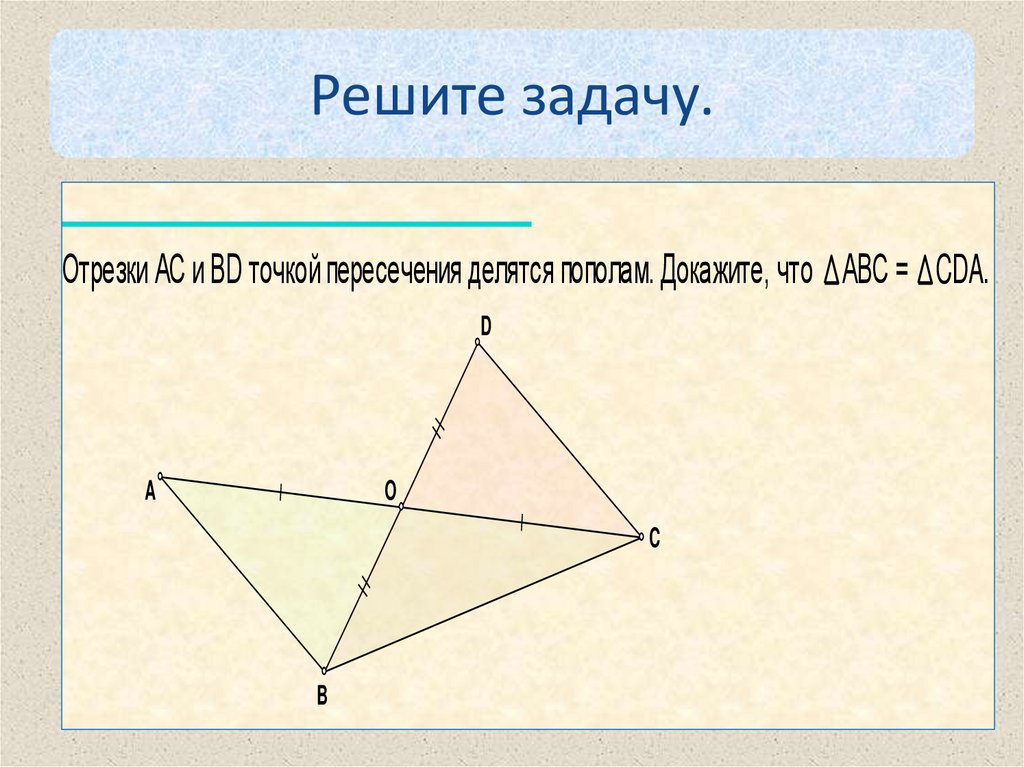
Решите задачу.
Отрезки АС и ВD точкой пересечения делятся пополам. Докажите, что АВС = CDA.
D
A
O
C
B