Похожие презентации:
Повторение материала по алгебре (7 класс)
1.
Повторениематериала по
алгебре за 7 класс.
Астафьева Екатерина
Санкт-Петербург
2024 г.
2.
Числовые выражения.Определение. Запись, которая состоит из чисел, знаков и скобок, а
также имеет смысл, называется числовым выражением.
Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы
можем посчитать значение числового выражения.
Определение. Если два числовых выражения записаны через знак
равно, то эти выражения образуют числовое равенство.
Вычислить значение выражения, содержащее букву, значит подставить в это выражение вместо буквы
данное в условии задания значение.
Определение. Выражение, не содержащее деления на выражение
переменными, называют целым выражением.
3.
Важен порядок выполнения арифметических действий!1.
Если выражение не имеет скобок, то надо выполнять действия в следующем порядке:
возведение в степень, умножение/деление, сложение/вычитание. Если имеется
несколько действий одной ступени, то их выполняют в порядке в котором они
записаны, то есть слева направо.
2. Если в выражении присутствуют скобки, то сначала выполняются действия в
скобках, а лишь затем все стальные действия в обычном порядке. При выполнении
действий в скобках, если их там несколько, следует пользоваться порядком
описанным в пункте 1.
3. Если выражение представляет собой дробь, то сначала вычисляются значении в
числителе и знаменателе, а потом числитель делится на знаменатель.
4.
Если в выражении присутствуют вложенные скобки, то выполнять действия следует
с внутренних скобок.
4.
1. Линейное уравнение с однойОпределение. Уравнение вида ax=b, где х-переменная, а и b некоторые числа, называют линейным уравнением с одной
переменной.
5.
2.Решение задач с помощью уравненийс одной переменной.
Для решение подобных задач вводится буквенное обозначение неизвестной величины из
условия. Чаще всего неизвестное обозначают буквой х.
При решении задач на составление уравнений удобно придерживаться такой
последовательности действий:
1. по условию задачи составить уравнение;
2. решить полученное уравнение;
3. выяснить, соответствует ли найденный корень смыслу задачи, и записать ответ.
Определение. Эту последовательность действий, состоящую из трёх шагов,
можно назвать алгоритмом решения текстовых задач.
6.
Проверять соответствие найденного корня условию задачи очень важно!Рассмотрим, например, такие задачи.
1. За 4 ч собрали 6 кг ягод, причём каждый час собирали одинаковое по массе количество ягод.
Сколько килограммов ягод собирали за 1ч?
2. Несколько мальчиков собрали 6 кг ягод. Каждый из них собрал по 4 кг. Сколько мальчиков
собирали ягоды?
По условию этих задач можно составить одно и то же уравнение 4х = 6, корнем
которого является число 1,5. Но в первой задаче ответ «полтора килограмма ягод за
час» является приемлемым, а во второй ответ «ягоды собирали полтора мальчика» нет. Поэтому вторая задача не имеет решений.
7.
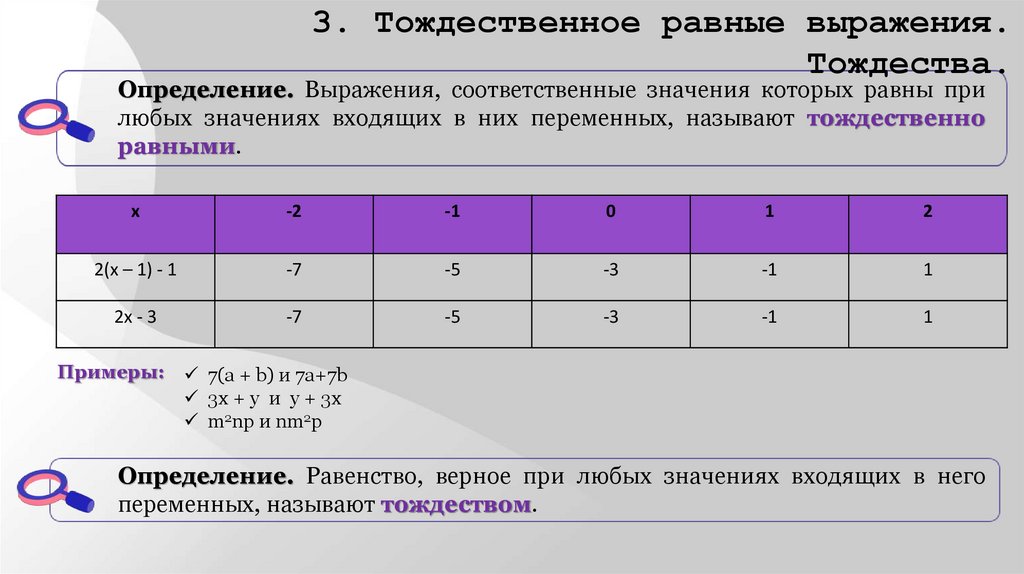
3. Тождественное равные выражения.Тождества.
Определение. Выражения, соответственные значения которых равны при
любых значениях входящих в них переменных, называют тождественно
равными.
х
-2
-1
0
1
2
2(х – 1) - 1
-7
-5
-3
-1
1
2х - 3
-7
-5
-3
-1
1
Примеры: 7(a + b) и 7а+7b
3х + у и у + 3х
m2np и nm2p
Определение. Равенство, верное при любых значениях входящих в него
переменных, называют тождеством.
8.
Определение. Замену одного выражения другим, тождественно равным ему,называют тождественным преобразованием выражения.
Для того, чтобы доказать, что данное равенство является тождеством (или доказать
тождество), используют такие приёмы (методы):
• тождественно преобразуют одну из частей данного равенства, получая другую часть;
• тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
• доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
9.
4.Степень с натуральным показатеОпределение. Выражение 52 называется степенью, число 5 - основанием
степени, число 2 - показателем степени.
Определение. Степенью числа а с натуральным показателем n, большим 1, называют
произведение n множителей, каждый из которых равен а.
Определение. Степенью числа а с показателем 1 называют само это число.
аn = аа ∙ … ∙ а , где n > 1
n множителей
а1 = а
Действие называется возведение в степень.
При возведении неотрицательного числа в степень получаем неотрицательное число.
10.
При возведении отрицательного числа в степень с чётным показателем получаемположительное число.
(-2)4 = 16
При возведении отрицательного числа в степень с нечётным показателем получаем
отрицательное число.
(-2)3 = -8
11.
5. Свойства степени с натуральным п12.
6. ОдночлеРассмотрим выражения:
2b;
1
ху2 ; -аb; m3 ∙ 3k 5 ;
3
3,14 2 pq3 ∙ (−7)r 2 t 4
Определение. Каждое из них представляет собой произведение чисел, переменных и
их степеней. Такие выражения называют одночленами.
Договорились также считать одночленами все числа, любые переменные и их степени.
Например, одночленами являются:
-5; 0,3; х; t 2 ; 23
Одночлены содержат только действия умножения и возведения в степень.
13.
Определение. Одночлен, который содержит только один числовой множитель, отличный отнуля, стоящий на первом месте, а все остальные множители – это степени с различными
основаниями. Такой вид одночлена называют стандартным видом одночлена.
Определение. Числовой множитель одночлена, записанного в стандартном виде, называют
коэффициентом одночлена.
Определение. Степенью одночлена называют сумму показателей степеней всех
переменных, входящих в него. Степень одночлена, который является числом, отличным от
нуля, считают равной нулю.
Примеры:
Степень одночлена −3,8




































 Математика
Математика








