Похожие презентации:
Теория вероятностей. Случайные события и вероятность
1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
2. Случайные события и вероятность
3.
Теоретико-вероятностные модели реальныхпроцессов и явлений, их применение при
решении прикладных задач
События в материальном мире можно разбить на три
категории – достоверные, невозможные и случайные.
Например, если подбросить игральную кость, то достоверно,
что число выпавших очков будет натуральным числом, не
возможно, чтобы это число равнялось 10, и возможно, что оно
будет равно 2. Однако, возможно также, что это число будет
равно 1,3,4,5,6.
Потребности практики привели математиков к
изучению случайных событий. Например, при организации
телефонной связи в некотором районе нужно знать число
вызовов в каждый момент времени, а оно случайным образом
изменяется с течением времени.
4.
При стрельбе из артиллерийского орудия надо знатьчисло снарядов, попавших в цель, а попадание в цель
является случайным событием. Методы теории вероятности
широко применяются в различных отраслях естествознания
и техники: в теории надежности, теории массового
обслуживания, в теоретической физике, геодезии, астрономии,
теории стрельбы, теории ошибок наблюдений, теории
автоматического управления, общей теории связи и во многих
других теоретических и прикладных науках. Теория
вероятностей служит также для обоснования математической
и прикладной статистики, которая в свою очередь
используется при планировании и организации производства,
при анализе технологических процессов, предупредительном
и приемочном контроле качества продукции.
5.
На первый взгляд может показаться, что в задачах ослучайных событиях ничего нельзя сказать об их исходе. И,
действительно, если бросить кость лишь один раз, то с
одинаковой вероятностью можно ожидать выпадения 1,2,3,4,5
или 6. Но при многократном повторении этого опыта
оказывается, что одни исходы будут появляться чаще, а
другие реже. Например, если подбросить кость 1200 раз, то
очень маловероятно, чтобы все время выпадало одно очко.
Гораздо вероятнее, что значения 1,2,3,4,5 и 6 будут появляться
примерно с одной и той же частотой.
Раздел математики, изучающий закономерности
случайных событий, называется теорией вероятностей. Эта
теория имеет дело не с отдельными событиями, а с
результатом проведения достаточно большого числа
испытаний, то есть с закономерностями массовых случайных
явлений.
6.
Основные понятия теории вероятностей.Аксиомы Колмогорова и их следствия.
I.Случайные события и случайные
величины.
1.Случайные события и их вероятности.
1.1.Случайный эксперимент. Случайные
события. Отношения между событиями.
7.
Определение.Случайный эксперимент S (опыт) – эксперимент,
результат которого не может быть точно
предсказан.
Определение.
Случайное событие (А, В, С и т.п.) – результат
случайного эксперимента. Это событие, которое
при заданном комплексе условий может как
произойти, так и не произойти.
Например, если брошена монета, то она может
упасть так, что сверху будет либо герб, либо
решка. Поэтому событие « при бросании монеты
выпал герб» - это случайное событие.
8.
Рассмотрим множество Ω всех возможныхвзаимно исключающих друг друга исходов
некоторого испытания ( эксперимента). Это
множество будем называть пространством
элементарных исходов. Число исходов, входящих в
Ω, может быть конечным или бесконечным.
Случайное событие А- некоторое подмножество
множества Ω.
Пример. Стрелок стреляет по мишени, разделенной
на 4 равные области. Выстрел – это случайный
эксперимент. Попадание в определенную область
мишени – это случайное событие.
Ω = {A,B,C,D,F}, где F – стрелок не
А В
С
попал в мишень
D
9.
Определение.Достоверное событие U – событие, которое в
данных условиях обязательно произойдет.
Невозможное событие V – событие, которое в
данных условиях никогда не произойдет.
Пример. В сосуде находится вода при нормальном
атмосферном давлении и температуре 200. В этом
случае событие « вода находится в жидком
состоянии» - достоверное событие, а событие «
вода находится в твердом состоянии» невозможное событие
10.
Определение. События А и В называютсянесовместными, если их совместное появление в
данном опыте невозможно, т.е. АВ=V, или,
другими словами, наступление одного из событий
исключает возможность наступления другого.
Примеры. 1. При бросании монеты появление
герба исключает появление решки, следовательно,
события « появился герб» и « появилась решка» несовместные события.
2. Бросаем кубик. События « число очков,
выпавших на кубике четное » и « число очков,
выпавших на кубике равно 4 » - совместные
события.
11.
Определение. Произведением (совмещением) двухсобытий А и В называется общая часть множеств
исходов, составляющих события А и В. Или
другими словами, совмещением двух событий А и
В называется новое событие АВ (или А В), в
результате которого происходит как событие А ,
так и событие В.
Определение. Суммой двух событий А и В
называется событие А+В (или А В) , состоящее в
наступлении хотя бы одного из этих событий: или
А, или В, или А и В вместе.
12.
Пример. Из ящика с деталями ( стандартные,нестандартные, окрашенные, неокрашенные)
наудачу извлекают деталь. Событие А – деталь
стандартная, событие В – деталь окрашенная.
Тогда событие А+В – деталь либо стандартная,
либо окрашенная, а событие АВ - деталь
стандартная и окрашенная.
Определение. Произведением нескольких
событий называется новое событие, состоящее в
совместном наступлении всех этих событий.
Определение. Суммой нескольких событий А1,
А2, …,Аn называется событие, соответствующее
объединению множеств А1, А2, …,Аn ( произойдет
хотя бы одно из указанных событий).
13.
Пример. Бросаем монету три раза. СобытияА - появление герба при первом бросании,
В - появление герба при втором бросании,
С - появление герба при третьем бросании.
Тогда АВС - появление герба при всех трех
бросаниях.
Определение. События А1, А2,..., Аn образуют
полную группу событий, если в результате
испытания обязательно должно произойти одно и
только одно из них. Это значит, что данные
события попарно несовместны и в сумме
образуют достоверное событие, т.е.,
АiАj = V (i j),
А1+ А2+... Аn = U.
14.
Пример. Стрелок произвел выстрел по мишени.Событие А- стрелок попал в цель, событие В –
промахнулся. Эти два события несовместны и в
результате
испытания
обязательно
какое-то
из
этих
A A U , A A V
событий произойдет. Ω={А,В}. События А и В
образуют полную группу.
Определение. События А и Ā называются
противоположными, если они образуют полную
группу событий, т.е. А+Ā=U, АĀ= V.
(Другими словами, событие Ā состоит в
n
n
ненаступлении
события
А).
A
A
;
i
i
i 1
i 1
В предыдущем
примере:
А- попадание, Ā=В –
промах.
15.
Для любых n событий имеют место формулыдвойственности: n
n
A A
i 1
i
i
i 1
A A U , A A V
Определение.
События называются равновозможными, если есть
основание считать, что одно из них не является
более возможным, чем другое.
Например, появление герба и появление решки при
бросании монеты – равновозможные события, так
как предполагается, что монета изготовлена из
однородного материала, имеет правильную
огранку и наличие чеканки не влияет на выпадение
той или иной стороны монеты.
16.
1.2.Вероятность события.Пример. Случайный эксперимент S – однократное
подбрасывание игральной кости. Пусть Х число
выпавших очков. А={Х=1}, В={Х-четно},
U={Х 6}, V={X>6}. События А и В –
несовместные события, А+В={1,2,4,6}, АВ=V.
Очевидно, что возможность того, что при бросании
игральной кости произойдет событие В больше,
чем возможность того, что произойдет событие А.
Встает вопрос: можно ли охарактеризовать эту
возможность каким- либо числом. Оказывается
можно. Это число и называют вероятностью
события.
17.
Таким образом, вероятность – есть число,характеризующее степень возможности появления
события.
Обозначение: P(A) – вероятность события A.
Найдем вероятности событий А и В. Каждый из
возможных результатов испытания ( испытание
состоит из в бросании игральной кости)
называется элементарным исходом. Элементарные
исходы обозначим w1, w2,…, wn. У нас 6
элементарных исходов: w1={X=1}, w2={X=2},
w3={X=3} , w4={X=4}, w5={X=5}, w6={X=6}.
18.
Легко видеть, что эти исходы образуютполную группу событий (они попарно
несовместны, в результате испытания одно из
событий обязательно произойдет), и
равновозможные. Те элементарные исходы, в
которых интересующее нас событие наступает,
назовем благоприятствующими. В нашем случае,
благоприятствующие исходы событию А w1={X=1} (один исход) и благоприятствующие
исходы событию В - w2={X=2}, w4={X=4},
w6={X=6}( 3 исхода).
Тогда P(A)=1/6, P(B)=3/6=1/2.
19.
Классическая модель.Пусть проводится эксперимент, который может
окончиться одним из n равновозможных
элементарных исходов. В этом эксперименте
может наступить интересующее нас событие А. Те
m элементарных исходов эксперимента, в которых
событие А наступает, называют
благоприятствующими этому событию.
20.
Определение. Вероятностью события Аназывают отношение числа благоприятствующих
этому событию элементарных исходов
эксперимента N A к их общему числу N, т.е.
NA
P(A)= N A/ N.
В этом определении предполагается, что
элементарные исходы несовместные,
равновозможные и образуют полную группу (т.е.
эксперимент заканчивается одним и только одним
исходом).
21.
Свойства.1)Вероятность достоверного события равна 1.
Действительно, если событие достоверно, то
каждый элементарный исход испытания
NA
благоприятствует событию U.
P(U)=NA/N=N/N=1.
2)Вероятность невозможного события равна 0.
Действительно, если событие невозможное, то
ни один из элементарных исходов испытания не
благоприятствует событию V.
P(V)=0/N=0.
3)Вероятность случайного события есть
положительное число, меньшее 1.
0<P(A)<1
22.
Действительно, случайному событиюблагоприятствует лишь часть из общего числа
элементарных исходов испытания. В этом случае
0<NA<N. Следовательно, 0<P(A)=NA/N<1.
NA
Итак, вероятность любого события удовлетворяет
неравенству:
0 P( A) 1
Построенная таким образом модель называется
классической моделью. Недостаток классической
модели – неприменима к испытаниям с
бесконечным числом исходов и в том случае, когда
исходы не равновозможные.
23.
Статистическая вероятность.Статистический подход к определению
вероятности применяется тогда, когда эксперимент
можно неоднократно повторить в неизменных
условиях.
Пусть проводится эксперимент S, в ходе
которого может произойти или не произойти
событие А.
Пусть n – число повторений эксперимента, nAчисло появлений события А в серии из n опытов.
Тогда nA/n – относительная частота появления
события А в серии из n опытов.
24.
Рассмотрим новую достаточно длиннуюсерию из n опытов примерно в тех же условиях и
снова найдем отношение nA/n и так несколько
серий. Если частота мало отличается от серии к
серии, колеблясь около некоторого числа p, то это
число принимают за вероятность события А.
Пример. Замечено, что при изготовлении деталей
на отлаженном станке в каждой партии из 1000
деталей от 2 до 4 бракованных. Тогда можно
утверждать что вероятность брака p=3/1000. Если
же в одних партиях 2-3 бракованных детали, а в
других 30-40, то о вероятности брака ничего
сказать нельзя( либо меняются условия работы,
либо станок не отлажен)
25.
Определение. Относительной частотой событияназывают отношение числа испытаний, в которых
это событие появилось, к общему числу фактически
проведенных испытаний.
Длительные наблюдения показали, что если в
одинаковых условиях производят опыты, в каждом
из которых число испытаний достаточно велико, то
относительная частота обнаруживает свойство
устойчивости.
26.
Это свойство состоит в том, что в различныхопытах относительная частота меняется мало (тем
меньше, чем больше произведено испытаний),
колеблясь около некоторого постоянного числа.
Это постоянное число есть вероятность события.
Итак, в качестве статистической
вероятности события принимают
относительную частоту или число, близкое к ней.
27.
Общая дискретная модель.Пусть эксперимент S имеет конечное или
счётное число исходов ω1, ω2, … , ωn, …
Эти исходы называются элементарными
событиями. Совокупность всех элементарных
событий, связанных с данным экспериментом,
называют дискретным пространством
элементарных событий или пространством
исходов и обозначают Ω.
Ω = { ω1, ω2, … , ωn, …}
28.
Предполагается, что в результате экспериментаможет быть зафиксирован один и только один
исход, и вероятности исходов р(ωi) заранее
известны, причём, выполнены аксиомы:
1) р(ωi) 0;
2) p( i ) 1,
wi .
i: i
Случайное событие А – любое подмножество
множества Ω.
29.
Вероятность события А – сумма вероятностейотдельных исходов, составляющих событие А,
то есть P( A) p( i )
i: i А
Следствия из аксиом и определения
вероятности
1.Пусть U – достоверное событие, тогда
Р(U) = p( i ) 1.
i: i
2.Для любого события А: 0 Р(А) 1.
30.
3.Пусть Ω = { ω1, ω2,…, ωn} и р(ωi) = р. ТогдаР(А) = p( i ) N A p
i: i А
1 p( i ) N p p 1 / N
i: i
то есть классическая модель – частный случай
общей дискретной модели.
31.
Геометрическая модель.Многие практические задачи приводят к
вопросам теории вероятности, которые не
укладываются в разобранную выше схему
конечного числа попарно несовместных исходов
испытаний. Пусть, например, стержень наудачу
разламывается на три части. Какова вероятность
того, что из получившихся отрезков можно будет
построить треугольник?
В этой задаче мы имеем бесконечное
множество исходов, так как разлом может попасть
на любую точку стержня. Здесь мы будем
пользоваться иным определением вероятности,
которое назовем геометрическим.
32.
Рассмотрим следующую модель. Пусть наотрезок АВ бросают наудачу точку. Назовем
вероятностью попадания этой точки на часть этого
отрезка отношение длины этой части к длине всего
отрезка ( если часть состоит из нескольких кусков,
то надо сложить длины этих кусков). Вместо
отрезка АВ можно взять некоторую
геометрическую фигуру, имеющую конечную
площадь и считать вероятностью попасть в часть X
этой фигуры отношение площадей указанной
части и всей фигуры.
33.
Итак, геометрическая вероятность – этовероятность попадания точки в некоторую область.
(отрезок, часть плоскости, шар, и т.д.)
Пусть Ω – область на плоскости, D Ω. μ(Ω), μ(D) –
площади этих областей.
В Ω наудачу бросается случайная точка ω.
Вероятность попадания в любую подобласть
области Ω зависит только от её площади. Тогда
P{ω D} = μ(D) / μ(Ω).
34.
Замечания.1.Такой подход распространяется и на n-мерный
случай
2.Геометрическая модель имеет ограниченную
область применения ввиду требования
равновозможности отдельных точек.
Пример 1. Вернемся к задаче о разламывании
стержня. Пусть на отрезок длины 1 бросают
наудачу две точки. Они разбивают отрезок на три
отрезка. Какова вероятность, что из полученных
трех отрезков можно сложить треугольник?
Заданный отрезок рассматриваем как отрезок [0,1]
числовой прямой. Тогда наудачу брошенные точки
имеют координаты – числа x и y, принадлежащие
35.
отрезку [0,1]. Но любую пару чисел можнорассматривать как координаты точки на
плоскости. Поскольку 0≤x≤1, 0≤y≤1, то эти точки
(x,y) наудачу брошены в квадрат со стороной 1.
Посмотрим теперь какую фигуру образуют точки,
координаты которых удовлетворяют условию
примера.
Для того, чтобы из этих трех отрезков можно
было построить треугольник, необходимо и
достаточно, чтобы длины этих отрезков
удовлетворяли неравенству треугольника.
36.
0x
1
y
При x≤y получаем: x<(y-x)+(1-y);
y-x<x+(1-y);
1-y<x+(y-x), что после
преобразований дает систему неравенств:
x 0, 5,
y x 0, 5,
y 0, 5,
x y,
Y
B
1
0,5
C
A
0,5
1
X
которой на плоскости XOY
соответствует треугольник ABC,
площадь которого S=1/8.
37.
0y
x
1
При x>y получаем: y<(x-y)+(1-x);
x-y<y+(1-x);
1-x<y+(x-y), что после
преобразований дает систему неравенств:
Y
1
0,5
M
N
K
0,5
1
y 0, 5,
y x 0, 5,
x 0, 5,
x y,
которой на плоскости XOY
X
соответствует треугольник NMK
площадь которого S=1/8.
38.
Площадь квадрата равна 1. Следовательно,вероятность построить треугольник равна
P=(1/8+1/8)/1=1/4.
Пример 2. (задача Бюффона) . На плоскости
проведено семейство параллельных прямых.
Расстояние между соседними прямыми равно m.
На эту плоскость наудачу бросается отрезок
длины m. Какова вероятность, что отрезок
пересекается хоть с одной прямой из этого
семейства?
Решение.
39.
xy
B
A
Рис. 1
Y
y=m sinx
m
Рис.2
π
X
Обозначим через y расстояние от верхнего конца
отрезка до ближайшей снизу прямой. Проведем
луч с началом в верхней (левой) точке отрезка,
параллельный прямым семейства и идущий
направо. Обозначим через x угол между этим
лучом и отрезком. Мы получили пару чисел,
удовлетворяющих неравенствам: 0≤x<π, 0≤y≤m.
Точка (x,y) с такими координатами наудачу
брошена в прямоугольник (рис2).
40.
Для того, чтобы отрезок пересекался хотя бы содной из прямых семейства, необходимо и
достаточно выполнение неравенства
y≤ |AB|=m sinx ,
которым на рисунке 2 определена заштрихованная
фигура. Найдем ее площадь:
S1 m sin x dx m cos x 2m.
0
0
Так как площадь прямоугольника, в который
наудачу брошена точка, S=πm, то искомая в
примере вероятность p=S1/S=2m/πm=2/π.
41.
Пример 3. (задача о встрече). Два студентаусловились встретится в определенном месте
между 12 и 13 часами дня. Пришедший первым
ждет второго в течении ¼ часа, после чего уходит.
Какова вероятность, что встреча состоится, если
каждый студент наудачу выбирает момент своего
прихода?
Решение.
0≤x≤1, 0≤y≤1, |y-x|≤1/4. Тогда
Y
y≤x+1/4, y≥x-1/4.
1
1/4
1/4
1
Sкв.=1, Sф=1-2(3/4·3/4·1/2)=1-9/16
= =7/16.
X
Следовательно, p=Sф/Sкв.=7/16.
42.
1.3. Элементы комбинаторики. Задачи нанепосредственный подсчет вероятностей
Комбинаторика изучает количество комбинаций
(подчиненное определенным условиям), которое
можно составить из элементов некоторого
заданного конечного множества.
Определение. Размещением называются
комбинации, составленные из n различных по m
элементов, которые отличаются либо составом
элементов, либо их порядком.
Пусть {a1,a2,…,an} – множество из n элементов.
Тогда любое упорядоченное его подмножество из
m элементов называется размещением из n
элементов по m.
43.
Например, рассмотрим множество A={1,2,3,,,,4,5}.Пусть m=3. Тогда можно рассмотреть следующие
размещения из 5 элементов по 3: (1,3,5), (5,3,1),
(4,2,1) и т.д.
Найдем число размещений без повторений из n
элементов некоторого множества по m. Первым
элементом x1 может стать любой элемент из n
элементов заданного множества, то есть получаем n
возможностей выбора. Если элемент x1 уже выбран,
то второй элемент x2 можно выбрать уже n-1
способом, так как повторение первого элемента не
допускается. Аналогично, при выбранных x1и x2,
третий элемент x 3 можно выбрать n-2 способами и
т.д. вплоть до элемента x , который можно выбрать
44.
n-(m-1) способами, так как до него уже выбраныпервые m-1 элементы, ни один из которых не
должен повториться. Тогда получаем, что число
размещений из n элементов по m элементов
выражается формулой:
n!
A n(n 1)...(n m 1)
.
(n m)!
Определение. Перестановками называются
комбинации, составленные из одних и тех же n
различных элементов и отличающиеся только
порядком их расположения. (или перестановка –
это взаимно однозначное отображение множества
первых n натуральных чисел в себя).
m
n
45.
Замечание.1) Размещения из n элементов по n элементов
называются перестановками из n элементов.
2) Число всевозможных перестановок pn=n!
Определение. Сочетаниями называются
комбинации, составленные из n различных
элементов по m элементов, которые отличаются
хотя бы одним элементом.
Например, из множества {a,b,c,d,f} можно
составить 10 сочетаний по 3 элемента в каждом:
{a,b,c}, {a,b,d}, {a,b,f}, {a,c,d}, {a,c,f}, {a,d,f},
{b,c,d}, {b,c,f}, {b,d,f}, {c,d,f}.
46.
Число сочетаний из n элементов по m элементовравно
n!
C
m !(n m)!
m
n
Примеры.
1. Сколько пятизначных чисел можно составить из
цифр {1,2,3,4,5}, так чтобы ни одна цифра не
повторялась?
Pn=n!=5!=120.
2. Сколько трехзначных чисел можно составить из
цифр {1,2,3,4,5}, так чтобы ни одна цифра не
повторялась?
A 5 4 3 60
3
5
47.
3) В аудитории 22 места. Сколькими способамиможно рассадить 15 студентов?
15
A22
22 21 ... (22 15 1) 22 21 ... 8.
4) Сколькими способами можно составить
команду из 4 человек для соревнований по бегу,
если имеется 7 бегунов.
7!
C
35.
4!(7 4)!
4
7
Замечание. Если бы команда выбиралась для
эстафетного бега, то число способов выбора было
бы равно A74 35 4! 35 24 840
так как играет роль порядок выбора спортсменов.
48.
5) Сколькими способами можно выбрать 2 деталииз ящика, содержащего 10 деталей.
10!
C
45.
2!(10 2)!
2
10
Свойства сочетаний.
1)Cn0 C00 1,
n!
0
Cn
0!(n 0)!
2)Cnm Cnn m ,
n!
n!
n m
C
, Cn
m !(n m)!
(n m)!(n n m)!
m
n
49.
n 1n
3)C C
1
n
n,
4) Ank Cnk pk
n!
n!
k
A
, Cn
(n k )!
k !(n k )!
k
n
Ank Cnk k ! Cnk pk .
50.
Упорядоченные выборкиВсе множество изучаемых объектов называется
генеральной совокупностью(г.с.). Число элементов
г.с. n - объем выборки. Любое множество
объектов, случайно выбранных из г.с. – случайная
выборка. Число элементов m выборки – объем
выборки.
Определение. Пусть {a1,a2,…,an} – множество из n
элементов или г.с. Упорядоченной выборкой
объема m из данной г.с. называется любое
упорядоченное подмножество из m его элементов.
51.
Пусть элементы выборки выбираются один задругим. Возможны два варианта.
1) Выборка с возвращением. Такие выборки –
упорядоченные множества, в которых допускаются
повторения.
2) Выборка без возвращения. Здесь элемент,
выбранный однажды, исключается из г.с. Такие
выборки – упорядоченные множества без
повторений. (m≤n).
52.
1. Схема выбора без возвращения.А)Пусть опыт состоит в выборе m элементов без
возвращения и без упорядочивания. Тогда
различными исходами следует считать m элементные подмножества исходного множества,
имеющие различный состав. Общее число
элементарных исходов при этом равно
n!
C
m !(n m)!
m
n
53.
Б)Пусть опыт состоит в выборе m элементов безвозвращения, но с упорядочиванием их по мере
выбора. Тогда различными исходами будут
упорядоченные m - элементные подмножества
исходного множества, отличающиеся либо
набором элементов, либо порядком их
следования. Общее число элементарных исходов
при этом равно
Anm n(n 1)(n 2)...(n m 1)
54.
2. Схема выбора с возвращением.а) Пусть опыт состоит в выборе m элементов с
возвращением, но без упорядочивания. Тогда
различными исходами следует считать m элементные подмножества исходного множества,
отличающиеся составом. Но при этом различные
наборы могут содержать повторяющиеся
элементы. Общее число элементарных исходов
при этом равно
C
m
n m 1
55.
Б)Пусть опыт состоит в выборе m элементов свозвращением и с упорядочиванием их в
последовательную цепочку. Тогда различными
исходами будут упорядоченные m - элементные
подмножества ( с повторениями) исходного
множества, отличающиеся либо составом
элементов, либо порядком их следования. Общее
число элементарных исходов при этом равно
nm
56.
Пример. В партии из N деталей имеется nстандартных. Наудачу отобраны m деталей. Найти
вероятность того, что среди отобранных деталей
ровно k стандартные.
Решение. Общее число возможных элементарных
исходов равно числу способов, которыми можно
извлечь m деталей из N деталей, то есть C Nm числу сочетаний из N элементов по m. Найдем
число благоприятных исходов. Нам надо выбрать k
k
C
стандартных деталей из n стандартных n
способами, при этом остальные m-k деталей
должны быть нестандартными. Выбрать же m-k
нестандартных деталей из N- m деталей можно C Nm nk
способами. Следовательно, число благоприятных
57.
исходов равноТогда
C C
k
n
m k
N n
p( A) Cnk CNm nk / CNm
58.
1.4.Операционные формулы теориивероятностей.
Правило сложения вероятностей.
Теорема 1. Вероятность появления одного из двух
несовместных событий, безразлично какого, равна
сумме вероятностей этих событий.
Р(А+В)=Р(А)+Р(В)
a1 , ... am
b1 , ... bn
Доказательство.
Обозначим исходы, благоприятные для
, ...через
, am
событияa1А,
, а для события bВ1 , –... , bn
через
. Вероятности этих исходов
обозначим соответственно
.
p1 , ...,через
pm и q1 , ..., q n
b1 , ... bn
59.
Тогда событию АUВ благоприятны все исходыa1 ,..., am , b1 ,..., bn
В силу того что события А и В несовместимы ,
среди этих исходов нет повторяющихся. Поэтому
вероятность события АUВ равна сумме
вероятностей этих исходов , т.е.
A B
a1 ,..., a m , b1 ,..., bn
.
A B
p( A B) p1 ... pm q1 ...qn .
Но
p1 ... pm P( A), q1 ... qn P( B),
а поэтому Р(А+В)=Р(А)+Р(В).
P( A B) P( A) P( B).
60.
Пример. Стрелок стреляет в мишень.Вероятность выбить 10 очков равна 0,3 , а
вероятность выбить 9 очков равна 0,6. Чему
равна вероятность выбить не менее 9 очков?
Решение. Событие А «выбить не менее 9
очков» является объединением событий
В – «выбить 10 очков» и С –«выбить 9 очков».
При этом события В и С несовместимы ,так
как нельзя одним выстрелом выбить и 9 и 10
очков. Поэтому по теореме 1 имеем:
P( A) P( B) P(C ) 0,3 0,6 0,9.
P( A) P( B) P(C ) 0,3 0,6 0,9.
61.
Следствие. Если события А1,…,Аn попарнонесовместимы, то вероятность объединения
этих событий равна сумме их вероятностей:
P( A1 ... An ) P( A1 ) ... P( An ).
P( A1 ... An ) P( A1 ) ... P( An ).
Доказательство. Если события A1 , ..., An попарно
несовместимы , то событие A1 ... An 1
несовместимо с событием An . В самом деле
( A1 ... An 1 ) An ( A1 An ) ... ( An 1 An ).
A1 ... An 1
Но при s<n имеем As
( A1
... An 1 )
An
An , и поэтому
а потому по теореме 1 имеем:
P( A1 ... An 1 An ) P( A1 ... An 1 ) P( An ).
( A1 ... An 1 ) An
62.
Применяя это же рассуждение к первомуслагаемому и продолжая далее, получаем после n-1
шага , что P( A ... A ) P( A ) ... P( A )
1
n
1
n
P( A1 ... An ) P( A1 ) ... P( An ).
Пример В цехе работают несколько станков.
Вероятность того, что за смену потребует наладки
ровно один станок , равна 0.2. Вероятность того,
что за смену потребуют наладки ровно два станка,
равна 0,13. Вероятность того, что за смену
потребуют наладки больше двух станков , равна
0.07. Какова вероятность того, что за смену
придется проводить наладку станков?
63.
Решение. В этом примере опыт состоит в том, чтопрошла смена и отмечено, сколько станков за эту
смену потребовало наладки. В этом опыте события
: А-«за смену потребовал наладки ровно один
станок», В- «за смену потребовали наладки ровно
два станка», и С- « за смену потребовали наладки
более двух станков» несовместимы. Нас же
интересует вероятность события AU BU C
P( A B C ) P( A) P( B) P(C )
0, 2 0,13 0, 07 0, 4.
64.
Выведем теперь связь между вероятностямипротивоположных событий.
Теорема 2. Для любого события А имеем:
P( A ) 1 P( A).
Для доказательства вспомним, что
A A U , P(U ) 1 и A A
Тогда по теореме 1 получаем:
1 P(U ) P( A A ) P( A) P( A ),
и, следовательно,
P( A ) 1 P( A).
65.
натуральное число от 100 до 999. Каковавероятность того, что хотя бы две его цифры
совпадают?
Решение. Опыт здесь состоит в том, что
наудачу выбирается число от 100 дл 999 и
смотрят , есть ли у него совпадающие цифры.
События «взяли наудачу число N» (N =100,
101, …, 999) равновероятны (в этом смысл
слова «наудачу») и образуют множество
исходов этого опыта. Число исходов n=900.
Нас интересует событие А – « у выбранного
числа совпадают хотя бы две цифры». Проще
, однако , подсчитать вероятность
противоположного события Ā - « у выбранного
À
66.
Каждое такое число есть размещение безповторений из 10 цифр по 3, не имеющих первым
элементом нуль. Следовательно,
m A A 10 9 8 9 8 9 8
( из числа всех трехэлементных размещений без
повторений надо вычесть число тех, у которых на
первом месте стоит нуль) и
3
10
2
9
2
92 8
P( A )
0,72.
900
Тогда по теореме 2
P( A) 1 P( A ) 0,28.
67.
В ряде случаев приходится вычислять вероятностьобъединения событий, которые могут быть
совместными.
Теорема 3. Вероятность появления хотя бы одного
из двух совместных событий равна сумме
вероятностей этих событий без вероятности их
совместного появления;
P( A B) P( A) P( B) P( AB).
Доказательство. Событие А состоит из компонент
A B и A B , а событие В – из компонент A B
и A B. Тогда
A B,
А В ( А В) ( А В ) ( А В) ( А В)
( А В) ( А В ) ( А В)
68.
И поскольку входящие в это разложениекомпоненты попарно не пересекаются, то
P( А
В) P( А
В) P( А
В ) P( А
В).
С другой стороны, имеем
Р( А) Р( А В) Р( А В ) и
Р( В) P( А В) Р( А В),
Ð( Â) Ð( À Â) Ð( À Â),
а потому
P( A B) P( A) P( B) P( AB).
69.
Следствия.n
1)P(A1+A2+...+An)= P( Ai ) P( Ai Aj ) P( Ai Aj Ak )
n 1
i 1
( 1) P( A1 A2 An )
i j
i j k
В частности , при n=3 имеем:
P( А В С ) Р( А) Р( В) Р(С ) Р( АВ )
Р( АС ) Р( ВС ) Р( АВС ).
2) P(A1+A2+...+An)=1– P( A1 A2 An ).
70.
Утверждение. Сумма вероятностей событий,образующих полную группу равна 1.
P(А1)+P( А2)+...P(Аn) = 1.
Доказательство. Пусть события А1, А2,..., Аn
образуют полную группу событий. Тогда данные
события попарно несовместны и в сумме
образуют достоверное событие, т.е.,
АiАj = V (i j),
А1+ А2+... Аn = U.
Следовательно, P(А1+ А2+... Аn) =P(U)=1.
С другой стороны, так как события А1, А2,..., Аn
несовместные, то
P(А1+ А2+... Аn) =P(А1)+P( А2)+...P(Аn) = 1.
71.
Условная вероятность.Пример. Из урны, в которой находятся 3 белых
и 2 черных шара, последовательно извлекают
два шара. Пусть А={Появление белого шара
при первом извлечении}, В={Появление
белого шара при повторном извлечении}.
1)Выбор с возвращением.
Р(В)=3/5 – не зависит от того, какой шар
был вынут при первом извлечении. В таком
случае говорят, что событие В не зависит от
события А.
Р(А)=3/5, →Р(АВ)=(3·3)/(5·5)=Р(А)·Р(В).
72.
2)Выбор без возвращения.Обозначим Р(В/А) - вероятность
события В при условии, что произошло
событие А. Такая вероятность называется
условной вероятностью. Аналогично
введем Р(В/Ā).
Очевидно Р(В/А)=2/4=1/2, Р(В/Ā)= 3/4 .
Т.е. в этом случае вероятность события В зависит
от того, произошло или нет событие А.
Р(АВ)=(3·2)/(5·4)=3/10=Р(А)·Р(В/А).
).
73.
Перейдем к определению условной вероятностиР(В/А).Применим статистический подход. Пусть
опыт S повторен N раз, при этом событие А
наблюдалось NА раз, событие АВ – NAB раз.
Условная частота появления события АВ в серии
из NA опытов равна
NAB /NA=(NAB/N)/(NA/N) P(AB)/P(A).
С другой стороны, при больших NA,
NAB /NA Р(В/А). Поэтому естественно принять
по определению
Р(В/А)=Р(АВ)/Р(А).
74.
Правило умножения вероятностей.Вероятность совместного появления двух событий
равна произведению вероятности одного из них на
условную вероятность другого, вычисленную в
предположении, что первое событие уже
наступило.
Р(АВ)= Р(А)Р(В/А)
Следствия:
1)Р(А)Р(В/А)=Р(В)Р(А/В);
2)P(A1A2...An)=Р(А1)Р(А2/А1)Р(А3/А1А2)...
Р(Аn/ A1A2...An-1).
75.
Статистическая независимость.Пусть событие В не зависит от события А
(появление события А не изменяет вероятность
появления события В) Тогда имеет место
равенство:
Р(В/А)=Р(В) .
Так как P(AB)= P(A)P(B/A) =P(BA)=P(B)P(A/B), то
P(A)P(B) =P(B)P(A/B), P(A)=P(A/B), то есть
условная вероятность события А в предположении,
что наступило событие В, равна безусловной
вероятности события А.
76.
Следствия1) Если В не зависит от А, то и А не
зависит от В, т.е. свойство независимости
взаимно.
2)Если А и В – независимы, то независимы
также Ā и В.
В частности для независимых событий
Р(АВ)=Р(А)Р(В) .
Часто за определение независимости принимают
последнее равенство.
77.
Определение. События А и В называютсястатистически независимыми, если
вероятность их совместного наступления
равна произведению их вероятностей.
Определение. События А1, А2,...Аn
называются независимыми в совокупности,
если для любого Pих
( A подмножества
A ...A ) P( A ) P( A )...P( A ),
k1
k2
km
k1
k2
km
m=2,3, ...n.
Если данное условие выполняется только для
m=2, то события попарно независимы.
Замечание. Из попарной независимости событий
не следует их независимость в совокупности.
78.
Пример. Четыре охотника стреляютодновременно и независимо друг от друга по
зайцу. Заяц подстрелен, если попал хоть один
охотник. Какова вероятность подстрелить
зайца если вероятность попадания для
каждого
равна 2/3
?
Решение.охотника
Перенумеруем
охотников
и
2
3
?
рассмотрим события А k - «попадание k-го
охотника», где k=1,2,3,4. Эти события по условию
задачи независимы и P(Ak )=2/3 при любом k. Нас
интересует вероятность события «заяц
подстрелен», т. е. A1 A2 A3 A4
Ak
P ( Ak )
2
3
A1 A2 A3 A4
:
P( A1
A2
A3
A4 ) P( A1 A2 A3 A4 ) 1 P( A1 A2 A3 A4 )
4
1
1
1 P( A1 ) P( A2 ) P( A3 ) P( A4 ) 1 1 0,988.
81
3
79.
Пример. Событие А может произойти в опытес вероятностью p. Опыт повторили
независимым образом n раз. Какова
вероятность того, что при этом событие А
произойдет хоть один раз?
Решение. Рассмотрим события Аk -«событие А
произошло при k-м повторении опыта», k=1,2,…n.
События Аk независимы, так как опыты
повторяются независимым образом. P(Аk)=p для
всех k. Нас интересует событие «опыт повторили
n
независимым образом n раз и при
этом событие А
Ak
произошло хотя бы один раз»- k 1 . Заметив, что
P Аk 1 p q
Āk независимы
и
, получаем:
n
n что
Ak
Ak
P( Ak ) p
n
Ak
k 1
Ak
P Ak 1 P( Ak ) 1 P( A1 ) P( A2 ) ... P( An ) 1 q n .
k 1
k 1
80.
nP( An ) lim (1 q ) 1
Интересно отметить, что lim
n
n
k 1
( поскольку 0<q<1 ), т. е. при достаточном
большом числе повторений опыта событие А
произойдет наверняка ( с вероятностью, как угодно
близкой к 1 ) хоть один раз. Про события, которые
происходят почти наверняка , принято говорить,
что они практически достоверны.
n
81.
1.5. Формула полной вероятности и формулаБайеса. Решение прикладных задач.
Пусть событие А может наступить одновременно
с одним из событий Hi (i=1,2,...n), образующих
полную группу событий. Тогда
Р(А)=Р(Н1)Р(А/Н1)+Р(Н2)Р(А/Н2)+...+
+ Р(Нn)Р(А/Hn) .
(вероятность события А, которое может произойти
при условии появления одного из несовместных
событий Н1, Н2,+..Нn , образующих полную
группу, равна сумме произведений вероятностей
каждого из этих событий на соответствующую
условную вероятность события А).
82.
Доказательство.А=АН1 + АН2 + … + АНn ,
причём, события АНi попарно несовместны. Тогда
Р(А) = P(АН1 + АН2 + … + АНn )=Р(АН1 )+Р(АН2 )+
… + Р(АНn) = Р(Н1) Р(А/Н1) + Р(Н2) Р(А/Н2)+ … +
Р(Нn) Р(А/Нn)
Замечание. События Нi называются гипотезами,
разбивающими событие А на частные случаи.
83.
Пример 1. В трёх одинаковых урнах находятсябелые и чёрные шары: в первой урне 1 ч, 2 б, во
второй – 1 ч, 3 б, в третьей – 2 ч, 2 б. Наудачу
выбирается урна, а из нее – один шар. Найти
вероятность того, что вынутый шар белый.
Решение.
А = {появление белого шара при однократном
вынимании}, Нi = {выбрана i – ая урна}
Р(А) =
=Р(Н1)·Р(А/Н1) + Р(Н2)·Р(А/Н2)+ Р(Н3)·Р(А/Н3)=
=1/3·2/3+1/3·3/4+1/3·1/2=23/36.
84.
Пример 2. Вероятность попадания в цель при одномвыстреле из орудия равна 0,9. Вероятность
поражения цели при k попаданиях (k≥1) равна
1-qk. Найти вероятность того, что цель будет
поражена, если сделать 2 выстрела.
Решение. А- цель поражена, если сделано 2
выстрела; H1- два раза попали в цель; H2- один раз
попали в цель; H3- ноль раз попали в цель.
P(H1)=0,9·0,9=0,81; P(H2)=0,9·0,1·2=0,18;P(H3)=0,12.
P(A/H1)=1-0,1·0,1=0,99; P(A/H2)=1-0,1=0,9;
P(A/H3)=0. Тогда по формуле полной вероятности
P(A)= P(A/H1)P(H1)+P(A/H2)P(H2)+P(A/H3)P(H3)=
=0,81·0,99+0,18·0,9+0·0,01=0,9639.
85.
Пример 3. Из m экзаменационных билетов kтрудных. Кто имеет больше шансов вытянуть
трудный билет - тот, кто берёт билет первым или
вторым?
Решение.
Н1 = {первым вытянут трудный билет},
Р(Н1)=k/m.
Н2 = {первым вытянут лёгкий билет},
Р(Н2)=(m –k)/m.
А = {вторым вытянут трудный билет}
Р(А) = Р(Н1) Р(А/Н1) + Р(Н2) Р(А/Н2)=
=k/m· (k–1)/(m–1)+(m –k)/m·k/(m–1)= k/m.
86.
Замечание. Если мы не знаем какой билет вытянулпервый студент, то вероятность вторым вытянуть
трудный билет равна вероятности вытянуть
первым трудный билет.
Из формулы полной вероятности легко
получаются формулы Байеса. Вероятности Р(Нi)
нам известны до опыта. Их называют априорными
вероятностями (то есть до опыта).
Пусть произведен опыт, в результате которого
наблюдалось событие А. Как следует изменить
вероятности гипотез? Вероятности Р(Нi/А) принято
называть апостериорными вероятностями (то есть
после опыта).
87.
РассмотримР(Нi·А)= Р(Нi )Р(А/Нi)=Р(А)Р(Нi /А), откуда
следуют формулы Байеса:
Р(Нi/А)= Р(Нi )Р(А/Нi) / Р(А) (при Р(А) 0) ,
i=1,2,...,n.
Данное равенство истолковывается следующим
образом: если существуют попарно исключающие
друг друга гипотезы H1,…,Hn, охватывающие
всевозможные случаи, и если известны вероятности
события А при каждой из этих гипотез, то по
формуле Байеса можно найти вероятность
справедливости гипотезы Hi (i=1,2,...,n) при
условии, что произошло событие А.
88.
Пример . В цеху стоят a ящиков с исправнымидеталями и b ящиков с бракованными деталями.
Среди исправных деталей p% отникелированы, а
из числа бракованных никелированы q% деталей (
в каждом ящике). Вынутая наугад деталь оказалось
никелированной. Какова вероятность, что она
исправна?
Решение. Имеем события H1- «деталь исправна» и
H2 – «деталь бракованная», а также событие А –
«деталь отникелирована». Нам надо найти
значение Р(H1│А). По условию имеем :
a
b
p
q
P ( H1 )
, P( H 2 )
, P ( A H1 ) , P ( A H 2 ) .
a b
a b
100
100
89.
Подставляем эти данные в формулу Байеса,получаем
a
p
a b 100
P( H1 A)
.
a
p
b
q
a b 100 a b 100
Значит, искомая вероятность равна
ap
P( H1 / A)
.
ap bq
90.
1.6. Формула Бернулли. Закон больших чисел.При введении понятия вероятности
отмечалось, что если вероятность некоторого
события А равна р, то вероятнее всего, что при
повторении испытания много раз относительная
частота благоприятных этому событию исходов
будет мало отличаться от значения р. Это
утверждение, называемое в теории вероятностей
законом больших чисел, лежит в основе всех
практических приложений этой теории – оно
позволяет с помощью вычисленных вероятностей
предсказывать частоту наступления данного
события в длинной серии независимых испытаний.
91.
Пусть производится n независимых испытаний, вкаждом из которых событие А может появиться
либо не появиться. Вероятность появления
события А в каждом испытании одна и та же и
равна p. Тогда вероятность ненаступления события
А в каждом испытании также постоянна и равна
q=1-p. Требуется найти вероятность того, что при n
испытаниях событие А появится ровно m раз и ,
следовательно, не произойдет событие А n-m раз.
Причем, не требуется, чтобы событие А
повторилось ровно m раз в определенном порядке.
92.
Выведем формулу Бернулли, позволяющуювычислить вероятность того, что в серии из n
независимых испытаний событие А , имеющее
вероятность р, встретиться m раз. Результат серии
из n испытаний можно записать в виде ряда из
букв А и Ā, имеющего длину n. Например, если
проведено семь испытаний, причем событие А
произошло во втором , третьем и пятом
испытаниях, то запишем результат данной серии в
виде ĀААĀАĀĀ.
93.
Так как испытания данной серии независимы другот друга, то для вычисления вероятности данного
исхода испытаний надо заменить в записи этой
серии каждую букву А ее вероятностью p , а
каждую букву Ā ее вероятностью 1-p и
перемножить эти числа.
Пример 1. Проводится серия из 8 независимых
испытаний. Событие А имеет вероятность р=0,7.
Чему равна вероятность того, что получиться
исход вида ААĀАAĀAĀ. ?
Решение. Заменяем каждую букву А на 0,7, а
каждую букву Ā на 1-0,7=0,3. Получаем
0,7×0,7×0,3×0,7×0,7×0,3×0,7×0,3=0,750,33.
À
0,7 5 0,33
94.
Вообще, если событие А имеет вероятность р, товероятность появления конкретной серии из n
испытаний, в которой это событие произошло m
раз, равна pmqn-m, где q=1-p
Теорема. Пусть вероятность события А равна р, и
пусть P n (m)- это вероятность того, что в серии из
n независимых испытаний это событие произойдет
ровно m раз. Тогда справедлива теорема Бернулли
n m
Pn (m) Cn p q .
Доказательство. Вероятность одного события,
состоящего в том, что в n испытаниях событие А
наступит ровно m раз и не наступит n-m раз, по
теореме умножения вероятностей равна pmqn-m.
m
m
95.
Число таких событий равно числу сочетаний из nm
элементов по m элементов, то есть Cn . Так как
события несовместные, то по теореме сложения
вероятностей несовместных событий искомая
вероятность равна сумме вероятностей всех
возможных событий:
Pn (m) Cn p q
m
m
n m
.
96.
Пример 2. Какова вероятность того, что при десятибросаниях игральной кости 3 очка выпадут ровно 2
раза?
Решение. Вероятность выпадения 3 очков при
одном бросании равна 1/6. Поэтому р=1/6, q=5/6.
Так как, кроме того, n=10 и m=2, то по формуле
Бернулли имеем:
1 5 10 9 5
Р 10 (2) С
.
10
2 6
6 6
2
2
10
8
8
97.
Следствия из формул Бернулли.Вероятность того, что в серии из n испытаний
событие А наступит:
1)Менее m раз –
Pn(0)+ Pn(1)+…+ Pn(m-1);
2) Более m раз –
Pn(m+1)+ Pn(m+2)+…+ Pn(n);
3) Не менее m раз –
Pn(m)+ Pn(m+1)+…+ Pn(n);
4) Не более m раз –
Pn(0)+ Pn(1)+…+ Pn(m).
98.
Пример 1.Монету бросают 6 раз. Найти вероятность того, что
герб выпадет:
а) менее 2 раз; б) не менее 2 раз.
Решение.
6
5
1 6 7
1
1 1 1
a) P P6 (0) Р 6 (1) С6 .
2
2 2 64 64 64
7 57
b) P( B) 1 ( P6 (0) Р 6 (1)) 1 .
64 64
99.
Пример 2. Сколько надо взять случайных цифр от 0до 9, чтобы вероятность появления среди них
цифры 7 была не менее 0,9.
Решение.
P=0,1 – вероятность появления цифры 7, в случае
если выбираем одну цифру. Тогда q=1-0,1=0,9.
Пусть А – хотя бы один раз появилась цифра 7,
если n раз выбираем по одной цифре.
P(A)=1-qn≥0,9 n≥22.
100.
Формулы для приближенного вычислениявероятностей при испытаниях Бернулли.
Вычисления по формуле Бернулли при больших m
и n затруднительны. В математике установлены
приближенные формулы, позволяющие находить
приближенные значения для Pn(m) и, что еще
важнее для практики, суммы значений Pn(m) ,
таких, что дробь m/n (относительная частота
появления события А ) лежит в данных границах.
По формуле Бернулли вероятность того, что в
серии из 100 подбрасываний монеты все 100 раз
выпадет герб, равна (1/2)100. Не столь мала, но все
же так же ничтожна вероятность и того, что цифра
выпадет не более 10 раз.
101.
Наиболее вероятно, что число выпадений гербабудет мало отличаться от 50.
Вообще, при большом числе испытаний
относительная частота появления события, как
правило мало отличается от вероятности этого
события. Математическую формулировку этого
утверждения дает принадлежащий Я.Бернулли
закон больших чисел, который в уточненной
редакции П.Л.Чебышевым форме гласит:
102.
Теорема. Пусть вероятность события А виспытании S равна р, и пусть проводятся серии,
состоящие из n независимых повторений этого
испытания. Через m обозначим число испытаний, в
которых происходило событие А. Тогда для любого
положительного числа а выполняется неравенство
m
pq
P p a 2
(*)
n
an
Поясним смысл этого неравенства. Выражение m/n
равно относительной частоте события А в серии
m
опытов, а n p - отклонению этой
относительной частоты от теоретического
значения р.
103.
mp a
n
Неравенство
означает, что
отклонение оказалось больше чем а. Но при
постоянном a с ростом n правая часть неравенства
(*) стремиться к нулю. Иными словами, серии в
которых отклонение экспериментальной частоты
от теоретической велико, составляют малую долю
всех возможных серий испытаний.
Из данной теоремы вытекает утверждение,
полученное Бернулли: в условиях теоремы при
любом значении а>0 имеем:
m
lim P p a 0.
n
n
104.
Для доказательства достаточно заметить, чтоpq
lim 2 0.
n a n
Пример . Сколько достаточно провести опытов, что
бы из них получить вероятность события с
точностью до 0,1 и чтобы р≈m/n с этой точностью
и с вероятностью 0,9?
Для решения достаточно найти такое n, чтобы
было выполнено неравенство pq2 0,1.
0,1 n
А так как q=1-p, то pq=p(1-p)≤1/4 и потому
достаточно указать n, удовлетворяющее
1
неравенству
0,1 , отсюда n≥250 .
4 0,12 n
105.
Как видим, даже получение вероятности событияиз опыта с такой незначительной точностью
требует большого числа экспериментов. Правда,
более глубокие теоремы показывают, что можно
ограничиться и меньшим числом опытов.
106. Случайные величины и случайные векторы, их числовые характеристики. Основные предельные теоремы.
107.
2. Случайные величины, связанные сданным вероятностным пространством.
2.1. Понятие случайной величины.
Случайной называют величину, которая в
результате испытания примет одно и только одно
возможное значение, заранее неизвестное и
зависящее от случайных причин, которые заранее
не могут быть учтены.
108.
Пример 1. В урне 2 белых и 3 чёрных шара.Последовательно вынимаем 2 шара. Пусть Х –
число вынутых белых шаров. С этим опытом
связаны следующие элементарные события:
ω1={чб}, ω2={бч}, ω3={чч}, ω4={бб}
Очевидно, Х – функция от элементарного события:
Х(ω1)=1, Х(ω2)=1, Х(ω3)=0, Х(ω4)=2.
Исход опыта является случайным, поэтому Х –
случайная величина. Функция Х(ωi) – случайная
величина, определённая на множестве
элементарных событий
Ω = { ω1, ω2, ω3, ω4}
109.
Пример 2.Опыт состоит в определении времени безотказной
работы прибора. Известно, что прибор заведомо
откажет за время t [0,T]. Введём элементарные
события
ωt = {прибор проработал время t, а затем отказал}.
Пусть Х – случайный момент отказа прибора.
Х=Х(ωt) = t – функция от элементарного события,
определённая на множестве элементарных
событий Ω = { ωt : t [0,T]}.
110.
Определение. Случайной величиной называетсяфункция Х=Х(ω), определённая на множестве
элементарных событий Ω.
Будем обозначать случайные величины
буквами X, Y, Z , и т.п., а их возможные значения
соответствующими строчными буквами x, y, z.
Определение.
Дискретной называют случайную величину, которая
принимает отдельные, изолированные возможные
значения с определенными вероятностями.
Число возможных значений дискретной величины
может быть конечным или бесконечным (счётным).
111.
Определение. Непрерывной называют случайнуювеличину, которая может принимать все значения
из некоторого конечного или бесконечного
промежутка.
Число
возможных
значений
непрерывной случайной величины бесконечно.
112.
2.2. Законы распределения случайнойвеличины.
Законом распределения случайной
величины называют правило, устанавливающее
связь между возможными значениями случайной
величины и соответствующими им вероятностями.
Ряд распределения:
x1
x2
x3
…
p1
p2
p3
…
n
xn
pn
Здесь pi = P{X= xi }, pi = 1. Такая таблица
i 1
называется рядом распределения.
(*)
113.
Замечание. Если множество возможных значенийслучайной величины бесконечное (счетное), то ряд
pi сходится и его сумма равна 1.
i 1
Нанесем на координатную плоскость точки (xi,pi).
Получим многоугольник распределения,
представляющий собой график зависимости (*).
p
(x2,p2)
(xn,pn)
(x1,p1)
(x3,p3)
x
114.
Пример. Производится 3 выстрела по мишени.Вероятность попадания при каждом выстреле
р=0,4. За каждое попадание стрелку засчитывается
5 очков. Построить ряд распределения случайной
величины Х – числа выбитых очков.
xi
pi
0
5
10
15
0,216 0,432 0,288 0,064
p1 = P{X= 0 } = (0.6)3 = 0.216,
p2 = P{X= 5 } = 3·0.4(0.6)2 =0.432,
p3 = P{X= 10 }=3·(0.4)20.6 = 0.288,
p4 = P{X= 15 }=(0.4)3 = 0.064,
4
pi = (0,4+0,6)3 = 1.
i 1
115.
Функция распределенияРяд и многоугольник распределения – законы
распределения дискретной случайной величины.
Введем более универсальную характеристику,
которая подходит и для непрерывных случайных
величин.
Определение. Функцией распределения
случайной величины Х называют функцию F(x),
определяющую вероятность того, что случайная
величина Х в результате испытания примет
значение, меньшее х, т.е.
F(x) = Р{ Х<х }.
116.
Определение. Случайная величина называетсянепрерывной, если ее функция распределения есть
непрерывная, кусочно-дифференцируемая функция
с непрерывной производной.
Свойства функции распределения.
1. 0 F(x) 1.
2. Р{ х1 Х < х2 } = F(x2) – F(x1).
(вероятность того, что случайная величина X
примет значения, заключенные в интервале [х1, х2)
равна приращению функции распределения на
этом интервале.
x
x
Доказательство.
{X<x2}={X<x1}U{x1≤X<x2},
1
2
117.
F(x2)=P(X<x2)=P(X<x1)+P(x1≤X<x2)==F(x1)+P(x1≤X<x2) Р{ х1 Х < х2 } = F(x2) – F(x1).
3.F(x) – неубывающая функция, то есть
F(x2) F(x1), если x2 > x1.
Доказательство. Пусть x2 > x1, тогда
F(x2) – F(x1)= Р{ х1 Х < х2 } ≥0 F(x2) F(x1).
lim Fl( x) 1
x
4.Р{ Х х }= 1 – F(x).
Доказательство.
Р{ Х х }=1-P(X<x)= 1 – F(x).
F ( x) 1.
5.F(+ ) = 1, так как lim
x
118.
6. F(– ) = 0, так как lim F ( x) 0.x
7. Функция F(x) – непрерывна слева, то есть
F( x– 0) = F(x).
8.Если Р{ Х = х0 } 0, то
Р{ Х = х0 } = F(xо + 0) – F(xо).
Следствия.
1.Если X – непрерывная случайная величина, то
P{X=x0}=0.
2.Если возможные значения случайной величины
принадлежат интервалу (a,b), то F(x)=0 при x≤a
и F(x)=1, при x≥b.
119.
Пример. Монета подбрасывается 1 раз. Х – числовыпадений «орла». Построить функцию
распределения.
xi
0
1
pi
0,5
0,5
х 0
0,
F(x) = Р{ Х<х } =
0.5, 0 x 1
1,
x 1
1
0,5
1
120.
Замечания.1)График функции распределения случайной
величины расположен в полосе, ограниченной
прямыми y=0 и y=1.
2)График функции распределения дискретной
случайной величины имеет ступенчатый вид.
121.
Плотность распределенияПусть случайная величина Х такова, что её
функцию распределения можно представить в виде
x
где f(t) 0,
F ( x) f (t )dt
f
(
t
)
dt
1.
Такая
случайная
величина
является
непрерывной, а функция f(x) называется
плотностью
распределения
вероятностей
непрерывной случайной величины Х.
122.
Если F(x) – дифференцируемая функция, тоf(x) = F’(x).
Замечание. Функция распределения определена и
для дискретных, и для непрерывных случайных
величин. Плотность распределения неприменима
для
описания
распределения
дискретных
f (t )dt
случайных величин.
х2
х1
.
123.
Утверждение. Вероятность того, что непрерывнаяслучайная величина X примет значение,
принадлежащее интервалу (x1, x2) равна
Р{ х1 < Х < х2 } = F(x2) – F(x1) =
х2
f (t )dt
х1
х2
Доказательство.
f (t )dt
f
(
t
)
dt
Р{ х1 ≤Х < х2 } = F(x2) – F(x1) =
х1
С другой стороны
Р{ х1 ≤Х < х2 }= Р{ X=х1}+ Р{ х1 < Х < х2 } = 0+
+Р{ х1 < Х < х2 } = Р{ х1 < Х < х2 }.
х2
х1
.
124.
Геометрический смысл: вероятность того, чтонепрерывная случайная величина принимает
значение, принадлежащее интервалу (x1, x2) равна
площади криволинейной трапеции, ограниченной
осью OX, кривой распределения f(x) и прямыми
y=x1 и y= x2.
125.
Вероятностный смысл плотности распределения.F ( x x) F ( x)
f ( x) lim
x 0
x
Разность F(x+ Δx) – F(x) определяет вероятность
того, что случайная величина X примет значение,
принадлежащее интервалу (x, x+Δx) . Тогда предел
отношения вероятности того, что непрерывная
случайная величина X примет значение,
принадлежащее интервалу (x, x+Δx), к длине этого
интервала, при условии, что длина данного
интервала стремится к нулю, равен значению
плотности распределения в точке x .
126.
2.3.Числовые характеристики случайныхвеличин.
2.3.1.Характеристика центра распределения
случайной величины – математическое
ожидание.
Определение и статистический смысл мат.
ожидания.
Закон
распределения
полностью
характеризует случайную величину. Однако часто
закон распределения неизвестен и приходится
ограничиваться меньшими сведениями.
127.
Пусть Х – дискретная случайная величина,принимающая конечное множество значений.
m
Пусть рi = {X = xi}, pi 1
i 1
Проводится n независимых повторений опыта S,
причём
X = xi в ni случаях (i = 1, 2, … , m). Тогда
n
1 m
X ср. xi ni xi pi
n i 1
i 1
при n → .
Естественно это значение принять за теоретическое
среднее величины X в эксперименте S.
128.
Определение. Математическим ожиданиемдискретной случайной величины X называется
сумма произведений всех ее возможных значений
на их вероятности:
M ( X ) xi pi ,
i 1
где xi – возможные значения случайной величины,
pi – соответствующие им вероятности (если
соответствующий ряд абсолютно сходится).
129.
Вероятностный смысл мат. ожидания.Пусть произведено n испытаний, в которых
случайная величина X примет m1 раз значение x1 ,
m2 раз значение x2,…., mk раз значение xk, причем
m1+m2 +….+ mk=n. Тогда сумма всех значений,
принятых случайной величиной, равна
k
xm
i 1
i
i
X - среднее арифметическое всех значений.
k
mk
m1 m2
X xi mi / n x1 x2 ...xk x1 1 x2 2 ... xk k ,
n n
n
i 1
где i mi / n относительная частота значения
xi
130.
Если число испытаний достаточно велико, то i pi(относительная частота появления события xi
приближенно равна вероятности появления этого
события).
Таким образом, мат. ожидание приближенно равно
среднему арифметическому наблюдаемых
значений случайной величины.
131.
Замечания.1) Из определения следует, что м. о. дискретной
случайной величины есть неслучайная величина.
2) Мат. ожидание больше наименьшего и меньше
наибольшего из возможных значений случайной
величины, то есть на числовой оси возможные
значения располагаются слева и справа от мат.
ожидания. В этом смысле м.о. характеризует
расположение распределения случайной величины
и поэтому называется центром распределения.
3) М. о. – число около которого группируется
среднее арифметическое в большой серии
измерений.
132.
Например, возьмем какой–то предмет и измеримего вес. Проведем n измерений этого предмета.
Пусть x1,x2,…,xk - серия повторных измерений.
Какие- тот измерения могли повторяться. Пусть
величина xi встретилась ni раз. Тогда
x1n1 x2 n2 ... xk nk k
X
xi pi
n
i 1
М.о. – истинный вес предмета
133.
Свойства математического ожидания.1). Если β – неслучайная величина, то М(β) = β.
Доказательство.
М(β)= β·1= β.
(рассматриваем постоянную величину как
дискретную случайную величину, принимающую
одно и то же значение β и принимает его с
вероятностью P =1).
134.
2). Если α – неслучайная величина, тоM(α Х) = α M(Х).
Доказательство.
n
n
M ( X ) ( xi ) pi xi pi M ( X ).
i 1
i 1
Произведение постоянной величины α на
дискретную случайную величину X рассматриваем
как дискретную случайную величину αX,
возможные значения которой равны αixi,
вероятности возможных значений равны pi.
135.
3).Математическое ожидание суммы двухслучайных величин равно сумме математических
ожиданий слагаемых: М(Х+Y) = М(Х)+M(Y).
Доказательство.
Пусть сл. величина X принимает значения xi
(i=1,…,n) c вероятностью pi, а сл. величина Y
принимает значения yi (i=1,…,k) c вероятностью qi.
Событие, состоящее в том, что сл. величина X
примет значения xi (i=1,2,…,n) c вероятностью pi ,
влечет за собой событие, которое состоит в том, что
сл. величина X+Y примет значения xi+y1, …,xi+yk
(i=1,2,…,n) вероятность которого по теореме
сложения вероятностей равна pi1+…+pik= pi .
136.
Аналогично, qj =p1j+…+pnj.Тогда
M(X+Y)=(x1+y1) p11 +(x1+y2) p12 +…+(x1+yk) p1k+
+(x2+y1) p21 +(x2+y2) p22 +…+(x2+yk) p2k+…+
+(xn+y1) pn1 +(xn+y2) pn2 +…+(xn+yk) pnk= x1( p11 + p12
+…+ p1k)+ x2( p21 +p22 +…+ p2k)+…+ xn(pn1 + pn2 +…+
pnk)+ y1( p11 +p21 +…+ pn1 )+y2(p12+p22…pn2)+ yk( p1k +
+p2k +…+ pnk)= x1p1 + x2p+…+ xpn+ y1q1+y2q2+…+
+ykqk =M(X)+M(Y).
137.
4).М. о. произведения двух независимых случайныхвеличин равно произведению их математических
ожиданий: М(Х·Y) = М(Х)·M(Y).
Доказательство.
Пусть сл. величина X принимает значения xi
(i=1,…,n) c вероятностью pi, а сл. величина Y
принимает значения yi (i=1,…,k) c вероятностью qi.
Произведением независимых сл. величин X и
Y называется сл. величина ХY, возможные значения
которой равны произведениям каждого возможного
значения сл. величины X на каждое возможное
значение сл. величины Y ; вероятности возможных
значений сл. величины Х·Y равны произведению
вероятностей возможных значений сомножителей.
138.
ТогдаM(XY)=x1y1 p1 q1+x1y2 p1q2 +…+x1ykp1qk+ x2y1 p2 q1
+x2y2 p2 q2 +…+x2ykp2 qk+…+ xny1 pn q1 +xny2 pn q2+
+…+xnyk pn qk= x1p1(y1q1+y2q2+…+ ykqk)+
+x2p2(y1q1+y2q2+…+ ykqk )+…+ xnpn(y1q1+y2q2+…+
ykqk) = (x1p1+ +x2p2+…+ xnpn )(y1q1+y2q2+…+ ykqk) =
=M(X)·M(Y).
139.
5).М. о. произведения нескольких независимыхслучайных величин равно произведению их
математических ожиданий.
6).М. о. суммы нескольких случайных величин
равно сумме их математических ожиданий.
7)
k
M ( i X i )
i 1
k
M ( X )
i 1
i
i
140.
Пример. Найти м.о. суммы числа очков, которыемогут выпасть при бросании двух игральных
костей.
1 способ.
x 2
p
1
36
3
4
5
6
7
8
9
10
11
12
2
36
3
36
4
36
5
36
6
36
5
36
4
36
3
36
2
36
1
36
1
2
3
4
5
6
5
M ( X ) 2 3 4 5 6 7 8
36
36
36
36
36
36
36
4
3
2
1
9 10 11 12
7.
36
36
36
36
2 способ. Пусть X - число очков, выпавших на 1
кубике, а Y – на втором.
141.
x1
2
p
1/6 1/6 1/6 1/6 1/6 1/6
Y
1
p
1/6 1/6 1/6 1/6 1/6 1/6
2
3
3
4
4
5
5
6
6
Тогда M(X)=(1+2+3+4+5+6)/6=7/2,
M(Y)=(1+2+3+4+5+6)/6=7/2,
M(X+Y)= M(X)+M(Y)=7.
142.
Определение. Математическим ожиданиемнепрерывной случайной величины X с плотностью
распределения f(x) называется число
M ( X ) x f ( x)dx
(если соответствующий интеграл абсолютно
сходится).
Если случайная величина У = g(X) – функция от
случайной величины Х, то её математическое
ожидание вычисляется по аналогичным
формулам.
143.
2.3.2. Характеристики рассеяния случайнойвеличины – дисперсия и стандартное
отклонение.
Рассмотрим две дискретные случайные величины:
X
-0,01 0,01
Y
-100 100
P
0,5 0,5
P
0,5
0,5
М.о. в обоих случаях одинаковые, а возможные
значения различны, причем случайная величина X
имеет возможные значения близкие к м.о. , а Y –
далекие от своего м.о. Следовательно, зная лишь
м.о. нельзя судить ни о том, какие возможные
значения сл. величина может принимать, ни о том,
как они рассеяны вокруг м.о. Поэтому наряду с
м.о. вводятся и другие характеристики.
144.
Определение. Дисперсией случайной величины Хназывается математическое ожидание квадрата её
отклонения от центра распределения, то есть
D(X)= M[(X – M(X))2].
Таким образом, для дискретной случайной
величины
D( X ) ( xi M ( X ))2 pi
i 1
Замечание. Дисперсия служит характеристикой
рассеяния возможных значений случайной
величины вокруг математического ожидания.
Например, в артиллерии важно знать насколько
кучно лягут снаряды вблизи цели, которая должна
быть поражена.
145.
Определение. Среднеквадратическим отклонениемслучайной величины Х (стандартным
отклонением, стандартом) называется число
σ(X) = √ D(X).
Свойства дисперсии и стандарта.
1. D(X)= M(X2) – M2(X).
Доказательство
D(X)=M[(X–M(X))2]=M[X2–2XM(X)+M2(X)]=
=M(X2)–2M(X)M(X) + M2(X)=M(X2)–M2(X).
2. Если C – неслучайная величина, то
D(С) = 0, σ(C) = 0.
Доказательство
D(C)=M(C–M(C))2= M(C-C) 2=M(0)=0
146.
3. Если C – неслучайная величина, тоD(СX) = С2 D(X), σ(CX) = |C|σ(X) .
Доказательство
D(CX)= M(C2X2) – M2(CX) = C2 (M(X2) – M2(X))
4. Если C – неслучайная величина, то
D(X +C) = D(X), σ(X+C) = σ(X)
Доказательство
D(X+C)=M[(X+C–M(X+C))2]= M[(X+C–M(X) – C)2]
= D(X).
147.
5.Дисперсия суммы двух независимых случайныхвеличин равна сумме дисперсий этих величин:
D(Х+Y) = D(Х) + D(Y).
Доказательство
D(Х+Y) = M((Х+Y)2)– M2(Х+Y) =M(Х2+2ХY +Y2) – (M(Х) + M(Y))2 =M(Х2 )+M(2ХY)+M(Y2) –
- (M2(Х)+ 2M(Х)·M(Y)+ M 2(Y))=M(Х2 ) - M 2(Х) +
+2M(Х)M(Y)+M(Y2) – M 2(Y) - 2M(Х)· M(Y)=
= D(Х) + D(Y).
6.Дисперсия разности двух независимых случайных
величин равна сумме их дисперсий:
D(Х–Y) = D(Х) + D(Y).
Доказательство
D(Х–Y) = D(Х) + D(–Y)= D(Х)+ D(Y) .
148.
7.Дисперсия суммы нескольких взаимнонезависимых случайных величин равна сумме
дисперсий этих величин:
D(Х 1+X 2+…Xn) = D(Х1) + D( X 2)+…+ D(Xn) .
Замечание.
Дисперсия имеет размерность, равную квадрату сл.
величины. Так как среднее квадратическое
отклонение есть корень из дисперсии, то его
размерность совпадает с размерностью случайной
величины. В тех случаях, когда желательно, чтобы
оценка рассеяния имела размерность случайной
величины, вычисляют среднее квадратическое
отклонение.
149.
Определение.Дисперсией непрерывной случайной величины X с
плотностью распределения f(x) называется число
D( X ) M (( X M ( X )) 2 ) ( x M ( x)) 2 f ( x) dx
(если соответствующий
сходится).
интеграл
абсолютно
150.
Утверждение. D( X )2
2
x
f
(
x
)
dx
M
( X ).
Доказательство.
D( X ) M (( X M ( X )) 2 ) ( x M ( X )) 2 f ( x)dx
2
x
f ( x )dx
( x 2 xM ( X ) M ( X )) f ( x)dx
2
2
2 xM ( X ) f ( x)dx
2
x
f ( x )dx
M ( X ) f ( x)dx
2
2M ( X ) xf ( x)dx M 2 ( X ) f ( x)dx
2
2
x
f
(
x
)
dx
M
( X ).
151.
Пример. Функция распределения сл. величины0, x 1
имеет вид:
F ( x) a b arcsin x, 1 x 1
1, x 1
Найти: a, b, M(X), D(X), P(1/2<X< √2/2).
Решение.
1) F ( 1) 0 a b arcsin( 1) a b 0
2
1
1
b
a ;b .
F (1) 1 a b arcsin(1) a
1
2
2
0, x 1
1 1
F ( x) arcsin x, 1 x 1
2
1, x 1
152.
0, x 11
2) f ( x) F ( x)
, 1 x 1
2
1 x
0, x 1
1
x
3) M ( X )
dx 0,
2
как
интеграл
от
нечетной
1
x
1
функции в симметричных пределах.
/2
x sin t
1
sin 2 t cos tdt
4) D( X )
dx 0
2
2
dx cos t dt / 2 1 sin t
1 1 x
1
/2
x2
/2
/2
1 cos 2t
1 t sin 2t
1
sin t dt
dt
.
/ 2
/ 2
2
2
4 / 2 2
1
2
1
5) ( X )
.
2
1
153.
21
2
2
1 1 1
5) P( X
) F ( ) F ( ) arcsin
2
2
2
2 2
2
1 1
1 1 1 1 1 1 1 1
arcsin .
2 2 4 2 6 4 6 12
2
154.
2.4. Многомерные случайные величины.Под n-мерной случайной величиной, или
случайным вектором, понимается упорядоченный
набор n случайных величин Х = (Х1, Х2, …, Хn).
Законом распределения дискретной n-мерной
случайной величины называется перечень
возможных значений этой величины, то есть
наборов чисел X i ( xi1 , xi2 ,..., xin ), i 1, 2,..., mi и их
вероятностей.
155.
Функция распределения случайного вектора.Функция распределения случайного вектора
Х = (Х1, Х2, …, Хn) определяется формулой
F(x1, x2, …, xn ) = Р{ Х1<х1, Х2<х2, ... , Хn<хn }.
В частности, для n=2: F(x, y) = Р{ Х<х, Y<y}.
Для двумерной случайной величины (X,Y) функция
F(x, y) – это вероятность того, что случайная точка
(x,y) попадает в бесконечный квадрат с вершиной в
точке (x,y), расположенный ниже и левее этой
Y
вершины.
(x,y)
X
156.
Свойства функции F(x, y).1. 0≤F(x, y) ≤1;
2. F(x, y) – неубывающая функция по каждому из
своих аргументов;
3.F(x, y) – непрерывная функция по каждому из
своих аргументов;
4. F(– , y) = F(x, – ) = F( – ,– ) = 0
5. F(+ ,+ ) = 1
6. F(x, + ) = F1(x), где F1(x) – функция
распределения случайной величины X,
F(+ , y) = F2(y) , где F2(y) – функция распределения
случайной величины Y.
Аналогичные свойства имеют место для функции
распределения n – мерного вектора - F(x1, x2, …, xn ).
157.
Плотность распределения.Пусть
F(x1, x2, …, xn ) =
где f(t1,t2, ... ,tn) 0,
x1
xn
x2
dt dt ... f (t , t ,..., t )dt
1
2
1
2
n
n
dt dt ... f (t , t ,..., t )dt 1.
1
2
1
2
n
n
Тогда Х = (Х1, Х2, …, Хn) – непрерывная случайная
величина, а f(x1 , x 2, ... ,xn) – плотность
совместного распределения непрерывных
случайных величин Х1, Х2, … , Хn.
158.
В частности, вероятность попадания случайнойвеличины Х = (Х1, Х2, …, Хn) в некоторую область
D Rn определяется как
P( X D) ... f ( x1 , x2 ,..., xn )dx1dx2 ...dxn
D
В точках непрерывности
F
f ( x1 , x2 ,..., xn )
x1 x2 ... xn
n
159.
Свойства функции f(x,y).1) f ( x, y) 0,
2)
f ( x, y)dxdy 1,
3) P(( X , Y ) D) f ( x, y )dxdy ,
D
4) f ( x, ydy f1 ( x) f X ( x),
f ( x, y)dx f ( y) f ( y).
2
2 F
5) f ( x, y )
.
x y
Y
160.
Частные (маргинальные) распределения.Зная закон совместного распределения
случайных величин Х1, Х2, … , Хn, можно
определить законы распределения отдельных
случайных величин.
Пусть Х = (Х, Y). x
Тогда F1(x) = F(x, + ) = dt1 f (t1 , t2 )dt2
x
f1 (t1 )dt1 ,
где f1(t1) = f (t1 , t 2 )dt2 – плотность
распределения случайной величины Х.
161.
Аналогично f2(t2) =f (t1, t2 )dt1
.
– плотность распределения случайной величины
Y.
Обратное, в общем случае, неверно, то есть,
зная распределения отдельных случайных
величин, не всегда возможно восстановить
совместный закон.
162.
Определение. Случайные .величины Х и Yназываются независимыми, если независимыми
являются события {X<x} и {Y<y} для любых
действительных чисел x и y.
Так как P(X<x,Y<y)= P(X<x)·P(Y<y) для
независимых случайных величин, то
F(x, y) = F1(x) F2(y).
Определение. Случайные величины Х1, Х2, … , Хn
называются статистически независимыми, если
F(x1, x2, …, xn ) = F1(x1) F2(x2) … Fn(xn ).
Для непрерывных независимых случайных
величин
f (x1, x2, …, xn ) = f1(x1) f2(x2) … fn(xn ).
163.
Условные распределения.Условным законом распределения одной из
сл. величин, входящих в систему (Х1, X2,…,Xn)
называется закон её распределения, вычисленный
при условии, что другие случайные величины
приняли определённое значение .
В частности, в случае системы двух дискретных
случайных величин (Х, Y) условным законом
распределения с.в.Y при условии, что X=xi
называется совокупность вероятностей .
P(Y y j , X xi )
P(Y y j / X xi )
; j 1, 2,..., m
P( X xi )
164.
Аналогично,P( X xi / Y y j )
P( X xi , Y y j )
P(Y y j )
; i 1, 2,..., n.
Определение. Условная плотность f(y/x)
непрерывной случайной величины Y при условии,
что X=x определяется равенством:
f (y/ x) = f (x, y) /f1(x), f1(x)= 0,
Аналогично,
f (x/ y) = f (x, y)/ f2(y), f2(y)= 0,
Таким образом, в общем случае
f (x, y) = f2(y)f (x / y) = f1(x)f (y / x)
165.
Математическое ожидание и дисперсияслучайного вектора.
Определение. Математическим ожиданием
случайного вектора Х = (Х1, Х2, …, Хn) называется
вектор M(Х) = (M(Х1), M(Х2), …, M(Хn))
Определение. М. о. двумерной случайной величины
(Х, Y) называется совокупность м.о. M(Х) и M(Y),
(то есть упорядоченная пара ((M(Х), M(Y))),
определяемая равенствами:
а) для дискретной случайной величины
n
m
M ( X ) xi pij ,
i 1 j 1
n
m
M (Y ) y j pij .
i 1 j 1
166.
б) для непрерывной случайной величиныM ( X ) x f ( x, y )dxdy x f1 ( x)dx,
M (Y ) y f ( x, y )dxdy y f 2 ( y )dy.
Определение. Пусть (X,Y)- система дискретных сл.
величин. Условным м. ожиданием дискретной сл.
величины Y при условии X = ximназывается
M (Y / X xi ) M (Y / xi ) y j p( y J / xi ),
j 1
p( y j / xi ) p(Y y j / X xi ).
где
n
Аналогично, M ( X / Y y j ) M ( X / y j ) xi p( xi / y j ),
i 1
p ( xi / y j ) p ( X xi / Y y j ).
167.
Определение. Пусть (X,Y)- система непрерывныхсл. величин. Условным м. ожиданием
непрерывной сл. величины Y при условии X = x
называется
M (Y / X ) y f ( y / x)dy,
Аналогично,
M ( X / Y ) x f ( x / y )dx.
168.
Определение. Дисперсией системы сл. величин(X,Y) называется совокупность (D(Х) и D(Y)), где
а) для дискретной случайной величины:
n
m
D( X ) ( xi M ( X )) 2 pij ,
i 1 j 1
n
m
D(Y ) ( y j M (Y )) 2 pij .
i 1 j 1
б) для непрерывной случайной величины:
D( X ) ( x M ( X )) 2 f ( x, y)dxdy
D(Y ) ( y M (Y )) 2 f ( x, y)dxdy
2
2
x
f
(
x
,
y
)
dxdy
M
( X ),
2
2
y
f
(
x
,
y
)
dxdy
M
(Y ).
169.
Характеристики меры связи случайных величин –ковариация и коэффициент корреляции.
Определение. Ковариацией случайных величин Х
и Y называется число, равное математическому
ожиданию произведения отклонений этих величин
от своих математических ожиданий.
Cov( X , Y ) M (( X M ( X )) (Y M (Y ))).
Для дискретных сл. величин:
n
m
Cov( X , Y ) ( xi M ( X ))( y j M (Y )) pij ,
i 1 j 1
Для непрерывных сл. величин:
Cov( X , Y ) ( x M ( X )) ( y M (Y )) f ( x, y)dxdy.
170.
Свойства ковариации.1) Cov( X , Y ) Cov(Y , X ).
2) Cov( X , Y ) M ( X Y ) M ( X ) M (Y )
M ( X Y ) M ( X ) M (Y ) Cov( X , Y ).
Доказательство.
Cov( X , Y ) M (( X M ( X )) (Y M (Y )))
M [ X Y M ( X ) Y M (Y ) X M ( X ) M (Y )]
M ( X Y ) M (M ( X ) Y ) M ( M (Y ) X ) M ( M ( X ) M (Y ))
M ( X Y ) M ( X ) M (Y ) M (Y ) M ( X ) M ( X ) M (Y )
M ( X Y ) M ( X ) M (Y ).
171.
3) D( X Y ) D( X ) D(Y ) 2Cov( X , Y ).Доказательство.
D( X Y ) M [(( X Y ) M ( X Y ))2 ]
M [( X Y ) 2M ( X Y ) ( X Y ) M ( X Y )]
2
2
M (( X Y )2 ) M (2M ( X Y ) ( X Y )) M (M 2 ( X Y ))
M ( X 2 ) 2M ( X Y ) M (Y 2 ) 2M ( X Y ) M ( X Y )
M ( X Y ) M ( X ) 2M ( X Y ) M (Y ) M ( X Y )
2
2
2
2
M ( X 2 ) 2M ( X Y ) M (Y 2 ) M 2 ( X ) 2M ( X ) M (Y )
M 2 (Y ) M ( X 2 ) M 2 ( X ) M (Y 2 ) M 2 (Y ) 2M ( X Y )
2M ( X ) M (Y ) D( X ) D(Y ) 2Cov( X , Y ).
172.
4)Если Х и Y– независимы, то Cov (Х, Y) = 0.Доказательство:
Cov( X , Y ) ( x M ( X ))( y M (Y )) f ( x, y)dxdy
Так как Х и Y– независимы, то f ( x, y) f1 ( x) f 2 ( y).
( x M ( X ))( y M (Y )) f1 ( x) f 2 ( y)dxdy
( x M ( X )) f1 ( x )dx ( y M ( y) f 2 ( y)dy 0,
так как
( x M ( X )) f ( x)dx xf ( x)dx M ( X ) f ( x)dx
1
1
1
M ( X ) M ( X ) f1 ( x)dx M ( X ) M ( X ) 0.
173.
Замечание. Если Cov(Х,Y) 0, случайные величиныX и Yзависимы. Однако, если Cov(Х,Y)=0, отсюда
не следует независимость случайных величин.
5.| Cov(Х,Y) | σ(X)· σ(Y) , причём, равенство
имеет место тогда и только тогда, когда случайные
величины связаны строгой линейной
зависимостью, то есть Y=αX+β.
Определение. Случайные величины называются
коррелированными, если их ковариация отлична от
нуля. Если Cov(Х,Y)=0, то случайные величины
называются некоррелированными.
174.
Пример. Приведем пример зависимых случайныхвеличин, ковариация которых равна 0. Пусть
плотность распределения – чётная функция. И
пусть Y = Х2, то есть случайные величины связаны
строгой функциональной зависимостью. Тогда
Cov( X , Y ) M ( X Y ) M ( X ) M (Y )
M (X 3) M (X ) M (X 2) 0
так как
3
x
f ( x)dx xf ( x)dx 0,
как интеграл от нечетной функции в симметричных
пределах.
175.
Определение. Коэффициентом корреляциислучайных величин Х и Y называется число
cov( X , Y )
( X ,Y )
.
( X ) (Y )
Свойства (Х,Y).
1) (Х,Y) = (Y, Х).
2) | (Х,Y) | 1, причём, = 1 тогда и только
тогда, когда случайные величины связаны строгой
линейной зависимостью.
3) Если Х и Y – независимы, то (Х, Y) = 0.
4) 2 (Х, Y) не меняется при линейных
преобразованиях случайных величин, то есть
2 (αХ+ β, Y+ ) = 2 (Х, Y).
176.
Статистический смысл (Х,Y).Коэффициент корреляции характеризует только
степень линейной зависимости между случайными
величинами и не может отражать более сложных
форм зависимости. Так как ( Х,Y)= 0 не только в
случае статистической независимости случайных
величин, но при определённых условиях и в случае
строгой функциональной зависимости, эта
характеристика не даёт исчерпывающего
представления о виде связи между величинами.
177.
2.5.Ковариационная матрица случайноговектора.
Ковариационной матрицей случайного
вектора Х = (Х1, Х2, …, Хn) называется матрица
K(X), элементами которой являются числа
Kij Cov( X i , X j ).
Заметим, что
Kii Cov( X i , X i ) M (( X i M ( X i )) 2 ) D( X i ).
Определитель ковариационной матрицы
называется обобщённой дисперсией. Её можно
использовать как меру рассеяния n-мерной
случайной величины.
178.
2.6. Понятие функции от случайной величины.Пусть Х – случайная величина, связанная с
данным экспериментом, g(x) – произвольная
функция от х. Случайная величина У называется
функцией от случайной величины Х, если У
принимает значение g(x) всякий раз, когда Х
принимает значение х.
Пример. Пусть Х – число бракованных деталей в
партии из 100 изделий. У – штраф за поставку
недоброкачественной продукции,
пропорциональный количеству бракованных
изделий У = g(Х) = kX.
179.
а) для дискретной случайной величины:M ( ( X )) ( xi ) pi ,
i 1
D( ( X )) ( ( xi ) M ( ( X ))) pi
2
i 1
б) для непрерывной случайной величины:
M ( ( X )) ( x) f ( x)dx,
D( ( X )) ( ( x) M ( ( x))) 2 f ( x) dx.
180.
2.7.Квантили распределения. Медиана имода.
xp
Пусть
p P{ X x p } f ( x)dx F ( x p ).
Точка xp называется квантилью уровня р
(р–квантилью) непрерывной случайной
величины Х с плотностью распределения f(x).
Если р = 0,5 – квантиль называется
медианой
f
(
x
)
dx
распределения Ме(X) .
P(X< Ме(X))= P(X> Ме(X))=1/2.
Геометрически: медиана – это абсцисса
точки, в которой прямая x= Ме(X) делит
пополам площадь фигуры, ограниченной
кривой распределения.
xp
181.
Мода распределения – точка, в которойплотность распределения имеет максимум.(
обозначается Мо(Х)).
2.8. Начальные и центральные моменты.
Определение. Начальным теоретическим
моментом порядка r случайной величины X
f ( x)dx ожидание
называется математическое
величины X r
:
r
- для дискретной
x
i pi
i 1
случайной величины
xp
r
x r f ( x )dx
- для непрерывной.
182.
Замечание. В частности, начальныйтеоретический момент первого порядка – это
мат. ожидание. Определение. Центральным
теоретическим моментом порядка r случайной
r
r M ((число
X M ( X ))) .
величины X называется
r
для
дискретной
(
x
M
(
X
))
p
i
i
i 1
случайной
величины
r
f ( x)dx
r
( x M ( X )) f ( x) dx - для непрерывной.
xp
Замечание. В частности, центральный
теоретический момент первого порядка равен
нулю:
1 M ( X M ( X )) M ( X ) M (M ( X ) M ( X ) M ( X ) 0.
183.
Центральный теоретический момент второгопорядка равен дисперсии:
2 M (( X M ( X ))2 ) D( X ).
Моменты случайной величины характеризуют
форму ее кривой.
Заметим,, что
2 M (( X M ( X ))2 ) M ( X 2 )f ( x)dxM 2 ( X ) 2 12 ;
xp
3 M (( X M ( X ))3 ) M ( X 3 3 X 2 M ( X ) 3 XM 2 ( X ) M 3 ( X ))
M ( X 3 ) 3M ( X 2 )M ( X ) 3M ( X )M 2 ( X ) M 3 ( X )
3 3 1 2 3 13 13 3 3 1 2 2 13 ;
184.
4 M (( X M ( X ))4 ) M ( X 4 ) 4 X 2 M 2 ( X ) 4 X 3M ( X ) 4 XM 3 ( X )M ( X ) 2 X M ( X ) 4 4 4 3 1 4 2
4
2
2
2
2 1
4
1
4 4 3 1 3 14 6 12 2 .
xp
f ( x)dx
4
1
2
1 2
185.
2.9. Основные дискретные и непрерывныераспределения и их числовые
характеристики.
2.9.1.Схема независимых испытаний Бернулли
и связанные с ней случайные величины.
Пусть в одних и тех же условиях проводится n
независимых испытаний, в каждом из которых
событие А может появиться (успех) с вероятностью
р или не появиться(неудача) с вероятностью q = 1-р.
Вероятности р и q считаются неизменными в
каждом испытании. Такая схема испытаний
называется схемой Бернулли, по имени Якоба
Бернулли, впервые рассмотревшего ее в своей книге
«Искусство возможного».
186.
Примеры. Многократное подбрасывание монет,игральных костей, извлечение разноцветных шаров
из одной и той же урны (с возвращением вынутого
шара), контроль качества одинаковых изделий в
партии из n изделий и т.п.
187.
Геометрическое распределение.Рассмотрим серию испытаний Бернулли. Сл.
величина Х - число испытаний, проведенных до
первого успеха. Построим ряд распределения
случайной величины Х.Пусть в первых (k-1)
испытаниях событие А не появилось, а в к –ом
испытании появилось. По теореме умножения
вероятностей P( X k ) qk 1 p.
1
pi p qp q p ...q p ... p
1.
1 q
i 1
(сумма членов бесконечно убывающей геом. прогрессии).
k 1
2
хk
1
2
3
pk
p
qp
q2p
...
k
...
qk-1p
...
188.
Найдем числовые характеристики геометрическогораспределения:
M ( X ) kq
k 1
k 1
p p kq
k 1
k 1
p (q )
k
k 1
q
1 q q p 1
k
p q p
2 .
p
2
(1 q)
p
p
k 1
1 q
Итак,
1
M (X ) .
p
189.
M (X ) k q2
2
k 1
k 1
p p k q
2
k 1
k 1
p k (q )
k
k 1
k
k 1
k
p kq p q kq p q (q )
k 1
k 1
k 1
q
1 q q
k
p q q p q
p q
2
1 q
k 1
(1 q)
2
q
(1 q) 2(1 q)q
1 q
p
p
p
2
4
3
(1 q)
(1 q)
(1 q)
1 q 1 q
p 3 2 .
p
p
190.
1 q 1q
D( X ) M ( X ) M ( X ) 2 2 2 .
p
p
p
2
2
Пример. Проводится стрельба по цели до первого
попадания. Вероятность попадания p=0.2. Найти
математическое ожидание и дисперсию сл.
величины X, если
а) стрелять можно неограниченное число раз;
б) в наличии 5 патронов.
Решение.
а)X 1 2
… K
… M(X)=1/p=1/0,2=5;
P
0,2
0,8·0,2
k 1
0,8
0,2 …
…
D(X)=q/p2=0,8/0,22=
=20.
191.
б) в наличии 5 патронов.X
P
1
2
3
4
5
0,2
0,8·0,2
0,82 0,2
0,83 0,2
0,84 0,2 0,85
M ( X ) 1 0, 2 2 0,8 0, 2 3 0,82 0, 2 4 0,83 0, 2
5 (0,8 0, 2 0,8 ) 3,3616;
4
5
M ( X 2 ) 1 0, 2 22 0,8 0, 2 32 0,82 0, 2 42 0,83 0, 2
52 (0,84 0, 2 0,85 ) 13,8704;
D( X ) 13,8704 (3,3616)2 2,57.
192.
Биномиальное распределение.Проводится серия испытаний Бернулли. Сл.
величина Х – число наступлений события А в серии
из n испытаний. Построим ряд распределения сл.
величины Х. Вероятность того, что Х=k, т.е. в
серии из n испытаний событие А наступит ровно k
раз, может быть подсчитана по формуле Pn (k ) Cnk pk qn k,.
k
C
где n – биномиальные коэффициенты (число
сочетаний из n элементов по k). Эта формула
называется формулой Бернулли, а рассматриваемый
закон распределения случайной величины Х
называется биномиальным законом, так как Pn (k )
– общий член в разложении бинома Ньютона:
( p q)n q n Cn1 pq n 1 Cn2 p 2 q n 2 Cnk p k q n k ... p n .
193.
Заметим, что в нашем случаеX 0
1
…
P Pn (0) q n Pn (1) Cn1 pq n 1 …
( p q)n ( p 1 p)n 1.
K
…
Pn (k ) Cnk p k q n k . …
n
Pn (n) p n
Найдем числовые характеристики биномиального
распределения.
n
X Xi ,
i 1
где Xi – число успехов в i-ом испытании ( число
появления события А в одном испытании).
Заметим, что Xi=0 или Xi=1. Тогда
n
n
i 1
i 1
M ( X i ) 1 p 0 q p M ( X ) M ( X i ) p pn;
194.
D( X i ) 1 p 0 q (M ( X i )) p p2
2
2
n
n
i 1
i 1
2
D( X ) D( X i ) ( p p 2 ) n ( p p 2 ) np(1 p) npq.
195.
Распределение Пуассона.Рассмотрим серию испытаний Бернулли, где n
– велико, а вероятность наступления события А в
каждом испытании р - очень мала. Такие события
называются редкими.
Пусть X – число наступления события А в серии из
n испытаний. Для определения вероятности k раз
наступления события А используем формулу
Бернулли: Pn (k ) Cnk pk qn k .
Если np при n ( -константа), то
k
e
биномиальное распределение
k k n k
Pn (k ) Cn p q
Это, так называемая, теорема Пуассона.
k!
.
196.
Доказательство.k n k
Pn (k ) C p q
k
n
n!
n(n 1)...(n k 1) k
k n k
n k
pq
p (1 p)
k !(n k )!
k!
n(n 1)...(n k 1)
np
1
k!
n n
k
n k
.
n k
n(n 1)...(n k 1)
lim Pn (k ) lim
1
n
n
k!
n n
n k
k
n(n 1)...(n k 1)
lim
1
k
k ! n
n
n
k
n k
n n 1 (n k 1)
lim
...
1
k ! n n n
n
n
n k
k
1 k 1
lim1 1 ... 1
1
k ! n n
n n
k
197.
lim 1k ! n n
k
n k
Pn (k ) C p q
k
n
k
k
lim 1 1 e
k ! n n n
k!
k
k
n k
n
k
e
.
k!
198.
Примеры редких событий.1)Завод в течение месяца выпускает несколько
тысяч деталей с малой вероятностью брака.
Например, в партии из 1000 деталей брак может
встретиться не более 10-15 раз.
2)Часто в качестве серии испытуемых объектов
удобнее брать не какое-то их число, а единицу
времени, в течение которой проводятся испытания,
или единицу площади, на которой расположены
испытуемые объекты. Например, число
неправильных соединений на АТС в течение часа,
число опечаток на страницу, число автомобильных
катастроф в неделю.
199.
Для отыскания вероятностей подобных случайныхвеличин удобным оказывается закон распределения
Пуассона, согласно которому вероятность того,
что случайная величина приняла значение k равна
Pn (k )
e
k
k!
.
k=0,1,2, ... , где - некоторый параметр. Заметим,
что
n
n
k e
k 0
k 0
k!
Pn (k )
n
k
k 0
k!
e
e e 1.
200.
Найдем числовые характеристики распределенияПуассона.
k
e
k
M ( X ) k Pn (k ) k
e
e
k!
k 0
k 0
k 0 k !
k 1 (k 1)!
n
n
n
k
n
k
k 1
m
n
e
k 1 m e
e e ,
k 1 (k 1)!
m 0 m !
k
2
k
k
n
n
n
n
e
k
k
2
2
2
M ( X ) k Pn (k ) k
e
e
k!
k!
k 0
k 0
k 0
k 1 (k 1)!
n
m 1
m 1
m 1
n
n
(
m
1)
m
k 1 m e
e
e
m!
m 0
m 0 m !
m 0 m !
n
2
e
e e e e 2 ,
m 1 (m 1)!
m 0 m !
s 0 s !
n
2
m 1
n
m
n
s
201.
ТогдаD( X ) M ( X 2 ) M 2 ( X ) 2 2 .
Пример. Радиоаппаратура состоит из 1000
элементов. Вероятность отказа одного элемента в
течение одного года работы равна 0,001 и не
зависит от состояния других элементов. Какова
вероятность отказа ровно двух и не менее двух
элементов за год?
k e 1k e 1 e 1
Решение: = np = 1000·0,001=1, Pn (k ) k ! k ! k ! .
e 1 1
Pn (2) 0,184.
2 2e
e 1 e 1
2
Pn (k 2) 1 P(k 2) 1 P(0) P(1) 1 1 0,2642.
1 1
e
202.
2.9.2.Некоторые непрерывные распределения.Равномерное распределение.
Случайная величина Х имеет равномерное на
[a, b] распределение, если
c, х [ a , b ]
f ( x)
0, x [a, b]
Заметим, что
b
b
f ( x)dx 1 c dx cx c(b a) 1
b
a
a
1
c
b a
a
203.
Таким образом,1
, х [ a, b]
f ( x) b a
0,
x [ a, b]
График функции плотности распределения:
f(x)
1/(b-a)
x
204.
Найдем функцию распределения:F ( x) 0, x a;
F ( x) 1, x b.
a x b , то
x
x
1
x a
F ( x) f ( x)dx
dx
b a a
b a
Если
0, x a
x a
F ( x)
,a x b
b a
1, x b.
205.
График функции распределения:F(x)
a
b
x
b
2
1
1 x b
M ( X ) x f ( x)dx
xdx
b a a
b a 2 a
b a
b a
;
2(b a)
2
2
2
206.
b3
b
1
1
x
2
2
2
M ( X ) x f ( x)dx
x dx
b a a
b a 3 a
b a
b ab a
;
3(b a)
3
2
2
2
b ab a (a b)
2
2
D( X ) M ( X ) M ( X )
3
4
2
2
2
2
2
2
2
4b 4ab 4a 3b 6ab 3a b 2ab a (b a)
;
12
12
12
3
3
2
(b a)
(X )
.
12
2
207.
Область применения: Время ожиданияобслуживания.
Для случайной величины, имеющей
равномерное распределение, вероятность того, что
случайная величина приняла значение из данного
интервала внутри отрезка [a,b] не зависит от
положения этого интервала на числовой оси и
пропорциональна длине этого интервала.
d a c a d c
P (c X d ) F ( d ) F (c )
.
b a b a b a
208.
Экспоненциальное (показательное) распределение.Случайная величина Х, принимающая
неотрицательные значения, имеет
экспоненциальное распределение с параметром ,
если
х 0
0,
f ( x) x
e , x 0,
где λ – постоянная положительная величина.
Показательное распределение характеризуется
одним параметром λ.
f(x)
Построим график
функции плотности.
λ
x
209.
Найдем функцию распределения:Пусть x>0, тогда
x
0
x
F ( x) f (t )dt 0dt e
t
dt
0
t
x
e
x
1 e .
0
Таким образом,
F(x)
0,
F ( x)
x
1 e ,
х 0
x 0.
1
x
210.
xx u dv e dx
M ( X ) x f ( x)dx x e dx
x
dx du v e /
0
x
x
xe x 1 x
e
x
e dx lim ( xe )
0
x
0
0
x
x
e
1
1 1 1
lim x lim
lim x .
x e
x
x e
x
x u dv e dx
M ( X ) x f ( x)dx x e dx
x
2
xdx
du
v
e
/
0
2
2
2
x
2
211.
2x 2e x 2 x
x
x
xe dx lim x 2( xe /
x e
0
0
0
x
2x 2
x
2 e
1 x
lim x
e dx) xlim
x
e
x e
0
0
2
1
2
2
lim x 2 2 .
x e
2 1 1
D( X ) M ( X ) M ( X ) 2 2 2 ;
1
(X ) .
2
2
212.
Итак, числовые характеристики показательногораспределения: M(X) = 1/ , D(X)= 1/ 2.
Область применения: Экспоненциальное
распределение хорошо характеризует нарушения
режима работы сложных систем.
Нормальное распределение.
Случайная величина Х распределена по
нормальному (или гауссову) закону, если
( x a )2
1
2 2
f ( x)
e
.
2
213.
x az
2
2
2
( x a )
(
x
a
)
1
1
1
2
2 2
2
e
dx
e
dx dz
dx
2
2
2
Действительно,
dx 2 dz
1
1
1
z2
z2
2 e dz
e dz
2
1.
Нормальное распределение определяется двумя
параметрами a и σ. Найдем вероятностный смысл
этих параметров.
214.
( x a )2( x a )2
1
1
2 2
2 2
M (X ) x
e
dx
xe
dx
2
2
x a
z
2
x a 2 z
dx 2 dz
1
ae dz
z
2
1
z2
(a 2 z ) e 2 dz
2
2
a
ze dz
a.
z2
ze dz 0 как интеграл от нечетной функции в
z2
симметричных пределах.
215.
x az
2
( x a )2
1
2 2
M (X ) x
e
dx
x a 2 z
2
dx 2 dz
2
2
1
1
2
z
2
z2
(a 2 z ) e 2 dz
a e dz
2
1
2 2
z2
1
z2
2 z e dz
2
a
2
z
e
dz
2
2a 2 z e dz 0
z2
как интеграл от нечетной
функции в симметричных пределах.
216.
a2
e dz
z
2
2
a
2
2
z e
2
z u
z2
dz
dz du
z2
ze dz dv
v
e
z2
2
2
e
1
z2
( z
e dz ) a 2
2 2
2
z2
2 2
2
1
z b
2
1
2b
2
( lim z 2
) a
( lim b2
)
2 b e b 2
2 b e
2
1
2
2
2
a
( lim
)
a
b2
b
2
2
2be
D( X ) M ( X 2 ) M 2 ( X ) a 2 2 a 2 2 .
2
2 2
(X ) .
217.
Итак, M ( X ) a, D( X ) 2 , ( X ) .Обозначение: X~N(a,σ) означает, что случайная
величина X распределена по нормальному закону с
параметрами a и σ.
Стандартным нормальным распределением
называют нормальное распределение с
параметрами а=0, =1. Плотность стандартного
нормального распределения
1
f ( x)
e
2
Эта функция табулирована.
x2
2
218.
График плотности распределения называютнормальной кривой ( кривой Гаусса). Пусть
( x a )2
1
2 2
f ( x)
e
.
2
Построим график плотности распределения.
1) D( f ( x)) ;
3) lim f ( x) 0;
2) f ( x) 0;
x
( x a )2
1
2( x a)
2
2
4) f ( x)
e
0 x a.
2
2
2
+
а
219.
x = a - точка максимума функции, f (a)1
.
2
5)График симметричен относительно прямой x = a.
6) f ( x)
1
3
2
( x a )2
2 2
(e
( x a )2
( x a))
( x a )2
2( x a)
3
(e
e
( x a))
2
2
2
( x a )2
2
1
( x a)
2
2
2 2
3
e
(1
)
0
(
x
a
)
2
2
x a
1
2
2
+
2 2
а-σ
+
а+σ
220.
x a - точки перегиба1
f (a )
e 1/ 2 .
2
f(x)
1
2
a-σ
a
a+σ
Чем меньше σ, тем уже холм кривой.
x
221.
Вероятность попадания в заданный интервалнормальной случайной величины.
Пусть X~ N(a, ). Тогда вероятность того, что
Х примет значение, принадлежащее интервалу
( , ) равна
( x a )2
1
2
2
P( X ) f ( x)dx
e
dx
2
x a
( a ) /
z2
z
1
2
e
dz
2 ( a ) /
dx dz
222.
12
1
2
где
( a ) /
0
( a ) /
0
z2
2
1
e dz
e dz
2
( a )/
z2
2
0
( a )/
e dz
0
a
a
e dz Ф
Ф
,
z2
2
x
z2
2
t2
2
1
Ф( X )
e
dt
2 0
- интеграл Лапласа, он табулирован.
223.
Функция распределенияx
x
F ( x) f (t )dt
1
e
2
(t a )
2 2
dt
z
dz
dt
x a
x a
1
2
1
z2 / 2
e
dz
2
z
2
2
0
e
z /2
2
dz e
z2 / 2
0
x a
z z2 / 2
d
dz
e
2 0
x a
2
1 z2 / 2
1
x a
e
dz Ф
.
2
2
2 0
1
2e
2
0
1
2
t a
2
dz
224.
Итак,1
x a
F ( x) Ф
.
2
Свойства интеграла Лапласа.
1)Ф x Ф( x) , то есть нечетная функция.
2)Ф 0 0.
3)Ф 1/ 2.
1
4) Если X~N(0,1), то F0 ( x) Ф x .
2
225.
Значения интеграла Лапласа задается таблицей.Вероятность попадания случайной величины
X~N(a,σ) в интервал (а-ε, а+ε):
P( X-a <ε )= P(a-ε<X <a+ε )=
a a
a a
Ф
Ф
Ф Ф 2Ф .
Правило трех сигм: если случайная величина
распределена нормально, то абсолютная величина
ее отклонения от математического ожидания не
превосходит утроенного среднеквадратического
отклонения. Можно непосредственно подсчитать,
что
P( X-a <3 ) = 2Ф(3)=2·0.49865=0,9973.
226.
Нормальное распределение играет особуюроль в теории вероятностей и ее приложениях. Чем
это объясняется? Ответ на этот вопрос дает
центральная предельная теорема: если случайная
величина Х представляет собой сумму очень
большого числа взаимно независимых случайных
величин, влияние каждой из которых на всю сумму
ничтожно мало, то Х имеет распределение,
близкое к нормальному.
227.
Распределение “хи-квадрат” ( 2 ).Пусть независимые случайные величины
Х1, Х2, …,Хn имеют стандартное нормальное
распределение (Xi~N(0,1)). Тогда сумма квадратов
этих величин
2 = Х12 + Х22 + … + Хn2
распределена по закону 2 с k=n степенями
свободы.
Если же эти величины связаны одним линейным
соотношением, например Х1 + Х2 + …+ Хn =nХср ,
то число степеней свободы k = n–1.
228.
Распределение Стьюдента.Пусть независимые случайные величины Х0,
Х1, Х2, …, Хn имеют стандартное нормальное
распределение. Тогда случайна величина
tn
X0
( X 12 X 22 ... X n2 ) / n
имеет распределение, которое называют tраспределением, или распределением Стьюдента, с
n степенями свободы.
С возрастанием числа степеней свободы
распределение Стьюдента быстро приближается к
нормальному.
229.
Распределение Фишера.Если U и V независимые случайные величины,
распределенные по закону 2 со степенями
свободы k1 и k2 , то величина
U
F
V
k1
k2
U
F
V
k1
k2
имеет распределение, которое называют
F-распределением,
или
распределением
Фишера, со степенями свободы k1 и k2 .
230.
4. 3. Предельные теоремы теориивероятностей.
Во многих задачах теории вероятностей
изучаются случайные величины, являющиеся
суммами большого числа других случайных
величин, т.е. зависящие от большого числа
случайных факторов. Определенные свойства таких
случайных величин описываются совокупностью
так называемых предельных теорем, которые, в
свою очередь, разбиваются на две группы теорем –
«закон больших чисел» и «центральная предельная
теорема».
231.
Группа теорем, называемых «закономбольших чисел», устанавливает устойчивость
средних значений: при большом числе испытаний
их средний результат может быть предсказан с
достаточной точностью. Другая группа теорем,
называемая «центральной предельной теоремой»,
устанавливает, что при достаточно общих и
естественных условиях закон распределения
суммы большого числа случайных величин близок
к нормальному.
232.
4.3.1. Неравенство ЧебышеваЕсли известна дисперсия случайной величины, то с
её помощью можно оценить вероятность
отклонения этой величины на заданное значение от
своего математического ожидания, причём, эта
оценка зависит лишь от дисперсии.
Соответствующую оценку даёт неравенство
Чебышёва.
Пусть Х – одномерная случайная величина с
числовыми характеристиками M(X) = m, D(X) = 2.
Тогда для 0 справедливо неравенство
2
P X m 2
233.
То есть вероятность попадания случайнойвеличины X вне интервала (m – ε, m + ε) тем
меньше, чем меньше σ.
m-ε
Следствие:
m
m+ε
P X m 1 2
2
Неравенства Чебышева можно использовать для
оценки вероятностей событий, связанных со
случайной величиной, распределение которой
неизвестно.
234.
Замечание. Если с.в. X имеет биноминальноераспределение с математическим ожиданием
M(X)=a=np и дисперсией D(X)=npq , неравенство
Чебышева имеет вид
P m np
npq
,
npq
P m np 1 2 .
2
Для относительной частоты m/n события А в n
независимых испытаниях, в каждом из которых
оно может произойти с вероятностью р,
неравенство Чебышева принимает вид
m
pq
P p 1
.
2
n
n
235.
4.3.2. Закон больших чисел. ТеоремаЧебышева.
Определение. Последовательность случайных
величин Y1, Y2, ..., Yn сходится по вероятности к
случайной величине Y, если 0
lim P Yn Y 1
n
Обозначение:
вер
Yn
Y
(n )
236.
Теорема Чебышёва.Пусть Х1, Х2, …, Хn – независимые случайные
величины, дисперсии которых ограничены одним и
тем же числом С, то есть D(Xi) C (i = 1, 2, …, n).
Тогда для 0
__
__
P X n M ( X n ) 1, где
lim
n
__
1 n
Х n Xi.
n i 1
То есть
__
вер
__
X n M (Xn)
( n )
237.
Доказательство.По следствию из неравенства Чебышева
D( X n )
2
c
1 P X n M ( X n ) 1 2 1
1
,
2
n
так как
1 n
1 n
1
c
D( X n ) D( X i ) 2 ( D( X i )) 2 n c .
n i 1
n i 1
n
n
Перейдем к пределу при n→∞
__
c
__
1 limP X n M ( X n ) lim(1 2 ) 1
n
n
n
__
__
вер
__
__
P X n M (Xn) 1
X n M (Xn)
lim
n
( n )
238.
Теорема Чебышева показывает, что среднееарифметическое большого числа случайных величин
как угодно мало отличается ( с вероятностью
близкой к 1) от среднего арифметического их
математических ожиданий.
Следствие 1. Если с.в. Х1, Х2, …, Хn независимы и
одинаково распределены, с математическим
ожиданием a и дисперсией σ2, то для любого ε>0
1 n
lim P X i a 1.
n
n i 1
__
То есть
вер
Xn a
( n )
239.
Следствие 2. (Теорема Бернулли). Если в условияхсхемы Бернулли вероятность наступления события
А в одном опыте равна р, а число наступлений
этого события при n независимых испытаниях
равно m, то для любого ε>0
m
lim P p 1.
n
n
Доказательство.
Применим теорему Чебышёва к случайным
величинам Хi схемы Бернулли (Xi – число успехов
в i-ом испытании)
240.
M(Xi)= 1·p + 0·q = p, D(Xi)= M(Xi2) – M2(Xi) = p –- p2 = p(1-p)=pq.
На промежутке [0,1] D(Xi)= p – p2 ¼ i, то есть
условия теоремы Чебышёва выполнены.
__
вер
Тогда.
Xn р
(n )
__
1 n
m
Но Х n X i
n i 1
n
где m – число успехов в серии из n испытаний, а
m/n – относительная частота успеха в серии из n
испытаний, то есть
m вер
р
n ( n )
241.
Полученный вывод об устойчивости относительнойчастоты оправдывает статистический подход к
определению вероятности как некоторого числа,
около которого колеблется относительная частота.
4.3.3. Закон квадратного корня.
Пусть Х1, Х2, …, Хn – независимые случайные
величины, D(Xi) = 2 (i = 1, 2, …, n).
2
Тогда
n
1
то есть
1
2
D[ X i ]
n
,
2
n i 1
n
n
n
1
[ Xi ]
n i 1
n
242.
Среднее арифметическое имеет в n раз меньшеестандартное отклонение. Если многократно
повторять независимые измерения и за
приближённое значение измеряемой величины
принять X то точность можно увеличить в n
раз.
243.
5.4.Понятие о центральной предельной теореме.ЦПТ утверждает, что при весьма широких
допущениях распределение суммы большого числа
сравнимых по дисперсиям независимых
случайных величин близко к нормальному. ЦПТ
объясняет, почему нормальное распределение
часто встречается на практике.
Пусть Х – случайная ошибка измерения
некоторой величины. Она связана, как правило, с
воздействием большого числа независимых
причин.
244.
Если ни одна из причин не доминирует, то Х = Х1+ Х2 +… + Хn распределена по нормальному
закону, независимо от того, каковы законы
распределения отдельных слагаемых.
Замечание. Занимаясь физикой и астрономией,
Гаусс заметил, что если ошибки измерения носят
случайный характер, то независимо от существа
эксперимента они распределяются по строго
определённому закону (нормальному закону
распределения). Этот закон был известен давно,
но, отдавая должное заслугам Гаусса в его
изучении и применении, его стали называть
гауссовым.
245.
Со временем выяснилось, что нормальноераспределение носит универсальный характер.
Годовое количество осадков в данном районе, рост
и вес взрослых людей, вес и размеры семян…
246. Статистические методы обработки экспериментальных данных
247.
3.1. Генеральная совокупность и выборка.Основная задача математической статистики –
получение выводов о массовых явлениях и
процессах по данным наблюдений над ними или
экспериментов.
Пусть, например, нужно измерить некоторую
величину. Можно выполнить 2, 3 и т.д. измерения.
Так как в результате каждого измерения получается
некоторое число, то в результате получим набор
чисел X1, …,Xn . Вопрос: какое из этих чисел или
какую функцию этих чисел следует принять за
значение измеряемой величины? Результат
произвольного измерения из-за влияния различных
ошибок является случайной величиной.
248.
Определение. Результат последовательных инезависимых наблюдений X1, …,Xn над случайной
величиной X называется случайной выборкой
объема n.
Генеральная совокупность – информационный
массив, подвергающийся статистической
обработке.
Выборка – часть генеральной совокупности,
подвергающаяся непосредственному
исследованию.
Повторной называют выборку, при которой
отобранный объект ( перед отбором следующего )
возвращается в генеральную совокупность.
249.
Бесповторной называют выборку, при которойотобранный объект в генеральную совокупность не
возвращается.
При повторной выборке все входящие в нее
случайные величины X1, …,Xn взаимно независимы
и имеют одинаковую функцию распределения F(x),
причем такую же, что и наблюдаемая величина. На
практике это означает, что измерения производятся
независимо друг от друга (полученные результаты
одних измерений не влияют на возможные
результаты других) . Величины X1, …,Xn имеют
одинаковое математическое ожидание M(Xi)=a, то
есть результаты измерений свободны от систематических ошибок (результаты в среднем не смещены
250.
относительно истинного значения M(X)=a). Так жеX1, …,Xn имеют одинаковые дисперсии
D(Xi)=D(X)=σ2, что называется равноточностью
измерений (например, когда измерения физической
величины проведены на одном и том же приборе
при одинаковых условиях).
Распределение случайной величины X
характеризуется рядом параметров (
математическое ожидание, дисперсия и так далее).
Эти параметры называются параметрами
генеральной совокупности.
251.
Объём выборки – число элементов в выборке.Признак – параметр, который мы изучаем при
статистическом исследовании генеральной
совокупности.
Пример: выборочный контроль партии изделий.
252.
3.2.Первичная обработка статистическихданных. Вариационный ряд и эмпирическая
функция распределения.
Пусть изучается случайная величина Х –
признак, которым обладает данная генеральная
совокупность.
Требуется из опыта определить её закон
распределения или экспериментально проверить
гипотезу о том, что Х подчинена тому или иному
закону. С этой целью над Х проводят ряд
независимых наблюдений.
253.
Пусть в n опытах Х приняла значения х1, х2,.
…, хn. Это первичный статистический материал.
Результаты измерений выстраивают в порядке
возрастания:
х1*< х2*< …< хk* (k n).
Пусть хi* встречается ni раз (i = 1, 2, ..., k).
Тогда n1 + n2 + … + nk = n – объём выборки.
Здесь ni – абсолютная частота, хi* –
варианта, wi = ni / n – относительная частота.
Построим таблицу (вариационный ряд):
хi* х1* х2*
…
х k*
wi
w1 w2
...
wk
254.
При большом числе измерений строятинтервальный вариационный ряд:
Ii
wi
х1 х2 х2 х3
w1
w2
…
хk хk+1
...
wk
В этом случае весь диапазон изменения
случайной величины X делят на несколько
интервалов, где wi = ni / n , где ni – число
измерений, попавших в данный интервал.
Если некоторое значение попало на границу
интервала, то иногда рекомендуют считать его
принадлежащим к обоим интервалам и
прибавлять к ni и ni+1 по 0,5.
255.
Для наглядности строят различные графикистатистического распределения и, в частности,
полигон и гистограмму.
Полигоном частот называют ломанную, отрезки
которой соединяют точки (x1,n1), (x2,n2), …,(xk,nk),
n
(xk-1,nk-1)
(x2,n2)
(x1,n1)
(x3,n3)
(xk,nk)
X
Полигоном относительных частот называют
ломанную, соединяющую точки (x1,w1), (x2,w2),
…,(xk,wk), где wi = ni / n .
256.
Вариационный ряд часто оформляют графически ввиде гистограммы – аналога графика плотности
распределения. Для этого весь интервал частот, в
котором заключены все наблюдаемые значения
разбивают на несколько частичных интервалов
длины xi и находят для каждого частичного
интервала сумму частот вариант, попавших в i –ый
интервал. Высота hi столбика гистограммы частот
определяется из условия
k
hi xi = ni , где ni n.
i 1
То есть площадь i- ого частичного прямоугольника
равна сумме частот вариант i- ого интервала.
Значит , площадь гистограммы частот равна сумме
всех частот, то есть объему выборки.
257.
Для гистограммы относительных частот высота hii-ого столбика гистограммы определяется из
условия
k
hi xi = wi , где wi 1
i 1
Пользуясь вариационным рядом, можно построить
эмпирическую функцию распределения случайной
величины Х.
Определение. Эмпирической функцией
распределения сл. величины Х называется частота
события {X<x} в данном статистическом
материале, то есть
F*(x) = Р*{ Х<х } = wi
i: xi x
258.
Пусть х фиксировано, тогда по теореме БернуллиF*(x) = Р*{ Х<х }
вер
Р{ Х<х }= F(x),
(n )
т.е. эмпирическая функция распределения сходится
по вероятности к истинной функции
распределения.
259.
3.3. Точечные оценки параметров.3.3.1.Понятие точечной оценки.
Пусть изучается случайная величина Х, закон
распределения которой F(x; ) содержит некоторый
неизвестный параметр . Задача – найти
подходящую оценку параметра по результатам n
независимых наблюдений над данной случайной
величиной.
Определение. Точечной оценкой * параметра
называется функция выборки *(х1, х2, …, хn),
значения которой принимаются в качестве
приближённого значения параметра.
Замечание. Так как * – функция от случайной
величины, то она является случайной величиной.
260.
Требования, предъявляемые к точечнымоценкам.
Для одного и того же параметра по одной и той
же выборке можно построить много различных
оценок. Для сравнения оценок между собой
вводятся следующие специальные характеристики.
1.Несмещённость.
Определение. Оценка * называется несмещенной,
если ее математическое ожидание равно истинному значению параметра , то есть M( *) = (то
есть при замене истинного значения параметра на
приближённое мы не делаем систематической
ошибки).
261.
2.Состоятельность.Определение. Оценка * называется состоятельной,
если при n→∞ она сходится по вероятности к
истинному значению оцениваемого параметра .
вер
,
*
( n )
то есть
lim P 1.
n
*
Точность оценки растёт с ростом числа измерений
262.
3.Эффективность.Пусть *i (i = 1, ..., k) – различные несмещённые
оценки одного и того же параметра . Оценка *i
считается лучшей по сравнению с другими, если её
дисперсия минимальна. Такая оценка называется
эффективной. (Эффективные оценки гарантируют
минимум среднеквадратической ошибки.)
Замечание. На практике не всегда удаётся
удовлетворить всем этим требованиям сразу. В
целях простоты расчётов чем-то жертвуют.
263.
Определение. Точностью оценки * называетсяквадрат отклонения оценки от истинного значения
, то есть M(( * - )2)=q2( *). Для несмещенных
оценок точность определяется величиной
дисперсии оценки q2( *) =D( * ).
264.
Метод максимального правдоподобия.Пусть задана модель F {F ( x, ), }
для схемы повторных независимых
наблюдений над некоторой случайной
X
X
,
...,
X
,
1
n
величиной
т. е. допустимые
функции распределения задаются
с точностью до значений некоторого параметра .
Такую модель называют параметрической, а
множество A возможных значений параметра –
параметрическим множеством. Пусть f ( x, )
плотность распределения наблюдаемой случайной
величины ( или вероятность события X=x в
дискретном случае) .
F
X 1 , ..., X n
265.
Тогда функция L( x, ) f ( x1; ) ... f ( xn , ) ,рассматриваемая при фиксированном x X как
функция параметра A , называется функцией
правдоподобия.
В дальнейшем предполагается, что
L( x, ) 0 и функция дифференцируема по .
F
X 1 , ..., X n
266.
Одним из наиболее универсальных методовоценивания неизвестных параметров распределений
является метод максимального правдоподобия. По
этому методу оценкой максимального
правдоподобия (о.м.п.) n* параметра α по выборке
X=(X1,…, Xn) является такая точка
параметрического множества A, в которой функция
правдоподобия L(x; ) при каждом Х=х достигает
максимума, т.е.
L(x ; n*)≥L(x; )
для или L(x; n ) sup L.( x; )
*
A
267.
Если для каждого x X максимум функции L(x;) достигается во внутренней точке множества A и
функция L(x; ) дифференцируема по , то о.м.п.
n* удовлетворяет уравнению правдоподобия
ln L( x; )
0
или
ln L( x; )
0, j 1,..., r, если ( 1 ,..., r )
j
268.
3.3.2. Оценки для математического ожидания идисперсии.
Пусть M(X) = m, D(X) = 2. Оба параметра не
известны. Пусть Х1, Х2, …, Хn – результаты n
независимых опытов над Х (повторная случайная
выборка). Положим
n
1
m* Х X i
n i 1
__
Проверим, выполняются ли в
требования к точечным оценкам.
этом
случае
269.
1) Несмещённость.n
n
1
1
M (m* ) M ( X ) M X i M ( X i )
n i 1
n i 1
1
nm m.
n
2)Состоятельность
По теореме Чебышёва
__
вер
m X M (X ) m
*
( n )
270.
3)Эффективностьn
n
1
1
D(m* ) D( X ) D( X i ) 2 D( X i )
n i 1
n i 1
1 2
2
2 n
.
n
n
(закон квадратного корня).
Эффективность оценки зависит от вида распреде ления. Доказано, что если Х имеет нормальное
распределение, то такая оценка эффективна.
271.
В качестве оценки для дисперсии рассмотрим__
n
1
*
2
D (Xi X )
n i 1
Теорема. Оценка D* является смещённой оценкой
для 2, причём
n 1 2
*
M (D )
n
.
Доказательство.
Сделаем следующие преобразования:
n
n
__
__
1
1
D* ( X i X ) 2 (( X i m) ( X m)) 2
n i 1
n i 1
__
1 n
(( X i m) 2 2( X i m)( X m) ( X m) 2 )
n i 1
272.
nn
__
1 n
2
1
( X i m) 2 ( X i m)( X m) ( X m) 2
n i 1
n i 1
n i 1
n
1 n
2
1
2
2
( X i m) ( X m) ( X i m) ( X m) n
n i 1
n
n
i 1
n
1 n
2
( X i m) 2 ( X m)( X i mn) ( X m) 2
n i 1
n
i 1
n
1 n
1
( X i m) 2 2( X m) X i 2m( X m) ( X m) 2
n i 1
n i 1
1 n
( X i m) 2 2( X m) X 2m( X m) ( X m) 2
n i 1
1 n
( X i m) 2 2( X m)( X m) ( X m) 2
n i 1
273.
Таким образом,n
1
D * ( X i m) 2 ( X m) 2
n i 1
n
1
Тогда M ( D* ) M ( ( X i m) 2 ( X m) 2 )
n i 1
n
1 n
1
M ( ( X i m) 2 ) ( X m) 2 M (( X i m)2 ) M ( X m) 2
n i 1
n i 1
n
n
1
1
1 2
2
2
D
(
X
)
2 D ( X i )
n D( X )
i
n i 1
n
n
i 1
1
n 1 2
2
2 n
.
n
n
2
Следовательно, оценка смещенная.
274.
Определение.Оценкой дисперсии при неизвестном
математическом ожидании называется величина
__
n
n
1
2
S2
2
(
X
X
)
i
n 1
n 1 i 1
Эта оценка несмещённая .
Оценка S2 называется выборочной дисперсией.
Можно показать, что S2 – состоятельная
оценка. В случае нормального распределения
S2 является асимптотически устойчивой, то
S
есть отношение
её дисперсии к минимально
возможной
1
при
n .
2
275.
2S=
S – выборочный стандарт.
Это состоятельная, но смещённая оценка ( ее
смещение убывает с увеличением n).
Число k=n-1 в формуле для оценки дисперсии
называется числом степеней свободы для оценки S2
Замечание.
Оценкой дисперсии при известном мат. ожидании
называется величина
n
1
S0 ( X i a ) 2
n i 1
2
S2
Эта оценка несмещённая и состоятельная.
276.
Замечание.На практике для S2 удобнее использовать такое
n
__
выражение: 2
1
2
2
S
Действительно,
( X i n( X ) )
n 1 i 1
n
1
1
2
2
2
2
(X i 2Xi X X )
S
(Xi X )
n 1 i 1
n 1 i 1
1 n 2
2 n
1 n
2
X
X
X
X
i
i
n 1 i 1
n 1 i 1
n 1 i 1
n
n
1 n 2
1
2
2
2
( X i 2 X X i nX )
( X i 2 XnX nX )
n 1 i 1
n 1 i 1
i 1
1 n 2
( X i nX 2 ).
n 1 i 1
n
__
277.
Вычисление оценки математического ожидания иоценки дисперсии упрощается, если отсчет
значений Xi вести от подходящим образом
выбранного начала отсчета и в подходящем
масштабе, то есть если сделать линейную замену
(кодирование) X i c hU i .Тогда
1 n
Ui .
X c hU , где U n
i 1
1 n
1 n
1
1 n
X X i (c hU i ) cn hU i
n i 1
n i 1
n
n i 1
c hU
278.
nn
__
1
1
2
2
2
2
2
S
( X i n( X ) )
(c hU i ) n(c hU )
n 1 i 1
n 1 i 1
1 n 2
2
2
2
2 2
(c 2chU i h U i ) nc 2nchU h U
n 1 i 1
n
n
1 2
2
2
2
2 2
nc 2ch U i h U i nc 2nchU h U
n 1
i 1
i 1
n
1
2
2
2 2
2chnU h U i 2nchU h U n
n 1
i 1
h n 2
2
Ui U n .
n 1 i 1
2
279.
Итак,n
h
2
2
2
S
Ui U n .
n 1 i 1
2
280.
3.3. 3. Оценка ковариации и коэффициентакорреляции
Пусть (Х1, Х2) – двумерная случайная величина.
n
__
__
1
K12*
( X 1i X 1 )( X 2i X 2 )
n 1 i 1
несмещённая оценка ковариации (эмпирическая
ковариация).
*
12
K
r12
S1S 2
– эмпирический коэффициент корреляции
281.
4.Интервальные оценки.4.1. Доверительный интервал и доверительная
вероятность.
Наряду с точечным оцениванием неизвестных
параметров распределений в математической
статистике используется оценивание с помощью
доверительных интервалов или (в случае векторного
параметра) доверительных множеств. Пусть * –
точечная оценка параметра . К каким ошибкам
может привести замена точного значения параметра
его точечной оценкой? Чтобы дать представление о
точности и надежности оценки, в мат. статистике
вводятся понятия доверительного интервала и
282.
Назначим достаточно большую вероятность p(например, p = 0,95) и найдём такое число , для
которого Р{ – * < }= p, то есть
Р{ * – < < * + }= p.
Последнее равенство означает, что с вероятностью
p случайный интервал Ip = ( *– , *+ ) накроет
неизвестное значение параметра . Вероятность p
называют доверительной вероятностью (или
надёжностью), а интервал Ip – доверительным
интервалом. Границы доверительного интервала –
доверительные границы.
283.
Определение. Интервал Ip = ( *– , *+ )называется доверительным интервалом
надёжности p для неизвестного параметра , если
Р{ * – < < * + }= p,
где * – точечная оценка параметра .
То есть доверительным интервалом параметра
называется интервал со случайными границами,
который накрывает истинное значение параметра
с заданной вероятностью, которая называется
доверительной вероятностью.
Величина α=1-p называется уровнем
значимости.
284.
При этом обычно требуют, чтобы вероятностивыхода за границы доверительного интервала были
равны между собой, то есть
Р{ < * - }= Р { > * + }= (1-p)/2=α/2.
Длина доверительного интервала,
характеризующая точность интервального
оценивания, зависит от объема выборки n и
доверительной вероятности p=1-α : при увеличении
объема выборки длина доверительного интервала
уменьшается, а с приближением доверительной
вероятности к единице – увеличивается.
285.
При решении некоторых задач применяютсяодносторонние доверительные интервалы, границы
которых определяются из условий
Р{ > * - }= p или Р { < * + }= p.
Эти интервалы называются соответственно
правосторонними и левосторонними
доверительными интервалами.
286.
4.2. Интервальная оценка центра нормальногораспределения, если известна дисперсия.
Пусть случайная величина X~ N(a, ). Пусть
дисперсия 2 известна (то есть известна точность
метода.), a – это неизвестный параметр, который
требуется оценить. Мы получили для центра
__
1 n
распределения точечную оценку Х n X i .
i 1
Эта случайная величина имеет распределение
N (a, / n ). Тогда случайная величина
U ( X a) /( / n)
имеет стандартное нормальное распределение
N (0, 1) независимо от параметра a. Кроме того,
функция U(a) непрерывна и строго монотонна.
287.
Зададим доверительную вероятность p иопределим доверительные границы из условия
Р{ X – a < }= p
__
__
n X a n
X a
P
P u
u
n
2
n
u
z
1
2
e
dz Ф(u ) Ф( u ) 2Ф(u ) p 1
2 u
Таким образом, по таблицам для функции Лапласа
находим значение up, удовлетворяющее уравнению
Ф(up) = p/2.
288.
ТогдаP
__
u1 / 2
X a
u1 / 2
1
n
P X u1 / 2
a X u1 / 2
1
n
n
То есть I X u1 / 2
, X u1 / 2
,
n
n
где u1 / 2 - квантиль стандартного нормального
распределения.
289.
4.3. Интервальная оценка центра нормальногораспределения, если дисперсия не известна.
Пусть сл. величина X~ N(a, ). Дисперсия 2
неизвестна, a – это параметр, который требуется
оценить. Точечная оценка для центра распределения
__
1 n
, а оценка
Х дисперсии
Xi
n
__
n
1
S2
( X i X )2 .
n 1 i 1
i 1
Тогда при доверительной вероятности 1-α
доверительный интервал для мат. ожидания имеет
вид
S
S
I X t1 / 2 (k )
, X t1 / 2 (k )
,
n
n
где t1 / 2 (k ) - квантиль распределения Стьюдента с
k = n-1 степенями свободы.
290.
По данным выборки__построим случайнуювеличину
X a
T
S
n
__
Х
Эта случайная величина имеет распределение
Стьюдента с k= (n – 1) степенями свободы.
Плотность этого распределения Sn-1(t)
выражается через Г – функцию и является
функцией чётной. Распределение Стьюдента
удобно тем, что не зависит от .
Зададим доверительную вероятность p и
определим доверительные границы из условия
Р{ X – a < }= p
291.
____
n X a n
X a
P
P t
t
S
S
S
S
n
n
t
2 Sn 1 ( )d p 1 .
0
По таблицам распределения Стьюдента при
заданном p определим tp (квантиль распределения
Стьюдента).
Таким образом
__
X a
S
S
P t1 / 2
t1 / 2 P X t1 / 2
a X t1 / 2
p
S
n
n
n
292.
4.4. Интервальная оценка дисперсии истандарта нормального распределения.
Пусть X~ N(a, ). Требуется оценить . Мат.
ожидание неизвесто. По данным выборки
построим случайную величину
2
S
2
2 (n 1)
V
S2
2
(n 1)
Она имеет распределение
n2 1 хи-квадрат с
(n–1) степенями свободы (распределение
Пирсона). Плотность этого распределения K n-1(χ)
также выражается через Г-функцию и имеет вид:
n 2 / 2
e
K ( , n 1)
2
2
n 1
2
( n 3) / 2
n 1
Г(
)
2
293.
Зададим доверительную вероятность pопределим доверительные границы из условия
и
S
P x1 2 (n 1) x2 1 K n 1 (v)dv
x1
x2
2
V
S2
2
(n 1)
Так как распределение не симметрично, то х1 и х2
можно выбрать по-разному. Выберем интервал так,
чтобы вероятности выхода за его пределы вправо и
влево были одинаковы и равны (1–p)/2.
n2 1
294.
Из последнего соотношения получаем:2 n 1
2
2 n 1
P S
S
x2
x1
2 2
2
2 2
P ( S z н S zв ) p ,
n
1
n
1
2
2
где z
z
,
,
в
н
x1
x2
V
S2
2
(n 1)
Величины zн , zв – табулированы в зависимости от
числа степеней свободы n – 1 и доверительной
вероятности p.
2
n 1
295.
Итак, если мат. ожидание неизвестно, тодоверительный интервал для дисперсии:
n 1
n 1
2
2
S
S
2
2
1 / 2 (n 1)
/ 2 (n 1)
2
если мат. ожидание известно, то доверительный
интервал для дисперсии:
S0
2
n
S0
2
1 / 2 (n)
2
n
2
/ 2 ( n )
2
296. Проверка статистических гипотез.
297.
5.Проверка статистических5.1.Понятие статистической гипотезы.
Статистической гипотезой (или просто гипотезой)
называют любое предположение о виде или
свойствах распределения наблюдаемых в
эксперименте случайных величин. Пусть для
исследуемого процесса сформулирована некоторая
гипотеза Н0 (ее называют основной или нулевой
гипотезой). В этом случае задача проверки этой
гипотезы заключается в конструировании такого
правила (алгоритма ), которое позволяло бы по
результатам соответствующих наблюдений (по
имеющимся статистическим данным) принять или
отклонить Н .
298.
Любое такое правило называют статистическимкритерием (или просто критерием) согласия для
гипотезы Н0. Если гипотеза Н0 однозначно
фиксирует распределение наблюдений, то ее
называют простой, в противном случае – сложной.
Пусть результат эксперимента описывается
некоторой случайной величиной Х=(Х1, …, Хn) и Н0
– некоторая гипотеза о ее распределении. Пусть,
далее Z=Z(Х) –некоторая статистика,
характеризующая отклонение эмпирических
данных от соответствующих (гипотезе Н0)
гипотетических значений, распределение которой в
случае справедливости Н0 известно (точно или хотя
бы приближенно).
299.
Тогда для каждого достаточно малого числа α > 0можно определить подмножество Z t : t Z ( x), x X ,
удовлетворяющее ( хотя бы приближенно) условию
P( z Z H 0 ) .
Любое такое подмножество Zα порождает
следующий критерий согласия для гипотезы Н0
: если z=Z(X) - наблюдавшееся значение
статистики Z(Х),
гипотеза Н0
z Zто при
отвергается; в противном случае считается , что
данные не противоречат Н0 (согласуется с Н0 );
z если
Z
другими словами,
, то гипотеза Н0
принимается (подчеркнем,
не
z что
Z факт
является доказательством истинности Н0).
t T (x)
t T1
300.
Если гипотеза Н0 истинна, то согласно указанномуправилу мы можем ее отвергнуть (т.е. принять
неправильное решение) с вероятностью, меньшей
или равной α. Число α называют уровнем
значимости критерия, а множество Zα –
критическим множеством (областью) для
гипотезы Н0. Статистику Z в описанной методике
называют статистикой критерия, а сам критерийкритерием Zα.
Итак, согласно описанной методике, критерий
определяется заданием соответствующей
критической области Zα в множестве значений
статистики Z при выбранном уровне значимости α.
301.
Для того чтобы иметь возможность сравниватьразличные критерии (порождаемые разными
статистиками Z) , надо ввести понятие
альтернативного распределения
(альтернативной гипотезы) и мощности
критерия.
Любое допустимое распределение FX=F
выборки
Х , отличающееся от гипотетического (т.е.
распределения при гипотезе Н0), называют
альтернативным распределением или
альтернативой. Совокупность всех
альтернатив называют альтернативной
F
:
302.
Функцией мощности критерия Zα называютследующий функционал на множестве всех
F
допустимых распределений
W ( F ) W (Z ; F ) P(Z Z F ).
Таким образом , W(F) – это вероятность попадания
значения статистики критерия в критическую
область, когда истинным распределением
наблюдений является распределение F.
Если F H1 , то значение W(F) называют
мощностью критерия при альтернативе F; оно
характеризует вероятность принятия правильного
решения (отклонение Н0) в ситуации, когда Н0
F
:
303.
5.2.Процедура проверки простойпараметрической гипотезы.
Из двух критериев с одним и тем же уровнем
значимости α лучшим считают тот, мощность
которого при альтернативах больше.
В процессе проверки гипотезы Но можно:
1)прийти к правильному решению;
2)отклонить гипотезу Но, когда она верна (ошибка
первого рода);
3)принять гипотезу Но, когда она ложна (ошибка
второго рода).
Обозначим: – вероятность ошибки первого рода
– уровень значимости,
– вероятность ошибки второго рода
304.
Вероятность 1– называют мощностью критерия.Это вероятность того, что не будет допущена
ошибка второго рода.
Гипотеза
критерий
Ошибка Вероятность
Но
Верна
принимается
1–
отвергается
ложна
Первого
рода
принимается Второго
рода
отвергается
1–
305.
Как найти критическую область?Для определения критической области задают
уровень значимости и учитывают вид
альтернативной гипотезы. Допустим, основная
гипотеза о значении неизвестного параметра
выглядит так: Но : = о
При этом альтернативная гипотеза может иметь
следующий вид: Н1 : > о ,
Н1 : < о ,
Н1 : о
Различают одностороннюю и двустороннюю
критические области.
Пусть f(z) –плотность распределения случайной
величины Z (критерия).
306.
Пусть f(z) –плотность распределения случайнойвеличины Z (критерия), при условии, что верна
гипотеза H0, а zp – квантиль распределения
функции Z.
1) Правосторонняя критическая область Z>zкр
определяется из условия Р{ Z>zкр }= .
Z1-α
Критическая область
размещается в правом
хвосте распределения
функции Z, то есть
удовлетворяет
неравенству Z>z1 -α
307.
2) Левосторонняя критическая область Z< zкропределяется из условия Р{ Z<zкр }= .
zα
Критическая область
размещается в левом
хвосте распределения
функции Z, то есть
удовлетворяет
неравенству Z<zα
308.
3) Двусторонняя критическая областьZ< zкр Z>zкр определяется из условия
Р{ Z<zкр }= Р{ Z>zкр }= /2.
Zα/2
Z 1-α/2
Критическая область размещается в обоих
хвостах распределения функции Z, то есть
удовлетворяет совокупности неравенств Z<zα/2 и
Z>z 1-α/2
309.
Таким образом, если вычисленное поэкспериментальным данным значение k попадает в
критическую область, гипотеза Но отвергается с
уровнем значимости , в противном случае нет
оснований отвергнуть гипотезу.
Итак, проверка параметрической гипотезы
статистической гипотезы при помощи критерия
значимости может быть разбита на следующие
этапы:
1) сформулировать проверяемую гипотезу H0 и
альтернативную гипотезу H1;
2) назначить уровень значимости α;
3) Выбрать статистику Z критерия для проверки
гипотезы H ;
310.
4) определить выборочное распределениестатистики Z при условии, что верна гипотеза H0;
5) в зависимости от формулировки альтернативной
гипотезы определить критическую область Vк
одним из неравенств Z<zα , Z>z 1 –α или
совокупностью неравенств Z<zα/2 и Z>z 1-α/2;
6) получить выборку наблюдений и вычислить
выборочное значение zв статистики критерия;
7) Принять статистическое решение:
- если zв Vk , то отклонить гипотезу H0 как не
согласующуюся с результатами наблюдений;
- еслиzв V / Vk , то принять гипотезу H0 как не
противоречащую результатам наблюдений;
311.
5.3. Проверка гипотезы о равенстве дисперсийдвух выборок (критерий Фишера).
Пусть генеральные совокупности X и Y
распределены по законам N(a1, 1). N(a2, 2).
Пусть X1, X2, ... , Xn1; Y1, Y2, ... , Yn2 –
независимые выборки из этих генеральных
совокупностей. Мат. ожидание не известно.
S12 , S22 – выборочные дисперсии. Пусть для
определённости S12 > S22. Требуется при заданном
уровне значимости проверить гипотезу
Но: 12 = 22
312.
В качестве критерия проверки нулевойгипотезы примем случайную величину
F = S12 / S22, которая, при условии справедливости
Но, имеет распределение Фишера с k1 = n1 – 1,
k2 = n2 – 1 степенями свободы.
1) Пусть Н1: 12 > 22
В этом случае для случайной величины F строят
правостороннюю критическую область, где
Fкр = F(1- ; k1, k2) – квантиль распределения
Фишера.
Если F< Fкр – нулевая гипотеза принимается с
уровнем значимости .
313.
2) Если конкурирующая гипотезаН1: 12 22,
то строят двустороннюю критическую область и
сравнивают F = S12 / S22 с табличным значением
для двустороннего критерия Фишера
F(1- /2; k1, k2). Если F< F(1- /2; k1, k2), то гипотеза
H0 принимается, в противном случае гипотеза H0
отвергается и принимается альтернативная
гипотеза Н1: 12 22.
314.
Замечание. В случае, если мат. ожидание известно,то в качестве критерия проверки нулевой гипотезы
Но: 12 = 22 рассматривают функцию критерия F
= S012 / S022, которая имеет распределение Фишера
с n1 и n2 степенями свободы.
1) Пусть Н1: 12 > 22,,
тогда если F< Fкр F(1- ; n1, n2), то нулевая
гипотеза принимается с уровнем значимости .
2) Если конкурирующая гипотеза Н1: 12 22, то
гипотеза H0 принимается при условии
F< F(1- /2; n1, n2).
315.
5.4. Проверка гипотезы о равенстве дисперсийзаданному числу.
Пусть X1, X2, ... , Xn– выборка из генеральной
совокупности, распределенная по нормальному
закону X~N(a, ). Значение дисперсии неизвестно.
S2 – выборочная дисперсия. Требуется при заданном
уровне значимости проверить гипотезу о
равенстве дисперсии заданному числу.
Но: 2 = 02
Пусть мат. ожидание неизвестно. В качестве
критерия проверки нулевой гипотезы примем
случайную величину Z = (n-1)S2 / 02, которая имеет
распределение χ2 c k =n-1 степенями свободы.
316.
Рассмотрим различные виды альтернативныхгипотез.
1) Н1: 2 > 02
В этом случае для случайной величины Z строят
правостороннюю критическую область.
Если Z< χ1-α2 (k)– нулевая гипотеза принимается с
уровнем значимости .
2) Н1: 2 < 02
Для случайной величины Z строят левостороннюю
критическую область.
Если Z>χα2 (k)– нулевая гипотеза принимается с
уровнем значимости .
317.
3) Н1: 2 ≠ 02В этом случае для случайной величины Z строят
двустороннюю критическую область.
Если χα/22 (k) < Z < χ1-α/22 (k)– нулевая гипотеза
принимается с уровнем значимости .
Замечание. Если мат. ожидание известно, то в
качестве критерия проверки нулевой гипотезы
примем случайную величину Z = nS02 / 02, где S02 –
оценка дисперсии при известном математическом
ожидании, а n – объем выборки.
318.
5.5.Проверка гипотезы о равенствематематических ожиданий двух выборок
(критерий Стьюдента)
Пусть генеральные совокупности X и Y
распределены по нормальным законам N(a1, 1) и
N(a2, 2), причём мат. ожидание неизвестно.
Дисперсии 1 и 2 неизвестны, но гипотеза о
равенстве дисперсий принимается.( 1 = 2 = )
Требуется при заданном уровне значимости
проверить нулевую гипотезу Но : а1 = а2,
т.е. требуется установить, значимо ли
различаются выборочные средние, найденные по
независимым выборкам объёмов n1 и n2.
319.
Пусть S12 , S22 – выборочные дисперсии,сводная оценка дисперсии
2
2
S
(
n
1
)
S
2
1
1
2 ( n2 1)
S cв
n1 n2 2
В качестве критерия проверки нулевой гипотезы
__
__
примем случайную величину
X Y
T
Sсв
1 1
n1 n2
которая при справедливости нулевой гипотезы
имеет распределение Стьюдента с с k = n1 + n2 – 2
степенями свободы.
t ( k) – квантиль распределения Стьюдента.
320.
Рассмотрим различные виды альтернативныхгипотез.
1) Н1: а1 > а2
В этом случае для случайной величины Т строят
правостороннюю критическую область.
Если Т< t 1-α (kсв)– нулевая гипотеза принимается с
уровнем значимости .
2) Н1: а1 < а2 (левосторонняя критическая
область) то нулевая гипотеза принимается с
уровнем значимости , при условии Т> t α (kсв).
3) Н1 : а1 а2
Строим двустороннюю критическую область
из условия P{|T| > t( ; k)} = , нулевая гипотеза
принимается при условии | Т | < t 1-α/2 (kсв).
321.
Замечание. Если дисперсии σ1 и σ2 известны, то вкачестве критерия проверки нулевой гипотезы
__
__
принимают случайную величину
X Y
U
2
1
n1
2
2
n2
,
которая имеет стандартное нормальное
распределение ( U~N(0,1) ). Гипотеза о равенстве
мат. ожиданий принимается , если :
1) U< u 1-α для альтернативной гипотезы Н1: а1 > а2
2) U> uα для альтернативной гипотезы Н1: а1 < а2
3) | U | < u 1-α/2 для альтернативной гипотезы
Н1 : а 1 а 2
322.
5.6.Проверка гипотезы о равенствематематического ожидания заданному числу.
Пусть X1, X2, ... , Xn– выборка из генеральной
совокупности, распределенная по нормальному
закону X~N(a, ). Значение мат. ожидания
неизвестно. X– оценка мат. ожидания. Требуется
при заданном уровне значимости проверить
гипотезу о равенстве мат. ожидания заданному
числу: Но: a=a 0
1. Пусть дисперсия неизвестна. В качестве критерия
проверки нулевой гипотезы примем случайную
__
величину
( X a0 ) n
t
, которая имеет
S
распределение Стьюдента с k степенями свободы.
323.
S2 – оценка дисперсии, k- число степеней свободы.Рассмотрим различные виды альтернативных
гипотез.
1) Н1: а > а0 (правосторонняя критическая
область).
Если t< t 1-α (k)– нулевая гипотеза принимается с
уровнем значимости .
2) Н1: а < а0 (левосторонняя критическая
область). Нулевая гипотеза принимается с
уровнем значимости , при условии t> t α (k).
3) Н1 : а1 а2
(двусторонняя критическая область) Нулевая
гипотеза принимается при условии | t | < t 1-α/2 (k).
324.
Замечание. Если дисперсия σ известна, то вкачестве критерия проверки нулевой гипотезы
принимают случайную величину
__
U
( X a0 ) n
,
которая имеет стандартное нормальное
распределение ( U~N(0,1) ). Гипотеза о равенстве
мат. ожидания заданному числу принимается, если :
1) U< u 1-α для альтернативной гипотезы Н1: а > а0
2) U> uα для альтернативной гипотезы Н1: а < а0
3) | U | < u 1-α/2 для альтернативной гипотезы
Н1 : а а 0
325.
5.7. Проверка гипотезы о виде распределения(критерий согласия 2)
Пусть закон распределения случайной
величины не известен, но есть основания
предполагать, что он имеет определённый вид.
Критерий значимости для проверки таких гипотез
называется критерием согласия.
Пусть гипотеза Но утверждает, что генеральная
совокупность распределена по закону с плотностью
распределения (х).По данным эксперимента
строится случайная величина, характеризующая
отклонение экспериментальных данных от
гипотетических. С её помощью осуществляется
326.
Для построения критерия 2 весь диапазонзначений Х разбивают на L интервалов [x i-1, xi]
(i =1, 2,..., N). Вероятность попадания в i-ый
интервал вычисляется с использованием
гипотетической плотности распределения (х):
xi
pi ( x)dx
xi 1
Из эксперимента вычисляют частоту попадания в
тот же интервал ni/n. При условии истинности
гипотезы
n вер
i
n
pi
( n )
327.
2L
(
n
/
n
p
)
(ni npi )
2
i
i
n
pi
npi
i 1
i 1
L
2
Построенную случайную величину при заданном
уровне значимости сравнивают с 2 ( ; k) –
квантилью распределения 2 с k = L – 1 – m
степенями свободы, где m – число оцениваемых
параметров. Например, если проверяется гипотеза
о нормальном распределении и для вычисления pi
параметры распределения оцениваются по той же
выборке, то k = L – 3.
328.
Если2 > 2 ( ; k) –
гипотеза отвергается с уровнем значимости . В
противном случае – принимается как не
противоречащая результатам эксперимента.
329. Статистический анализ зависимостей
330.
6. 1. Элементы регрессионного анализа. Методнаименьших квадратов.
На практике часто возникает ситуация, когда есть
предположение о функциональной зависимости
величины у от величины х.
y = f(x; a1, a2, …,am) (1)
Причем, вид функции f известен, а параметры
неизвестны. Например:
у = a1+ a2х или у = a1+ a2х + a3х2
Для отыскания неизвестных значений
параметров проводят эксперименты. Но так как
результаты эксперимента имеют случайные ошибки,
то по ним нельзя найти точные значения
параметров, а только их оценки.
331.
Поэтому ставится задача отыскания наилучшихоценок параметров по результатам N
экспериментов.
Пусть Уi – возможный результат i-ого эксперимента.
Y1, Y2, …, YN – взаимно независимые случайные
величины. Xi – точка, в которой проводился i-ый
эксперимент. Предполагается, что Xi – неслучайные
величины. На практике это означает, что ошибками
в их определении можно пренебречь.
Аргумент Х иногда называют регулируемым
фактором, а результат эксперимента У – откликом.
332.
Пусть Zi – случайная ошибка i-огоэксперимента, причем ее математическое ожидание
равно нулю, а D(Zi) = 2/wi, где wi – известные числа
(веса измерений), а 2 обычно не известно. Тогда
математическую модель эксперимента можно
записать в виде
Yi = f(Xi ; a1, a2, …,am) + Zi ( i = 1, 2, …, N ),
что равносильно равенствам
М(Yi) = f(Xi ; a1, a2, …, am) ( i = 1, 2, …, N ).
D(Yi) = D(Zi) = 2/wi .
(2)
333.
Таким образом, значение функции f в точке Xiпредставляет собой теоретическое среднее
значение возможных результатов экспериментов в
i-ой точке.
Зависимость (2) называют регрессией.
Уравнение (1) называют уравнением регрессии, а
отыскание оценок неизвестных параметров и
исследование получаемых моделей –
регрессионным анализом.
Вид функции регрессии обычно определяют
из практических соображений.
В регрессионном анализе принято строить
оценки по методу наименьших квадратов (МНК).
334.
Определение. Оценками параметров a1, a2, …,amпо МНК называются такие величины a1*, a2*,
…,am*, для которых взвешенная сумма квадратов
отклонений результатов эксперимента от значений
функции регрессии достигает наименьшего
значения:
N
[Y f ( X ; a , a ,..., a )] w min
i 1
i
i
*
1
*
2
*
m
2
i
(3)
Мы ограничимся регрессиями, линейными
относительно параметров a1, a2, …,am, т.е. вида
f(X ; a1, a2, …,am) = a1 1(Х)+ a2 2(Х)+ …+am m(Х)
(4)
335.
Функции 1(Х), 2(Х), …, m(Х), по которымпроизводится разложение регрессии, называются
базисными функциями.
Значение базисных функций будем
рассматривать только на множестве точек Xi ( i =
1, 2, …, N ), в которых проводился эксперимент.
Поэтому каждой функции j ставится в
соответствие N-мерный вектор ( j(Х1), j(Х2),
…, j(ХN)).
Функции 1(Х), 2(Х), …, m(Х) называются
линейно независимыми на множестве точек Xi
( i = 1, 2, …, N ), если линейно независимы
соответствующие векторы. Базисные функции
линейно независимые.
336.
Для регрессий вида (4) задача отысканияоценок мо МНК имеет единственное решение,
которое можно записать в общем виде. Обозначим
N
Q(a1* , a2* ,..., an* ) [Yi (a1* 1 ( X i ) a2* 2 ( X i ) ... am* ( X i ))]2 wi
i 1
Найдём минимум этой функции из условия:
N
Q
*
*
*
2
[
Y
(
a
(
X
)
a
(
X
)
...
a
i
1 1
i
2
2
i
m ( X i ))] j ( X i ) wi 0
*
a j
i 1
( j = 1, 2, …, m )
337.
Получаем систему m линейных уравнений с mнеизвестными
*
a1
N
N
1 ( X i ) j ( X i )wi a ( X ) ( X )w ...
*
2
i 1
N
N
i 1
i 1
i 1
2
i
j
i
i
am* m ( X i ) j ( X i ) wi Yi j ( X i ) wi
( j = 1, 2, …, m ) (5)
N
Введём обозначения ( X ) ( X ) w ( , ) a
i 1
k
i
( k = 1, 2, …, m ; j = 1, 2, …, m )
j
i
i
k
j
kj
338.
NY ( X )w (Y , ) b
i 1
i
j
i
i
j
j
( j = 1, 2, …, m )
A = ||a kj|| , B = (b1, b2, ... , bm)T, * = (a1*, a2*, …,am*)
Тогда последняя система может быть записана в
матричном виде
A * = B (6) * = A –1 B.
Существование обратной матрицы следует из
предположения о линейной независимости
базисных функций.
339.
Оценки параметров регрессии вида (4) ,полученные по МНК, наилучшие оценки, то есть
имеют наименьшую дисперсию в классе всех
несмещённых оценок.
340.
Ортогонализация базиса.Очевидно, формулы для оценок параметров
упрощаются, если в системе (6) матрица А
диагональная,
то
есть
N
akj k ( X i ) j ( X i ) wi ( k , j ) kj k
2
i 1
Соответствующие базисные функции в этом случае
называются ортогональными. Обозначим их T1, T2,
..., Tm.
Тогда разложение регрессии по ортогональному
базису имеет вид
M(Yi) = 1T1 (Xi) + 2T2 (Xi) + ... + m Tm (Xi)
( i = 1, 2, …, N )
341.
Система (5) в этом случае упрощаетсяj·(Tj, Tj) = (Y, Tj) ( j = 1, 2, …, m )
Отсюда получим
N
N
2
Y
T
(
X
)
w
/
T
j*= (Y, Tj) / (Tj, Tj) = i j i i j ( X i ) wi
i 1
i 1
( j = 1, 2, …, m )
Рассмотрим один из методов ортогонализации
базиса.
Пусть 1(Х), 2(Х), …, m(Х) – произвольный базис.
Положим Т1 = 1.
Т2 ищем в виде
Т2 = 2 + 2 Т1,
( 2 , T1 )
где 2 определим из условия (Т2 , Т1) = 0 2 T 2
1
342.
ДалееТ3 = 3 + 3 Т1+ 3Т2,
где 3, 3 определим из условия
(Т3 , Т1) = 0, (Т3 , Т2) = 0
3
( 3 , T1 )
T1
2
,
3
( 3 , T2 )
T2
2
.
И так далее до построения всего ортогонального
базиса.
k 1
Tk k ckjT j , где
j 1
ckj
( k , T j )
Tj
2
.
343.
Если предположить, что 1 1, 2 x, тоT1 1,
N
2
( 2 , T1 )
T1
2
xw
i 1N
i
i
w
i 1
X взв.
i
T2 x X взв.
то есть
N
Заметим, что если wi=1, то 2 X , так как wi N .
i 1
Ортогональность двух функций не нарушается,
если одну из них умножить на любое число. Для
удобства расчетов T2 берут T2 ( x X взв. ) / h , где
h выбирают так, чтобы T2 принимали целые
значения и не имели общих множителей.
344.
Тогдаx X взв.
yлин. x
,
h
N
N
где
Yi wi
YT
i 1 ( X i ) wi
i 1
*
i 1
;
1 N
N
2
w
T
(
X
)
w
i
1 i i
*
1
*
1
*
2
*
2
i 1
i 1
N
N
YT ( X )w Y X w
2* i N1
i 2
i
i
T ( X )w
i 1
2
2
i
i
i N1
i
i
i
X w
i 1
2
i
i
.
345.
Для построения квадратичной модели добавимновую базисную функцию 3 и строим базисный
многочлен Т3 = 3 + 3 Т1+ 3Т2, где ( , T ) ,
3
3
( 3 , T2 )
T2
2
3
.
1
2
T1
2
x X взв.
2
3
X
, тогда
h
Пусть
Т3 = X2 + 3 ·1+ 3X
N
X i wi
N
X X w
2
3 i 1 N
w
i 1
2
; 3 i 1N
i
2
X
i wi
i
i 1
yкв. T T T y лин. T
*
1 1
*
2 2
i
*
3 3
*
3 3
i
N
X w
3
i N1
i
i
2
X
i wi
i 1
.
346.
6.2. Свойства оценок параметров регрессионноймодели.
Из выражения
N
N
i 1
i 1
2
*j YT
(
X
)
w
/
T
i j
i
i
j ( X i )wi ,
( j = 1, 2, …, m )
легко вывести свойства оценок параметров
регрессионной модели.
1.Любая оценка j* строится только по
соответствующей базисной функции Tj и не зависит
от остальных. Это удобно при достраивании
моделей.
347.
2. Любая оценка j* – линейная функция отрезультатов эксперимента Yi и несмещённая
оценка истинного значения параметра j, то есть
М ( j*) = j, что следует из линейности
математического ожидания и ортогональности
базисных функций.
Действительно N
N
*
2
M ( j ) M ( YT
i j ( X i ) wi / T j ( X i ) wi )
i 1
i 1
N
1
Tj
M (Y )T ( X )w
N
2
1
i 1
N
i
j
i
i
i 1
T j 2 ( X i ) wi
1
(
T
(
X
)
T
(
X
)
T
(
X
))
T
(
X
)
w
(T j , T j ) j
i
2 2
i
m m
i
j
i
i
2 1 1
2 j
T j i 1
Tj
348.
3. Дисперсия оценки в силу независимости величинYi равна
D( j ) D(
2
Tj
1
Tj
N
1
i 1
Tj
YT ( X i ) wi )
2 i j
N
2
2
D
(
Y
)
T
(
X
)
w
i
j
i
i
4
i 1
2
N
2
T
4 j ( X i ) wi
Tj
i 1
2
Таким образом, среднеквадратичная ошибка
оценки
( j*)= T
j
полученная дисперсия является наименьшей среди
дисперсий всех линейных несмещённых оценок
параметра j.
349.
4. cov( j , k) = 0, j k, то есть оценки попарнонекоррелированы. Это следует из независимости
величин Yi.
5. Обозначим рассчитанные по модели значения
Y*(Xi) = 1*T1 (Xi) + 2*T2 (Xi) + ... + m *Tm (Xi)
Тогда отклонения эмпирических значений Yi от
расчитанных по модели
Yi = Yi – Y*(Xi)
ортогональны всем базисным функциям. Это
можно использовать для проверки правильности
вычислений.
Действительно:
(Y – Y*, Tj) = (Y, Tj) – j*( Tj, Tj) = (Y, Tj) – (Y, Tj) =
350.
6. 3. Проверка адекватности модели регрессии.Определение. Регрессионная модель называется
адекватной, если предсказанные по ней значения
переменной Y согласуются с результатами
эксперимента.
Обычно начинают с линейной модели и затем
повышают степень многочлена, пока модель не
станет адекватной, то есть гипотеза об ее
истинности не будет противоречить результатам
эксперимента.
Для проверки гипотезы об адекватности модели
регрессии вычисляют остаточную дисперсию (
дисперсию адекватности.)
351.
N1
2
Sад2 .
(
Y
)
i wi ,
kад. i 1
где kад.= N-m – число степеней свободы
дисперсии адекватности, N- число точек, в которых
проводился эксперимент, а m – число оцениваемых
параметров в модели ( для линейной модели m =2,
для квадратичной модели m =3).
Yi Yi Yi* ( xi )
отклонение средних Yi от проверяемой модели
регрессии.
352.
Если истинная функция регрессии имеет тот жевид, что и рассматриваемая модель, то дисперсия
адекватности служит несмещенной оценкой
истинной дисперсии эксперимента и ее можно
сравнивать с другими подобными оценками. В
частности, может быть проведена независимая
серия измерений для получения оценки
дисперсии эксперимента S2эксп.
Если в каждой точке проводилось несколько
измерений, то за независимую оценку дисперсии
можно взять сводную оценку дисперсии
S k
S
,k k число степеней свободы
k
сводной дисперсии.
N
2
св .
i 1
N
i 1
2
i
N
i
св .
i
i 1
i
353.
Если Sад2 . Sсв2 .- нет оснований сомневаться впригодности модели; если Sад2 . Sсв2 . , то находят
отношение F Sад2 . / Sсв2 . и применяют односторонний
критерий Фишера.
2
2
2
2
S
S
S
S
H0 : ад. св.
; H1 : ад. св.
F ( , kад. , kсв. ) квантиль распределения Фишера ,
где α – уровень значимости.
Если
F F ( , kад. , kсв. ),
то модель противоречит результатам эксперимента
и отвергается с уровнем значимости α.
354.
Построение доверительных интервалов.Оценки параметров регрессии j * являются
точечными оценками истинных значений
параметров j . Если результаты экспериментов
независимы и подчинены нормальному закону
распределения с дисперсией 2 , то доверительные
интервалы с доверительной вероятностью p=1-α
для j определяются по формулам:
j
Tj
*
j
j , j 1, 2,..., m где
N
2
T
j ( X i )wi
i 1
t1 / 2 (k ) S
j
;
Tj
- нормы базисных функций;
- несмещенная оценка дисперсии 2 с числом
степеней свободы k;
S2
355.
t1 / 2 (k ) - квантиль распределения Стьюдента356.
6.4.Анализ корреляционных зависимостей.Во многих задачах требуется установить
зависимость изучаемой случайной величины У от
одной или нескольких других величин.
Мы будем рассматривать одномерную задачу.
Строгая функциональная зависимость У от Х
реализуется редко, так как обе величины или одна
из них подвержены ещё действию случайных
факторов, причём, среди них могут быть факторы,
общие для Х и У. В этом случае возникает
статистическая зависимость.
Например, если Y зависит от случайных
факторов Z1, Z2,U1 ,U2 , а Х от Z1, Z2, V1, то между
Х и У есть статистическая зависимость.
357.
Определение. Статистической называютзависимость, при которой изменение одной из
величин влечёт распределение вероятностей другой.
В частности, если статистическая зависимость
проявляется в том, что при изменении одной из
величин изменяется среднее значение другой, то в
этом случае статистическая зависимость называется
корреляционной.
Пример. Пусть У – урожай зерна, а Х – количество
внесённых в почву удобрений. С одинаковых по
площади участков земли снимают разный урожай.
Средний же урожай является функцией от
количества удобрений, то есть связан с Х
корреляционной зависимостью.
358.
Пусть (Х,У) – непрерывная двумерная случайнаявеличина. Она характеризуется некоторой
плотностью совместного распределения (х,у).
При каждом фиксированном х получим своё
распределение для у, называемое условным
распределением. Центр этого распределения
называют условным математическим ожиданием
M (Y / xi ) y ( y / xi )dy
Аналогично при фиксированном у:
M ( X / yi ) x ( x / yi )dx.
359.
Определение. Зависимость математическогоожидания М (Y/x) случайной величины У от
значений величины х называется функцией
регрессии У на Х, М(Y/x)= f(x).
Аналогично М(Х/у)= g(у) – функция регрессии Х
на У.
360.
Линейная корреляция.Определение. Корреляционная зависимость между
Х и У называется линейной корреляцией, если
функции регрессии
у = f(x) = М[Y/x]
х = g(у) = М[Х/у]
есть прямые.
Можно доказать, что уравнения этих прямых
таковы:
y
y my ( x mx ) регрессия У на Х,
x
1 y
y my
( x mx ) регрессия Х на У.
x
361.
Здесь ( Х,У) =корреляции.
cov( X , У )
х у
– коэффициент
362.
Свойства прямых регрессии.1. Обе прямые регрессии проходят через центр
совместного распределения (mx,my).
2. Так как 1, то прямая регрессии У на Х идёт
более полого.
3. Прямые регрессии совпадают = 1, то есть
Х и У связаны линейной функциональной
зависимостью.
4. Среди всех прямых, описывающих зависимость
между Х и У, прямая регрессии У на Х реализует
минимум для суммы квадратов отклонений У от
соответствующих точек прямой, измеренных вдоль
оси У. Прямая регрессии Х на У обладает
аналогичным свойством, только отклонения
363.
измеряются по горизонтали.364.
Оценка коэффициентов корреляции поопытным данным.
В качестве точечной оценки коэффициента
корреляции по результатам независимых
экспериментов (Хi,Уi) (i = 1, 2, ..., N) принимается
эмпирический коэффициент корреляции
N
( x x)( y y)
*
12
K
r
Sх S у
i 1
i
i
N
N
2
(
x
x
)
*
(
y
y
)
i
i
2
i 1
i 1
N
N
1 N
xi yi xi yi
N i 1 i 1
i 1
N
N
N
1
1
( xi 2 ( xi ) 2 )( yi 2 ( yi ) 2 )
N
N i 1
i 1
i 1
365.
По эмпирическому коэффициенту корреляцииможно построить доверительный интервал для
истинного коэффициента корреляции с заданной
доверительной вероятностью р. Проще всего для
этой цели воспользоваться номограммами,
приведёнными в таблицах математической
статистики.
Уравнения эмпирических прямых регрессии
задаются так:
y y
x x
r
Sy
Sx
y y 1 x x
Sy
r Sx
– регрессия У на Х
– регрессия Х на У.
366.
Проверка гипотезы о существованиилинейной зависимости между величинами
( то есть о том, что истинный коэффициент
корреляции не равен нулю)
Пусть построен доверительный интервал
с заданным уровнем значимости.
Считается, что линейная зависимость между
величинами существует, если значение = 0 не
принадлежит найденному доверительному
интервалу. H0: XY = 0 ; H1: XY ≠ 0 .
Если гипотеза принимается, то можно
пользоваться уравнениями эмпирических прямых
регрессии для предсказания значения одной
переменной по значению другой.
367.
Однако предсказанное значение может иметьбольшую погрешность.
Для проверки гипотезы H0: XY = 0 при
альтернативной гипотезе H1: XY ≠ 0 можно
использовать следующий критерий. Линейная
зависимость между X и Y не существует, если
r
t1 / 2 (n 2)
t1 / 2 (n 2)
n 2 t
2
1 / 2
(n 2)
,
где
- квантиль распределения Стьюдента
368.
Если принята гипотеза о существованиилинейной зависимости между случайными
величинами X и Y, то , зная доверительный
интервал для коэффициента корреляции, можно
сделать вывод о силе взаимосвязи между X и Y.
Если доверительный интервал примыкает к 1 или к
-1, то говорят, что связь сильная. Если
доверительный интервал примыкает к 0, говорят,
что связь слабая. Если доверительный интервал
расположен примерно посредине интервала (-1, 0)
или (0,1), то связь средней величины.
















































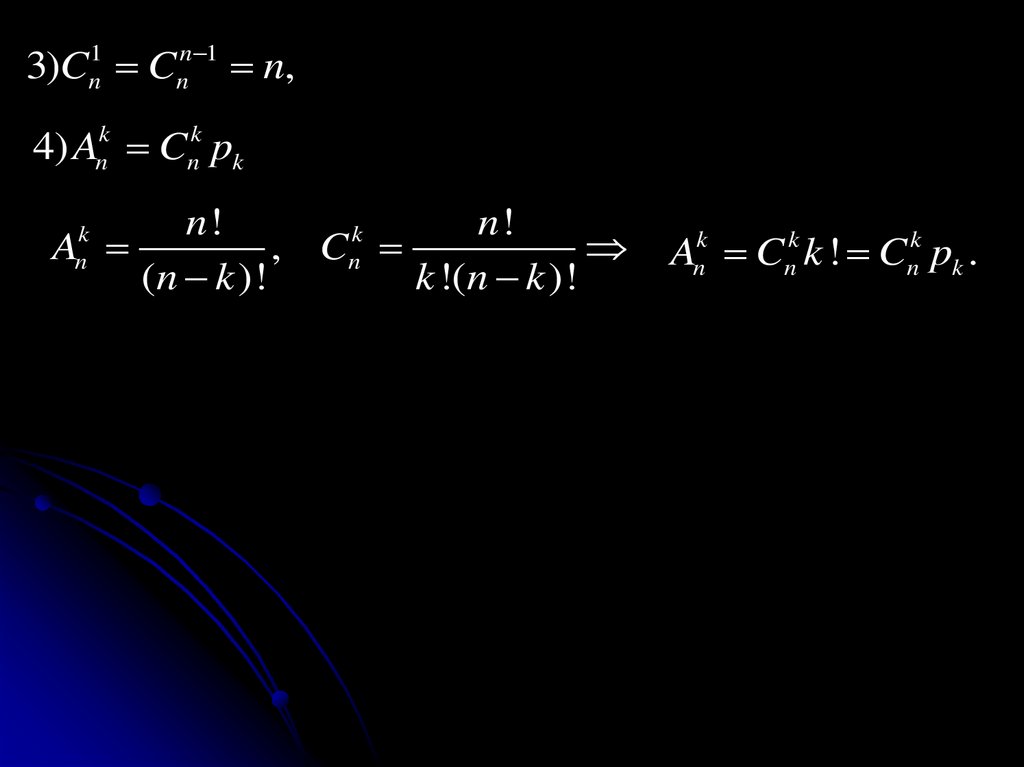







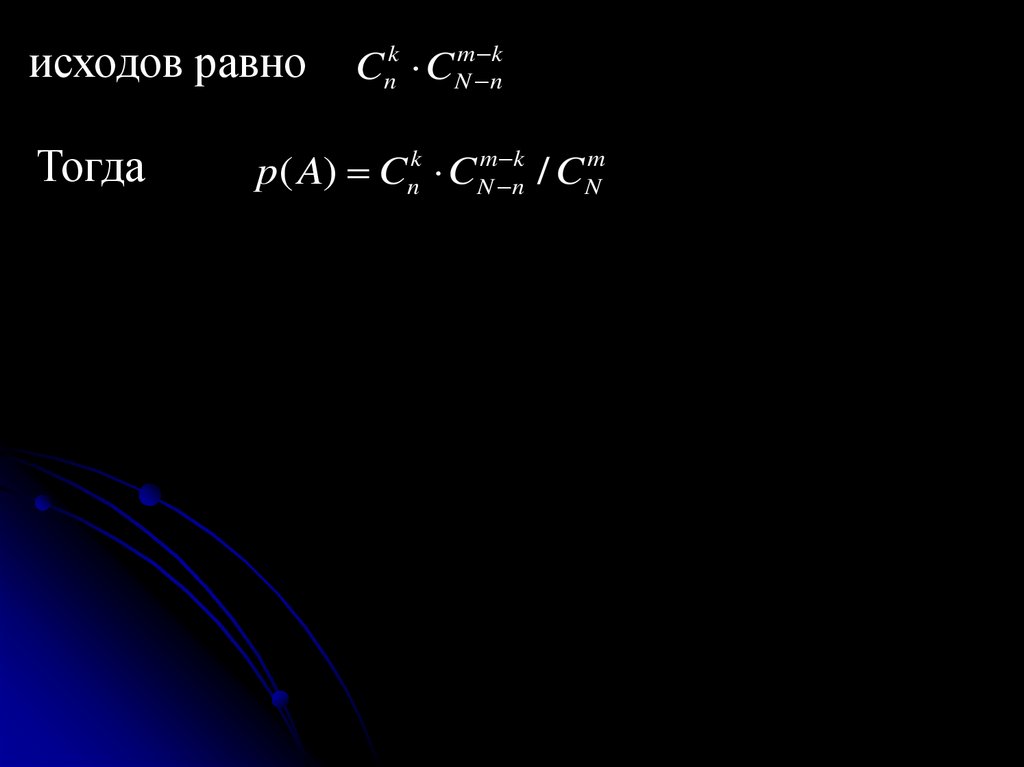






















































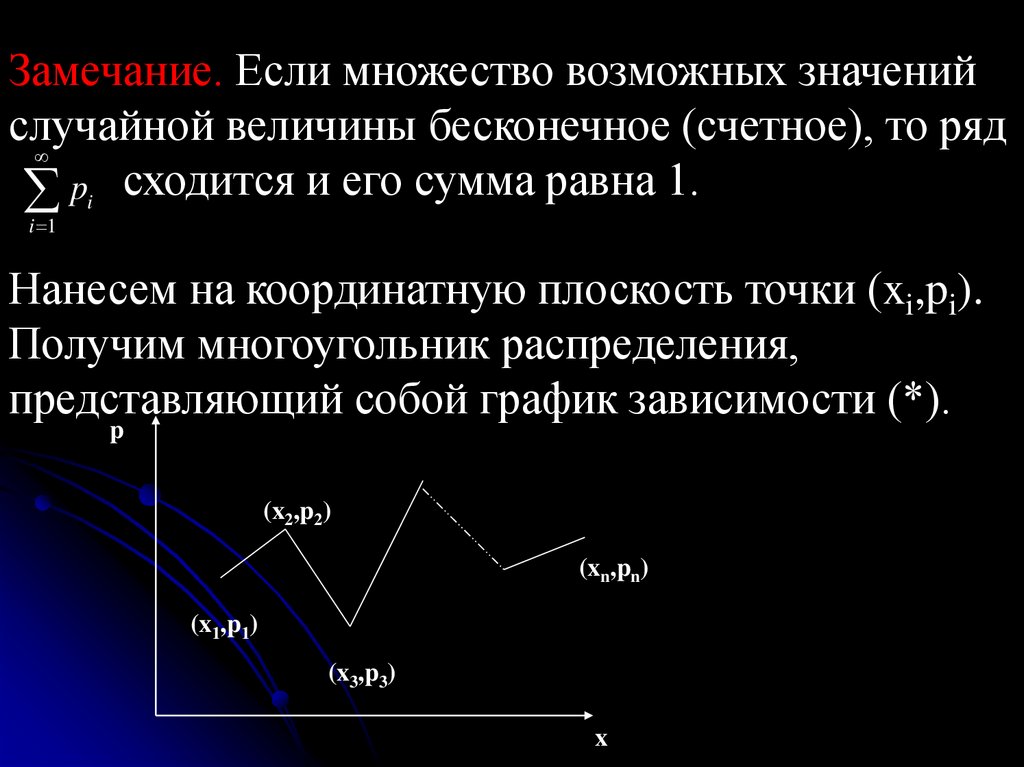



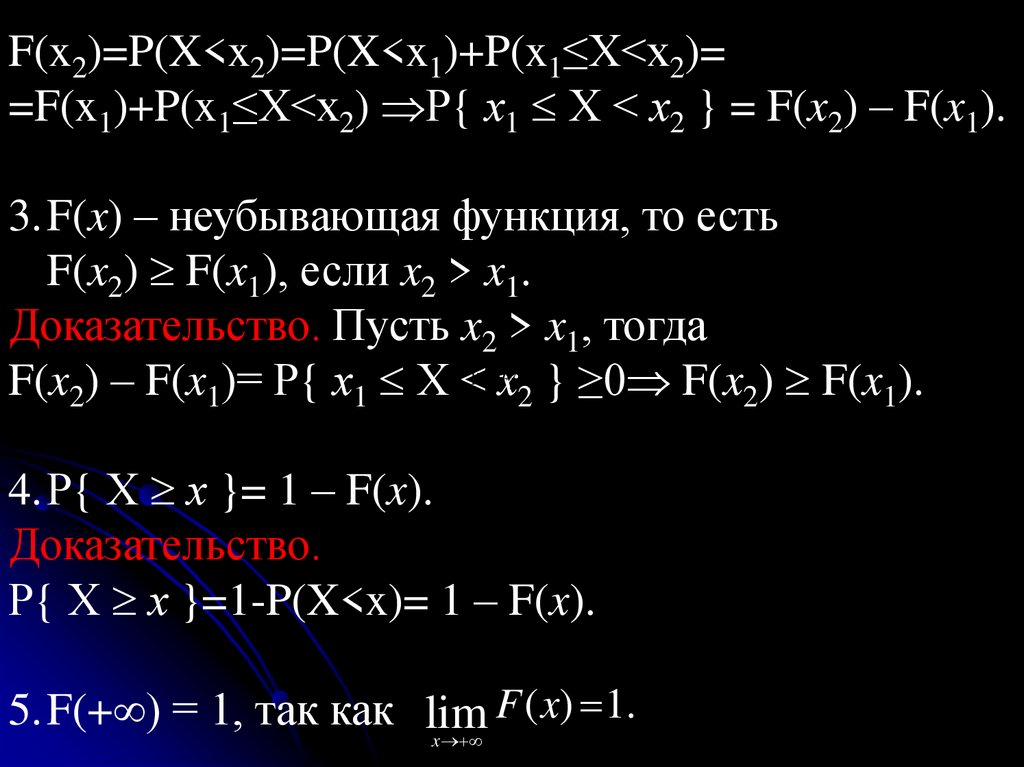


















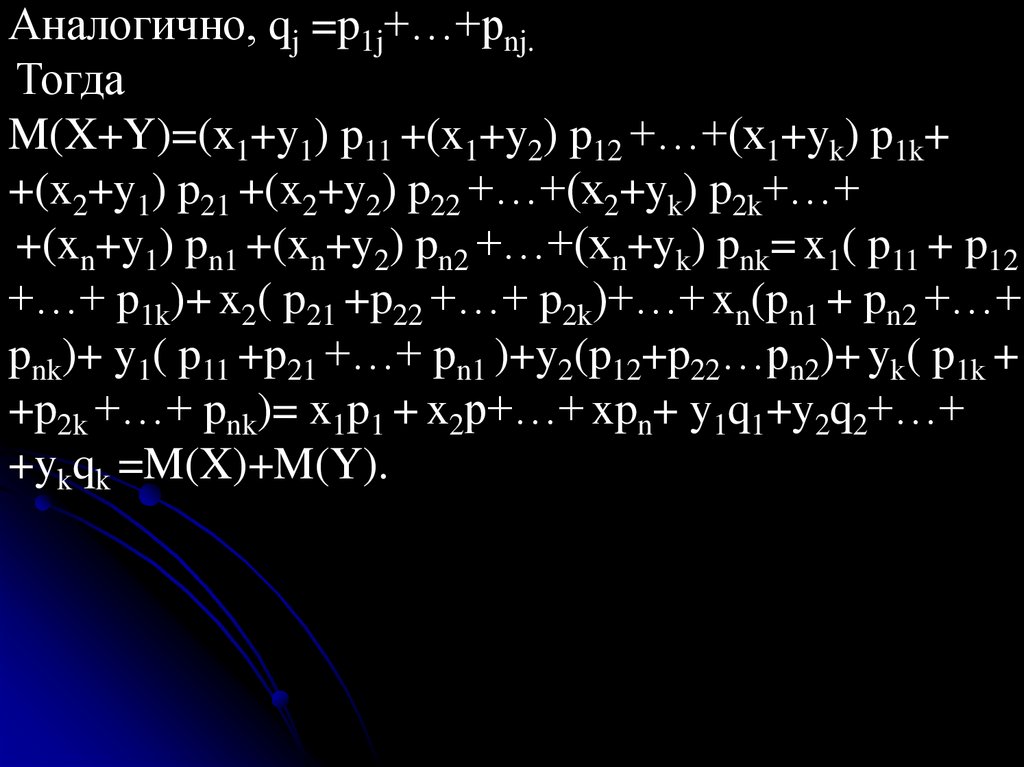

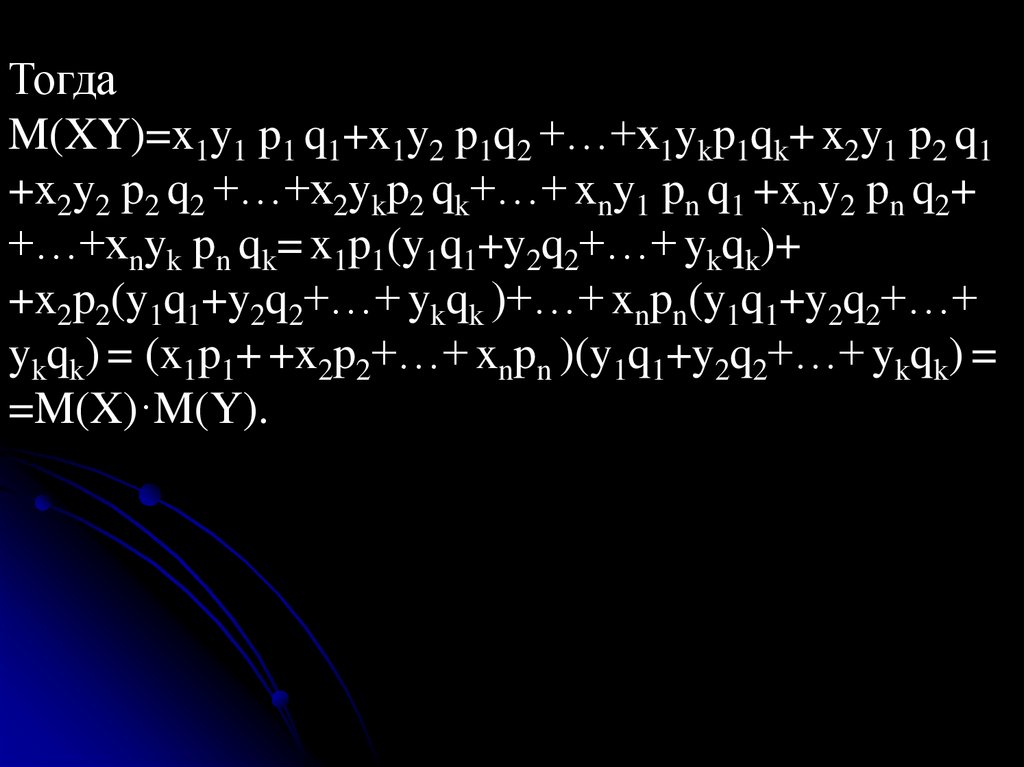







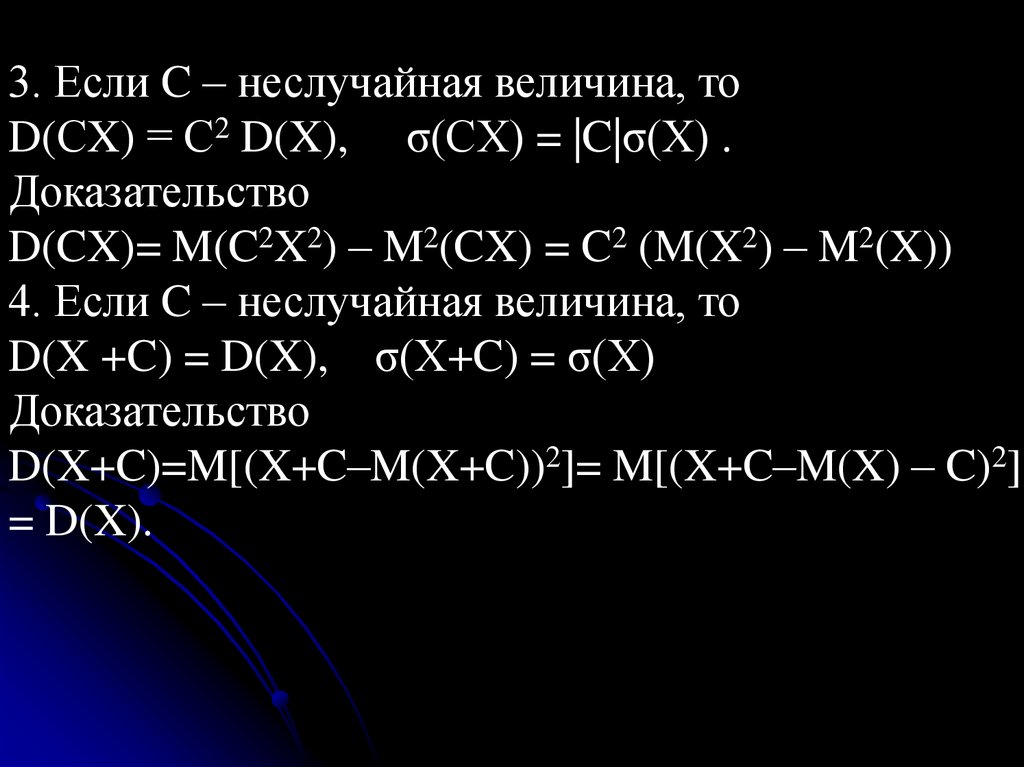






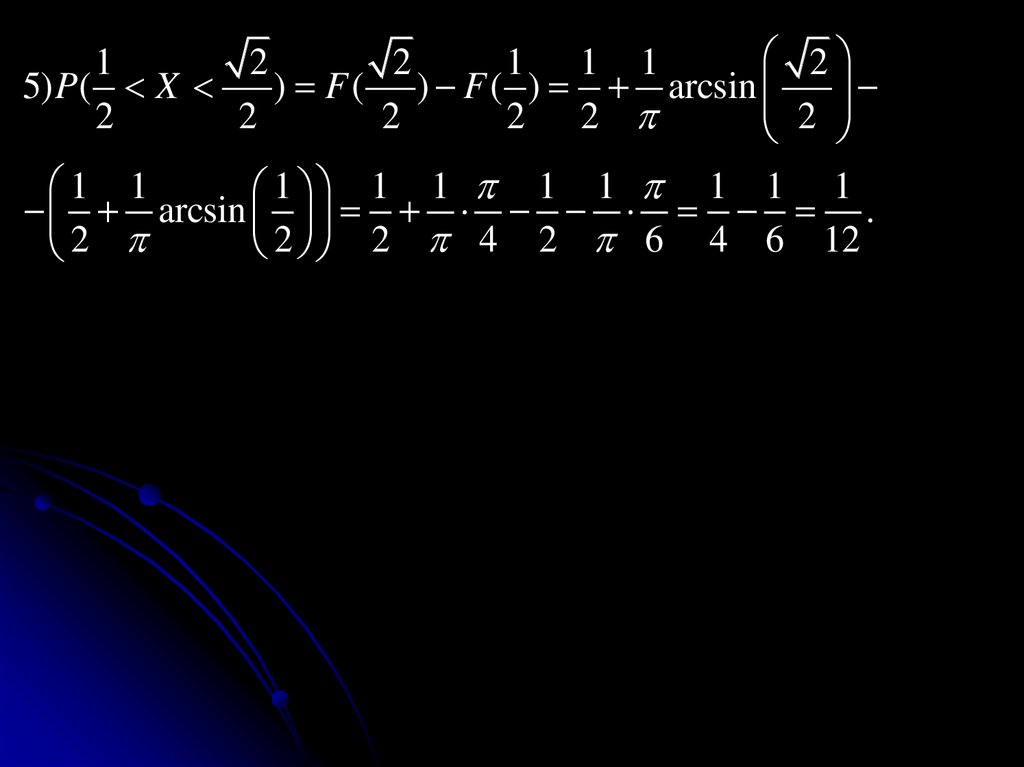

















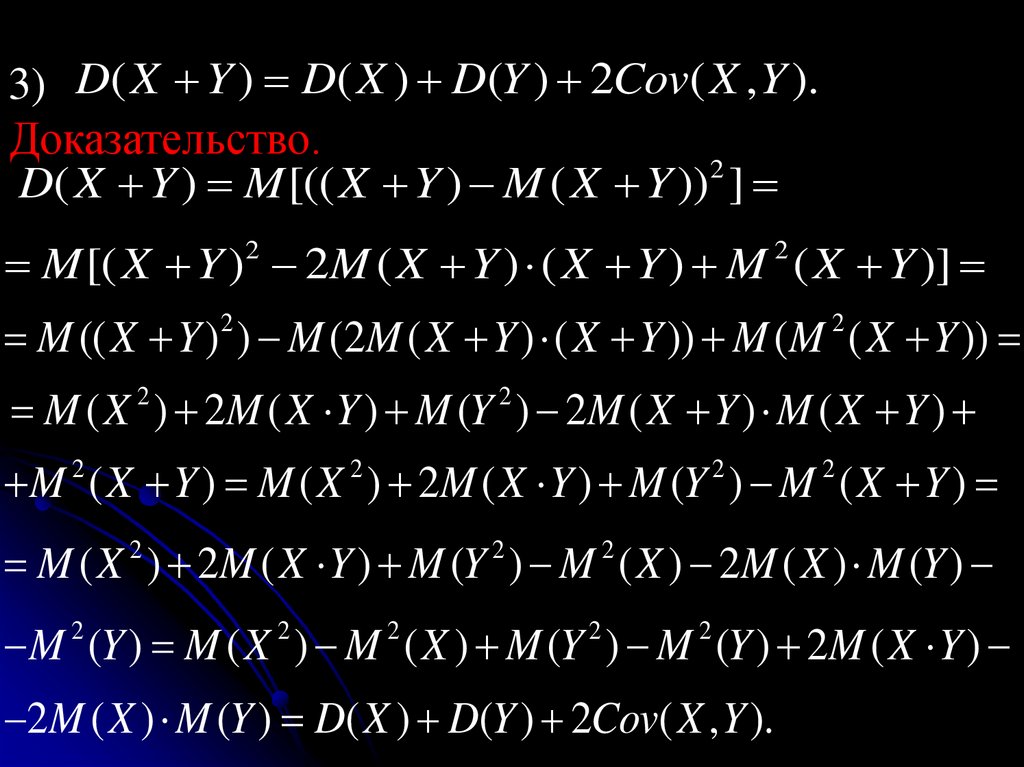
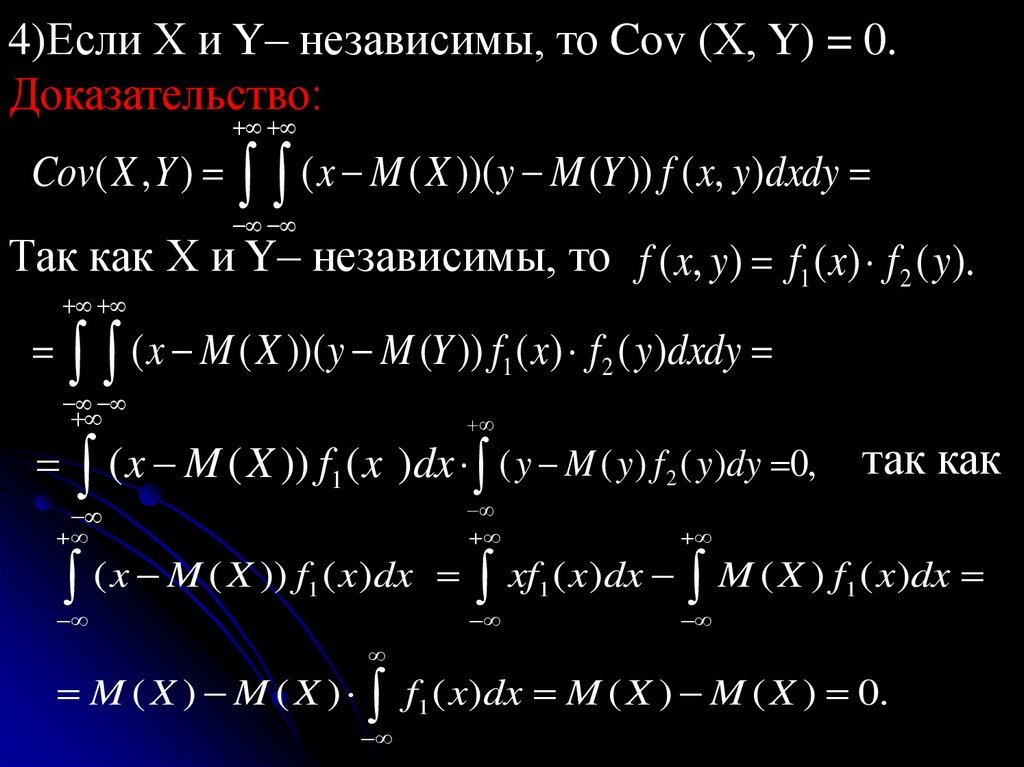











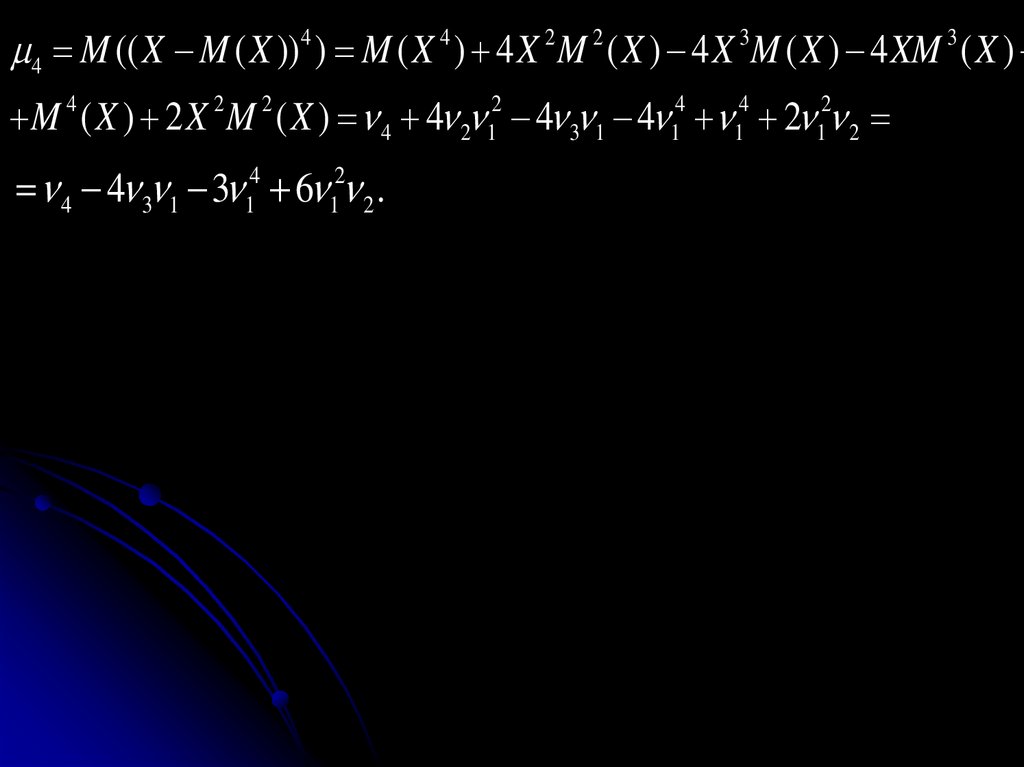









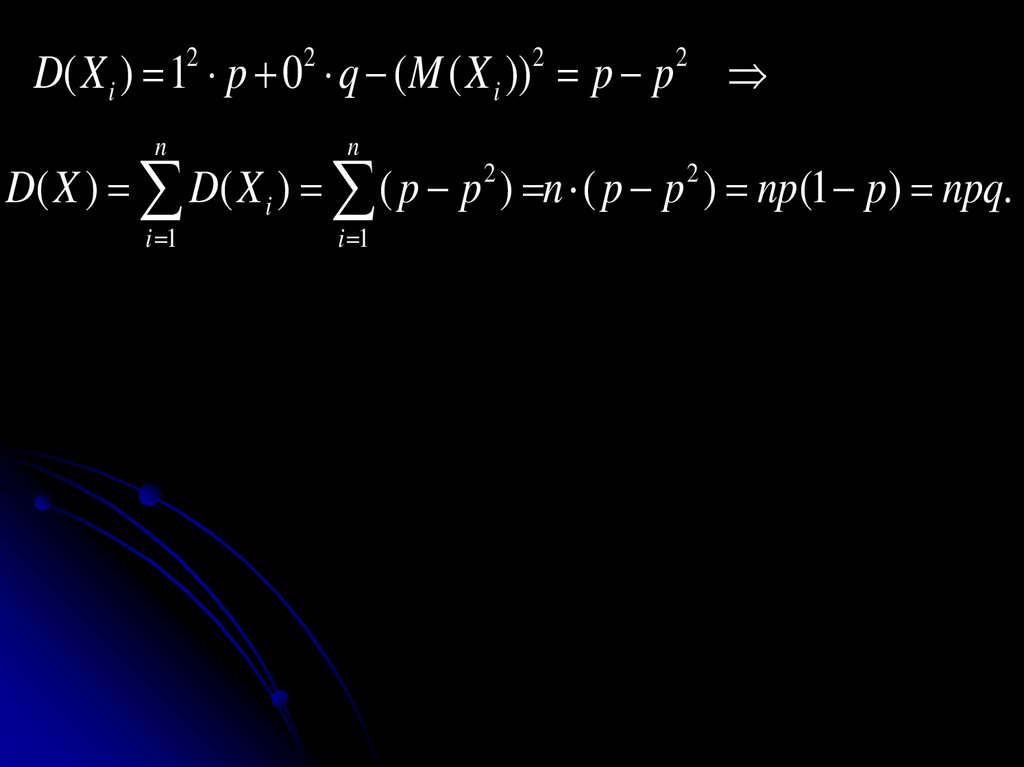
























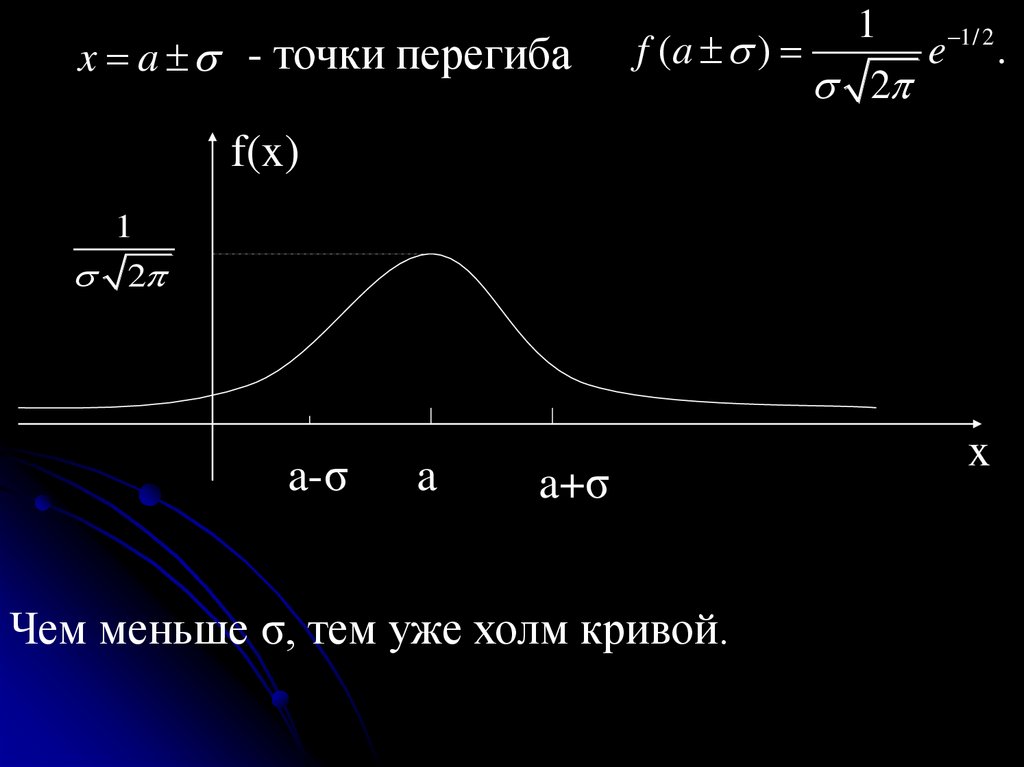
























































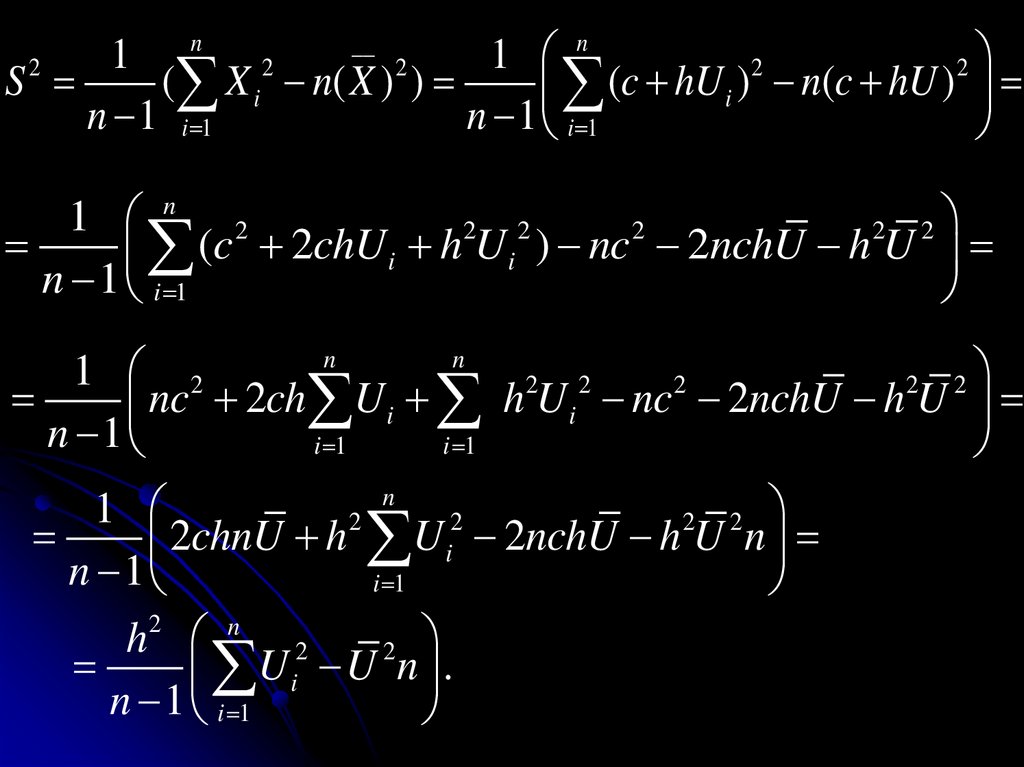

























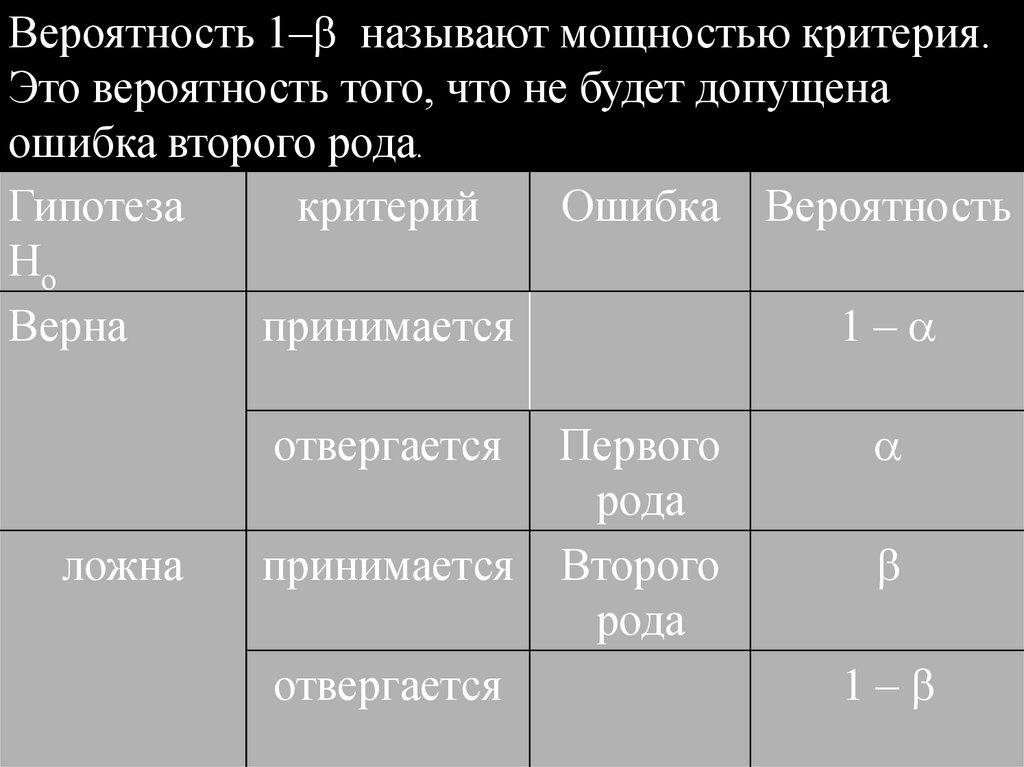






























































 Математика
Математика








