Четырёхугольники, их свойства и признаки

1.

Тутубалина Дина Алексеевна
учитель математики Спец ПУ
г. Орлова Кировской области

2.

Четырёхугольник – это фигура,
состоящая из четырёх точек и
четырёх, последовательно
соединяющих их, отрезков
А
D
В
Никакие три из данных
точек не должны лежать
на одной прямой, а
соединяющие их отрезки
С не должны пересекаться
A, В, С, D – вершины
АВ, ВС, СD, DА – стороны
АС, ВD - диагонали

3.

Определение
Параллелограмм – четырёхугольник,
у которого противоположные
стороны попарно параллельны
В
А
АВ//СD
ВС//АD
С
D
АВСD - параллелограмм

4.

1 свойство
Свойства и признаки
параллелограмма
2 свойство
3 свойство
4 свойство
1 признак
2 признак
3 признак

5.

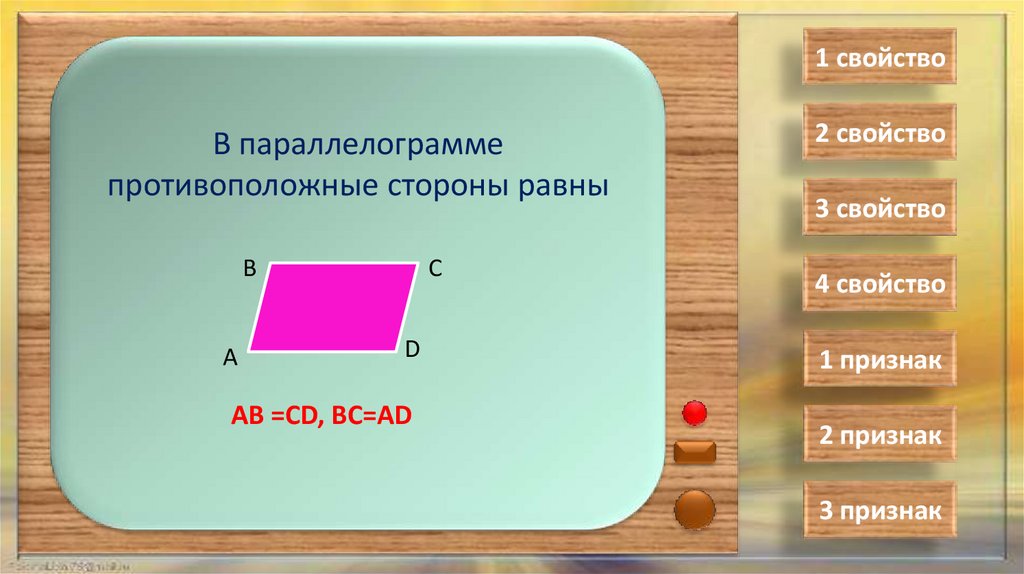
1 свойство
В параллелограмме
противоположные стороны равны
В
А
С
D
АВ =СD, ВС=АD
2 свойство
3 свойство
4 свойство
1 признак
2 признак
3 признак

6.

1 свойство
В параллелограмме
противоположные углы равны
2 свойство
3 свойство
В
С
4 свойство
А
D
А= С, В = D
1 признак
2 признак
3 признак

7.

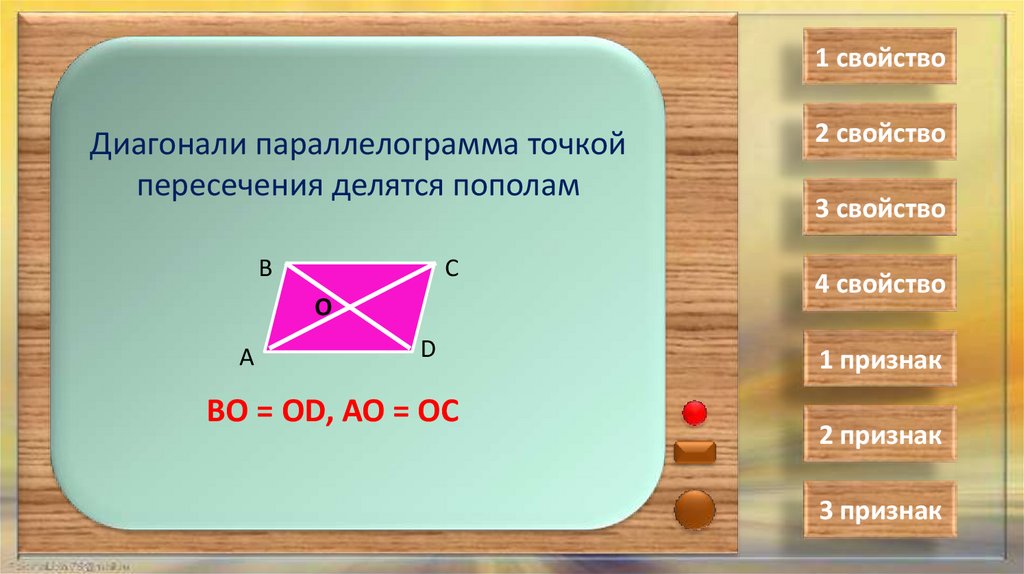
1 свойство
Диагонали параллелограмма точкой
пересечения делятся пополам
В
С
О
А
D
ВО = ОD, АО = ОС
2 свойство
3 свойство
4 свойство
1 признак
2 признак
3 признак

8.

1 свойство
Сумма углов, прилежащих к одной
стороне, равна 180°
В
С
D
А
2 свойство
3 свойство
4 свойство
1 признак
А + В = С+ D = В+ С = А+ D
2 признак
=180°
3 признак

9.

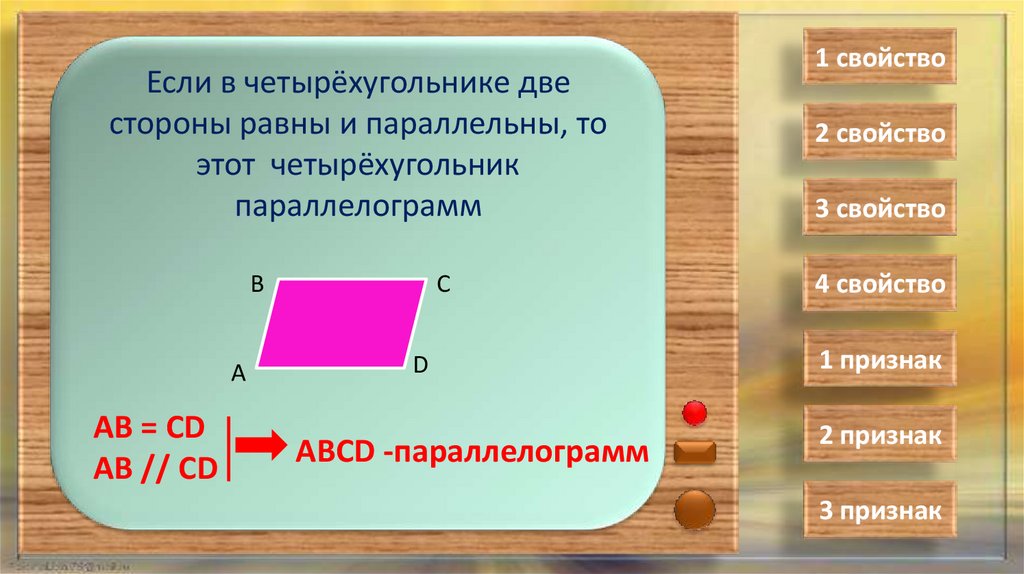
Если в четырёхугольнике две
стороны равны и параллельны, то
этот четырёхугольник
параллелограмм
В
А
АВ = СD
АВ // СD
С
D
АВСD -параллелограмм
1 свойство
2 свойство
3 свойство
4 свойство
1 признак
2 признак
3 признак

10.

1 свойство
Если в четырёхугольнике
противоположные стороны попарно
равны, то этот четырёхугольник
параллелограмм
2 свойство
3 свойство
4 свойство
В
С
1 признак
А
АВ = СD
ВС = АD
D
АВСD - параллелограмм
2 признак
3 признак

11.

1 свойство
Если в четырёхугольнике диагонали
пересекаются и точкой пересечения
делятся пополам, то этот
четырёхугольник параллелограмм
2 свойство
3 свойство
4 свойство
В
С
О
А
ВО = ОD
АО = ОС
D
1 признак
2 признак
АВСD - параллелограмм
3 признак

12.

Определение
Прямоугольником называется
параллелограмм, у которого все
углы прямые
В
С
А
D
А = В= С= D = 90°

13.

1 свойство
Свойства и признаки
прямоугольника
2 свойство
признак

14.

1 свойство
Все свойства параллелограмма
В
А
С
D
2 свойство
признак

15.

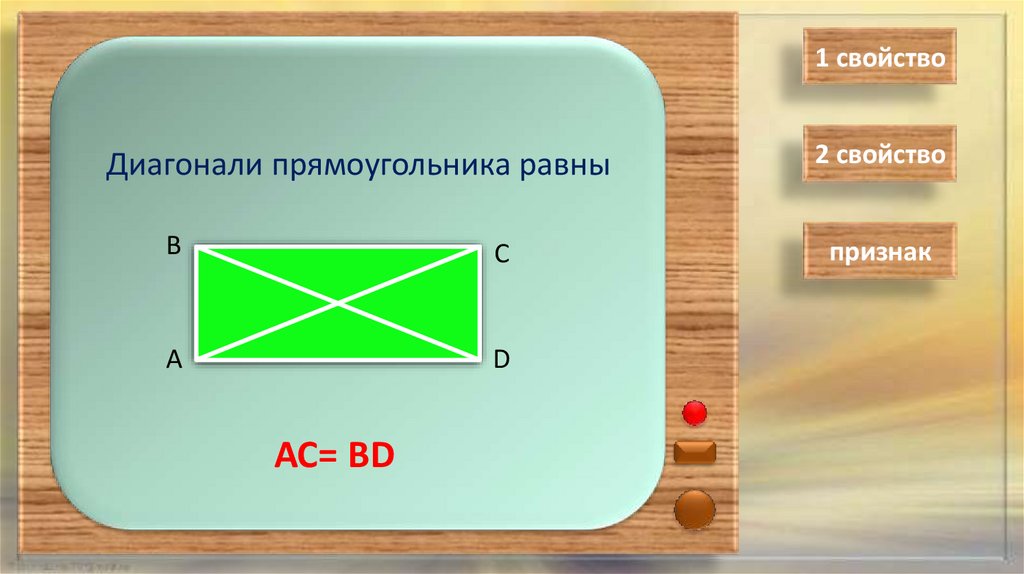
1 свойство
Диагонали прямоугольника равны
В
С
А
D
АС= ВD
2 свойство
признак

16.

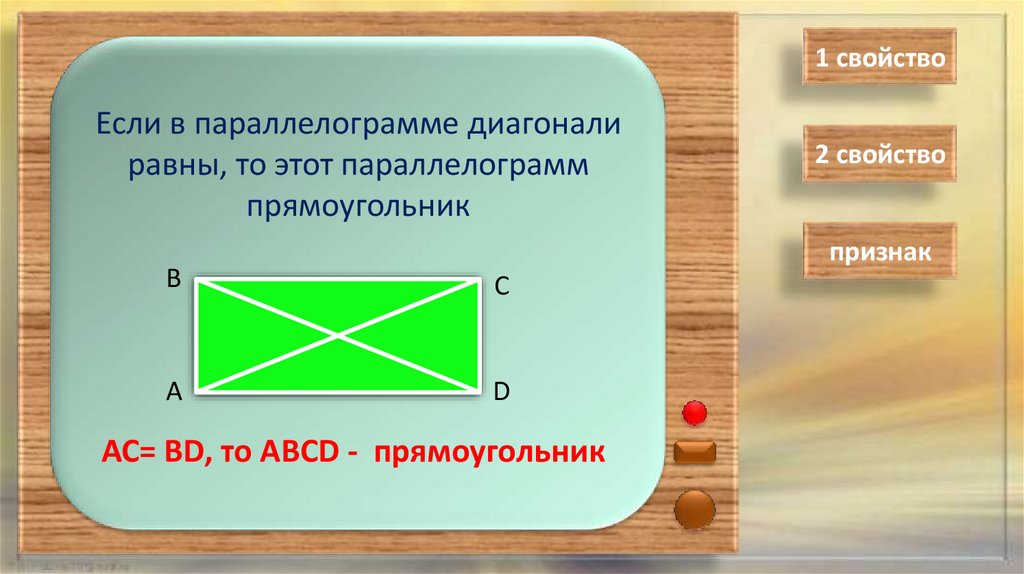
1 свойство
Если в параллелограмме диагонали
равны, то этот параллелограмм
прямоугольник
2 свойство
признак
В
С
А
D
АС= ВD, то АВСD - прямоугольник

17.

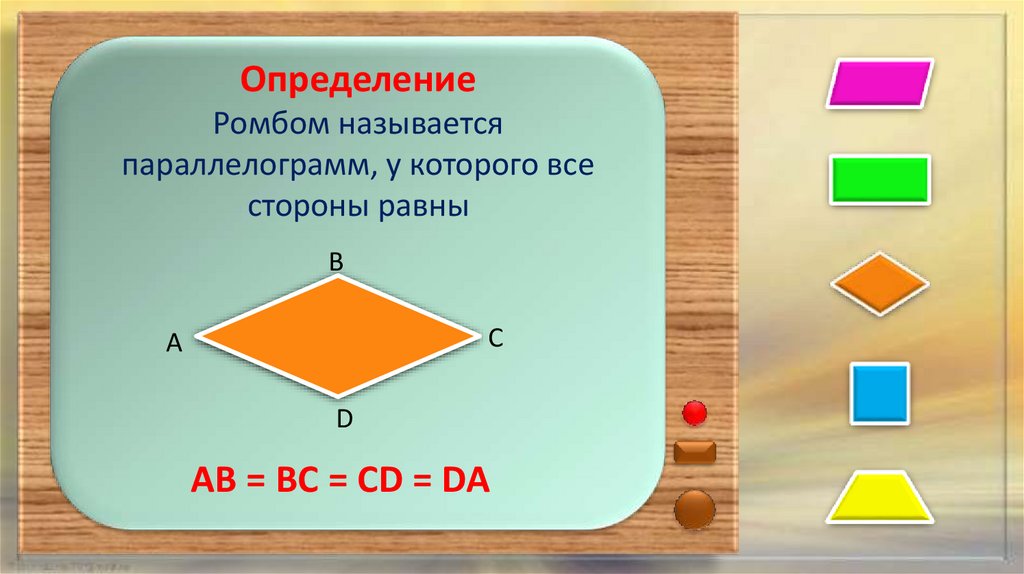
Определение
Ромбом называется
параллелограмм, у которого все
стороны равны
В
С
А
D
АВ = ВС = СD = DA

18.

1 свойство
Свойства и признаки ромба
2 свойство
3 свойство
1 признак
2 признак
3 признак

19.

1 свойство
Все свойства параллелограмма
В
С
2 свойство
3 свойство
1 признак
А
D
2 признак
3 признак

20.

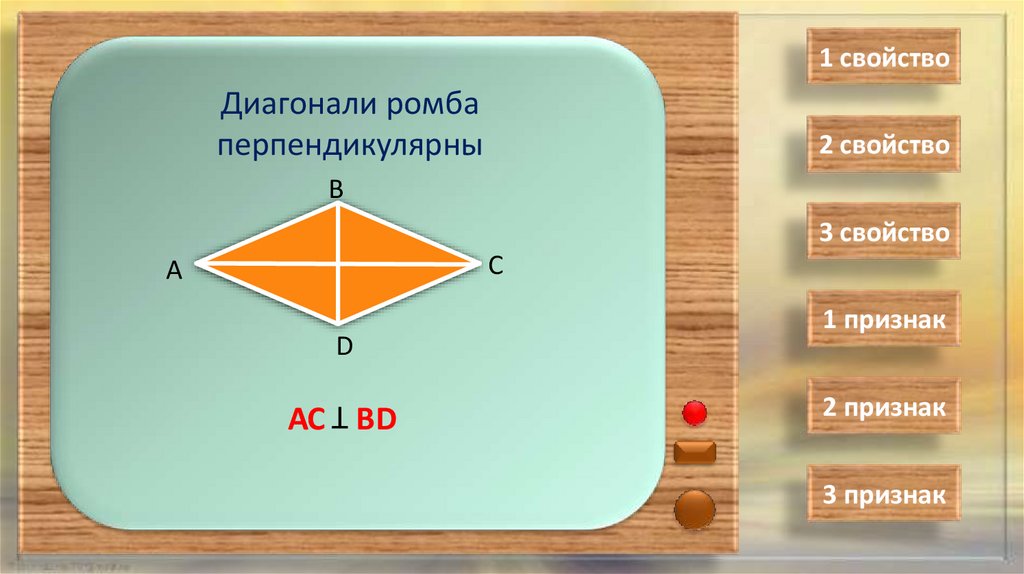
1 свойство
Диагонали ромба
перпендикулярны
2 свойство
В
3 свойство
А
Τ
D
Т
АС ВD
С
1 признак
2 признак
3 признак

21.

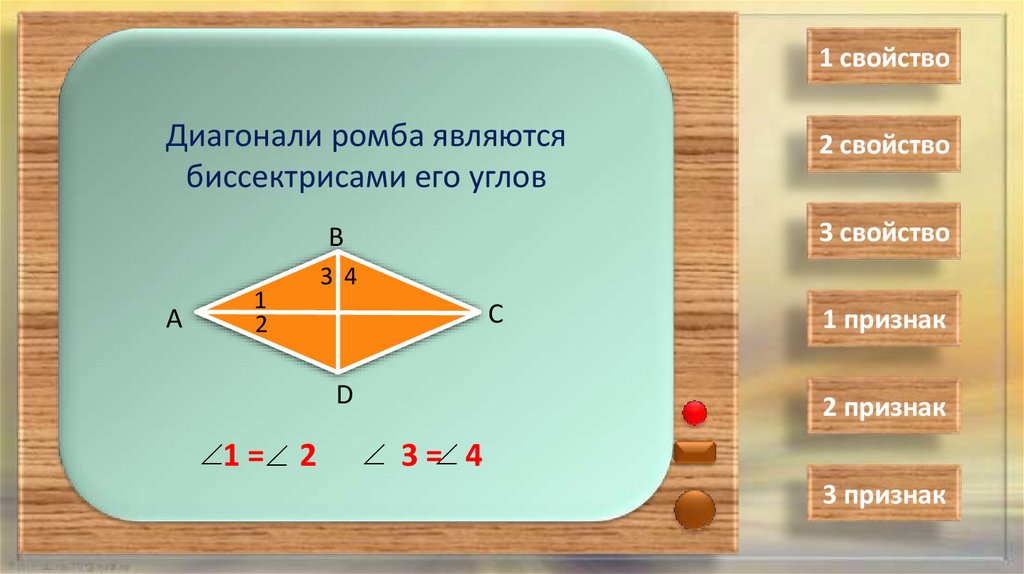
1 свойство
Диагонали ромба являются
биссектрисами его углов
3 свойство
В
А
1
2
3 4
С
D
1 = 2
2 свойство
1 признак
2 признак
3 = 4
3 признак

22.

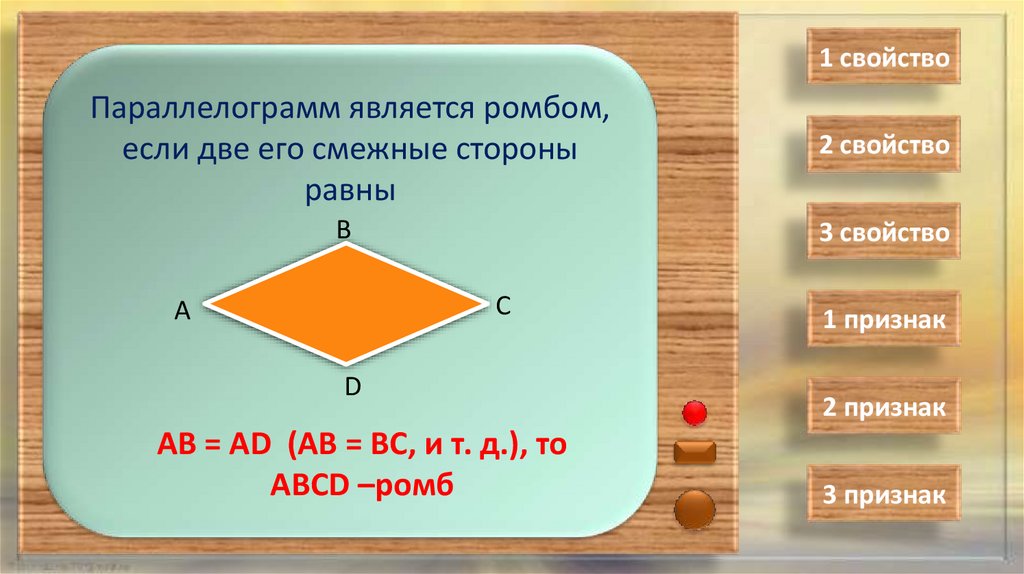
1 свойство
Параллелограмм является ромбом,
если две его смежные стороны
равны
2 свойство
В
3 свойство
С
А
D
АВ = АD (АВ = ВС, и т. д.), то
АВСD –ромб
1 признак
2 признак
3 признак

23.

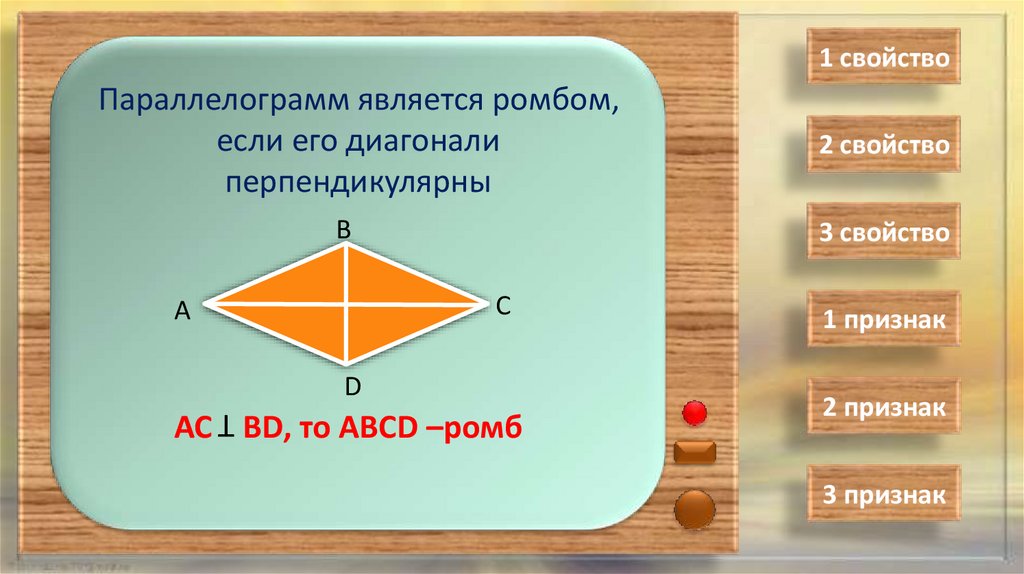
1 свойство
Параллелограмм является ромбом,
если его диагонали
перпендикулярны
2 свойство
В
3 свойство
С
А
D
Т
АС ВD, то АВСD –ромб
1 признак
2 признак
3 признак

24.

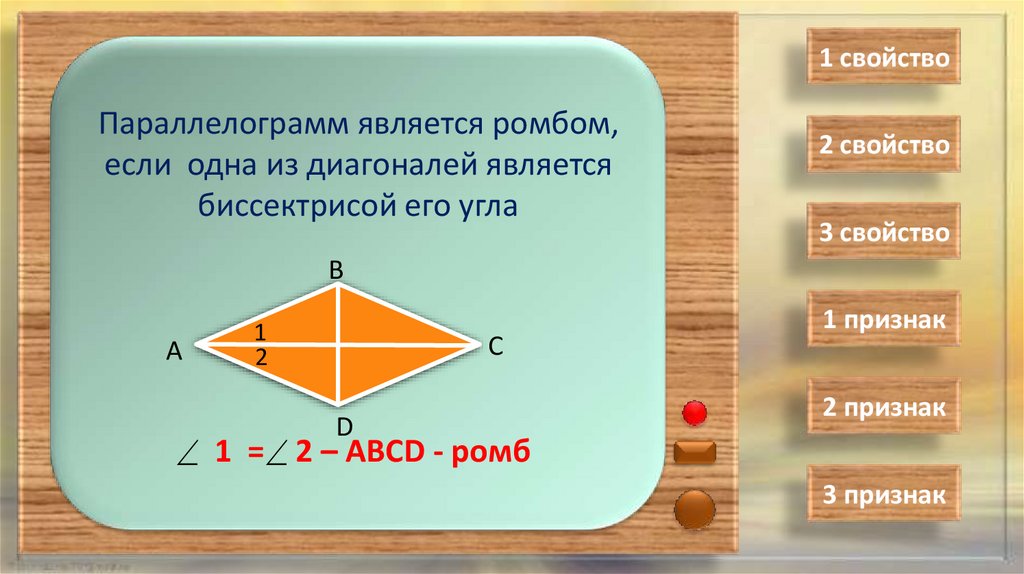
1 свойство
Параллелограмм является ромбом,
если одна из диагоналей является
биссектрисой его угла
2 свойство
3 свойство
В
А
1
2
С
D
1 признак
2 признак
1 = 2 – АВСD - ромб
3 признак

25.

Определение
Квадратом называется
прямоугольник, у которого все
стороны равны
В
С
А
D
АВ = ВС = СD= DА

26.

1 свойство
Свойства и признаки
квадрата
2 свойство
3 свойство
4 свойство
5 свойство
признак

27.

1 свойство
Все углы квадрата прямые
В
С
А
D
2 свойство
3 свойство
4 свойство
5 свойство
А = В = С = D = 90°
признак

28.

1 свойство
Диагонали квадрата равны
В
2 свойство
С
3 свойство
D
А
АС = ВD
4 свойство
5 свойство
признак

29.

1 свойство
Диагонали квадрата
взаимно перпендикулярны
В
С
А
D
Т
АС ВD
2 свойство
3 свойство
4 свойство
5 свойство
признак

30.

1 свойство
Диагонали квадрата точкой
пересечения делятся пополам
В
С
О
А
2 свойство
3 свойство
4 свойство
D
5 свойство
АО = ОС , ВО = ОD
признак

31.

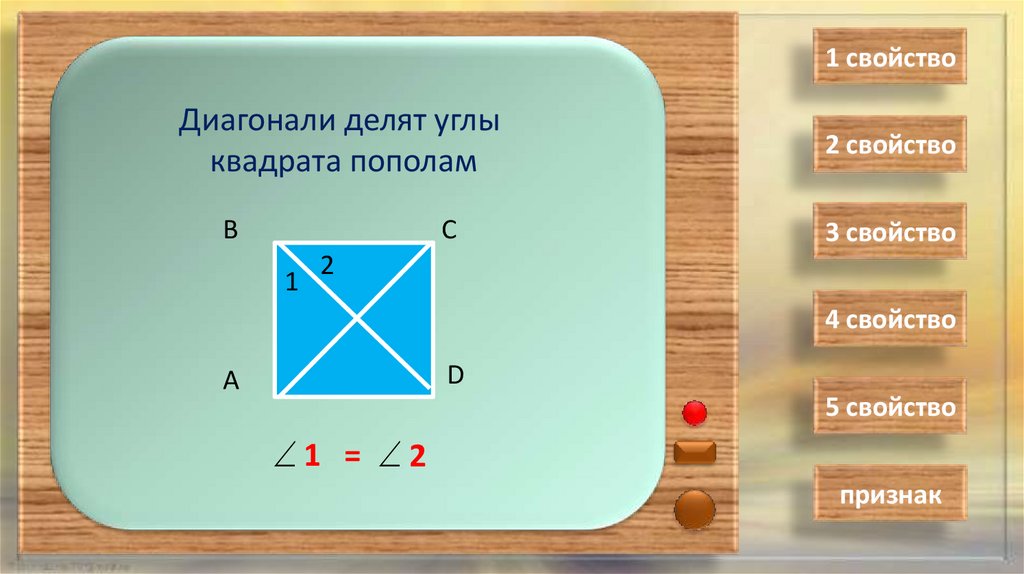
1 свойство
Диагонали делят углы
квадрата пополам
В
С
1
2 свойство
3 свойство
2
4 свойство
D
А
5 свойство
1 = 2
признак

32.

1 свойство
Прямоугольник является
квадратом, если он
обладает каким-нибудь
признаком ромба
В
С
2 свойство
3 свойство
4 свойство
5 свойство
А
D
признак

33.

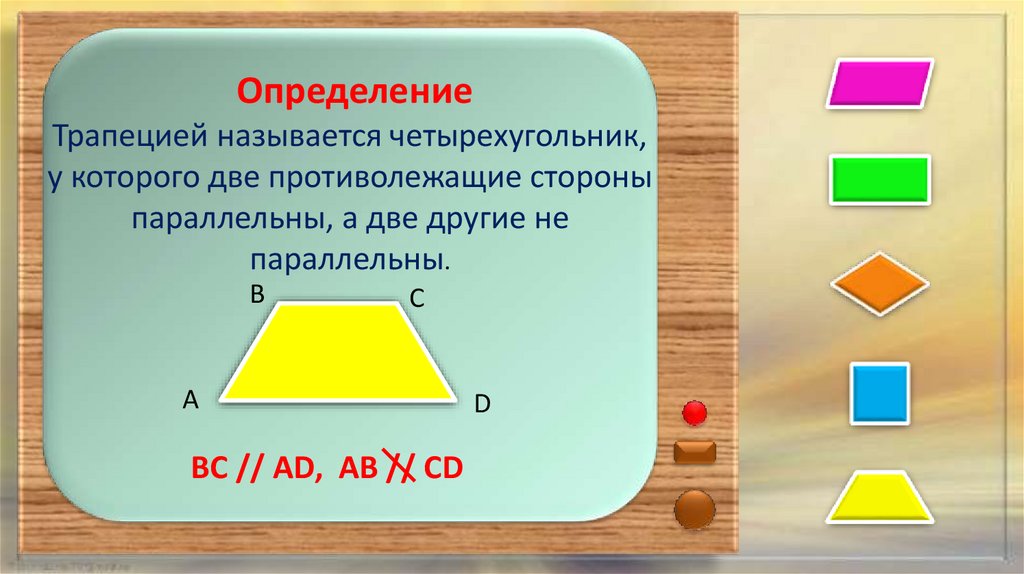
Определение
Трапецией называется четырехугольник,
у которого две противолежащие стороны
параллельны, а две другие не
параллельны.
В
С
А
ВС // AD, АВ // СD
D

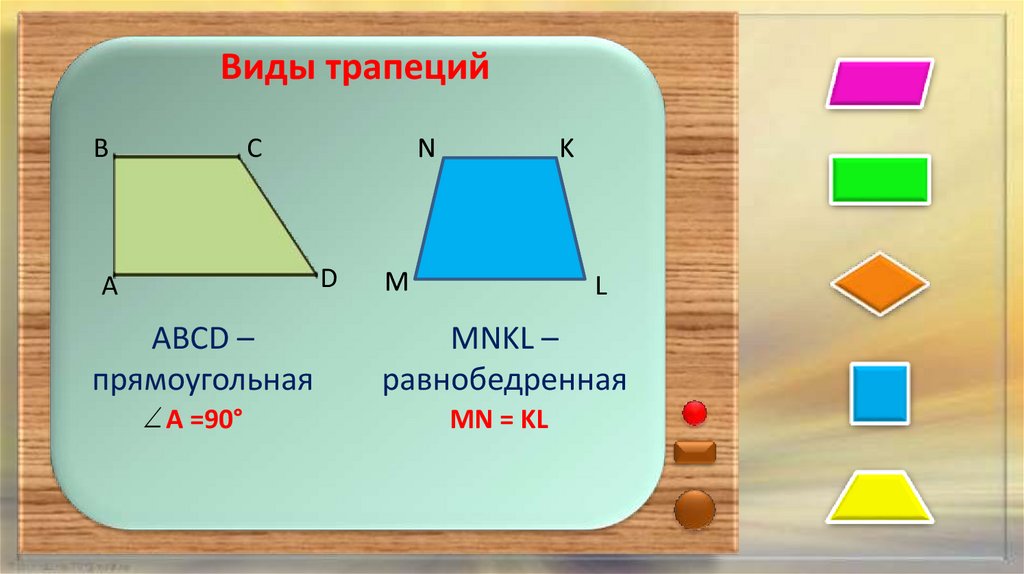
34.

Виды трапеций
В
С
N
D
А
ABCD –
прямоугольная
А =90°
K
М
L
MNKL –
равнобедренная
МN = KL

35.

1 свойство
Свойства и признаки
равнобедренной
трапеции
2 свойство
1 признак
2 признак

36.

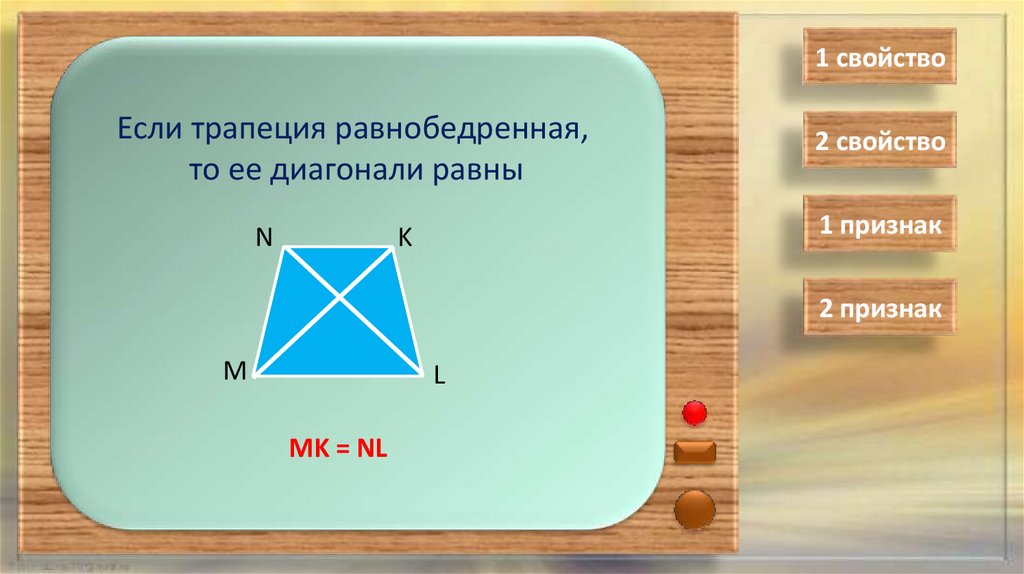
1 свойство
Если трапеция равнобедренная,
то ее диагонали равны
N
2 свойство
1 признак
K
2 признак
М
L
MK = NL

37.

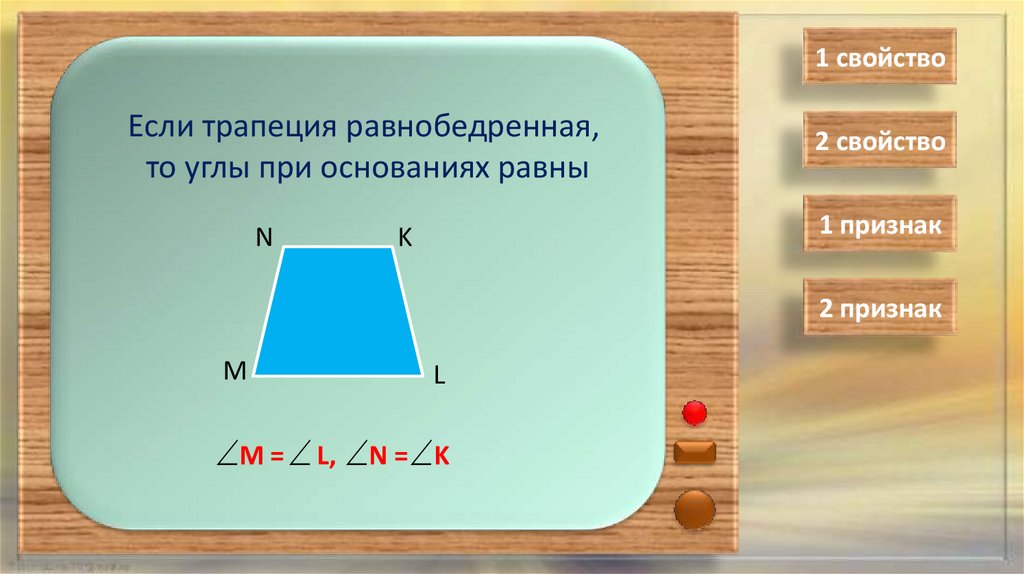
1 свойство
Если трапеция равнобедренная,
то углы при основаниях равны
N
2 свойство
1 признак
K
2 признак
М
L
M = L, N = K

38.

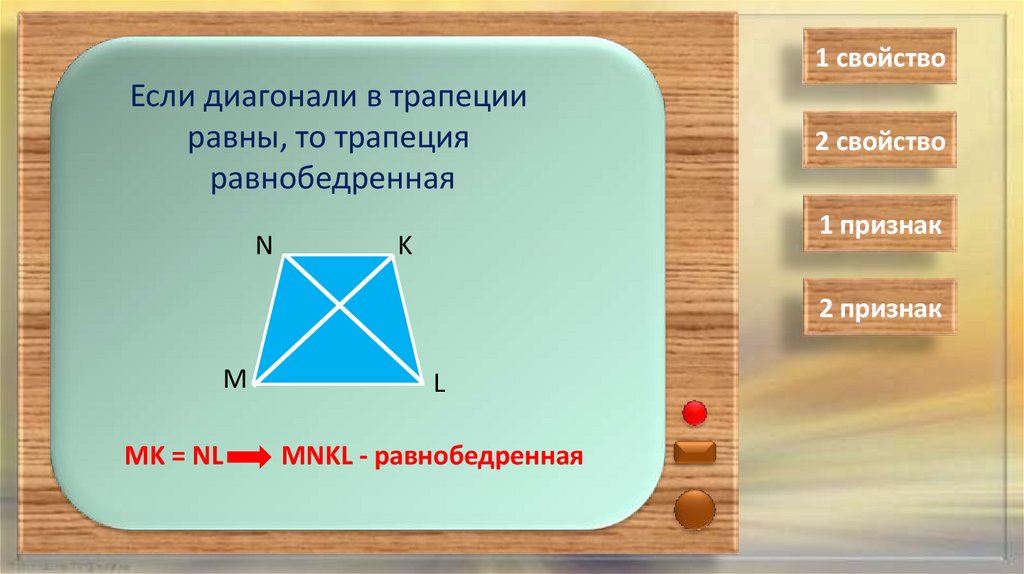
1 свойство
Если диагонали в трапеции
равны, то трапеция
равнобедренная
N
2 свойство
1 признак
K
2 признак
М
MK = NL
L
MNKL - равнобедренная

39.

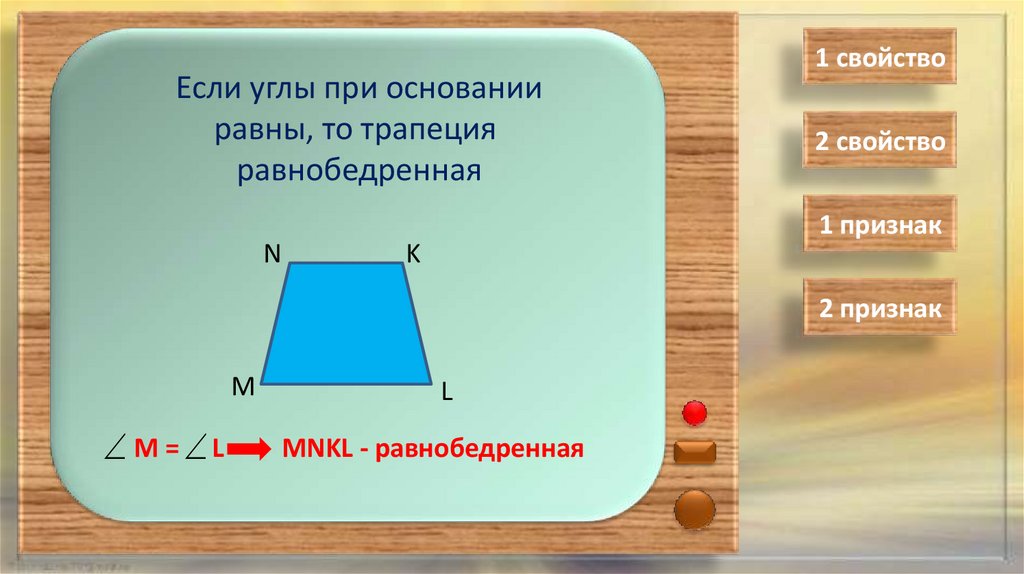
Если углы при основании
равны, то трапеция
равнобедренная
1 свойство
2 свойство
1 признак
N
K
2 признак
М
M = L
L
MNKL - равнобедренная

40.

Источники информации
http://pedsovet.su/_ld/379/69498365.jpg
http://www.picrolls.com/slide/51/52028-Wide-screen_Drawings_Vol_1_No_17.jpg