Натуральные числа. Повторение курса математики 5 класса

1.

Сенина Г., Сенин В., МАОУ СОШ №4 г. Корсаков, 2023
6
Натуральные числа.
Повторение курса
математики 5 класса
http://seninvg07.narod.ru/
метапредмет – задача

2.

Ц
Задачи урока
За ученого трех
неученых дают
На примерах
учимся
Порядок больше
всего помогает
ясному усвоению
?
повторение
целеполагание

3.

Ц
Задачи урока
• Арифметические действия с
многозначными натуральными
числами.
• Использование при
вычислениях
переместительного и
сочетательного свойств
сложения и умножения,
распределительного свойства
умножения.
• Округление натуральных
чисел.
Уважаемых шестиклассников будет
сопровождать знаменитый кот
Серафим со своими вопросами и
заданиями.
54 199
5
0,56 34,1 676
7
8
11
1
95
- Прочитайте числа.
- На какие группы их можно разделить?
- Дайте название каждой группе чисел.
целеполагание

4.

?
Математическая разминка
Вычислите:
вхождение в тему урока и создание условий для осознанного восприятия нового материала

5.

Работаем с книгой
Натуральные числа
?
1, 2. 3, 4, 5, 6, 7, 8. 9, 10, 11, 12, …
Нуль не является натуральным числом.
Сумма чисел
?
Число с, которое получают в результате
сложения чисел а и b, называют суммой. Числа а
и b, которые складывают, называют
слагаемыми. Суммой называют и выражение
вида а + b.
Переместительное
свойство сложения
?
Сумма чисел не изменяется при перестановке
слагаемых: а + b = b + а.
Например, 234 + 375 = …
Сочетательное
свойство сложения
?
Чтобы прибавить к числу сумму двух чисел,
можно сначала прибавить первое слагаемое, а
потом к полученной сумме прибавить второе
слагаемое: a + (b + с) = (а + b) + с = a + b + с.
Например, 23 – (27 + 49) = …
организация и самоорганизация учащихся. организация обратной связи

6.

Работаем с книгой
Свойство нуля при
сложении
?
От прибавления нуля число не изменяется:
a + 0 = 0 + a = a.
Например, 405 + 0 = …
Разность чисел
?
Вычитание — это действие, с помощью
которого по сумме и одному из слагаемых
находят другое слагаемое. Число а, из которого
вычитают, называют уменьшаемым, число b,
которое вычитают, называют вычитаемым, а
число с, которое получают в результате
вычитания из числа а числа b, называют
разностью. Разностью называют и выражения
вида
а – b.
а – b = с.
организация и самоорганизация учащихся. организация обратной связи

7.

Работаем с книгой
Свойство
вычитания
суммы uз числа
?
Чтобы вычесть сумму из числа, можно вычесть
из этого числа одно слагаемое, а потом из
полученной разности вычесть другое слагаемое:
а – (b + с ) = а – b – с, если b + с < а или b + с = а.
Например, 456 – (56 + 237) = …
Свойство
вычитания
числа uз суммы
?
Чтобы из суммы вычесть число, можно вычесть
его из одного слагаемого, а к полученной
разности прибавить другое слагаемое:
(а + b) – с = a + (b – с), если с < b или с = b;
(о + b) – с = (a – с) + b, если с < а или с = а.
Например, (118 + 236) – 18 = …
Свойства нуля
при вычитании
?
Если из числа вычесть нуль, оно не изменится:
a – 0 = а. На пример, 1003 – 0 = ...
При вычитании равных чисел получится нуль:
a – a = 0. Например, 349 – 349 = ...
организация и самоорганизация учащихся. организация обратной связи

8.

Работаем с книгой
Произведение чисел
?
Умножить число a на число b — значит найти
сумму b слагаемых, каждое из которых равно a.
Числа a и b которые перемножают, называют
множителями, а число с, которое получают в
результате умножения чисел a и b. называют
произведением. Произведением называют и
выражение вида
ab. a ∙ b = с .
Переместительное
свойство умножения
?
Произведение чисел не изменяется при
перестановке множителей:
a∙b=b∙а.
Например, 23 ∙ 4 = …
организация и самоорганизация учащихся. организация обратной связи

9.

Работаем с книгой
Сочетательное
свойство умножения
?
Чтобы умножить число на произведение двух
чисел, можно сначала умножить его на первый
множитель а потом полученное произведение
умножить на второй множитель:
a • (b • с) = (а • b) • с.
Например, 5•(2 • 87) = …
Для любого числа п:
n • 1 = n; 1 • п = п; 0 • n = 0; n • 0 = 0.
Например, 1 • 45 = … ; 0 • 87 = … .
Распределительное
свойство умножения
относительно
сложения
?
Чтобы умножить сумму на число, можно
умножить на это число каждое слагаемое и
сложить получившиеся произведения:
(а + b ) с = ас + bс.
Например. 82 • 7 = (80 + 2) • 7 = …
организация и самоорганизация учащихся. организация обратной связи

10.

Работаем с книгой
Распределительное
свойство умножения
относительно
вычитания
?
Чтобы умножить разность на число можно
умножить на это число уменьшаемое и
вычитаемое и из первого произведения вычесть
второе.
(а – b) с = ас – bc.
Например, 99 • 6 = (100 – 1) • 6 = …
Степень числа
Частное чисел
Свойства деления
Числовые и
буквенные
выражения
Уравнение
Делитель, кратное
Простое число
Свойство
делимости
Признаки делимости
организация и самоорганизация учащихся. организация обратной связи

11.

К
Наши задачи
1. Найдите ошибки в примерах и исправьте их:
а) 19 + 27 = 36; в) 27 + 42 = 69;
д) 49 + 32 = 71;
б) 37 - 19 = 16; г) 74 - 56 = 18;
е) 49 - 32 = 17.
2. Вычислите:
а) 42 : 7 • 8;
60 • 5 : 10;
630 : 9 • 3;
б) 72 : 8 • 3;
44 : 4 • 2;
360 : 4 : 3;
в) 12 • 3 : 9;
46 : 2 • 3;
280 : 4 : 7;
г) (37 + 11) : 24;
(53 - 39) • 6;
49 : (71 - 64).
3. Используя только цифры 0 и 6, запишите все трёхзначные числа. Найдите
сумму этих чисел и разделите её на 422.
4. Выполните сложение:
а) 40 000 + 4000 + 900 + 50 + 7;
б) 6 000 000 + 40 000 + 2000 + 600 + 1;
в) 700 000 + 9000 + 300 + 20;
г) 2000 + 900 + 5.
практикум

12.

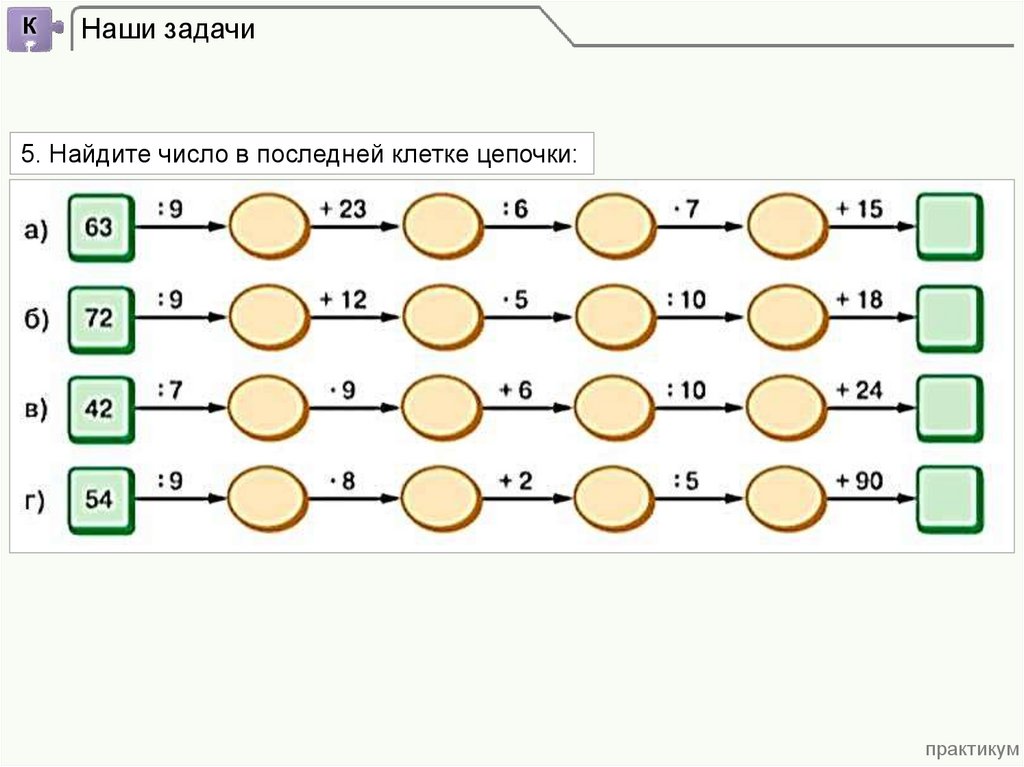
К
Наши задачи
5. Найдите число в последней клетке цепочки:
практикум

13.

?
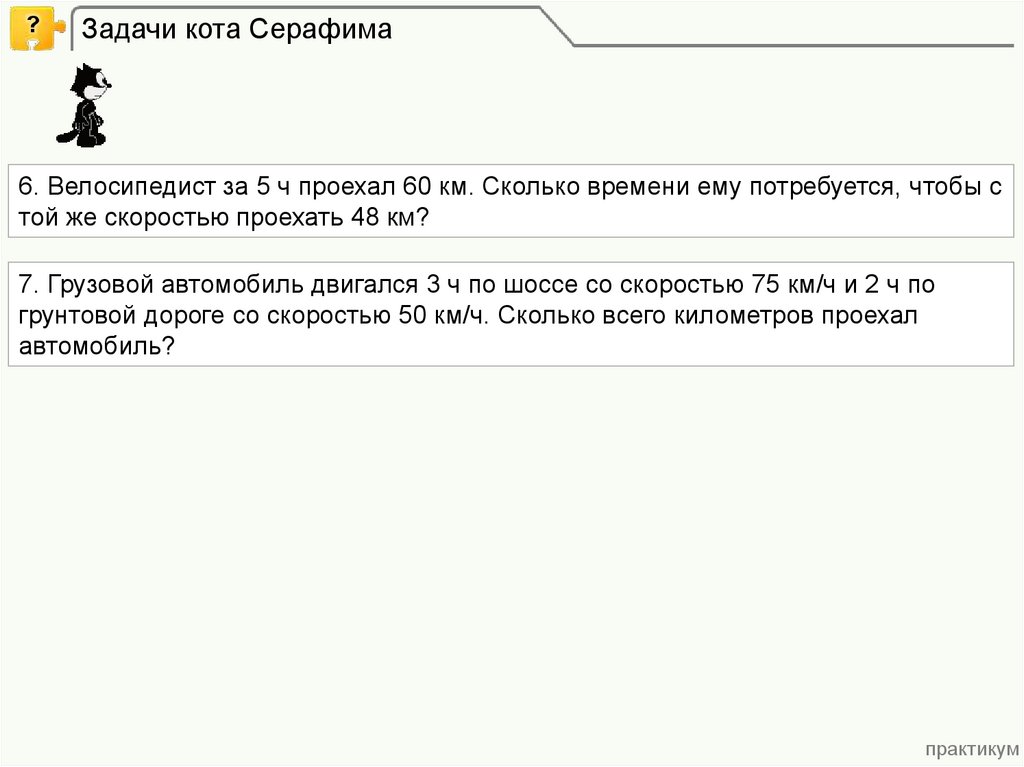
Задачи кота Серафима
6. Велосипедист за 5 ч проехал 60 км. Сколько времени ему потребуется, чтобы с
той же скоростью проехать 48 км?
7. Грузовой автомобиль двигался 3 ч по шоссе со скоростью 75 км/ч и 2 ч по
грунтовой дороге со скоростью 50 км/ч. Сколько всего километров проехал
автомобиль?
практикум

14.

?
Проверь себя
1. Запишите самое маленькое натуральное число.
2. Запишите самое большое трёхзначное число.
Запишите цифрами число:
3. Десять миллионов сто тысяч двадцать.
4. Шесть миллиардов двадцать миллионов пять.
5.15 млрд 3 млн 20 тыс.
Верно ли высказывание (ответьте да или нет)?
6. За числом две тысячи девятьсот девяносто девять
следующее натуральное число — три тысячи.
7. Число, на единицу меньшее десяти миллионов, — это
девять миллионов.
проверка полученных результатов. коррекция

15.

Д
Итоги
Вычислите:
а) 745 + 476;
б) 472 – 398;
в) 2842 : 7; д ) 47 – 24 – 39;
г) 342 • 25; е) 840 : 12 + 15;
ж) 24 • (327 – 276);
з) (247 + 578) : 25.
Какие трудности вы испытывали на уроке?
Домашнее задание: стр. 4 – 7. Вычислите.
подведение итогов. рефлексия. домашнее задание