Эконометрика. Базовые элементы эконометрики

1. Эконометрика – наука, предметом изучения которой является количественное выражение взаимосвязей экономических явлений и

процессов
С.Фишер
«,,,Занимается
разработкой
и
применением
статистических методов для измерения взаимосвязей
между экономическими переменными»
С.Айвазян
«,,,объединяет совокупность методов и моделей,
позволяющих придавать количественные выражения
качественным зависимостям»

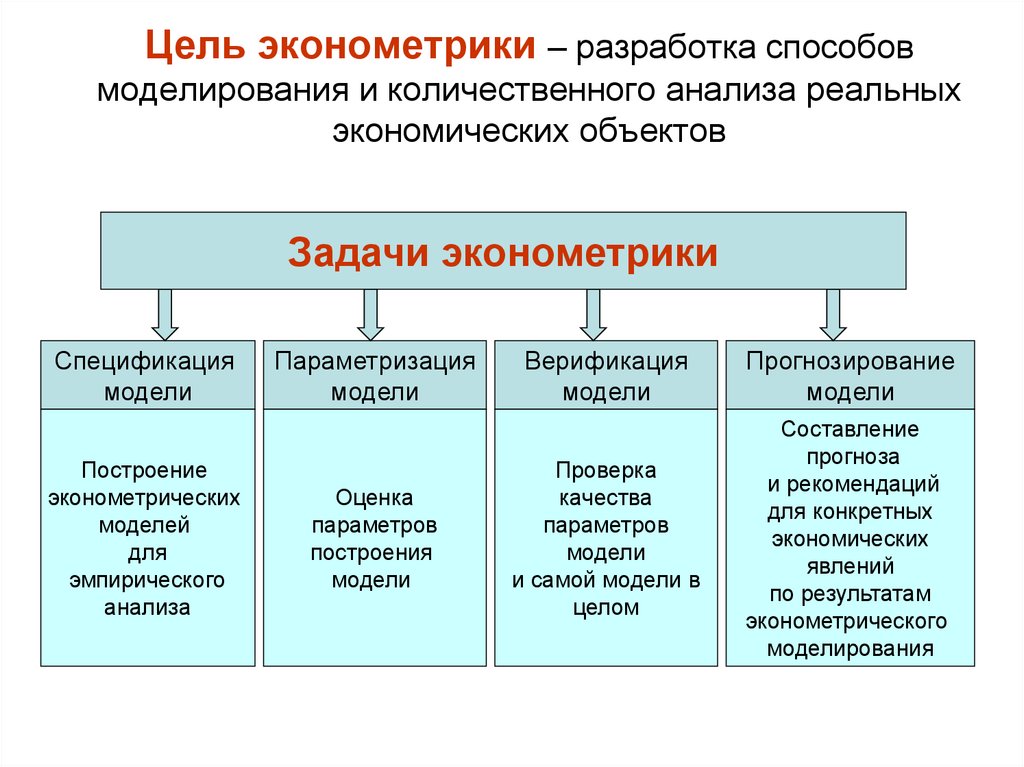
2. Цель эконометрики – разработка способов моделирования и количественного анализа реальных экономических объектов

Задачи эконометрики
Спецификация
модели
Построение
эконометрических
моделей
для
эмпирического
анализа
Параметризация
модели
Оценка
параметров
построения
модели
Верификация
модели
Прогнозирование
модели
Проверка
качества
параметров
модели
и самой модели в
целом
Составление
прогноза
и рекомендаций
для конкретных
экономических
явлений
по результатам
эконометрического
моделирования

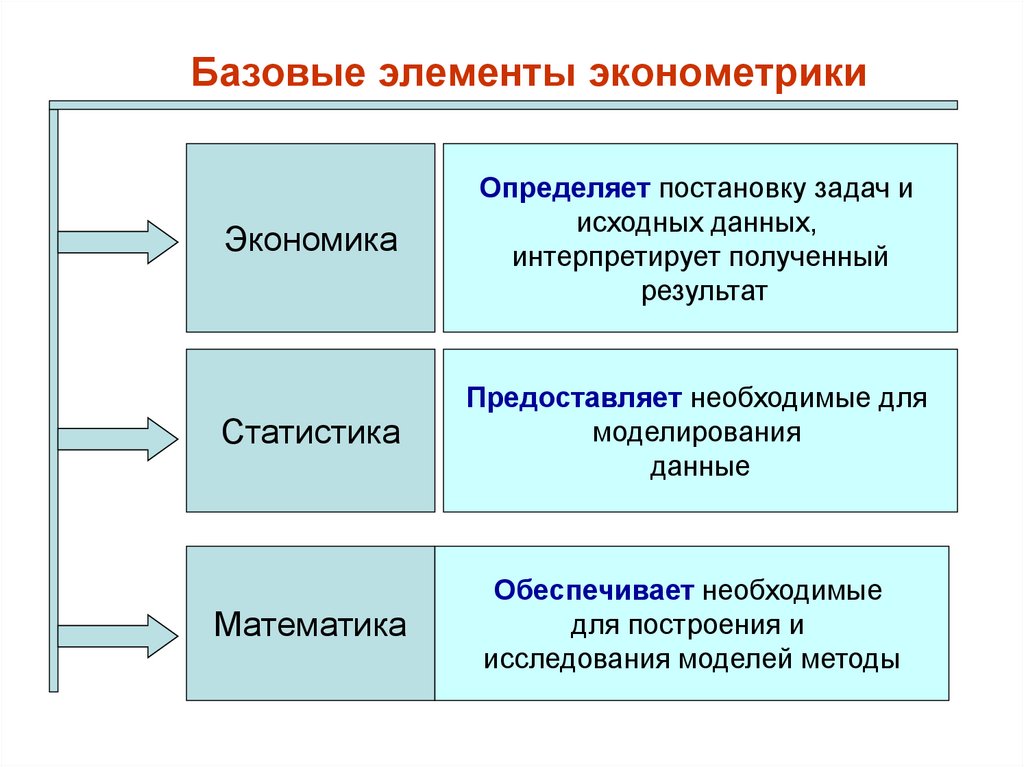
3. Базовые элементы эконометрики

Экономика
Определяет постановку задач и
исходных данных,
интерпретирует полученный
результат
Статистика
Предоставляет необходимые для
моделирования
данные
Математика
Обеспечивает необходимые
для построения и
исследования моделей методы

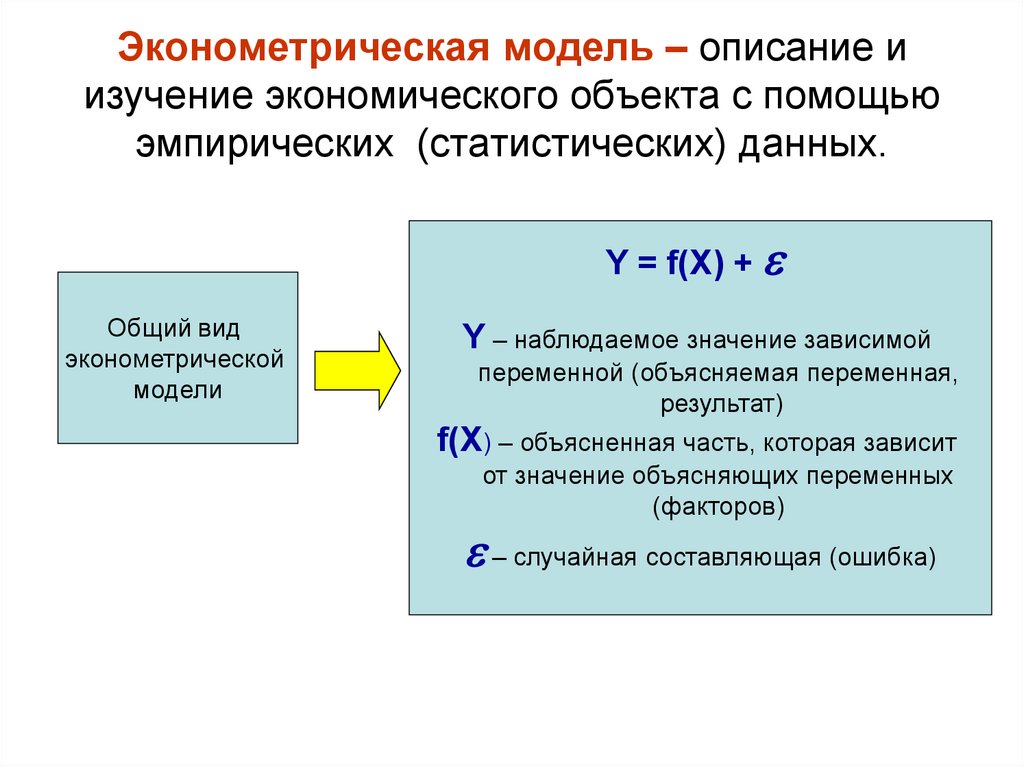
4. Эконометрическая модель – описание и изучение экономического объекта с помощью эмпирических (статистических) данных.

Y = f(X) +
Общий вид
эконометрической
модели
Y – наблюдаемое значение зависимой
переменной (объясняемая переменная,
результат)
f(X) – объясненная часть, которая зависит
от значение объясняющих переменных
(факторов)
– случайная составляющая (ошибка)

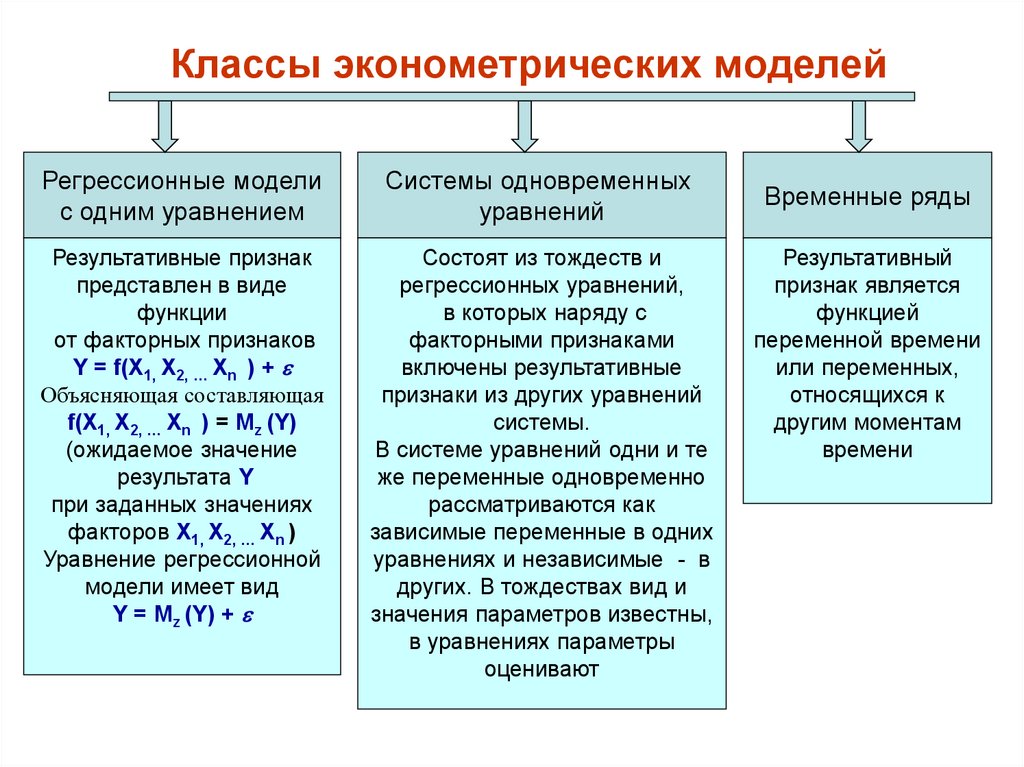
5. Классы эконометрических моделей

Регрессионные модели
с одним уравнением
Системы одновременных
уравнений
Результативные признак
представлен в виде
функции
от факторных признаков
Y = f(X1, X2, … Xn ) +
Объясняющая составляющая
f(X1, X2, … Xn ) = Mz (Y)
(ожидаемое значение
результата Y
при заданных значениях
факторов X1, X2, … Xn )
Уравнение регрессионной
модели имеет вид
Y = Mz (Y) +
Состоят из тождеств и
регрессионных уравнений,
в которых наряду с
факторными признаками
включены результативные
признаки из других уравнений
системы.
В системе уравнений одни и те
же переменные одновременно
рассматриваются как
зависимые переменные в одних
уравнениях и независимые - в
других. В тождествах вид и
значения параметров известны,
в уравнениях параметры
оценивают
Временные ряды
Результативный
признак является
функцией
переменной времени
или переменных,
относящихся к
другим моментам
времени

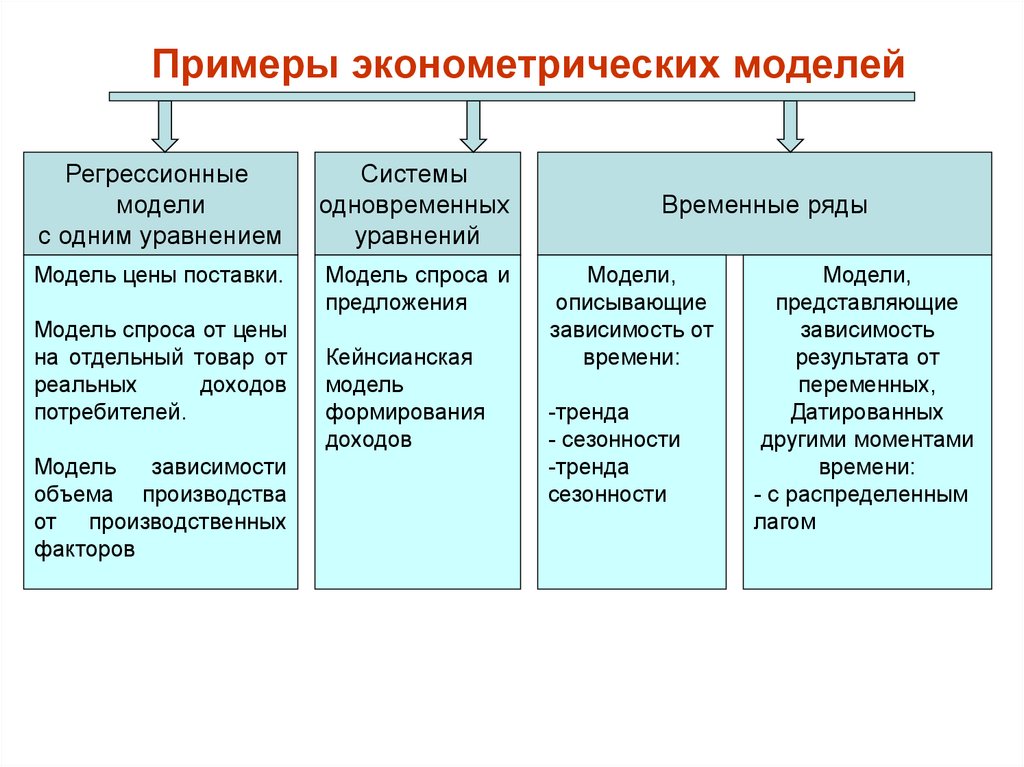
6. Примеры эконометрических моделей

Регрессионные
модели
с одним уравнением
Системы
одновременных
уравнений
Модель цены поставки.
Модель спроса и
предложения
Модель спроса от цены
на отдельный товар от
реальных
доходов
потребителей.
Модель
зависимости
объема производства
от производственных
факторов
Кейнсианская
модель
формирования
доходов
Временные ряды
Модели,
описывающие
зависимость от
времени:
-тренда
- сезонности
-тренда
сезонности
Модели,
представляющие
зависимость
результата от
переменных,
Датированных
другими моментами
времени:
- с распределенным
лагом

7. Типы экономических данных, используемых в эконометрических исследованиях.

Пространственные
данные
характеризуют ситуацию по
конкретной переменной
(или набору переменных),
относящейся к пространственно
разделенным сходным объектам
в один и тот же момент времени.
Временные ряды
отражают изменения
(динамику)
какой-либо переменой на
промежутке времени.
набор сведений
по разным объектам,
взятым за один и тот же
период времени
набор сведений, характеризующий
один и тот же объект,
за разные
периоды времени
Объем производства предприятий региона,
численность студентов институтов города
ежеквартальные данные по инфляции,
данные по средней заработной плате,

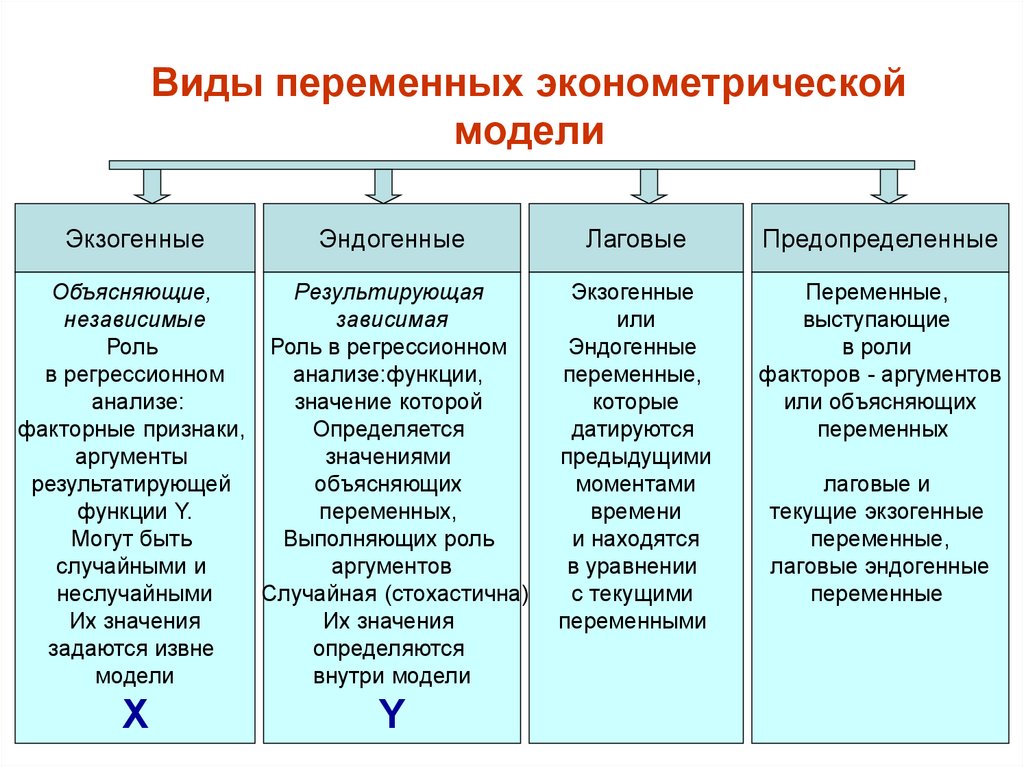
8. Виды переменных эконометрической модели

Экзогенные
Эндогенные
Объясняющие,
Результирующая
независимые
зависимая
Роль
Роль в регрессионном
в регрессионном
анализе:функции,
анализе:
значение которой
факторные признаки,
Определяется
аргументы
значениями
результатирующей
объясняющих
функции Y.
переменных,
Могут быть
Выполняющих роль
случайными и
аргументов
неслучайными
Случайная (стохастична)
Их значения
Их значения
задаются извне
определяются
модели
внутри модели
X
Y
Лаговые
Предопределенные
Экзогенные
или
Эндогенные
переменные,
которые
датируются
предыдущими
моментами
времени
и находятся
в уравнении
с текущими
переменными
Переменные,
выступающие
в роли
факторов - аргументов
или объясняющих
переменных
лаговые и
текущие экзогенные
переменные,
лаговые эндогенные
переменные

9. Этапы эконометрического моделирования

Постановочный
Формируют
цель
исследования
(анализ,
прогноз,имитация
развития,
управленческое
решение
и
т.д.),
определяют
экономические
переменные модели
Априорный
Анализируют изучаемое экономическое явление:
формируют и формализируют информацию, известную
до начала моделирования
Параметризации
Определяют вид экономической модели, выражают в
математической форме взаимосвязь между ее
переменными, формулируют исходные предпосылки и
ограничения модели
Информационный Собирают необходимую статистическую информацию
Идентификация
модели
Проводят статистический анализ модели, оценивают
качество ее параметров
Верификации
модели
Проверяют истинность модели, определяют насколько
соответствует
построенная
модель
реальному
экономическому явлению

10. Основные понятия

Временный ряд – это ряд последовательно
расположенных во времени числовых
показателей,
которые
характеризуют
уровень состояния и изменения явления
или процесса.
Отдельные наблюдения временного ряда
называются уровнями этого ряда.
Основные элементы временного ряда:
показатели времени t, уровень ряда y.

11. Компоненты временных рядов

• Значения уровней временных рядов
экономических показателей складываются
из составляющих (компонентов):
• тренда
• сезонной
• циклической
• случайной

12.

• Устойчивую тенденцию во временном ряду более
или менее свободную от случайных колебаний
называют трендом (ut)
• Во временных рядах тенденция может быть
представлена:
- тенденцией среднего уровня, когда значения в
отдельные
моменты
времени
выступают
математическими ожиданиями ряда динамики
- тенденцией дисперсии, которая представляет
собой тенденцию изменения отклонений между
эмпирическими уровнями и детерминированной
компонентой ряда

13.

• Повторяющиеся в каждом временном
периоде колебания, связанные с изменением
времени года называют в зависимости от
периода колебания:
- не превышающие года – сезонные (st)
компоненты временного ряда
(например: природные, климатические условия)
- более года - циклические (vt) компоненты
временного ряда
(например: демографические циклы)

14.

• Тренд,
сезонная,
циклическая
составляющие называются регулярными
(систематическими)
компонентами
временного ряда
• Если из временного ряда удалить
регулярный компонент, то останется
случайный компонент (et)

15.

• Если временный ряд представлен в
виде суммы составляющих
компонентов, модель называется
аддитивной формой
yt = u t + st + vt + et

16.

• Если временный ряд представлен в виде
произведения составляющих компонентов,
модель называется мультипликативной
формой
yt = u t * st * vt * et

17.

• Если временный ряд представлен в виде
произведения
систематических
составляющих компонентов и суммы
случайной компоненты, модель называется
смешанной формой
yt = u t * st * vt + et

18.

yt -уровни временного ряда
u t – временный тренд
st – сезонный компонент
vt - циклическая составляющая
et - случайный компонент

19. Расчет показателей динамики во временных рядах. Прогнозироавание на основе показателей временного ряда

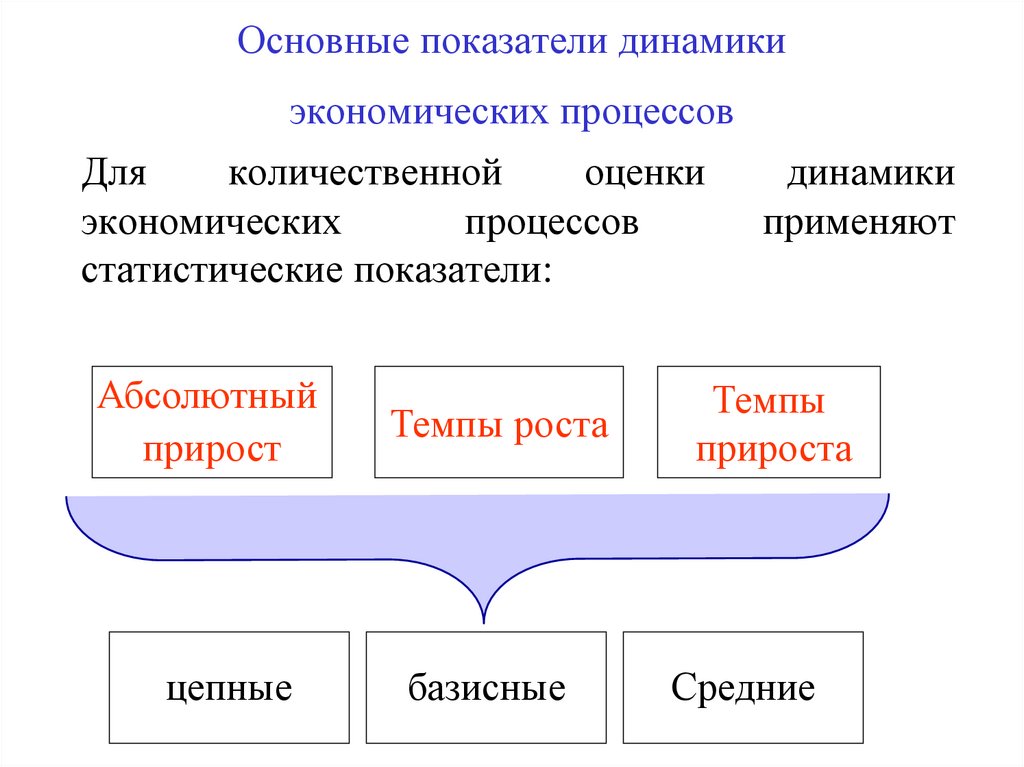
20. Основные показатели динамики экономических процессов

Для
количественной
оценки
экономических
процессов
статистические показатели:
динамики
применяют
Абсолютный
прирост
Темпы роста
Темпы
прироста
цепные
базисные
Средние

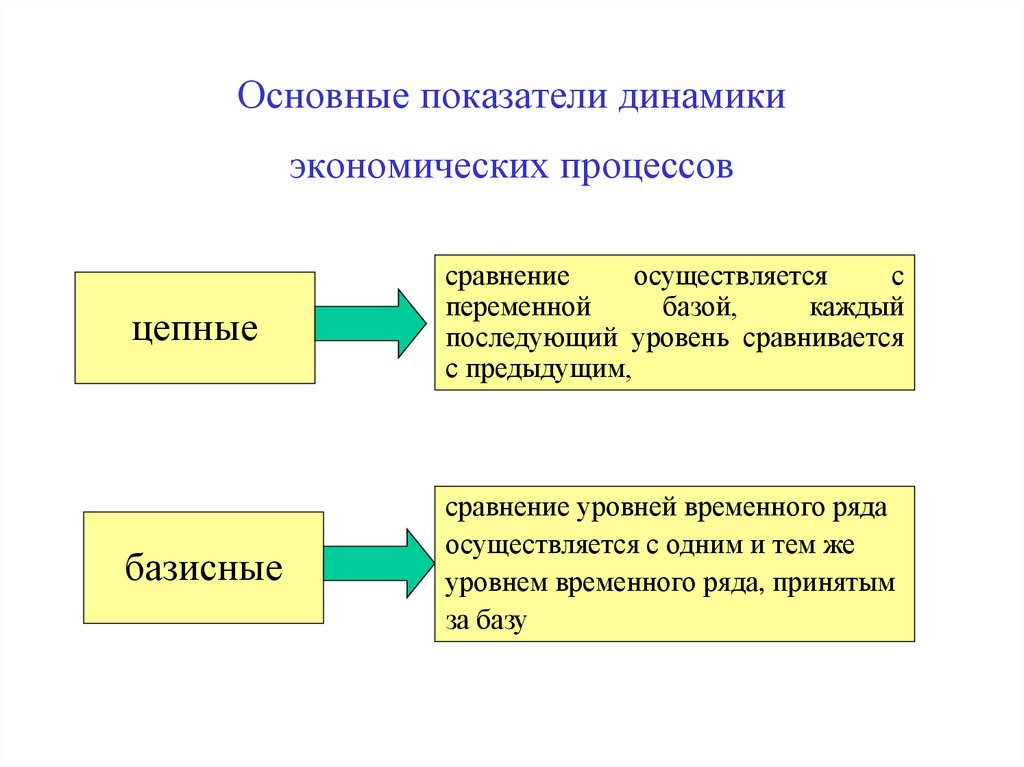
21. Основные показатели динамики экономических процессов

цепные
сравнение
осуществляется
с
переменной
базой,
каждый
последующий уровень сравнивается
с предыдущим,
базисные
сравнение уровней временного ряда
осуществляется с одним и тем же
уровнем временного ряда, принятым
за базу

22. Формулы для вычисления цепных, базисных и средних абсолютных приростов, темпов роста и темпов прироста

Абсолютный
прирост
Темп роста
Темп
прироста
Цепной
yц t yt yt 1
yt
Tц
100%
yt 1
K ц Tц 100%
Базисный
yb t yt yb
yt
Tб
100%
yб
Средний
( yn yt ) T ( yn )1/(n 1) 100%
yt
t
y1
(n 1)
Обозначение
K b Tb 100%
K t T t 100%

23. Для получения прогнозного значения на один шаг вперед к последнему наблюдению добавляют значение среднего абсолютного прироста:

ˆ
y n 1 y n y
уn - значение показателя в п точке временного ряда,
yn 1 - прогнозное значение показателя в точке п + 1,
ŷ - значение среднего прироста временного ряда.

24. Прогнозное значение на i шагов вперед

ˆ n 1 yn T
y
ŷn 1 - прогнозная оценка значения показателя в точке
п + i,
T
- средний темп роста, выраженный в относительных
величинах.

25. Пример

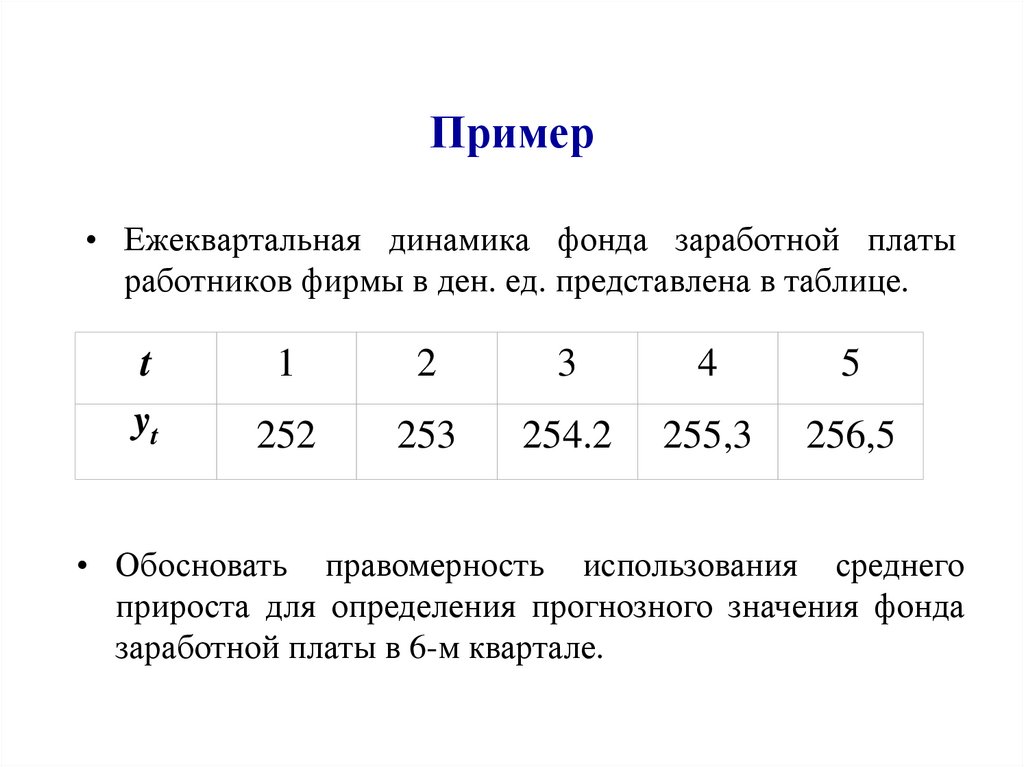
• Ежеквартальная динамика фонда заработной платы
работников фирмы в ден. ед. представлена в таблице.
t
yt
1
2
3
4
5
252
253
254.2
255,3
256,5
• Обосновать правомерность использования среднего
прироста для определения прогнозного значения фонда
заработной платы в 6-м квартале.

26.

Цепные абсолютные приросты:
y5 y5 y4 = 253 - 252 = 1,
y2 y2 y1 = 254,2 - 253 = 1,2,
y3 y3 y 2 = 255,3 - 254,2 = 1,1,
y 4 y4 y3 =256,5 - 255,3 = 1,2.
Цепные абсолютные приросты изменяются от 1 до 1,2. Их
изменения примерно одинаковы, что свидетельствует о близости
ежеквартальной динамики фонда заработной платы фирмы к
линейной. Поэтому правомерно определить прогнозное значение
у6 c помощью среднего прироста y :
y ( y5 y1 ) /( n 1) = (256,5 -252)/(5 -1) = 1,125,
ˆ y5 y =256,5 + 1,125 =257,625.
y

27.

• Изменение ежеквартальной динамики фонда
заработной
платы
работников
фирмы
происходило примерно с постоянным темпом
роста в течение 5 rварталов. Фонд заработной
платы в 1-м квартале составлял 252 ден. ед., а в
5-м квартале — 256,5 ден. ед.
• Определить прогноз фонда заработной платы
работников фирмы в 6-м квартале, используя
средний темп роста.

28. По условию, изменение фонда заработной платы происходило примерно с постоянным темпом роста в течении 5 кварталов. Поэтому

правомерно использовать
средний темп роста для расчета прогноза фонда в 6-м
квартале.
Средний темп роста составит:
1 /( n 1)
Tt ( y n / y1 )
* 100%
T ( y5 / y1 )1/ 4 *100% = (256,5/252)1/4 • 100 % = 100,44 %.
Таким образом, прогноз величины фонда заработной платы
сотрудников фирмы составит:
yˆ 6 y5T = 256,5 *100,44 =257,6 ден. ед.

29. Модели кривых роста в прогнозировании

30.

Уравнение линии тренда — это формула,
которая находит линию, которая лучше всего
соответствует точкам данных
Тренды бывают
по направлению
•восходящий (бычий)
•нисходящий (медвежий)
•боковой.
по скорости
•сильный тренд
•слабый тренд

31.

Кривые роста выбирают из трех классов
функций
Первый класс - кривые, которые используются для
описания процессов с монотонным характером развития
и отсутствием пределов роста
Второой класс - кривые, имеющие предел роста в
исследуемом периоде (кривые насыщения)
Третий класс - кривые насыщения имеющие точки
перегиба (S - образные кривые)

32.

ПОЛИНОМ (греч., от polys многий, и
nomos часть, член) – численная величина,
состоящая
из
нескольких
членов,
соединенных между собою знаками: плюс
или минус
Полиномиальный тренд применяется для
описания значений временных рядов,
попеременно возрастающих и убывающих.

33.

Порядок полинома – это показатель
наивысшей степени, используемой в полиноме
уt = а0 + а1t + а2t2 + а3t3 + ...
Параметр а0 является начальным уровнем
ряда при t = 0
а1 - линейный прирост,
а2 - ускорение роста,
а3 - изменение ускорения роста

34.

Полином первой степени
у t = a 0 + a 1t
на графике изображается в виде прямой и
используется для описания процессов,
развивающихся равномерно во времени

35.

Полином второй степени
уt = а0 + а1t + а2t2
на графике изображается в виде параболы,
применяется в тех случаях, когда процесс
развивается равноускоренно
При
а2 > 0 ветви параболы направлены вверх
а2 < 0 ветви параболы направлены вниз

36.

Полином третьей степени
уt = а0 + а1t + а2t2+ а3t3
У полинома третьей степени знак
прироста ординат может изменяться один
или два раза

37.

Оценки параметров полиномов определяются
методом наименьших квадратов
Уравнение для определения коэффициентов
прямой

38.

Решение
системы,
т.
е. нахождение
коэффициентов системы a0, a1 производится
по формулам Крамера
Систему нормальных уравнений можно
упростить и уменьшить абсолютные значения
величин, если перенести начала координат в
середину ряда динамики

39.

40.

Уравнение полинома второй степени (параболы), после
переноса начала координат в середину ряда динамики

41.

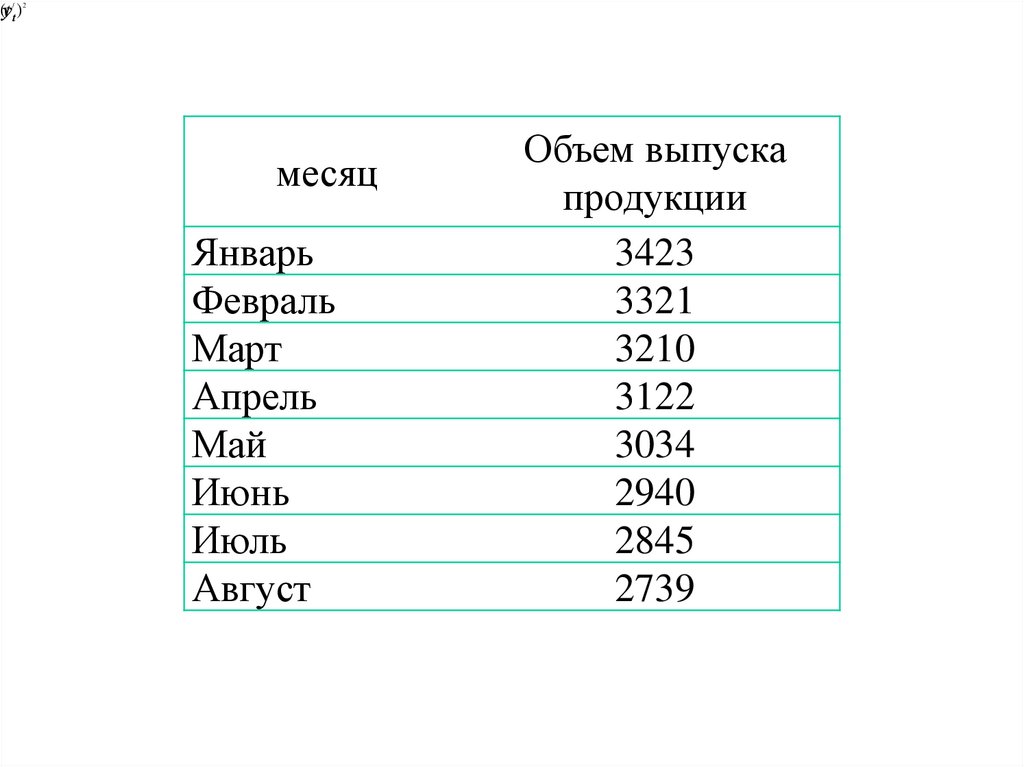
Пример
По данным выпуска продукции фирмы за 8
месяцев произвести расчет
• коэффициентов a0 и a1 линейного тренда и
прогноз на месяц вперед
• коэффициентов параболического тренда a0, a1,
a3 прогноз на месяц вперед

42.

(tyt/ ) 2
месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Объем выпуска
продукции
3423
3321
3210
3122
3034
2940
2845
2739

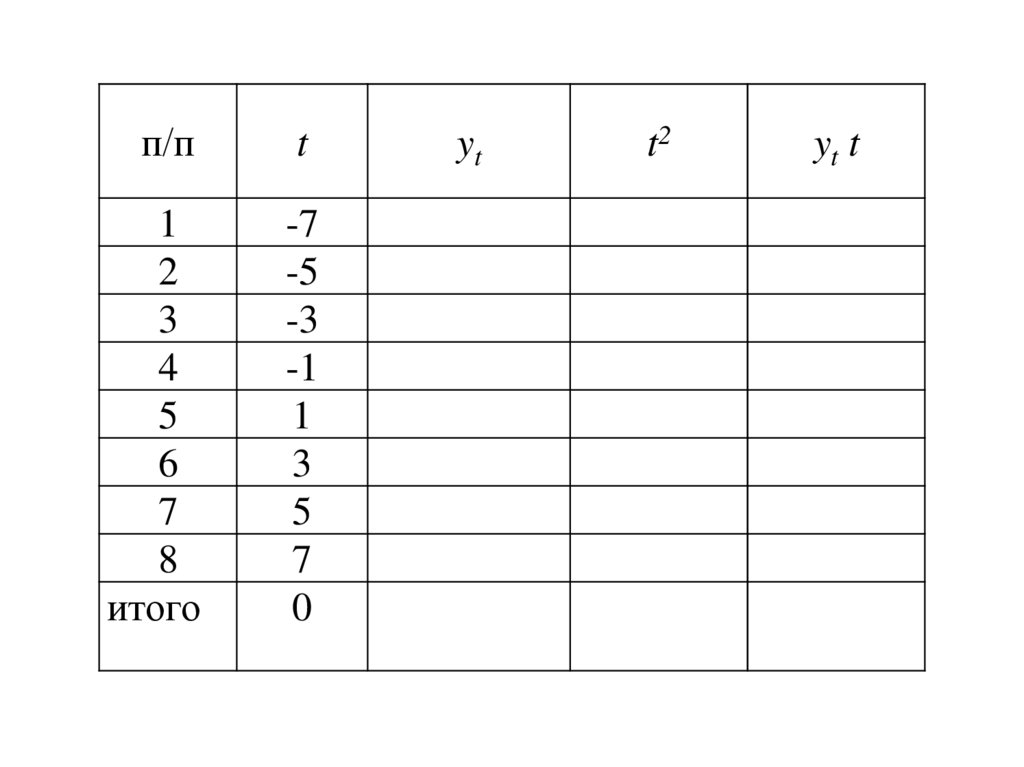
43.

Вспомогательная таблица
п/п
1
2
3
4
5
6
7
8
итого
t
yt
t2
yt t

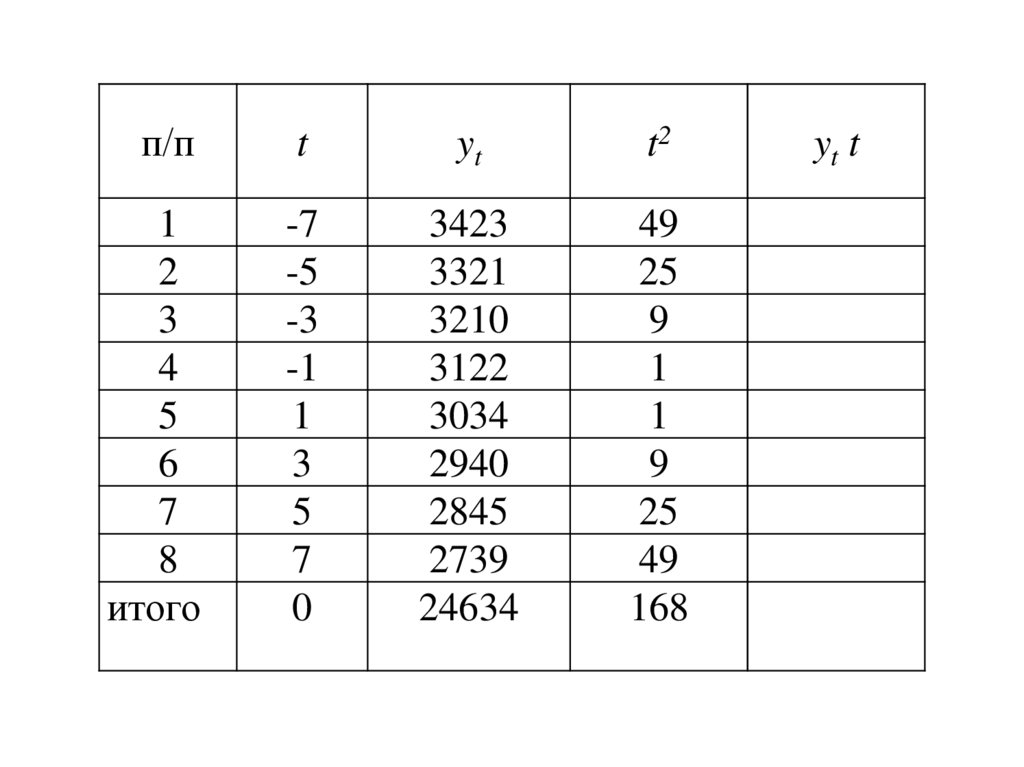
44.

п/п
t
1
2
3
4
5
6
7
8
итого
-7
-5
-3
-1
1
3
5
7
0
yt
t2
yt t

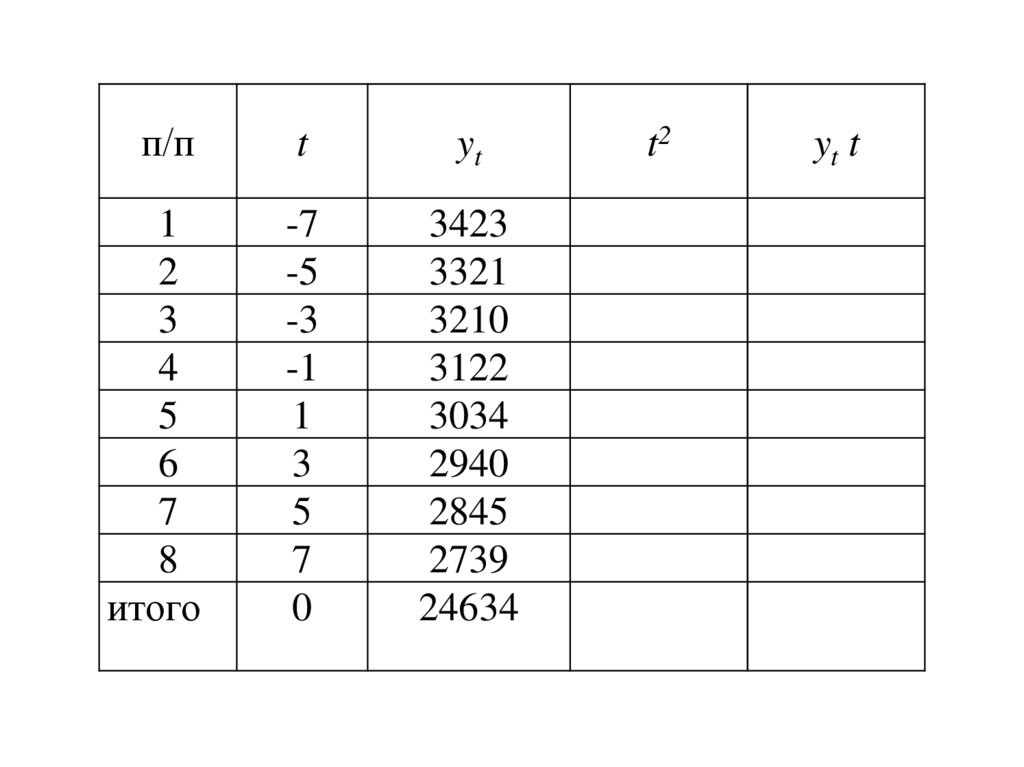
45.

п/п
t
yt
1
2
3
4
5
6
7
8
итого
-7
-5
-3
-1
1
3
5
7
0
3423
3321
3210
3122
3034
2940
2845
2739
24634
t2
yt t

46.

п/п
t
yt
t2
1
2
3
4
5
6
7
8
итого
-7
-5
-3
-1
1
3
5
7
0
3423
3321
3210
3122
3034
2940
2845
2739
24634
49
25
9
1
1
9
25
49
168
yt t

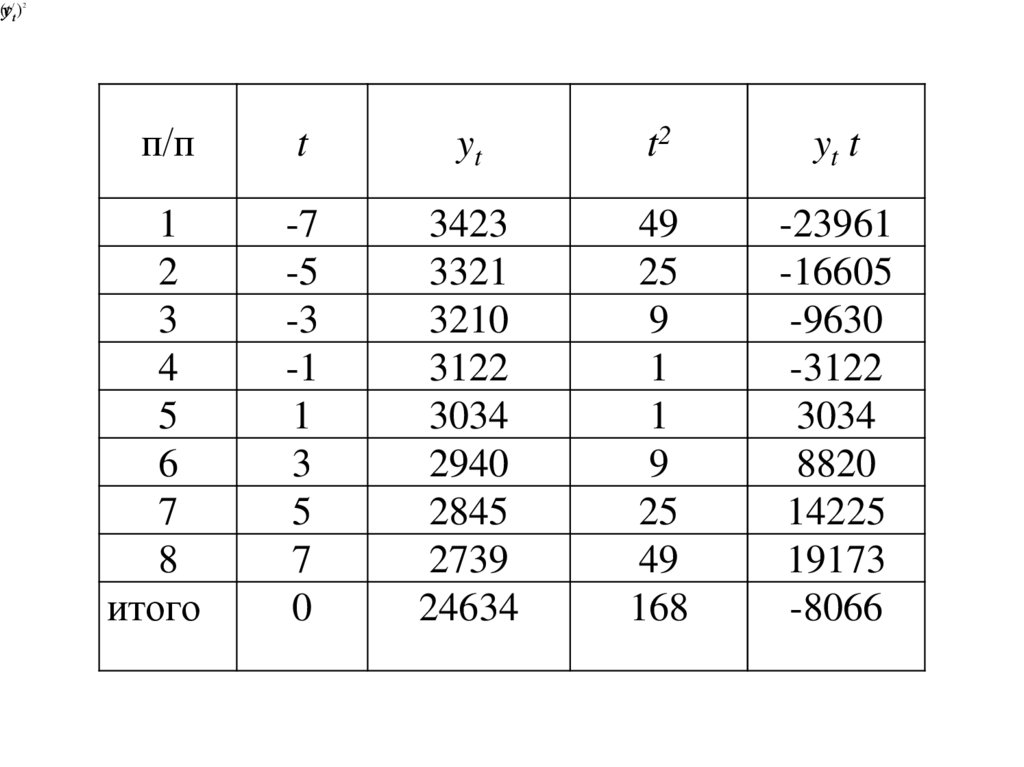
47.

(tyt/ ) 2
п/п
t
yt
t2
yt t
1
2
3
4
5
6
7
8
итого
-7
-5
-3
-1
1
3
5
7
0
3423
3321
3210
3122
3034
2940
2845
2739
24634
49
25
9
1
1
9
25
49
168
-23961
-16605
-9630
-3122
3034
8820
14225
19173
-8066

48.

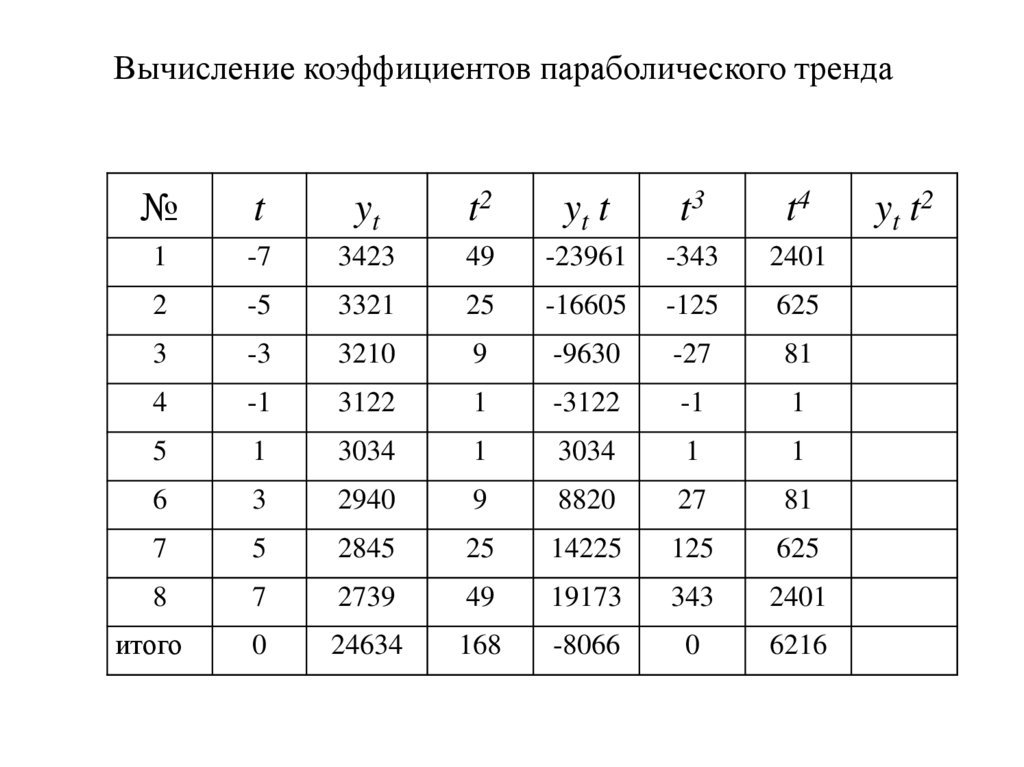
49.

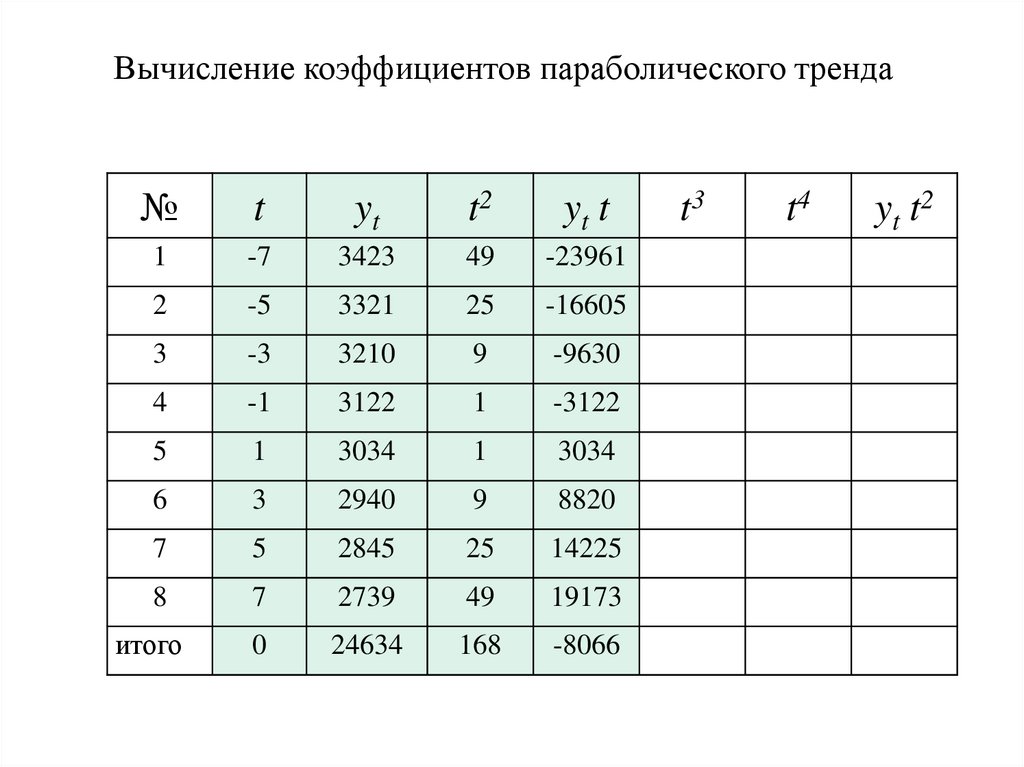
Вычисление коэффициентов параболического тренда
№
t
yt
t2
yt t
1
-7
3423
49
-23961
2
-5
3321
25
-16605
3
-3
3210
9
-9630
4
-1
3122
1
-3122
5
1
3034
1
3034
6
3
2940
9
8820
7
5
2845
25
14225
8
7
2739
49
19173
итого
0
24634
168
-8066
t3
t4
yt t2

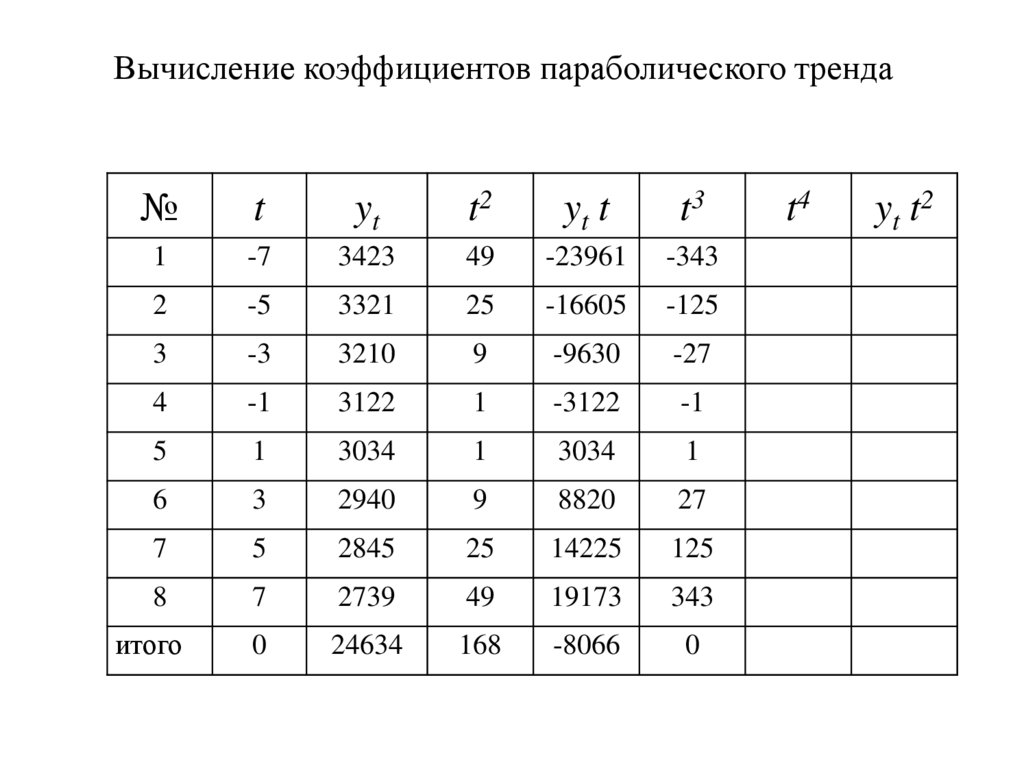
50.

Вычисление коэффициентов параболического тренда
№
t
yt
t2
yt t
t3
1
-7
3423
49
-23961
-343
2
-5
3321
25
-16605
-125
3
-3
3210
9
-9630
-27
4
-1
3122
1
-3122
-1
5
1
3034
1
3034
1
6
3
2940
9
8820
27
7
5
2845
25
14225
125
8
7
2739
49
19173
343
итого
0
24634
168
-8066
0
t4
yt t2

51.

Вычисление коэффициентов параболического тренда
№
t
yt
t2
yt t
t3
t4
1
-7
3423
49
-23961
-343
2401
2
-5
3321
25
-16605
-125
625
3
-3
3210
9
-9630
-27
81
4
-1
3122
1
-3122
-1
1
5
1
3034
1
3034
1
1
6
3
2940
9
8820
27
81
7
5
2845
25
14225
125
625
8
7
2739
49
19173
343
2401
итого
0
24634
168
-8066
0
6216
yt t2

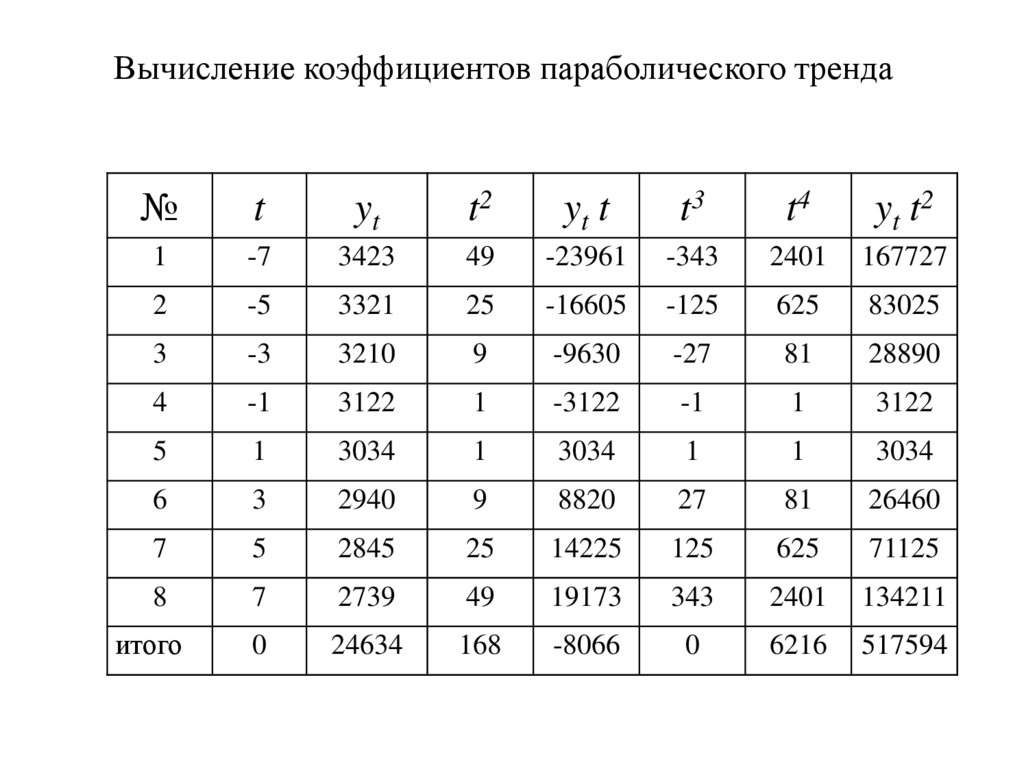
52.

Вычисление коэффициентов параболического тренда
№
t
yt
t2
yt t
t3
t4
yt t2
1
-7
3423
49
-23961
-343
2401
167727
2
-5
3321
25
-16605
-125
625
83025
3
-3
3210
9
-9630
-27
81
28890
4
-1
3122
1
-3122
-1
1
3122
5
1
3034
1
3034
1
1
3034
6
3
2940
9
8820
27
81
26460
7
5
2845
25
14225
125
625
71125
8
7
2739
49
19173
343
2401
134211
итого
0
24634
168
-8066
0
6216
517594

53.

Коэффициенты параболического тренда
= 3077,05
= -48,01
= 0,105

54.

Уравнение параболического тренда:
величина среднего уровня ряда при t=0 составляет
3077,05,
среднемесячное уменьшение выпуска продукции
составляет 48,01
ускорение роста выпуска продукции составляет 0,105,
что свидетельствует о снижении выпуска продукции за
исследуемый период в среднем на 5%

55.

Прогноз выпуска продукции на 9-й месяц

56.

Прогноз выпуска продукции на 9 месяц параболический тренд:
Разница прогнозных значений показателей линейного тренда и
параболического составляет 6,31 (1%)

57.

ЗАДАНИЕ:
По данным курса доллара за 9 дней произвести расчет
прогнозных показателей на последующие 10 и 11 дни
03.09.2024
90,0013
02.09.2024
91,1868
01.09.2024
91,1868
31.08.2024
91,1868
30.08.2024
91,4548
29.08.2024
91,4449
28.08.2024
91,4807
27.08.2024
91,7745
24.08.2024
91,6012