Похожие презентации:
Расширение понятия числа до комплексных чисел (урок 1.1)
1. Развитие понятия о числе
Тема 1:2. Урок 1.1
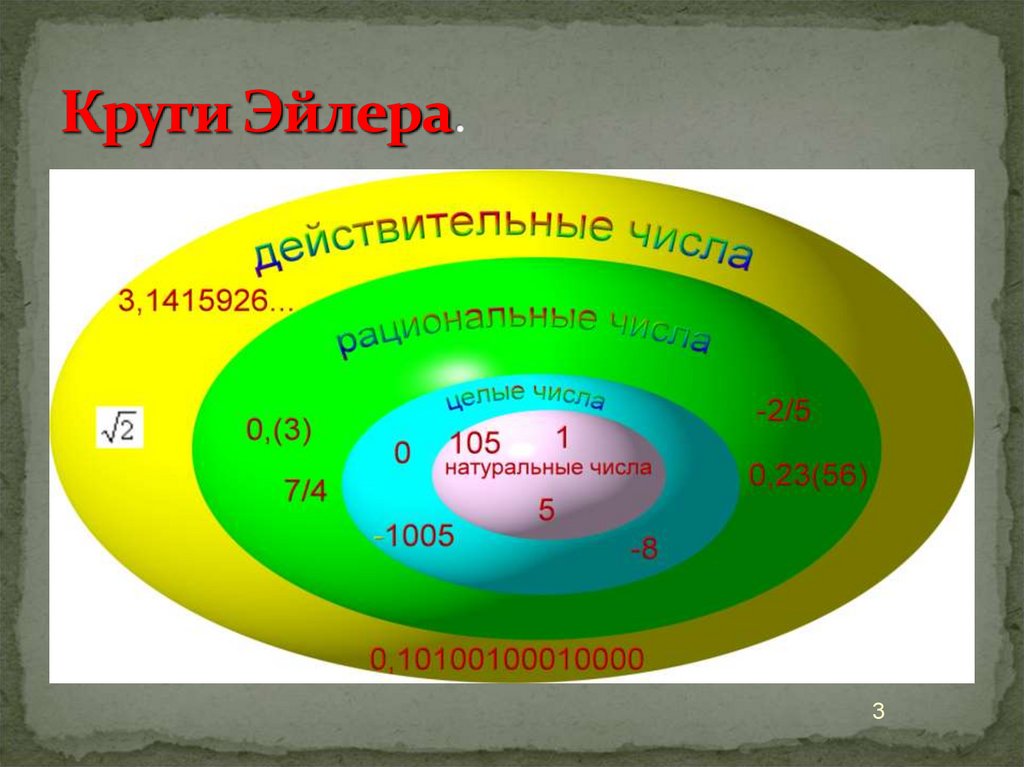
Расширение понятия числа до комплексных чисел .3. Круги Эйлера.
34. Натуральные числа
запиши в конспект5.
6.
7.
Замечание: действие вычитания не всегдавозможно на множестве натуральных чисел.
Например: от 3 нельзя отнять 5
Замечание : действие деления также не
всегда возможно на множестве натуральных
чисел.
Например: 2 не делится на 7
8. Целые числа
9.
запиши в конспект10.
11.
12.
13.
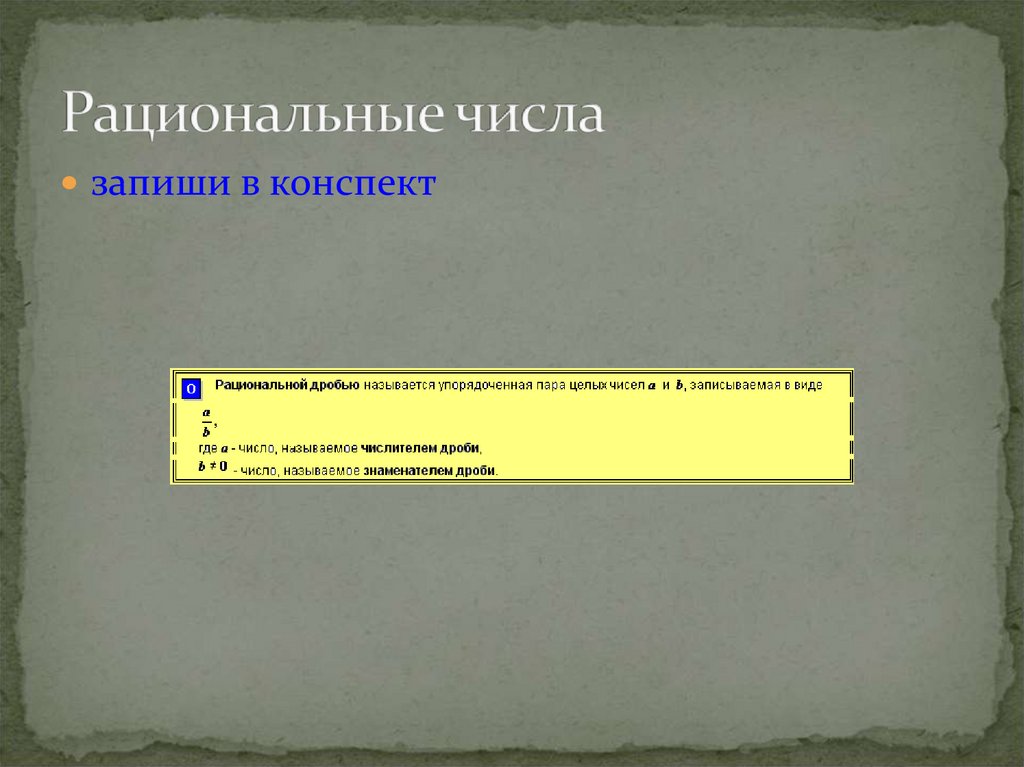
14. Рациональные числа
запиши в конспект15.
16.
17.
3 5 - смешанная дробь8
18.
19. Действительные числа запиши в конспект
Множество рациональных чисел замкнутоотносительно операций сложения, вычитания,
умножения и деления(т.е. эти действия над
рациональными числами дают рациональное
число)
Вместе с тем, например, операция извлечения
квадратного корня требует расширение
понятия числа. Эту потребность удовлетворяют
числа, которые называются иррациональными
2,
3
5,
1
,.... иррациональные числа
7
20.
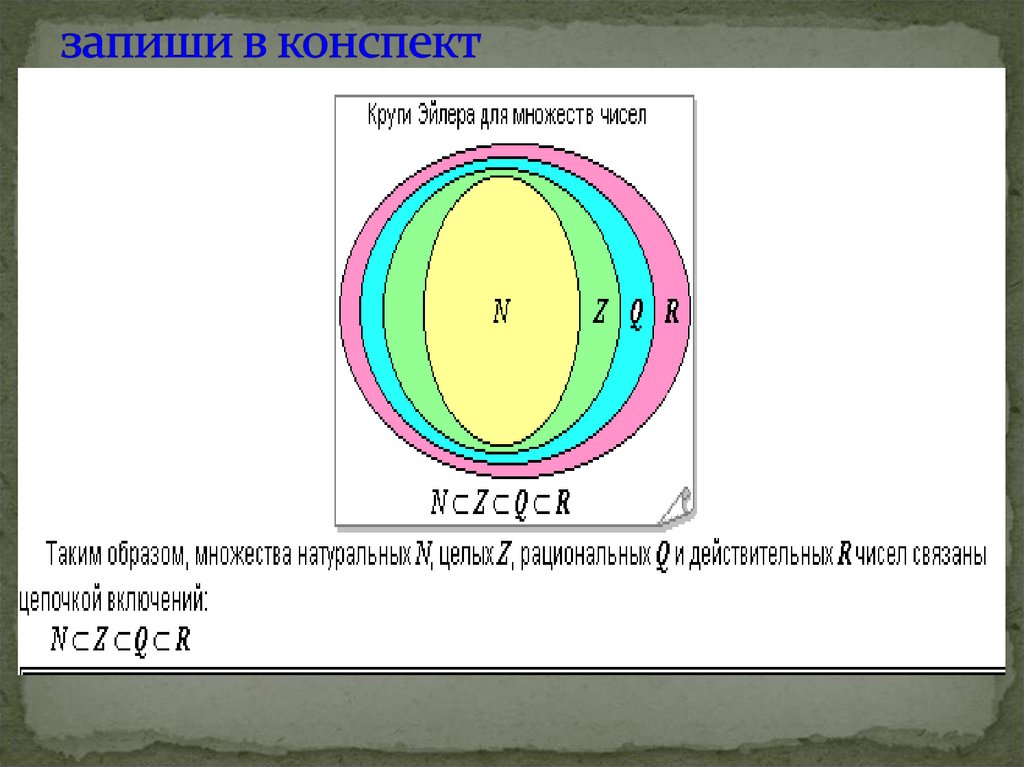
Определение : Множеством действительных чиселназывается объединение множества рациональных
чисел и множества иррациональных чисел.
Обозначение:R
21. запиши в конспект
22. Комплексные числа
Когда появились квадратные уравнения оказалось,что не всегда можно найти его корни.например
уравнение
х 1 0
приводит нас к
2
х 1
которое не имеет
2
корней в действ.числах
23. запиши в конспект
i 1любое комплексно е число
можно записать
2
z a bi _ где _ a; b R
a действительная
b мнимая _ части
комплексно го _ числа
24.
Мнимаяединица
i – начальная буква французского
слова
imaginaire – «мнимый»
25. Например,
3636
36 36
363636
( (( 111))) 36
36
1
6
i
36( (11 )36
1
6
i
1)
36
1
6
i
6i
Сделай сам(запиши в конспект):
900
1
4
12,25
26. Определение 3. запиши в конспект Два комплексных числа называются сопряженными, если они отличаются друг от друга только
27.
28.
29.
30.
31. Домашнее задание
1 реши уравнения2 запиши степени мнимой единицы
32. Решите уравнение запиши в конспект
Решите уравнениеx 4x 5 0
2
x 2 x 17 0
2
x 4 x 13 0
2
x 4x 8 0
2
x 10 x 29 0
2
33.
2 ;3 3 2iiii4342431
2
i
i
(
(
1
1
)
)
i
i
i
;
i
;
2
1
1
;
;
2
1
4
3
3
3
2
2
2
2
2
3
2
i
i
i
i
i
(
i
i
i
(
1
)
i
i
;
4
3
2
i
1
;
4
3
2
i
1
;
iiii332 4
i
i
i
i
i
i
i
i
i
i
(
(
1
1
i
(
(
1
1
)
)
i
i
;
;
i
2
2
3
2
i
i
i
i
i
(
1
i
i
i
i
i
(
ii2ii53i4344i 4 i iiii2i(2ii4i3i3 i 3 i1 ( (() ( i 1 11 1) i))ii)i iii i i i ; i i ;i;i; ;i3 2ii222 2 ( (1( ) 1
iiii5545545i4i iii3444(3443iii
1
)
i
;
3
2
i
i
i
i
(
1
2
2
2
i
1
i
i
;
i
i
i
(
1
)
i
i
i
(
1
i
i
1
1
i
i
i
i
;
;
i
i
i
i
i
(
(
1
1
4
4
3
3
2
2
5
4
2
iiii345i545i 5
i
i
1
i
i
;
i
i
1
i
i
;
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
1
i
i
;
3
3
2
2
4
4
4
i
i
i
(
1
)
1
;
3
2
66565i
54i54i
24
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
i
i
i
1
1
i
i
;
i
;
4
3
i
1
i
i
;
3
6
5
5
2
2
2
5
4
iiii5566i6 4i4ii 5
i
i
i
(
1
i
i
i
i
1
;
i
i
i
i
i
2
i
i
i
i
55 ii
22
i
1
1
;
;
1
1
i
i
i
i
;
;
ii45i6656
i4i4 i5 5ii5 iii11 iiii i ii;i; 2iii222 11;;
i
i
6
i4i7i677676i i i i i5665665 i1 i i i i ii
11 i ii i ; i i ii
;; i i2i225 5 41 4;11;;
i6 1ii iii(
ii 1
iii7 i ii
i ;)ii ii i i 1 1i i;i; 11 i
iiii666767
(
(
1
1
i
i
;
;
5i5i 66 ii
22)) ii
i
i
(
1
i
i
;
7
i
(
1
i
i
;
5i5 i6 6ii6
2)
2)
i
i
i
i
i
i
i
1
1
;
;
i
i
(
1
)
i
7
7
7
1 1;;i
;55ii;;
ii5ii875877i i i i i76767 6i iii i i ii
i i (i(ii (
2 1 1i
)i1)2 )i
ii i16 6
;
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
i
i
i
;
;
i
i
i
i
i
i
1
.
8
7
i
i
1
.
.
8
7
i 77 8 i 66 7 i i i 1;
34. Комплексные числа
Определение 1. Числа видаa + bi,
где a и b – действительные числа,
i – мнимая единица,
называются комплексными.
a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.
35.
VII в.н.э.-квадратный корень из
положительного числа
имеет два значения –
положительное и
отрицательное,
а из отрицательных
чисел квадратные корни
извлечь нельзя:
нет такого числа х,
чтобы
х2 = -9.
36. В XVI веке
в связи с изучениемкубических уравнений
оказалось необходимым
извлекать квадратные корн
из отрицательных чисел.
Первым учёным,
предложившим ввести
числа новой природы,
был Джорж Кордано.
37.
Он предложила а а
Кордано назвал такие величины
“чисто отрицательными” или даже
“софистически отрицательными”,
считая их бесполезными и
стремился не применять их.
38. Название “мнимые числа” ввёл французский математик и философ Р. Декарт
в 1637году
39. один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare (мнимый)
в 1777году





























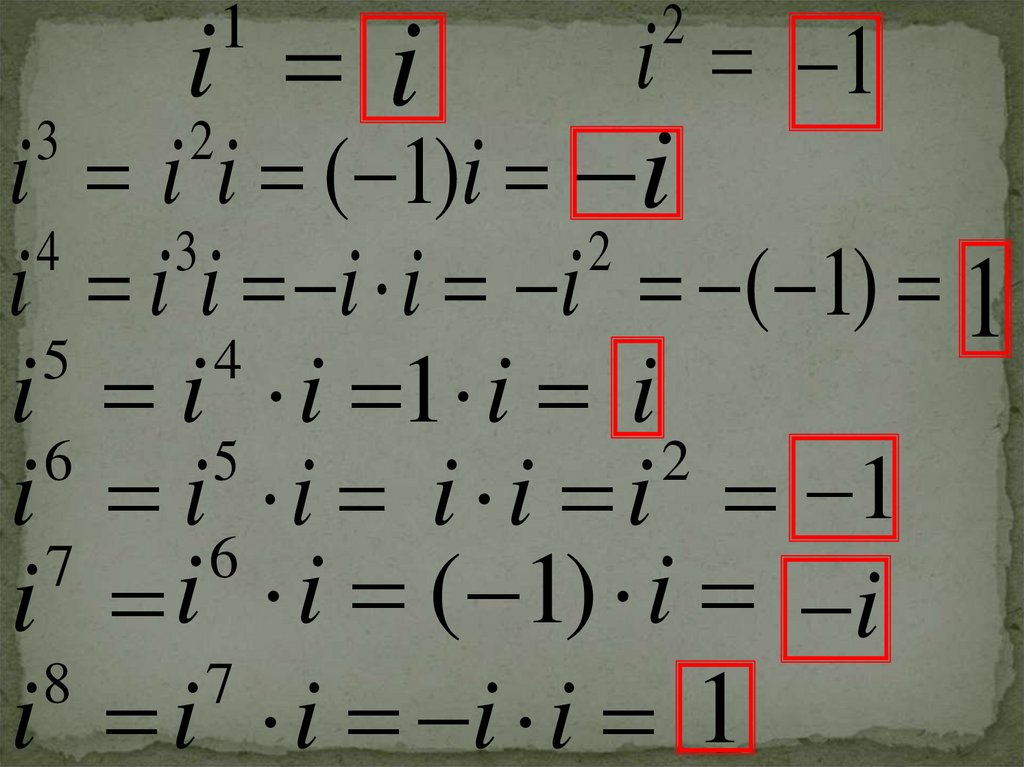






 Математика
Математика








