Работа по графику производной

1.

Работа по графику
производной
Презентация создана учителем математики АЛВС «Динамо СанктПетербург»
Конторовой Е.В.
Использованы задания открытого банка заданий ЕГЭ по математике

2.

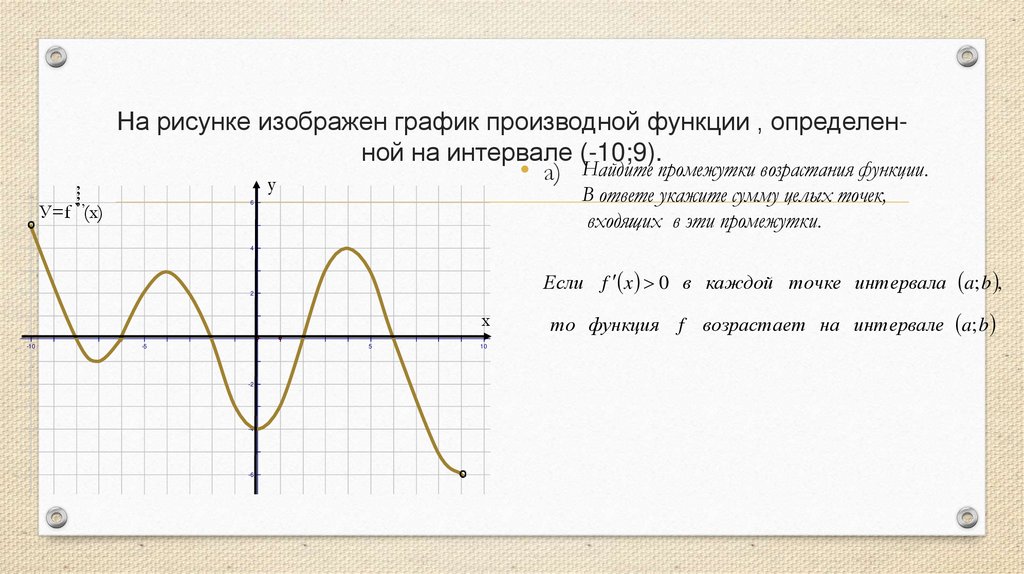
На рисунке изображен график производной функции , определенной на интервале (-10;9).
• а) Найдите промежутки возрастания функции.
у
8
У=f ̀̀̓̓̓̓ (x)
В ответе укажите сумму целых точек,
входящих в эти промежутки.
6
4
Если f x 0 в каждой точке интервала a; b ,
2
х
-10
-5
5
-2
-4
-6
10
то функция f возрастает на интервале a; b
15

3.

На рисунке изображен график производной функции , опредепромежутки возрастания функции.
• а) Найдите
ленной на интервале
(-10;9).
8
У=f ̀̀̓̓̓̓ (x)
6
В ответе укажите сумму целых точек,
входящих в эти промежутки.
у
4
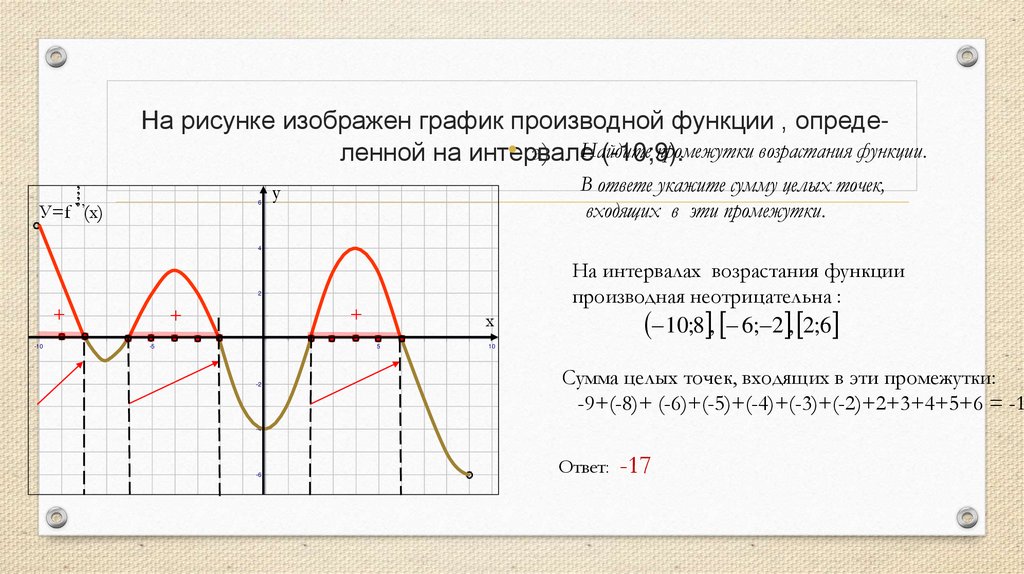
На интервалах возрастания функции
производная неотрицательна :
2
+
-10
+
+
-5
5
-2
10;8 , 6; 2 , 2;6
х
10
15
Сумма целых точек, входящих в эти промежутки:
-9+(-8)+ (-6)+(-5)+(-4)+(-3)+(-2)+2+3+4+5+6 = -17
-4
-6
Ответ: -17

4.

На рисунке изображен график производной функции , опредепромежутки возрастания функции.
• б) Найдите
ленной на интервале
(-10;9).
8
У=f ̀̀̓̓̓̓ (x)
6
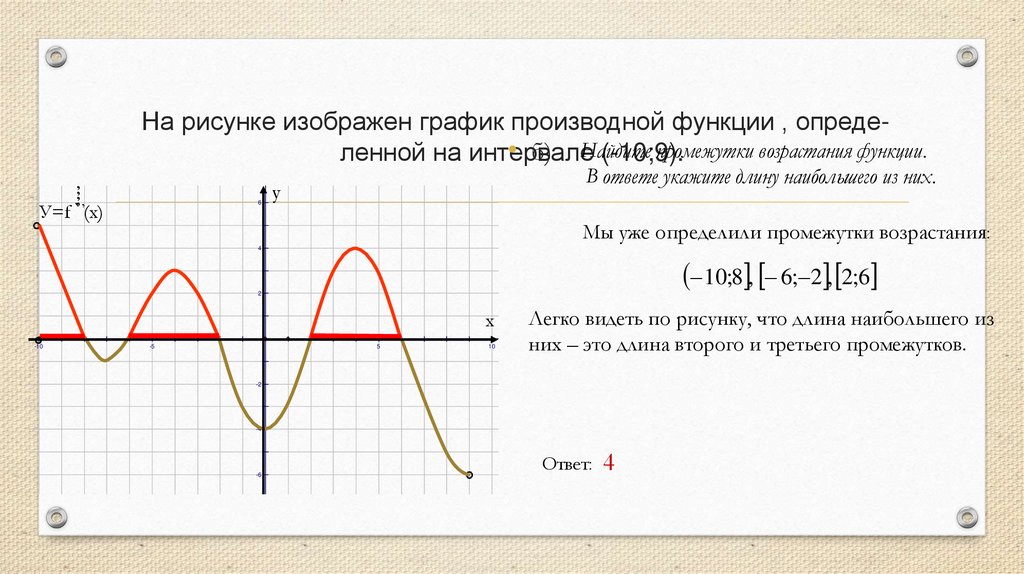
В ответе укажите длину наибольшего из них.
у
Мы уже определили промежутки возрастания:
4
10;8 , 6; 2 , 2;6
2
х
-10
-5
5
10
Легко видеть по рисунку, что длина наибольшего из
них – это длина второго и третьего промежутков.
15
-2
-4
-6
Ответ: 4

5.

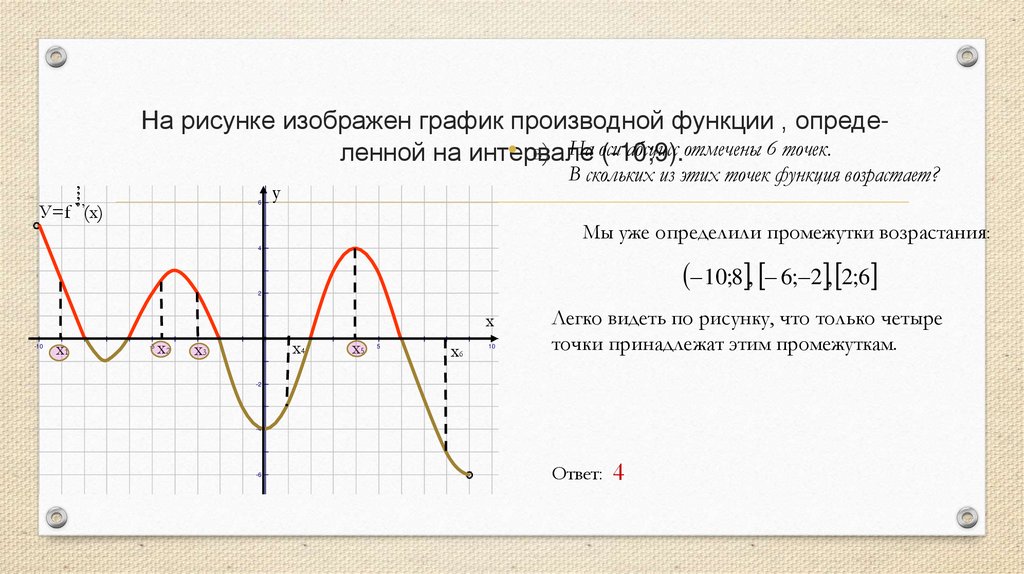
На рисунке изображен график производной функции , опредеабсцисс отмечены 6 точек.
• в) На оси
ленной на интервале
(-10;9).
8
У=f ̀̀̓̓̓̓ (x)
6
В скольких из этих точек функция возрастает?
у
Мы уже определили промежутки возрастания:
4
10;8 , 6; 2 , 2;6
2
х
-10
х1
-5
х2
х4
х3
х5
5
х6
10
Легко видеть по рисунку, что только четыре
точки принадлежат этим промежуткам.
15
-2
-4
-6
Ответ: 4

6.

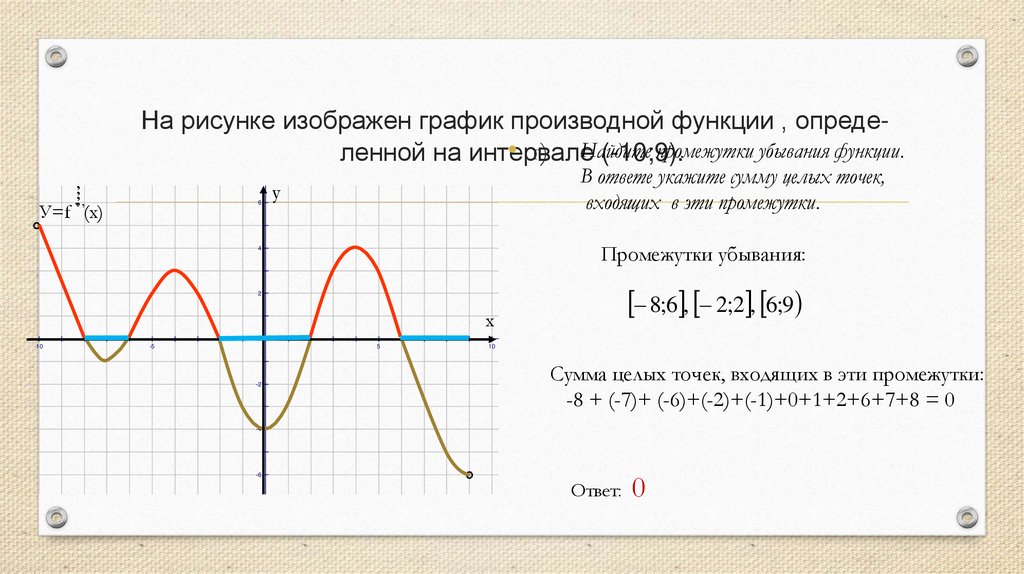
На рисунке изображен график производной функции , опредепромежутки убывания функции.
• г) Найдите
ленной на интервале
(-10;9).
8
У=f ̀̀̓̓̓̓ (x)
6
В ответе укажите сумму целых точек,
входящих в эти промежутки.
у
Промежутки убывания:
4
8;6 , 2;2 , 6;9
2
х
-10
-5
5
-2
10
15
Сумма целых точек, входящих в эти промежутки:
-8 + (-7)+ (-6)+(-2)+(-1)+0+1+2+6+7+8 = 0
-4
-6
Ответ: 0

7.

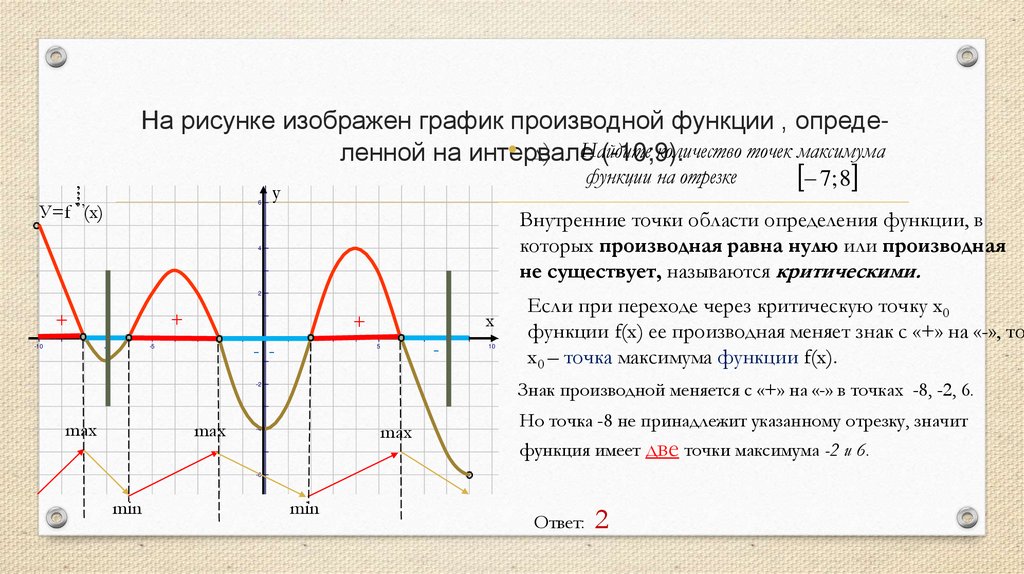
На рисунке изображен график производной функции , опредеколичество точек максимума
• д) Найдите
ленной на интервале
(-10;9).
8
У=f ̀̀̓̓̓̓ (x)
6
функции на отрезке
у
Внутренние точки области определения функции, в
которых производная равна нулю или производная
не существует, называются критическими.
4
2
+
+
-
-10
х
+
- -
-5
-
5
max
10
Если при переходе через критическую точку х0
функции f(x) ее производная меняет знак с «+» на «-», то
х0 – точка максимума функции f(x).
15
Знак производной меняется с «+» на «-» в точках -8, -2, 6.
-2
max
max
-4
Но точка -8 не принадлежит указанному отрезку, значит
функция имеет две точки максимума -2 и 6.
-6
min
7; 8
min
Ответ: 2

8.

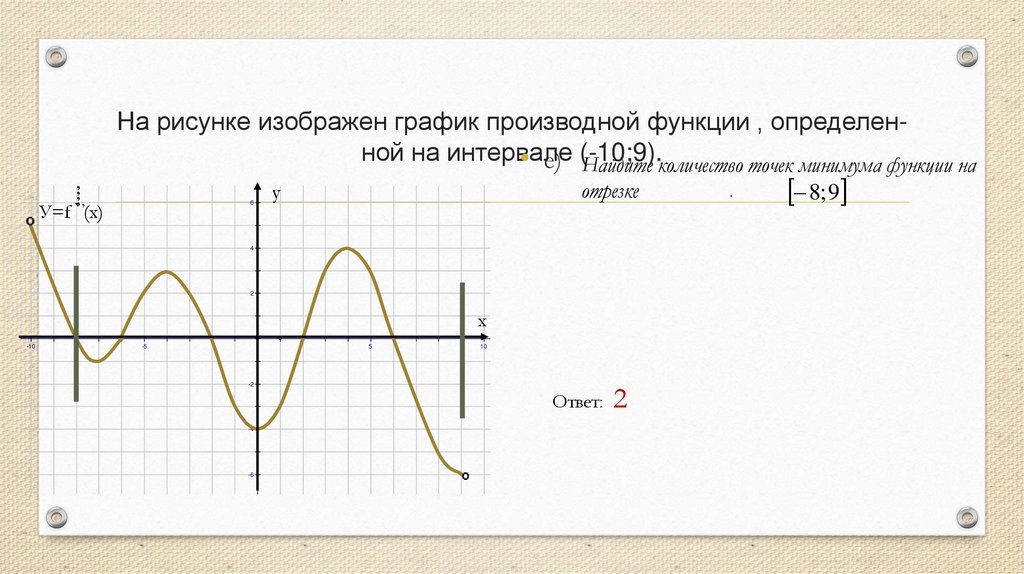
На рисунке изображен график производной функции , определенной на интервале
• е) (-10;9).
Найдите количество точек минимума функции на
8
У=f ̀̀̓̓̓̓ (x)
6
отрезке
у
4
2
х
-10
-5
5
-2
-4
-6
10
15
Ответ: 2
.
8; 9

9.

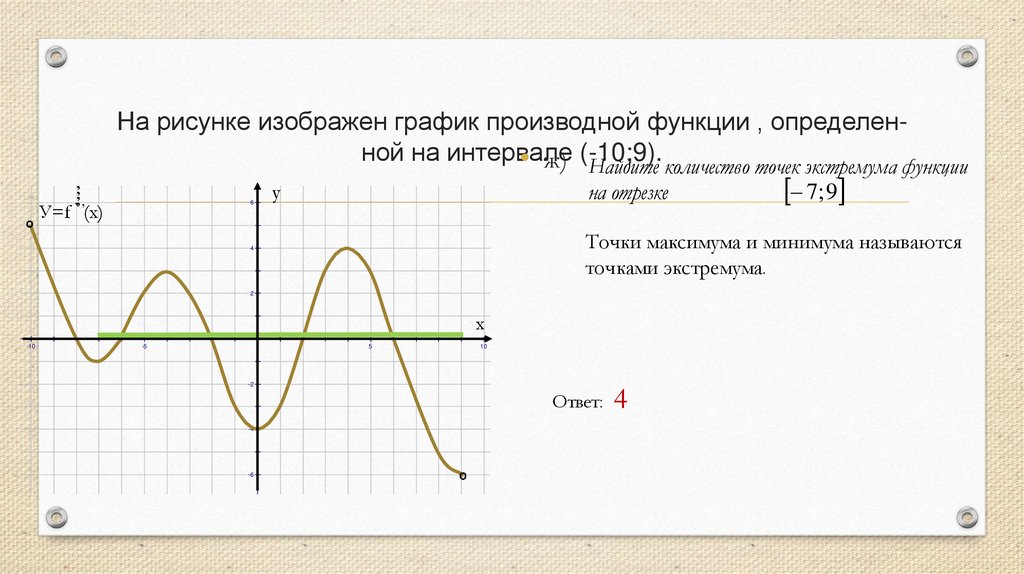
На рисунке изображен график производной функции , определенной на интервале
• ж) (-10;9).
Найдите количество точек экстремума функции
8
У=f ̀̀̓̓̓̓ (x)
6
на отрезке
у
Точки максимума и минимума называются
точками экстремума.
4
2
х
-10
-5
5
-2
-4
-6
7; 9
10
15
Ответ: 4

10.

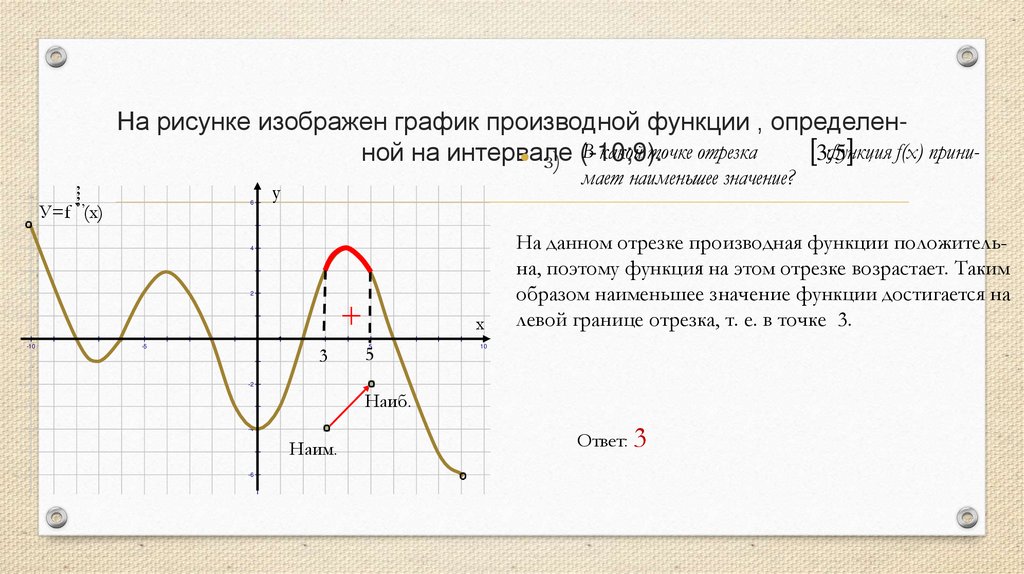
На рисунке изображен график производной функции , определенВ какой точке отрезка
f(x) прини 3функция
; 5
ной на интервале
• з) (-10;9).
8
У=f ̀̀̓̓̓̓ (x)
6
мает наименьшее значение?
у
4
2
+
-10
-5
3
х
5
5
10
На данном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Таким
образом наименьшее значение функции достигается на
левой границе отрезка, т. е. в точке 3.
15
-2
Наиб.
-4
Наим.
-6
Ответ: 3

11.

На рисунке изображен график производной функции , определенной на
интервале (-10;9).
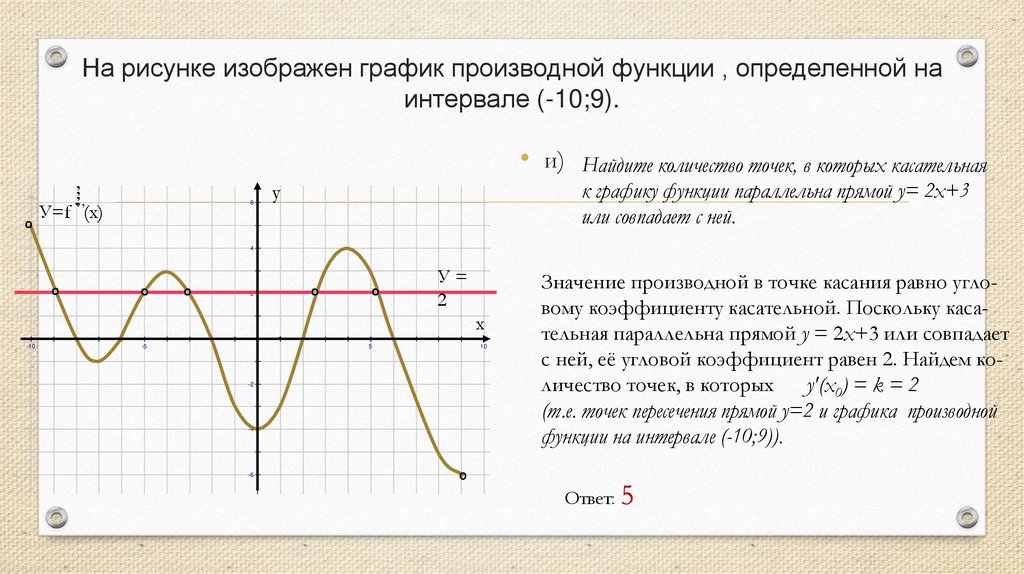
• и) Найдите количество точек, в которых касательная
8
У=f ̀̀̓̓̓̓ (x)
6
к графику функции параллельна прямой у= 2х+3
или совпадает с ней.
у
4
У=
2
2
х
-10
-5
5
-2
-4
10
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = 2x+3 или совпадает
с ней, её угловой коэффициент равен 2. Найдем количество точек, в которых
y'(x0) = k = 2
(т.е. точек пересечения прямой у=2 и графика производной
функции на интервале (-10;9)).
15
-6
Ответ: 5