Линейная алгебра и аналитическая геометрия 1 семестр. Модули

1.

Линейная алгебра
и аналитическая геометрия
1 семестр. Модули
1. Матрицы и определители. Системы линейных
алгебраических уравнений (СЛАУ).
2. Геометрические векторы.
3. Прямая на плоскости. Прямая и плоскость в
пространстве. Кривые второго порядка.
Поверхности второго порядка.
4. Комплексные числа. Многочлены.
1

2.

Линейная алгебра
и аналитическая геометрия
Литература
[1] Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. СПб.: Лань, 2015.
[2] Натансон И.П. Краткий курс высшей математики. -СПб.: Лань, 2009.
[3] Клетеник Д. В. Сборник задач по аналитической геометрии. -СПб.:
Лань, 2011.
[4] Сборник задач по математике для втузов, т. 1. ред. Ефимов А.В и
Поспелов А.С. М.:Физматлит, 2014.
Учебно-методическая литература
[5] Выборнов А.Н., Вегера Ж.Г., Ляшенко В.С. Векторная алгебра и
аналитическая геометрия. -М.: РТУ МИРЭА, 2023.
https://ibc.mirea.ru/books/share/54862/
[6] Баланкина Е.С.Кривые второго порядка. -М.: РТУ МИРЭА, 2023.
https://ibc.mirea.ru/books/share/54609/
[7] Выборнов А.Н., Вегера Ж.Г. Элементы высшей алгебры -М.:
РТУ МИРЭА, 2023. https://ibc.mirea.ru/books/share/54861/
2

3.

Линейная алгебра
и аналитическая геометрия
Модуль 1.
Матрицы и определители
Лекция 1. Матрицы, виды матриц.
Операции над матрицами
3

4.

Матрицы. Виды матриц
a11 a12
a21 a22
Anxm =
a
n1 an 2
a1m
a2 m
anm
Обозначения матриц:
A, B, C ,
Anxm ,
{aij }, {aij }n×m ,
aij
A1xm = ( a11 a12 ... a1m ) - матрица-строка
a11
a
Anx1 = 21 - матрица-столбец
...
a
n1
4

5.

Матрицы
a11 a12
a21 a22
Квадратная матрица Anxn =
a
n1 an 2
a1n
a2 n
ann
Элементы квадратной матрицы, для которых i=j
называются диагональными.
Диагональ матрицы, на которой они находятся, главной диагональю.
5

6.

Матрицы
Квадратная матрица, у которой все элементы, кроме
диагональных, равны 0, называется диагональной:
a11 0
0 a22
0
0
0
0
ann
Единичной матрицей называется диагональная
матрица, у которой элементы, стоящие на главной
диагонали, равны 1:
1 0 ... 0
Enxn = 0 1 ... 0
0 0 ... 1
6

7.

Матрицы
Квадратная матрица называется треугольной,
если все ее элементы, стоящие ниже (или выше)
главной диагонали, равны нулю:
a11 a12
0 a22
A=
0
0
a1n
a2 n
ann
Верхняя треугольная
a11 0
a21 a22
A=
a
n1 an 2
0
0
ann
Нижняя треугольная
7

8.

Операции над матрицами
1. Равенство матриц
Матрица А называется равной матрице В, если они
одинакового размера
и их соответствующие элементы равны.
=
Anxm Bnxm , если ∀i, j ∈ N : 1 ≤ i ≤ n, 1 ≤ j ≤ m
выполнено : aij = bij .
8

9.

Операции над матрицами
2. Транспонирование матриц.
Если элементы каждой строки матрицы А записать
в том же порядке в столбцы матрицы В, то матрица В
называется транспонированной матрицей и
обозначается АТ .
Очевидно, что ( Am× n )T = Bn× m
Пример 1. Дана матрица А, получить матрицу АТ.
Решение:
A
(
)
1 −4
1
0
5
Т
=
,
( А ) 0 1 .
− 4 1 −2
5 −2
9

10.

Операции над матрицами
3. Сложение матриц
Суммой матриц А и В одинаковых размеров
называется матрица С тех же размеров и с элементами
равными
cij = aij + bij для всех i и j: 1 ≤ i ≤ n, 1 ≤ j ≤ m.
1 −1
−1 11
0 − 2 , B =
−2 0 .
Пример 2. Найти С=А+В, если A =
−1 0
1 1
Решение:
1 − 1 −1 11 0 10
C = A + B = 0 − 2 + −2 0 = −2 − 2 .
−1 0 1 1 0 1
10

11.

Операции над матрицами
4. Умножение матрицы на число
Произведением матрицы А любой размерности на
число k называется матрица С той же размерности и с
элементами равными
cij
kaij для всех i и j: 1 ≤ i ≤ n, 1 ≤ j ≤ m.
1 −1
Пример 3. Найти С=2А, если=
A 0 − 2 .
−1 0
Решение:
− 2
1 −1 2
C = 2 A = 2 0 − 2 = 0 − 4 .
0
−1 0 −2
11

12.

Операции над матрицами
5. Умножение матриц
Произведением матрицы Аnxm на матрицу Вmxk
называется матрица Сnxk= A ⋅ B с элементами,
равными
cij =
ai1 ⋅ b1 j + ai 2 ⋅ b2 j + ... +aim ⋅ bmj
для всех i и j: 1 ≤ i ≤ n, 1 ≤ j ≤ k .
12

13.

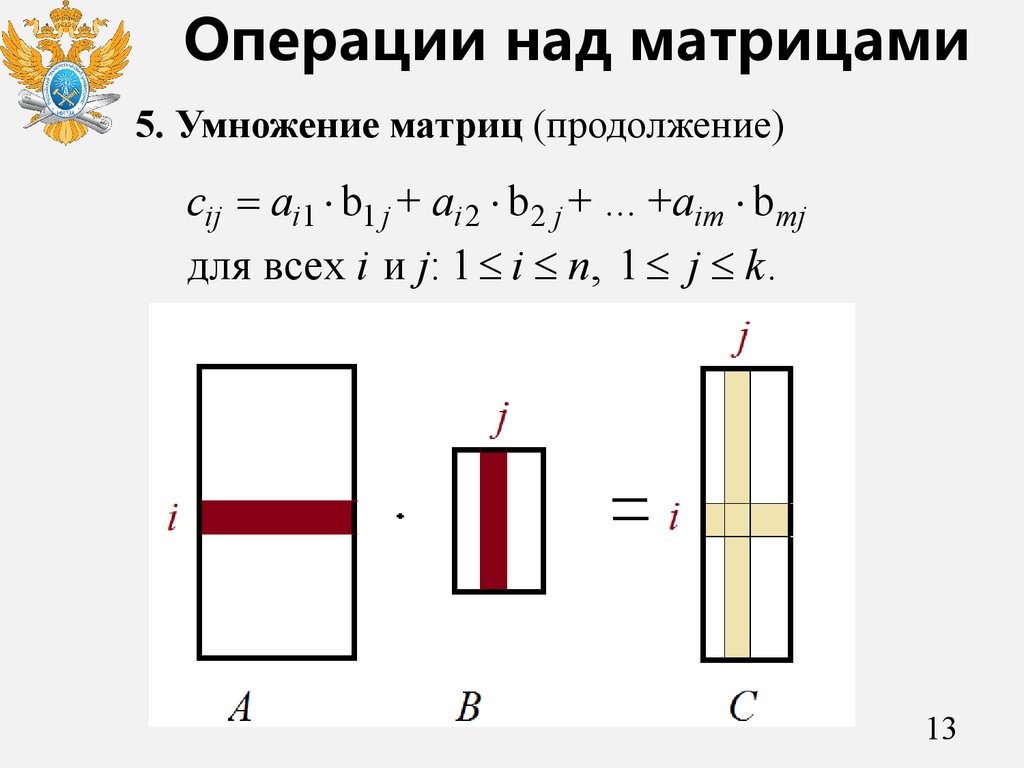
Операции над матрицами
5. Умножение матриц (продолжение)
cij =
ai1 ⋅ b1 j + ai 2 ⋅ b2 j + ... +aim ⋅ bmj
для всех i и j: 1 ≤ i ≤ n, 1 ≤ j ≤ k .
13

14.

Операции над матрицами
5. Умножение матриц (продолжение)
cij =
ai1 ⋅ b1 j + ai 2 ⋅ b2 j + ... +aim ⋅ bmj
для всех i и j: 1 ≤ i ≤ n, 1 ≤ j ≤ k .
Пример 4. Найти С= A ⋅ B, если
1 4
,
А 2× 2 =
5 − 2
Решение:
c11
A2×2 ⋅ B2×3 = C2×3 =
c21
5
B 2× 3 =
0
4 − 1
2 3
c12
c22
(
)
c13
5
12
11
=
.
c23 25 16 −11
14

15.

Операции над матрицами
Пример 5. Найти С= A ⋅ B, если
1 -1
=
А3×2 =
0 1 ,
B2×3
1
0
(
)
5 4 −1
0 2 3
Решение:
5 2 -4
A3×2 ⋅ B2×3 = C3×3 = 0 2 3 .
5 4 -1
15

16.

Операции над матрицами
Пример 6. Найти D= B ⋅ A , если
B2×3
=
(
1 -1
5 4 -1 ,
А3×2 0 1
=
0 2 3
1
0
)
Решение:
4 -1
B2×3 ⋅ A3×2 = D2×2 =
.
3 2
16

17.

Операции над матрицами
6. Возведение матрицы в степень
n-ой степенью матрицы A называется такая
матрица An , которая получена умножением матрицы А
саму на себя n раз:
n
A = A ⋅ A ⋅... ⋅ A
n − раз
17

18.

Свойства операций над матрицами
Свойства операции сложения матриц:
1. A+ B = B + A – коммутативность.
2. ( A + B ) + C = A + ( B + C )
– ассоциативность.
3. α ⋅ ( A + B) = α ⋅ A + α ⋅ B
– дистрибутивность
относительно сложения матриц.
4. (α + β) ⋅ A = α ⋅ A + β ⋅ A – дистрибутивность
относительно сложения чисел.
Ο – существует противоположная
5. ∃ (-A) : A+(-A) =
матрица (-А) и нулевая матрица Ο.
18

19.

Свойства операций над матрицами
Свойства операции умножения матрицы на число:
1. (α ⋅ β) ⋅ A = α ⋅ (β ⋅ A) = β ⋅ (α ⋅ A) – ассоциативность.
O – существование нулевой матрицы.
2. 0 ⋅ A =
19

20.

Свойства операций над матрицами
Свойства операции транспонирования матриц
( )
1. AT
T
T
3. ( A + B ) = AT + BT .
= A.
T
T
αAT .
2. ( αA) =
BT AT .
4. ( AB ) =
T
, ( AB )kxn
Доказательство 4: Пусть Anxm , Bmxk тогда ( AB )
nxk
AmT xn , BkTxm , тогда BkTxm ⋅ AmT xn =
Fkxn
T
=
D AB, =
C D ; C
=
D=
ij
ji
(
T
T
)
=
B A
m
m
∑ A jl Bli
l =1
m
∑=
( B ) ( A ) ∑ Bli Ajl
T
T
ij
il
lj
=l 1 =l 1
(
⇒ BT AT
)
ij
T
=
( AB )ij
20

21.

Свойства операций над матрицами
Свойства операции умножения матриц
1. A ⋅ B ≠ B ⋅ A ̶ операция умножения матриц
некоммутативна.
2. A ⋅ E = E ⋅ A = A ̶ существование единичной матрицы
3. ( A + B ) ⋅ C = A ⋅ C + B ⋅ C
̶ дистрибутивность.
4. A ⋅ ( B + C ) = A ⋅ B + A ⋅ C
̶ дистрибутивность.
5. A ⋅ B ⋅ C = ( A ⋅ B ) ⋅ C = A ⋅ ( B ⋅ C )
̶ ассоциативность.
21

22.

Свойства операций над матрицами
2. A ⋅ E = E ⋅ A = A
Доказательство: Пусть
C
a11 a12
a21 a22
a
n1 an 2
Anxm , Emxm тогда C = ( AE )nxm ;
a1m 1 0 ... 0
a2 m 0 1 ... 0
⋅
,
... ... ... ...
anm 0 0 ... 1
cij = ai1 ⋅ e1 j + ai 2 ⋅ e2 j + ... +aim ⋅ emj =aij ⋅ e jj = aij .
22

23.

Свойства операций над матрицами
5. A ⋅ B ⋅ C = ( A ⋅ B ) ⋅ C = A ⋅ ( B ⋅ C )
Доказательство: Пусть Anxm , Bmxk
тогда ( AB )nxk ;
( А( B ⋅ C ) )nxs .
( AB )nxk , тогда Ckxs , а D = ( ( AB ) С )nxs . ( B ⋅ C )mxs , тогда F =
k
d ij = ∑ ( AB )il clj ,
l =1
m
f ij = ∑ aip ( BC ) pj ,
p =1
k m
d ij ∑ ∑ aip bpl ⋅ clj .
aip bpl ,
( AB )il = ∑=
=p 1
=l 1
p =1
m
k
( BC ) pj = ∑ bpl clj ,
l =1
k m
m
k
f ij = ∑ aip ∑ bpl clj .
=
p 1=
l 1
k m
d ij ∑ ∑ aip bpl =
=
⋅ clj ∑ ∑ aip ⋅ bpl=
⋅ clj f ij
p 1
=l 1 =p 1
=l 1 =
(
)
23

24.

Матричные уравнения
Пример 7. Решить матричное уравнение:
−2 0
5 − 3
2⋅
+ 3⋅ X =
.
2 − 1
−5 1
Решение:
−4 0
5 − 3
4 − 2 + 3⋅ X =
−5 1 ,
5 − 3 −4 0
=
3⋅ X
−
,
−5 1 4 − 2
1 9 − 3
,
X=
⋅
3 −9 3
9 − 3
3⋅ X =
−9 3 ,
3 − 1
X=
−3 1 .
24

25.

Матричные уравнения
Пример 8. Решить матричное уравнение:
5 − 1 −2 3
4⋅ X =
−5 1 . 2 − 1
−12 16
4⋅ X =
12 − 16
−3 4
X =
.
3 − 4
25

26.

Матричные уравнения
Пример 9. Решить матричное уравнение:
−2 0
5 − 3
2 − 1 ⋅ X =
−5 1 .
Пример 10. Решить матричное уравнение:
−2 0
5 − 3
X −
⋅X +
=0.
2 − 1
−5 1
2
26

27.

Линейная алгебра
и аналитическая геометрия
Модуль 1.
Матрицы и определители
Определители.
Основные свойства определителей.
Вычисление определителей
2727

28.

Определители
a11 a12
Квадратная матрица Anxn = a21 a22
a
n1 an 2
det A
=
∑
по всем
подстановкам
a1n
a2 n
ann
a1k1 ⋅ a2 k2 ⋅ ... ⋅ ankn ⋅ ( −1)
σ
Определителем квадратной матрицы размерами nxn
называется число, равное сумме n! слагаемых, каждое
из которых представляет собой произведение элементов
этой матрицы, взятых по одному из каждой строчки и из
каждого столбца со знаком «+», если подстановка,
образованная индексами элементов, входящих в
произведение, четна и со знаком «-», если нечетна. 28

29.

Перестановки
Перестановкой порядка n называется набор
чисел 1, 2, …, n, переставленных в определенном
порядке.
Обозначение: Pn = ( i1 , i2 , i3 ,..., in ).
Например: пусть n=2.
Возможны 2 перестановки:
=
P2 (1,
=
2 ) , P2 ( 2, 1) ;
(1, 2):=
i1 1,=
i2 2
(2, 1):
i1 2,=
i2 1
=
Если для какой-нибудь пары ( ik , il ) окажется, что при
k < l обнаружится, что ik > il , то будем говорить, что
этой паре в перестановке соответствует инверсия.
В зависимости от четности количества инверсий
перестановку называют четной или нечетной. 29

30.

Перестановки
=
n 3;=
P3
(1, 2,3)
Возможные перестановки 123 132 213 231 312 321
Рассмотрим перестановку 132 :
пара (1,3) : большее число 3 правее меньшего числа 1, инверсии нет;
пара (1,2) : большее число 2 правее меньшего числа 1, инверсии нет;
пара (3,2) : меньшее число 2 правее большего числа 3, инверсия!!!
Перестановка 132 нечетная.
P6 = ( 5,6, 4, 2,3,1)
30

31.

Перестановки
Транспозицией называется операция над
перестановкой, в которой два любых элемента
меняются местами.
Лемма. Всякая транспозиция меняет четность
перестановки.
( i1, i2 , i3 ,..., ik , ik +1,...in ) → ( i1, i2 , i3 ,..., ik +1, ik ,...in )
( i1, i2 , i3 , i4 , i5 , i6 ,...., in )
( i1, i2 , i4 , i5 , i6 , i3 ,...., in ) Всего 6-3=3 транспозиция; ik и il : ( l − k )
(l − k ) − 1
( i1, i2 , i6 , i4 , i5 , i3 ,...., in ) Всего 2 транспозиции;
(
Общее число транспозиций: 2 l − k
) − 1, четность перестановки меняется.
31

32.

Подстановки
Из двух перестановок ( i1 , i2 , i3 ,..., in ) и ( j1 , j2 , j3 ,..., jn )
одних и тех же чисел 1, 2, 3, …, n можно составить
новый объект
i1 i2 i3 ... in
σ
− подстановка.
j1 j2 j3 ... jn
Подстановкой называется взаимно-однозначное
отображение множества, состоящего из n чисел на
себя.
Подстановку называют четной, если перестановки,
из которых она состоит имеют одинаковую четность,
и нечетной в противоположном случае.
1 2 3
1 3 2
σ
− ?
σ
− четная подст. =
3 2 1
1 2 3
32

33.

Подстановки
Транспозицией подстановки называют любую
перестановку ее столбцов.
Лемма. Транспозиция подстановки не меняет ее
четность.
1 2 3 ... n
σ
− подстановка.
j1 j2 j3 ... jn
Для четной подстановки σ - ε ( σ ) =1.
Для нечетной подстановки σ - ε ( σ ) =−1.
=
det A
∑
по всем
подстановкам
a1k1 ⋅ a2 k2 ⋅ ... ⋅ ankn ⋅ ε ( σ )
33

34.

Определители
Мономом называется произведение n элементов
матрицы А, в которое входит по одному элементу
из каждой строки и каждого столбца.
Например:
a11 a12
=
A
, a11 ⋅ a22 , a12 ⋅ a21
a21 a22
(
)
a11 a12 a13
A = a21 a22 a23 , a11a22 a33 , a11a23a32
a31 a32 a33
34

35.

Определители
Пример 1: Указать мономы матрицы А, отличные от 0.
2 −1 10 2
0
1
3
7
A=
0 0 3 1
0 0 0 −1
2 ⋅ 1 ⋅ 3 ⋅ ( −1) =−6.
35

36.

Определители
Определителем квадратной матрицы размерами nxn
называется число, равное сумме всевозможных
мономов этой матрицы, взятых со знаком «+», если
подстановка, образованная индексами элементов,
входящих в произведение, четна и со знаком «-», если
нечетна.
A
(
)
a11 a12
, a11 ⋅ a22 , a12 ⋅ a21.
a21 a22
det A =
a11 a12
= a11 ⋅ a22 − a12 ⋅ a21.
a21 a22
36

37.

Определители
a11 a12 a13
A = a21 a22 a23 ,
a31 a32 a33
a11a22 a33 , a11a23a32 , a12 a23a31 ,
a12 a21a33 , a13a21a32 , a13a22 a31.
a11 a12 a13
a23
det A a=
21 a22
a31 a32 a33
a11a22 a33 + a12 a23a31 + a13a21a32 −
− a13a22 a31 − a12 a21a33 − a11a23a32 .
37

38.

Определители 3-его порядка
Правило Саррюса
det A = a11a22 a33 + a12 a23a31 + a13a21a32 −
− a13a22 a31 − a12 a21a33 − a11a23a32 .
a11 a12 a13
a21 a22 a23
a31 a32 a33
38

39.

Определители
Пример 2: Вычислить определитель матрицы А.
2 −1 10 2
0
1
3
7
A=
0 0 3 1
0 0 0 −1
2 ⋅ 1 ⋅ 3 ⋅ ( −1) =−6.
a11a22 a33a44
i: 1 2 3 4
нет инверсий! ⇒ "+", ε=1
j: 1 2 3 4
det A = −6.
39

40.

Определители
Пример 3: Вычислить определитель матрицы А.
(
)
5
3
−
A=
−1 2
det A = 5 −3 = 5 ⋅ 2 − ( −1) ⋅ ( −3) = 7.
−1 2
40

41.

Определители
Пример 4: Вычислить определитель матрицы А.
3 0 −1
A = 2 1 2
0 5 1
3 0 −1
det A 2=
1 2
0 5 1
= 3 ⋅ 1 ⋅ 1 + 0 ⋅ 2 ⋅ 0 + ( −1) ⋅ 2 ⋅ 5 − ( ( −1) ⋅ 1 ⋅ 0 + 0 ⋅ 2 ⋅ 1 + 3 ⋅ 2 ⋅ 5) =
3 − 10 − ( 3 ⋅ 2 ⋅ 5) =−7 − 30 =−37.
41

42.

Свойства определителей
det A
=
∑
по всем
подстановкам
1. det A=det AT.
a1k1 ⋅ a2 k2 ⋅ ... ⋅ ankn ⋅ ε ( σ )
a11 a12
a21 a22
an1 an 2
a1n
a2 n
ann
ai1 j1 ⋅ ai2 j2 ⋅ ... ⋅ ain jn :
i1 i2 i3 i4 ... in
j j j j ... j
n
1 2 3 4
T
T
T
a j1i1 ⋅ a j2i2 ⋅ ... ⋅ a jnin :
j1 j2 j3 j4 ... jn
i i i i ... i
n
1 2 3 4
42

43.

Свойства определителей
2. Если в определителе поменять местами две
строки (два столбца), то знак определителя
поменяется на противоположный.
a11 a12 ....a1k ....a1l ... a1n
a21 a22 ....a2 k ...a2l ... a2 n
.......................................
...............ai1k ..................
........................ai2l ...........
an1 an 2 ... ank ...anl ... ann
a11 a12 .................... a1n
a21 a22 .................... a2 n
........................................
........................ai1l ...........
...............ai2 k .....................
an1 an 2 .................... ann
...ai1k ⋅ ... ⋅ ai2l ...
...ai1l ⋅ ... ⋅ ai2 k ...
1 2 ... i1.... i2 ... in
j j ... k .... l ... j
n
1 2
1 2 ... i1.... i2 ... in
j j ... l.... k ... j
n
1 2
43

44.

Свойства определителей
2. Если в определителе поменять местами две
строки (два столбца), то знак определителя
поменяется на противоположный.
Пример 1.
det A =
a11 a12
= a11 ⋅ a22 − a12 ⋅ a21 ,
a21 a22
det A′ =
a12
a22
a11
= a12 ⋅ a21 − a11 ⋅ a22 .
a21
44

45.

Свойства определителей
3. Если квадратная матрица имеет два одинаковых
столбца (строки), то ее определитель равен 0.
a12
a
A = 22
a
n2
a12
a22
an 2
a1n
a2 n
ann
a12
a
B = 22
a
n2
a12
a22
an 2
a1n
a2 n
ann
det A = det B,
det B = − det A,
det A = − det A,
det A = 0.
45

46.

Свойства определителей
4. Если квадратная матрица имеет ряд, состоящий из
нулей, то ее определитель равен 0.
a11 0 a1n
a21 0 a2 n
= ai11 ⋅ 0 ⋅ ai3 3 ...ain n +a j11 ⋅ 0 ⋅ a j3 3 ...a jn n + ... = 0.
an1 0 ann
46

47.

Свойства определителей
5.Умножение всех элементов ряда квадратной матрицы
на число, эквивалентно умножению определителя
на это число.
a11 λa12
a21 λa22
an1 λan 2
a1n
a2 n a
=
1i1 λa2i2 a3i3 ...anin +a1 j1 λa2 j2 a3 j3 ...anjn + ... =
ann
(
)
(
(
)
)
=
λ a1i1 a2i2 a3i3 ...anin +a1 j1 a2 j2 a3 j3 ...anjn + ... =
a11 a12
a
a22
= λ 21
an1 an 2
a1n
a2 n
.
ann
47

48.

Свойства определителей
6. Если два ряда квадратной матрицы пропорциональны,
то ее определитель равен 0.
a11 λa11
a21 λa21
an1 λan1
a1n
a11 a11 a1n
a
a21 a2 n
a2 n
=
λ 21
=
0.
ann
an1 an1 ann
48

49.

Свойства определителей
7. Если каждый элемент некоторого ряда квадратной
матрицы представить в виде суммы двух слагаемых, то
определитель этой матрицы равен сумме двух
определителей матриц, все элементы которых, кроме
элементов выделенного ряда, те же, что у исходной
матрицы, а на месте выделенного ряда у первой
матрицы располагается ряд из первых слагаемых, а у
второй – ряд из вторых слагаемых.
a11 a12 + a 12
a21 a22 + a 22
an1 an 2 + a n 2
a1n
a2 n
ann
49

50.

Свойства определителей
(
a11 a12 + a 12
a21 a22 + a 22
an1 an 2 + a n 2
)
a1n
a2 n
=
ann
(
)
=
ε1a1i1 a2i2 + a 2i2 a3i3 ...anin +ε2 a1 j1 a2 j2 + a 2 j2 a3 j3 ...anjn + ... =
(
) (
)
= ε1a1i1 a2i2 a3i3 ...anin +ε2 a1 j1 a2 j2 a3 j3 ...anjn + ... + ε1a1i1 a 2i2 a3i3 ...anin +ε2 a1 j1 a 2 j2 a3 j3 ...anjn + ... =
a11 a12
a21 a22
an1 an 2
a1n a11 a 12
a2 n a21 a 22
+
ann an1 a n 2
a1n
a2 n
.
ann
50

51.

Свойства определителей
a11 a12
a
a22
A = 21
a
n1 an 2
a1n
a2 n
ann
Линейная комбинация столбцов матрицы есть столбец:
b1 λ a + λ a +
b λ1a11 + λ 2a12 +
21
2 22
2 = 1
...
b λ1an1 + λ 2 an 2 +
n
λ n a1n
λ n a2 n
λ n ann
51

52.

Свойства определителей
8. Если к столбцу (строке) матрицы прибавить
линейную комбинацию остальных столбцов
(строчек), то ее определитель не изменится.
a11 a12
a
a22
A = 21
a
n1 an 2
a1n
a2 n
ann
a11 + λ1a12
a21 + λ1a22
an1 + λ1an 2
a11 a12
a21 a22
an1 an 2
a12 a1n
a22 a2 n
=
an 2 ann
a1n λ1a12
a2 n λ1a22
+
ann λ1an 2
a12
a22
an 2
0
a1n
a2 n
ann
52

53.

Свойства определителей
9. Если столбец (строка) матрицы есть линейная
комбинация остальных столбцов (строчек), то ее
определитель равен 0.
λ 2 a12 + λ 3a13
λ 2 a22 + λ 3a23
λ 2 a n 2 + λ 3a n 3
a12
a22
an 2
λ 2 a12
λ a
=2 22
λ 2 an 2
a1n λ 3a13
a2 n λ 3a23
+
ann λ 3an 3
a12
a22
an 2
a1n
a2 n
=
ann
a12
a22
an 2
a13 a1n
a23 a2 n
0
=
an 3 ann
53

54.

Свойства определителей
10. Определитель матрицы есть линейная
однородная функция элементов фиксированного
ряда.
∑
det A
=
по всем
подстановкам
det A
n
a1k1 ⋅ a2 k2 ⋅ ... ⋅ ankn ⋅ ε ( σ )
n
=
aij Aij ,
det A ∑ aij Aij .
∑
j 1 =i 1
54

55.

Свойства определителей
det A
n
n
=
aij Aij ,
det A ∑ aij Aij .
∑
j 1 =i 1
a11 a12 a13
a23
det A a=
21 a22
a31 a32 a33
a11a22 a33 + a12 a23a31 + a13a21a32 −
− a13a22 a31 − a12 a21a33 − a11a23a32 =
= a11 ( a22 a33 − a23a32 ) + a12 ( a23a31 − a21a33 ) + a13 ( a21a32 − a22 a31 )
55

56.

Свойства определителей
Миноры и алгебраические
дополнения
a11 a12 ... a1 j ... a1n
a a ... a ... a
2j
2n
21 22
... ... ... ... ...
A=
ai1 ai 2 ... aij ... ain
... ...
... ... ...
an1 an 2 ... anj ... ann
M ij - минор, соответствующий элементу aij
Aij =
det=
A
n
i+ j
( −1)
M ij .
n
i+ j
Aij ∑ ( −1)
∑ aij =
=j 1 =j 1
aij M ij
56

57.

Свойства определителей
a11 a12 a13
=
det A a=
a23
21 a22
a31 a32 a33
a11 ( a22 a33 − a23a32 ) + a12 ( a23a31 − a21a33 ) + a13 ( a21a32 − a22 a31 ) =
a22 a23
a21 a23
a21 a22
= a11
− a12
+ a13
.
a31 a32
a32 a33
a31 a33
57

58.

Методы вычисления определителей
∑
=
det A
по всем
подстановкам
n
a1k1 ⋅ a2 k2 ⋅ ... ⋅ ankn ⋅ ε ( σ )
det A = ∑ aij Aij ,
j =1
Aij =
i+ j
( −1)
M ij .
a11 a12 ... a1 j ... a1n
a21 a22 ... a2 j ... a2 n
... ... ... ... ...
ai1 ai 2 ... aij ... ain
... ... ...
... ...
an1 an 2 ... anj ... ann
M ij - минор, соответствующий элементу aij
58

59.

Методы вычисления определителей
det A
=
∑
по всем
подстановкам
a1k1 ⋅ a2 k2 ⋅ ... ⋅ ankn ⋅ ε ( σ )
Пример 1. Вычислить определитель матрицы:
a11 0
0 a22
0
0
0 det=
A a11a22 ⋅ ... ⋅ ann ⋅ ε (=
σ ) a11a22 ⋅ ... ⋅ ann .
0
... n
σ 1 2=
1 2 ... n - четная подстановка, ε ( σ ) 1
ann
Пример 2. Вычислить определитель матрицы:
det A a1n a2 n −1 ⋅ ... ⋅ an1 ⋅ ε ( σ )
0
a1n =
0 ...
0 ... a2 n −1 0
...
...
... σ = 1 2 ... n
a
n n − 1 ... 1
...
0
0
n1
n ( n − 1)
σ = ( n − 1) + ( n − 2 ) + ( n − 3) + ... + 1 =
, ε ( σ ) = ( −1)n ( n −1) 2
2
det A =a1n a2 n −1 ⋅ ... ⋅ an1 ⋅ ε ( σ ) =( −1)n ( n −1) 2 a1n a2 n −1 ⋅ ... ⋅ an1.
59

60.

Методы вычисления определителей
det A
=
∑
по всем
подстановкам
a11 a12
0 a22
A =
0
0
ak11 ⋅ ak2 2 ⋅ ... ⋅ akn n ⋅ ε ( σ )
a11 0
a
a22
A = 21
a
n1 an 2
a1n
a2 n
ann
0
0
ann
det=
A a11a22 ⋅ ... ⋅ ann .
Пример 3. Вычислить определитель матрицы:
−1
A= 6
11
−2
0 0 0 =
det A a11a22 a33a44 ⋅ ε ( σ ) ,
1 0 0
2 3 4
0=
3 0 σ 1=
, σ 0, ε ( σ ) =1,
7 8 −1
1 2 3 4
det A = ( −1) ⋅ 1 ⋅ 3 ⋅ ( −1) = 3.
60

61.

Методы вычисления определителей
=
det A
∑
по всем
подстановкам
ankn ⋅ an −1kn −1 ⋅ ... ⋅ a2 k2 ⋅ a1k1 ⋅ ε ( σ )
Пример 4. Вычислить определитель матрицы:
−8 11 =
4
−1
det A a41a32 a23a14 ⋅ ε ( σ ) ,
6
1
1
0
A=
3 2 1
0 0 σ 4=
11 −7 11=
−2
1 2 3 4 , σ 6, ε ( σ ) =1,
0
0
0
det A = ( −2 ) ⋅ ( −7 11) ⋅ 1 ⋅ 11 = 14.
61

62.

Методы вычисления определителей
n
det A = ∑ aij Aij ,
Aij =
i+ j
( −1)
j =1
Пример 5. Вычислить определитель матрицы:
M ij .
4
−8 11
−1
1
1 0
A= 6
11 −7 11 0 0
−2
0
0
0
4
−1
−8 11
n
6
1
1
0
= ∑ a4=
A4 j a=
A41
det A
41
j
11 −7 11 0 0 j =1
−2
0
0 0
−8 11
4
1 = 14
= ( −2) ⋅ ( −1)4 +1 ⋅ 1
1 0 = 2 ⋅ 11 ⋅ ( −1)1+ 3 ⋅ 1
−7 11 0
−7 11 0 0
62

63.

Методы вычисления определителей
det A
n
n
=
aij Aij ,
det A ∑ aij Aij .
∑
j 1 =i 1
Пример 6. Вычислить определитель матрицы:
−1 4 −1 7
A= 1 1 1 2
1 − 2 1 −3
−1 3 4 −2
−1 4 −1 7
−1 4 −1 7
1
1 1 2
0 5 0 9
=
=
1 −2 1 −3
0 2 0 4
−1 3 4 −2
0 −1 5 −9
det A
1+1
= ( −1) ⋅ ( −1)
5 0 9
⋅ 2 0 4 = ( −1) ⋅ 5 ⋅ ( −1)3+ 2 ⋅ 5 9 = 5 ⋅ ( 20 − 18 ) = 10.
2 4
−1 5 −9
63

64.

Свойства определителей
11) Определитель произведения двух матриц
An×n и Bn×n равен произведению их определителей
det ( A ⋅ B
=
) det ( A) ⋅ det ( B ) .
64

65.

Линейная алгебра
и аналитическая геометрия
Модуль 1.
Матрицы и определители
Метод Крамера решения СЛАУ
Обратная матрица
Решение СЛАУ с помощью обратной матрицы
65

66.

Метод Крамера решения СЛАУ
b1 ,
a11 x1 + a12 x2 + ... + a1m xm =
a x + a x + ... + a x =
b2 ,
21 1
22 2
2m m
...
bn .
an1 x1 + an 2 x2 + ... + anm xm =
a11 a12
a
a22
=
An×n 21
a
n1 an 2
a11 a12
a21 a22
a
n1 an 2
a1n
a2 n
=
,X
ann
a11 a12
a
a22
Пусть det A 21
an1 an 2
x1
x
2
=
, B
...
x
n
a1n
a2 n
≠ 0,
ann
a1m x1 b1
a2 m x2 b2
⋅
=
... ...
anm x b
m n
b1
b
2 ,
...
b
n
A⋅ X =
B.
66

67.

Метод Крамера решения СЛАУ
b1 , ⋅ A11
a11 x1 + a12 x2 + ... + a1n xn =
a x + a x + ... + a x = b , ⋅ A
21 1
22 2
2n n
2
21
...
bn , ⋅ An1
an1 x1 + an 2 x2 + ... + ann xn =
a11 x1 ⋅ A11 + a12 x2 ⋅ A11 + ... + a1n xn ⋅ A11 =b1 ⋅ A11 ,
a x ⋅ A + a x ⋅ A + ... + a x ⋅ A =b ⋅ A ,
21 1
21
22 2
21
2n n
21
2
21
...
an1 x1 ⋅ An1 + an 2 x2 ⋅ An1 + ... + ann xn ⋅ An1 =bn ⋅ An1.
x1 ( a11 ⋅ A11 + a21 ⋅ A21 + ... + an1 ⋅ An1 ) +
+x2 ( a12 ⋅ A11 + a22 ⋅ A21 + ... + an 2 ⋅ An1 ) +
............................................................
+xn ( a1n ⋅ A11 + a2 n ⋅ A21 + ... + ann ⋅ An1 ) =
=b1 ⋅ A11 + b2 ⋅ A21 + ... + bn ⋅ An1.
67

68.

Метод Крамера решения СЛАУ
a11 a12
a21 a22
a
n1 an 2
x1 ( a11 ⋅ A11 + a21 ⋅ A21 + ... + an1 ⋅ An1 ) +
a1n x1 b1
a2 n x2 b2
⋅
=
... ...
ann x b
n n
+x2 ( a12 ⋅ A11 + a22 ⋅ A21 + ... + an 2 ⋅ An1 ) +
............................................................
+xn ( a1n ⋅ A11 + a2 n ⋅ A21 + ... + ann ⋅ An1 ) =
=b1 ⋅ A11 + b2 ⋅ A21 + ... + bn ⋅ An1.
a11 a12 a1n
a
a22 a2 n
x1 ⋅ 21
=
an1 an 2 ann
b1 a12
b2 a22
bn an 2
det A1
x1 =
.
det A
a1n
a2 n
,
ann
x1 ⋅ det A= det A1 ,
68

69.

Теорема Крамера
det A1
=
x1 det A ,
det A2
=
,
x2
det A − формулы Крамера.
...
det An
xn =
.
det A
Теорема 1. Пусть определитель матрицы системы n линейных алгебраических уравнений с n неизвестными отличен
от 0, det A ≠ 0, тогда решение этой системы существует,
единственно и дается формулами Крамера.
69

70.

Следствия теоремы Крамера
Следствие 1. Если известно, что система n
линейных алгебраических уравнений с n
неизвестными не имеет решений, то ее
определитель равен 0.
Следствие 2. Если известно, что система n
линейных алгебраических уравнений с n
неизвестными имеет более одного
решения, то ее определитель равен 0.
70

71.

Следствия теоремы Крамера
Однородная СЛАУ:
0,
a11 x1 + a12 x2 + ... + a1n xn =
a x + a x + ... + a x =
0,
21 1
22 2
2n n
...
0,
an1 x1 + an 2 x2 + ... + ann xn =
0
0
X − тривиальное решение.
=
...
0
Следствие 3. Для того, чтобы система n
линейных алгебраических однородных
уравнений с n неизвестными имела
нетривиальное решение, необходимо,
чтобы ее определитель был равен 0.
71

72.

Метод Крамера решения СЛАУ
Пример 1. Решить СЛАУ:
0,
x1 − x2 + x3 =
−1,
x1 + 2 x3 =
x2 − x3 =
1.
1 −1 1
A = 1 0 2 ,
0 1 −1
0
B = −1 .
1
1 −1 1
det A =1 0 2 =1 − 2 − 1 =−2 ≠ 0
0 1 −1
0 −1 1
det A1 =−1 0 2 =−1 − 2 + 1 =−2,
1 1 −1
det A1 −2
x1 =
= =1,
det A −2
1 0 1
det A2 = 1 −1 2 = 1 + 1 − 2 = 0,
0 1 −1
x2 =
det A2
0
=
= 0,
det A −2
1 −1 0
det A3 = 1 0 −1 =1 + 1 =2,
0 1 1
det A3 2
x3 =
= =−1.
det A −2
1
X = 0 .
−1
72

73.

Метод Крамера решения СЛАУ
Пример 2. Решить СЛАУ:
1,
3 x − 2 y =
6 x − 4 y =
0.
det A =3 −2 =0, det Ax =1 −2 =−4 ≠ 0, det A =3 1 =−6 ≠ 0.
6 −4
0 −4
6 0
det A ⋅ x = det Ax ,
det A ⋅ y = det A ,
y
0 ⋅ x= − 4,
0 ⋅ y = − 6.
СЛАУ не имеет решений.
1,
3 x − 2 y =
3 x − 2 y =
0.
73

74.

Метод Крамера решения СЛАУ
Пример 3. Решить СЛАУ:
5 0,
=
det A 3=
9 15
=
Ax
det
det A ⋅ x = det Ax ,
det A ⋅ y = det A ,
y
3x + 5 y = 4,
9 x + 15 y = 12.
4=
5 0,
12 15
0 ⋅ x =0,
0 ⋅ y =0,
+ 5 y 4,
+ 5 y 4,
3x=
3x=
3x + 5 y= 4,
9 x +=
15 y 12, 3x =
+ 5 y 4,
x
X = 4 − 3x .
5
4 0.
=
Ay 3=
det
9 12
y=
4 − 3x
.
5
74

75.

Обратная матрица
a11 a12
a
a22
An×n = 21
a
n1 an 2
a1n
a2 n
ann
Матрица Bn×n называется обратной к матрице An×n ,
если A ⋅ B = B ⋅ A = En×n .
A ⋅ B ⋅ C = ( A ⋅ B ) ⋅ C = A ⋅ ( B ⋅ C ),
А ⋅ Е = Е ⋅ А = А.
A−1 - обратная к А.
Теорема 1. Если матрица имеет обратную матрицу, то
обратная матрица единственная.
Предположим противное:
A ⋅ B = B ⋅ A = En ×n ,
A ⋅ B ′ = B ′ ⋅ A = En ×n .
Тогда B = B ⋅ E = B ⋅ ( A ⋅ B′) =( B ⋅ A) ⋅ B′ = E ⋅ B′ = B′.
75

76.

Обратная матрица
Теорема 2. Для того, чтобы матрица имела обратную
матрицу необходимо и достаточно, чтобы det A ≠ 0.
Необходимость. Пусть A−1 - матрица, обратная к А. Тогда
(
)
(
)
( )
det A ⋅ A−1 = det E = 1, но det A ⋅ A−1 = det ( A) ⋅ det A−1 = 1,
следовательно, det A ≠ 0.
Достаточность. Пусть det A ≠ 0.
Рассмотрим
n
∑ aij Aij = det A,
j =1
Aij =
i+ j
( −1)
M ij .
n
∑ aij Akj = 0.
j =1
76

77.

Обратная матрица
n
n
∑ aij Akj = 0.
∑ aij Aij = det A,
j =1
j =1
Рассмотрим квадратную матрицу В с элементами
bij =
A ji
det A
n
. Матрица С=АВ имеет элементы
n
Akj
1 n
1, k = i,
cik= ∑ aij ⋅ b jk= ∑ aij ⋅
=
aij ⋅ Akj=
∑
det A=
det A j 1
0, k ≠ i.
j 1 =j 1
Аналогично, С ′ = ВA имеет элементы
n
n
Aik
1 n
1, k = j,
ckj′ = ∑ bki ⋅ aij= ∑ aij ⋅
aij ⋅ Aik=
=
∑
det A=
det A j 1
0, k ≠ j.
i 1 =j 1
B = A−1.
77

78.

Обратная матрица
C1 ⋅ C2 ⋅ C3 = (C1 ⋅ C2 ) ⋅ C3 = C1 ⋅ (C2 ⋅ C3 )
Теорема 3. Если матрицы An×n и Bn×n имеют обратные
матрицы, то и их произведение имеет обратную матрицу,
причем
−1
−1 −1
AB
B
A .
=
( )
(
)
(
)
A
A
AA
= E.
( AB ) ( B A=) ( ( AB ) B )=
( A ( BB ))=
−1 −1
−1 −1
=
AB
B
A
E
=
,
B
A ( AB ) E.
( )
−1 −1
−1
−1
−1
−1
−1
78

79.

Обратная матрица
Теорема 4. Если матрица An×n имеет обратную
матрицу, то и AT имеет обратную матрицу,
причем
−1 T
T −1
= A
A
.
( )
( )
A (A )
E=
, (A ) A
E.
=
T
−1 T
( AB ) = BT AT
T
T
T
( C1C2 ) = C2T C1T
A
−1 T
( ) (
−1 T
A =
−1
T
)
T
T
A A= E=
E.
79

80.

Вычисление обратной матрицы
An−×1n
=
B=
: bij
A ji
det A
.
1. Матрица квадратная;
2. Вычисляем определитель, det A ≠ 0;
3. Вычисляем Aij ; находим союзную матрицу D
DT
;
B=
det A
4. Вычисляем
5. Заполняем матрицу B = A−1.
80

81.

Вычисление обратной матрицы
(
)
−2 4 .
3
Пример 4. Найти матрицу обратную данной: A = 1
det A = −2 4 =( −2 ) ⋅ 3 − 1 ⋅ 4 = ( −10 ) ≠ 0,
1 3
A11 = ( −1) 1+1⋅ 3 = 3, A12 = ( −1) 1+ 2⋅ 1 = −1,
A21 =( −1) 2 +1⋅ 4 =−4, A22 =( −1) 2 + 2⋅ ( −2 ) =−2,
−4
3
−10 −10
=
A−1 =
−
−
1
2
−10 −10
3
− 10
1
10
4
10
.
2
10
81

82.

Решение СЛАУ с помощью
обратной матрицы
b1 ,
a11 x1 + a12 x2 + ... + a1n xn =
a x + a x + ... + a x =
b2 ,
21 1
22 2
2n n
...
bn .
an1 x1 + an 2 x2 + ... + ann xn =
a11 a12
a
a22
A 21
a
n1 an 2
x1
x
2
=
, B
...
x
n
a1n
a2 n
=
,X
ann
b1
b
2 ,
...
b
n
A⋅ X =
B.
A⋅ X =
B.
A−1 ⋅ ( A ⋅ X ) = A−1 ⋅ B,
(
)
A−1 ⋅ A ⋅ X = A−1 ⋅ B,
E ⋅ X = A−1 ⋅ B,
=
X A−1 ⋅ B.
82

83.

Решение СЛАУ с помощью
обратной матрицы
A⋅ X = B
X = A−1 ⋅ B
Пример 5. Найти решение СЛАУ
21,
3x1 − 2 x2 + 4 x3 =
9,
3x1 + 4 x2 − 2 x3 =
2 x1 − x2 − x3 =
10.
3 −2 4
A= 3 4 −2 , B=
2 −1 −1
21
9 .
10
3 −2 4
det A =3 4 −2 =−12 + 8 − 12 − (32 + 6 + 6) =−60.
2 −1 −1
A11 =
−6, A12 =
−1, A13 =
−11,
( −1) 1+1⋅ −41 −−21 =
( −1) 1+ 2⋅ 23 −−21 =
( −1) 1+3⋅ 23 −41 =
A21 =
−6, A22 =
−11, A23 =
−1,
( −1) 2+1⋅ −−21 −41 =
( −1) 2+ 2⋅ 23 −41 =
( −1) 2+3⋅ 23 −−21 =
A31 =
−12, A32 =
18, A33 =
18,
( −1) 3+1⋅ −42 −42 =
( −1) 3+ 2⋅ 33 −42 =
( −1) 3+3⋅ 33 −42 =
83

84.

Решение СЛАУ с помощью
обратной матрицы
bij =
A ji
det A
.
−6, A12 =
−1, A13 =
−11,
A11 =
( −1) 1+3⋅ 23 −41 =
( −1) 1+ 2⋅ 23 −−21 =
( −1) 1+1⋅ −41 −−21 =
A21 =
−6, A22 =
−11, A23 =
−1,
( −1) 2+ 2⋅ 23 −41 =
( −1) 2+3⋅ 23 −−21 =
( −1) 2+1⋅ −−21 −41 =
A31 =
−12, A32 =
18, A33 =
18,
( −1) 3+3⋅ 33 −42 =
( −1) 3+1⋅ −42 −42 =
( −1) 3+ 2⋅ 33 −42 =
1 −6 −6 −12 1 6 6 12
A=
−1 −11 18 =
1 11 −18 .
−60 −11 −1 18 60 11 1 −18
A⋅ X = B
21 5
6
6
12
1
X =A−1 ⋅ B = 1 11 −18 ⋅ 9 = −1 .
60 11 1 −18
10 1
−1
X = A−1 ⋅ B
84

85.

Решение матричных уравнений
Пример 6. Решить матричное уравнение:
−2 0
5 − 3
2 − 1 ⋅ X =
−5 1 .
A⋅ X = B
X = A−1 ⋅ B
det A= −2 0 = 2 ≠ 0,
2 −1
A11 =( −1) 1+1⋅ ( −1) =−1, A12 =( −1) 1+ 2⋅ 2 =−2,
A21 = ( −1) 2 +1⋅ 0 = 0, A22 = ( −1) 2 + 2⋅ ( −2 ) = −2,
A−1
−1 0
2
− 1 0
=
2
.
=
X
−2 −2
−1 −1
2
2
1 0
− 2
5 − 3
=
−5 1
−1 −1
5
− 2
0
3
2 .
2
85

86.

Решение матричных уравнений
Пример 7. Решить матричное уравнение:
10 26 3 4
X ⋅A= B
X ⋅
=
.
−10 − 7 −1 5
X = B ⋅ A−1
Пример 8. Решить матричное уравнение:
−1 2
1
0 1 ⋅ X ⋅ 2
0 −2
=
4 1
− 12
.
−4
A⋅ X ⋅ B =
C,
A−1 A ⋅ X ⋅ B ⋅ B −1= A−1 ⋅ C ⋅ B −1 ,
X = A−1 ⋅ C ⋅ B −1.
86

87.

Линейная алгебра
и аналитическая геометрия
Модуль 1.
Матрицы и определители
Ранг матрицы. Теорема КронекераКапелли. Метод исключения Гаусса решения
СЛАУ
87

88.

Минор матрицы
Минором порядка k матрицы An m называют определитель,
который составлен из элементов этой матрицы, стоящих на
пересечении произвольно выбранных k строк и k столбцов с
сохранением порядка.
x
j1 j2 ... jk
M i i ... i
k
1 2
88

89.

Ранг матрицы
Рангом матрицы называют число, равное
максимальному порядку ненулевых миноров этой
матрицы.
r = rangA
r = RgA
Свойство. Если ранг матрицы равен r, то матрица имеет
хотя бы один ненулевой минор порядка r, а все ее
миноры больших порядков равны нулю.
89

90.

Ранг матрицы
Минор М матрицы А называют базисным, если
выполнены два условия:
а) М не равен 0;
б) его порядок равен рангу матрицы А.
Строки и столбцы матрицы А, в которых расположен
базисный минор называются базисными.
Пример 3. Вычислить ранг матрицы
1 2 0
−1 3 3
0 1 2
1 2 0
−1 3 3
1 2 0
1 2 0
1 2 0
1 2 0
90

91.

Ранг матрицы
Пример 4. Назвать какой-нибудь базисный минор матрицы
1 0 -2 4 7
−1 4 -1 4 7
1 0 -2 4 7
91

92.

Ранг матрицы
Теорема 1. При транспонировании матрицы ее ранг не
изменяется.
i1 i2 ... ik
M j j ... j
k
1 2
j1 j2 ... jk
M i i ... i
k
1 2
92

93.

Ранг матрицы
Пример 4. Вычислить ранг матрицы
1 0 -2 4 7
−1 4 -1 4 7
1 0 -2 4 7
93

94.

Вычисление ранга матрицы.
Метод окаймляющих миноров
Минор М’ матрицы А называется окаймляющим для
минора М, если он получается из последнего
добавлением одной новой строки и одного нового
столбца матрицы А.
Теорема 2. Если для некоторого ненулевого минора
матрицы А все окаймляющие его миноры равны 0, то он
является базисным.
94

95.

Вычисление ранга матрицы
Пример 5. Найти ранг матрицы
2 -4 3 1 0
1 -2 1 -4 2
0
1
-1
3
1
4 -7 4 -4 5
95

96.

Элементарные преобразования
строк и столбцов матрицы
1. Умножение строки матрицы на число
2. Перестановка двух строк в матрице;
3. Добавление к i-ой строке матрицы ее k-ой строки,
помноженной на число λ.
Свойство 1. Каждое элементарное преобразование имеет
обратное элементарное преобразование
Свойство 2. Каждое элементарное преобразование над
матрицей можно трактовать как умножение матрицы А на
некоторую матрицу.
96

97.

Вычисление ранга матрицы.
Метод элементарных преобразований
Сведение матрицы к ступенчатой форме:
все нулевые строки располагаются под ненулевыми;
первый ненулевой элемент в каждой строке расположен
правее первого ненулевого элемента предыдущей
строки.
Теорема 3. Ранг матрицы не изменяется при элементарных
преобразованиях ее строк и столбцов
Ранг матрицы равен числу ненулевых строк в ее
ступенчатой форме
Пример 5. Найти ранг
матрицы и какой-нибудь из ее
базисных миноров
2 -4 3 1 0
1 -2 1 -4 2
0
1
-1
3
1
4 -7 4 -4 5
97

98.

Ранг матрицы.
Теорема о базисном миноре
Ряды матрицы называются линейно-независимыми, если их
линейная комбинация равна нулевому ряду только тогда, когда
все коэффициенты линейной комбинации равны 0.
Ряды матрицы называются линейно-зависимыми, если
существует их линейная комбинация, равная нулевому ряду, при
том не все коэффициенты линейной комбинации равны 0.
Теорема 4 (о базисном миноре). Базисные строки (столбцы)
матрицы А линейно независимы. Любые строки (столбцы)
матрицы А, не являющиеся базисными, являются линейными
комбинациями базисных строк (столбцов).
98

99.

Решение СЛАУ методом Гаусса
Теорема 5. Элементарные преобразования расширенной
матрицы СЛАУ не изменяет ее решения.
0,
−2 x1 + 3 x3 =
1,
− x1 − 3 x2 + 4 x3 =
3 x1 − 3 x2 − 2 x3 =
−1.
99

100.

Теорема Кронекера-Капелли
Теорема 6. (Теорема Кронекера-Капелли)
Для совместности системы необходимо и достаточно,
чтобы ранг матрицы системы был равен рангу ее
расширенной матрицы.
Теорема 7.
Если ранг матрицы совместной системы равен числу
неизвестных, то система имеет единственное решение.
Теорема 8.
Если ранг матрицы совместной системы меньше
числа неизвестных, то система имеет бесконечно много
решений.
100

101.

Решение СЛАУ методом Гаусса
Пример 7. Решить СЛАУ
3,
3x1 + x2 − x3 =
2,
x1 + 2 x2 − x3 =
4 x1 + 3x2 − 2 x3 =
4.
Пример 8. Решить СЛАУ
0,
x1 − x2 + x3 =
x + 2 x =
−1,
1
3
x − x =
3 1,
2
0.
x1 + x2 + x3 =
Пример 9. Решить СЛАУ
2,
2 x1 + 3x2 − x3 + x4 =
x + 2 x + x − x =
1
2
3
4 1,
3 x + 5 x =
3,
2
1
1.
x1 + x2 − 2 x3 + 2 x4 =
101

102.

Линейная алгебра
и аналитическая геометрия
Модуль 1.
Матрицы и определители. СЛАУ
Фундаментальная система
решений однородной СЛАУ.
Теорема о структуре общего решения
совместной неоднородной системы
102

103.

Однородные СЛАУ
0,
a11 x1 + a12 x2 + ... + a1n xn =
a x + a x + ... + a x =
0,
21 1
22 2
2n n
...
0.
am1 x1 + am 2 x2 + ... + amn xn =
a11 a12
a
a22
A mxn = 21
a
m1 am 2
Ο,
A⋅ X =
x1
a1n 0
0
a 2 n 0 X = x2 , Ο = 0 .
,
nx1
mx1
...
...
0
x
0
amn 0
n
Система имеет только тривиальное решение: RgA = n
Система имеет нетривиальные решения: RgA < n
103

104.

Однородные СЛАУ
Фундаментальная система решений
Любой набор из n-r линейно-независимых столбцов –
решений однородной СЛАУ называют
фундаментальной системой решений этой СЛАУ.
n – количество неизвестных, r – ранг матрицы СЛАУ.
0,
x1 + x2 + x3 =
0,
2 x1 − 3x2 + x3 =
3x1 − 2 x2 + 2 x3 =
0.
104

105.

Однородные СЛАУ
Фундаментальная система решений
0,
x1 − 2 x2 − 3x3 =
−2 x + 4 x + 6 x =
0.
1
2
3
105

106.

Теорема о структуре общего
решения неоднородной СЛАУ
чрнс
B и
X
Пусть
- частное решение СЛАУ A ⋅ X =
известна фундаментальная система решений
{X , X ,..., X } соответствующей однородной
(1)
(2)
(k )
Ο. Тогда любое решение СЛАУ
A⋅ X =
A⋅ X =
B можно представить в виде
системы
X
= X
чрнс
+ C1 ⋅ X
(1)
+ C2 ⋅ X
(2)
(k )
+ ... + Ck ⋅ X .
106

107.

Общее решение неоднородных СЛАУ
−3,
2 x1 + x2 − 3x3 − x4 =
−1,
x1 + x2 − x3 − 2 x4 =
x1 − 3x2 − 5 x3 + 10 x4 =
−5.
−1,
x1 − x2 + x3 − x4 =
x + x + 2 x + 3x =
3,
1
2
3
4
2 x + 4 x + 5 x + 10 x =
2
3
4 10,
1
−6.
2 x1 − 4 x2 + x3 − 6 x4 =
107

108.

Общее решение неоднородных СЛАУ
0,
x1 − x2 + x3 − x4 =
x + x + 2 x + 3x =
0,
1
2
3
4
2 x + 4 x + 5 x + 10 x =
0,
1
2
3
4
0,
2 x1 − 4 x2 + x3 − 6 x4 =
1 −1
A = 1 1
2 4
2 −4
1
→ 0
0
0
1 −1
2 3
5 10
1 −6
−1 1
2 1
0 0
0 0
−1 1 −1 1 −1 −1
3 → 0 2 1 4
4 →
10 0 6 3 12 12
−6 0 −2 −1 −4 −4
−1 −1
4 4 ; базисный минор M12
12
0 0
0 0
108

109.

Общее решение неоднородных СЛАУ
1 −1 1 −1 −1
0 2 1 4 4 ; базисный минор M12
12
0 0 0 0 0
0 0 0 0 0
1
1.
−1, x1 = 1,
− x3 + x4 − 1, x1 − x2 =
2
x1 − x2 =
чрнс
X
.
=
2x =
=
=
x
x
2,
2
4,
− x3 − 4 x4 + 4,
2
2
0
2
− x3 + x4 ,
x1 − x2 =
2x =
− x3 − 4 x4 ,
2
2.
3
− x3 − x4 ,
x1 =
2
x3
x2 =
− − 2 x4 ,
2
− x3 + x4 ,
x1 − x2 =
x3
− − 2 x4 ,
x2 =
2
−1.5 −1
−0.5 −2
ФСР :
, .
1 0
0 1
0
109

110.

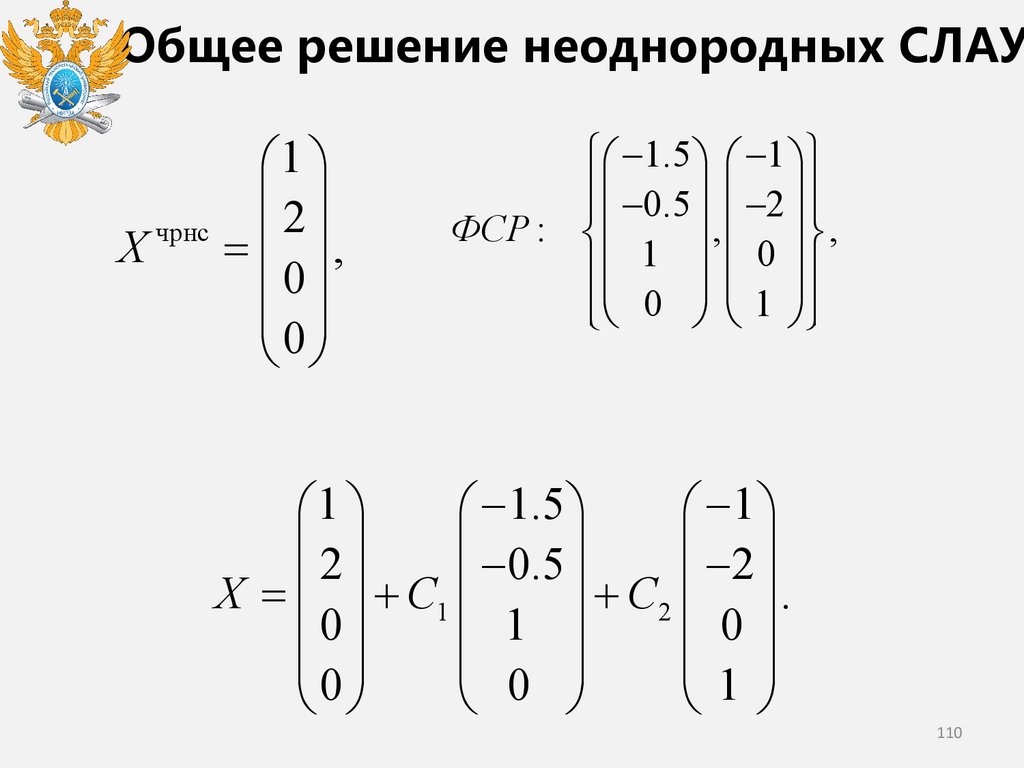
Общее решение неоднородных СЛАУ
1
2
чрнс
X
= ,
0
0
−1.5 −1
−0.5 −2
ФСР :
, ,
1
0
0 1
1
−1.5
−1
2
−0.5
−2
X=
+ C1
+ C2 .
0
1
0
0
0
1
110

111.

Вычисление обратной матрицы с
помощью элементарных преобразований
Элементарные преобразования
строк и столбцов матрицы
1. Умножение строки матрицы на число
2. Перестановка двух строк в матрице;
3. Добавление к i-ой строке матрицы ее k-ой строки,
помноженной на число λ.

112.

Вычисление обратной матрицы с
помощью элементарных преобразований
A ⋅=
X E, =
X A−1.
P1 ⋅ A ⋅ X = P1 ⋅ E ,
P2 ⋅ ( P1 ⋅ A) ⋅ X = P2 ⋅ ( P1 ⋅ E ) ,
..........................................,
Pn ⋅ (...P2 ⋅ ( P1 ⋅ A) ) ⋅ X = Pn ⋅ (...P2 ⋅ ( P1 ⋅ E ) ) ,
112

113.

Вычисление обратной матрицы с
помощью элементарных преобразований
Вычислить матрицу, обратную данной
с помощью элементарных преобразований
(
−3 2
1 4
)
0 −1
0
1 −2 −3
−2 5 0
113

114.

Решение СЛАУ методом Гаусса
114