Простейшие преобразования графиков функций

1. Простейшие преобразования графиков функций.

2. Цели урока:

Научить студентов преобразованию графика
функции с использованием параллельного
переноса, растяжения, сжатия вдоль оси
координат, а также применению всех
перечисленных видов для одной функции.
Способствовать развитию наблюдательности,
умения анализировать, преобразовывать графики
данных функций, побуждать учеников к
самоконтролю своей учебной деятельности,
научить сравнивать, делать выводы, находить
аналогию.
Воспитать умение строить, преобразовывать
графики линейной функции, квадратичной
функции и обратной пропорциональности.
Воспитать такие качества личности, как
познавательная активность, самостоятельность.

3. Содержание темы:

I. Параллельный перенос вдоль оси Оу.
II. Растяжение и сжатие вдоль оси Оу.
III. Параллельный перенос вдоль оси Ох.
IV. Растяжение и сжатие вдоль оси Ох.
V. Преобразование графика функции с
использованием всех четырех видов
преобразования.

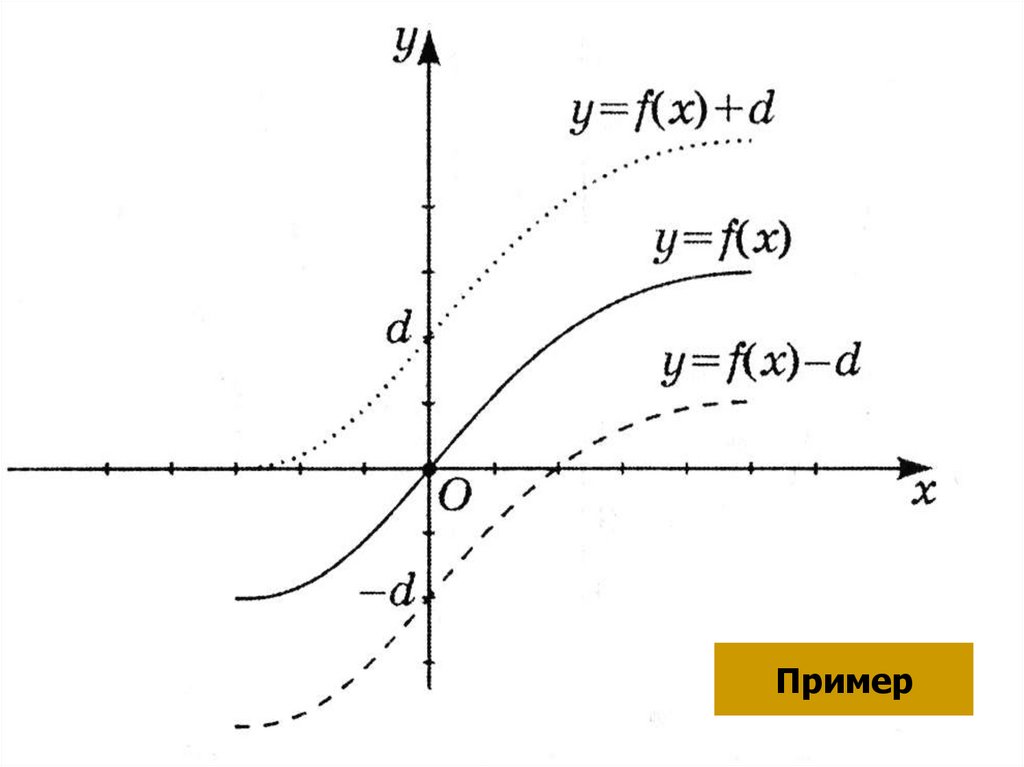
4. I. Параллельный перенос вдоль оси Оу

График функции у=f(x)+d получаем из
графика функции у=f(x) параллельным
переносом на расстояние d вдоль оси Оу,
в положительном направлении при d >0
и в отрицательном направлении при d
<0.

5.

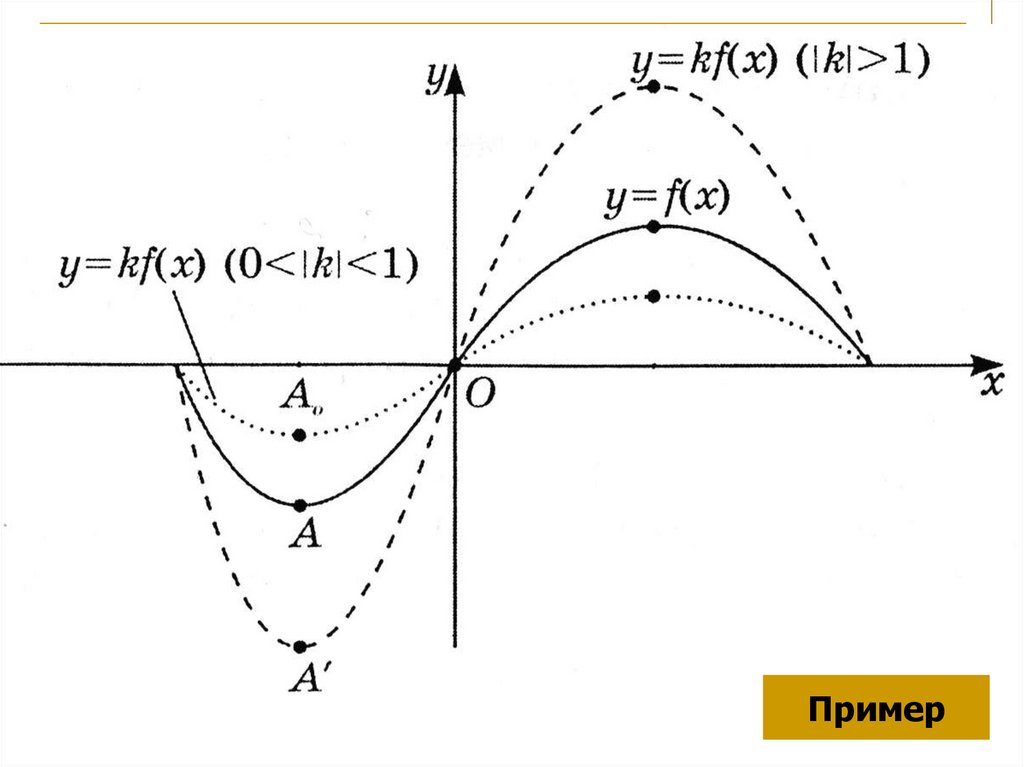
Пример

6. II. Растяжение и сжатие вдоль оси Оу.

График функции y=kf(x) получаем из
графика функции y=f(x) при |k|> 1
растяжением в |k| раз вдоль оси Оу, а
при 0 < |k| < 1 – сжатием в |k| раз
вдоль оси Оу.

7.

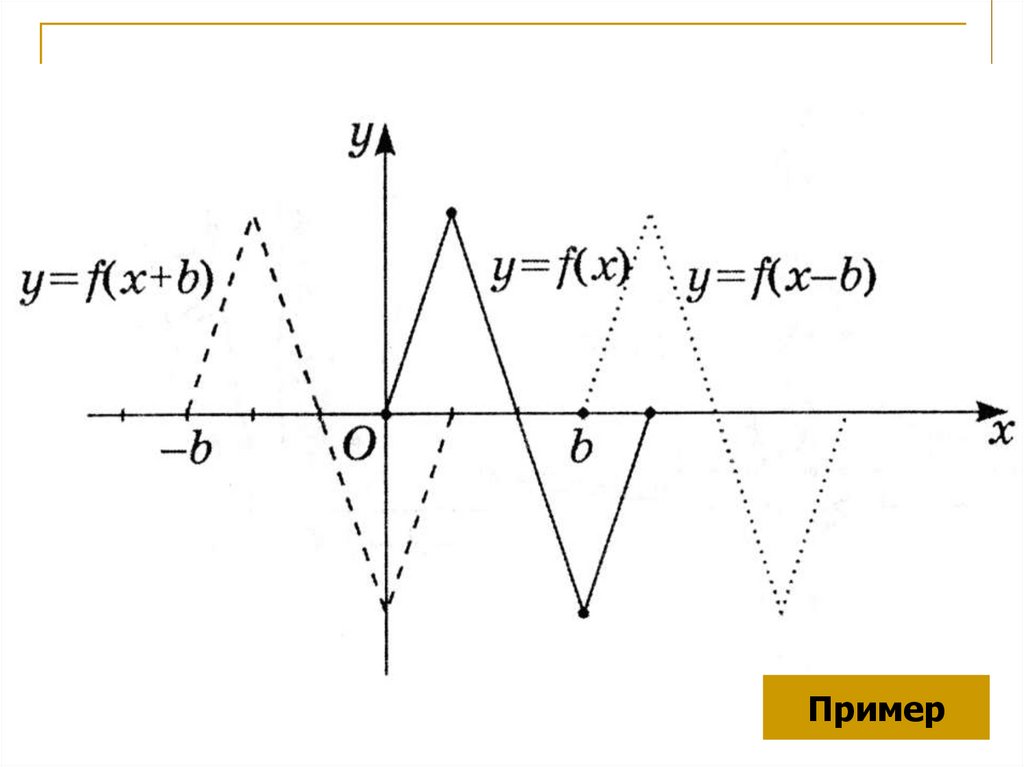
Пример

8. III. Параллельный перенос вдоль оси Ох.

График функции у=f(x+b) получаем путем
параллельного переноса графика функции
у=f(x) вдоль оси Ох на |b| единиц в
положительном направлении при b <0 и в
отрицательном направлении – при b >0.

9.

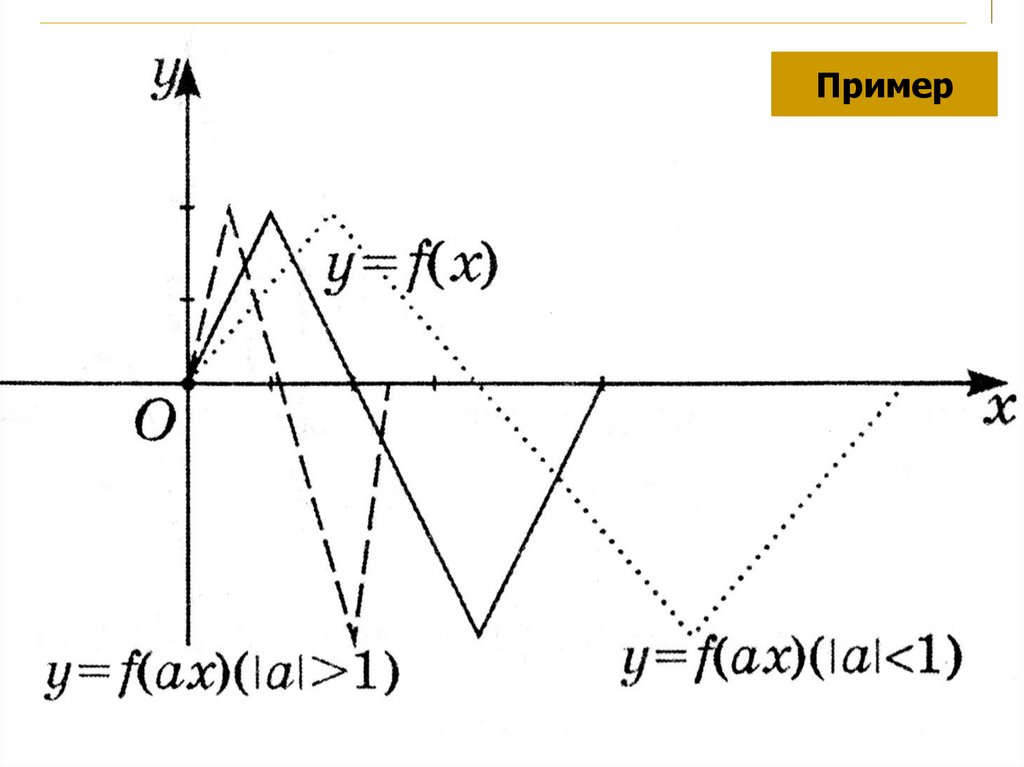
Пример

10. IV. Растяжение и сжатие вдоль оси Ох.

График функции y=f(аx) получаем из графика
функции y=f(x) сжатием в |a| раз вдоль оси
Ох при |a| > 1 и растяжением в
вдоль оси Ох при |a| < 1.
1
а
раз

11.

Пример

12. V. Преобразование графика функции с использованием всех четырех видов преобразования

График функции y=kf(аx+b)+d
получаем из графика функции y=f(x),
используя все приведенные четыре
вида преобразования.

13. Пример 5

Построим график функции:
у 2 х 2 12 х 19
Решение: Сначала выделим полный квадрат для
данного трехчлена:
у 2 х 12 х 19 2( х 6 х) 19
2
2
2(( х 6 х 9) 9) 19
2
2( х 3) 18 19
2
2( х 3) 1
2

14.

Выполним следующие преобразования:
построим график функции
у х2 ;
параболу параллельно перенесем вдоль оси Ох в
положительном направлении на три единицы;
полученную параболу растянем от оси Ох в 2 раза;
затем к полученной параболе применим симметричность
относительно прямой у=0;
последнюю параболу параллельно перенесем вдоль оси Оу на
одну единицу в отрицательном направлении.

15.

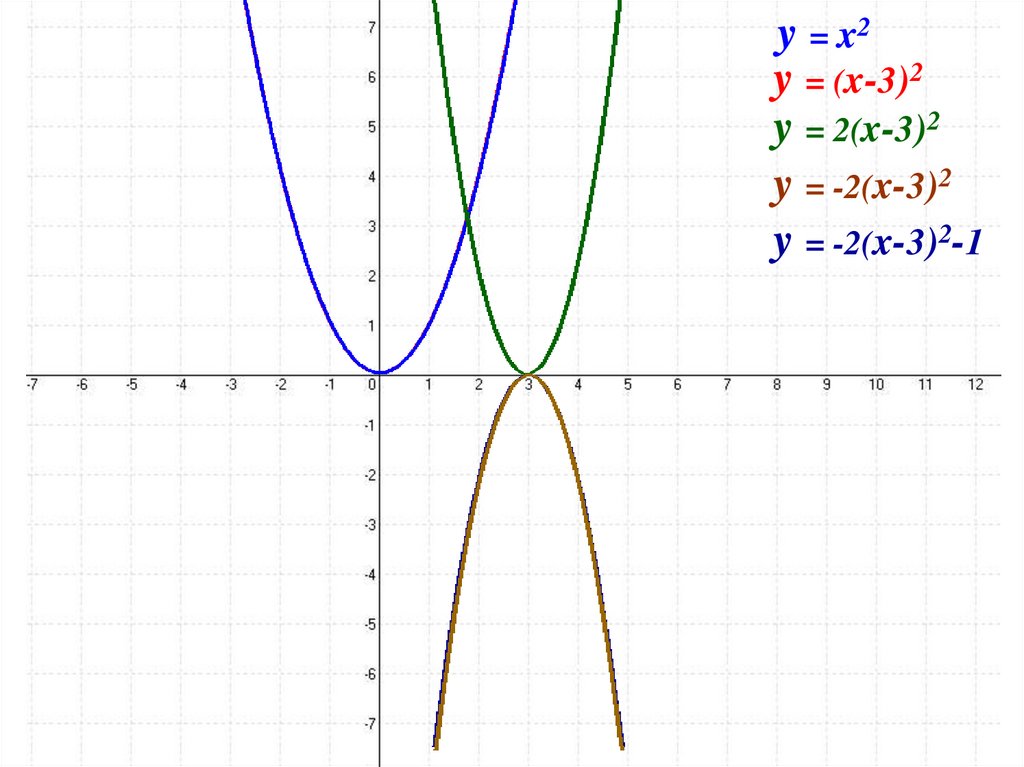
y = x2
y = (x-3)2
y = 2(x-3)2
y = -2(x-3)2
y = -2(x-3)2-1

16.

Выполните задание
Постройте в одной и той же системе
координат графики функций
у=-0,5х2; у=-0,5х2 -4; у=0,5(х+4)2; у=-0,5(х+1)2 -3.
Выполненные задания отправить на почту
преподавателя [email protected]