Похожие презентации:
Колебательное движение
1.
Тема:«Колебательное
движение»
2.
Механические колебанияСвободные
Гармонические
колебания
Вынужденные
Математический
маятник
Груз на пружине
Резонанс
Период
Частота
Амплитуда
Формулы периодов
для математического
маятника и груза на пружине
Закон гармонических
колебаний
3.
Механические колебания – это физическиепроцессы, точно или почти точно повторяющиеся через
одинаковые промежутки времени.
СВОБОДНЫЕ
возникают в
системе под
действием
внутренних сил
(упругости,
тяжести) после
кратковременного
воздействия
внешних сил.
Амплитуда
уменьшается из-за
потерь энергии на
преодоление сил
трения и
сопротивления.
Затухающие.
ВЫНУЖДЕННЫЕ
совершаются телами
под действием
внешних периодически
меняющихся сил.
Амплитуда
постоянна,
т.к. потеря энергии
восполняется работой
внешней
вынуждающей силы
АВТОКОЛЕБАНИЯ
незатухающие
колебания, которые
могут существовать
в системе без
воздействия на нее
внешних
периодических сил, за
счет источника
энергии (часы с
маятником)
4. Условия существования колебаний:
наличие устойчивого положенияравновесия (ΣF=0);
наличие в колеблющемся теле
избыточной энергии (Ер≠ 0);
наличие результирующей силы,
отличной от нуля;
силы трения в системе малы.
5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ:
• смещение (х) – отклонение тела от положения равновесия вданный момент времени;
• амплитуда (xm) – модуль максимального смещения точки от
положения равновесия;
• период (Т) – время одного полного колебания;
Т = t/n, где n – число полных колебаний
• частота (ν) число колебаний в единицу времени;
ν = n / t ; ν = 1 / Т – линейная частота [ѵ] = 1/c = 1 Гц (Герц)
ω0 =2π/Т – циклическая частота колебаний [ѡ0]= рад/с
•фаза колебаний (φ) определяет состояние колебательной
системы в любой момент времени; φ = ѡ0t + φ0 [φ] = рад
6. Резонанс (лат. resono – «откликаюсь»)
Резонанс(лат. resono – «откликаюсь»)
- это резкое возрастание амплитуды вынужденных
колебаний, возникающее, когда частота
собственных колебаний совпадает с частотой
вынуждающей силы: ω=ω0
7.
Математический маятник – этоточечное тело (мат точка),
подвешенное к нерастяжимой и
невесомой нити.
Пружинный маятник - это тело,
подвешенное на пружине и совершающее
колебания вдоль вертикальной оси под
действием силы упругости пружины.
8.
9.
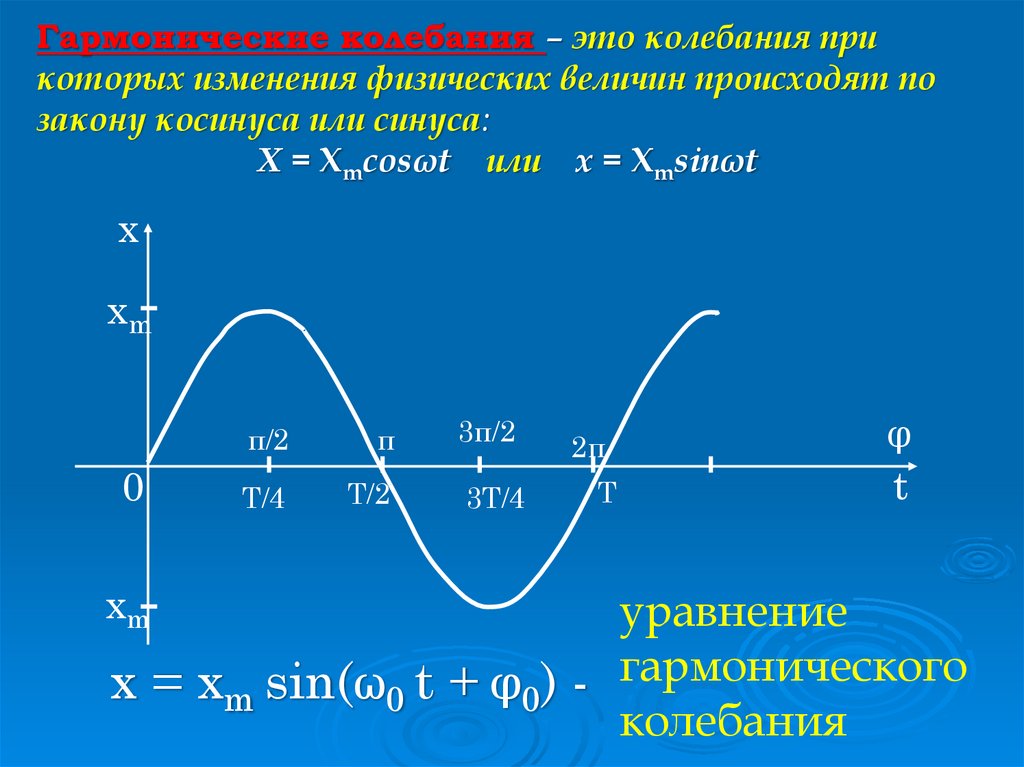
Гармонические колебания – это колебания прикоторых изменения физических величин происходят по
закону косинуса или синуса:
Х = Xmcosωt или х = Xmsinωt
x
xm
0
xm
π/2
π
3π/2
T/4
T/2
3T/4
2π
T
φ
t
уравнение
x = xm sin(ω0 t + φ0) - гармонического
колебания
10.
Во всех трех случаях для синихкривых φ0 = 0:
а ) красная кривая отличается от
синей только большей
амплитудой (x'm > xm);
b ) красная кривая отличается от
синей только значением периода
(T' = T / 2);
с ) красная кривая отличается от
синей только значением
начальной фазы
(φ0’= -π/2 рад).
11.
Графики тела,совершающего гармонические колебания
координаты x(t):
скорости υ(t):
ускорения a(t):
12.
Задача: напишите уравнение гармоническогоколебания, если максимальное ускорение точки
49,3 см/с2 , период колебания 2 с, а смещение
точки в начальный момент времени 25 мм.
Дано:
СИ
Решение.
аmax =49,3см/с2 0,493м/с2 x = xm sin(ω0t+ φ0)
T = 2c
х0=25мм
х(t) - ?
0,025м
Из уравнения гармонических колебаний для
ускорения:
am = ω02xm → xm = am / ω02
ω0 = 2π / T = 2π / 2 = π.
am = 4π2 xm/T2
xm = am T2/4π2 = 0,493*4/4*9.86
= 0,05 (м)
При t = 0 х = х0=0,025м; значит уравнение
примет вид: 0,025 = 0,05sin φ0
φ0 = arcSin(0,025/0,05) = π / 6.
Ответ: х = 0,05 Sin(πt + π/6).
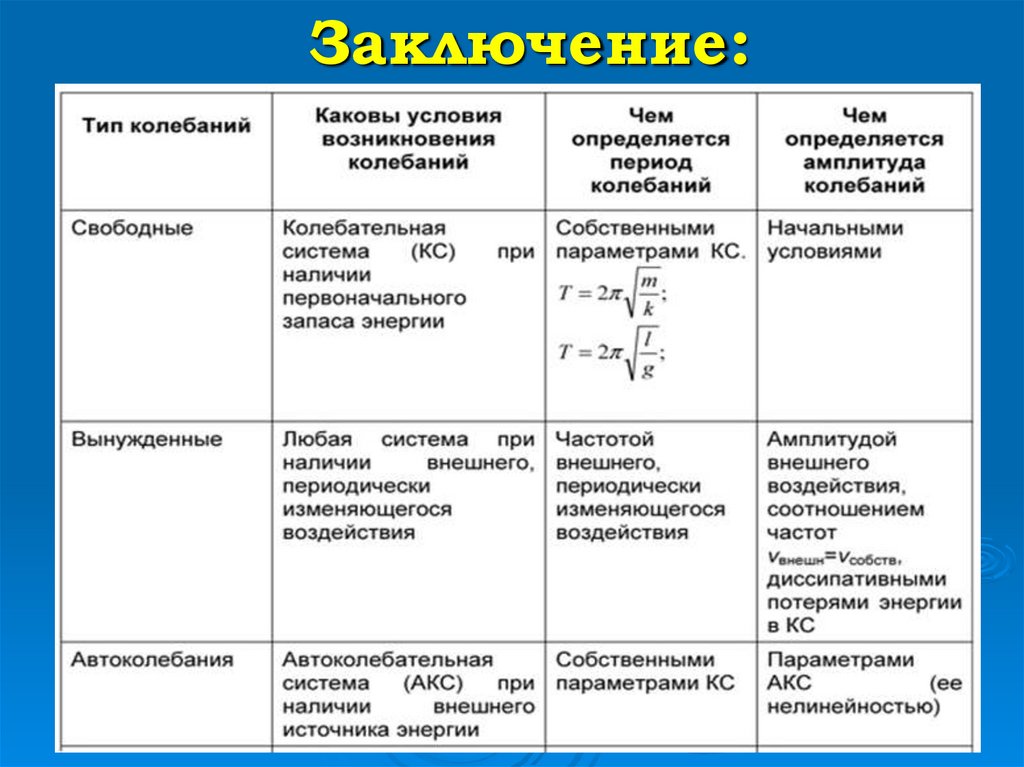
13. Заключение:
14. Домашнее задание:
1. Гармонические колебания описываются уравнением:х = 0,01Sin(3πt + π/6).
Определите: А) амплитуду колебаний;
Б) циклическую частоту;
В) начальную фазу;
Г) период колебаний.
2. Определите жесткость пружины, если прикреплённый
к ней груз совершает 20 колебаний за 30 с.
3. Материальная точка массой 10 г совершает
гармонические колебания с частотой 1 Гц. Амплитуда
колебаний 0,05м. Определите:
А) максимальную силу, действующую на точку;
Б) Полную энергию материальной точки.












 Физика
Физика








