Похожие презентации:
Механические колебания
1.
Д.з. § 13,14(до стр. 63) Работа попрезентации: сделать записи в
тетради по слайдам 12-17, решить
задачи по тексту слайда 18.
Механические колебания
Физика – 11
2021 - 2022 учебный год
2.
Колебания– это движение или процессы, которые точно
или приблизительно повторяются через
определенный промежуток времени.
В зависимости от физической природы различают:
Механические Электромагнитные
Другие
колебания
колебания
колебания
Колеблющиеся Колеблющиеся
Колеблющиеся
величины:
величины: заряд
величины:
координата,
конденсатора, сила
температура,
скорость,
тока, напряжение,
давление,
ускорение,
вектор напряженности
плотность и
сила...
электрического поля,
пр.
вектор магнитной
индукции
3.
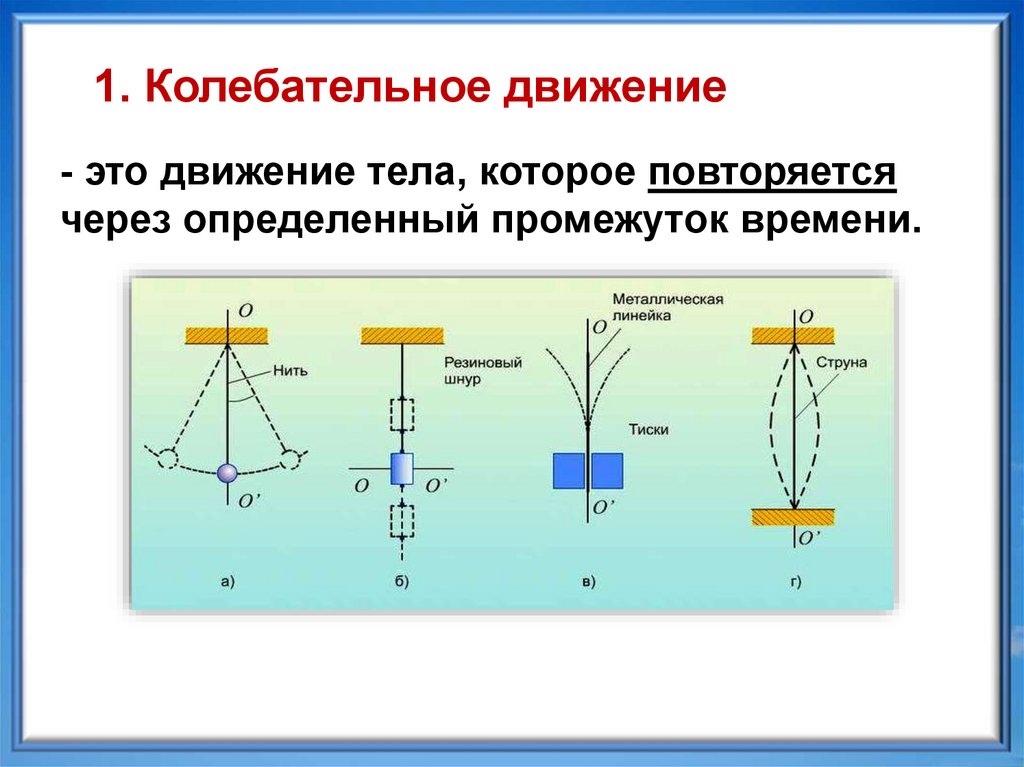
1. Колебательное движение- это движение тела, которое повторяется
через определенный промежуток времени.
4.
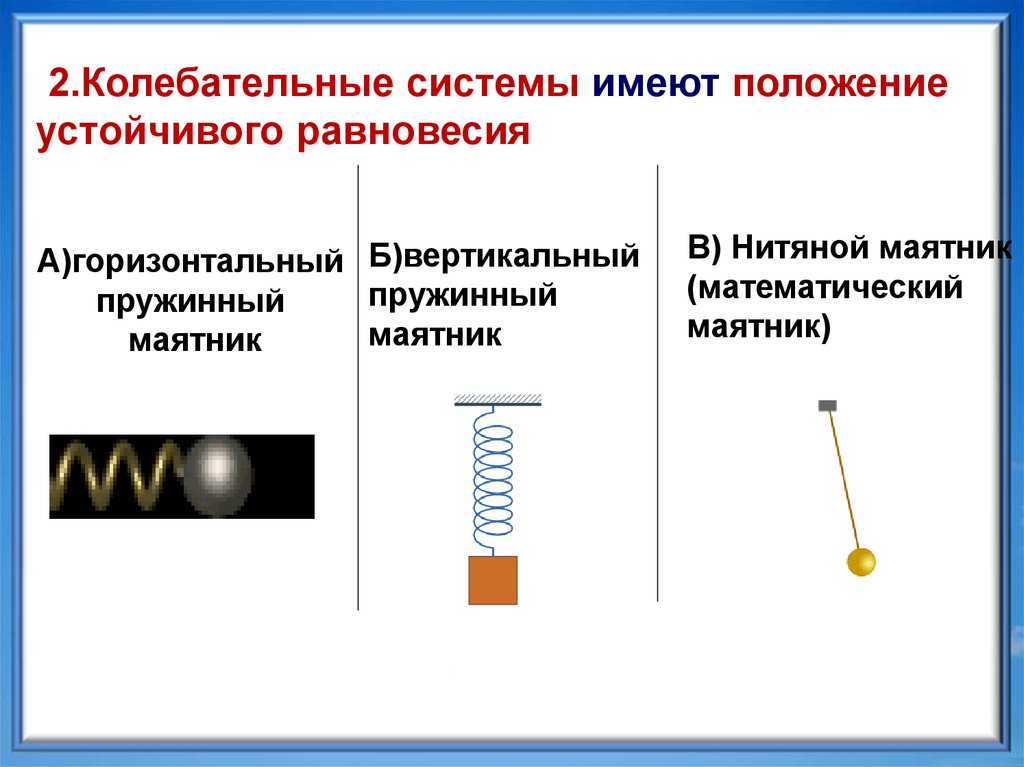
2.Колебательные системы имеют положениеустойчивого равновесия
А)горизонтальный Б)вертикальный
пружинный
пружинный
маятник
маятник
В) Нитяной маятник
(математический
маятник)
5.
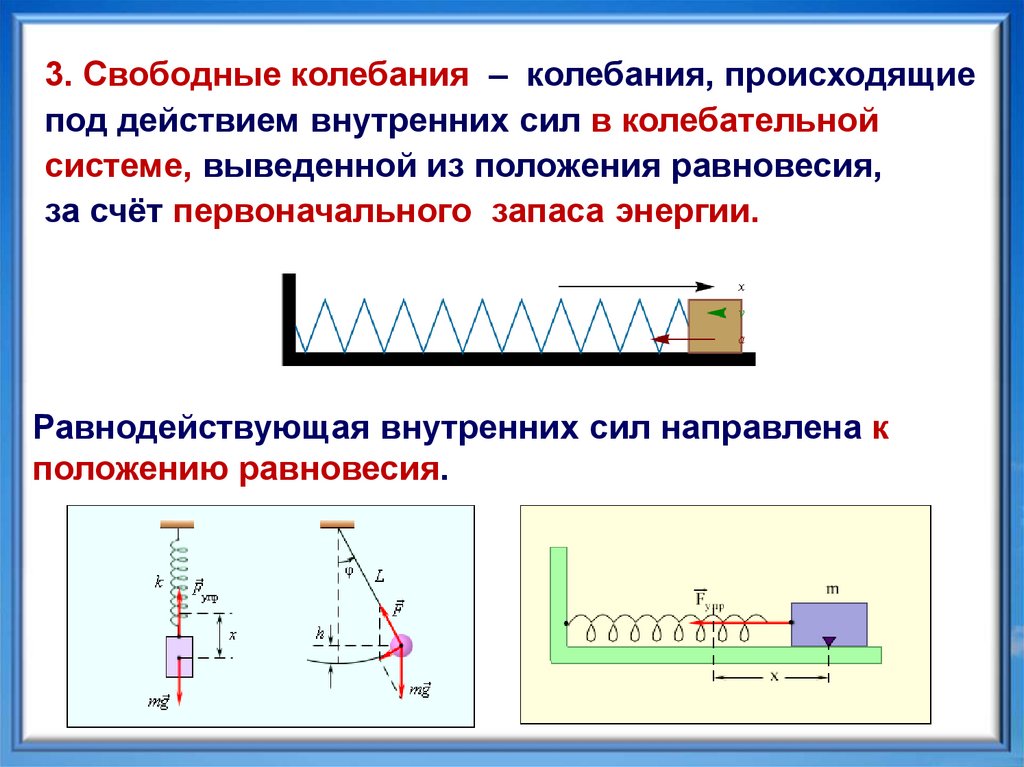
3. Свободные колебания – колебания, происходящиепод действием внутренних сил в колебательной
системе, выведенной из положения равновесия,
за счёт первоначального запаса энергии.
Равнодействующая внутренних сил направлена к
положению равновесия.
6.
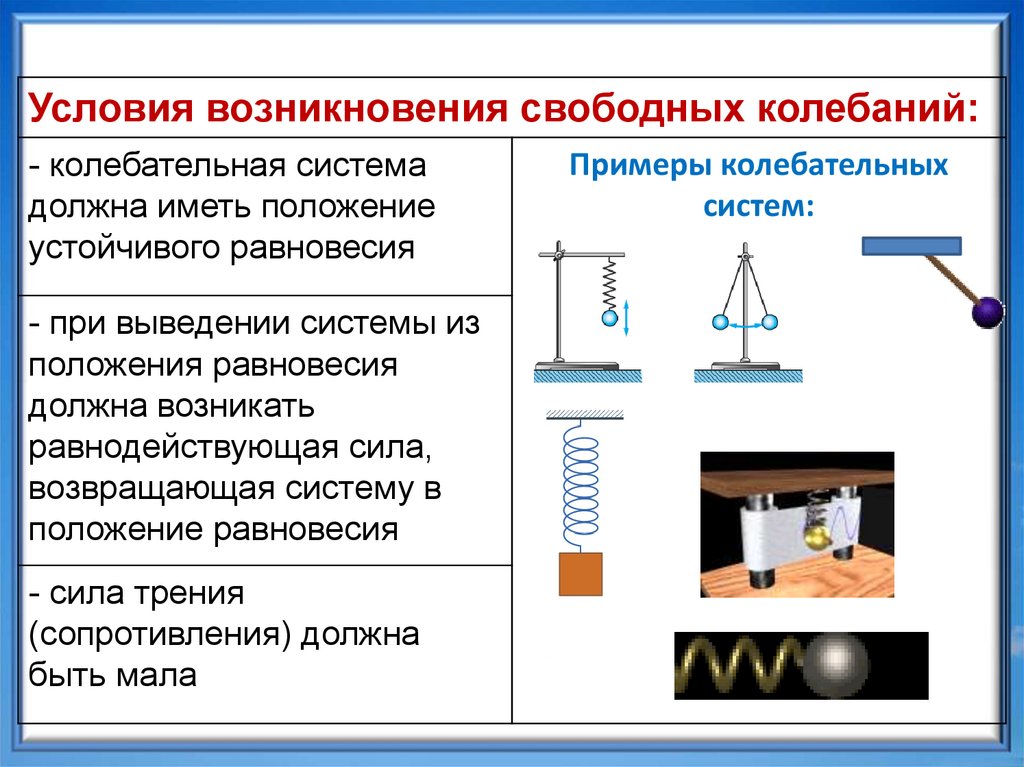
Условия возникновения свободных колебаний:- колебательная система
должна иметь положение
устойчивого равновесия
- при выведении системы из
положения равновесия
должна возникать
равнодействующая сила,
возвращающая систему в
положение равновесия
- сила трения
(сопротивления) должна
быть мала
Примеры колебательных
систем:
7.
4. Амплиnуда колебаний хm - модуль наибольшегосмещения тела от положения равновесия.
Определяется начальными условиями (энергией).
5. Период колебаний Т– промежуток времени,
в течение которого происходит одно полное
колебание.
t
Т
N
6. Частота колебаний ν - это число колебаний в
единицу времени.
N
ν
t
1
ν Гц
с
1
Т
ν
8.
7. Колебания груза на пружинеПо II закону Ньютона:
ma Fупр mg N
В проекциях на ОХ:
0
х
max ( Fупр ) х
max kx
Уравнение движения:
k
ax x
m
ax ~ x
Проекция ах ускорения тела
прямо пропорциональна его
координате х, взятой с
противоположным знаком.
9.
8. Уравнение движения груза на пружинеk
ax x
m
х
а
а х
k
х x
m
х ~ x
ax ~ x
скорость – это первая производная
координаты по времени
ускорение – это первая производная
скорости по времени
ускорение – это вторая производная
координаты по времени
- при свободных колебаниях координата
изменяется так, что вторая производная
координаты хꞌꞌ по времени пропорциональна
координате х, взятой с противоположным
знаком.
10.
8. Уравнение движения груза на пружинеОбозначим
k
для пружинного маятника
m
2
0
х x
2
0
(1)
Решение уравнения (1):
Скорость:
х хm cos 0 t
х 0 хm sin 0 t
2
Ускорение: a х 0 хm cos 0 t
Решение уравнения (1):
х хm sin 0 t
Периодические изменения физической величины в
зависимости от времени, происходящие по формуле синуса
или косинуса, называется гармоническими колебаниями.
11.
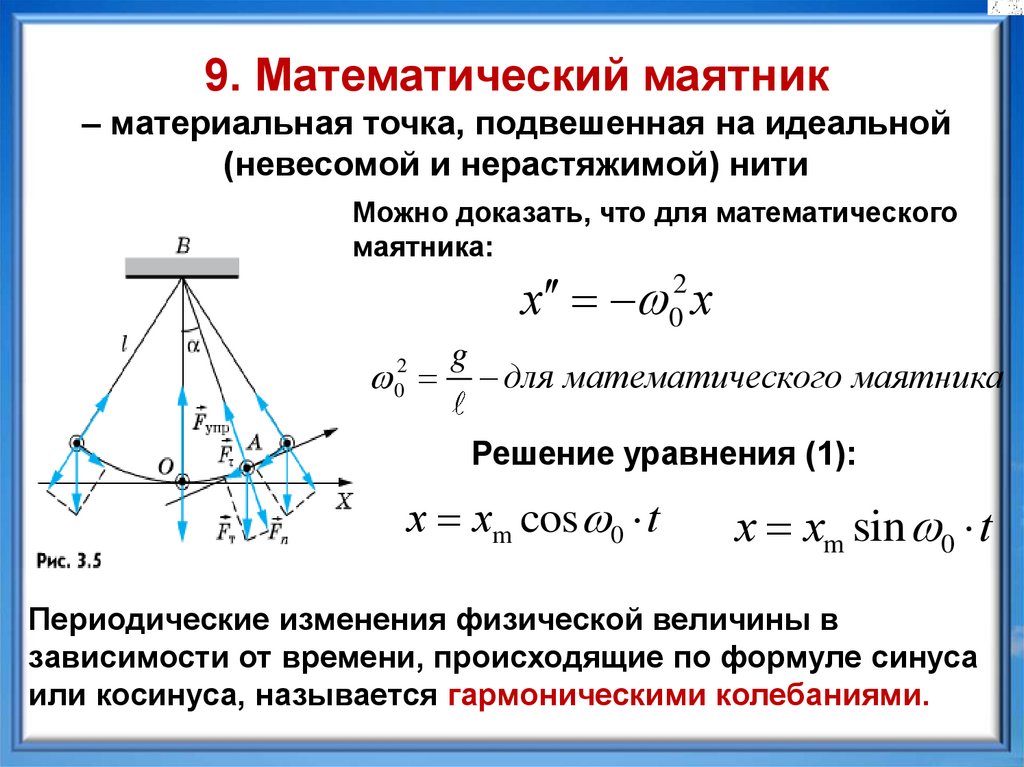
9. Математический маятник– материальная точка, подвешенная на идеальной
(невесомой и нерастяжимой) нити
Можно доказать, что для математического
маятника:
2
0
х x
2
0
g
для математического маятника
Решение уравнения (1):
х хm cos 0 t
х хm sin 0 t
Периодические изменения физической величины в
зависимости от времени, происходящие по формуле синуса
или косинуса, называется гармоническими колебаниями.
12.
10. Физический смысл ω0х хm cos 0 t
Через время Т при увеличении аргумента косинуса
на ω0Т значение координаты повторяется.
Наименьший период у косинуса 2π.
Приравняем: ω0Т = 2π
2
0
2
Т
ω0 – циклическая частота –
это число колебаний не за 1 с,
а за 2π секунд.
ω0 – циклическая частота измеряется в рад/с
13.
11.Период колебаний груза на пружине Т0Т 2
2
2
m
Т
2
0
k
k
m
m
Т 2
k
12.Период колебаний математического маятника Т
2
2
Т
2
0
g
g
Т 2
g
14.
13. Фаза колебаний φх хm cos 0 t
х хm cos
φ
φ = ω0Т– фаза колебаний – аргумент косинуса или
синуса – определяет при заданной амплитуде
состояние колебательной системы в любой
момент времени, измеряется в радианах.
Фаза колебаний определяет значения координаты,
скорости, ускорения, изменяющихся тоже по
гармоническому закону.
15.
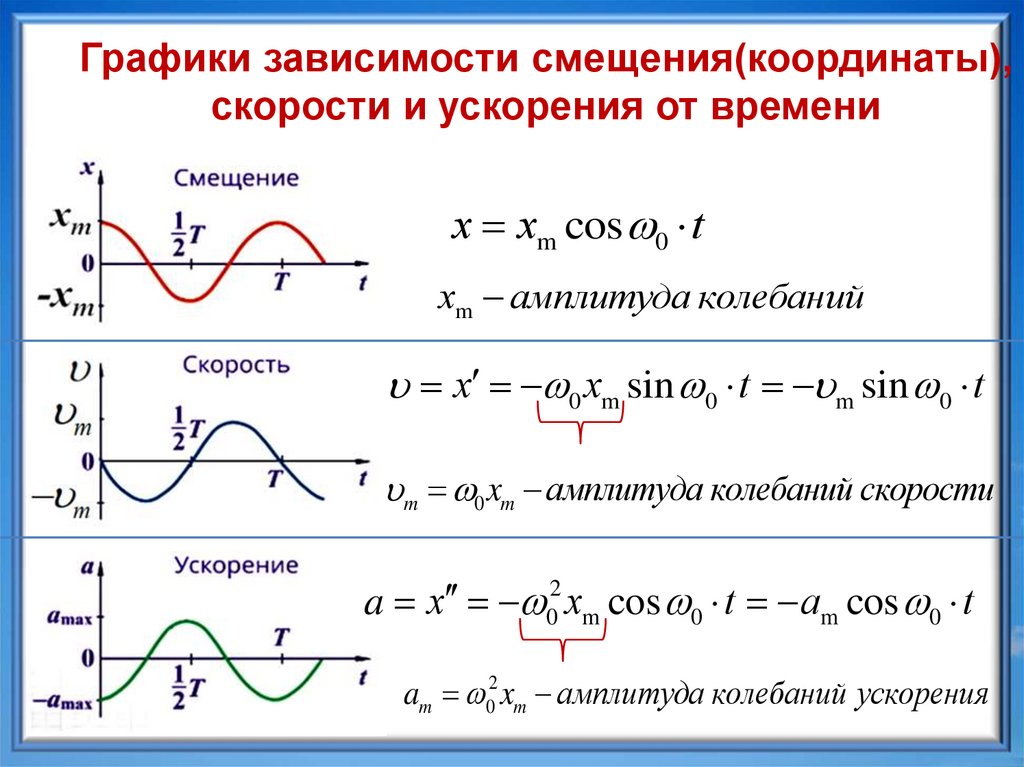
Графики зависимости смещения(координаты),скорости и ускорения от времени
х хm cos 0 t
хm амплитуда колебаний
х 0 хm sin 0 t m sin 0 t
m 0 xm амплитуда колебаний скорости
a х 02 хm cos 0 t аm cos 0 t
am 02 xm амплитуда колебаний ускорения
16.
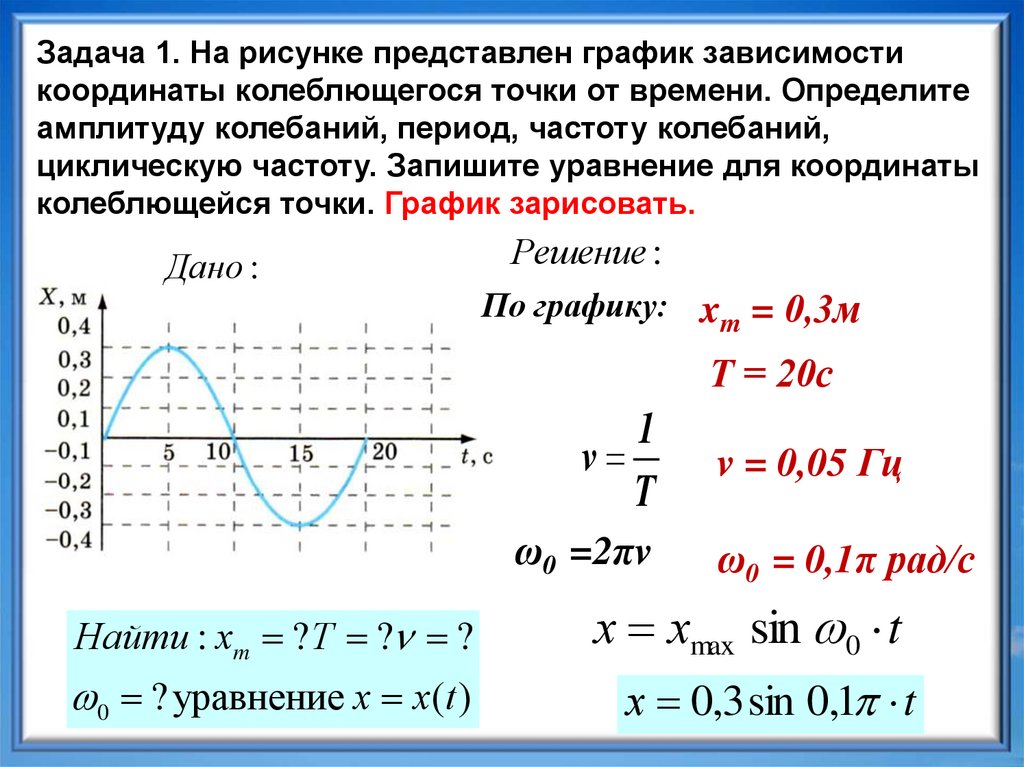
Задача 1. На рисунке представлен график зависимостикоординаты колеблющегося точки от времени. Определите
амплитуду колебаний, период, частоту колебаний,
циклическую частоту. Запишите уравнение для координаты
колеблющейся точки. График зарисовать.
Дано :
Решение :
По графику: xm = 0,3м
Т = 20с
1
ν
Т
ω0 =2πv
Найти : хm ? Т ? ?
0 ? уравнение х х(t )
v = 0,05 Гц
ω0 = 0,1π рад/с
х хmax sin 0 t
х 0,3 sin 0,1 t
17.
Задача 2. Материальная точка совершаетгармонические колебания согласно уравнению
х 2 cos( t )
3
4
в котором все величины заданы в единицах СИ. Найти
амплитуду, начальную фазу φ0 и период колебаний.
Решение :
Дано :
х 2сos ( t )
3
4
xm ?
0 ?
Т ?
х хm cos( 0 t 0 )
х 2 cos( t )
3
4
если t = 0
0
3
рад / с
Т
хmax 2 м
0
2
0
4
Т
2
3
6( с )
18.
Решить задачу. Запишите уравнение гармоническогоколебательного движения точки х(t), совершающей
колебания с амплитудой хm = 8 см, если за t = 1 мин
совершается N = 120 колебаний и начальная фаза
колебаний равна φ0 = 45°.
Дано :
хm 8cм 0,08 м
t 1мин 60с
N 120
0
4
x x(t )
Решение :
х хm cos( 0 t 0 )











 Физика
Физика








