Похожие презентации:
Многогранники
1. Многогранники
МНОГОГРАННИКИЗайцев, Сачалин , Соловьев, Емелин .11 НА
2. Содержание
ПризмаПараллелепипед
Пирамида
Далее
3. Призма
Две грани которогоявляются (равными) многоугольниками, лежащими
в параллельных плоскостях, а остальные грани —
параллелограммами, имеющими общие стороны с
этими многоугольниками.
Виды призм
Прямая
Наклонная
Правильная
Далее
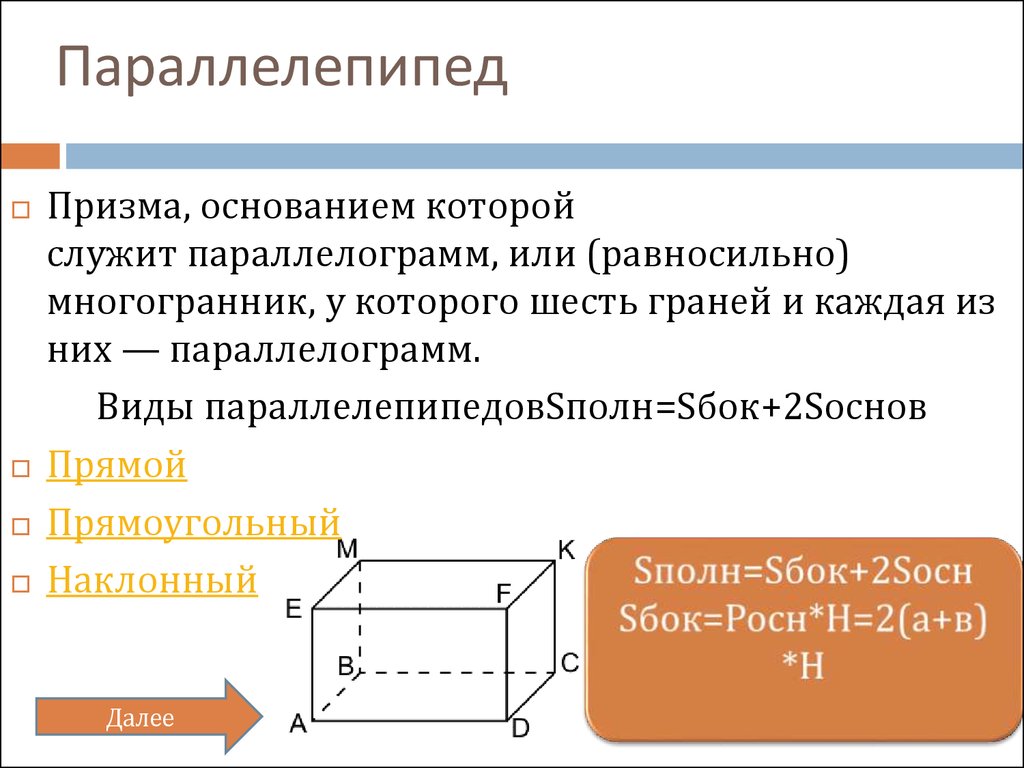
4. Параллелепипед
Призма, основанием которойслужит параллелограмм, или (равносильно)
многогранник, у которого шесть граней и каждая из
них — параллелограмм.
Виды параллелепипедовSполн=Sбок+2Sоснов
Прямой
Прямоугольный
Наклонный
Далее
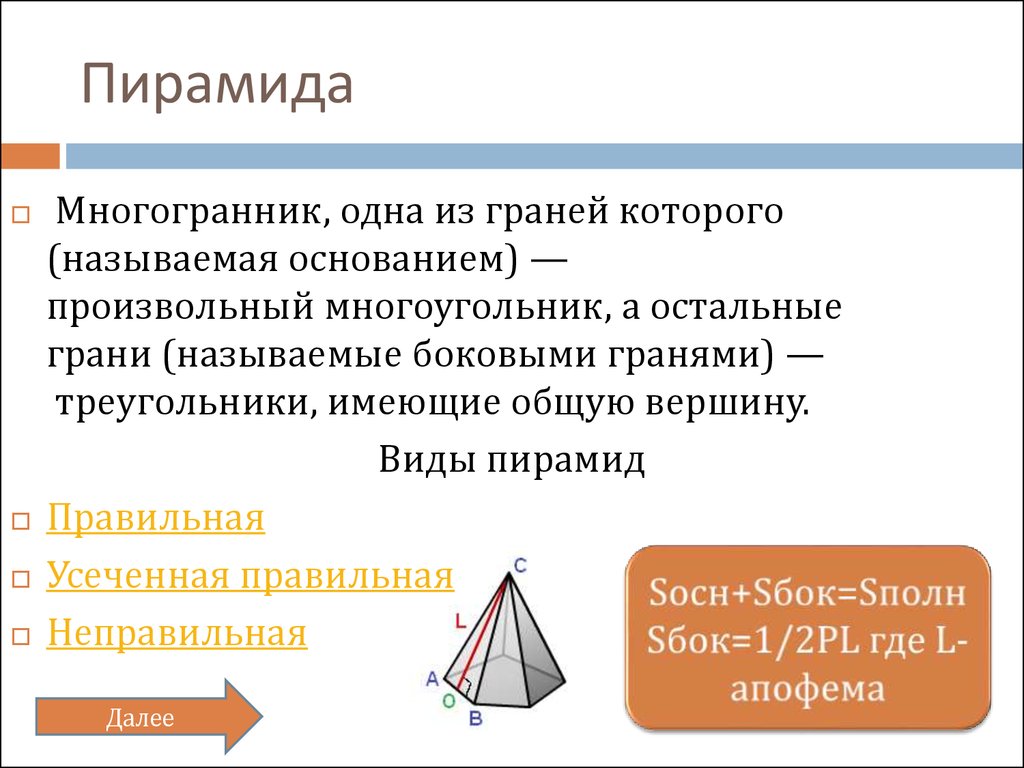
5. Пирамида
Многогранник, одна из граней которого(называемая основанием) —
произвольный многоугольник, а остальные
грани (называемые боковыми гранями) —
треугольники, имеющие общую вершину.
Виды пирамид
Правильная
Усеченная правильная
Неправильная
Далее
6. Наклонная
Призма боковые ребра которой неперпендикулярны основанию.
Свойства
Боковые рёбра не перпендикулярны
В основании лежат произвольные
многоугольники
7. Правильная
Правильная призма — это прямая призма,основанием которой является правильный
многоугольник.
Свойства
Основания правильной призмы являются пр
авильными многоугольниками.
Боковые грани правильной призмы являютс
я равными прямоугольниками.
Боковые ребра правильной призмы равны.
8. Прямая
Прямой призмой называют призму, боковыеребра которой перпендикулярны к
плоскостям оснований.
Свойства
Все боковые грани прямой призмы
являются прямоугольниками.
Высота прямой призмы равна длине
бокового ребра.
Боковые ребра перпендикулярны
плоскостям.
9. Прямой
В основании лежит параллелограмм , а рёбраперпендикулярны к основанию.
Свойства
4 ребра прямоугольники.
10. Прямоугольный
Прямоугольный параллелепипед - это прямой параллелепипед, восновании которого прямоугольник.
Свойства
Примерами прямоугольного параллелепипеда служат классная
комната, кирпич, спичечный коробок или системный
блок компьютера.
Длины трёх рёбер прямоугольного параллелепипеда, имеющих
общий конец, называют его измерениями. Прямоугольный
параллелепипед с равными измерениями называется кубом. Все
шесть граней куба — равные квадраты.
Квадрат длины диагонали прямоугольного параллелепипеда равен
сумме квадратов трёх его измерений.
11. Наклонный
Все его грани – параллелограммы, апротивоположные грани — равные
параллелограммы.
Свойства
Диагонали параллелепипеда пересекаются в
одной точке и делятся в этой точки пополам.
12. Правильная
Пирамида называется правильной, если основанием еёявляется правильный многоугольник, а вершина проецируется в центр
основания. Тогда она обладает такими свойствами:
Свойства
боковые рёбра правильной пирамиды равны;
в правильной пирамиде все боковые грани — конгруэнтные
равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать вокруг
неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских
углов при вершине пирамиды равна , а каждый из них соответственно ,
где n — количество сторон многоугольника основания;
площадь боковой поверхности правильной пирамиды равна половине
произведения периметра основания на апофему.
13. Усеченная правильная
Усеченной пирамидой называется многогранник, у котороговершинами служат вершины основания и вершины ее сечения
плоскостью, параллельной основанию.
Свойства
Основания усеченной пирамиды — подобные многоугольники.
Боковые грани усеченной пирамиды — трапеции.
Боковые ребра правильной усеченной пирамиды равны и
одинаково наклонены к основанию пирамиды.
Боковые грани правильной усеченной пирамиды — равные
между собой равнобедренные трапеции и одинаково наклонены
к основанию пирамиды.
Двугранные углы при боковых ребрах правильной усеченной
пирамиды равны.
14. Неправильная
Пирамида называется неправильной, если в её основаниилежит неправильный многоугольник , или если в основании
правильный многоугольник, но вершина пирамиды не
проектируется в центр основания.












 Математика
Математика








