Представление чисел в позиционных системах счисления

1. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ

МК
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ
В ПОЗИЦИОННЫХ
СИСТЕМАХ СЧИСЛЕНИЯ
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ

2. Общие сведения

МК
МК
Общие сведения
!
Система счисления – это способ записи чисел.
Унарные
Непозиционные
Узелки
Камни
Римская {I, V, X, L, C, D, M}
Кириллическая
Позиционные
Двоичная {0, 1}
Восьмеричная {0, 1, 2, 3, 4, 5, 6, 7}
Двенадцатеричная {0, 1, …, 9, T, E}
Шестнадцатеричная
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

3. Позиционные системы счисления

МК
МК
Позиционные системы счисления
!
Система счисления называется позиционной, если
количественный эквивалент цифры зависит от её
положения (места, позиции) в записи числа.
Основное достоинство любой позиционной системы
счисления – возможность записи произвольного числа
ограниченным количеством символов.
Основание
Название
Базис
q=2
Двоичная
1, 2, 4, 8, 16, 32, …
q=3
Троичная
1, 3, 9, 27, 81, 243, …
q=8
Восьмеричная
1, 8, 64, 512, …
q = 16
Шестнадцатеричная
1, 16, 256, 4096, …

4. Позиционная система счисления

МК
МК
Позиционная система счисления
!
Представление числа в виде суммы разрядных
слагаемых называется развёрнутой формой записи
числа в системе счисления с основанием q.
Свернутая
форма
Развернутая
форма

5. Перевод чисел в 10-ую систему

МК
МК
Перевод чисел в 10-ую систему
!
Алгоритм перевода в 10-ую систему счисления:
1. Записать развёрнутую форму числа .
2. Представить все числа, фигурирующие в
развёрнутой форме, в 10-ой системе счисления
3. Вычислить значение полученного выражения.
2 1 0 -1

6. Схема Горнера

МК
МК
Схема Горнера
Перевести в 10-ую систему счисления:
1 = 1
1 0 = 2
1·2+0
1 0 0 = 4
2·2+0
1 0 0 1 = 9
4·2+1
1 0 0 1 0 = 18
9·2+0
1 0 0 1 0 1 = 37
18·2+1
1 0 0 1 0 1 1 = 75
37·2+1
?
По схеме Горнера перевести
в 10-ую систему счисления:
1100110011
10100011
20213 2 2

7. Пример решения

МК
МК
Пример решения

8. Пример решения

МК
?
Пример решения
Все четырехбуквенные слова, составленные из пяти букв
M, A, G, I, P записаны в алфавитном порядке.
1
2
3
4
5
6
7
AAAA
AAAG
AAAI
AAAM
AAAP
AAGA
…
M
P
Каким по счету в списке слов будет GIMP?
Решение:
Введем обозначения:
A
G
I
0
1
2
3
4
Получаем список чисел в пятеричной системе счисления:
1
2
3
4
5
6
7
0000
0001
0002
0003
0004
0010
…
GIMP: 12345 = 1∙53 + 2∙52 + 3∙51 + 4 = 125 + 50 + 15 + 4 = 194
Ответ: 195

9. Перевод целого десятичного числа в систему счисления с оcнованием q

МК
Перевод целого десятичного числа
в систему счисления с оcнованием q
МК
Для перевода целого десятичного числа в систему
счисления с основанием q следует:
1) последовательно выполнять деление данного числа и
получаемых целых частных на основание новой системы
счисления до тех пор, пока не получится частное, равное
нулю;
2) полученные остатки, являющиеся цифрами числа в
новой системе счисления, привести в соответствие
алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая
его, начиная с последнего остатка.

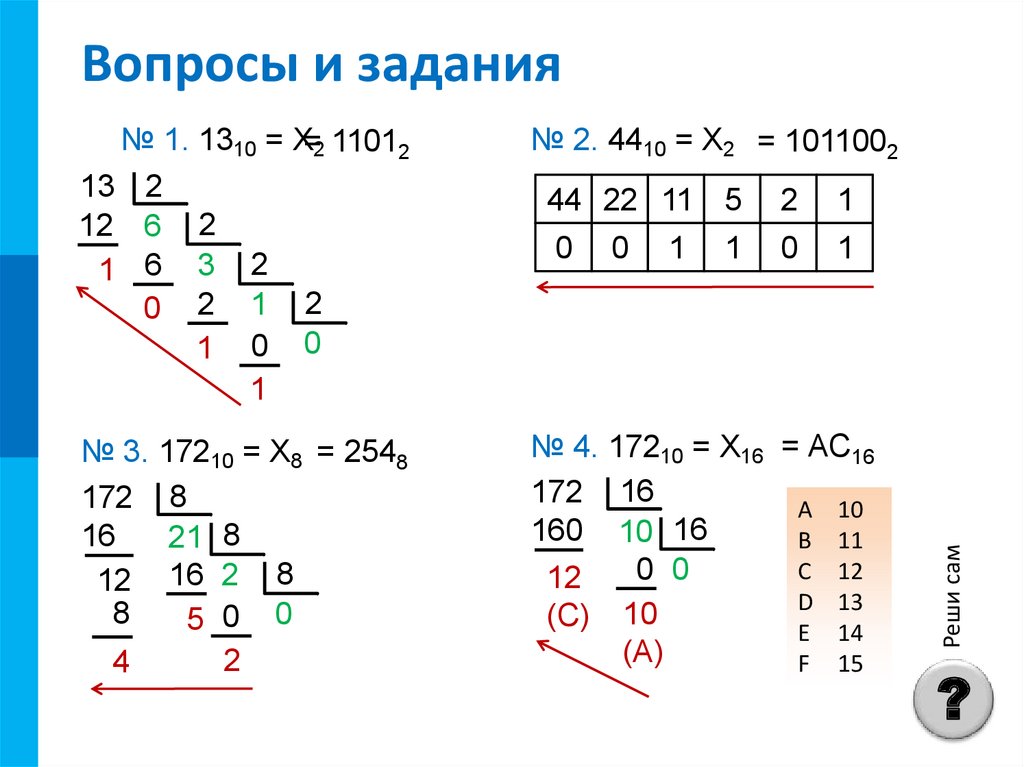
10. Вопросы и задания

МК
МК
№ 1. 1310 = Х=2 11012
13 2
12 6 2
1 6 3 2
0 2 1 2
1 0 0
1
№ 2. 4410 = Х2 = 1011002
№ 3. 17210 = Х8 = 2548
172 8
16
21 8
12 16 2 8
8
5 0 0
2
4
№ 4. 17210 = Х16 = АС16
172 16
A 10
160 10 16
B 11
C 12
0 0
12
D 13
(С) 10
E 14
(А)
F 15
44 22 11 5
2
1
0
0
1
0
1
1
Реши сам
Вопросы и задания
?

11. Решите самостоятельно

МК
Решите самостоятельно
№ 5. Переведите десятичные числа в указанные системы
счисления.
а) 10010
=X
1100100
2
2
е) 23310
б) 18710
=X
273
8 8
ж) 30210 = X
456
8 8
=X
11101001
2
2
в) 257210 = A0C
X16 16
з) 380210 = X
EDA
16 16
г) 145810 = X
21313
5
5
и) 95010 = X
12300
5
5
д) 5310
к) 4110
=X
1222
3
3
= 1112
X3 3
ОТВЕТ

12. Перевод целого десятичного числа в двоичную систему счисления

МК
Перевод целого десятичного числа
в двоичную систему счисления
МК
Для перевода числа Х (X≤10000) в двоичную систему
счисле-ния можно воспользоваться таблицей степеней
двойки.
№ 6. 529 = Х = 1000010001
10
2
2
Реши сам
Решение:
Представим число в виде суммы степеней двойки, для этого:
• возьмем максимально возможное значение, не превышающее исходное число (512 < 529);
• найдем разность между исходным числом и этим
значением (17);
• выпишем степень двойки, не превышающее эту разность
и т. д.
52910 = 512 + 17 = 512 + 16 + 1 =
= 29 + 24 + 20 = 10000100012
210
29
1024 512
28
27
26
25
24
23
22
21
20
256
128
64
32
16
8
4
2
1
?

13. Решите самостоятельно

МК
Решите самостоятельно
№ 7. Переведите десятичные числа в двоичную систему
счисления, используя таблицу степеней двойки:
210
29
1024 512
а) 9710
28
27
26
25
24
23
22
21
20
256
128
64
32
16
8
4
2
1
=X
1100
0012
2
г) 8410
=X
1010100
2
2
б) 32810 = X
101001000
2
2
д) 29210 = X
100100100
2
2
в) 109010 = X
10001000010
2
2
е) 54710 = X
1000100011
2
2
ОТВЕТ

14. Перевод десятичной дроби в систему счисления с основанием q

МК
Перевод десятичной дроби в
систему счисления с основанием q
МК
№ 8. 0,37510 = Х2 = 0,0112
0,375
х
2
0,75
х
2
0,750
1,50
х
0,5
2
1,0
Операция
0,375 · 2
0,75 · 2
0,5
Результат
0,750
1,500
1,000
Реши сам
Для перевода конечной десятичной дроби в систему
счисления с основанием q следует:
1) последовательно умножать данное число и получаемые
дробные части произведения на основание новой
системы счисления до тех пор, пока дробная часть
произведения не станет равна нулю или не будет
достигнута требуемая точность представления числа;
2) полученные целые части (цифры числа) привести в
соответствие алфавиту новой системы счисления;
3) составить дробную часть числа в новой системе
счисления, начиная с целой части первого произведения.
?

15. Решите самостоятельно

МК
Решите самостоятельно
№ 9. Переведите десятичные дроби в систему счисления с
указанным основанием (с точностью до трех знаков после
запятой):
а) 0,62510 = X
0,101
2
2
0,110
г) 0,75010 = X
2
2
б) 0,24510 = X
0,175
8
8
0,100
д) 0,12510 = X
8
8
в) 0,46010 = X
0,75С
16
16
0,5D7
е) 0,36510 = X
16
16
ОТВЕТ

16. Решите самостоятельно

МК
Решите самостоятельно
№ 10. Переведите смешанные десятичные числа в систему
счисления с указанным основанием (с точностью до трех
знаков после запятой):
При переводе смешанных чисел из десятичной системы счисления в
любую другую отдельно (по разным правилам) переводится целая и
дробная части.
а) 98,7510
= 1100010,110
X2
2 г) 43,12510
=X
101011,001
2
2
б) 100,37510 = 144,300
X8
8
д) 16,7810
в) 121,12110 =≈ X
79,1EF
16
16
е) 750,75010 == X
2EE,C00
16
16
=
X8
≈ 20,617
8
ОТВЕТ

17. Перевод чисел из системы счисления с основанием р в систему счисления

МК
МК
Перевод чисел из системы
счисления с основанием р в систему
счисления
с основанием q
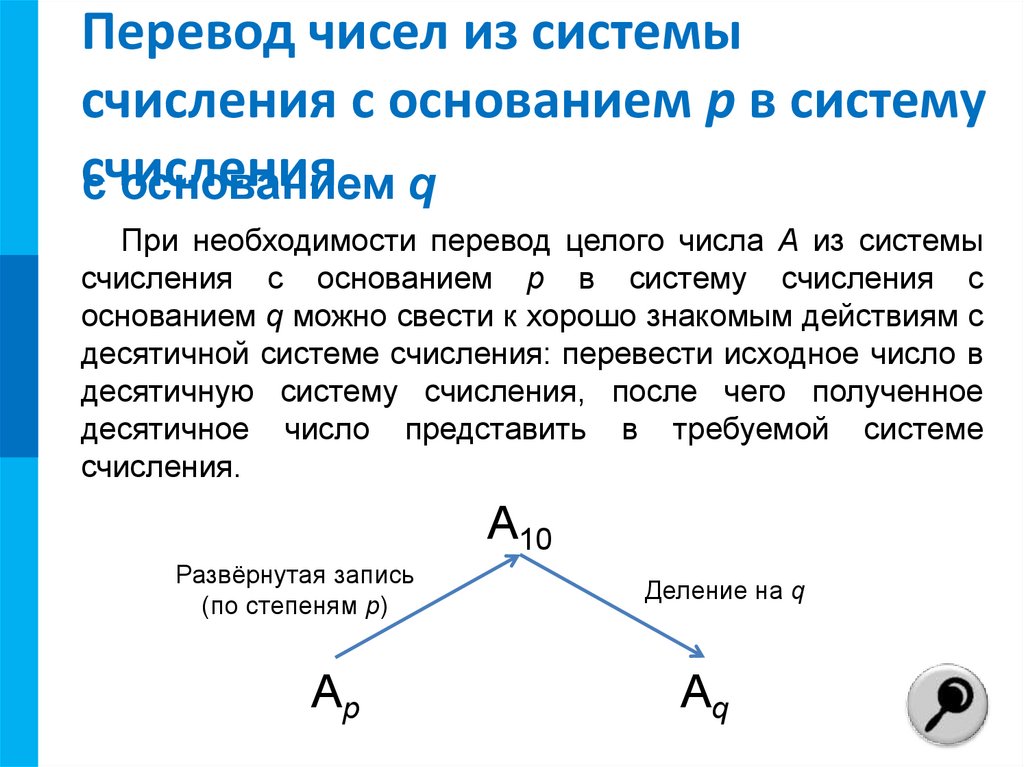
При необходимости перевод целого числа А из системы
счисления с основанием p в систему счисления с
основанием q можно свести к хорошо знакомым действиям с
десятичной системе счисления: перевести исходное число в
десятичную систему счисления, после чего полученное
десятичное число представить в требуемой системе
счисления.
А10
Развёрнутая запись
(по степеням p)
Аp
Деление на q
Аq

18. Быстрый перевод чисел в компьютерных системах счисления

МК
Быстрый перевод чисел в
компьютерных системах счисления
МК
Способ
«быстрого»
переводаоснован
основанна
натом,
том, что
что каждой
Способ
«быстрого»
перевода
цифре числа в системе счисления, основание которой q
кратно степени двойки, соответствует число, состоящее из n
(q=2n) цифр в двоичной системе счисления. Замена
восьмеричных цифр двоичными тройками (триадами) и
шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод. Для этого:
1) данное двоичное число надо разбить справа налево на
группы по n цифр в каждой;
2) если в последней левой группе окажется меньше n
разрядов, то её надо дополнить слева нулями до нужного
числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное
число и записать её соответствующей цифрой системы
счисления с основанием q = 2n.

19. Перевод целых чисел между двоичной и восьмеричной системами счисления

А
МК
2
Восьмеричные
цифры заменяем
триадами
Триады меняем на
восьмеричные
цифры
А8
А8
№ 11. 11001012 = Х8 = 1458
001100101
1
4
5
№ 12. 3028 = Х2 = 110000102
3
0
2
0 1 1 0 0 00 1 0
Цифра →
?
Двоичный
Триада
код
0
→
0
0
0
1
→
0
0
1
2
→
0
1
0
3
→
0
1
1
4
→
1
0
0
5
→
1
0
1
6
→
1
1
0
7
→
1
1
1

20. Перевод целых чисел между двоичной и 16-ной системами счисления

Перевод целых чисел между
двоичной и 16-ной системами
счисленияА
МК
Цифра →
2
16-ные цифры
заменяем
тетрадами
А16
Тетрады меняем на
16-ные цифры
А16
№ 13. 11011012 = Х16 = 6D16
01101101
6
D
№ 14. 5A316 = Х2 = 101101000112
5
A
3
01011010 0011
?
Двоичные
Тетрадакоды
0
→
0
0
0
0
1
→
0
0
0
1
2
→
0
0
1
0
3
→
0
0
1
1
4
→
0
1
0
0
5
→
0
1
0
1
6
→
0
1
1
0
7
→
0
1
1
1
8
→
1
0
0
0
9
→
1
0
0
1
A (10) →
1
0
1
0
B (11) →
1
0
1
1
C (12) →
1
1
0
0
D (13) →
1
1
0
1
E (14) →
1
1
1
0
F (15) →
1
1
1
1

21. Перевод дробной части между двоичной и восьмеричной системами

Перевод дробной части между
двоичной и восьмеричной
?
системами
Чтобы записать правильную двоичную дробь в системе счисления
МК
с основанием q = 2n, достаточно:
1) двоичное число разбить слева направо на группы по n цифр в
каждой; если в последней правой группе окажется меньше n
разрядов, то её надо дополнить справа нулями до нужного
числа разрядов;
2) рассмотреть каждую группу как n-разряд- Цифра → Триада
ное двоичное число и записать её
0
→ 0 0 0
соответствующей цифрой.
0, 1 1 1 0 1 0
0,
7
2
№ 16. 0,1328 = Х2 = 0,001011012
3
2
0, 1
0, 0 0 1 0 1 10 1 0
1
→ 0
0
1
2
→ 0
1
0
3
→ 0
1
1
4
→ 1
0
5
→ 1
0
6
→ 1
1
7
→ 1
1
Реши сам
№ 15. 0,111012 = Х8 = 0,728
0
1
0
?1

22. Решите самостоятельно

МК
Решите самостоятельно
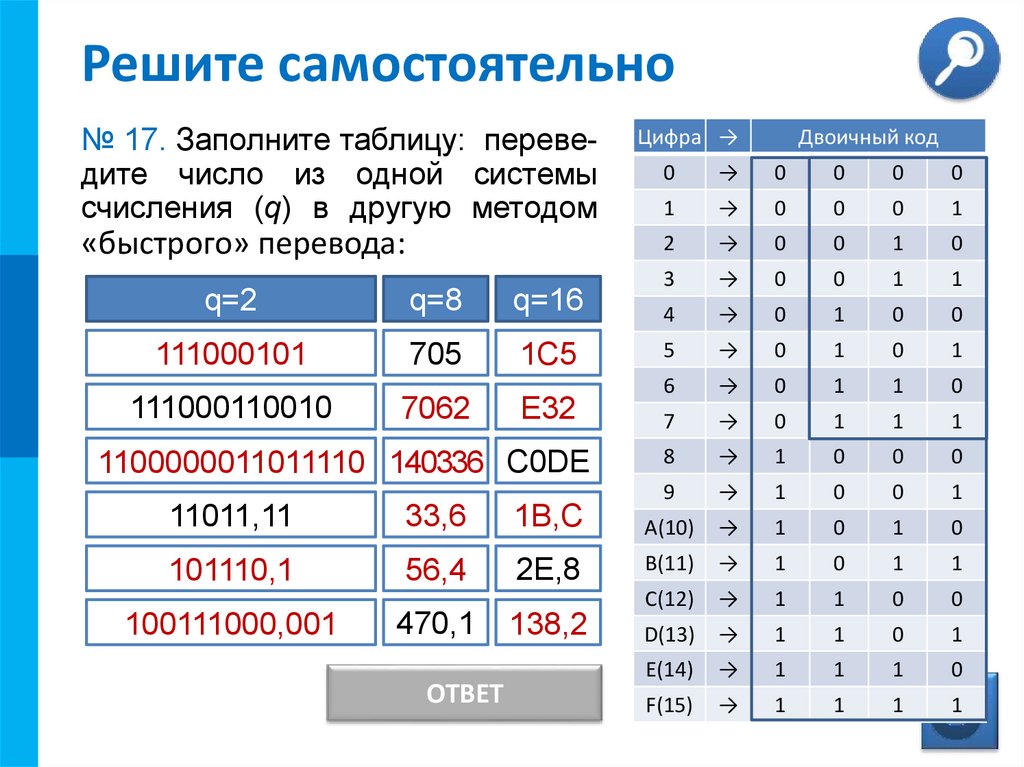
№ 17. Заполните таблицу: переведите число из одной системы
счисления (q) в другую методом
«быстрого» перевода:
q=2
q=8
q=16
111000101
705
1C5
111000110010
7062
E32
1100000011011110 140336 C0DE
Цифра →
Двоичный код
0
→
0
0
0
0
1
→
0
0
0
1
2
→
0
0
1
0
3
→
0
0
1
1
4
→
0
1
0
0
5
→
0
1
0
1
6
→
0
1
1
0
7
→
0
1
1
1
8
→
1
0
0
0
9
→
1
0
0
1
11011,11
33,6
1B,С
А(10)
→
1
0
1
0
101110,1
56,4
2E,8
B(11)
→
1
0
1
1
C(12)
→
1
1
0
0
D(13)
→
1
1
0
1
E(14)
→
1
1
1
0
F(15)
→
1
1
1
1
100111000,001
470,1
ОТВЕТ
138,2

23. Вопросы и задания

МК
МК
Вопросы и задания
Задание 3. Все 5-буквенные слова, составленные из
букв
А, Б и В, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА
5. АААББ
…
Какие слова находятся в этом списке на 51-м и 200-м
местах?
Решение:
Слово в трехбуквенном алфавите можно рассматривать,
как запись слова в троичной системе в 5-разрядном
представлении. Тогда А – 0, Б – 1, В – 2.

24. Вопросы и задания

МК
МК
Вопросы и задания
Задание 3 (решение).
А – 0, Б – 1, В – 2.
При такой записи незначащие нули в начале (слева)
тоже записываются:
1. ААААА = 000003 = 010
2. ААААБ = 000013 = 110
3. ААААВ = 000023 = 210
4. АААБА = 000103 = 310
…
…
= *****3 = 5010
51. ?
= *****3 = 19910
200. ?
Аналогично
Чтобы
понять,
надо
какое
перевести
слово
соответствует
в
троичную систему
этому счислечислу,
надочисло
ния
перевести
199. его в троичную систему
199 3 счисления и при
необходимости
дополнить
198 66 3
слева «0»66
до 22
пяти3разрядов.
1
0 21 7 3
50 31 6 2 3
48 16 3 1 0 0
3
2 15 5
2
3
3
1
1
0 0
2
На 51-м месте в списке стоит 19910 = 211013 → ВББАБ
1
число 51-1 = 50, а на 200-м –
Ответ:
→ВББАБ
АБВБВ
5010 = АБВБВ
012123 и
число 200-1=199.