Численное моделирование распространения одномерных волн горения в газовых смесях

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
Национальный исследовательский ядерный университет «МИФИ»
КАФЕДРА №97
«Суперкомпьютерное моделирование в инженерно-физических процессах»
ОТЧЕТ
Учебная практика(научно-исследовательская работа)
на тему:
«Численное моделирование распространения одномерных волн горения в газовых смесях на основе водорода»
Выполнил:
Студент группы Б21-221
Денисов В.А.
Научный руководитель:
Киверин А.Д.
г.Москва, 2024

2.

Вступление
Ламинарные волны горения предварительно перемешанной
смеси
vlam>vu
2

3.

Цель:исследовать зависимость скорости
ламинарного горения от состава смеси на
основе водорода.
Задачи:
Ознакомление с физико-химическими моделями и
лабораторным пакетом NRG, которые
используются для решения задач горения
Провели расчеты по тестовым постановкам задач о
ламинарном горении для валидации, верификации
и оценки вычислительной эффективности
реализованных в NRG алгоритмов
3

4.

Математическая модель
∂ρ ∂ρu
+
=0
∂t ∂x
∂ ρ Y k ∂ ρ uY k ∂ ρ Y k V k
+
=
+ ρ ω̇ k
∂t
∂x
∂x
Где x – пространственная координата,
t — время,
ρ — плотность,
Y k — массовая доля k-ого типа частиц,
u — кордината вектора скорости,
V k — k-ая скорость диффузии частиц,
ω̇k — мощность химического источника
4

5.

hk ∂ Y k
∂ ( ρ E) ∂ (ρ u E) ∂
∂T
∂
+
=
(uσ − u p)+[
(κ (T)
)+ρ ∑
(
)]
∂t
∂x
∂x
∂x
∂x
k mk ∂ t
1 2
E= ϵ+ u — удельная суммарная энергия,
2
ϵ — удельная внутренняя энергия,
κ (T ) - теплопроводность,
D k (T) — коэффициент диффузии k-ого типа частиц,
hk - энтальпия образования k-ого вещества,
mk - молярная масса k-ого вещества
5

6.

2
∂ρu ∂ρu ∂
+
=
(σ − p)
∂t
∂x
∂x
4
∂u
σ = μ (T)
3
∂x
Где T — температура,
p - давление,
μ (T ) - коэффициент вязкости,
σ - компонента тензора вязких напряжений
Температурные зависимости коэффициентов вязкости,
диффузии и теплопроводности для отдельных компонент
смеси вычисляются из первых принципов молекулярнокинетической теории[1].
1. Ю.Варнатц, У.Масс, Р.Диббл «Горение. Физические и химические аспекты,
моделирование, эксперименты, образование загрязняющих веществ», 2006
6

7.

Постановка задачи
Первый вариант постановки задачи на поиск скорости
ламинарного горения.
U
θ
ρf
Где θ = ρ
V lam=
b
ρ f , ρ b - плотности
свежей смеси и продуктов
горения соответственно
7

8.

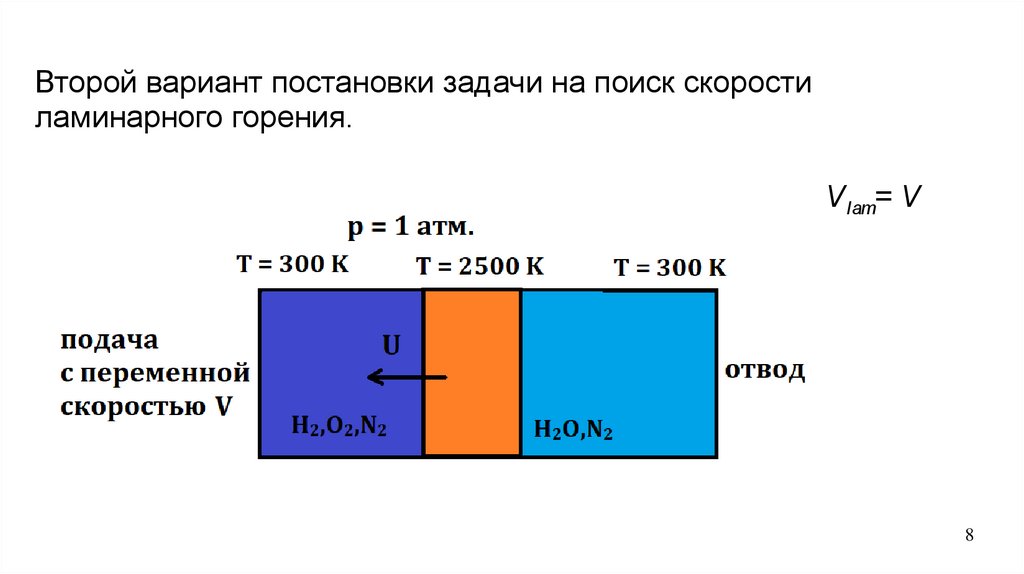
Второй вариант постановки задачи на поиск скорости
ламинарного горения.
V lam= V
8

9.

Численная схема решения
На платформе вычислительного пакета NRG реализован
алгоритм решения уравнений динамики химически
активных газовых смесей в приближении малых чисел
Маха, предложенный Fire Dynamics Simulator (FDS).
Алгоритм типа предиктор-коррекор имеет второй порядок
точности по времени и пространству. Это позволило
выполнить детальные расчеты процессов горения газовых
смесей малой интенсивности.
9

10.

Результаты
10

11.

Выводы
Лабораторный пакет NRG, использующий детальные
физико-химические модели, был применен для решения
задачи нахождения нормальной скорости горения
Полученная зависимость ламинарной скорости горения от
мольной доли водорода в смеси лежит в пределах
погрешности экспериментальных данных
Показана сходимость решения задачи о ламинарной
скорости горения при измельчении расчетной сетки
11

12.

Планы
Использование исследованной постановки задачи в
качестве бенчмарка для определения вычислительной
эффективности пакета NRG при использовании
вычислительных систем различной архитектуры, в том
числе суперкомпьютеров с общей и разделенной памятью
Использование полученных результатов для
профилирования и оптимизации пакета NRG с целью
улучшения эффективности решения задач горения с
использованием широкого круга архитектур
вычислительных систем
12

13.

Спасибо за внимание!
13

14.

График сходимости скорости и распределения
величин для второй постановки задачи
14