Похожие презентации:
Численное моделирование развития возмущений в ударном слое на пластине в потоке смеси колебательно возбужденных газов
1.
Семинар академика Фомина В.М.«Задачи аэрофизики и газовой динамики»
25 марта 2015 г., НГУ
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
РАЗВИТИЯ ВОЗМУЩЕНИЙ В УДАРНОМ СЛОЕ
НА ПЛАСТИНЕ В ПОТОКЕ СМЕСИ
КОЛЕБАТЕЛЬНО ВОЗБУЖДЕННЫХ ГАЗОВ
Решетова А.И.
Научный руководитель:
д.ф.-м.н. Поплавская Т.В.
2.
Мотивация1. Malik M.R., Anderson J.D. Real gas effect on hypersonic boundary layer stability //
Physics of Fluid A. 1991. Vol. 3, No. 5. pp. 803-821.
2. Осипов А.И, Уваров А.В Кинетические и газодинамические процессы в
неравновесной молекулярной физике // Успехи физических наук, т. 162, № 11, 1992г.
3. В.В. Лунёв Течение реальных газов с большими скоростями. - 2007 с.500.
4. Anderson J.D. Hypersonic and high temperature gas dynamics. 1989. 702pp.
5. Bertolotti F.P. The influence of rotational and vibrational energy relaxation on boundary
layer stability // Journal of Fluid Mechanics. 1998. Vol. 372. pp. 93-118.
6. Fujii K., Hornung H.G. Experimental investigation of high-enthalpy effects on attachmentline boundary-layer transition // AIAA Journal . 2003. V0l. 41, No. 7.
7. Григорьев Ю.Н., Ершов И.В. Устойчивость течений релаксирующих молекулярных
газов // Новосибирск: Изд-во СО РАН, 2012. 230с.
8. Гапонов С.А., Петров Г.В. Устойчивость пограничного слоя неравновесно
диссоциирующего газа // Новосибирск: Наука, 2013. 95с.
9. Кириловский С.В. , Поплавская Т.В., Цырюльников И.С. Применение пакета
ANSYS FLUENT для решения задач воздействия акустических волн на гиперзвуковой
ударный слой на пластине // Математическое моделирование. 2013. т.25. N 9.
10. С. В. Кириловский, А.А. Маслов, Т. В. Поплавская, И. С. Цырюльников Влияние
колебательной релаксации на развитие возмущений в ударном слое на пластине //
ЖТФ (в печати)
2
3.
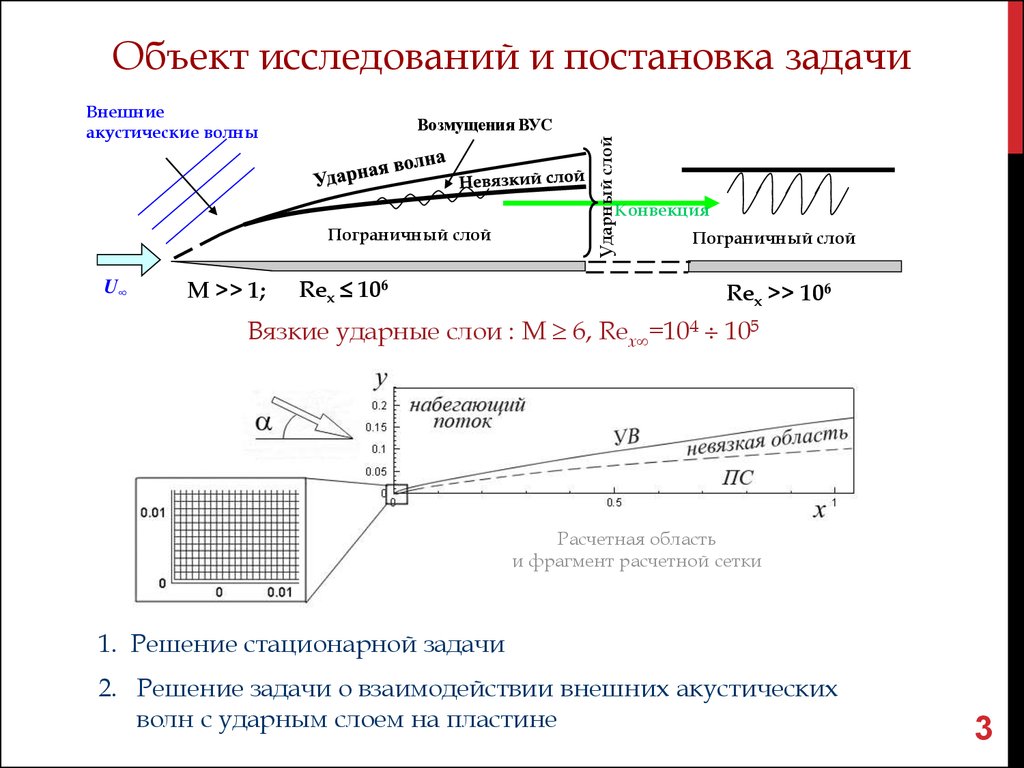
Объект исследований и постановка задачиВнешние
акустические волны
Ударный слой
Возмущения ВУС
Конвекция
Пограничный слой
U∞
M >> 1;
Rex 106
Пограничный слой
Rex >> 106
Вязкие ударные слои : М 6, Rex =104 105
Расчетная область
и фрагмент расчетной сетки
1. Решение стационарной задачи
2. Решение задачи о взаимодействии внешних акустических
волн с ударным слоем на пластине
3
4.
Развитие возмущений на пластинеЭкспериментальные исследования ИТ-302М ИТПМ
Маслов А.А., Миронов С.Г., Цырюльников И.С.
Состав потока
в рабочей части
ИТ-302:
Воздух; СО2
Смесь воздуха и СО2
Численное моделирование (ANSYS Fluent)
Кириловский С.В., Поплавская Т.В.
форкамера
коническое сопло
критическое
сечение
акустические Развитие возмущений
волны
III
M
P
T
I
Течение в сопловом тракте
аэродинамической трубы
II
Обтекание пластины
4
5.
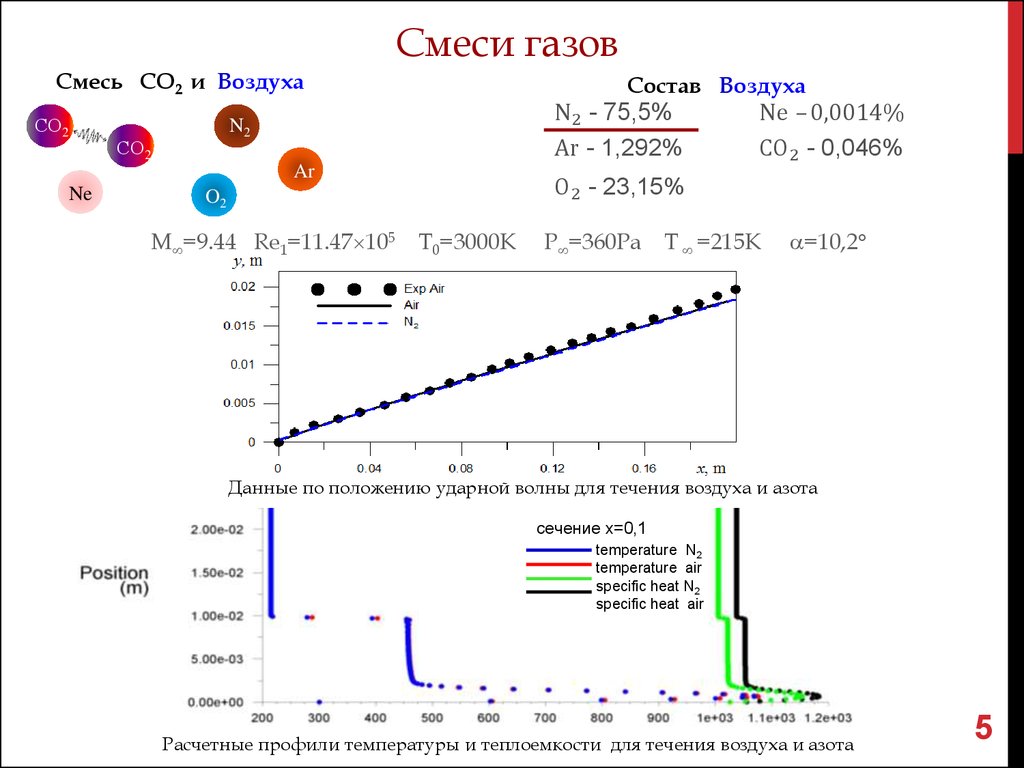
Смеси газовСмесь СО2 и Воздуха
СО2
N2 - 75,5%
Ar - 1,292%
N2
СО2
Ar
Ne
Состав Воздуха
O2
M =9.44 Re1=11.47 105 T0=3000K
Ne – 0,0014%
CO2 - 0,046%
O2 - 23,15%
P =360Pa
T =215K
=10,2
Данные по положению ударной волны для течения воздуха и азота
сечение х=0,1
temperature N2
temperature air
specific heat N2
specific heat air
Расчетные профили температуры и теплоемкости для течения воздуха и азота
5
6.
Колебательное движение в молекулахСО2
1
2
Моды:
симметричные
валентные колебания
θv :
деформационные
колебания
1920K
960K
СО2
СО2
СО2
СО2
СО2
асимметричные
валентные колебания
симметричные
колебания
3340K
3380K
Константы скорости релаксации k2 группы 2
Уровней молекулы CO2 при столкновениях
с молекулами М (Т=300К)
Смесь СО2 и N2
СО2
N2
3
СО2
M
k2 (мм рт.ст.)-1 с-1
CO2
194
N2
650
N2
В. Виттеман СО2-лазер // М. «Мир». 1990
N2
6
7.
Термодинамическая модельc p f T
Термически
совершенный газ
c p f T
равновесный vt f
c p f T , t
неравновесный
vt ~ f
Иерархия времён релаксационных процессов
Макроскопический уровень
описания колебательной релаксации
с помощью двухтемпературной модели
релаксационных течений
tt rt vv vt ~ f
Уравнение Ландау-Теллера
для каждой колебательной степени свободы:
devib 1 eq
evib evib
dt vt
evib –
eq
evib
vt –
колебательная энергия (неравновесная)
e v
v
Ttr
1
R
колебательная энергия
(равновесная)
время колебательной релаксации
7
8.
Основные уравненияУравнения сохранения:
u 0
t
u u u p
импульса
t
4
4
( CO 2 N 2 )
n ( CO 2 CO2 )
e
u
e
p
T
u
q
qtvn
энергии
t
t
tr
tv
t
n 1
n 1
( CO CO )
( CO N )
evn u evn qtvn 2 2 qtvn 2 2
колебат. энергии
t
массы
UDS
+
UDF
n=1,…4
k теплопроводность,
сp,0 теплоёмкость поступательно-вращательных степеней свободы,
2
2
T I тензор вязких напряжений, et c p dTtr p u энергия газа
3
2
n
eq
n
n
n
колебательная энергия газа,
ev
e n
Ttr
1
R
ev
e n
Tv
1
R
n 1,..4
vt время колебательной релаксации,
поток энергии между поступательными и колебательными степенями свободы
n
eq
qtvn CO2 CO2 CO2 CO2 ev evn
СО2
vt
n ( CO2 N 2 )
tv
q
СО2
eq n n
(CO2 N 2 ) ev ev
СО2
vt
N2
9
9.
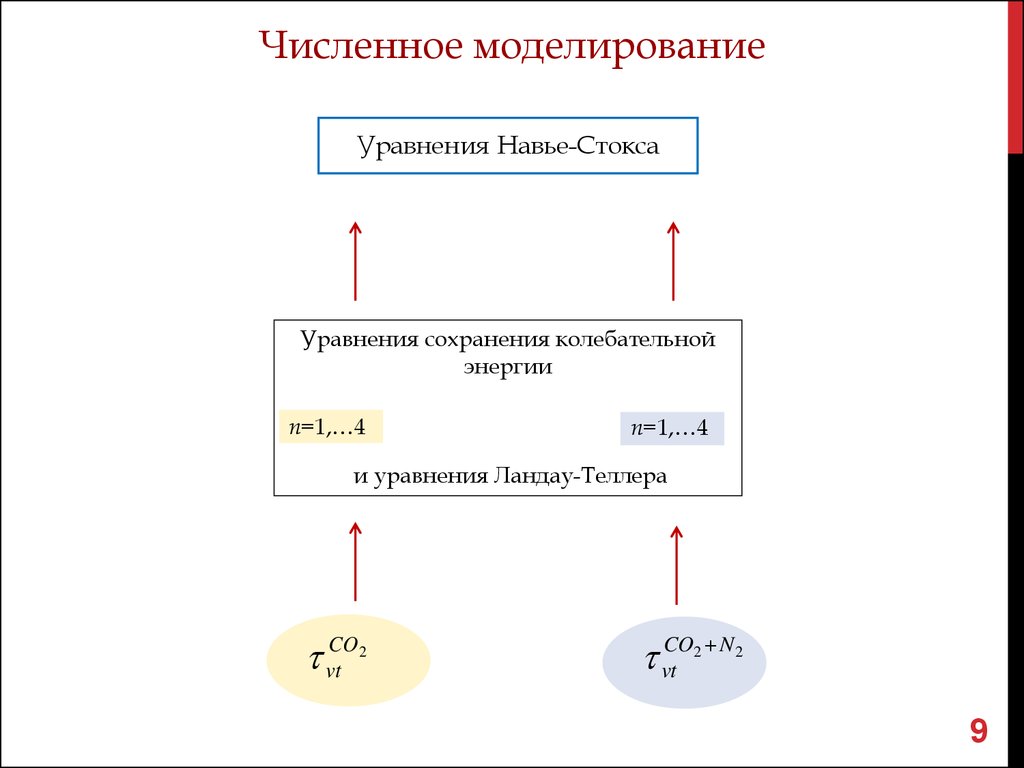
Численное моделированиеУравнения Навье-Стокса
Уравнения сохранения колебательной
энергии
n=1,…4
n=1,…4
и уравнения Ландау-Теллера
vtCO
2
vtCO N
2
2
9
10. Времена колебательной релаксации газов
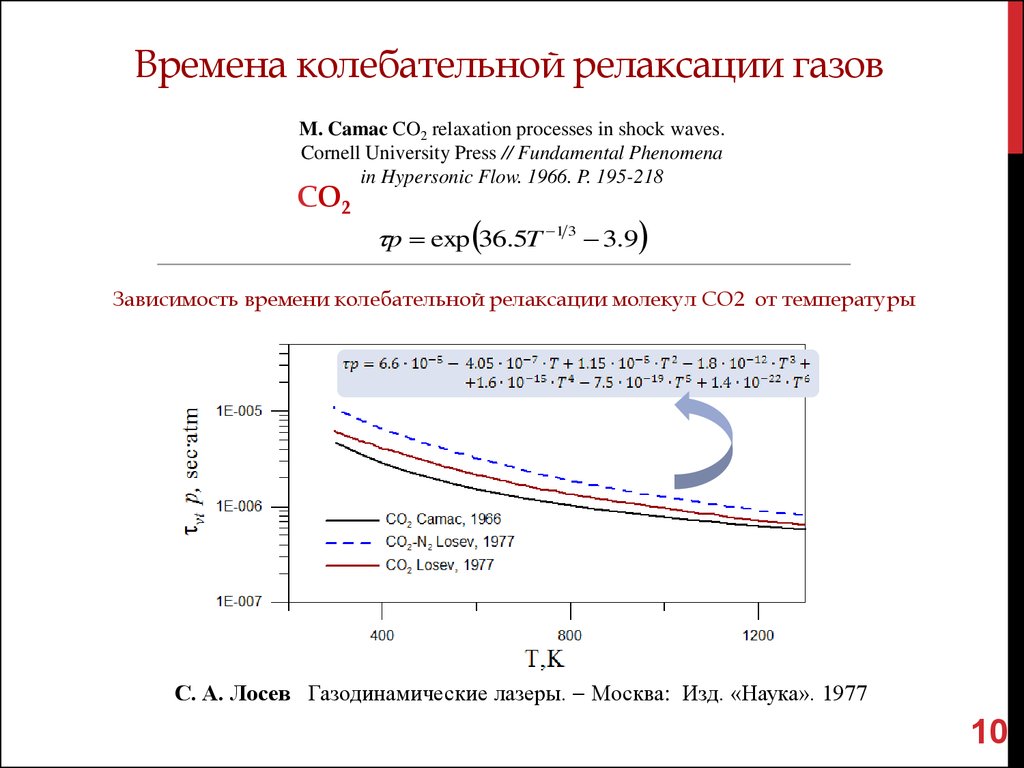
M. Camac CO2 relaxation processes in shock waves.Cornell University Press // Fundamental Phenomena
in Hypersonic Flow. 1966. P. 195-218
СО2
p exp 36.5T 1 3 3.9
Зависимость времени колебательной релаксации молекул СО2 от температуры
С. А. Лосев Газодинамические лазеры. Москва: Изд. «Наука». 1977
10
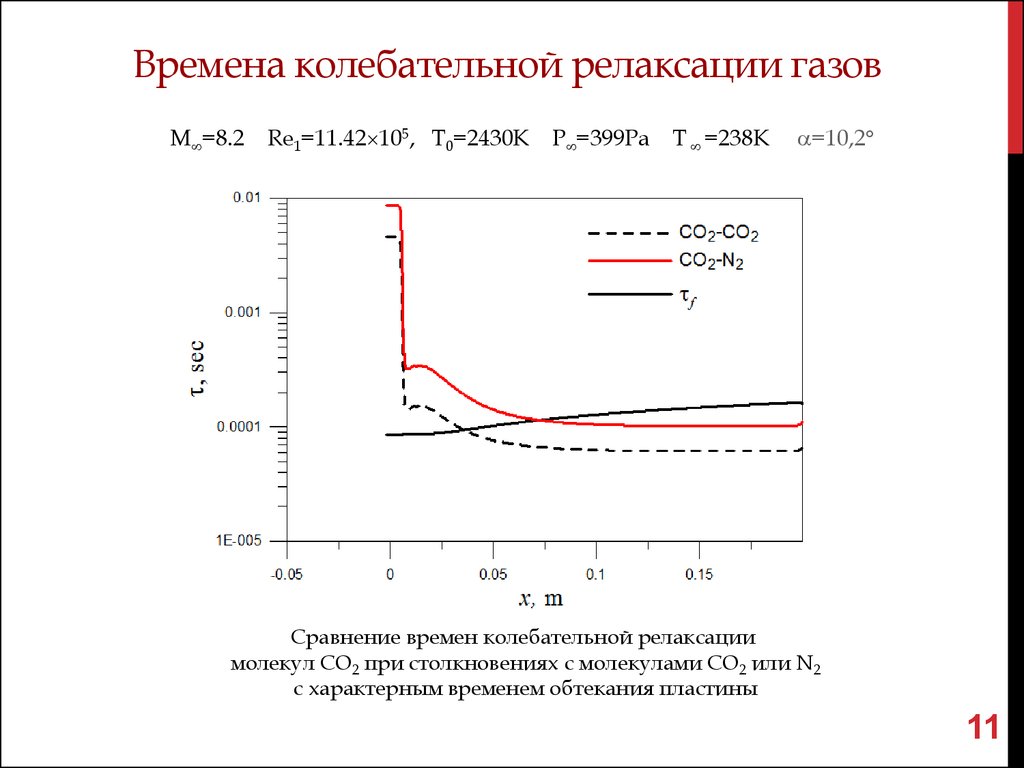
11. Времена колебательной релаксации газов
M =8.2Re1=11.42 105, T0=2430K P =399Pa
T =238K
=10,2
Сравнение времен колебательной релаксации
молекул СО2 при столкновениях с молекулами СО2 или N2
с характерным временем обтекания пластины
11
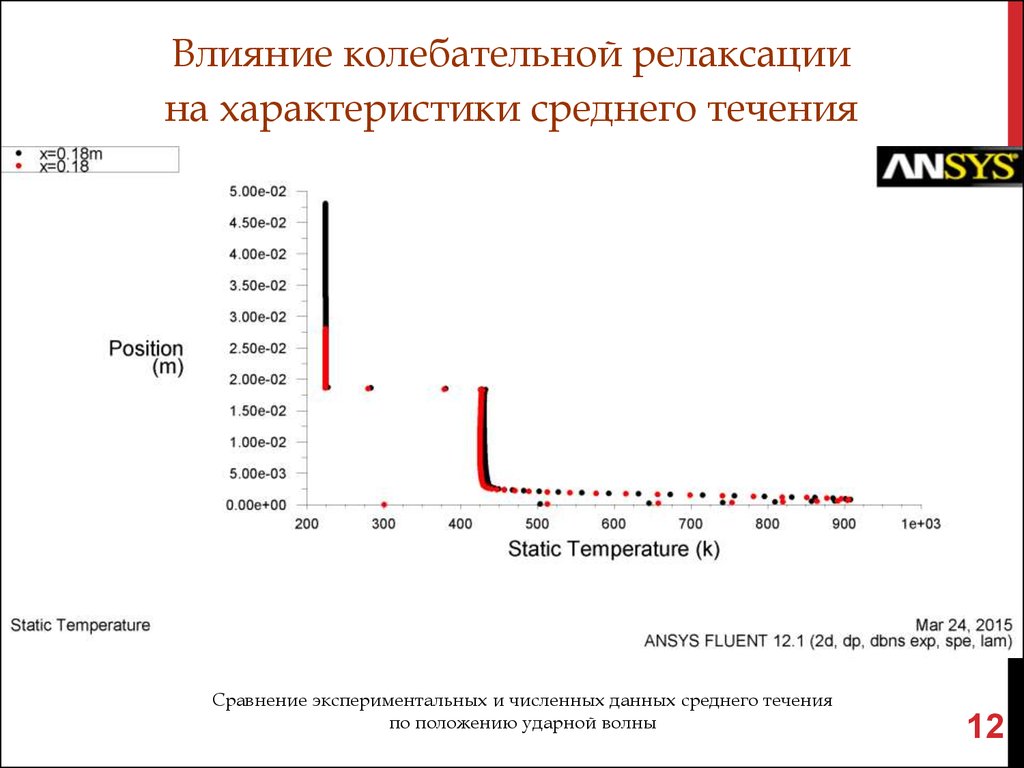
12.
Влияние колебательной релаксациина характеристики среднего течения
M =8.37, Re1=12.3 105, T =224K, p =382Па, =10,2 non-eq
Сравнение экспериментальных и численных данных среднего течения
по положению ударной волны
12
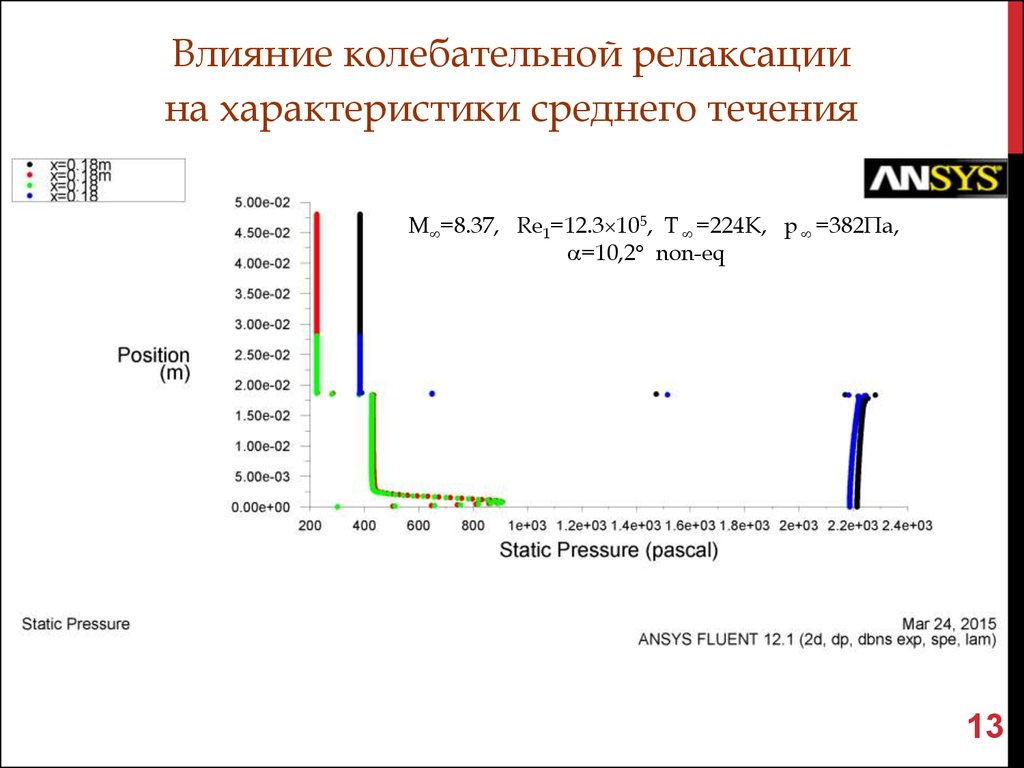
13.
Влияние колебательной релаксациина характеристики среднего течения
M =8.37, Re1=12.3 105, T =224K, p =382Па, =10,2 non-eq
M =8.37, Re1=12.3 105, T =224K, p =382Па,
=10,2 non-eq
13
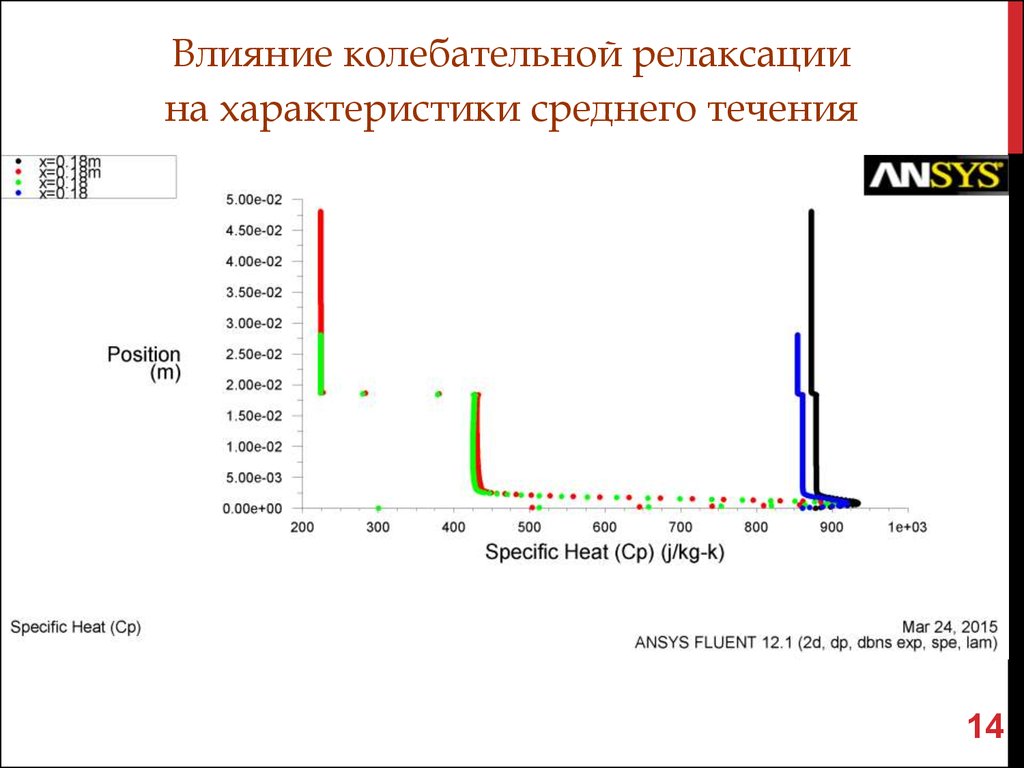
14.
Влияние колебательной релаксациина характеристики среднего течения
M =8.37, Re1=12.3 105, T =224K, p =382Па, =10,2 non-eq
14
15.
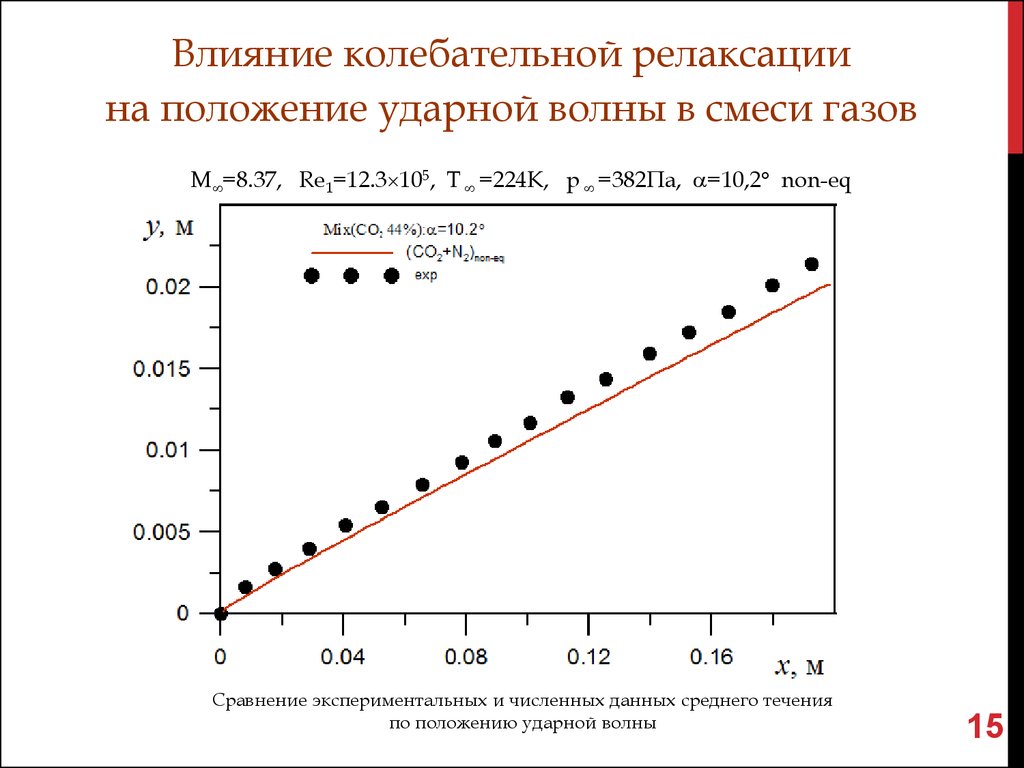
Влияние колебательной релаксациина положение ударной волны в смеси газов
M =8.37, Re1=12.3 105, T =224K, p =382Па, =10,2 non-eq
Сравнение экспериментальных и численных данных среднего течения
по положению ударной волны
15
16. Развитие возмущений в ударном слое
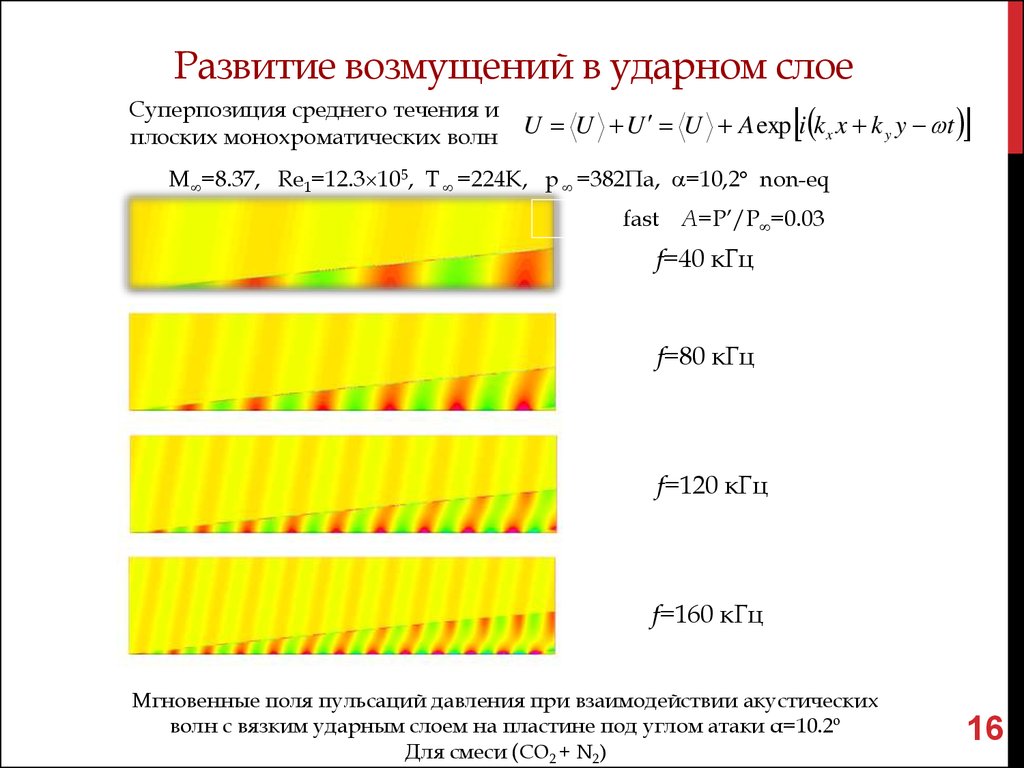
Суперпозиция среднего течения иплоских монохроматических волн U U U U A exp i k x k
x
y
y t
M =8.37, Re1=12.3 105, T =224K, p =382Па, =10,2 non-eq
fast
A=P’/P∞=0.03
f=40 кГц
f=80 кГц
f=120 кГц
f=160 кГц
Мгновенные поля пульсаций давления при взаимодействии акустических
волн с вязким ударным слоем на пластине под углом атаки α=10.2º
Для смеси (СО2 + N2)
16
17. Развитие возмущений в ударном слое
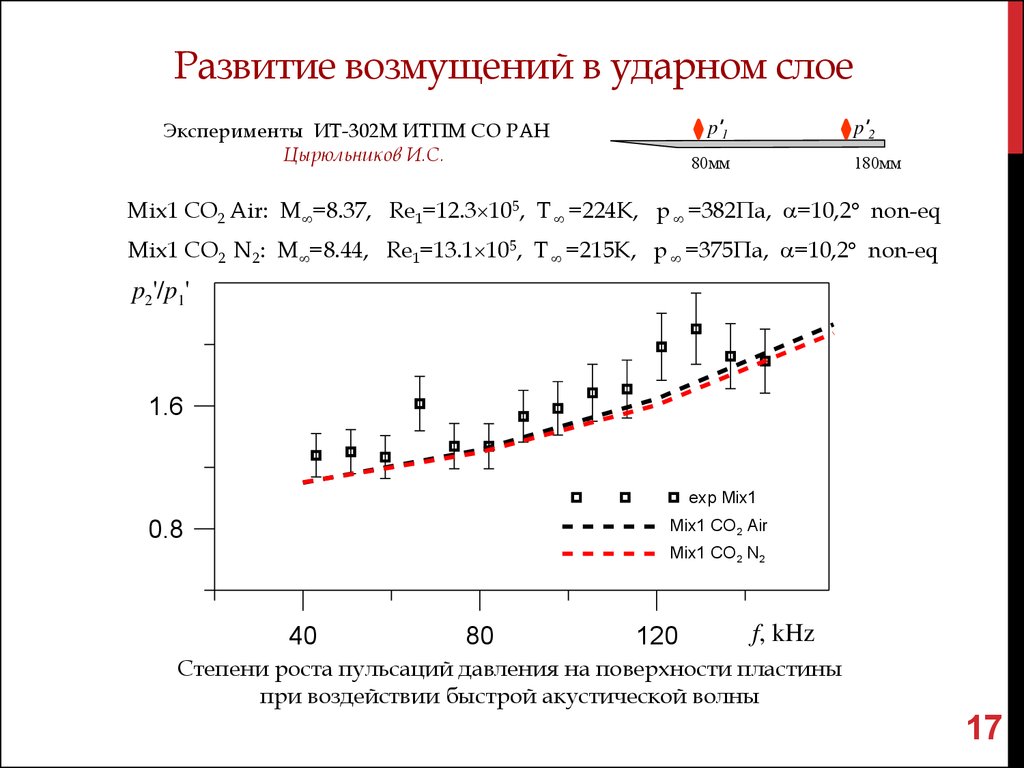
Эксперименты ИТ-302М ИТПМ СО РАНЦырюльников И.С.
p′1
p′2
80мм
180мм
Mix1 CO2 Air: M =8.37, Re1=12.3 105, T =224K, p =382Па, =10,2 non-eq
Mix1 CO2 N2: M =8.44, Re1=13.1 105, T =215K, p =375Па, =10,2 non-eq
p2'/p1'
1.6
exp Mix1
Mix1 CO2 Air
0.8
Mix1 CO2 N2
40
80
120
f, kHz
Степени роста пульсаций давления на поверхности пластины
при воздействии быстрой акустической волны
17
18. Планы на будущее
• Провести параметрические расчёты для:a. различных температур торможения;
b. различных концентраций СО2 в смеси с N2;
• Выступление на МНСК в апреле 2015г.;
Заключение
• Выполнено численное моделирование обтекания пластины под углом атаки в
потоке смеси воздуха и СО2 и смеси азота и СО2 для условий экспериментов в
аэродинамической трубе ИТ-302М ИТПМ СО РАН с учетом колебательной
релаксации молекул СО2 в рамках двухтемпературной модели релаксационных
течений;
• Для гиперзвуковых ударных слоев получены данные по динамике развития
возмущений на модели, обтекаемой гиперзвуковыми потоками смесей азота и
углекислого газа с учетом возбуждения и релаксации колебательных степеней
свободы молекул СО2 при столкновениях с молекулами других газов.
• Получено согласие расчетных и экспериментальных данных по
характеристикам среднего течения и развития возмущений.
Работа выполнена при поддержке гранта Правительства РФ (Договор № 14.Z50.31.0019)
для поддержки исследований под руководством ведущих ученых
18
19. Спасибо за внимание
СПАСИБО ЗА ВНИМАНИЕ19








 Физика
Физика Химия
Химия








