Построение сечений тетраэдра и параллелепипеда

1. Построение сечений тетраэдра и параллелепипеда.

2. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

3.

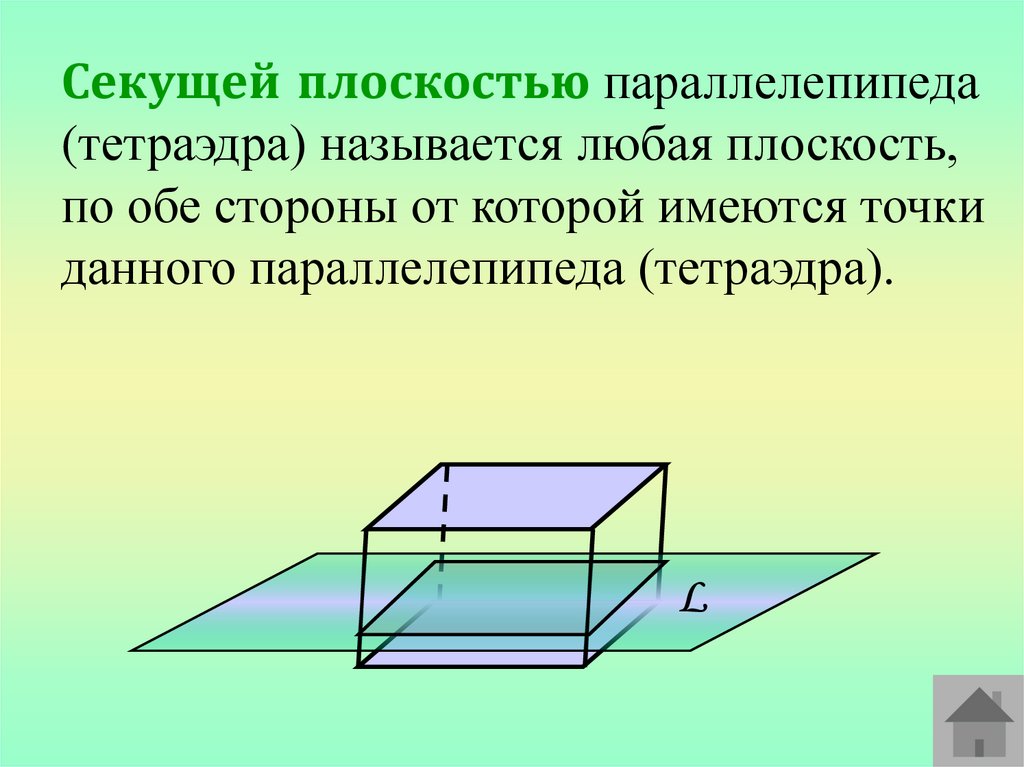
Секущей плоскостью параллелепипеда
(тетраэдра) называется любая плоскость,
по обе стороны от которой имеются точки
данного параллелепипеда (тетраэдра).
L

4.

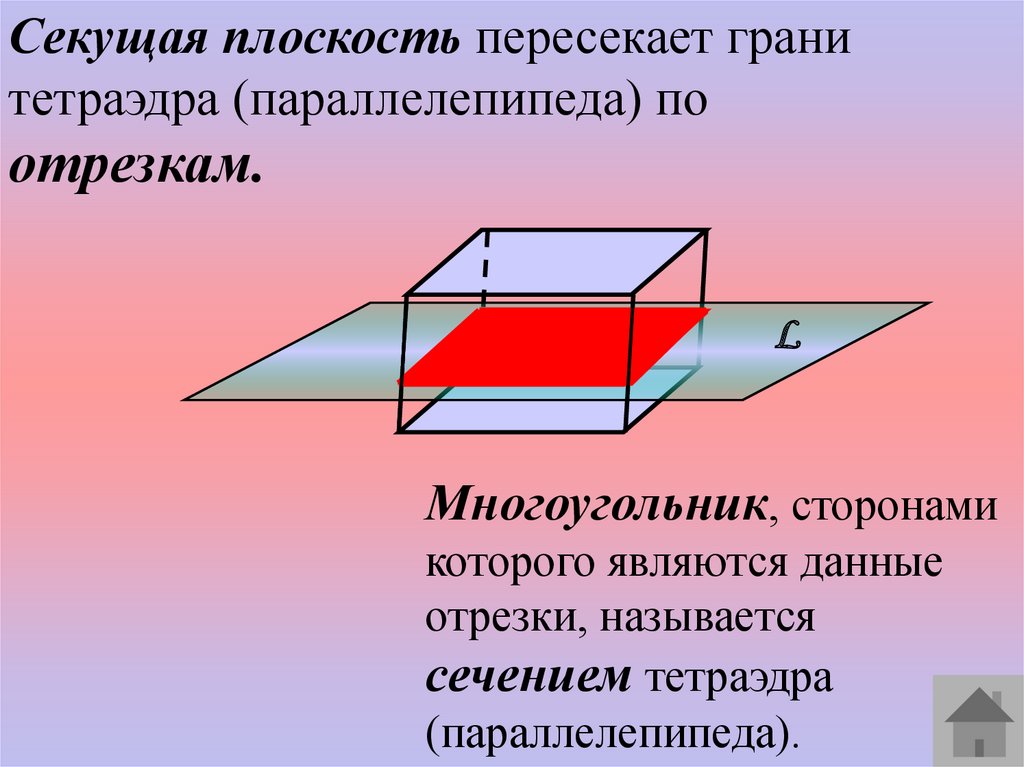
Секущая плоскость пересекает грани
тетраэдра (параллелепипеда) по
отрезкам.
L
Многоугольник, сторонами
которого являются данные
отрезки, называется
сечением тетраэдра
(параллелепипеда).

5. При этом необходимо учитывать следующее:

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает
параллельные
грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна
точка, принадлежащая плоскости сечения, то надо
построить дополнительную точку. Для этого
необходимо найти точки пересечения уже
построенных прямых с другими прямыми,
лежащими в тех же гранях.

6.

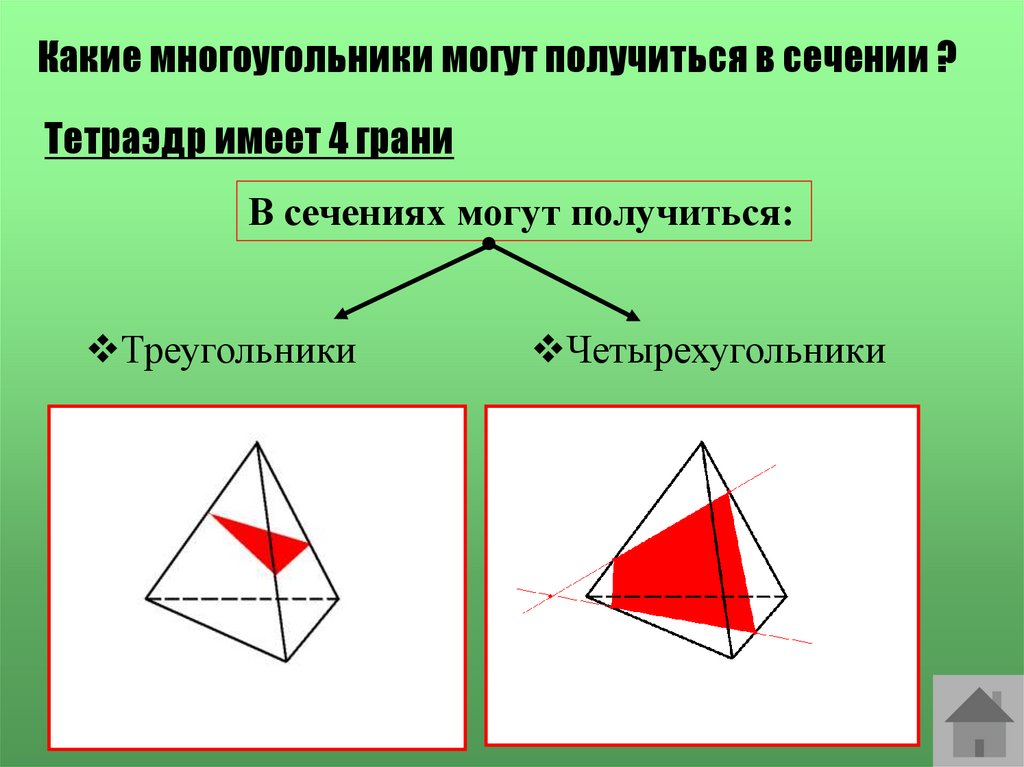
Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут получиться:
Треугольники
Четырехугольники

7.

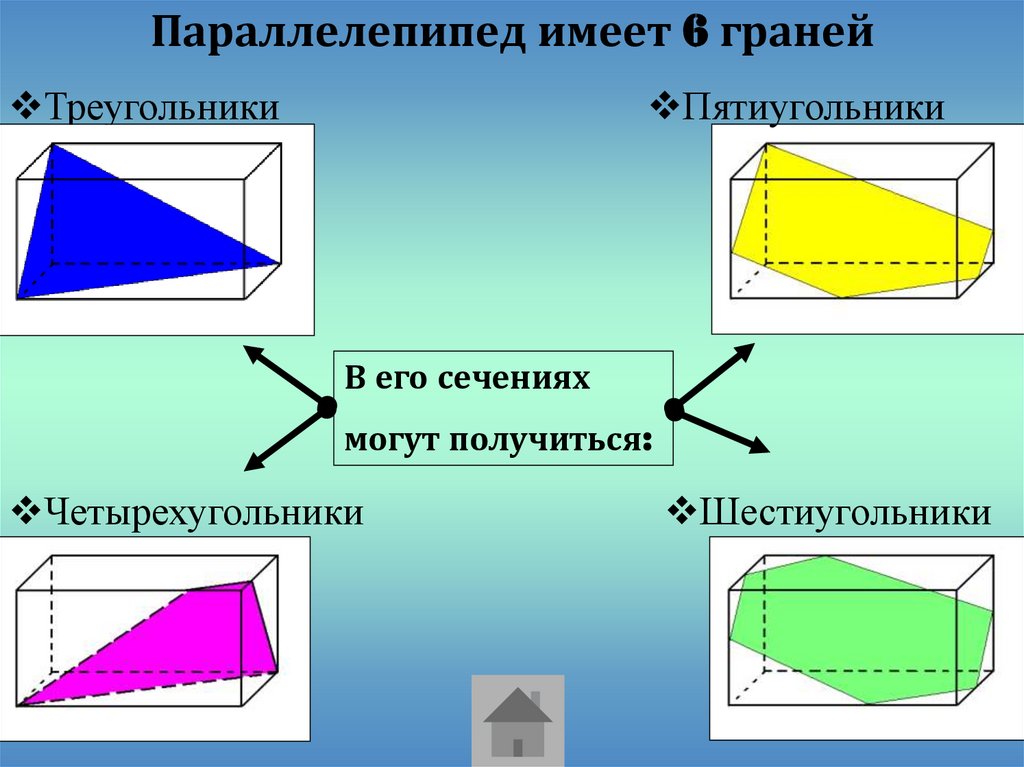
Параллелепипед имеет 6 граней
Треугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольники
Шестиугольники

8.

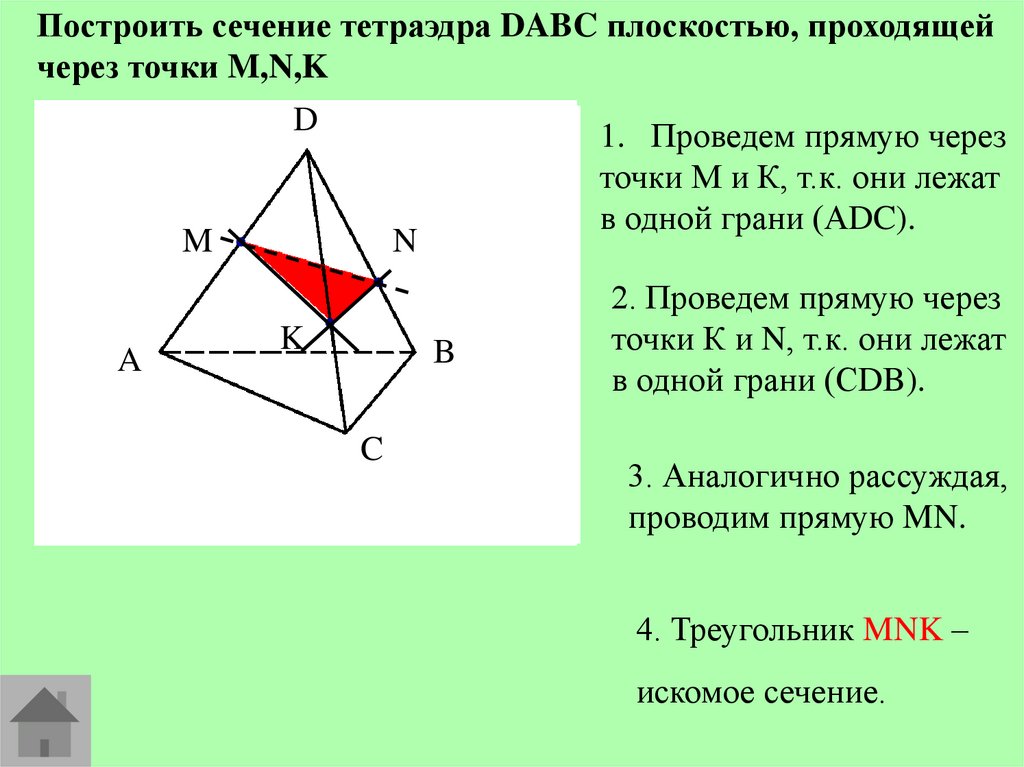
Построить сечение тетраэдра DABC плоскостью, проходящей
через точки M,N,K
D
M
AA
1. Проведем прямую через
точки М и К, т.к. они лежат
в одной грани (АDC).
N
K
BB
C
C
2. Проведем прямую через
точки К и N, т.к. они лежат
в одной грани (СDB).
3. Аналогично рассуждая,
проводим прямую MN.
4. Треугольник MNK –
искомое сечение.

9.

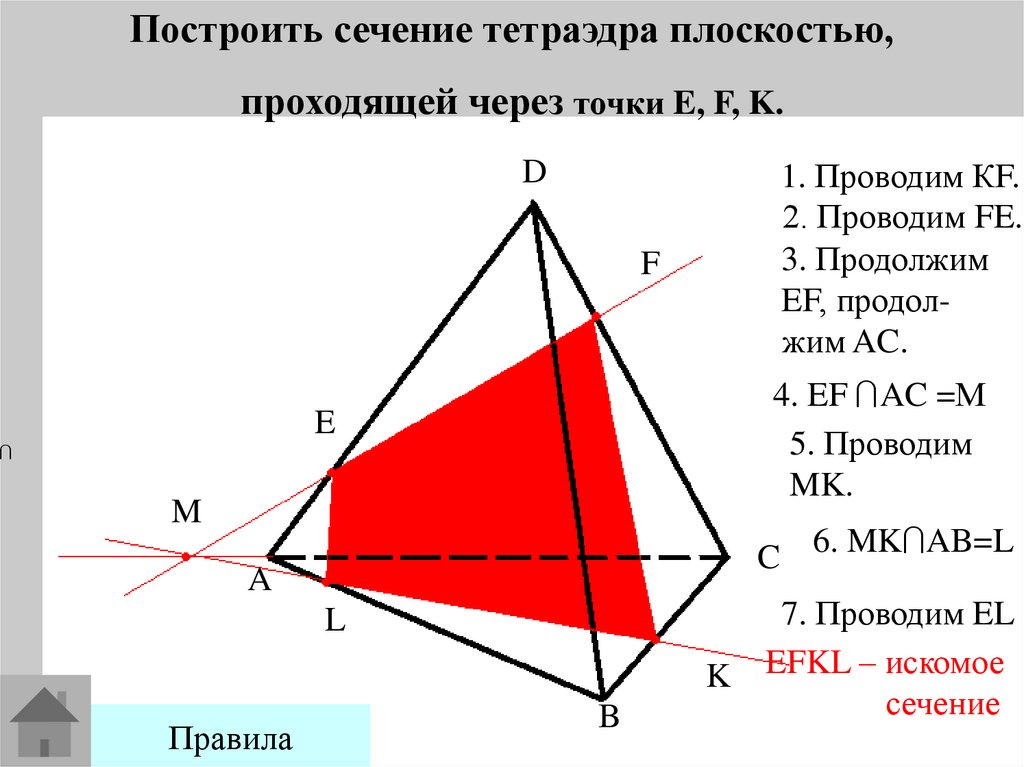
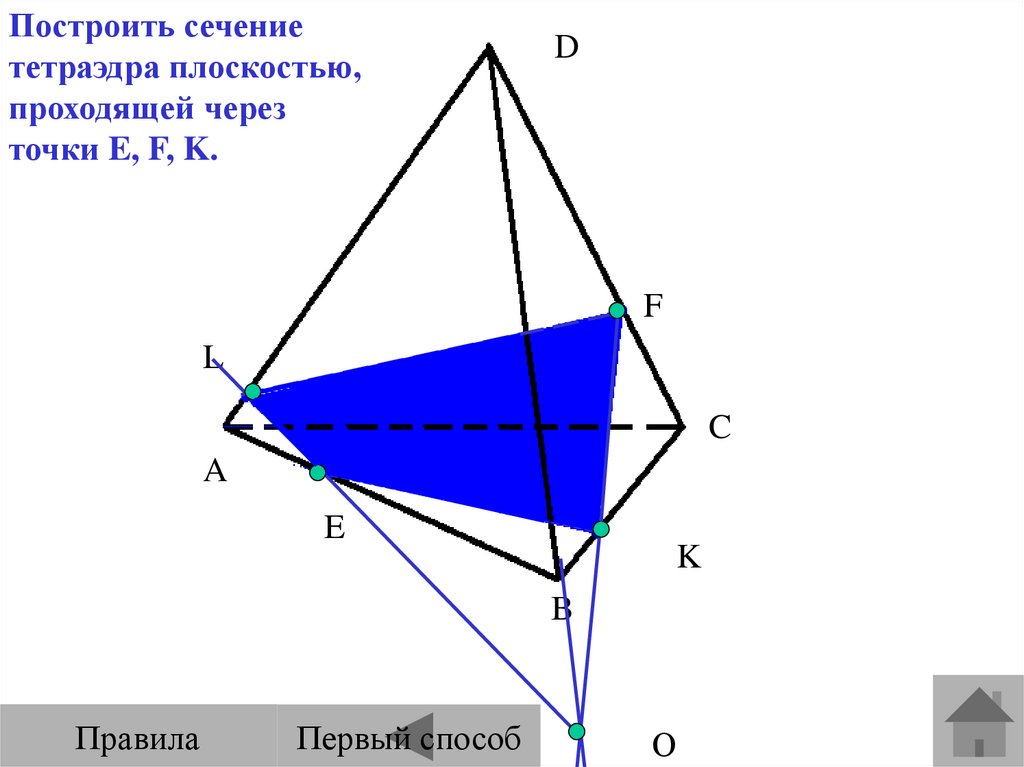
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
1. Проводим КF.
2. Проводим FE.
3. Продолжим
EF, продолжим AC.
D
F
4. EF AC =М
5. Проводим
MK.
E
M
C 6. MK AB=L
A
L
K
Правила
B
7. Проводим EL
EFKL – искомое
сечение

10.

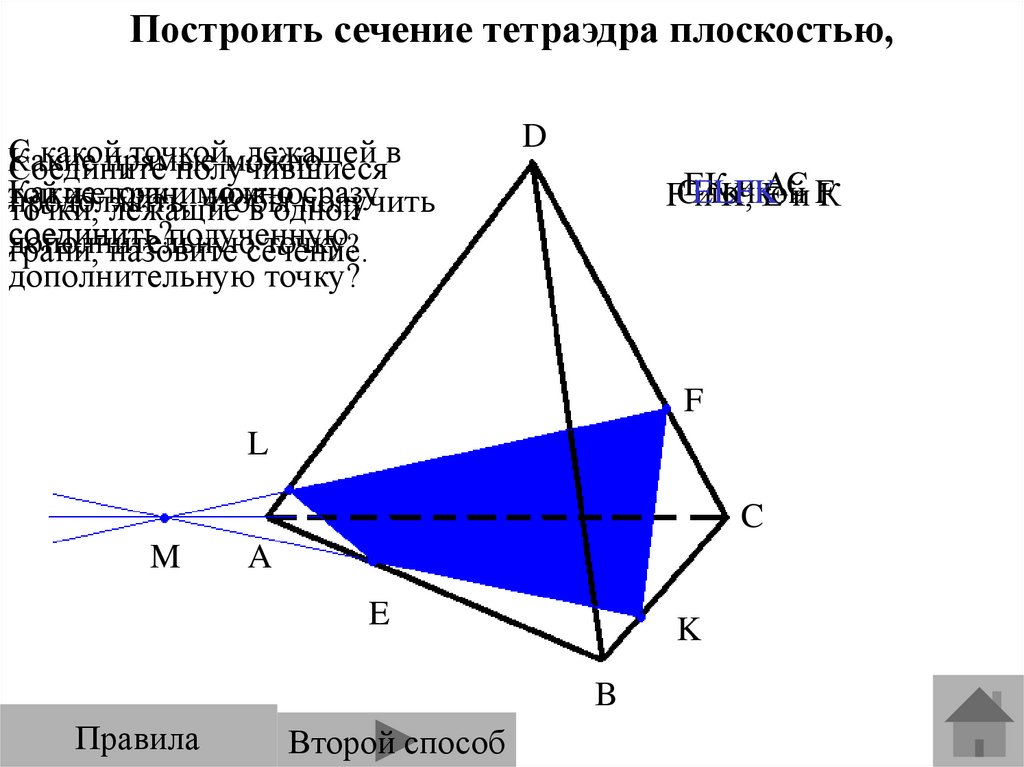
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
С
какойпрямые
точкой,
лежащей в
Какие
можно
Соедините
получившиеся
Какие
сразу
той
жеточки
граниможно
можно
продолжить,
чтобы
получить
точки,
лежащие
в одной
соединить?
соединить
полученную
дополнительную
точку?
грани, назовите
сечение.
дополнительную точку?
D
иЕ
АС
ЕLFK
FСЕК
иточкой
K,
и FК
F
L
C
M
A
E
K
B
Правила
Второй способ

11.

Построить сечение
тетраэдра плоскостью,
проходящей через
точки E, F, K.
D
F
L
C
A
E
K
B
Правила
Первый способ
О

12.

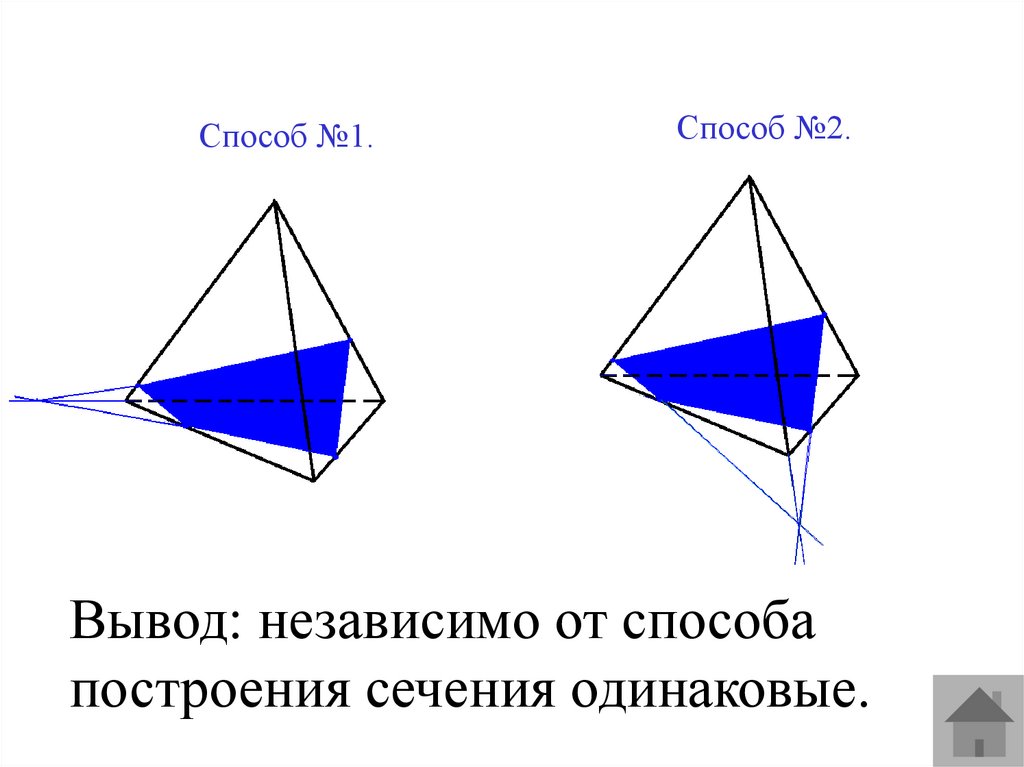
Способ №1.
Способ №2.
Вывод: независимо от способа
построения сечения одинаковые.

13.

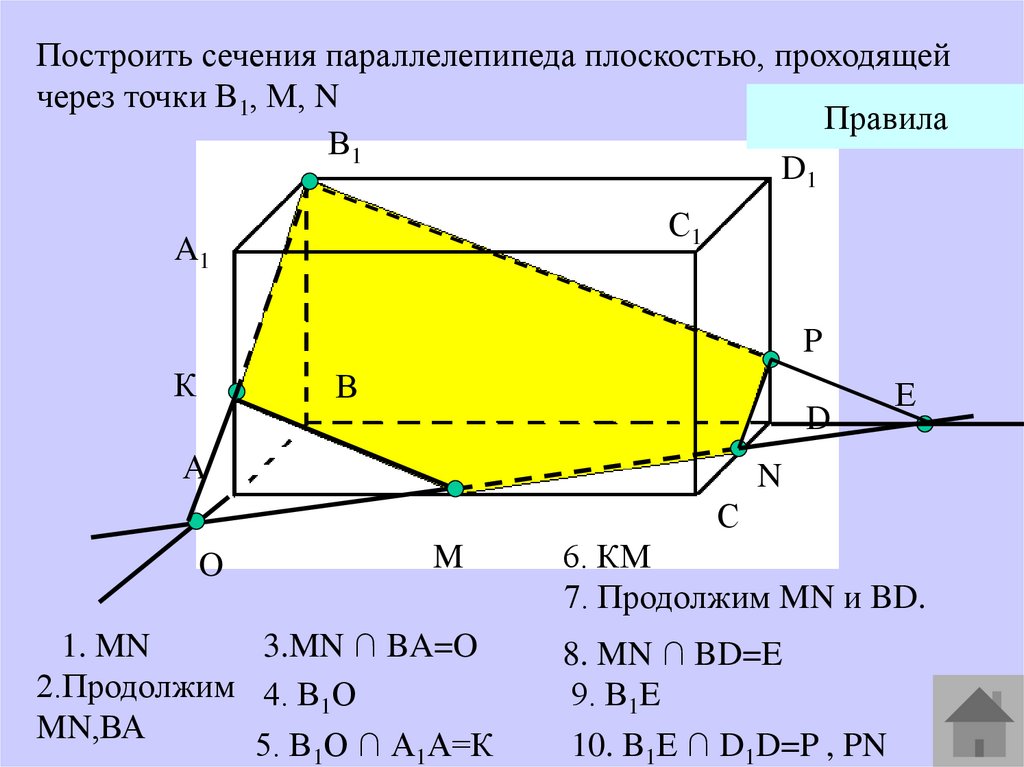
Построить сечения параллелепипеда плоскостью, проходящей
через точки В1, М, N
Правила
В1
D1
С1
A1
P
К
В
D
А
Е
N
С
O
M
1. MN
3.MN ∩ BA=O
2.Продолжим 4. В1О
MN,ВА
5. В1О ∩ А1А=К
6. КМ
7. Продолжим MN и BD.
8. MN ∩ BD=E
9. В1E
10. B1Е ∩ D1D=P , PN

14.

Построить сечение параллелепипеда плоскостью,
проходящей через точки M,A,D.
В1
D1
E
A1
С1
В
А
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – сечение.
М
D
С

15.

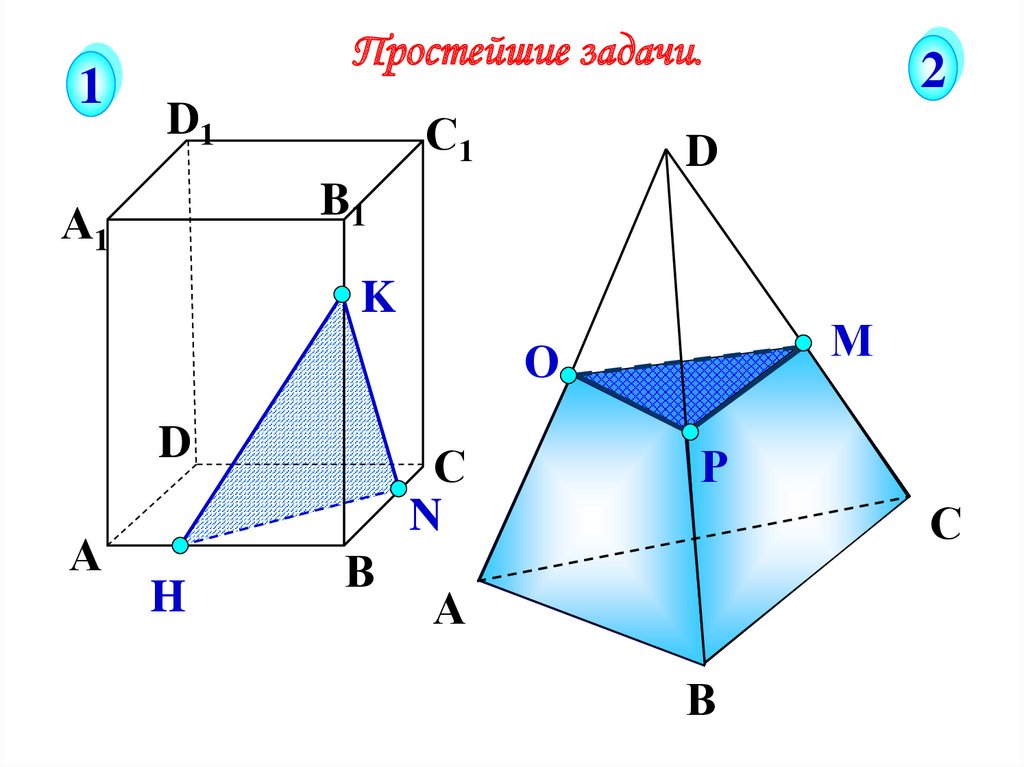
1
Простейшие задачи.
D1
С1
D
B1
А1
K
М
О
D
А
2
H
С
N
В
Р
С
А
В

16.

D
3
Простейшие задачи.
D
4
О
С
С
А
А
О
В
В

17.

Диагональные сечения.
5
С1
D1
А1
С
D
А
D1
А1
B1
В
6
С1
B1
С
D
А
В

18.

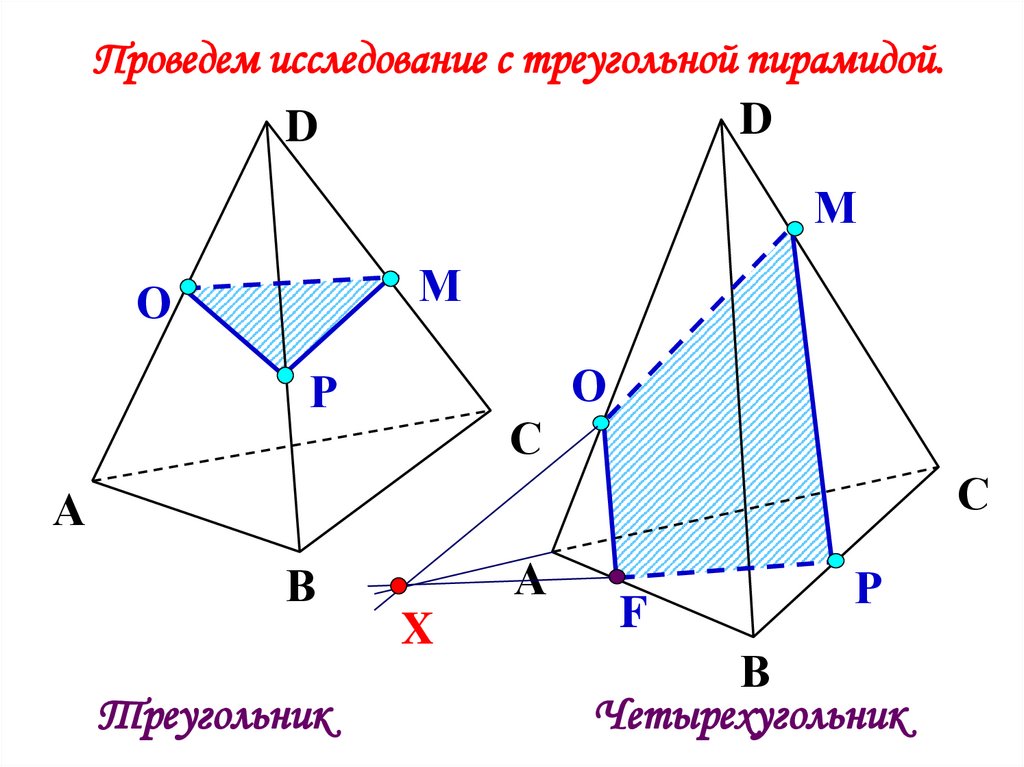
Проведем исследование с треугольной пирамидой.
D
D
М
М
О
О
Р
С
С
А
А
В
X
Треугольник
F
Р
В
Четырехугольник

19.

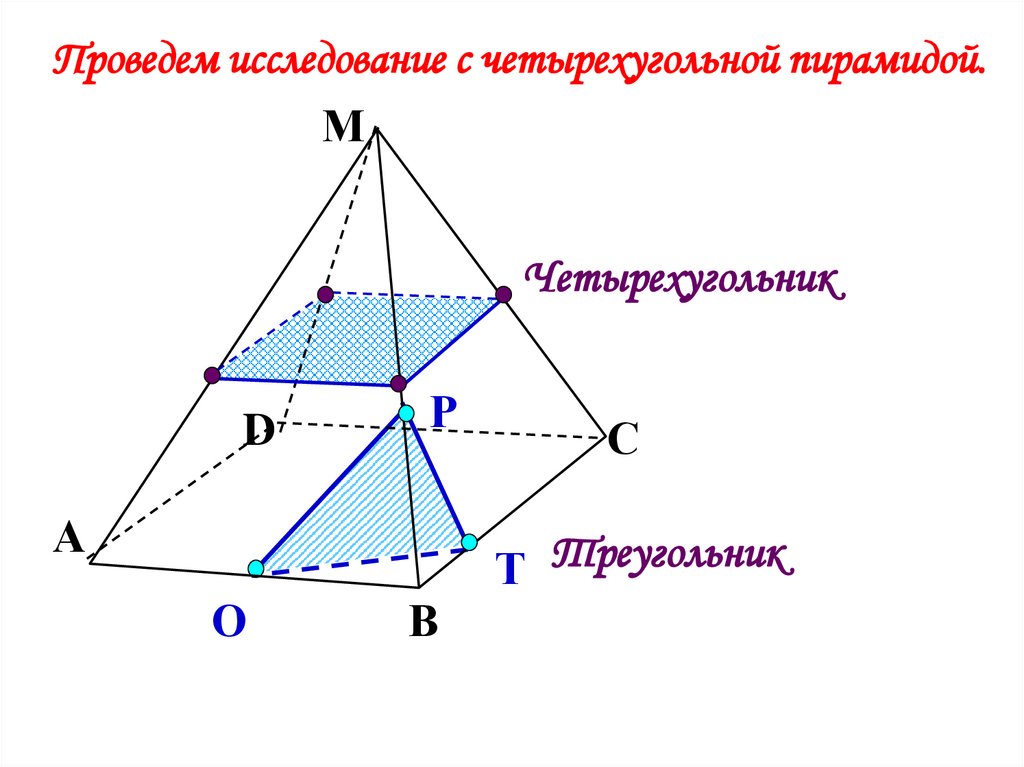
Проведем исследование с четырехугольной пирамидой.
М
Четырехугольник
D
Р
А
С
Т Треугольник
О
В

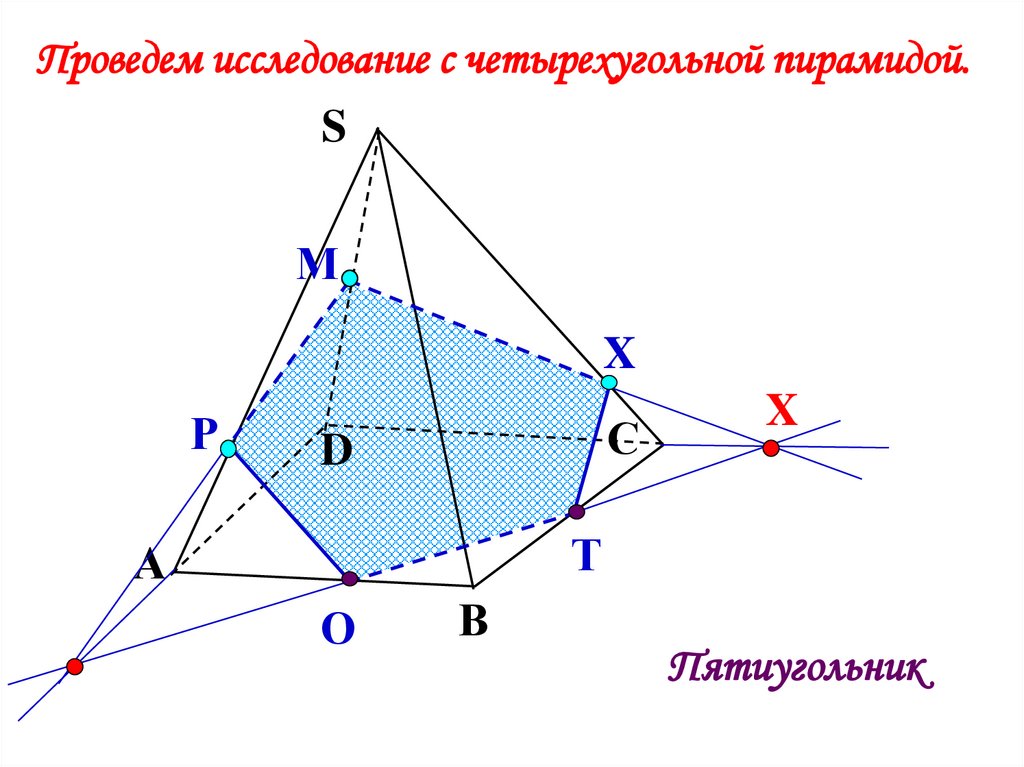
20.

Проведем исследование с четырехугольной пирамидой.
S
М
X
Р
С
D
X
Т
А
О
В
Пятиугольник

21.

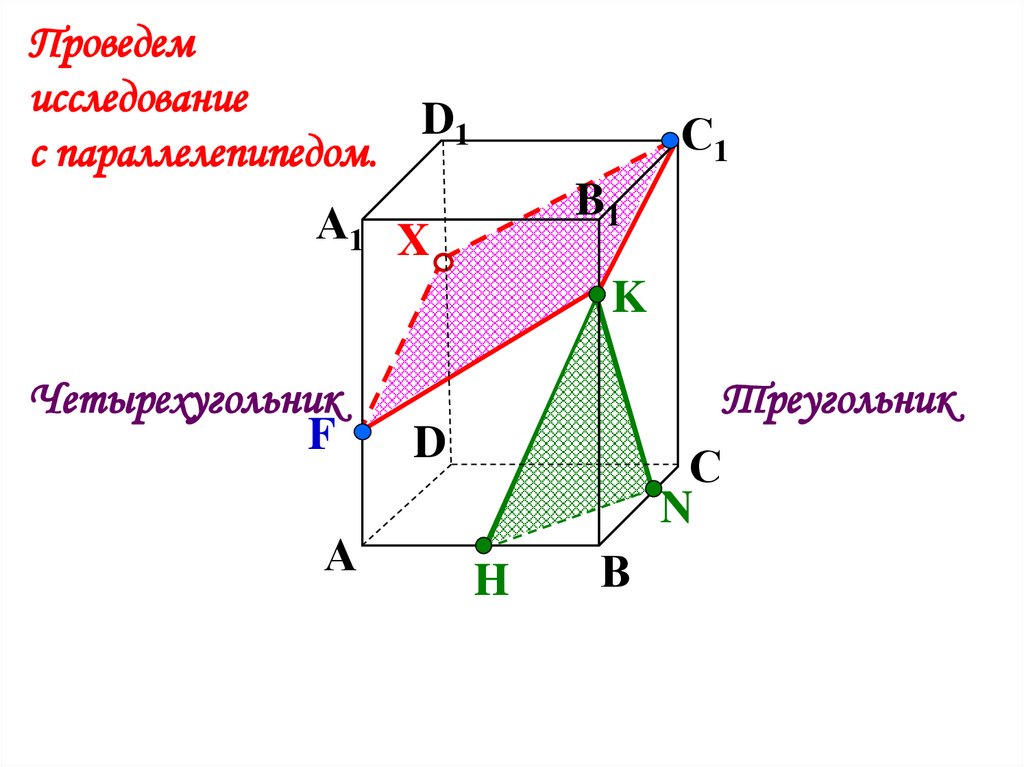
Проведем
исследование
D1
с параллелепипедом.
С1
B1
А1 X
K
Четырехугольник
F
А
Треугольник
D
С
N
H
В

22.

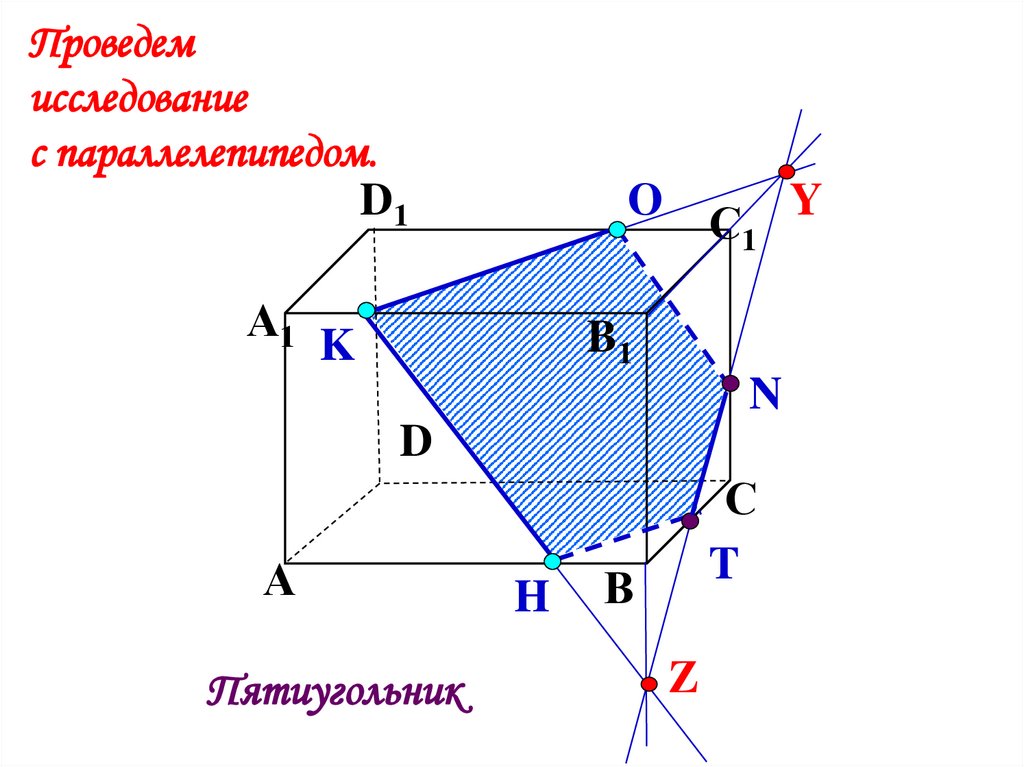
Проведем
исследование
с параллелепипедом.
D1
А1
О
С1
B1
K
N
D
А
Пятиугольник
H
С
T
В
Z
Y

23.

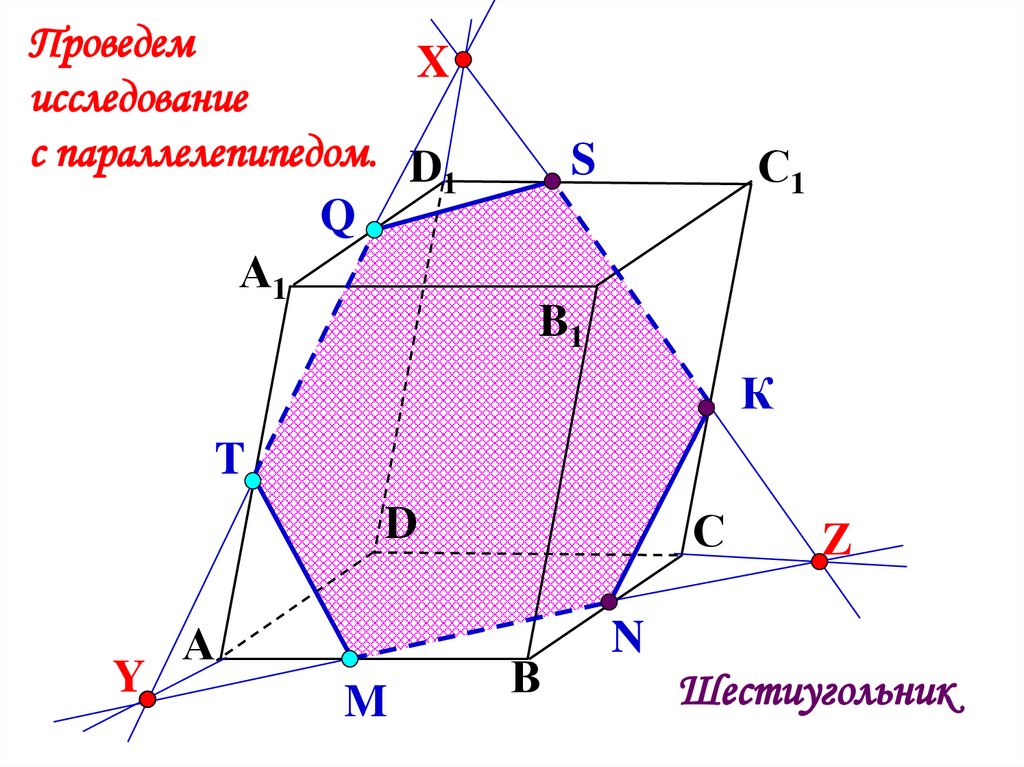
Проведем
X
исследование
с параллелепипедом. D
1
Q
А1
С1
S
B1
К
T
С
D
Y
А
M
В
Z
N
Шестиугольник

24.

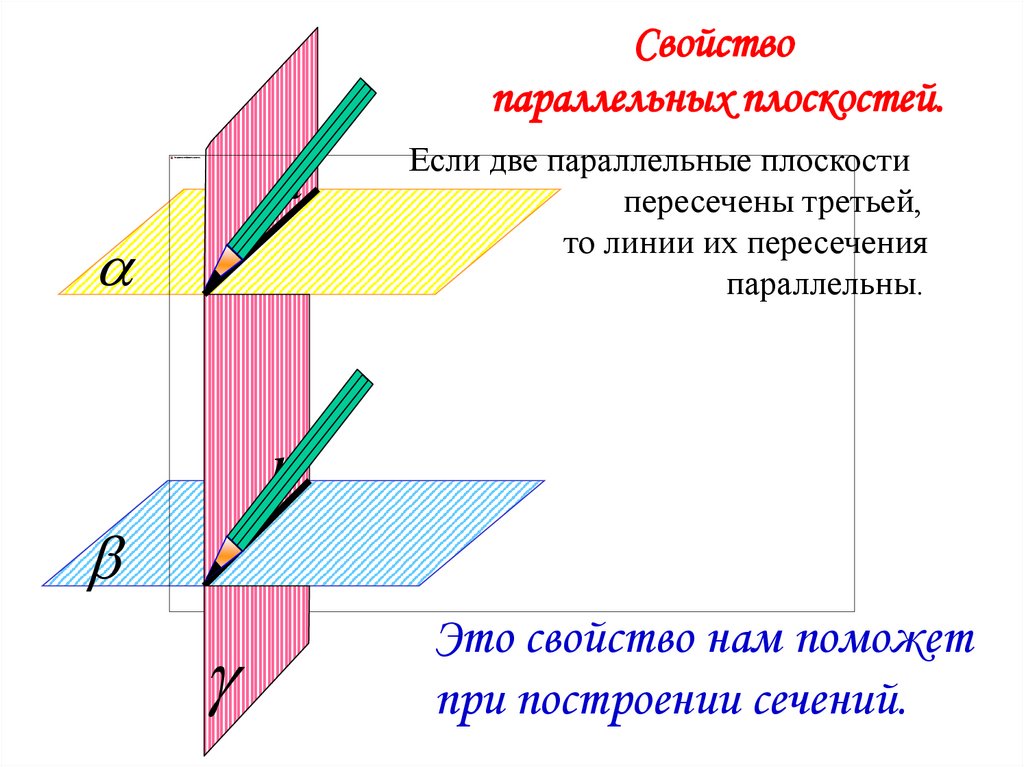
Свойство
параллельных плоскостей.
а
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
b
Это свойство нам поможет
при построении сечений.

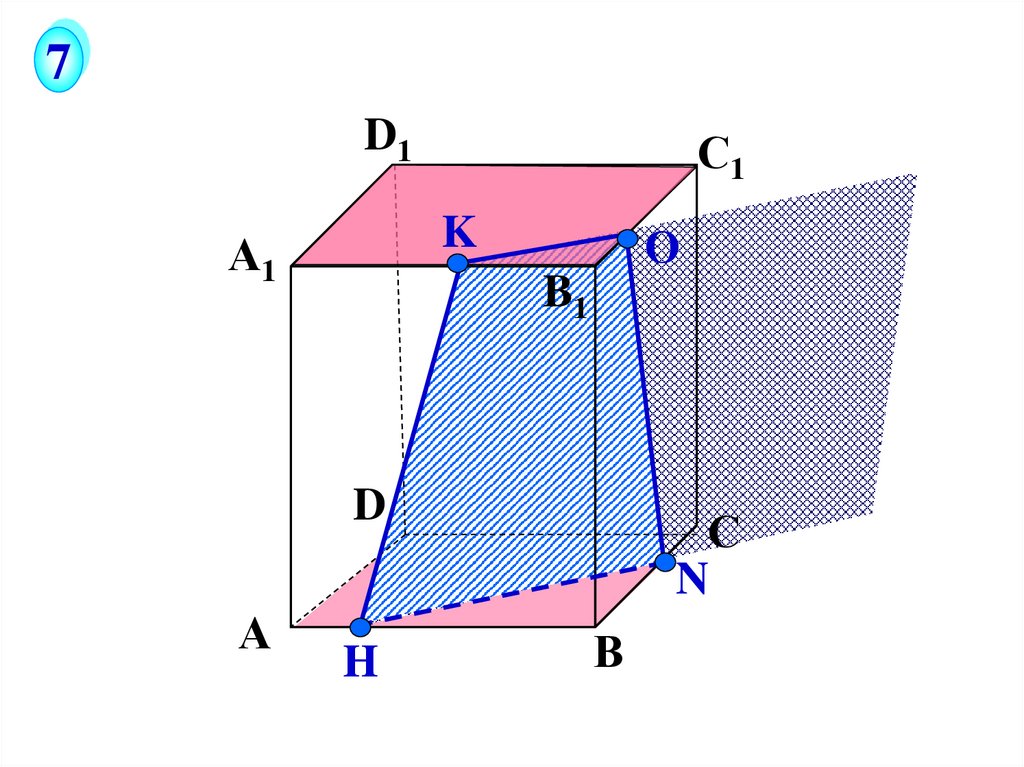
25.

7
D1
С1
K
А1
О
B1
D
А
H
С
N
В

26.

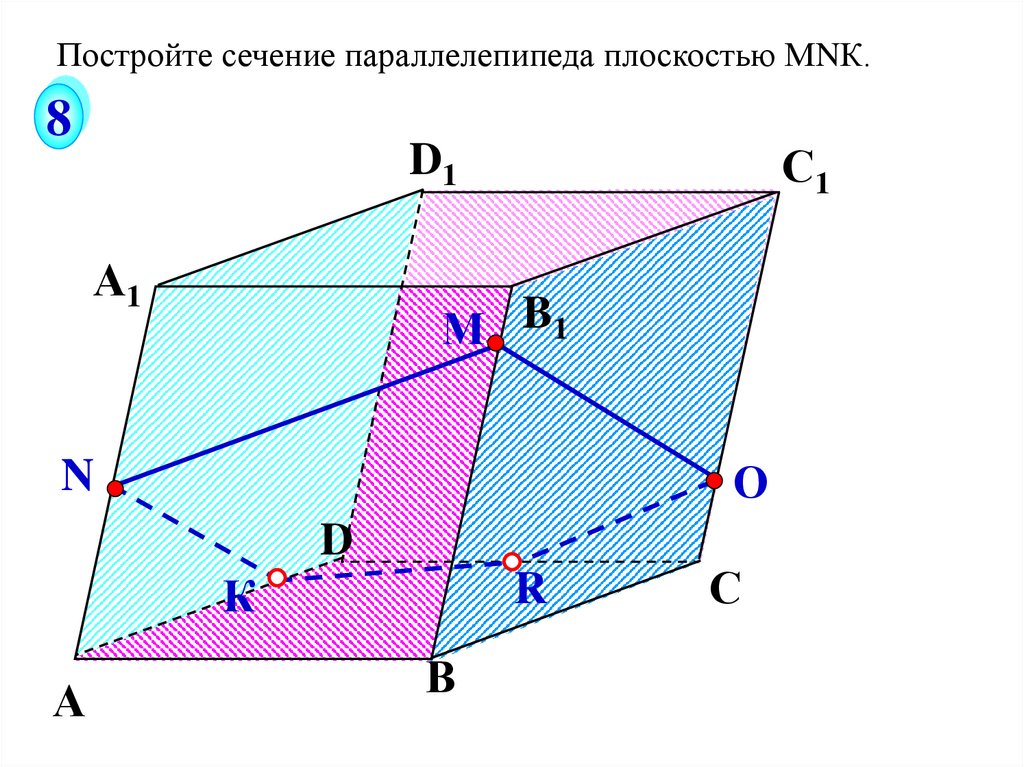
Постройте сечение параллелепипеда плоскостью МNК.
8
С1
D1
А1
М B1
О
N
D
К
А
R
В
С

27.

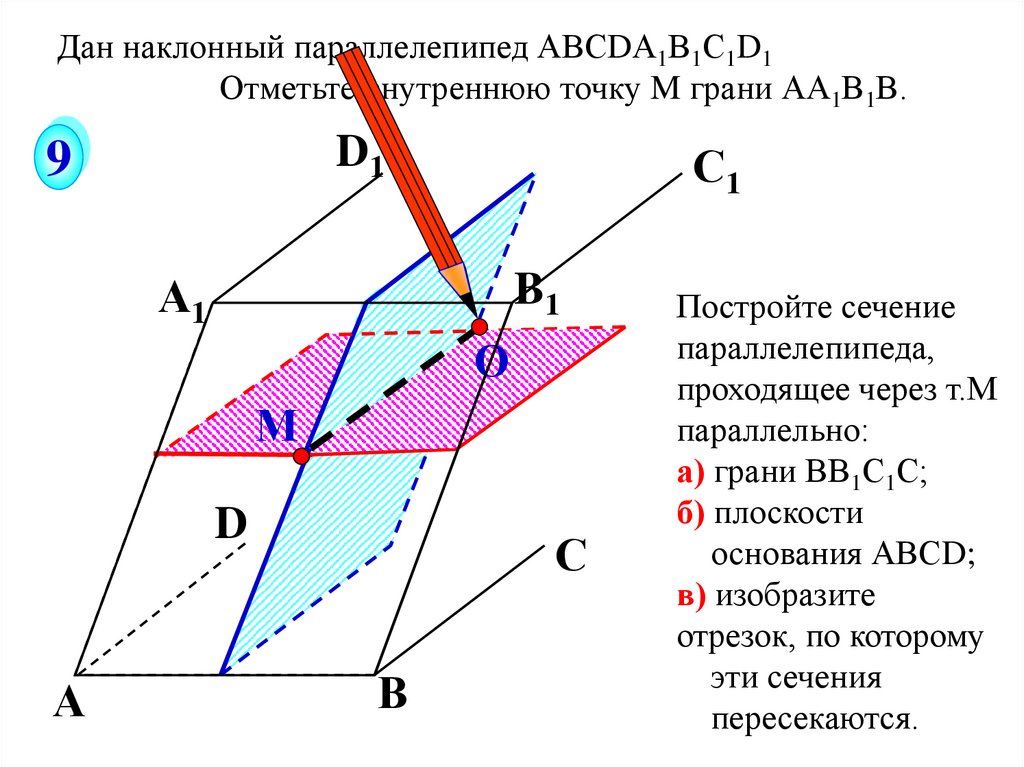
Дан наклонный параллелепипед АВСDА1В1С1D1
Отметьте внутреннюю точку M грани АА1В1В.
D1
9
С1
А1
B1
О
М
D
А
С
В
Постройте сечение
параллелепипеда,
проходящее через т.М
параллельно:
а) грани ВВ1С1С;
б) плоскости
основания АВСD;
в) изобразите
отрезок, по которому
эти сечения
пересекаются.

28.

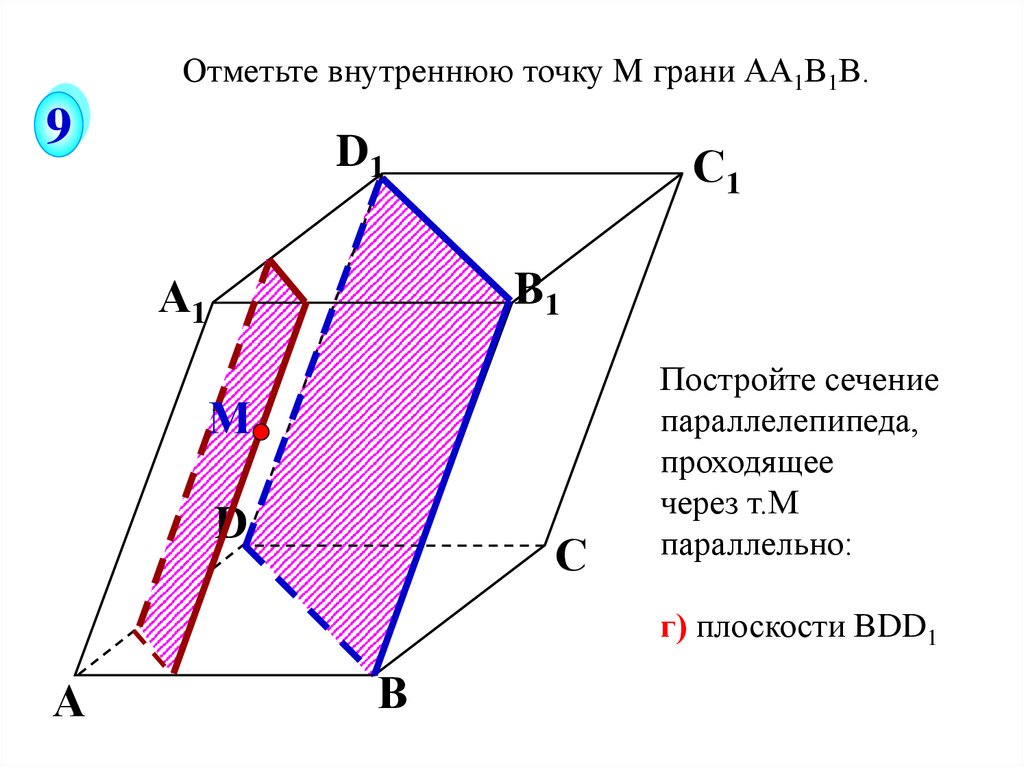
Отметьте внутреннюю точку M грани АА1В1В.
9
D1
А1
С1
B1
М
D
С
Постройте сечение
параллелепипеда,
проходящее
через т.М
параллельно:
г) плоскости ВDD1
А
В

29.

Блиц-опрос.
D1
С1
K
А1
Верите ли вы, что прямые НК
и ВВ1 пересекаются?
B1
D
А
H
С
В

30.

Блиц-опрос.
D1
С1
К
А1
B1
Н
D
А
С
N
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

31.

Блиц-опрос.
D1
А1
К
А
С1
М
B1
Н
D
В
Верите ли вы, что прямые НК
и МР пересекаются?
Р
С
N
На чертеже есть
ещё ошибка!

32.

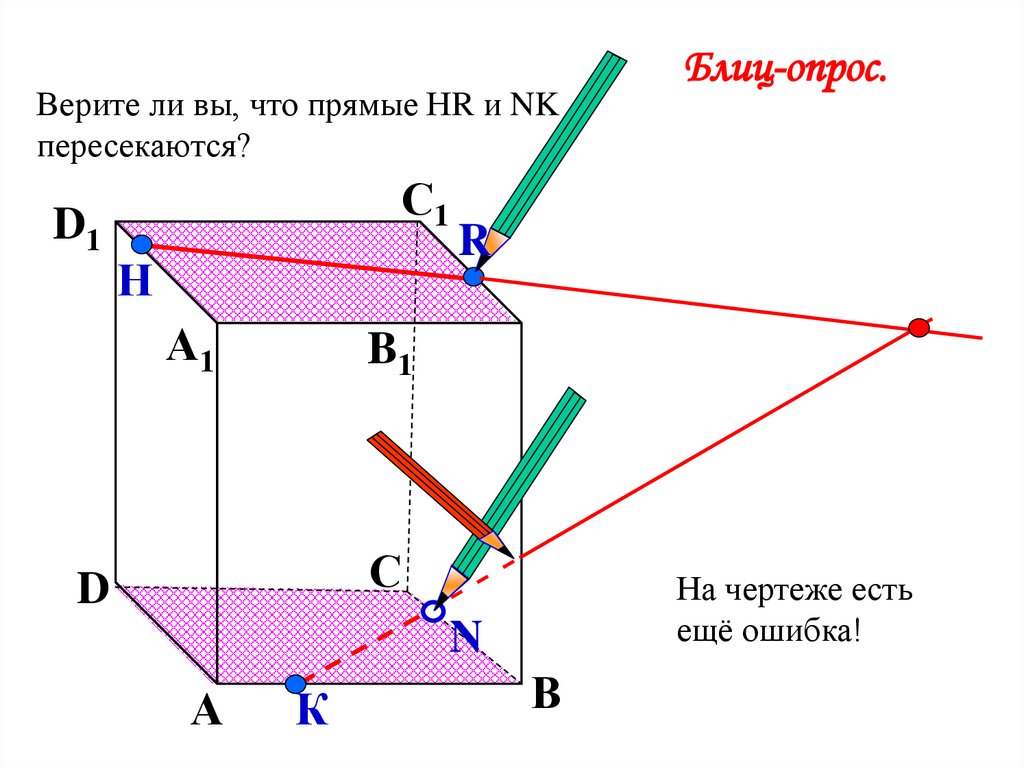
Верите ли вы, что прямые НR и NK
пересекаются?
D1
С1
Н
А1
R
B1
С
D
На чертеже есть
ещё ошибка!
N
А
Блиц-опрос.
К
В

33.

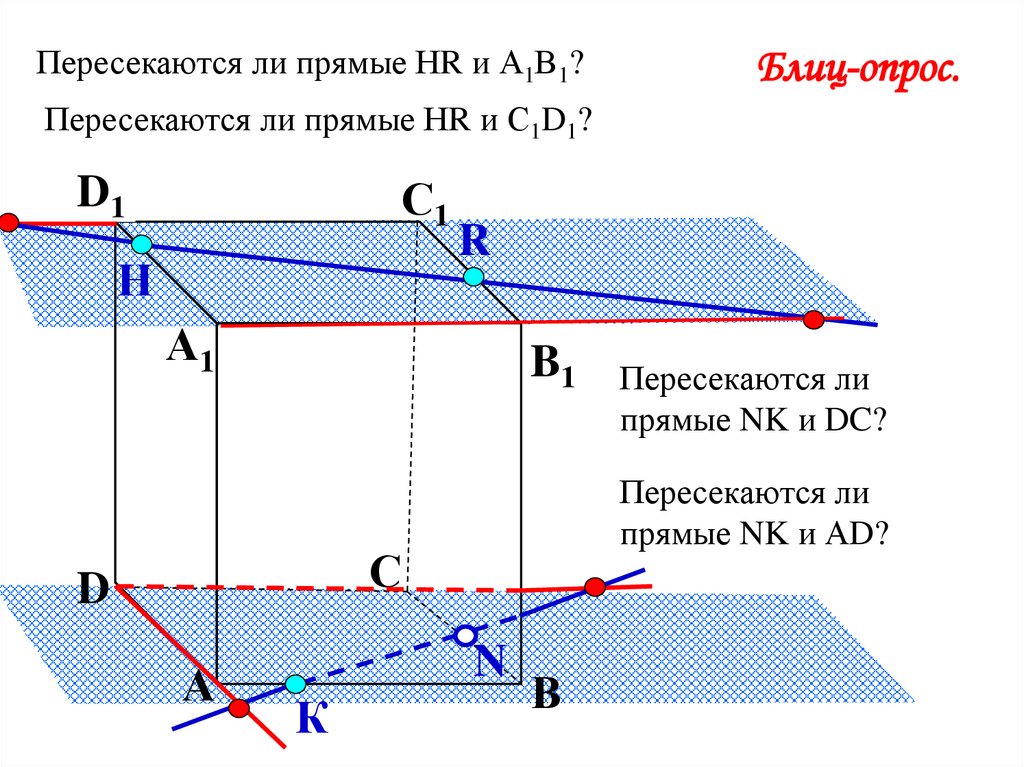
Пересекаются ли прямые НR и А1В1?
Блиц-опрос.
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

34.

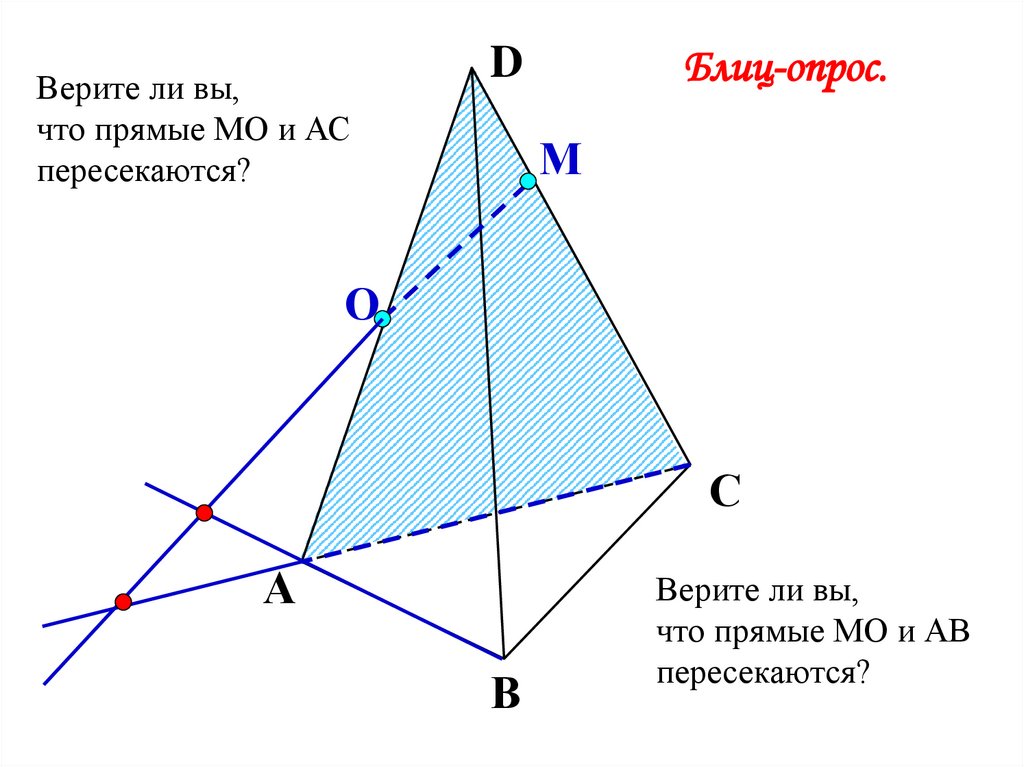
Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

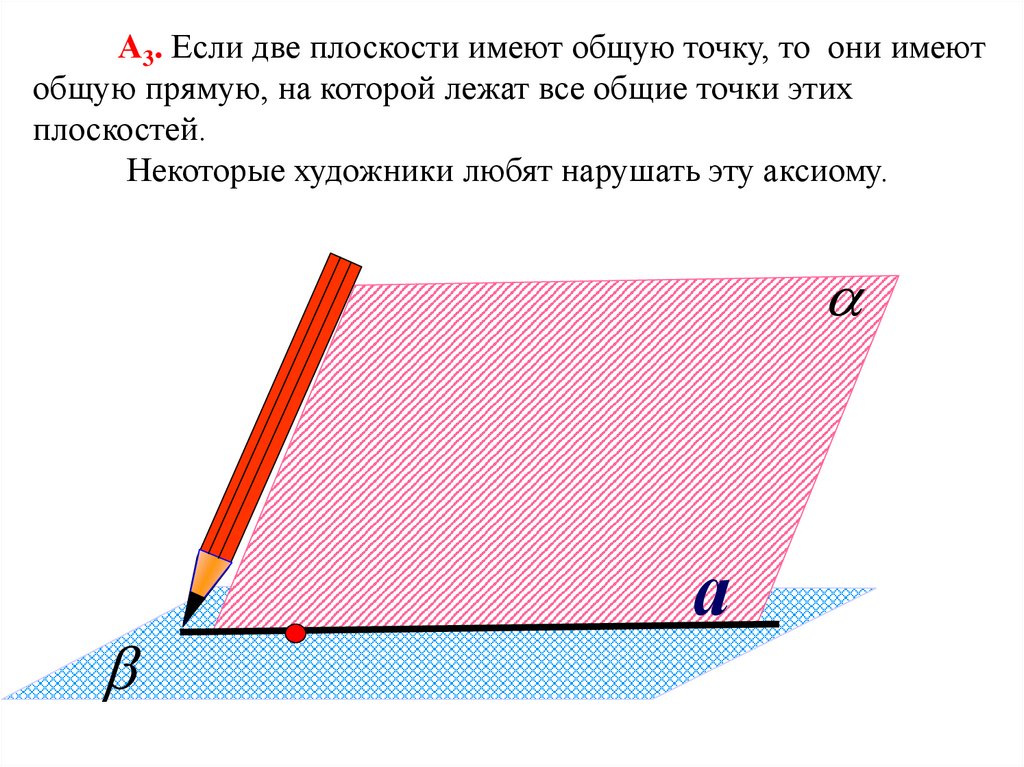
35.

А3. Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих
плоскостей.
Некоторые художники любят нарушать эту аксиому.
а

36.

Это интересно!
Многие художники, искажая законы перспективы,
рисуют необычные картины. Кстати, эти рисунки очень
популярны среди математиков. В сети Internet можно найти
множество сайтов, где публикуются эти невозможные объекты.
Популярные художники Морис Эшер, Оскар Реутерсвард,
Жос де Мей и другие, удивляли своими картинами
математиков.
http://www.im-possible.info/english/art/mey/mey2.html
http://alone.sammit.kiev.ua/moremind/illusion/index.html
http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/a

37.

"Такое может нарисовать только тот, кто делает
дизайн, не зная перспективы..."
Жос де Мей

38.

Законы геометрии часто нарушаются в компьютерных играх.
Поднимаясь по этой лесенке, мы остаёмся на том же этаже.
А2. Если две точки прямой
лежат в плоскости, то все точки
прямой лежат в этой плоскости.
а
Лесенки здесь быть не может!
а

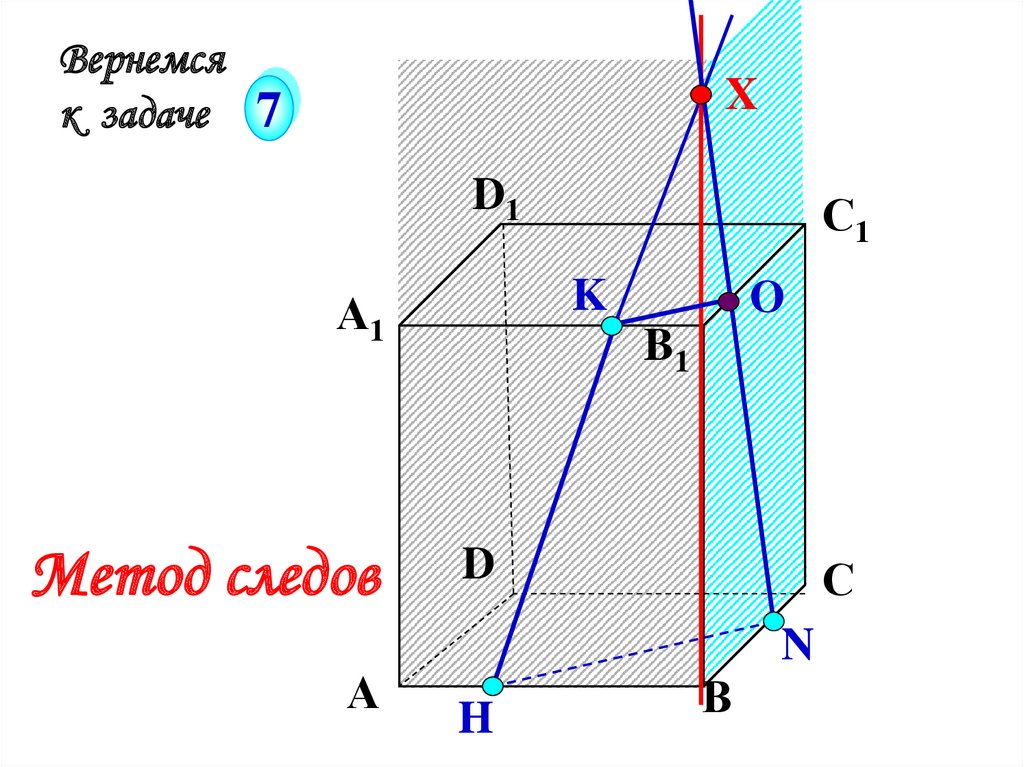
39.

Вернемся
к задаче 7
X
D1
А
О
K
А1
Метод следов
С1
B1
D
С
N
H
В

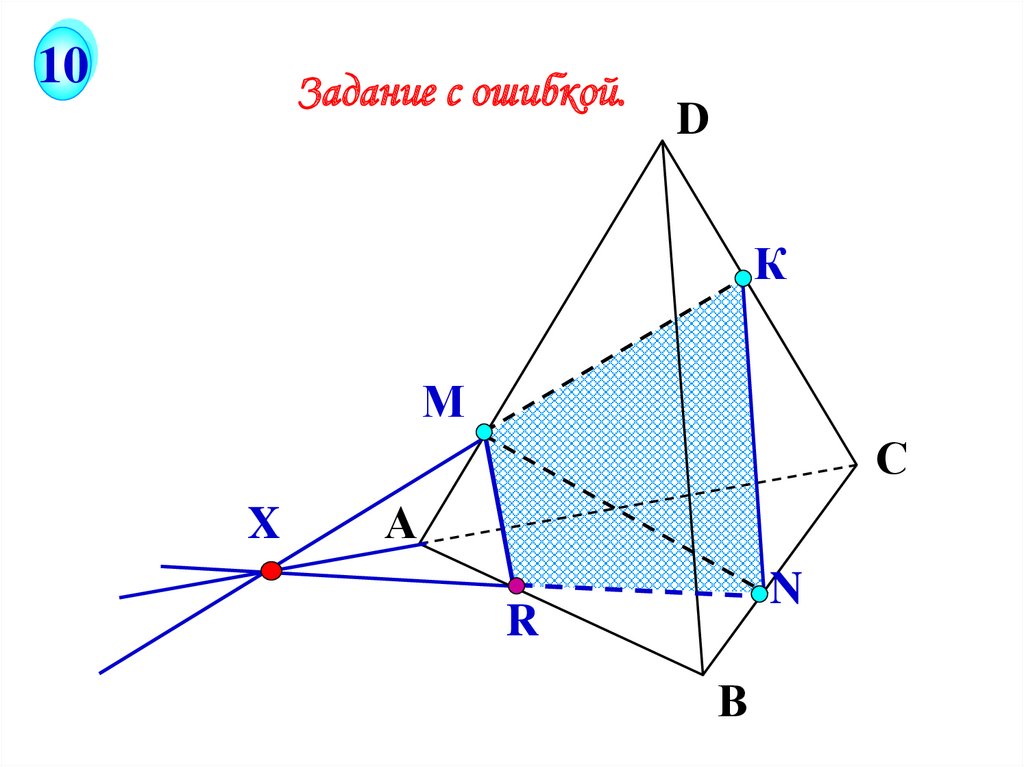
40.

10
Задание с ошибкой.
D
К
М
С
X
А
N
R
В

41.

11
О
D1
А1
С1
B1
K
N
D
А
H
С
Z
В
X
Y

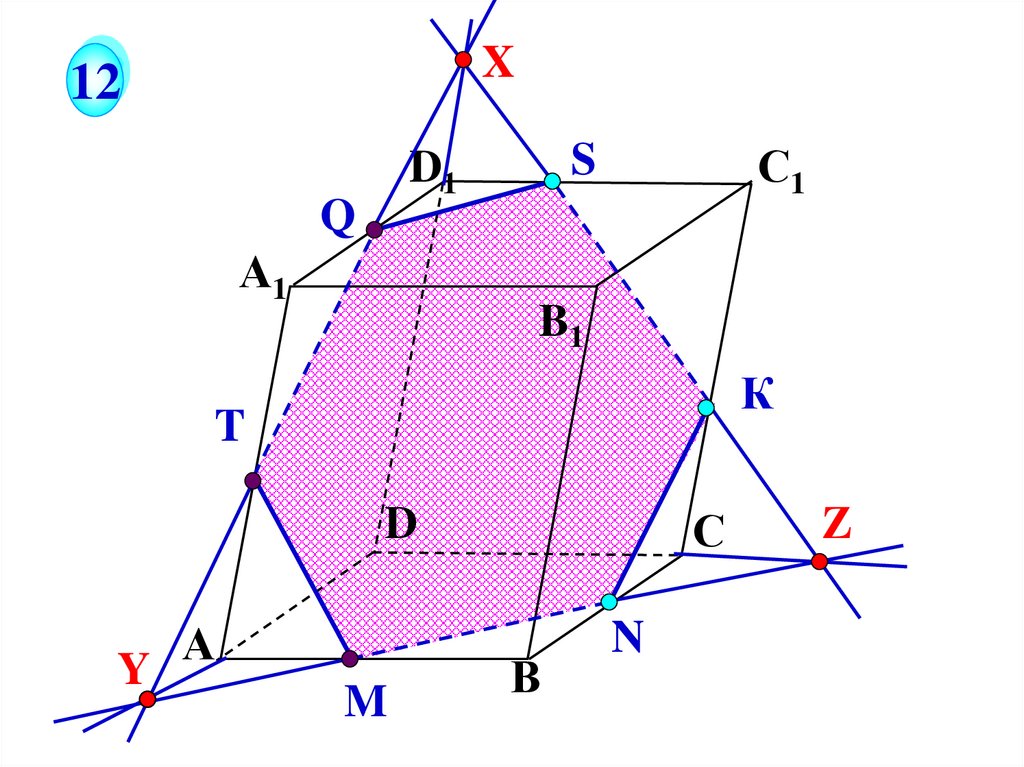
42.

X
12
Q
А1
С1
S
D1
B1
К
T
С
D
Y
А
M
В
N
Z

43.

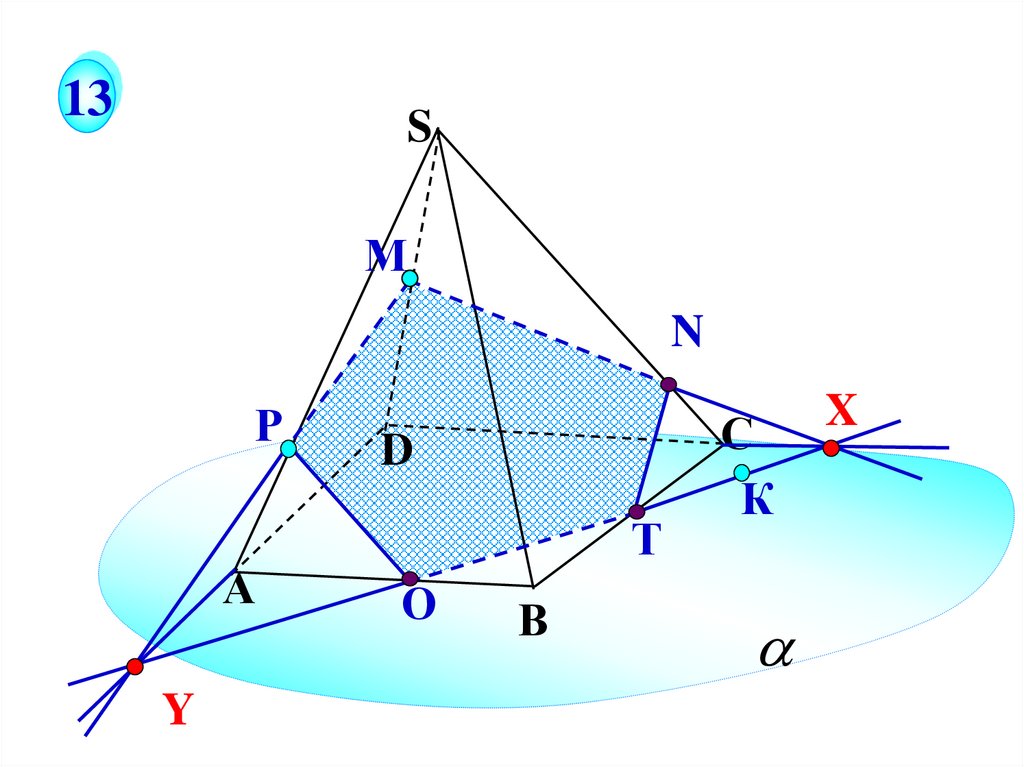
13
S
М
N
Р
А
Y
D
Т
О
В
С
К
X

44.

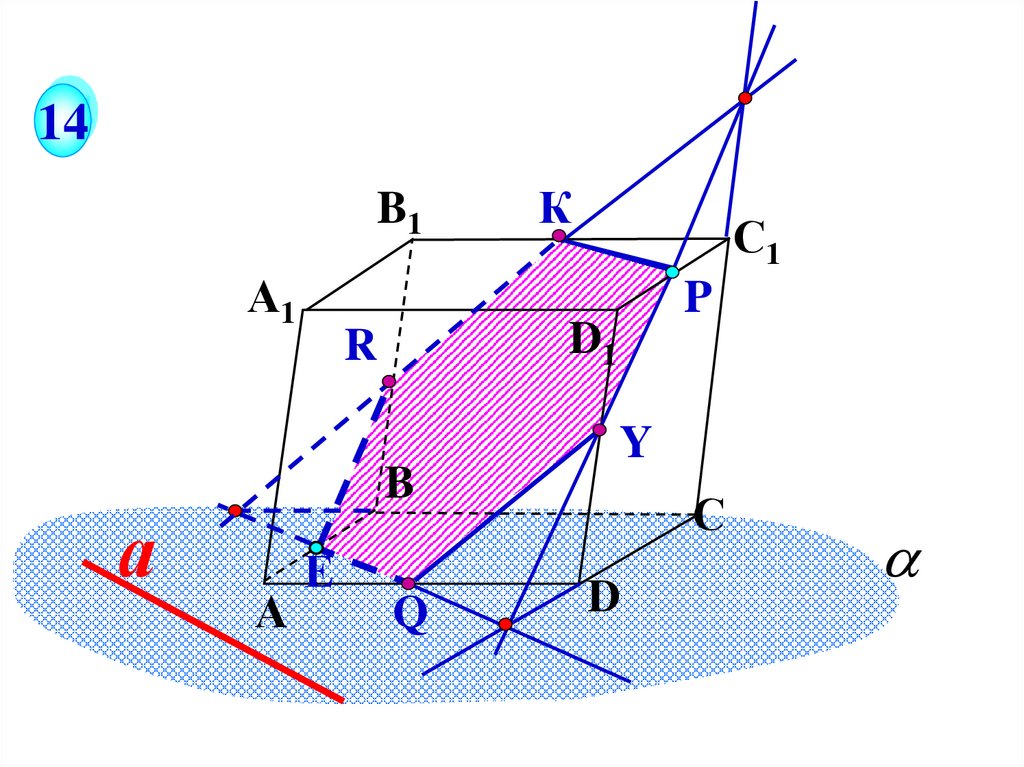
14
B1
А1
А
С1
P
D1
R
B
а
К
Е
Q
Y
С
D

45.

ВЫ МНОГОЕ УЗНАЛИ
И МНОГОЕ УВИДЕЛИ!
ТАК ВПЕРЕД, РЕБЯТА:
ДЕРЗАЙТЕ И ТВОРИТЕ!
СПАСИБО ЗА ВНИМАНИЕ.