Похожие презентации:
Производная функции. Определение
1.
ПРОИЗВОДНАЯФУНКЦИИ
2.
Определение:Предел отношения приращения функции к
приращению аргумента при ∆х → 0
называется производной функции f(x) в
точке х0:
у
lim
y
x 0 х
Производная – это скорость
изменения функции!
Штрих обозначает
действие
нахождения
производной
3.
КАКИМ ОБРАЗОМ МОЖНО ЗАПИСАТЬПРОИЗВОДНУЮ
у dу
y f ( x) y
х dх
4.
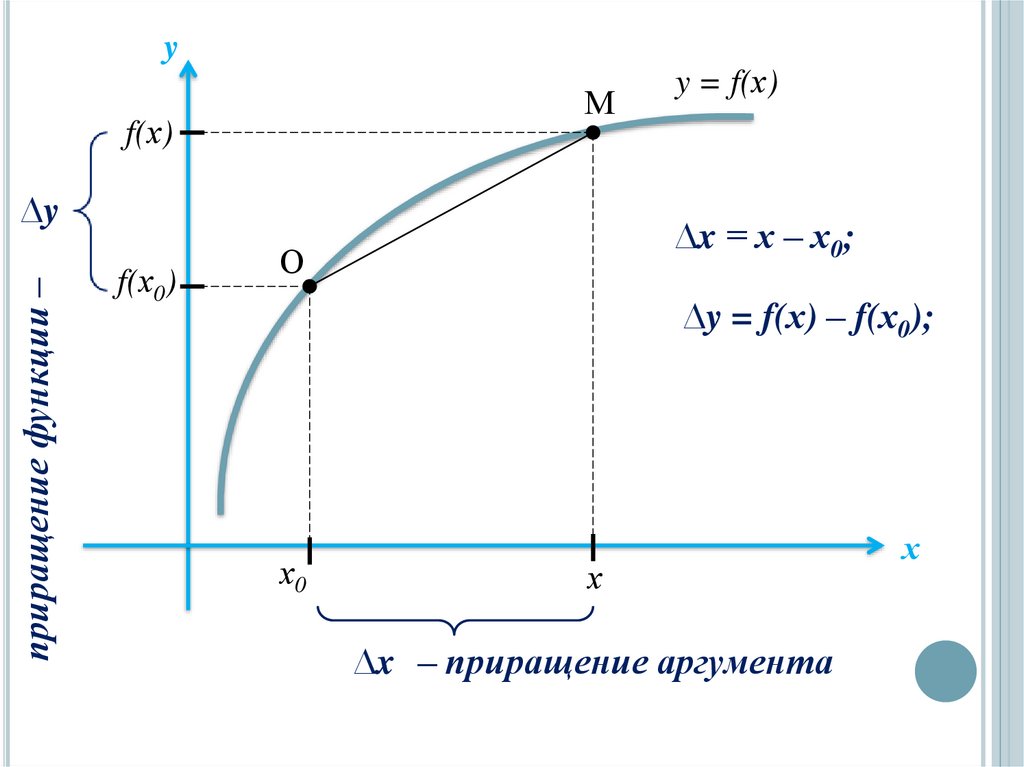
yМ
f(х)
приращение функции –
∆y
f(х0)
y = f(х)
∆x = х – х0;
О
∆y = f(х) – f(х0);
х0
х
∆x – приращение аргумента
х
5.
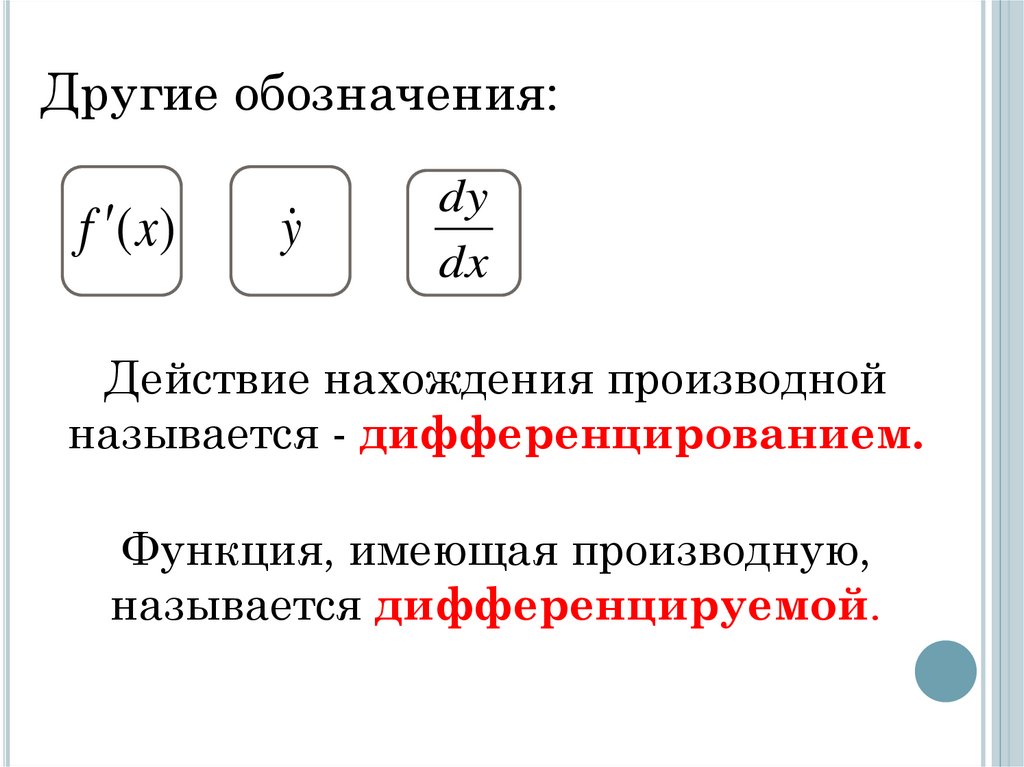
Другие обозначения:f (x)
y
dy
dx
Действие нахождения производной
называется - дифференцированием.
Функция, имеющая производную,
называется дифференцируемой.
6.
ОБЩЕЕ ПРАВИЛО ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ:1) y y f ( x x)
2) y f ( x x) f ( x)
y f ( x x) f ( x)
3)
x
x
y
4) y lim
x 0 x
7.
Правила дифференцированияU V W U V W
С U С U
U V U V V U
U V W U V W V U W W U V
U U V U V
2
V
V
U 1
U
С С
С
С
V
2
V
V
8.
Производные элементарных функций1)
С 0 , С постоянная
2)
x 1
x n x
1
4) х
3)
n
n 1
2 x
5)
1
1
2
x
x
СТЕПЕННЫЕ
ФУНКЦИИ
9.
Производные элементарных функцийa a lna
7) e e lne e
6)
x
x
x
8)
x
x
ПОКАЗАТЕЛЬНЫЕ
ФУНКЦИИ
1
log a x
х lna
1
9) lnx
х
0,4343
10) lgx
х
ЛОГАРИФМИЧЕСКИЕ
ФУНКЦИИ
10.
Производные элементарных функций11)
12)
sinx cosx
cosx sinx
13)
1
tgx
2
cos x
14)
1
ctgx 2
sin x
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
11.
Математический диктантx
С U
С
1
x
cosx
n
x
e
x
sinx
U V
lnx
tgx
a
x
U V
ctgx
х
U
V
12.
Вычисление производных элементарных функций1) y x
3 x
y x
3
3) y x
3 1
3x
2
7
y 7x
2, 4
y 2,4 x
5
y 5 x
2) y x
4) y x
x n x
n
3
6
1, 4
6
n 1
13.
Вычисление производных элементарных функций5 ) y 4х 2x 3x 10
2
3
4
6) y 3х 6 x
0,5
0,008
7 ) y 3х 1,5x 7x 0,35
4
8) y
2
1
5
x х x ,
x
a x a n x
n
n 1
С 0
U V U V
x0 2
x0 1
14.
Вычисление производных элементарных функций9 ) y 2 tgx 5 lnx 4
U V U V
x
10 ) y 8 ctgx 2 cosx 7 lg x 0,136
2
11 ) y 2 log 2 x 3 x 10 x
3
3
4
12) y 3 cos x 4 sin х 2e 5 x, x0 0
x
15.
Д/З Выучить формулы!Вычислить производные:
1) y 1,2x 4х 3x 1,2х 0,007
5
2
3
2) y lgx 3 ctgx 9 6 lnx
x
3) y 5x 2x 3x 2x
2
2
Вычислить производные в заданных точках:
4) y 7x 13х 5x 3, x0 6,5
3
3
2
5) y 4x 1,5x 9х
x0 1,4
2
2
3
16.
Вычисление по правилу произведенияU V U V U V
1) у = x∙sinx;
у′ = (x∙sinx)′ = (x)′∙sinx + x∙(sinx)′ =
U
V
= 1∙sinx + x∙cosx = sinx + x∙cosx
17.
2) y x ey x e
x
U V U V U V
x
x e x e
x
x
1 e x e e 1 x
x
x
x
3) y x 3x 2 x 8
2
2
3
3
y x 3 x 2 x 8 2 x 8 x 3 x
2
3
2 x 3 2 x 3 8 6 x 2 0 x 2 3x
4 x 4 16 x 6 x 3 24 6 x 4 18 x 3
10 x 4 24 x 3 16 x 24
18.
4) y' (4) y' (1) ?y 1 2 x x
U V U V U V
y 1 2 x x x 1 2 x
1 2x
1
0 2 x
1 2 x 2 x
2 x
2 x
7
1 2 4
5,75
4
y ' ( 4) 2 4
4
2 4
1
1 2 1
2,5
2
y ' (1) 2 1
2
2 1
y ' (4) y ' (1) 5,75 2,5 3,25
19.
5) 1 2 x x 1 2 x x x 1 2 x3
3
3
1
3
0 2 3x x
1 2x
2 x
3
1 2x
2
6 x x
2 x
3
1 2 1
2
y ' (1) y (1) 6 1 1
1 2 13 1
2 1
2
1
6
1 5,5
2
20.
Вычисление по правилу дроби1 2х
1) у
;
3 5х
U U V UV
2
V
V
1 2х
1 2 х 3 5 х 1 2 х 3 5 х
у
2
3 5х
3 5 х
2 3 5 х 1 2 х 5 6 10 х 5 10 х
11
2
2
2
3 5 х
3 5 х
3 5 х
21.
2)1 sin x
у
;
1 sin x
U U V UV
2
V
V
1 sin x 1 sin x 1 sin x 1 sin x 1 sin x
у
2
1 sin x
1 sin x
cos x 1 sin x 1 sin x cos x
2
1 sin x
2 cos x
cos x cos x sin x cos x sin x cos x
2
2
1 sin x
1 sin x
22.
Вычислить производную в заданной точке:3)
2 3х
у
1 2х
2
2 3x
у
1 2x
2
x0 1
2 3x 1 2x 2 3x 1 2x
2
2
1 2 x
2
2
2
6
x
12
x
4
6
x
6 x 1 2 x 2 3x 2
2
2
1 2 x
1 2 x
2
6x 6x 4
2
1 2 x
2
6 6 4
y ( 1)
4
2
1 2
23.
е ху
2х
х
4)
U U V UV
2
V
V
2
x
2
x
2
е х
e x 2 х e x 2 х
у
2
2 х
2х
х
2
e 2 x 2 x e x 2
2x e 4x 2 e 2x
x
x
4x2
2 x e x 2e x 2 x 2
2
4x
2
x
2
4x2
x ex ex x2
2
2x
x
2
24.
U U V UV2
V
V
6 x 3 ln x
5) у
;
2
2 x
2
2
6 x 3 ln x 6 x 3 ln x 2 x 6 x 3 ln x 2 x
у
2
2
2 x
2 x2
3
2
6
2
x
6 x 3 ln x 2 x
x
2
2 x2
6
6
2
2
12 6 x 3x 12 x 6 x ln x 6 x ln x 6 x 3x 12
x
x
2 2
2 2
2 x
2 x
2
25.
Самостоятельно вычислить производную в заданной точке:y (25) y 4 ?
y
(
0
)
?
2) y 4 x х x 2e
y (0) ?
3) y 2 x 8e cos x
1) y 3 x x
2
2
3
x
x
2 4х
4) у
2 х
9 ln х 4 x
5) у
2
2х
3
y ( 6) ?
y (1) ?
26.
Производная сложной функцииf(x) = f ( u(x) )
f′(x) = f′(u) ∙ u’
Пример:
1) у = (2x – 7)14;
u
u(x) = 2x – 7;
f(u) = u14;
у′ = f′(u) ∙ u′(x) = 14u13 ∙ 2 = 28(2x – 7)13
27.
3) у 3 5 x5
4) у
;
3
f(x) = f ( u(x) )
f′(x) = f′(u) ∙ u′(x)
10
7 x 2
5) у 2 х 3;
6
10 ) у e
*
6) у e
2 x 15
7) у ln x x 9
3
8) у sin 2 x
2
2
9 ) у 3 sin x 3
*
3 2 x 4
2
1








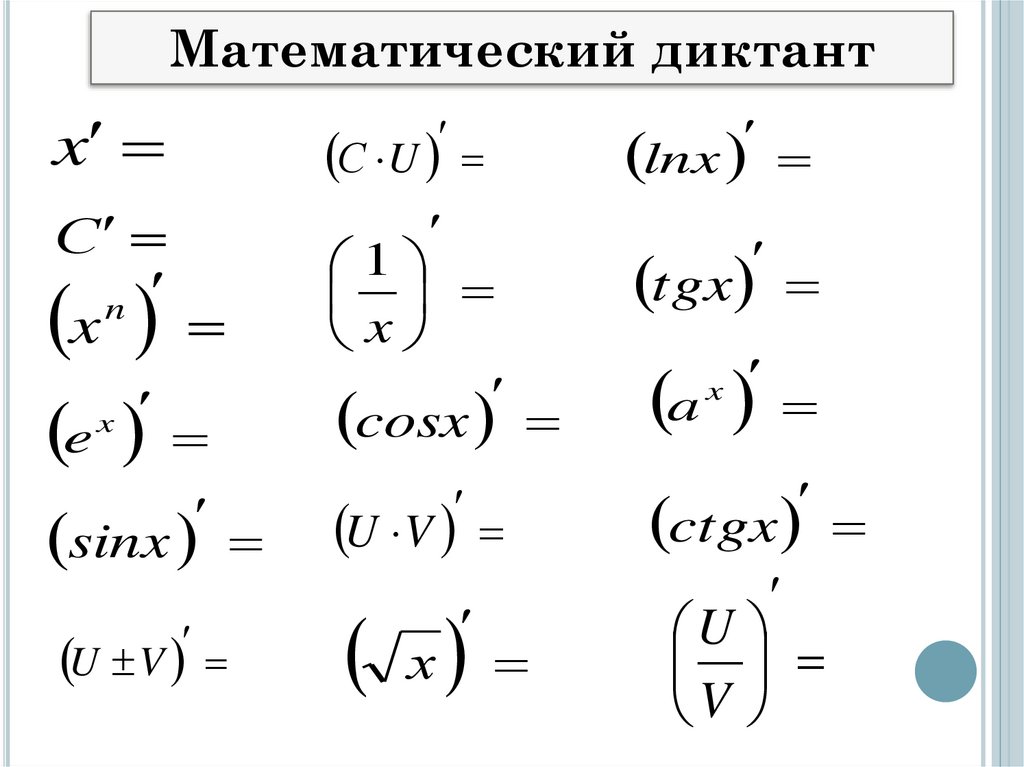






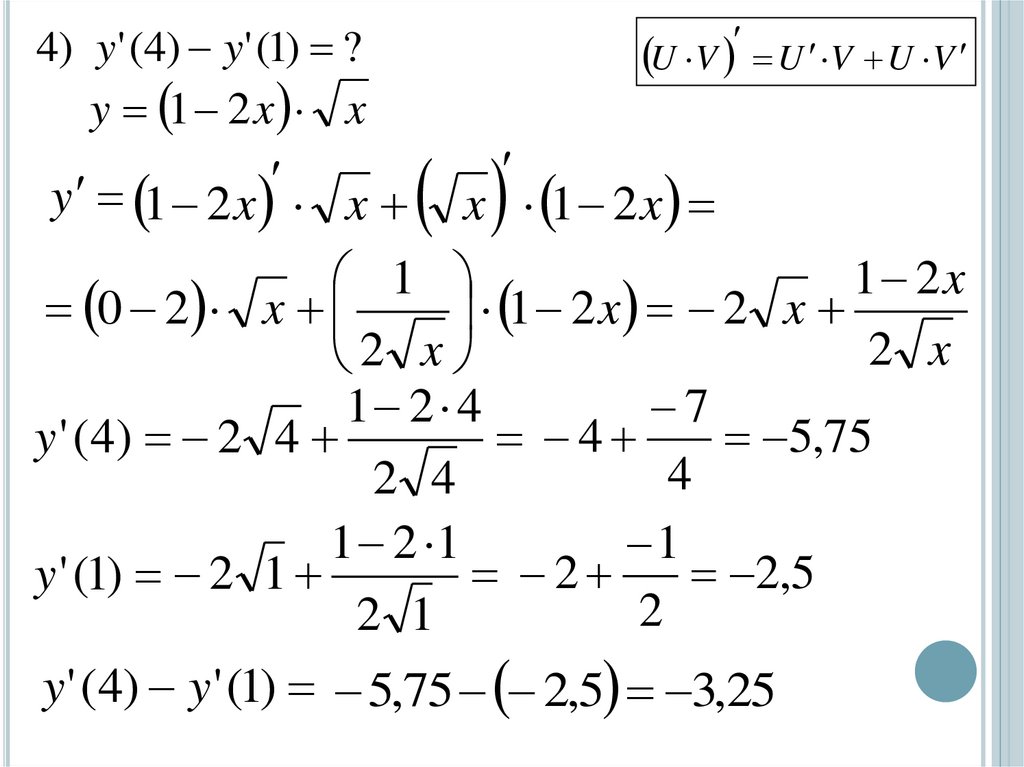
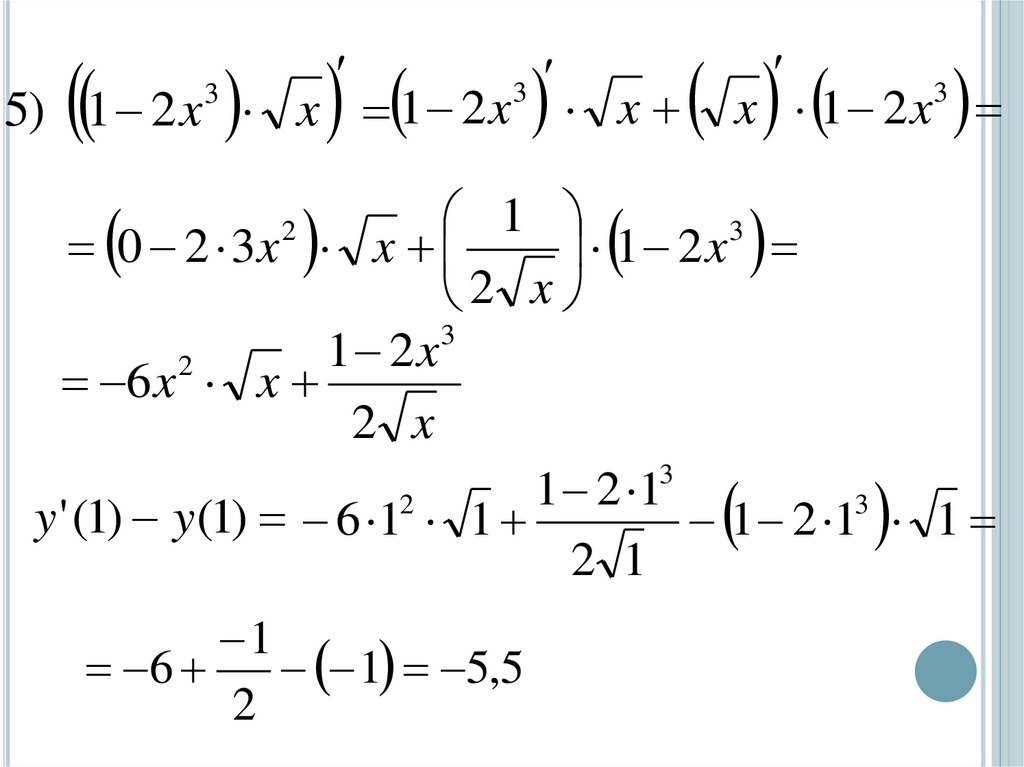

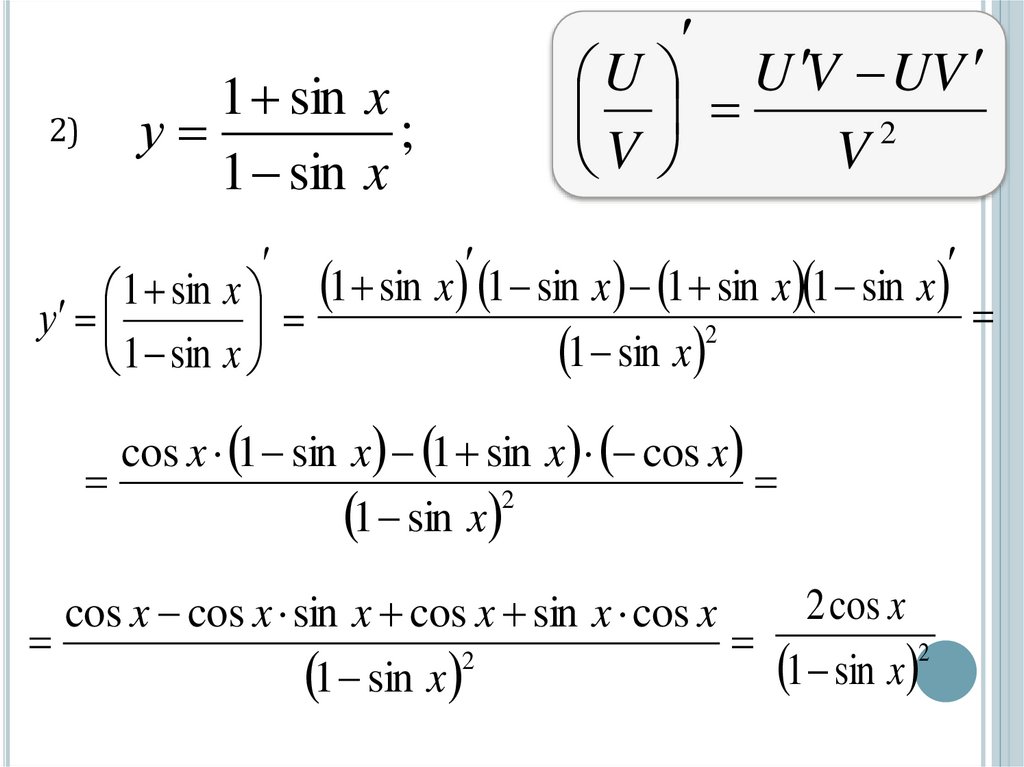

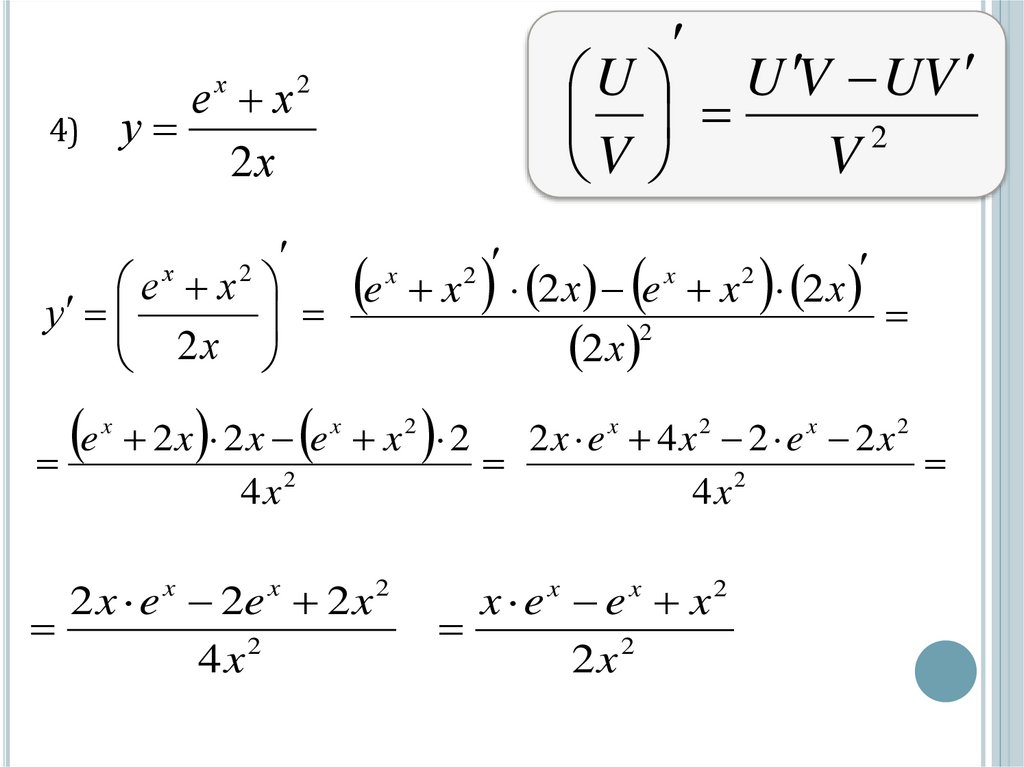
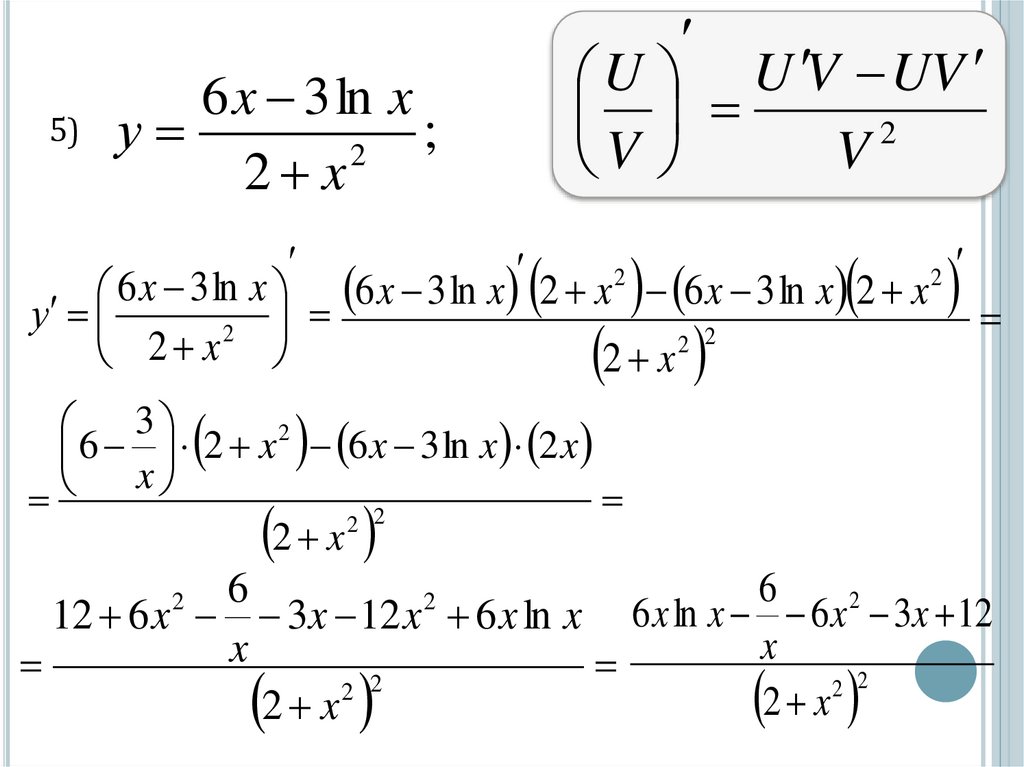


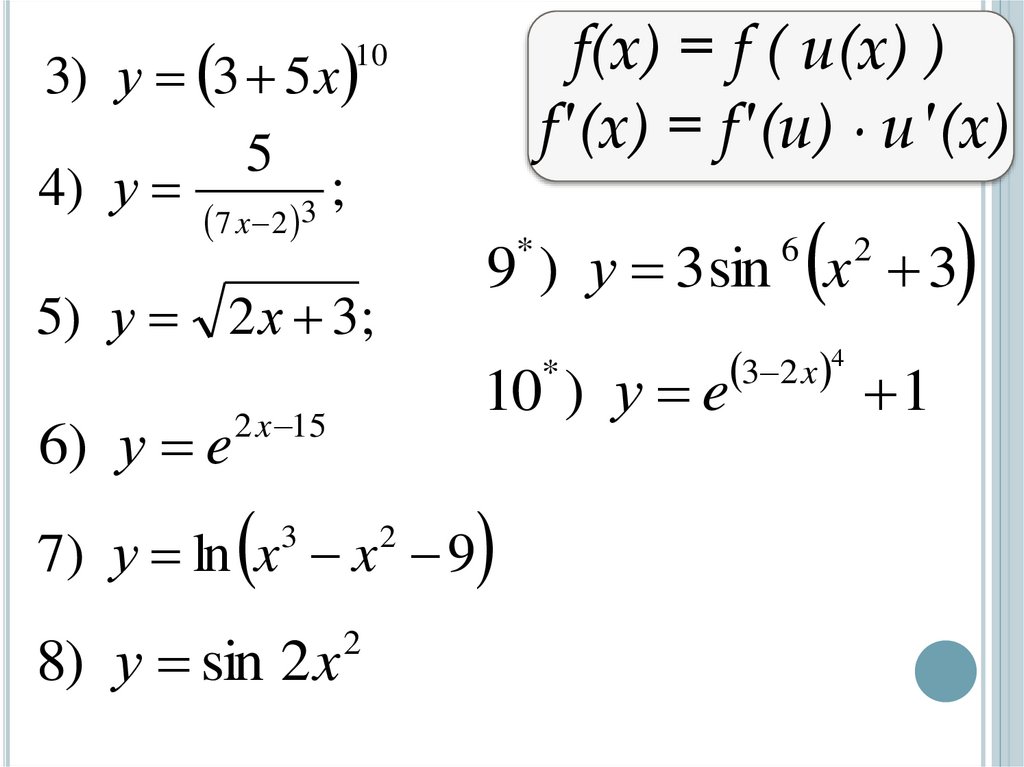
 Математика
Математика








