Пересекающиеся, параллельные и скрещивающиеся прямые в пространстве

1.

Пересекающиеся, параллельные
и скрещивающиеся прямые в
пространстве.

2.

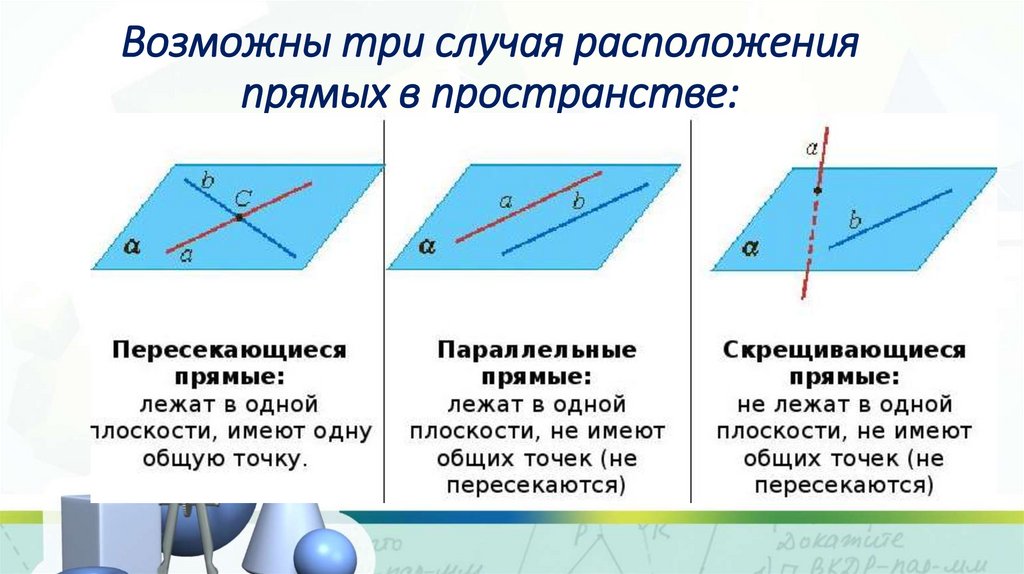
Возможны три случая расположения
прямых в пространстве:

3.

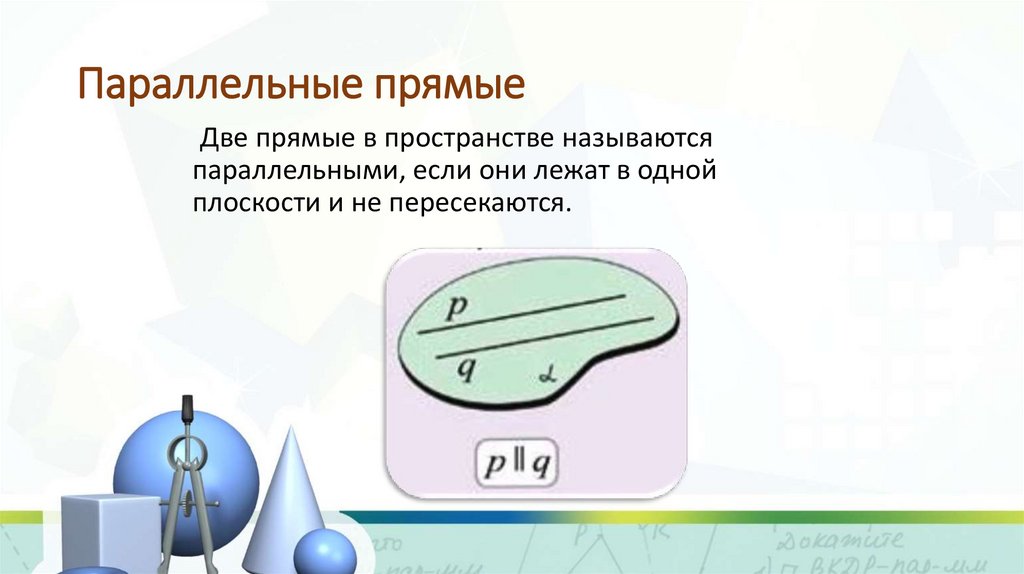
Параллельные прямые
Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются.

4.

5.

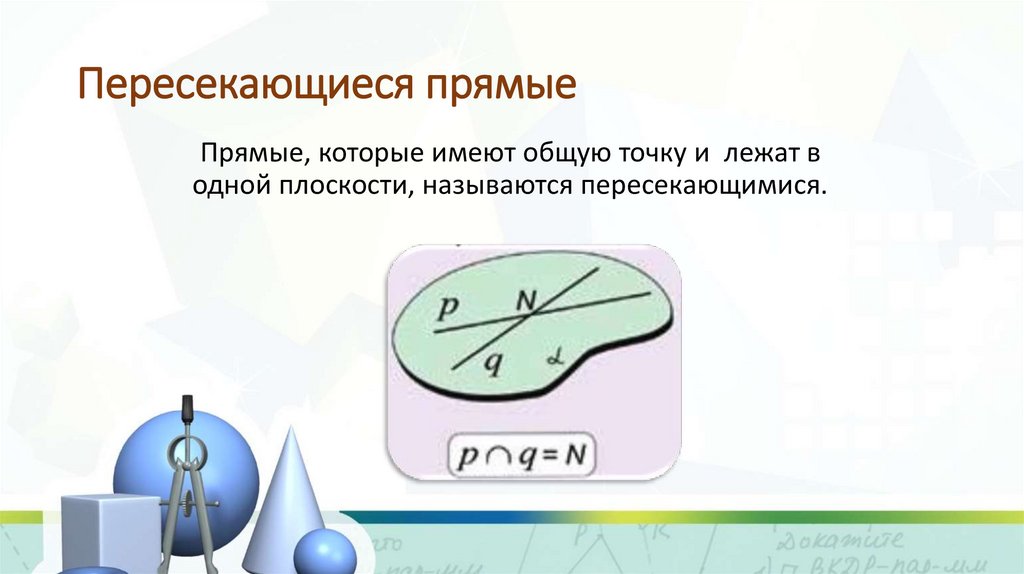
Пересекающиеся прямые
Прямые, которые имеют общую точку и лежат в
одной плоскости, называются пересекающимися.

6.

7.

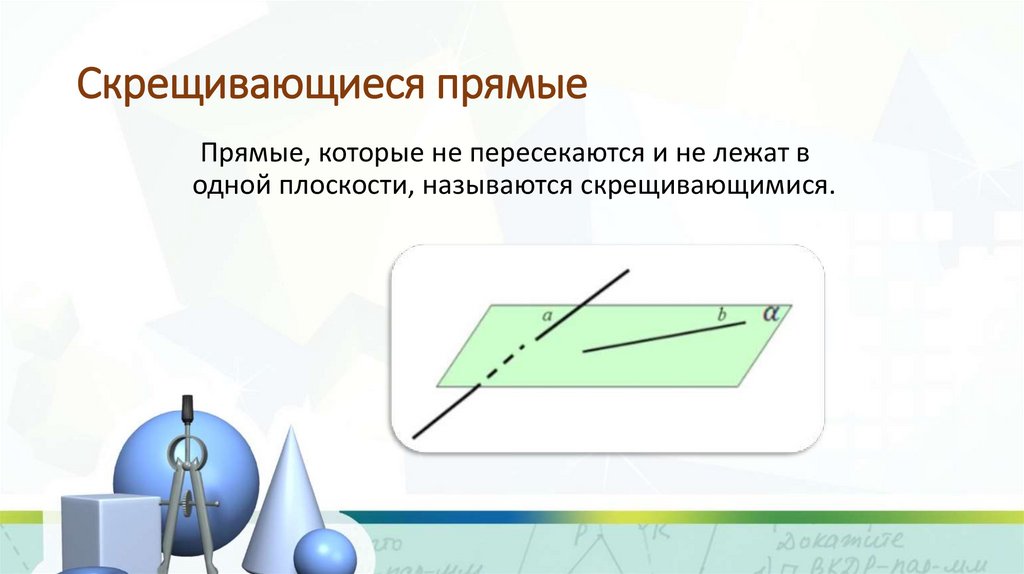
Скрещивающиеся прямые
Прямые, которые не пересекаются и не лежат в
одной плоскости, называются скрещивающимися.

8.

9.

Теорема:
Через две параллельные прямые
проходит плоскость и притом только одна.

10.

Теорема.
Через точку в пространстве, не
принадлежащую данной прямой,
проходит прямая, параллельна
данной, и притом только одна.

11.

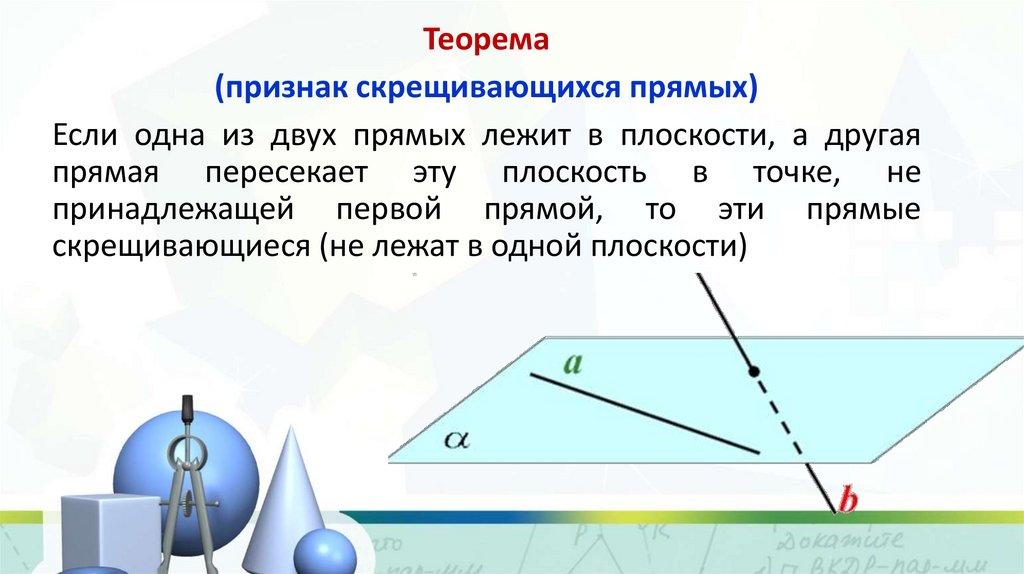
Теорема
(признак скрещивающихся прямых)
Если одна из двух прямых лежит в плоскости, а другая
прямая пересекает эту плоскость в точке, не
принадлежащей первой прямой, то эти прямые
скрещивающиеся (не лежат в одной плоскости)

12.

Пользуясь изображением, запишите:
1) точки, которые принадлежат плоскости
грани ВSС;
2) точки которые не лежат в плоскости
грани ВSС;
3) общие точки плоскостей граней АSС и
АВS;
4) прямую пересечения плоскостей граней
АВС и SAC;
5) плоскость, которая проходит через
прямые АВ и ВS;
6) плоскость, которая не содержит прямых
АВ и ВS.

13.

Опираясь на рисунок, укажите пары
параллельных и скрещивающихся отрезков.
Параллельные
Скрещивающиеся

14.

Задача № 1
Известно, что точки А,В,С,D лежат в одной плоскости.
Определите, могут ли прямые АВ и СD:
а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.

15.

Задача № 2
Известно, что точки А,В,С,D не лежат в одной плоскости.
Определите, могут ли прямые АВ и СD:
а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.

16.

Правильная пирамида SABCD пересечена плоскостью KLNM,
Задача 3 параллельной основанию

17.

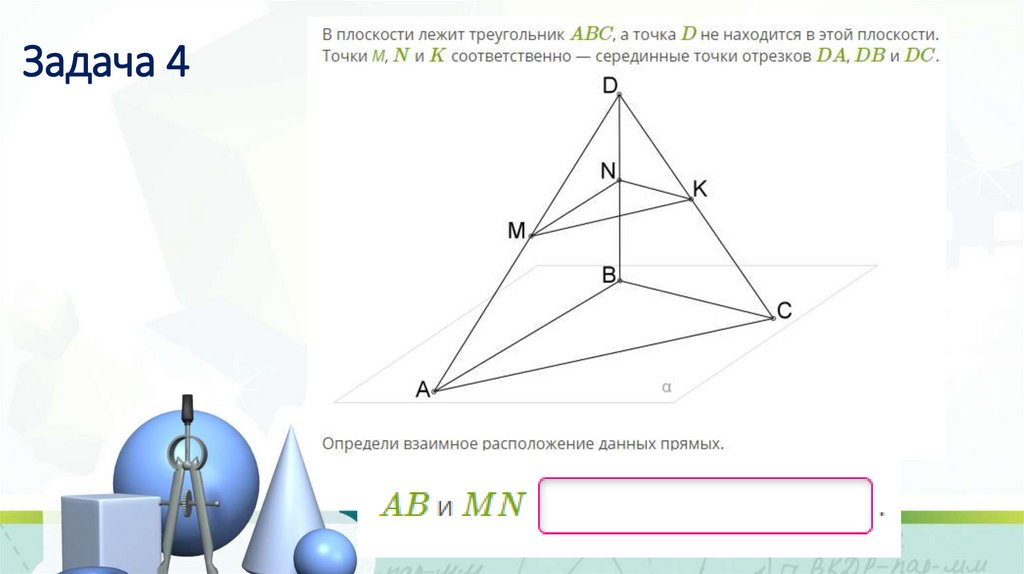
Задача 4

18.

Задача 5

19.

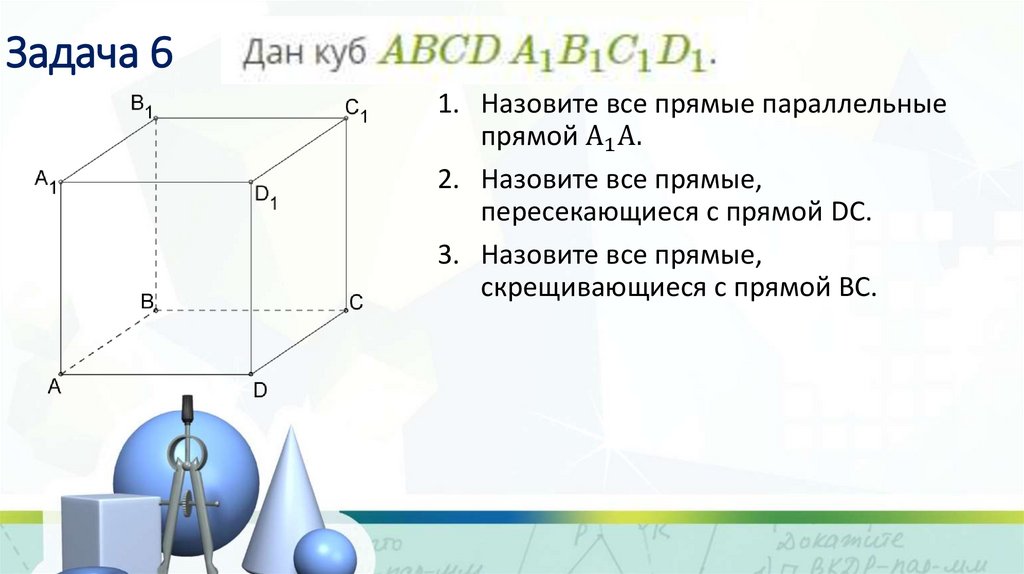
Задача 6
1. Назовите все прямые параллельные
прямой А1 А.
2. Назовите все прямые,
пересекающиеся с прямой DC.
3. Назовите все прямые,
скрещивающиеся с прямой ВС.