Презентация по геометрии _Прямоугольник, ромб, квадрат_ (8 кл)

1.

Учебное занятие по геометрии в 8 классе

2.

Цели учебного занятия:
• Ввести определения прямоугольника,
ромба, квадрата как частных видов
параллелограмма, изучить их
свойства и признаки, закрепить
полученные знания при решении
задач.
•Повторить, обобщить, систематизировать
знания учащихся о параллелограммах.

3.

•Прямоугольник
•Ромб
•Квадрат
•Решение задач
•Тест

4.

ПРЯМОУГОЛЬНИК
Прямоугольник – это
параллелограмм, у которого
все углы прямые.

5.

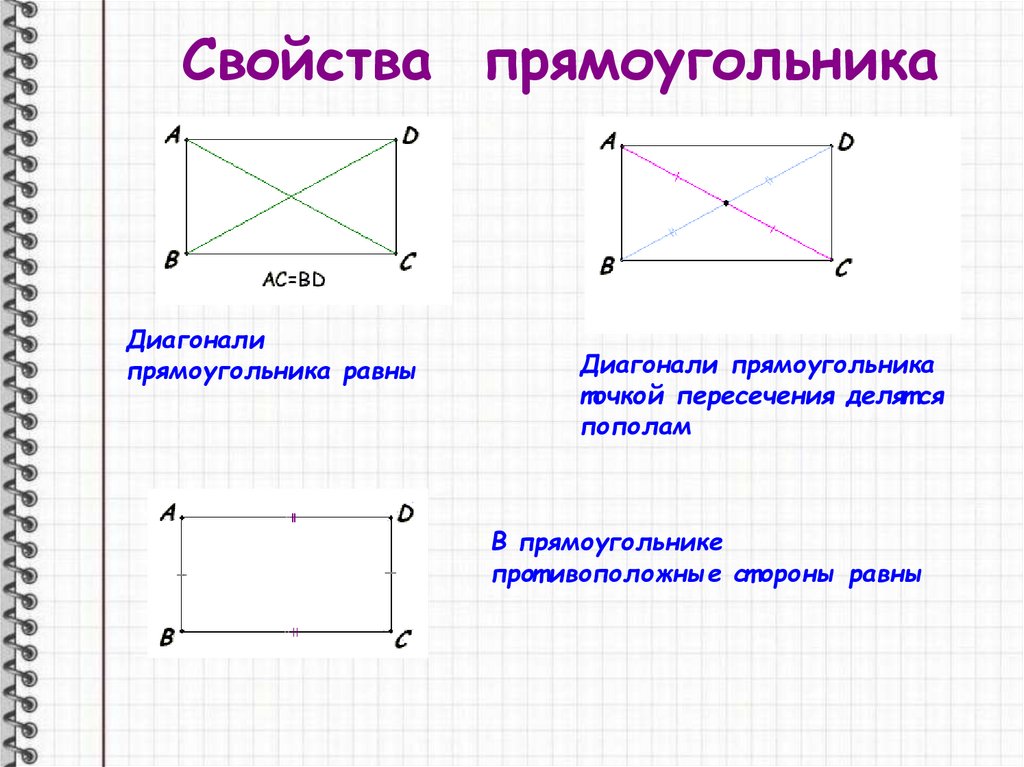
Свойства прямоугольника
Диагонали
прямоугольника равны
Диагонали прямоугольника
точкой пересечения делят ся
пополам
В прямоугольнике
прот ивоположные ст ороны равны

6.

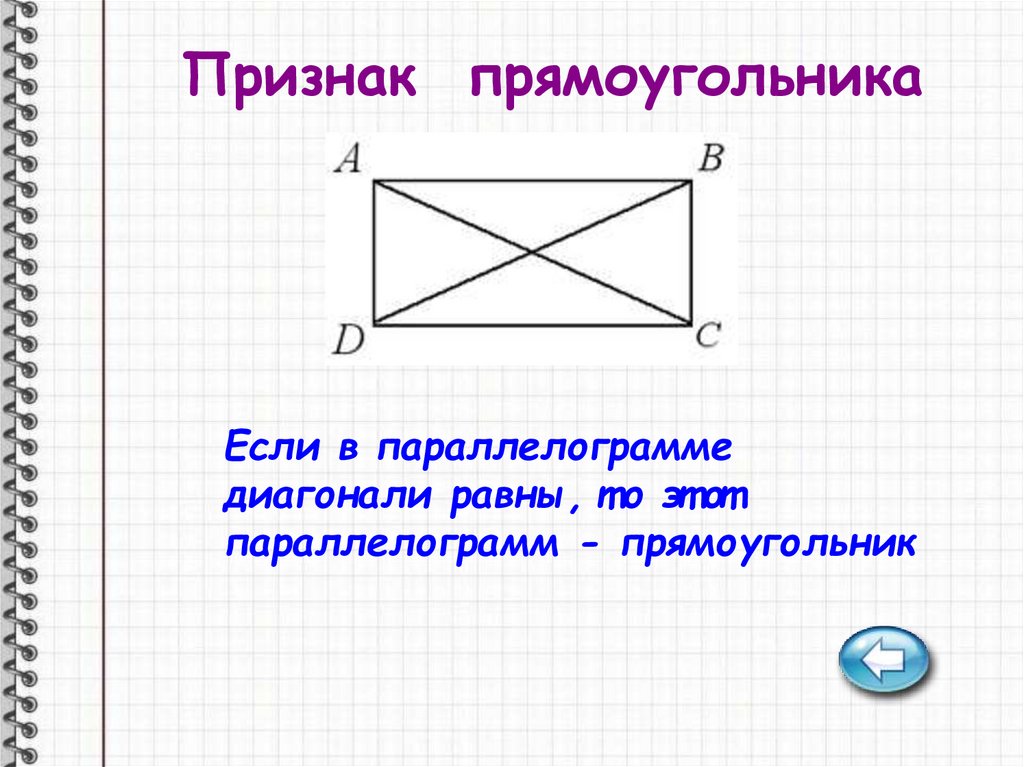
Признак прямоугольника
Если в параллелограмме
диагонали равны, т о эт от
параллелограмм - прямоугольник

7.

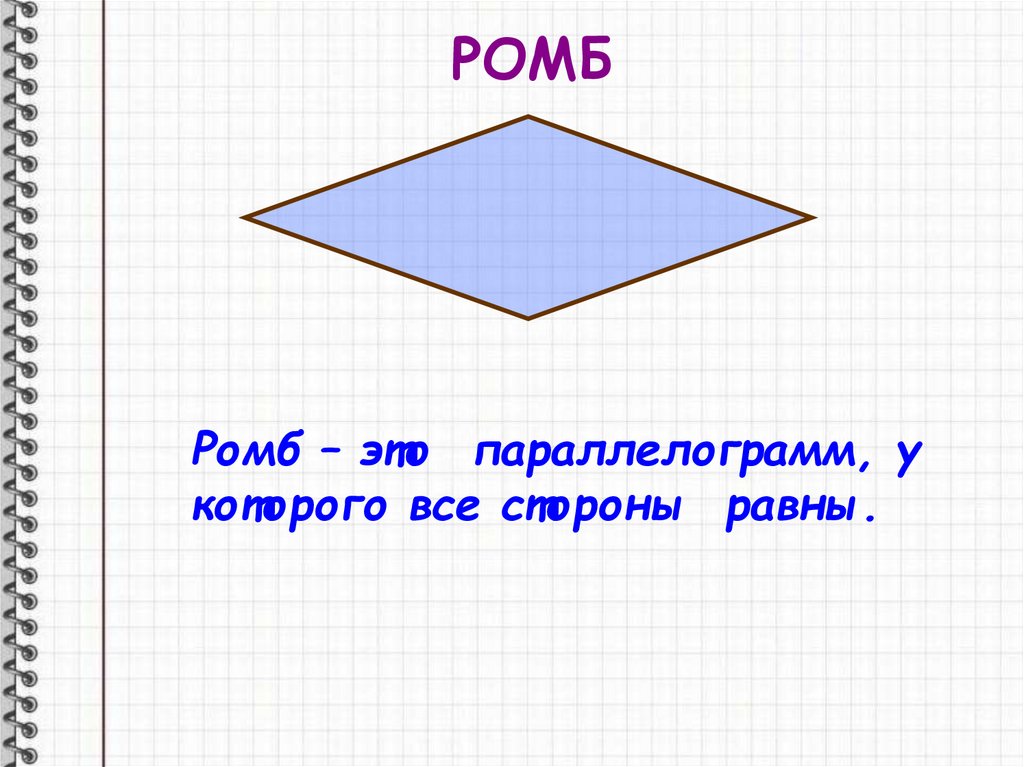
РОМБ
Ромб – это параллелограмм, у
которого все стороны равны.

8.

Слово ромб
произошло от
греческого слова
rombos – “бубен”.
Впервые термин
употребляется у
древнегреческих
учёных Герона и
Паппа
Александрийского

9.

СВОЙСТВА РОМБА
• Диагонали ромба
взаимно
перпендикулярны и
в т очке пересечения
делят ся пополам.
• Диагонали
ромба являют ся
биссект рисами
его углов.

10.

ПРИЗНАК
РОМБА
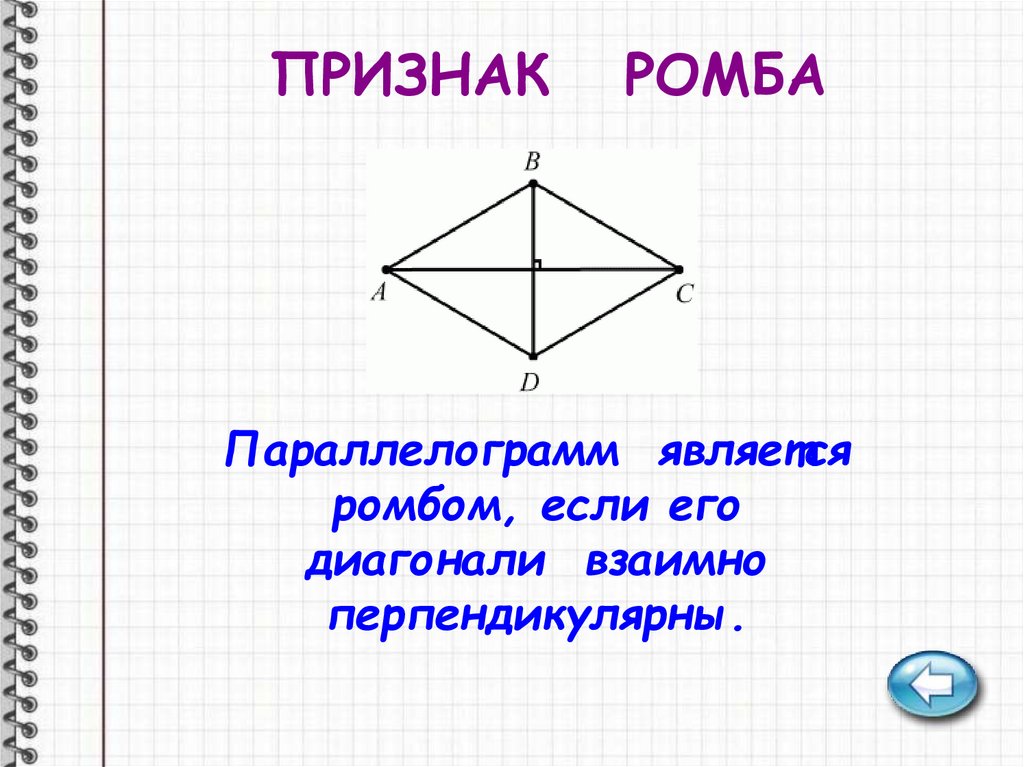
Параллелограмм является
ромбом, если его
диагонали взаимно
перпендикулярны.

11.

КВАДРАТ
Квадрат ом называет ся прямоугольник,
у кот орого все ст ороны равны
Квадрат ом называет ся ромб,
у кот орого все углы прямые

12.

Слово квадрат
Квадратом
произошло от
также называют
латинского слова возведение
quadratus –
в степень 2
“четырехугольный”
(от guattuor χ²
“четыре”).
3²
5²
Y²

13.

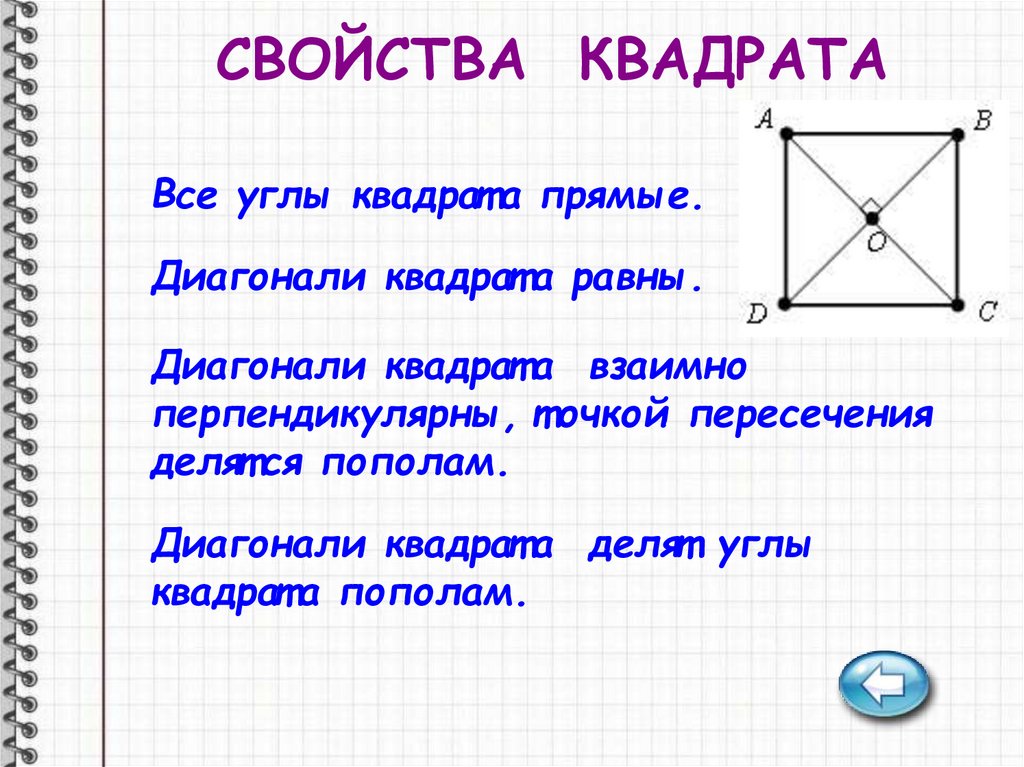
СВОЙСТВА КВАДРАТА
Все углы квадрат а прямые.
Диагонали квадрат а равны.
Диагонали квадрат а взаимно
перпендикулярны, т очкой пересечения
делят ся пополам.
Диагонали квадрат а делят углы
квадрат а пополам.

14.

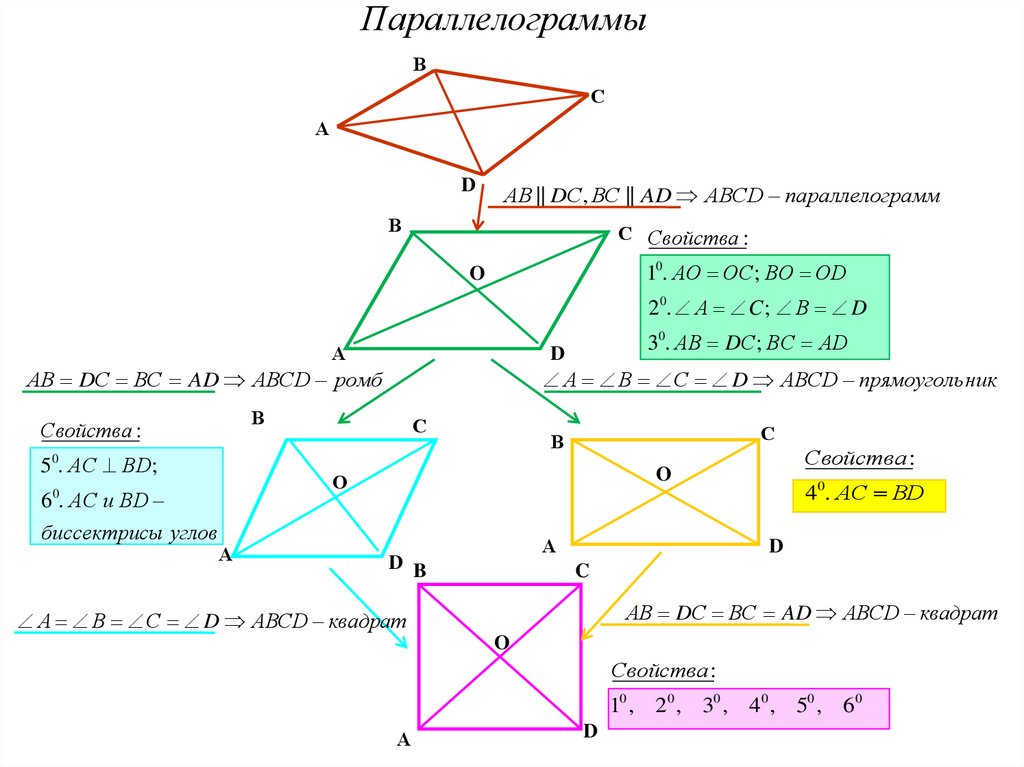
Параллелограммы
С
В
А
D
АВ || DС , ВС || AD АВСD параллелограмм
В
С Свойства :
10. АО АС ; ВО ОD
O
20. А C ; В D
А
D
АВ DС ВС AD АВСD ромб
А В С D АВСD прямоугольник
В
Свойства :
50. АС ВD;
30. АВ DС ; ВС АD
С
С
В
О
6 . АС и ВD
биссектрисы углов
0
А
А
Свойства :
O
D
B
4 0. АС ВD
D
C
АВ DС ВС AD АВСD квадрат
А В С D АВСD квадрат
O
Свойства :
А
D
10 , 20 , 30 , 40 , 50 , 60

15.

Параллелограммы
В
С
А
D
АВ || DС , ВС || AD АВСD параллелограмм
В
С Свойства :
10. АО ОС ; ВО ОD
O
20. А C ; В D
А
D
АВ DС ВС AD АВСD ромб
50. АС ВD;
6 . АС и ВD
биссектрисы углов
А В С D АВСD прямоуголь ник
В
Свойства :
30. АВ DС ; ВС АD
С
С
В
О
0
А
Свойства :
O
А
D B
40. АС ВD
D
C
АВ DС ВС AD АВСD квадрат
А В С D АВСD квадрат
O
Свойства :
10 , 20 , 30 , 40 , 50 , 60
А
D

16.

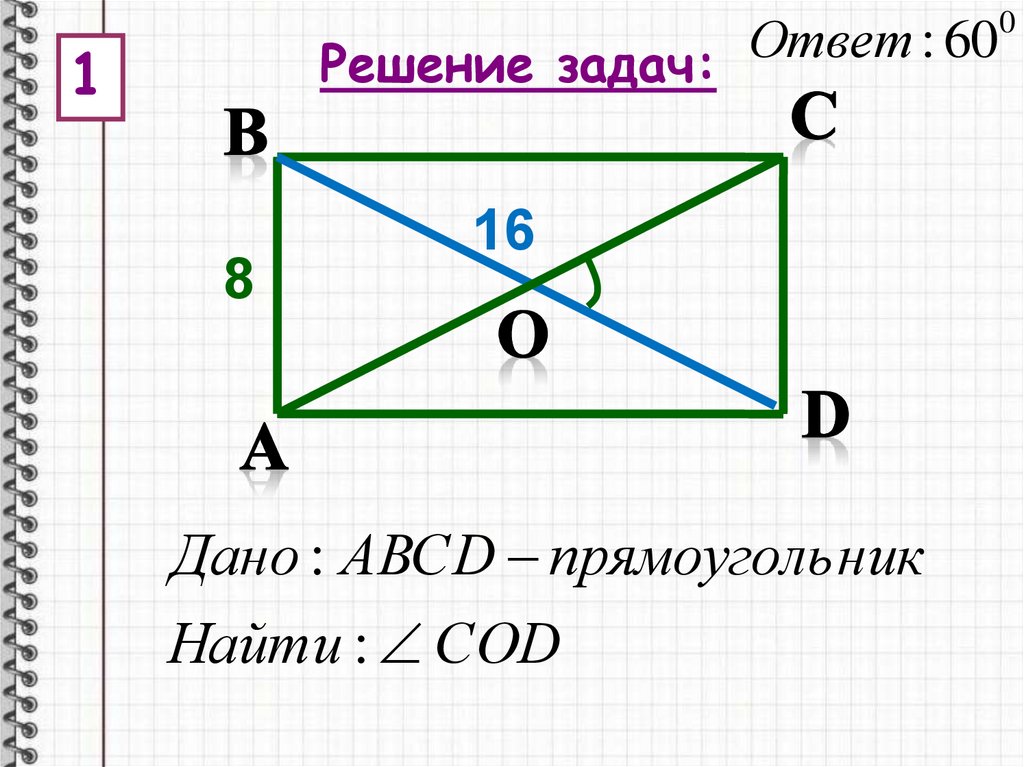
Ответ
:
60
Решение задач:
1
8
16
Дано : АВСD прямоуголь ник
Найти : СОD
0

17.

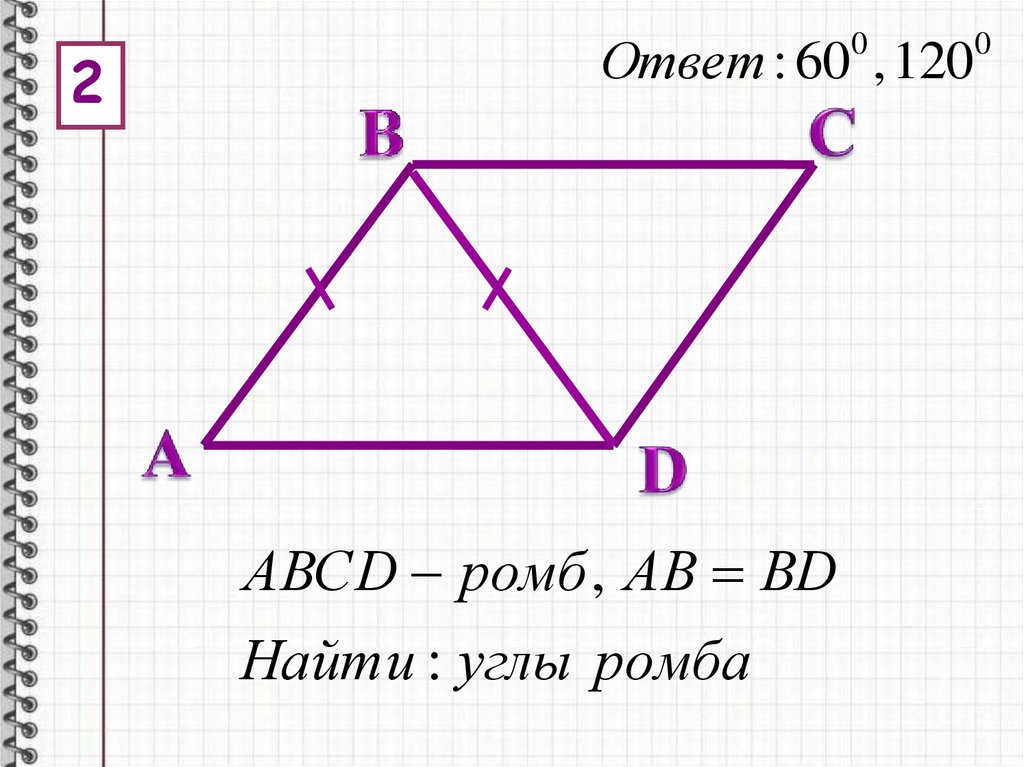
2
Ответ : 60 , 120
0
АВСD ромб , АВ ВD
Найти : углы ромба
0

18.

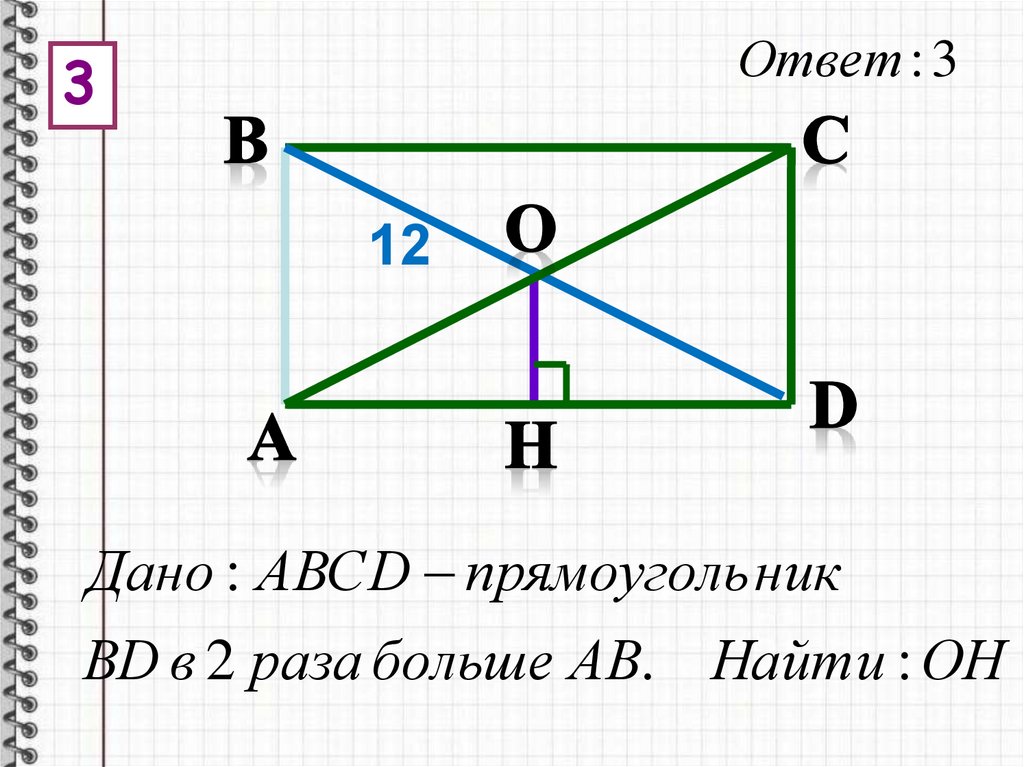
Ответ : 3
3
12
Дано : АВСD прямоуголь ник
ВD в 2 раза больше АВ. Найти : ОН

19.

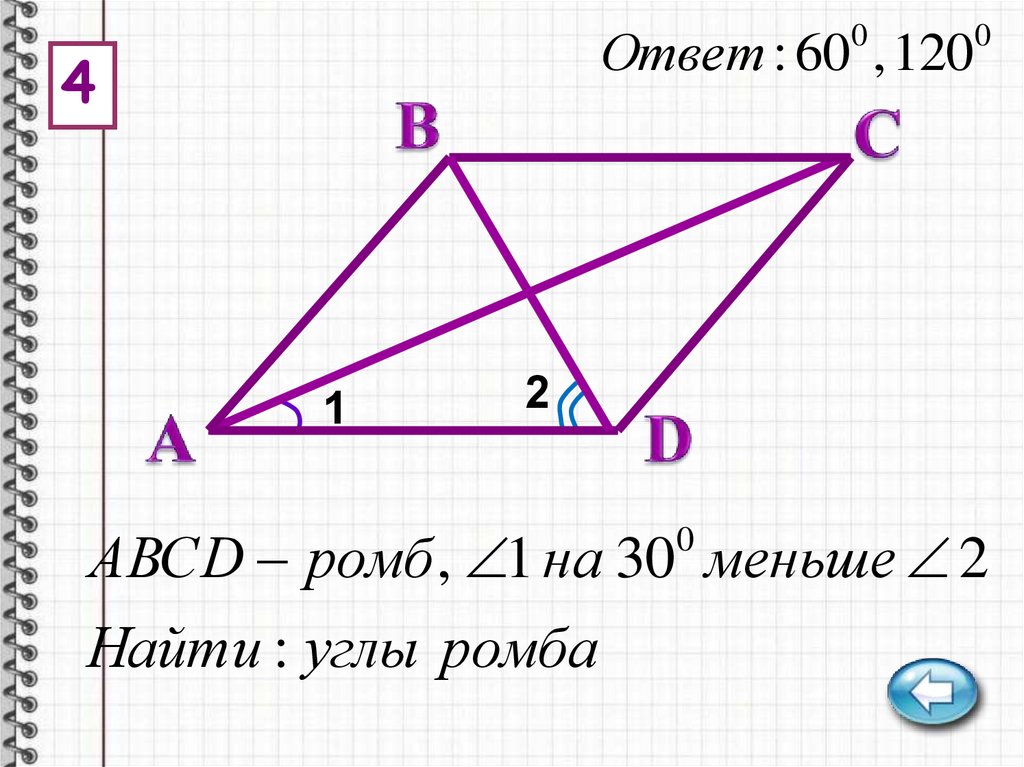
Ответ : 60 , 120
0
4
1
0
2
АВСD ромб , 1 на 30 меньше 2
Найти : углы ромба
0

20.

Проверочная работа
1 – параллелограмм
2 – прямоугольник
3 – ромб
4 – квадрат
Для каждого из 10 утверждений, основанных
на свойствах данных параллелограммов,
укажите номер той фигуры, которой это
утверждение принадлежит первоначально.

21.

Проверочная работа
Вариант 1
Вариант 2
В параллелограмме:
1. Односторонние углы равны
2. Диагональ делит на равные
равнобедренные треугольники
3. Сумма односторонних углов
4. Диагонали равны
5. Диагональ делит на равные
треугольники
6. Углы равны и диагонали перпендикулярны
7. Диагонали делят на равные
равнобедренные треугольники
8. Диагонали- биссектрисы и
равны между собой
9. Все стороны равны
10. Смежные стороны равны и
перпендикулярны
1. Диагонали перпендикулярны
2. Один угол прямой и диагонали
биссектрисы
3. Противоположные стороны
равны
4. Смежные стороны равны
5. Диагонали делят на равные
прямоугольные треугольники
6. Диагонали делят на равнобедренные треугольники
7. Диагональ делит на равные
прямоугольные треугольники
8. Диагонали перпендикулярны и
равны
9. Все углы равны
10. Диагонали точкой пересечения делятся пополам

22.

Ответы к проверочной работе
Вариант 1
1. 2
2. 3
3. 1
4. 2
5. 1
6. 4
7. 4
8. 4
9. 3
10. 4
Вариант 2
1. 3
2. 4
3. 1
4. 3
5. 3
6. 2
7. 2
8. 4
9. 2
10. 1

23.

Домашнее задание
Задача 1.
Диагонали прямоугольника АВСD пересекаются в
точке О, АВО = 36 . Найдите АОD.
Задача 2.
Найдите периметр ромба ABCD, если В = 120 ,
а BD=8 см.
Задача 3.
Периметр ромба ABCD равен 16 см. Высота,
опущенная к стороне AD из вершины B, равна
2 см. Найдите углы ромба.
-