Задача безусловной оптимизации

1. Задача безусловной оптимизации

J(x)
min
x R
n
x
• методы решения ЗБО являются алгоритмическим фундаментом для решения общей
НП-задачи
• непосредственно возникает во многих
ИУСкогда ограничения отсутствуют
приложениях,
(решение алгебраических систем уравнений)
• методы решения ЗБО могут применяться в
задачах с неактивными ограничениями

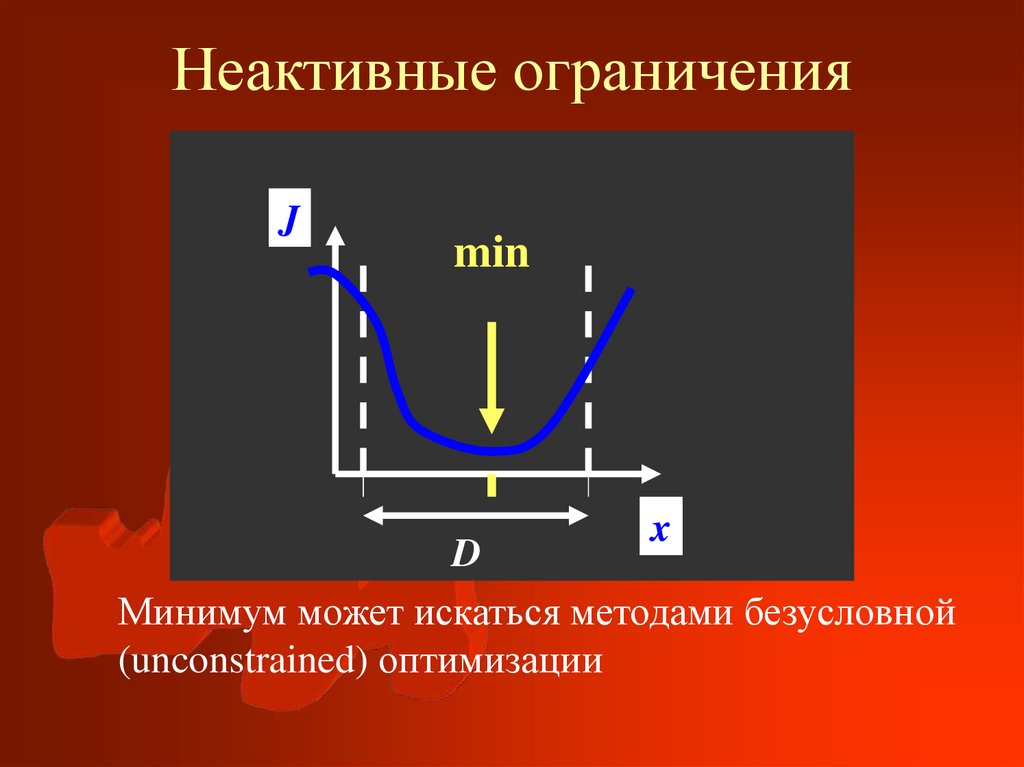
2. Неактивные ограничения

J
ИУС
min
x
D
Минимум может искаться методами безусловной
(unconstrained) оптимизации

3. Три основные метода сведения задач с ограничениями (НП-задач) к ЗБО

• Метод замены переменных
• Метод штрафных функций
• Метод модифицированных функций
ИУС
Лагранжа

4. Метод замены переменных (стр. 154, разд. 2.2.2 )

min , x 0
J(x)
x
Замена : x = y
2
2
J(x) = J(y ) = F(y)
- < y < +
ИУС
Применяется при наличии «простых» или
интервальных ограничений вида:
a x b

5.

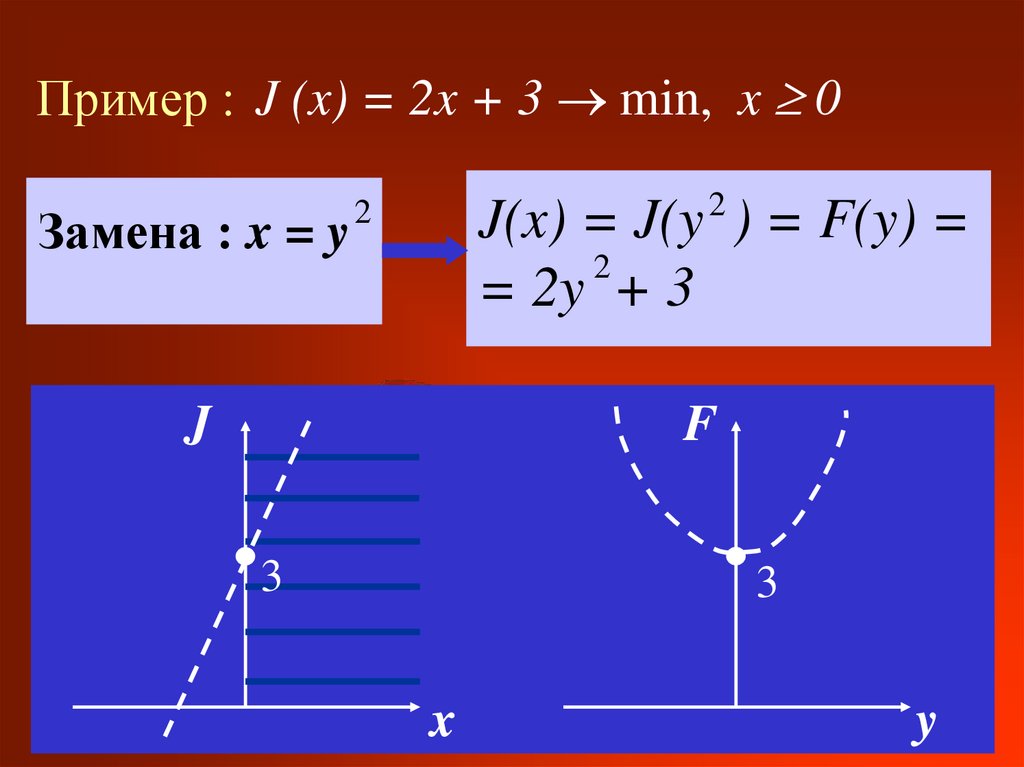
Пример : J (x) = 2x + 3 min, x 0
Замена : x = y
J(x) = J(y 2 ) = F(y) =
2
= 2y + 3
2
J
F
ИУС
3
3
x
y

6. Замена переменных – некоторые проблемы

• Вместо исходных простых
функционалов можем получить
более сложные с различными
особенностями и сингулярностями
• Применение
ИУС метода оправдано в
относительно простых случаях, либо
на начальных этапах оптимизации

7. Метод штрафных функций

Продемонстрируем основную идею на примере
задачи с ограничением - равенством:
2
J(x) = x
1
2
+x
2
min, x = 2
1
ИУС
Здесь минимизатор очевиден: x* = ( 2, 0)

8.

Согласно общей идее МШФ исходная задача
заменяется на вспомогательную последовательность
задач с неограниченно растущим параметром
J (x) = x + x + (x - 2 ) min,
1
2
2
2
2
ИУС
x*( ) x*
1
при
x

9.

Уравнения линий уровня функций J
x
2
=0
>0
1
x
ИУС
2
1

10. Метод точных штрафных функций (модифицированных функций Лагранжа)

Продемонстрируем основную идею на примере
следующей задачи с ограничением - равенством:
3
J(x) = x min, g(x) = x + 1 = 0
ИУС
Здесь минимизатор снова очевиден: x* = - 1
(но мы будем поступать формально)

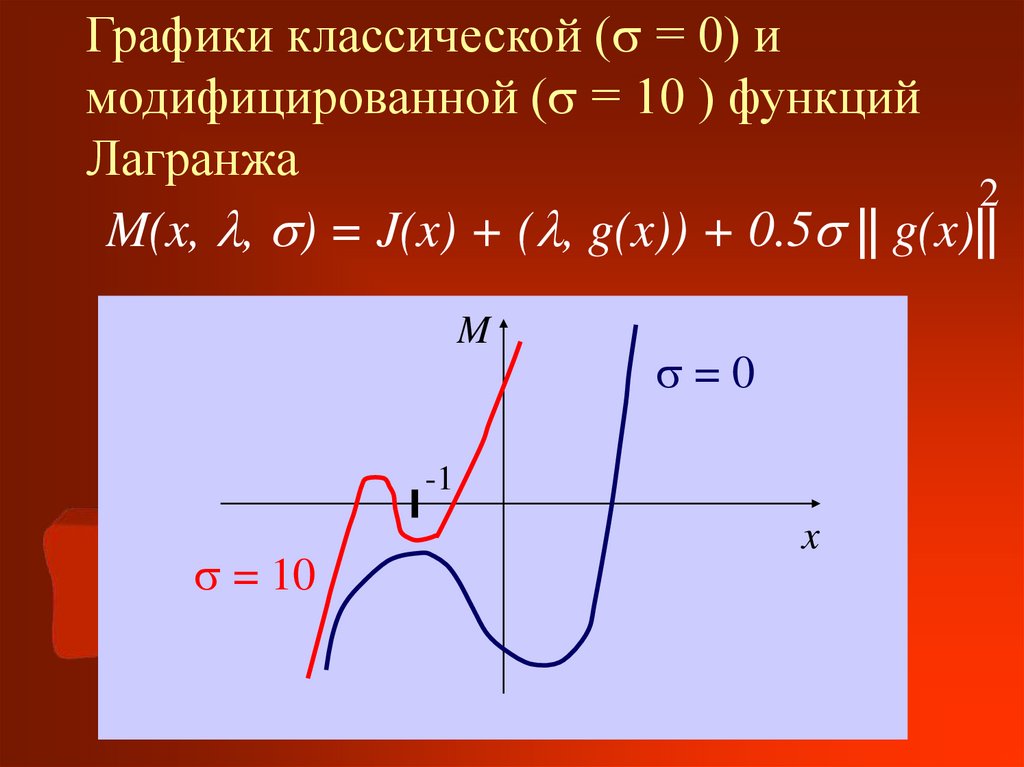
11. Графики классической ( = 0) и модифицированной ( = 10 ) функций Лагранжа

Графики классической ( = 0) и
модифицированной ( = 10 ) функций
Лагранжа
2
M(x, , ) = J(x) + ( , g(x)) + 0.5 || g(x)||
M
=0
-1
ИУС
= 10
x

12. Основные выводы

• Метод МФЛ является гибридом метода штрафных
функций и классического метода множителей
Лагранжа
• В методе МФЛ отсутствует неограниченно растущий
параметр – это хорошо, т.к. степень обусловленности
задачи оказывается существенно меньше, чем в методе
штрафных функций
• Недостаток 1: в искомой точке функция М имеет
лишь локальный минимум, а сама может быть
ИУСснизу
неограниченной
• Недостаток 2: параметр должен превышать
некоторое пороговое значение (в примере выше оно
равно 6), которое трудно определять алгоритмически

13. Основные рекомендации по решению задач с ограничениями

• Вначале попытаться решить задачу без учета
ограничений – может быть они окажутся неактивными
• Далее попытаться применить замену переменных для
снятия ограничений и обратиться к методам
безусловной оптимизации
• Если задача все еще не решена использовать на первом
этапе МШФ, а затем перейти для уточнения решения к
ИУС
методу МФЛ
• Если все попытки не дают результата, обратиться к
специальным методам оптимизации, ориентированным
на работу в условиях ограничений

14. Обратимся теперь к изучению базовых методов и алгоритмов безусловной оптимизации (далее будем считать, что ограничения уже

отсутствуют)
ИУС

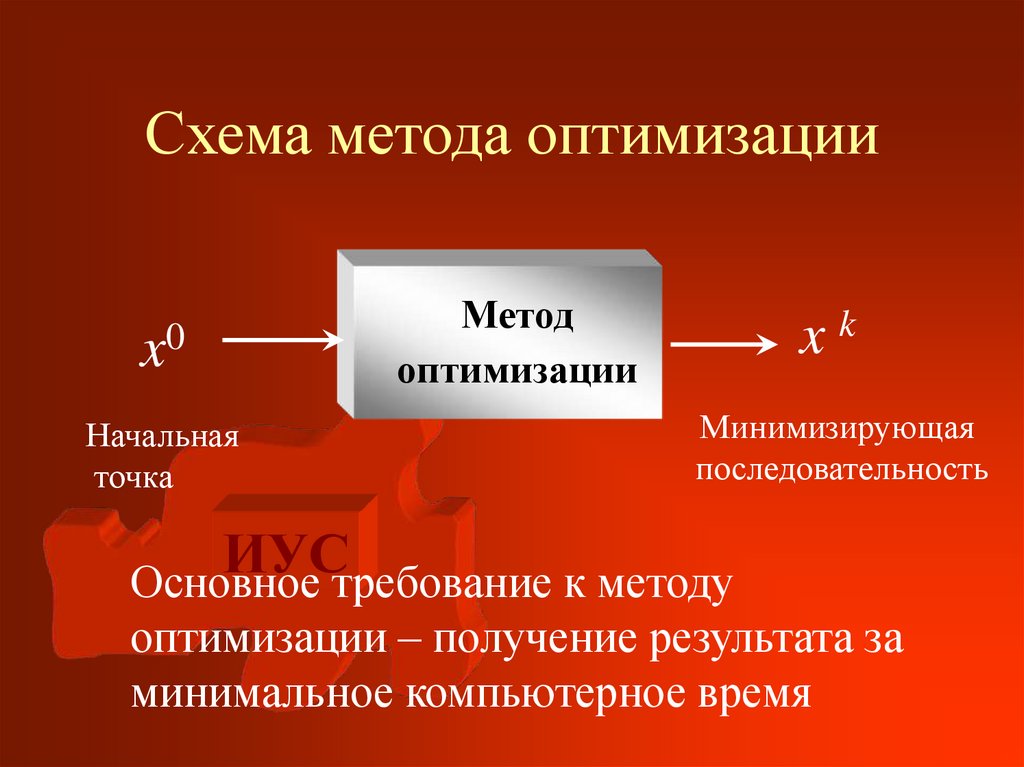
15. Схема метода оптимизации

x0
Начальная
точка
Метод
оптимизации
xk
Минимизирующая
последовательность
ИУС
Основное требование к методу
оптимизации – получение результата за
минимальное компьютерное время

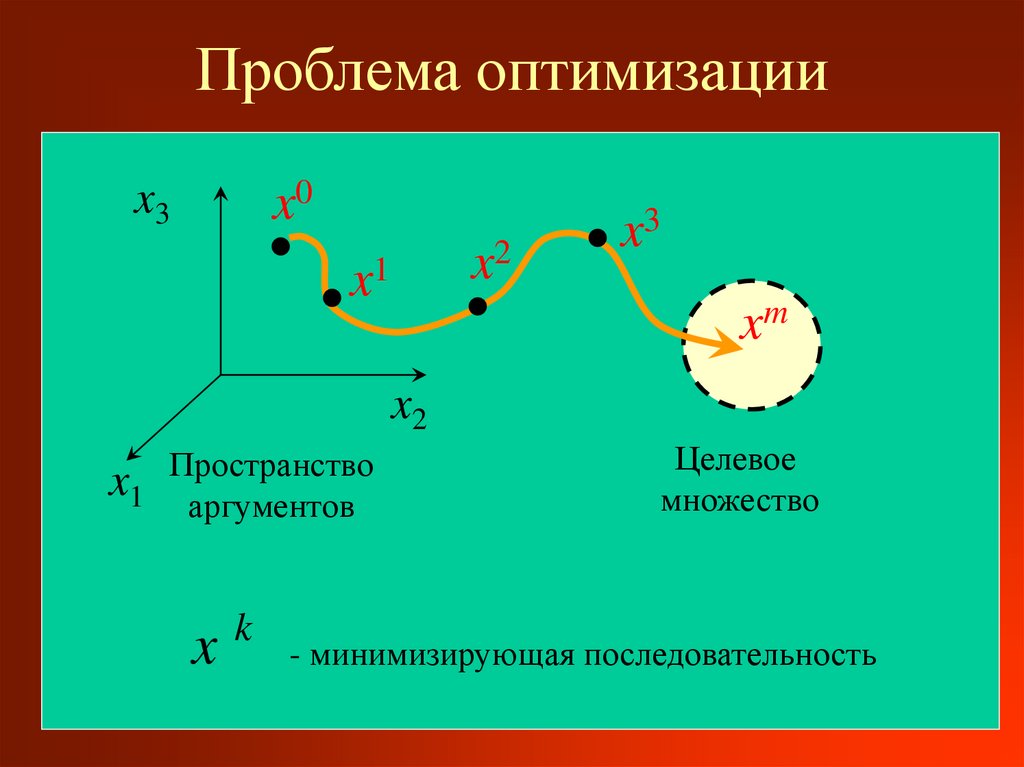
16. Проблема оптимизации

x0
x3
x2
x1
x3
xm
x2
Пространство
x1 аргументов
Целевое
множество
ИУС
x
k
- минимизирующая последовательность

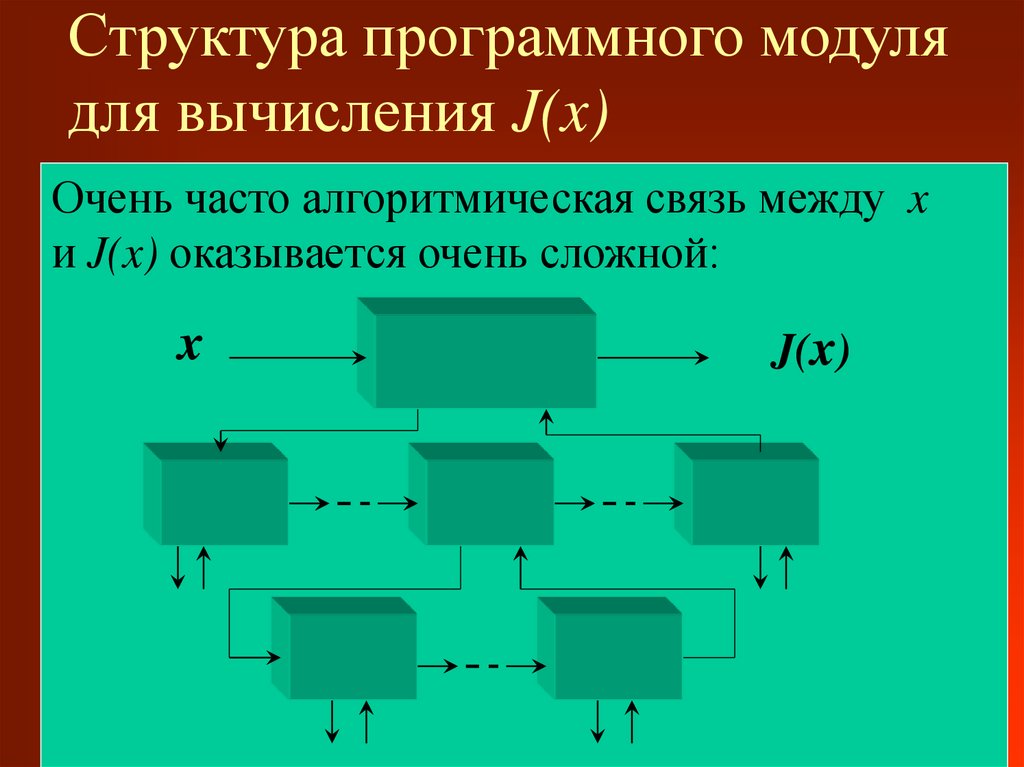
17. Структура программного модуля для вычисления J(x)

Очень часто алгоритмическая связь между x
и J(x) оказывается очень сложной:
x
J(x)
ИУС

18. Основные трудности

В процессе минимизации J(x) мы часто имеем
нечто подобное:
10.2342776 Скорость сходимости
10.2342774 является
неудовлетворительной.
10.2342773
Много
Процедура
10.2342771
часов
минимизации требует
10.2342768 слишком много
реального
10.2342763 времени
времениИУС
……………
3.5000000 -искомый минимум

19. Итак, основные трудности :

• Медленная сходимость
• Jamming (заклинивание) – когда
процесс оптимизации полностью
останавливается задолго до
достижения оптимальной точки
ИУС
Для иллюстрации этой ситуации рассмотрим
наиболее простой метод оптимизации

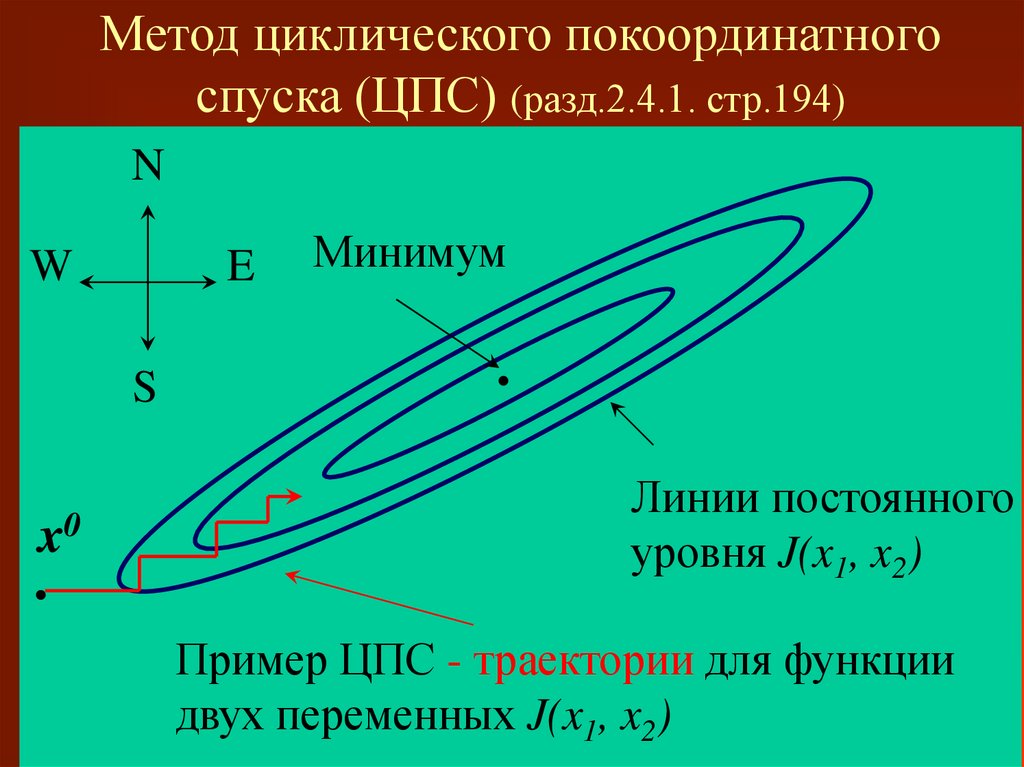
20. Метод циклического покоординатного спуска (ЦПС) (разд.2.4.1. стр.194)

N
W
E
Минимум
S
x0
ИУС
Линии постоянного
уровня J(x1, x2)
Пример ЦПС - траектории для функции
двух переменных J(x1, x2)

21. Медленная сходимость

Линии
постоянного
уровня подобны
узкому глубокому
оврагу
ИУС
ЦПС траектория
Когда мы имеем больше
двух переменных
ситуация может быть
более сложной (в этом
случае мы можем иметь
многомерные овраги)

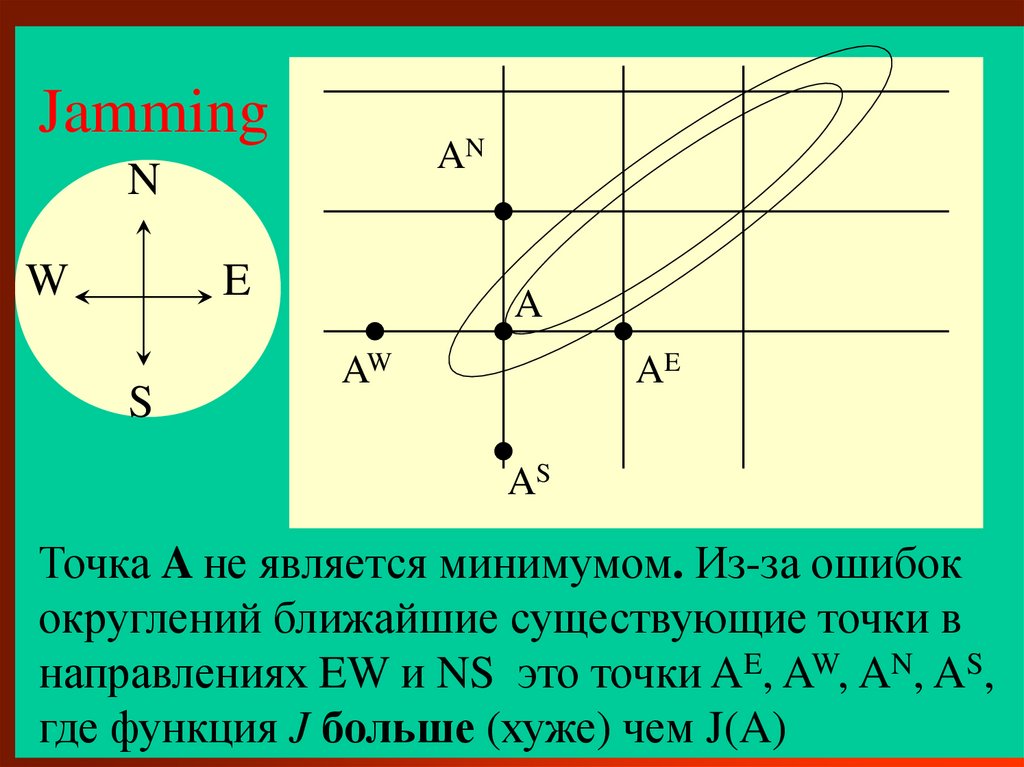
22.

Jamming
AN
N
W
E
S
A
AW
AE
AS
ИУС
Точка A не
является минимумом. Из-за ошибок
округлений ближайшие существующие точки в
направлениях EW и NS это точки AE, AW, AN, AS,
где функция J больше (хуже) чем J(A)

23. Выводы

• Аналогичные трудности возникают для большинства
известных методов оптимизации
• К сожалению очень часто точка заклинивания
ошибочно принимается за точку минимума и задача
оптимизации считается решенной
• Очень часто мы считаем, что ошибки округления и
дискретность разрядной сетки есть что-то
малозначимое, однако в проблемах численного анализа,
моделирования и оптимизации это не так
ИУС являются алгоритмической
• Методы оптимизации
базой для общих систем выбора и принятия решений и
недооценка вышеприведенных замечаний может
приводить к досадным ошибкам

24. Очень печальный пример

Monograph “Optimal control by mathematical
programming”, Prentice-Hall, Inc.Englewood Cliffs,
New Jersey, 1971.
By Professor of Electrical Engineering University of
Illinois Urbana B. Kuo and Associate Professor of
Automatic Control Rensselaer Polytechnic Institute
ИУС
of Connecticut Hartford D. Tabak

25. Optimal control problems for dynamical systems

Печальный пример
Optimal control problems for
dynamical systems
Пример. Заданы уравнения процесса:
y1(i+1) – y1(i) = T(i+1) (- y12(i) + y2(i) + u(i))
y2(i+1) – y2(i) = T(i+1) y1(i) , i= 0, 1, …, 11
Проблема заключается в выборе такой
ИУС
управляющей
последовательности u(i), чтобы
достичь заданной целевой области в
пространстве переменных y1, y2 и обеспечить
минимум заданному функционалу J

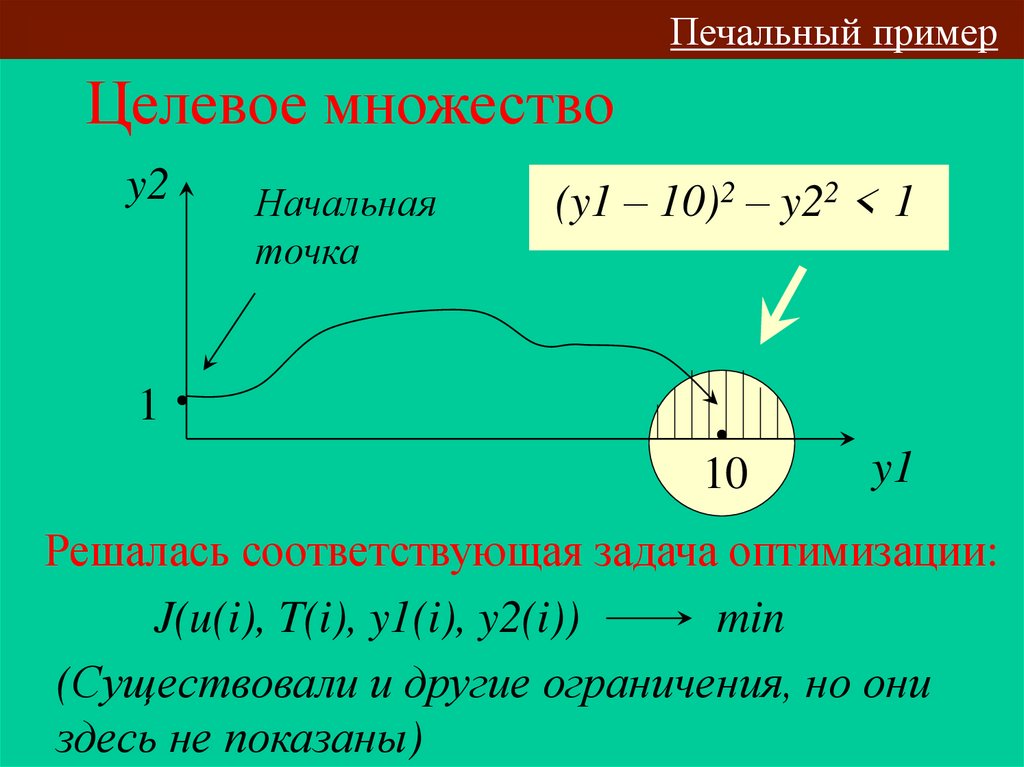
26. Целевое множество

Печальный пример
Целевое множество
y2
Начальная
точка
(y1 – 10)2 – y22 < 1
1
10
y1
РешаласьИУС
соответствующая задача оптимизации:
J(u(i), T(i), y1(i), y2(i))
min
(Существовали и другие ограничения, но они
здесь не показаны)

27. Методы использованные в монографии

Печальный пример
Методы использованные в монографии
Сформулированная задача оптимизации
содержала 48 переменных и 37 ограничений и
была решена методом
последовательной безусловной
минимизации (штрафных функций),
разработанным
ИУС известными американскими
авторами Фиакко и Мак-Кормиком

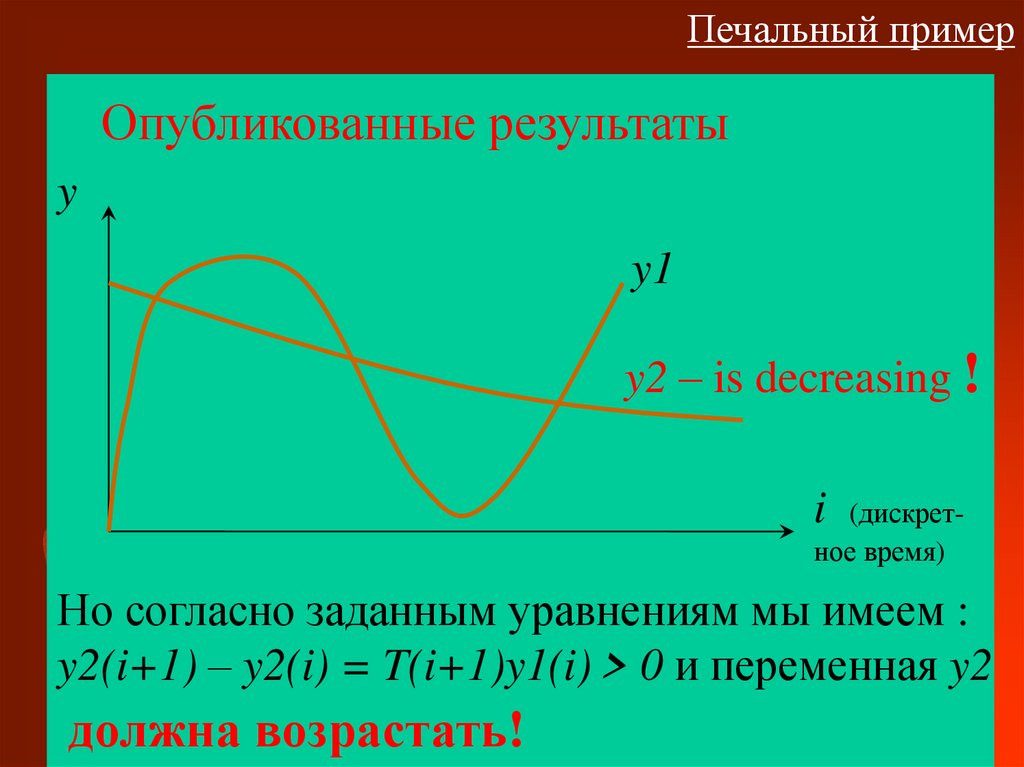
28. Опубликованные результаты

Печальный пример
Опубликованные результаты
y
y1
y2 – is decreasing !
ИУС
i (дискретное время)
Но согласно заданным уравнениям мы имеем :
y2(i+1) – y2(i) = T(i+1)y1(i) > 0 и переменная y2
должна возрастать!

29. Выводы

Печальный пример
Выводы
• Полученные численные результаты даже
качественно не соответствуют уравнениям системы
• Авторы не заметили этого
• Они получили точку заклинивания (jamming point) и
остановились задолго до минимума
• Практические результаты применения подобных
численных исследований могут быть весьма
ИУС
плачевными
• Мы должны уделять большое внимание корректному
применению методов оптимизации и принятия
решений