Одновременная измеримость двух физических величин. Вводные замечания

1.

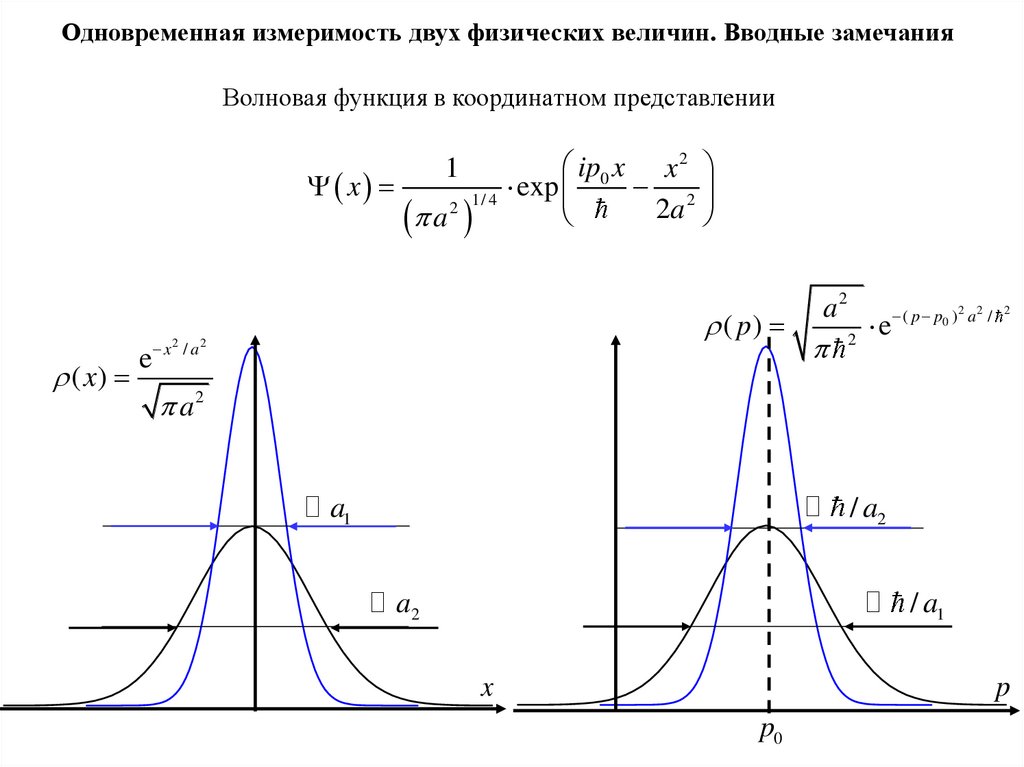
Одновременная измеримость двух физических величин. Вводные замечания
Волновая функция в координатном представлении
ip0 x x 2
x
exp
2
2 1/ 4
2a
a
1
e x / a
2
( x)
( p)
2
a2
( p p0 ) a /
e
2
2
2
2
a2
/ a2
a1
/ a1
a2
p
x
p0

2.

Соотношение неопределённости координата-импульс
Графические соображения
p x
Непосредственное вычисление дисперсий координаты и импульса
p p x x p x
2
2
2
2
2
4
Чем точнее определена координата (т.е., чем меньше дисперсия координаты),
тем неопределённее значение импульса и наоборот!

3.

Одновременная измеримость двух физических величин. Определение
Пусть в серии экспериментов (формально бесконечной), проводимых с системой,
находящейся в одном и том же состоянии, измеряют какую-то физическую величину.
В результате измерений получают одно и то же значение этой величины.
В другой серии экспериментов, проводимых над той же системой в том же состоянии,
измеряют другую физическую величину и для неё всё время получают одно и то же
значение. Тогда эти две величины называются одновременно измеримыми!
Более формальное определение. Если в данном состоянии системы при измерении
двух величин с вероятностью единица получают одни и те же значения, то эти
величины одновременно измеримы! Отсюда следует математическое утверждение:
операторы двух одновременно измеримых физических величин имеют общий базис
собственных волновых функций
n :
fˆ n f n n , gˆ m g m m

4.

Коммутативность операторов одновременно измеримых величин
Если две величины одновременно измеримы, то их операторы коммутируют
между собой
fˆ , gˆ 0
Доказательство. Справедливы равенства
fˆ gˆ n f n g n n , gˆ fˆ n g n f n n
fˆ , gˆ n 0
Для произвольной волновой функции
an n , fˆ , gˆ an fˆ , gˆ n 0
n
n
Вопрос: а если коммутатор операторов двух физических величин равен нулю, будут
ли эти величины одновременно измеримы?

5.

Рассмотрим два эрмитовых оператора
ˆ
ˆ †,
ˆ ,
ˆ
ˆ † ,
ˆ iCˆ
Введём также операторы
ˆ
ˆ a,
ˆ
ˆ b; a a , b b
1
1
Вопрос
ˆ † ?,
ˆ ,
ˆ † ?,
ˆ ?
1
1
1
1

6.

Ответ
ˆ†
ˆ ,
ˆ ,
ˆ†
ˆ ,
ˆ iCˆ
1
1
1
1
1
1
Рассмотрим функционал
2
ˆ i
ˆ 0,
J dx
1
1
В развёрнутом виде
ˆ
ˆ i
ˆ
ˆ
J dx 1 i 1
1
1
С помощью операции транспонирования «перебросить» действие оператора
ˆ i
ˆ
1
1
на функцию
ˆ i
ˆ
1
1

7.

Результат
†
ˆ
ˆ i
ˆ
ˆ
J dx 1 i 1
1
1
Перемножить операторы в скобках с учётом коммутатора соответствующих величин?

8.

Результат
ˆ 2 i
ˆ ,
ˆ
ˆ2
J dx 2
1
1
1 1
Или
ˆ 2 Cˆ
ˆ2
J dx 2
1
1
Положим, что
a , b
Тогда
dx ˆ 12 , dx ˆ 12 , C dx Cˆ
2
2
J C 0
2
2
2
Условие неотрицательности функционала при любых
?

9.

Условие неотрицательности функционала при любых
C2
4
2
2
Найти явный вид условия неотрицательности функционала при
ˆ pˆ ,
ˆ xˆ

10.

Условие неотрицательности функционала при
ˆ pˆ ,
ˆ xˆ
Называется соотношением неопределённости Гейзенберга
p x
2
2
2
4
Физический смысл соотношения неопределённости в общем случае
Если операторы двух величин коммутируют, то возможно создать состояние системы,
в котором дисперсии этих величин равны нулю – т.е. эти величины одновременно
измеримы. И наоборот, в случае некоммутирующих операторов дисперсии
соответствующих величин ВСЕГДА отличны от нуля – эти величины одновременно
не измеримы!

11.

Найти волновые функции, минимизирующие соотношение неопределённости для пары
координата-импульс, т.е. когда
p x
2
2
2
4
Указание: в этом случае функционал обращается в ноль
2
ˆ i ˆ 0
J dx
1
1

12.

Дифференциальное уравнение
d
p
i
x
x
0
0 x 0
i dx
Или
d x
ip0 x x0
dx
x
Ответ
ip x x x0 2
x C exp 0
0, metr 2
2