Похожие презентации:
Случайные события. Курс лекций «Метрология»
1. Случайные события
Курс лекций «Метрология»2. Литература
Гмурман В.Е. Теория вероятностей иматематическая статистика: учеб. пособие для
бакалавров.
3. Испытания и события
Испытание – эксперимент с очерченным набором возможныхвзаимоисключающих результатов.
Событие – результат испытания.
Существует три вида событий:
1. Достоверное событие – событие, которое обязательно
произойдет, если будет осуществлена определенная совокупность
условий.
2. Невозможное событие – событие, которое заведомо не
произойдет, если будет осуществлена определенная совокупность
условий.
3. Случайное событие – событие, которое при осуществлении
определенной совокупности условий может либо произойти, либо
не произойти.
4. Случайные события
События называют несовместными, если появление одного изних исключает появление других событий в одном и том же
испытании.
Несколько событий образуют полную группу, если в результате
испытания появится хотя бы одно из них.
События называют равновозможными, если есть основание
считать, что ни одно из них не является более возможным, чем
другое.
5. Классическое определение вероятности
Вероятность события А – отношение числа m исходов,благоприятствующих событию А, к общему числу n
равновозможных несовместных элементарных исходов,
образующих полную группу.
где m – число элементарных исходов, благоприятствующих А;
n – число всех возможных элементарных исходов испытания.
Свойства вероятности:
1. Вероятность достоверного события равна 1.
2. Вероятность невозможного события равна 0.
3. Вероятность случайного события есть положительное число,
заключенное между 0 и 1.
6. Основные формулы комбинаторики
Перестановки – комбинации, состоящие из одних и тех же nразличных элементов и отличающиеся только порядком их
расположения.
Размещения – комбинации, составленные из n различных
элементов по m элементов, которые отличаются либо составом
элементов, либо их порядком.
Сочетания – комбинации, составленные из n различных
элементов по m элементов, которые отличаются хотя бы одним
элементом.
7. Относительная частота
Относительная частота – отношение числа испытаний, вкоторых событие появилось, к общему числу фактически
произведенных испытаний.
где m – число появлений события;
n – общее число испытаний.
8. Относительная частота
Определение вероятности не требует, чтобы испытанияпроводились в действительности.
Определение относительной частоты предполагает, что испытания
были проведены фактически.
Вероятность вычисляют до опыта, а относительную частоту –
после опыта.
Свойство устойчивости: в сериях испытаний относительная
частота изменяется мало (тем меньше, чем больше число
испытаний), колеблясь около вероятности появления события.
9. Статистическая вероятность
Недостатки классического определения вероятности:1.Число элементарных исходов испытания конечно.
2.Элементарные события – равновозможные.
Статистическая вероятность события – относительная
частота появления события или число, близкое к ней.
Недостаток статистического определения вероятности:
неоднозначность статистической вероятности.
10. Геометрическая вероятность
Геометрическая вероятность – вероятность попадания точкив область: отрезок, часть поверхности или объема.
1. Вероятность попадания точки на отрезок длиной l, являющийся
частью отрезка длиной L:
11. Геометрическая вероятность
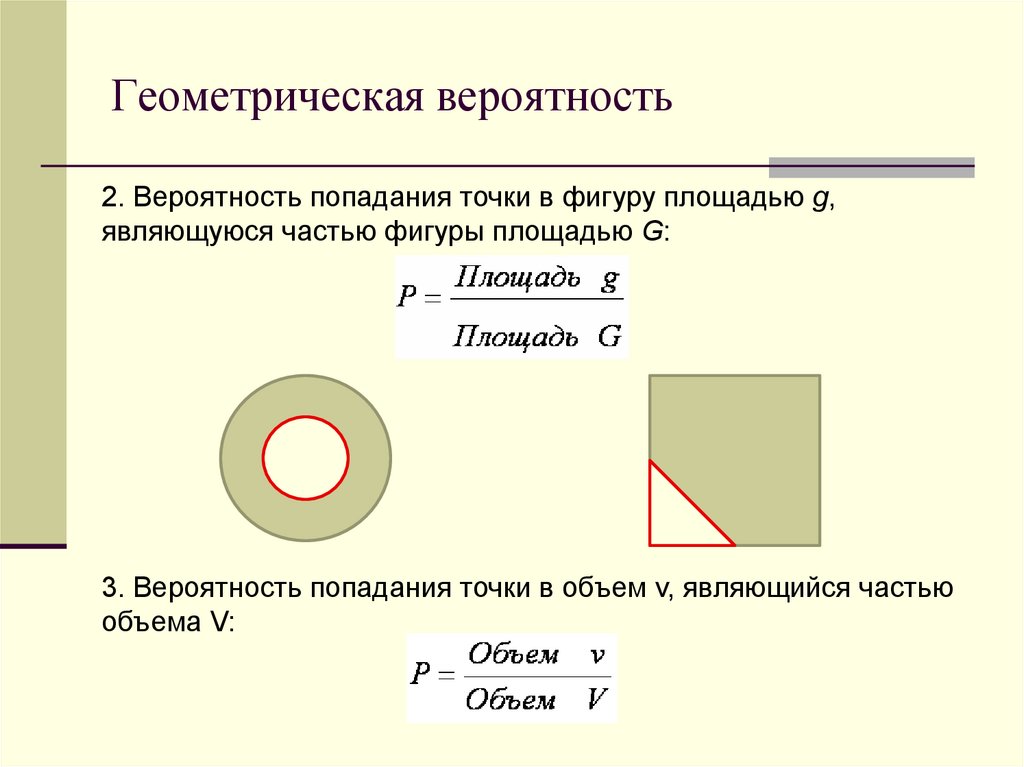
2. Вероятность попадания точки в фигуру площадью g,являющуюся частью фигуры площадью G:
3. Вероятность попадания точки в объем v, являющийся частью
объема V:
12. Маловероятные события
Принцип практической невозможности маловероятныхсобытий: если случайное событие имеет очень малую
вероятность, то на практике можно считать, что в единичном
испытании это событие не наступит.
Уровень значимости – малая вероятность, при которой в
данной задаче событие можно считать практически невозможным.
Обычно принимают уровень значимости из интервала от 0,01 до
0,05.
13. Теорема сложения вероятностей несовместных событий
Сумма событий – событие, которое состоит в появлении хотябы одного из этих событий.
Вероятность появления одного из нескольких попарно
несовместных событий, безразлично которого:
Сумма вероятностей событий, образующих полную группу, равна
единице:
Сумма вероятностей противоположных событий равна единице:
14. Теорема умножения вероятностей независимых событий
Произведение событий – событие, которое состоит всовместном появлении всех этих событий.
Вероятность совместного появления нескольких событий,
независимых в совокупности:
Событие B называют независимым от события A, если
появление события A не изменяет вероятности события B.
Несколько событий называют независимыми в совокупности,
если независимы каждые два из них, а также каждое событие и
все возможные произведения остальных.
Вероятность появления хотя бы одного из нескольких событий,
независимых в совокупности:
15. Теорема умножения вероятностей зависимых событий
Условная вероятность PA(B) – вероятность события В,вычисленная в предположении, что событие А уже наступило.
Если события A и B являются независимыми:
Вероятность совместного появления двух событий :
Вероятность совместного появления n событий :
16. Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двух совместныхсобытий:
Если события являются несовместными:
17. Полная вероятность
Вероятность события А, которое может наступить лишь приусловии появления одного из несовместных событий В1, В2 … Вn ,
образующих полную группу:
18. Вероятность гипотез Формулы Бейеса
Пусть событие А может наступить лишь при условии появленияодного из несовместных событий В1, В2 … Вn , образующих
полную группу и называемых гипотезами.
Произведено испытание, в результате которого появилось
событие А.
Условная вероятность любой гипотезы Bi после проведения
испытания вычисляется по формуле Бейеса:
19. Формула Бернулли
Вероятность того, что при n испытаниях событие А осуществитсяровно k раз, равна:
p – вероятность того, что событие A наступит в единичном
испытании (одинакова для всех испытаний),
q = 1 - p – вероятность того, что событие A не наступит в
единичном испытании.


















 Математика
Математика








