Похожие презентации:
Случайные события. Вероятность. Основные теоремы сложения и умножения вероятностей
1. Случайные события Вероятность Основные теоремы сложения и умножения вероятностей
2. Теория вероятностей
математическая наука, изучающаязакономерности случайных явлений
3. Классическое определение вероятности
Определение: Вероятностью событияА называется отношение числа
благоприятных этому событию случаев
к общему числу всех случаев
m
P( A)
n
4. Свойства вероятности
m n1 - вероятность достоверного события;
n n
1.
P ( A)
2.
0
P ( A) 0
n
3.
0≤P(A)≤1
- вероятность невозможного события;
- вероятность любого события.
5. Относительная частота
Определение: Относительной частотойназывается отношение числа испытаний, в
которых событие появилось к общему числу
фактически произведенных испытаний
m
P
(
A
)
- относительная частота события А
n
или статистическая вероятность, m- число
появлений события,n – общее число
испытаний.
Отличие вероятности от относительной
частоты: вероятность вычисляют до опыта, а
относительную частоту – после опыта.
6.
Опр. Событие называется случайнымпо отношению к данному испытанию
(опыту), если при осуществлении этого
испытания (опыта) оно может наступить
или не наступить.
Событие обозначается:
A, B, C ,....
7.
Определения1. Событие , которое в результате
опыта обязательно произойдет
называется достоверным.
2. Событие, которое в результате
опыта никогда не наступит называется
невозможным.
3. Если одновременно одно
событие влечет за собой другое и
наоборот, такие события называются
равносильными.
8.
4. События называются несовместными,если наступление одного из них исключает
наступление любого другого.
5. События называются
равновозможными, если в результате
испытания по условиям симметрии ни одно
из этих событий не является объективно
более возможным.
9.
6. События называютсяединственно возможными, если появление в
результате испытания одного и только
одного из них является практически
достоверным событием.
10.
7. Несколько событий образуютполную группу, если они являются
единственно возможными и
несовместными исходами испытания.
Это означает, что в результате
испытания обязательно должно
произойти одно и только одно из этих
событий.
11.
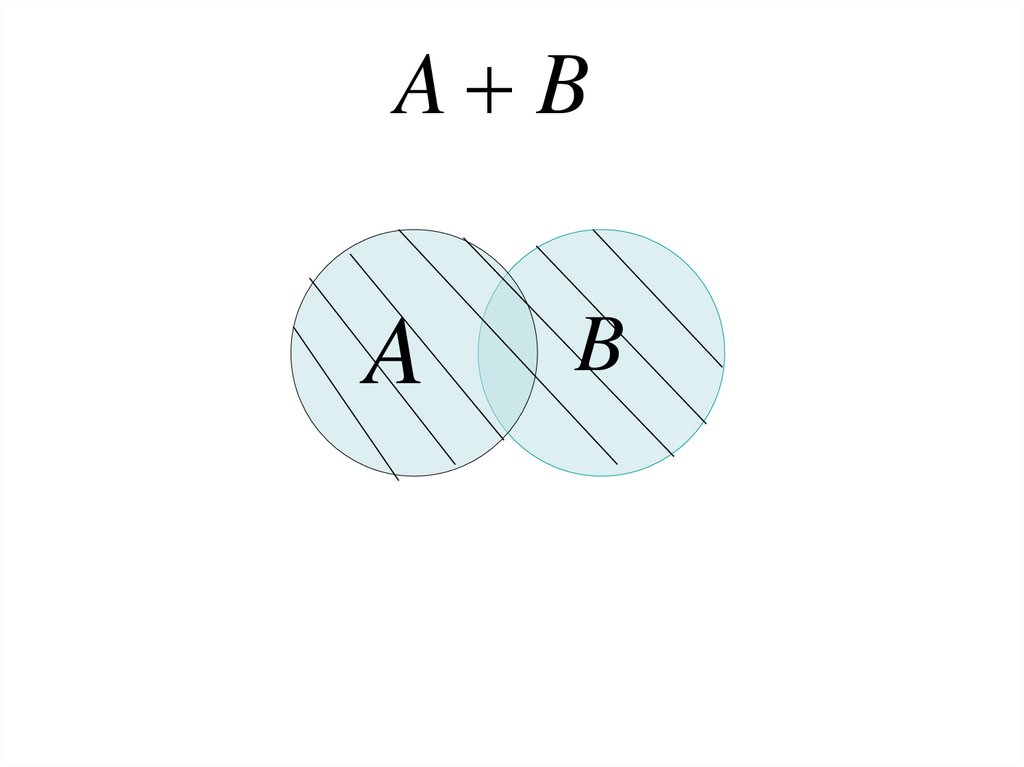
A BA
B
12.
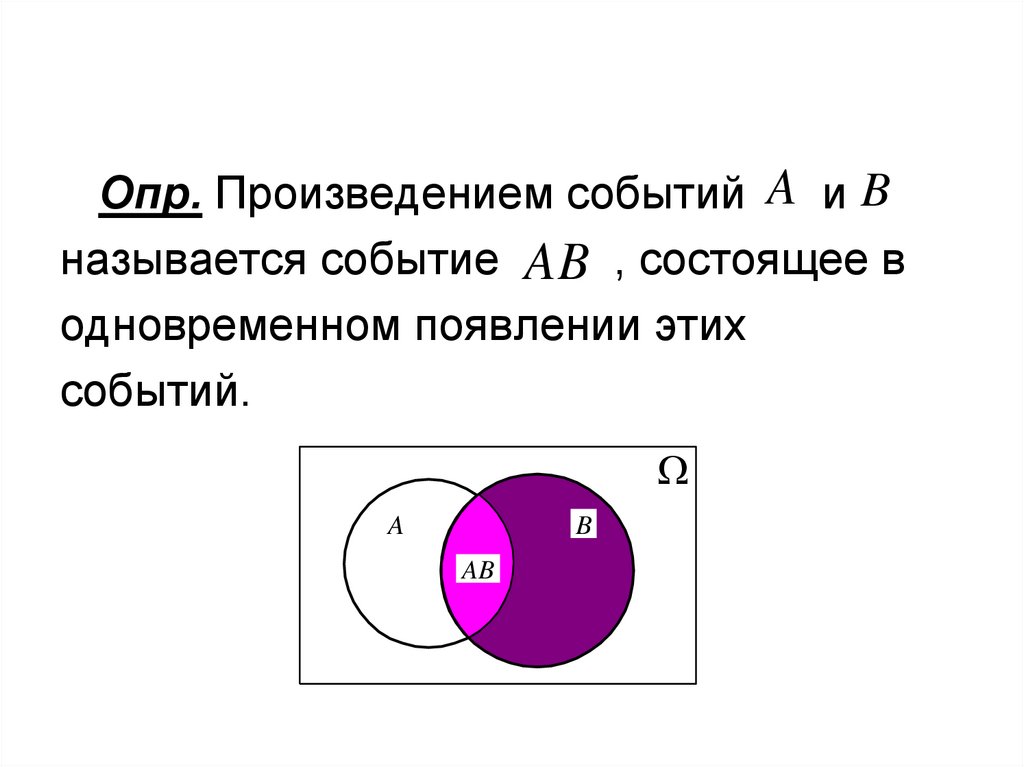
Опр. Произведением событий A и Bназывается событие AB , состоящее в
одновременном появлении этих
событий.
A
B
AB
13.
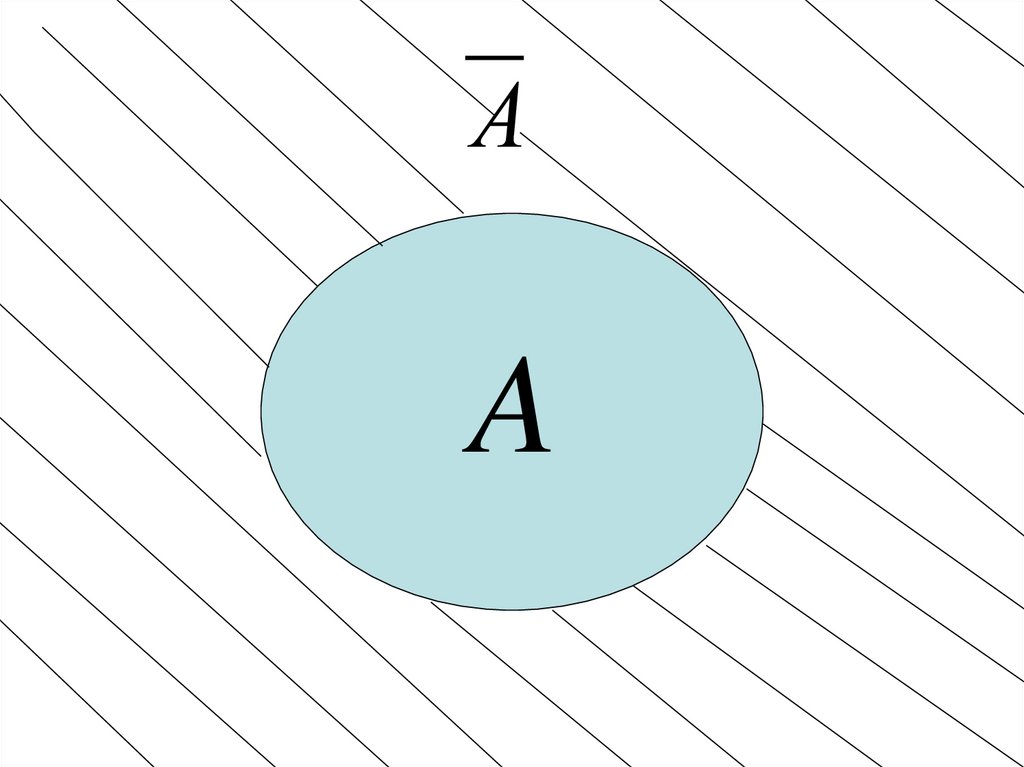
• Опр. Событие А называетсяпротивоположным событию A , если
оно считается наступившим тогда и
только тогда, когда A не наступает.
14.
АA
15.
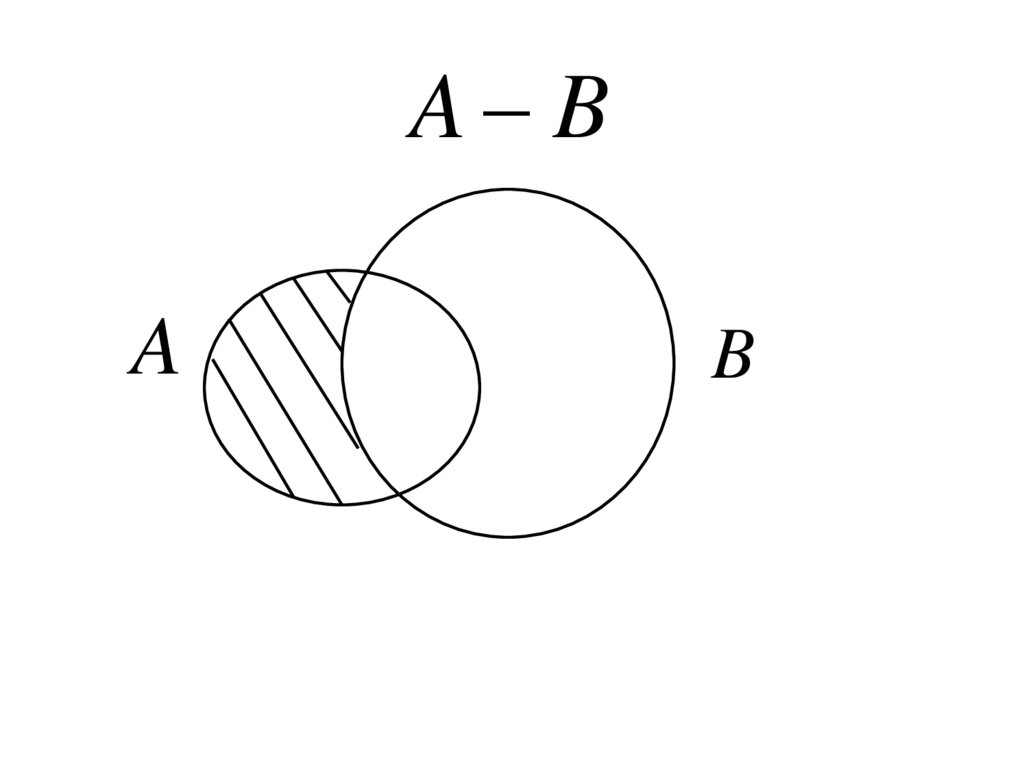
Опр. Разностью A B двух событийA и B называется событие, которое
состоится, если событие A произойдет, а
событие B не произойдет.
16.
A BA
B
17. Правило сложения вероятностей
Если события несовместны, товероятность их суммы равна
сумме
вероятностей этих событий:
P A B P A P B
18.
Для суммы совместных событий используетсяформула:
P A B P A P B P(AB)
19.
• Опр. Условной вероятностью PB Aсобытия A относительно события B
называется вероятность осуществления
события A при условии, что событие B
уже произошло.
20.
P ABPB A
P B
P AB P B PB A
21.
• Опр. События называютсянезависимыми, если наступление одного
не меняет шансов появления другого .
Если события A и B независимы, то
P AB P A P B
22. Основные теоремы сложения и умножения
• Для совместных событий:P( А В) P( А) P( В) P( АВ);
• Для несовместных событий:
P( А В) P( А) P( В);
• Для независимых событий:
P( AB) P( A) P( B);
• Для зависимых событий:
P AB P A PA B















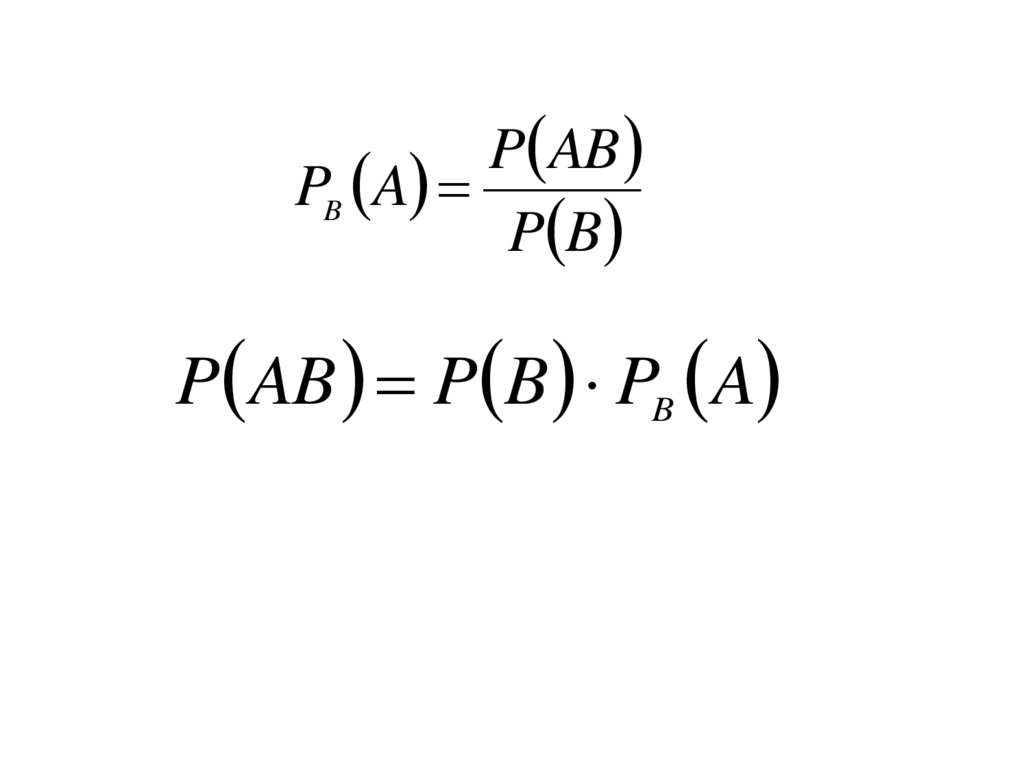



 Математика
Математика








