Похожие презентации:
Решение задач при помощи уравнений
1.
Решение задач при помощиуравнений
Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42»
Рыбина М.В.
2.
ПОВТОРИМ!• Уравнение – это равенство, содержащее
букву, значение которой надо найти.
• Решить уравнение – значит найти все его
корни.
• Корнем уравнения называют такое число,
при подстановке которого в уравнение
вместо неизвестного получается верное
числовое равенство.
3.
Алгоритм решения задач с помощьюуравнений:
1. Неизвестную величину нужно обозначить
буквой;
2. Используя условия задачи, составить уравнение;
3. Решить это уравнение;
4. Ответить на вопрос задачи.
4.
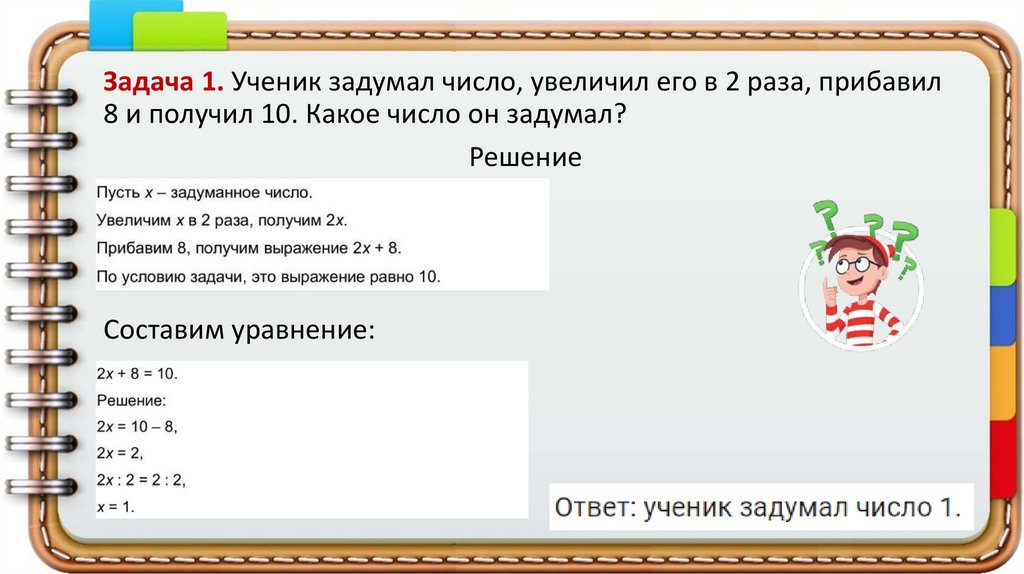
Задача 1. Ученик задумал число, увеличил его в 2 раза, прибавил8 и получил 10. Какое число он задумал?
Решение
Составим уравнение:
5.
Задача 2. В одном баке воды было в 4 раза больше, чем в другом. Из первогобака перелили в другой 36 литров и воды в баках стало поровну. Сколько
литров воды было в каждом баке?
Решение
Пусть x л — количество воды, которое было до переливания во втором баке.
Тогда в первом баке её было 4x л.
После переливания в первом баке осталось (4x –36) л воды, а во втором
стало (x+36) л.
По условию задачи известно, что после переливания в обоих баках воды стало
поровну. Составим уравнение:
4x –36=x+36.
4х – х = 36 + 36
3х = 72
х = 72:3
х = 24 – во 2 баке
24 4 = 96 (л) – в 1 баке
Ответ: 96 л и 24 л
6.
Задача 3. В группе детского сада 26 детей и мальчиков на 4 больше, чемдевочек. Сколько мальчиков и девочек в группе?
Решение:
Пусть х – количество девочек в группе.
Тогда мальчиков: х + 4.
Всего детей в группе 26.
Уравнение имеет следующий вид:
x + х + 4 = 26
2х = 26 – 4
2х = 22
x = 22 : 2
x = 11 – количество девочек в группе.
Тогда мальчиков: 11 + 4 = 15 человек.
Ответ: в группе 11 девочек и 15 мальчиков.
7.
Задача 4. У двух подруг была равная сумма денег. Первая купила 5одинаковых шоколадок, и у неё осталось 50 рублей. Вторая купила 3
шоколадки за ту же цену, и у нее осталось 120 рублей. Какова цена одной
шоколадки?
Решение:
Пусть х – рублей цена одной шоколадки.
Тогда у первой девочки было (5х + 50) рублей.
У второй девочки было (3х + 120) рублей.
Так как у подруг было равное количество денег, приравняем полученные
выражения:
5х + 50 = 3х + 120
5х – 3х = 120 – 50
2х = 70
x = 70 : 2
x = 35 рублей – цена одной шоколадки
Ответ: шоколадка стоит 35 рублей.
8.
Задача 5. Расстояние от одного города до другого катер по течению проплылза 5 часов, а против течения за 6 часов. Скорость течения реки 2 км/ч. Найдите
собственную скорость катера.
Пусть х км/ч. – скорость катера в стоячей воде (собственная скорость катера).
Тогда скорость катера по течению (х + 2) км/ч. Скорость против течения (х – 2)
км/ч. Так как путь находится по формуле: S = v · t. При этом расстояние между
городами не меняется, то есть по течению и против течения катер прошёл
одно и то же расстояние. Путь по течению равен 5(х + 2) км. Путь против
течения равен 6(х – 2) км.
Составим уравнение:
5(х + 2) = 6(х – 2)
5х + 10 = 6х – 12;
5х – 6х = – 12 – 10;
– х = – 22;
x = 22.
Ответ: собственная скорость катера 22 км/ч.
9.
Задание 1Выберите правильный ответ.
Задумали число, прибавили к нему 5, в сумме получили 15. Какое
уравнение для этой задачи составлено верно?
10.
Задание 2• Составьте уравнение по условию задачи и выделите
правильный ответ.
• Первое число на 5 больше второго, а сумма этих чисел равна 25.
Примите за неизвестное меньшее число.
11.
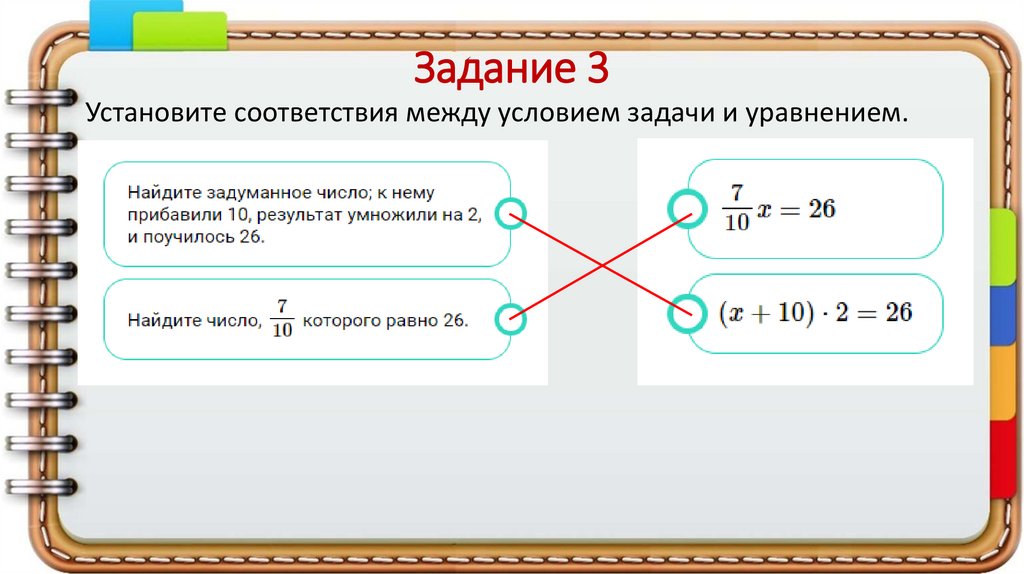
Задание 3Установите соответствия между условием задачи и уравнением.
12.
Задание 4• Выберите правильные ответы.
• Первое число на 6 меньше второго, а сумма этих чисел равна 32.
Найдите эти числа.
13.
Задание 5• Выделите подходящее уравнение.
• Рубашка стоит 1000 рублей. При покупке этой рубашки в
выходные дни даётся скидка 20 %. Составьте уравнение для
нахождения цены рубашки со скидкой.
14.
Задание 615.
Задание 7Между домами, в которых живут Леонид и Виктор, лежит
прямая дорога длиной 600 км. Друзья договорились
встретиться в кафе, расположенном возле этой дороги между
их домами. Леонид выехал из дома на маршрутном такси, а
Виктор — на легковом автомобиле, скорость которого
на 18 км/ч больше, чем скорость маршрутного такси.
Известно, что каждый из друзей потратил на
дорогу 4 ч. Найди скорость маршрутного такси и скорость
легкового автомобиля.
66
84
16.
Задание 8• Паша и Слава насобирали одинаковое число орехов. Паша
отдал Славе 15 орехов, и у него осталось в 6 раз(-а) меньше,
чем у Славы. Найди количество орехов, которое насобирал
каждый мальчик.
Паша
Слава
6(х – 15) = (х + 15)
Было
Х
Х
Осталось
Х – 15
Х + 15
21
17.
Задание 9В пакете лежат конфеты. Если раздавать их детям
по 5 конфет каждому, то не хватит 2 конфет, а если раздать
по 4 конфеты, то в пакете ещё останется 16 конфет.
Сколько конфет в пакете?
Решение
Пусть количество детей х. Тогда количество конфет в пакете или 5х
– 2, или 4х + 16.
5х - 2 = 4х + 16,
5х – 4х = 16 + 2,
х = 18
5 18 – 2 = 88 Ответ: 88 конфет
18.
Рефлексия19.
Домашнее задание:• Выучить алгоритм § 5 п. 42
• Выполнить в тетради: № 5.102; 5.103 стр.92
20.
Использованные источники:• https://resh.edu.ru/subject/lesson/6874/conspect/237888/
• https://www.yaklass.ru/p/matematika/6-klass/preobrazovaniebukvennykh-vyrazhenii-14441/etapy-resheniia-lineinykh-uravnenii14617/re-7950e951-6005-483a-9808-3c33abe5b238
• https://resh.edu.ru/subject/lesson/6892/conspect/237950/


















 Математика
Математика