Решение задач с помощью систем уравнений

1.

«Решение задач с помощью
систем уравнений»

2.

Цели урока:
Обобщение и систематизация знаний
учащихся по данной теме;
Организовать деятельность учащихся по
самостоятельному применению знаний
по данной теме;
Создать условия для развития
алгоритмического , логического и
творческого стиля мышления учащихся;
Подготовиться к контрольной работе;
Обеспечить развитие у школьников
способности к оценочным действиям.

3.

Этапы игры:
Организационный
II. Проверка домашнего задания
III. Конкурс «Разминка»
IV. Конкурс «Математическая эстафета»
V. Конкурс «Найдите ошибку»
VI. Конкурс «Кто быстрее ?»
VII. Конкурс капитанов.
VIII. Итоги урока – КВН.
IX. Рефлексия.
I.

4.

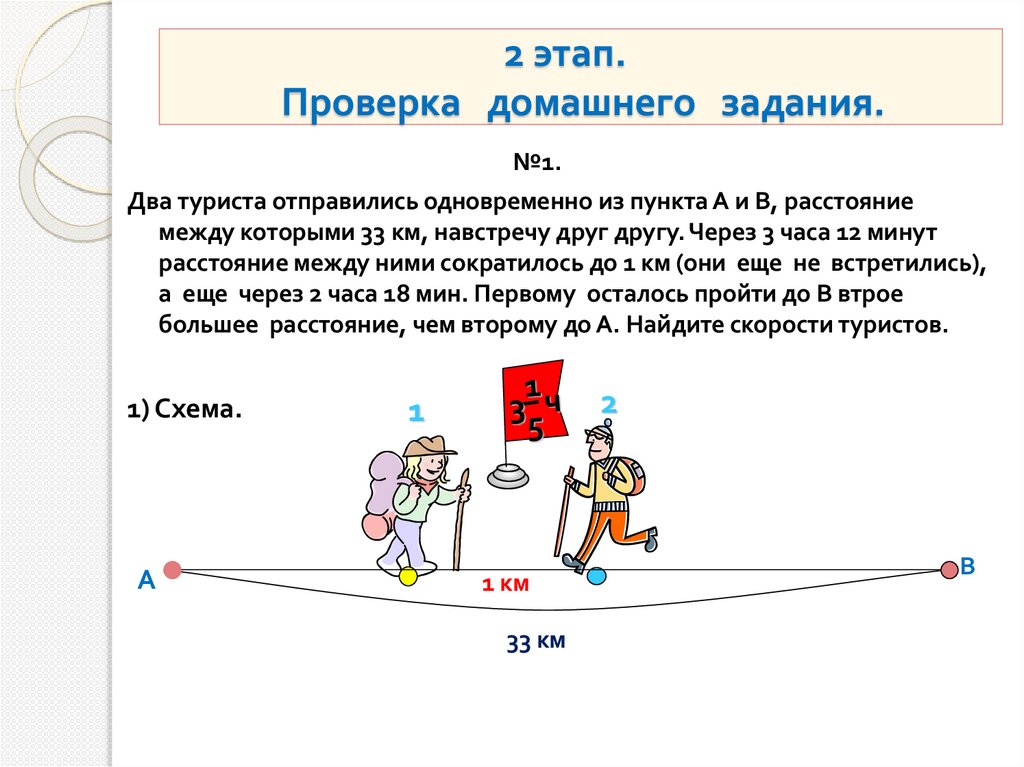
2 этап.
Проверка домашнего задания.
№1.
Два туриста отправились одновременно из пункта А и В, расстояние
между которыми 33 км, навстречу друг другу. Через 3 часа 12 минут
расстояние между ними сократилось до 1 км (они еще не встретились),
а еще через 2 часа 18 мин. Первому осталось пройти до В втрое
большее расстояние, чем второму до А. Найдите скорости туристов.
1) Схема.
А
2
1
1 км
33 км
В

5.

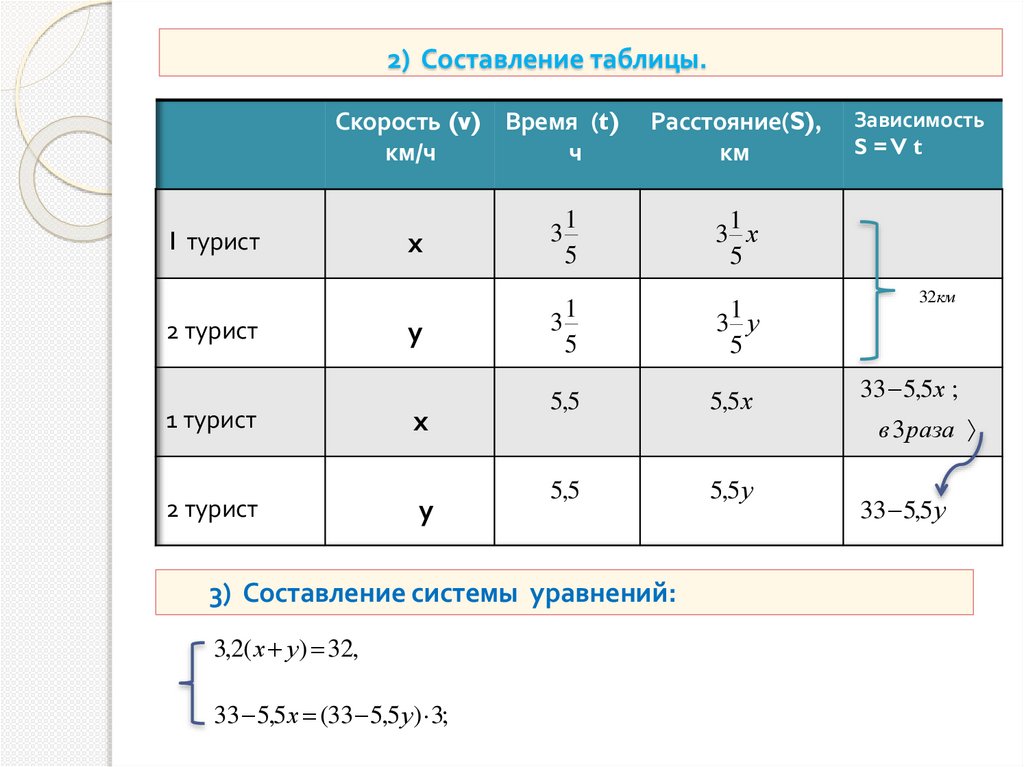
2) Составление таблицы.
Скорость (v) Время (t)
км/ч
ч
1 турист
2 турист
1 турист
2 турист
Расстояние(S),
км
х
3
1
5
1
3 х
5
у
1
3
5
1
3 у
5
5,5
5,5х
5,5
5,5 у
х
у
3) Составление системы уравнений:
3,2( х у) 32,
33 5,5х (33 5,5 у) 3;
Зависимость
S =V t
32км
33 5,5х ;
в 3 раза
33 5,5 у

6.

4) Решение системы уравнений:
х у 10,
33 5,5х 99 16,5 у;
х у 10,
16,5 у 5,5х 99 33;
х у 10,
16,5 у 5,5х 66 | 5,5
х у 10,
3 у х 12;
4 у 22,
х у 10;
у 5,5
х 4,5
Ответ: скорость первого туриста – 4,5 км/ч, второго – 5,5 км/ч.

7.

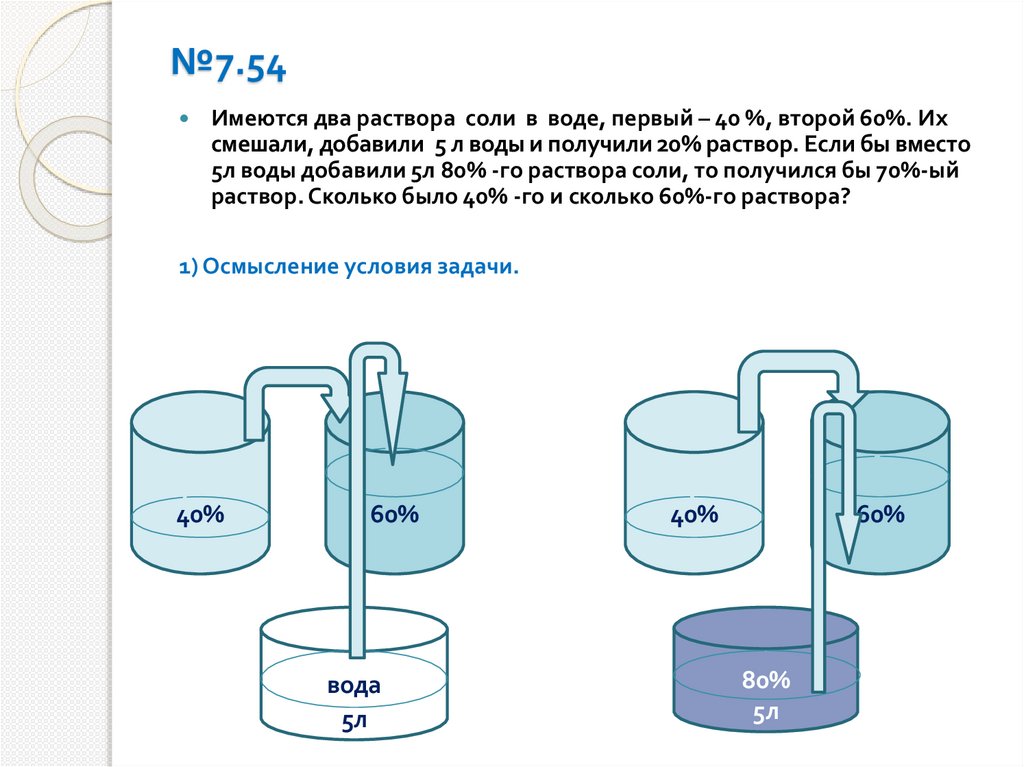
№7.54
Имеются два раствора соли в воде, первый – 40 %, второй 60%. Их
смешали, добавили 5 л воды и получили 20% раствор. Если бы вместо
5л воды добавили 5л 80% -го раствора соли, то получился бы 70%-ый
раствор. Сколько было 40% -го и сколько 60%-го раствора?
1) Осмысление условия задачи.
40%
60%
вода
5л
40%
60%
80%
5л

8.

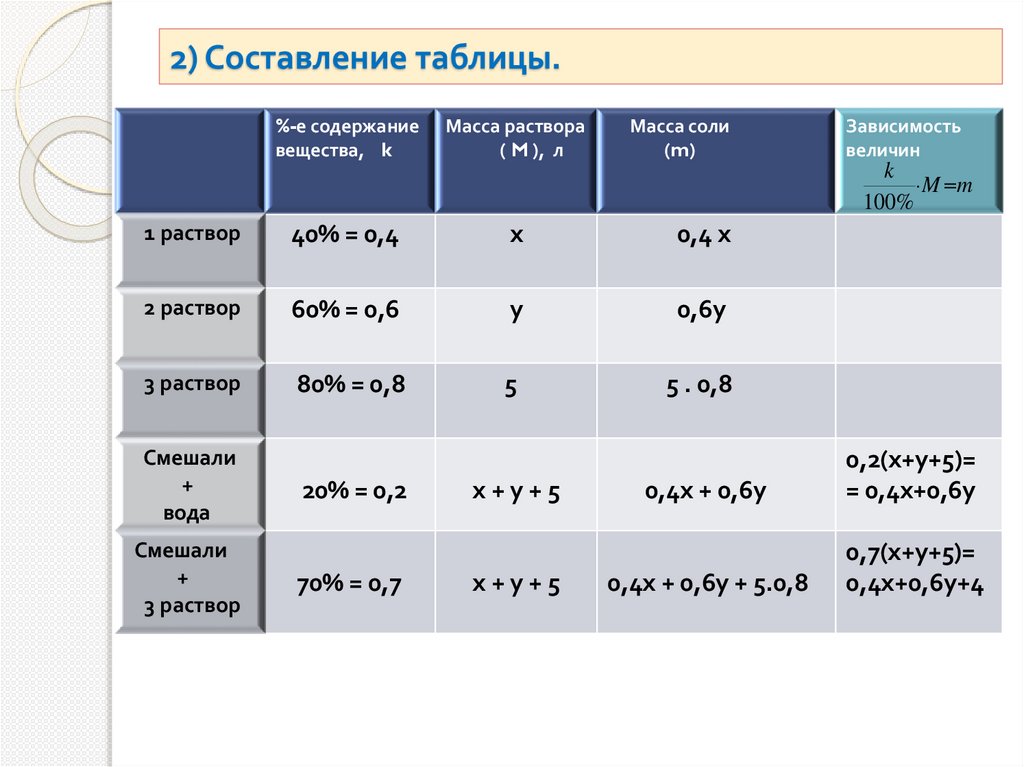
2) Составление таблицы.
%-е содержание
вещества, k
Масса раствора
( M ), л
Масса соли
(m)
Зависимость
величин
k
M m
100%
1 раствор
40% = 0,4
х
0,4 х
2 раствор
60% = 0,6
у
0,6у
3 раствор
80% = 0,8
5
5 . 0,8
Смешали
+
вода
Смешали
+
3 раствор
20% = 0,2
70% = 0,7
х+у+5
х+у+5
0,4х + 0,6у
0,2(х+у+5)=
= 0,4х+0,6у
0,4х + 0,6у + 5.0,8
0,7(х+у+5)=
0,4х+0,6у+4

9.

3) Составление и решение системы уравнений:
0,2( х у 5) 0,4 х 0,6 у, | 0,2
0,7( х у 5) 0,4 х 0,6 у 4; | 0,7
х у 5 2 х 3 у,
10
х у 5 (0,4 х 0,6 у 4)
;
7
х 2 у 5,
4
6
40
х у 5 х у
;
7
7
7
х 2 у 5,
3
1
5
х у ; | 7
7
7
7
х 2 у 5,
3х у 5; | 2
х 2 у 5,
6 х 2 у 10;
5х 5
х 1;
у 2.
Ответ: 40% раствора было – 1 литр , а 60% - 2 литра.

10.

4 этап.
«Математическая эстафета».
От пристани А одновременно отправились вниз по течению катер и плот.
Катер прошел 96 км, затем повернул обратно и вернулся в А через 14
1
часов. Известно, что скорость катера по течению в 1 раза больше
3
скорости катера против течения. На каком расстоянии от А катер
встретил плот на обратном пути?
1) схема
t = 14 ч
Vсоб.
V соб.
V плота
Vтеч.- у км/ч
А

11.

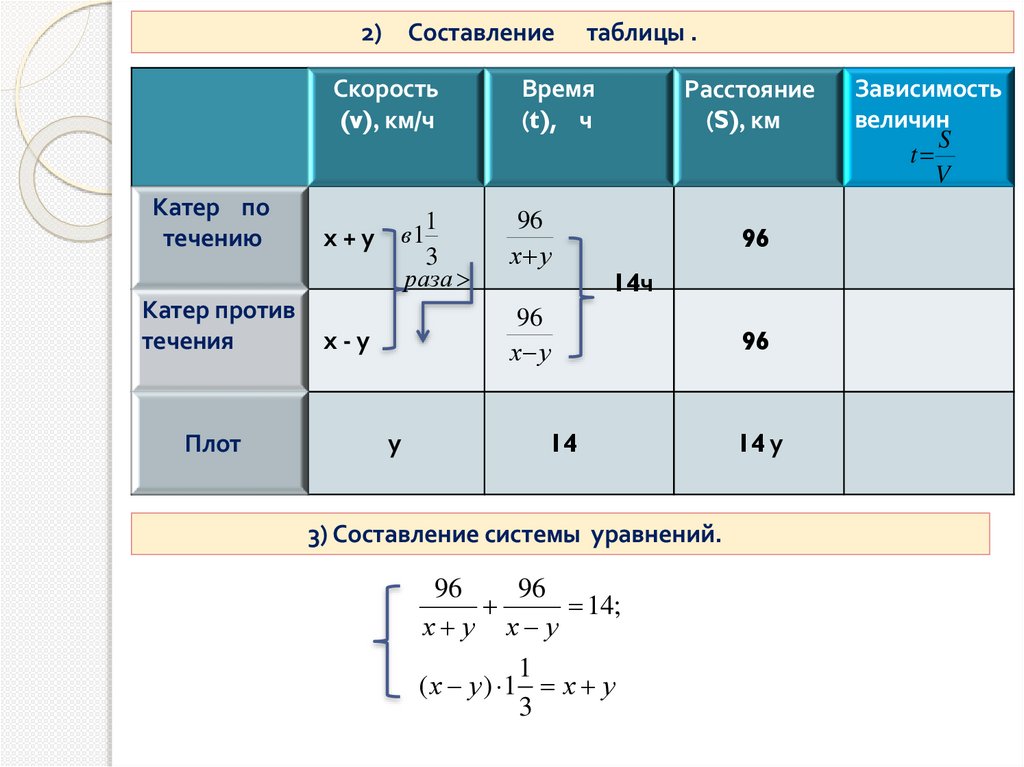
2)
Составление
Скорость
(v), км/ч
Катер по
течению
Катер против
течения
Плот
х+у
1
в1
3
раза
таблицы .
Время
(t), ч
96
х у
Расстояние
(S), км
96
14ч
96
х у
х-у
у
14
3) Составление системы уравнений.
96
96
14;
х у х у
1
( х у ) 1 х у
3
96
14 у
Зависимость
величин
S
t
V

12.

4) Решение системы уравнений.
48
48
7,
х у
х у
4 х 4 у 3 х 3 у;
48
48
7,
х у
х у
х 7 у;
48
48
7,
8у
6у
х 7 у;
6
8
7,
у
у
х 7 у;
7 у 14,
х 7 у;
у 2,
х 14.

13.

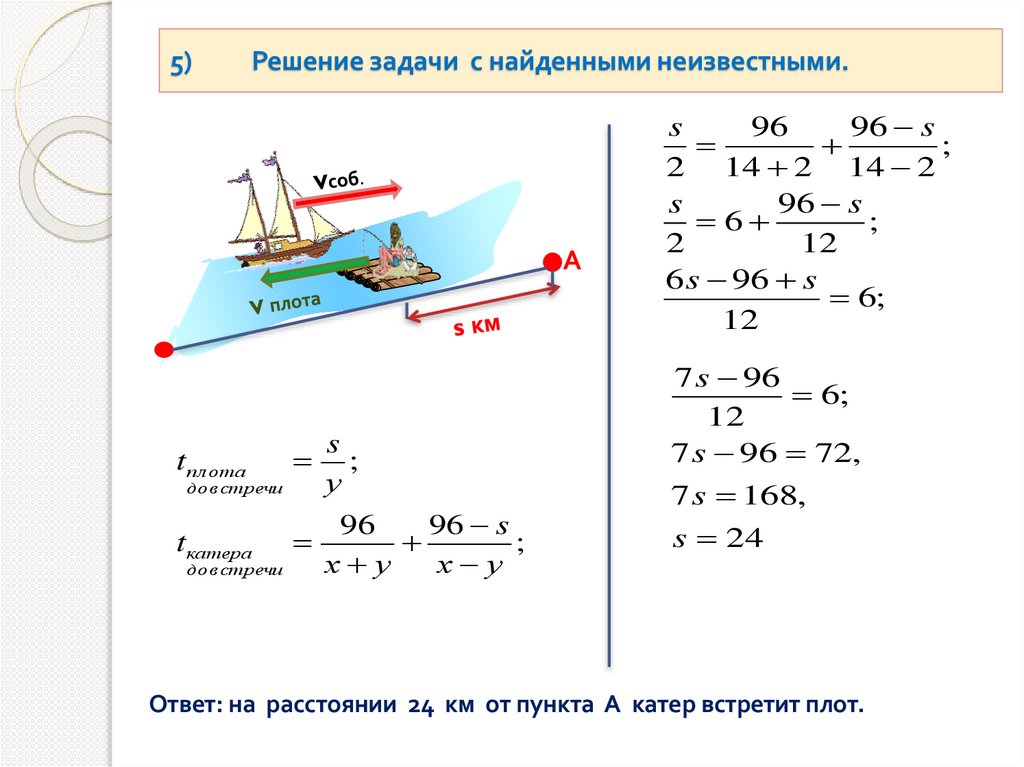
5)
Решение задачи с найденными неизвестными.
А
s
;
у
до в стречи
96
96 s
tкатера
;
х у
х у
до в стречи
tпл ота
s
96
96 s
;
2 14 2 14 2
s
96 s
6
;
2
12
6 s 96 s
6;
12
7 s 96
6;
12
7 s 96 72,
7 s 168,
s 24
Ответ: на расстоянии 24 км от пункта А катер встретит плот.

14.

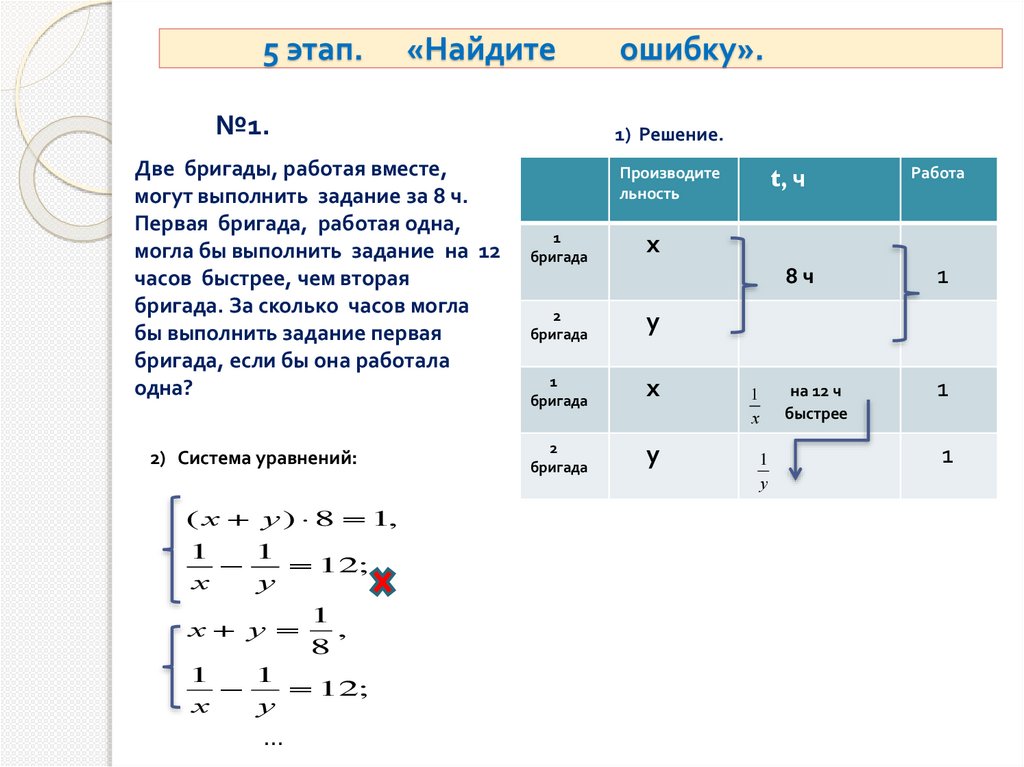
5 этап.
«Найдите
№1.
Две бригады, работая вместе,
могут выполнить задание за 8 ч.
Первая бригада, работая одна,
могла бы выполнить задание на 12
часов быстрее, чем вторая
бригада. За сколько часов могла
бы выполнить задание первая
бригада, если бы она работала
одна?
2) Система уравнений:
( х у ) 8 1,
1
1
12;
х
у
1
х у
,
8
1
1
12;
х
у
…
ошибку».
1) Решение.
Производите
льность
1
бригада
t, ч
Работа
8ч
1
на 12 ч
быстрее
1
х
2
бригада
у
1
бригада
х
2
бригада
у
1
х
1
у
1

15.

5 этап. «Найдите ошибку»
№2. Турист проплыл на лодке по
реке из города А в город В и
обратно за 7 часов. Найдите
скорость течения реки, если
известно, что турист проплывает
2 км против течения за то же
время, что и 5 км по течению, а
расстояние между городами
равно 20 км.
v
1) Составим таблицу:
V,
км/ч
По
течению
х+у
Против
течения
х-у
По
течению
х+у
Против
течения
х-у
t, ч
S, км
20
20
х у
20
х у
7ч
5
5
х у
2
х у
20
=
2
соб.
2) Составим и решим систему уравнений:
v
теч
vпр теч= vсоб – vтеч ; vпо теч= vсоб+ vтеч
20
20
7,
х у
х у
5( х у ) 2( х у );
20
20
7,
х у
х у
5 х 5 у 2 х 2 у;
.............

16.

5 этап. «Найдите ошибку»
№3.
При смешивании 40%-го
раствора соли с 10%-м
раствором получили 800 г
раствора с концентрацией соли
21,25%. Сколько граммов
каждого раствора было для
этого взято?
2)
1) Составим таблицу.
m, масса
соли
% -ое
содержание
М, масса
раствора
1
раствор
40% = 0,4
х
0,4 х
Составим и решим систему уравнений.
2
раствор
10%=0,1
у
0,1 у
х у 800,
0,4 х 0,1 у
21,25;
800
х у 800,
Смешанный
раствор
21,25%= 0,
2125
х + у = 800
0,4 х 0,1 у 17000;
х 800 у ,
0,4(800 у ) 0,1 у 17000;
...............
0,4х+0,1у

17.

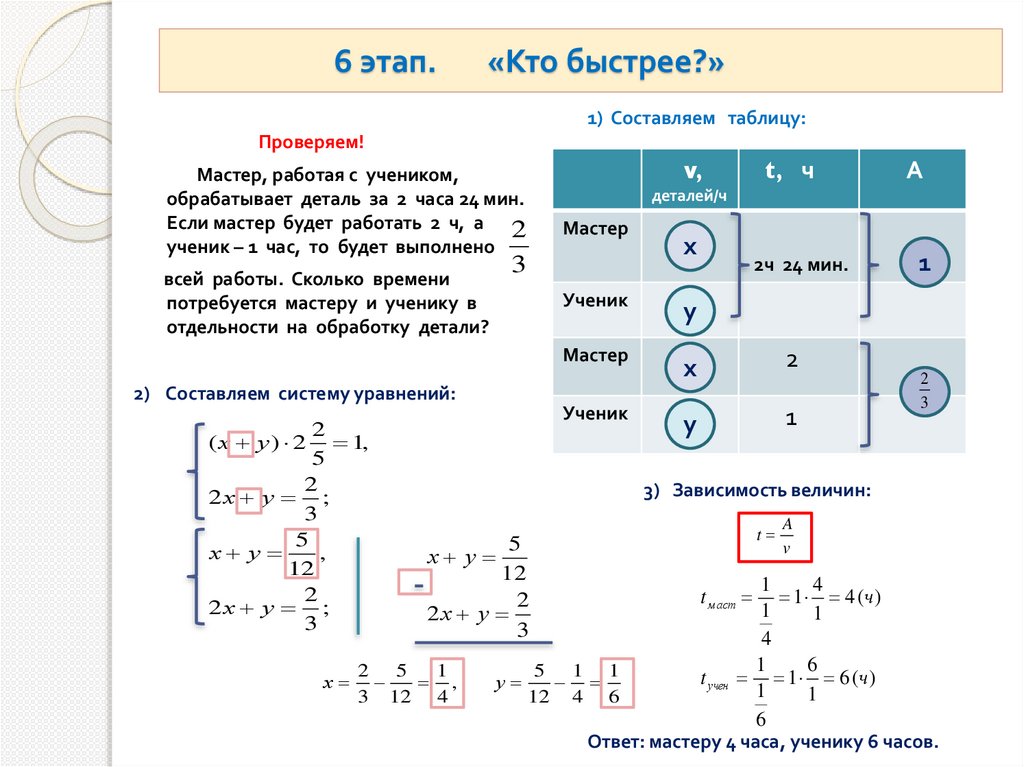
6 этап.
«Кто быстрее?»
1) Составляем таблицу:
Проверяем!
Мастер, работая с учеником,
обрабатывает деталь за 2 часа 24 мин.
Если мастер будет работать 2 ч, а 2
ученик – 1 час, то будет выполнено
всей работы. Сколько времени
потребуется мастеру и ученику в
отдельности на обработку детали?
v,
t, ч
А
2ч 24 мин.
1
деталей/ч
Мастер
3
Ученик
Мастер
х
у
х
2
у
1
2) Составляем систему уравнений:
2
( х у ) 2 1,
5
2
2х у ;
3
5
х у
,
12
2
2х у ;
3
х
Ученик
2
3
3) Зависимость величин:
5
х у
12
2
2х у
3
2 5
1
,
3 12 4
t
A
v
1
4
1 4 (ч)
1
1
4
1
6
5 1 1
t учен 1 6 (ч)
у
1
1
12 4 6
6
Ответ: мастеру 4 часа, ученику 6 часов.
t м аст

18.

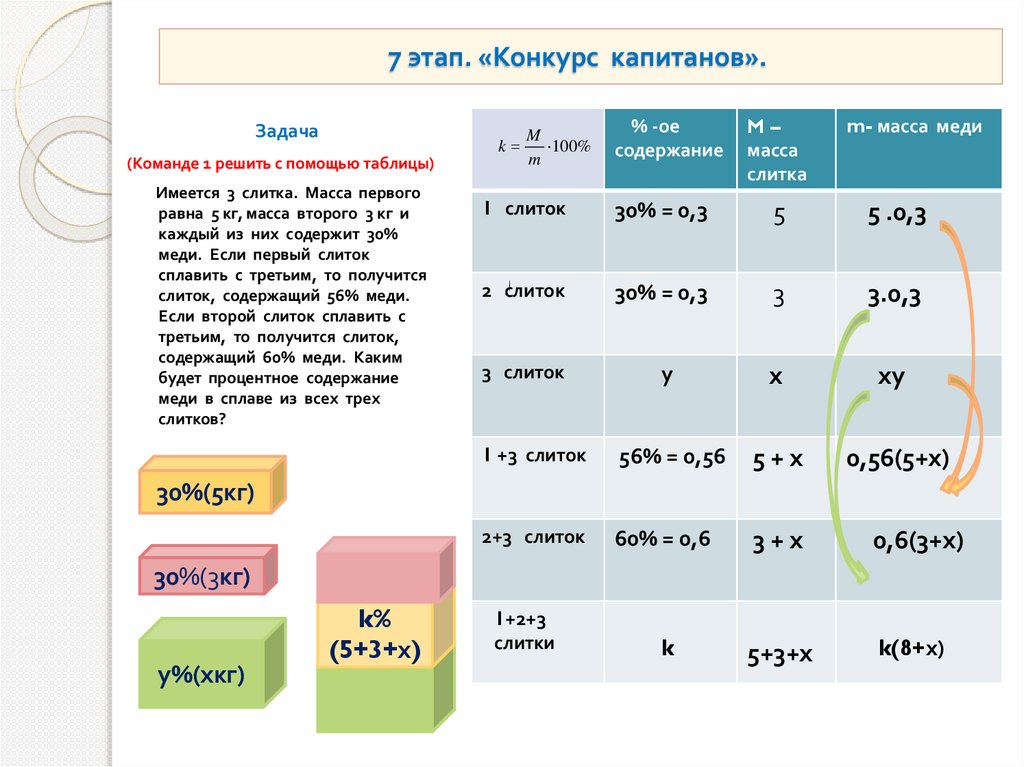
7 этап. «Конкурс капитанов».
Задача
(Команде 1 решить с помощью таблицы)
Имеется 3 слитка. Масса первого
равна 5 кг, масса второго 3 кг и
каждый из них содержит 30%
меди. Если первый слиток
сплавить с третьим, то получится
слиток, содержащий 56% меди.
Если второй слиток сплавить с
третьим, то получится слиток,
содержащий 60% меди. Каким
будет процентное содержание
меди в сплаве из всех трех
слитков?
m- масса меди
% -ое
содержание
M–
масса
слитка
1 слиток
30% = 0,3
5
5 .0,3
2 слиток
30% = 0,3
3
3.0,3
3 слиток
у
х
ху
1 +3 слиток
56% = 0,56
5+х
0,56(5+х)
2+3 слиток
60% = 0,6
3+х
0,6(3+х)
1+2+3
слитки
k
5+3+х
k(8+х)
k
M
100%
m
30%(5кг)
30%(3кг)
у%(хкг)
k%
(5+3+х)

19.

2) Составим и решим систему уравнений.
0,56(5 х ) 1,5 ху,
0,6(3 х ) 0,9 ху;
2,8 0,56 х 1,5 ху,
1,8 0,6 х 0,9 ху;
0,56 х ху 1,3,
0,6 х ху 0,9
2) 5 3 10 18 ( кг ) масса
сплава
3) 1,5 0,9 10 0,69 9,3 (кг ) масса
меди в сплаве
4) k
9,3
2
100% 51 %
18
3
0,04 х 0,4
х 10 (кг ) масса 3 го сплава
0,6 10 10 у 0,9
6 10 у 0,9
10 у 6,9
у 0,69
0,69 69% процентное содержание меди в 3 сплаве
2
Ответ : 51 % содержание меди в сплаве из всех трех слитков.
3

20.

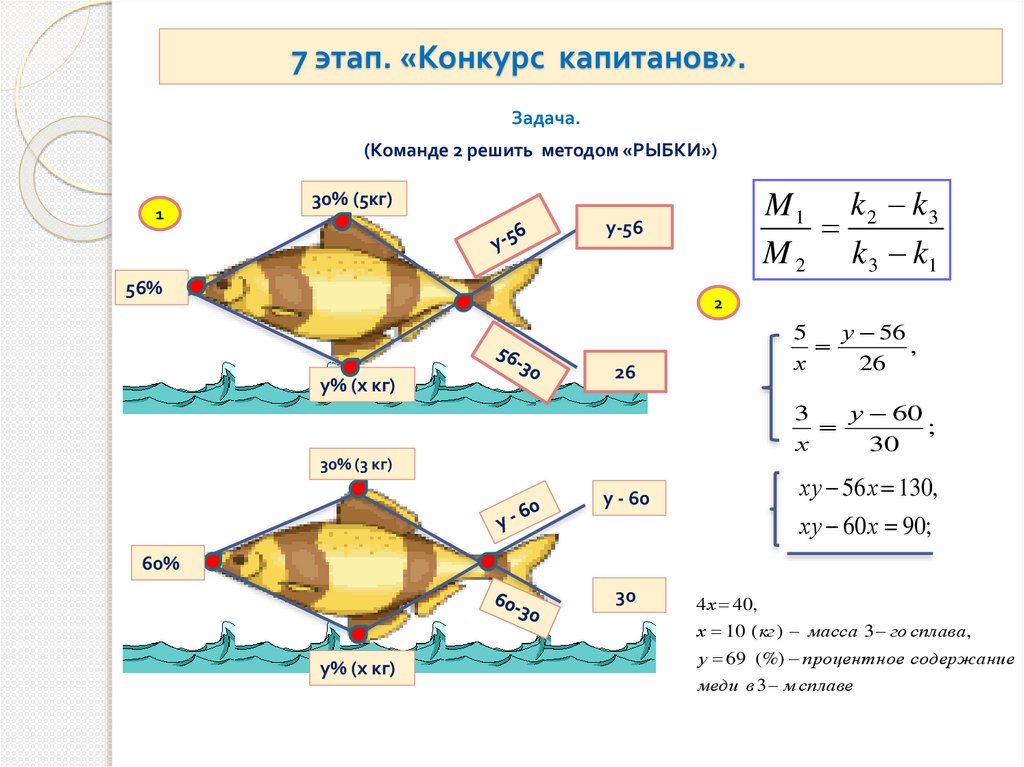
7 этап. «Конкурс капитанов».
Задача.
(Команде 2 решить методом «РЫБКИ»)
1
M 1 k 2 k3
M 2 k 3 k1
30% (5кг)
у-56
56%
2
у% (х кг)
26
5
у 56
,
х
26
3
у 60
;
х
30
30% (3 кг)
у - 60
ху 56 х 130,
ху 60 х 90;
60%
30
у% (х кг)
4 х 40,
х 10 (кг ) масса 3 го сплава,
у 69 (%) процентное содержание
меди в 3 м сплаве

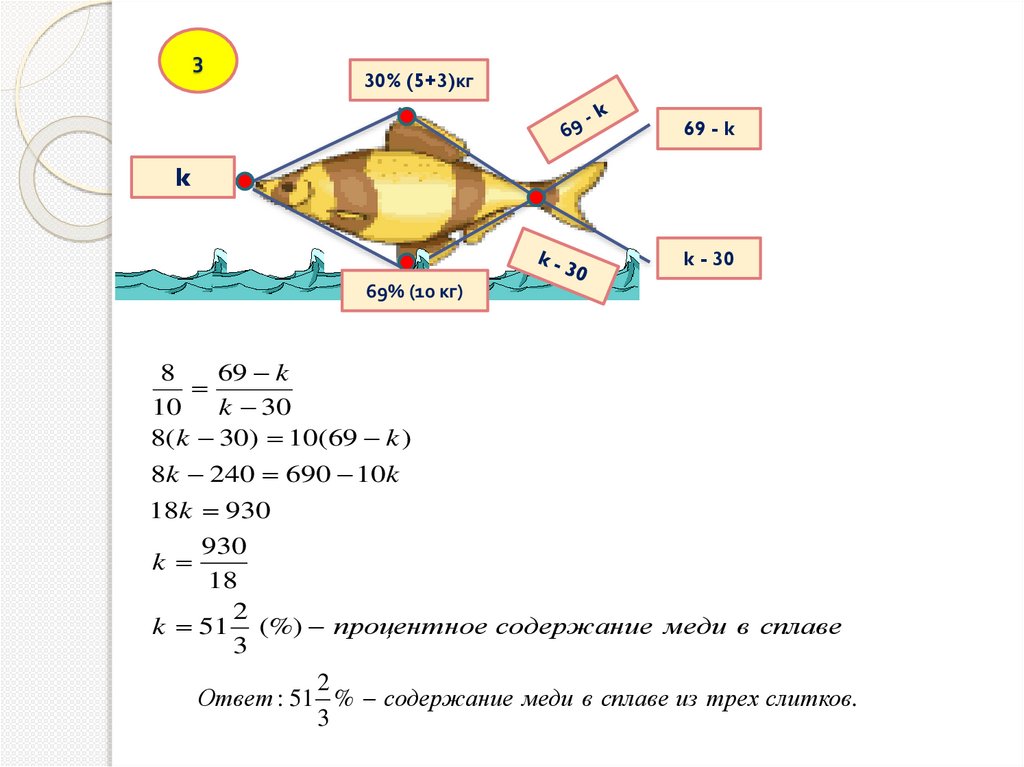
21.

3
30% (5+3)кг
69 - k
k
k - 30
69% (10 кг)
8
69 k
10
k 30
8( k 30) 10(69 k )
8k 240 690 10k
18k 930
930
k
18
2
k 51 (%) процентное содержание меди в сплаве
3
2
Ответ : 51 % содержание меди в сплаве из трех слитков.
3

22.

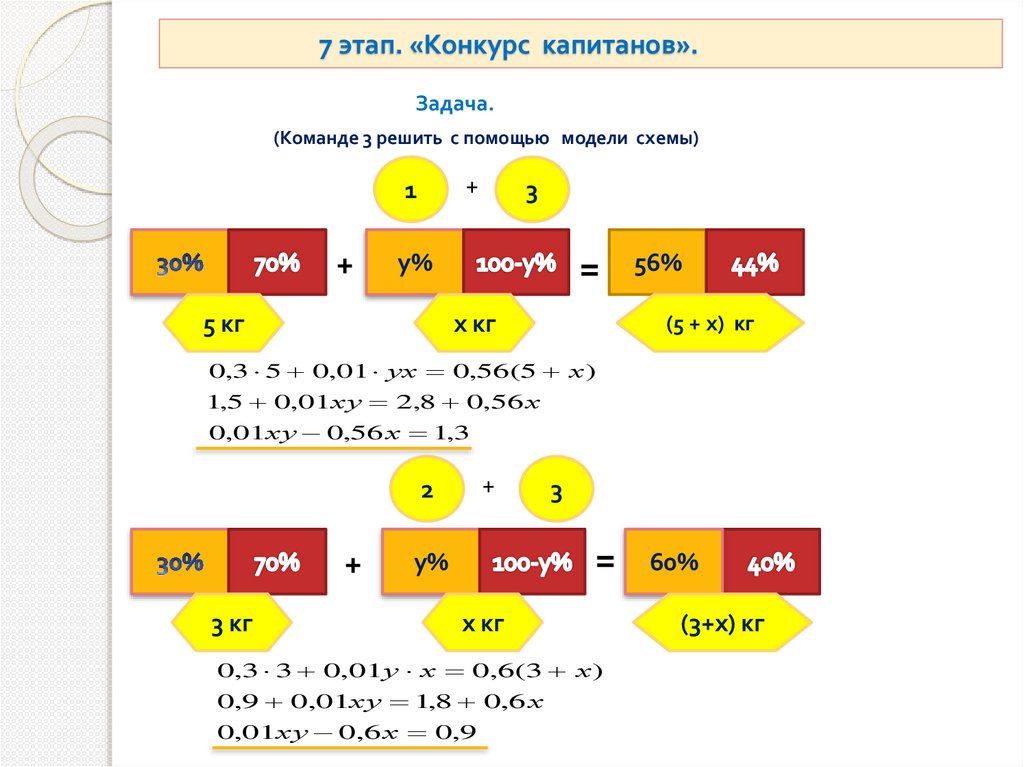
7 этап. «Конкурс капитанов».
Задача.
(Команде 3 решить с помощью модели схемы)
+
1
+
3
=
у%
5 кг
х кг
56%
(5 + х) кг
0,3 5 0,01 ух 0,56(5 х )
1,5 0,01ху 2,8 0,56 х
0,01ху 0,56 х 1,3
2
+
3 кг
+
3
=
у%
х кг
0,3 3 0,01 у х 0,6(3 х )
0,9 0,01ху 1,8 0,6 х
0,01ху 0,6 х 0,9
60%
(3+х) кг

23.

Получаем систему уравнений:
0,01 ху 0,56 х 1,3,
0,01 ху 0,6 х 0,9;
0,04 х 0,4
х 10 ( кг ) масса 3 го слитка
0,01 10 у 0,6 10 0,9
0,1 у 0,9 6
0,1 у 6,9
у 69 (%) процентное содержание меди в 3 м сплаве
1
+
2
3
=
+
5+3
кг
+
10
кг
0,3 8 0,69 10 0,01 k 18
2,4 6,9 0,18k
0,18k 9,3
k 9,3 : 0,18
2
k 51 (%) содержание меди в сплаве из 3 х слитков
3
Ответ : 51
2
% содержание меди в сплаве из трех слитков.
3
18 кг

24.

8 этап. Итоги игры:
1.
2.
3.
4.
5.
6.
7.
Повторили и систематизировали знания по теме:
«Решение задач с помощью систем уравнений»
Повторили табличный метод решения задач на движение
между пунктами и по реке, на производительность, на
концентрацию и процентное содержание.
Повторили три способа решения задач на процентное
содержание (концентрацию) : 1) табличный; 2) метод
«рыбки»; 3) с помощью модели – схемы.
Учились искать ошибки как в своих решениях, так и в
решениях товарищей.
Учились грамотно объяснять и доказывать верность своего
решения.
Помогали товарищам решать задачи по данной теме в
случаи их затруднения.
Учились контролировать уровень своих знаний с помощью
интернета.

25.

9 этап.
РЕФЛЕКСИЯ.
1.На уроке я работал…
2.Своей работой на уроке я…
3.Урок для меня показался….
4.За урок я …
1. активно / пассивно
2. доволен / не доволен
3. коротким / длинным
4. не устал / устал
5.Мое настроение…
5. стало лучше / стало хуже
6.Материал урока мне был….
6.
7.Домашнее задание мне кажется….
7. интересно / не интересно
8. На каком уровне в большей степени
осуществлялось общение в группе?
8.
понятен / не понятен
полезен / бесполезен
интересен / скучен
легким / трудным
обмен информацией
взаимодействие
взаимопонимание
были равномерно
задействованы все уровни

26.

Используемые интернет – ресурсы:
Картинки рыбок взяты с сайта
http://fantasyflash.ru/anime/index.php?kont=sea&n=1
Картинки парусника, лодки, плота, реки, туристов
взяты с сайта http://le-savchen.ucoz.ru/
Картинка КВН http://www.kzgazeta.ru/news1220.html