Похожие презентации:
Доверительный интервал для математического ожидания случайной величины при неизвестной дисперсии и малой выборке. Лекция 5
1. Лекция 5
Доверительный интервал дляматематического ожидания случайной
величины при неизвестной дисперсии
и малой выборке
2.
Определим доверительный интервал дляматематического ожидания нормально
распределенной случайной величины при
неизвестной дисперсии и малой выборке
(объем выборки n < 30 ) по доверительной
вероятности γ .
3.
Для построения доверительного интервалаиспользуем распределение Стьюдента c (n -1)
степенями свободы:
4.
Теорема 1. Если элементы выборки {x1, x2,..., xn},независимы и каждый из них распределяется
нормально с параметрами (a,σ2), то случайная
величина
имеет распределение Стьюдента с (n -1)
степенями свободы.
5.
из теоремы =>6.
Итак, для нахождения границ доверительногоинтервала для математического ожидания а,
отвечающего доверительной вероятности γ, введем
вспомогательную случайную величину
где DB находится по выборке.
7.
С одной стороны, имеемс другой —
8.
Из условиянаходим квантиль tγ.
Искомый интервал для математического
ожидания а получен:
9.
Задача 7На контрольных испытаниях случайно выбранных из партии
15 осветительных ламп были определены средняя
продолжительность работы лампы
= 3000 ч и
среднеквадратическое отклонение σ = 20 ч.
Найти с вероятностью γ =0,99 доверительный интервал для
средней продолжительности работы лампы в целом для
партии.
10.
РешениеПоскольку объем выборки n =15 , что меньше 30, то выборка
— малая.
Доверительный интервал для средней продолжительности
службы лампы во всей партии (генеральная средняя —
математическое ожидание a) определяется неравенством
11.
По таблице распределения Стьюдента:при γ = 0,99,
n–1 = 15–1 = 14 имеем квантиль tγ =2,98.
12.
13.
Вычислим:Тогда получим:
Итак, доверительный интервал для математического
ожидания a :
3000-15,94<a<3000+15,94 ,
или
2984,06<a<3015,94 .
14.
Т.о., с вероятностью 0,99 можно утверждать, что средняяпродолжительность службы лампы для всей партии
колеблется в пределах от 2984,06 до 3015,94 ч.
15.
Доверительный интервал для дисперсии случайнойвеличины с неизвестным математическим ожиданием
Построим доверительный интервал для дисперсии
случайной величины с нормальным распределением при
неизвестном математическом ожидании.
Задача 8
Определить доверительный интервал для дисперсии
нормально распределенной случайной величины с
неизвестным математическим ожиданием по доверительной
вероятности γ.
Задача решается с помощью распределения χ2 с (n -1)
степенями свободы:
16.
Теорема 2.Если элементы выборки {x1, x2, …, xn } независимы и каждый
из них распределяется нормально с параметрами (a, σ2 ),
то
и DB — независимы,
причем
распределено нормально с параметрами (a, σ2/n),
случайная величина
имеет распределение χ2 с (n -1) степенями свободы.
17.
По теореме 2Величины χ12, χ22 находятся из уравнений
18.
После подстановкив неравенство
получаем
19.
Искомый интервал для математического ожидания σ2:20.
Доверительный интервал для вероятности успеха в схемеБернулли и параметра λ распределения Пуассона
Определим доверительный интервал для вероятности успеха
в схеме Бернулли.
Задача 9
Пусть в n независимых испытаниях успех наступил x раз.
Найти доверительный интервал для вероятности p успеха в
одном испытании по доверительной вероятности γ .
21.
РешениеРассмотрим случай, когда n — велико. Тогда эффективной
оценкой вероятности p успеха в одном испытании является
относительная частота успеха
По теореме Муавра-Лапласа относительная частота w имеет
нормальное распределение с параметрами
22.
Рассмотрим вспомогательную случайную величинукоторая, следовательно, имеет стандартное распределение
независимо от значения p.
При больших n тогда имеем:
23.
Найдем из этого приближенного равенства квантиль uγ (прил.1 или с помощью компьютерных вычислений).
24.
25.
26.
27.
Решая неравенствоотносительно p, получим, что с вероятностью ≈ γ
выполняется следующее условие:
28.
Заменяя значения p и q в левой и правой частях этогонеравенства их оценками p* =w и q* =1-w,
получаем, что доверительный интервал для вероятности
успеха в схеме Бернулли приближенно имеет вид
29.
Задача 10Пусть {x1, x2, …, xn } — выборка из генеральной
совокупности, имеющей распределение Пуассона с
неизвестным параметром λ :
где x принимает неотрицательные целочисленные значения
x =0,1,2, ... .
Найти доверительный интервал для параметра λ по
доверительной вероятности γ .
30.
РешениеРассмотрим случай, когда n — велико.
Тогда доверительный интервал для параметра λ приближенно
имеет вид
где
— выборочное среднее;
uγ — квантиль стандартного распределения.




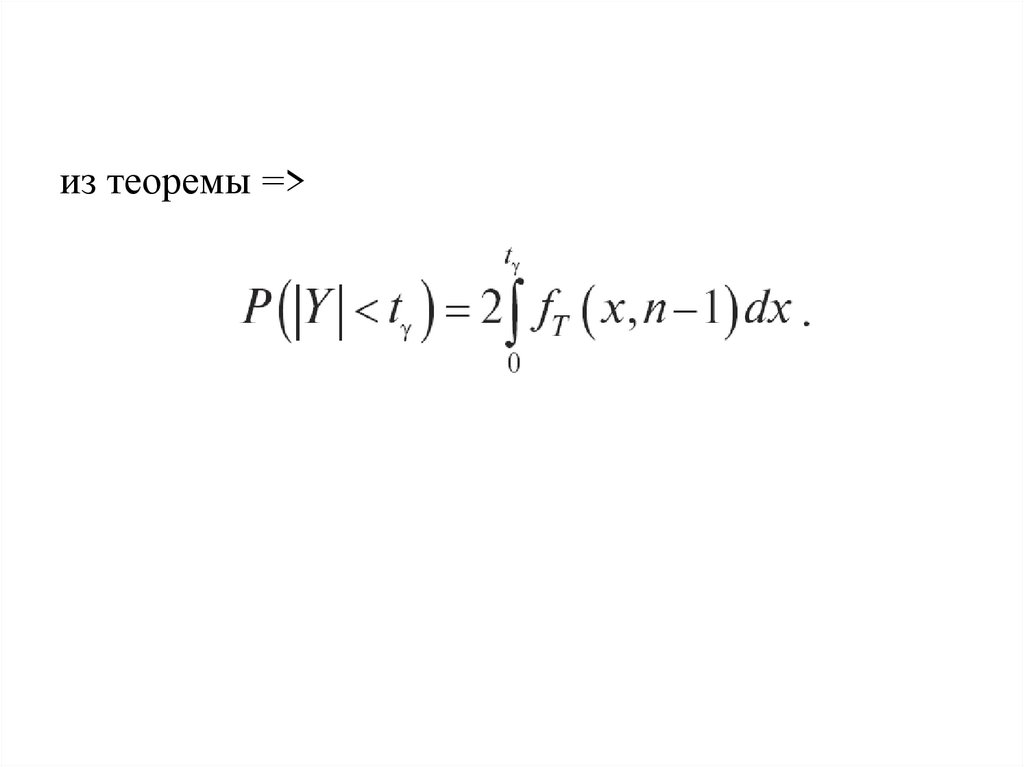
























 Математика
Математика








