Похожие презентации:
Случайная величина
1. Случайная величина
2. Определение
Случайная величина имеет нормальноераспределение с параметрами a и σ, если её
плотность распределения имеет вид:
1
x
e
2π σ
x a 2
2σ 2
3. Функция распределения
1F x
e
2π σ
Функция распределения,
функцию Лапласа
t a 2
2σ 2
dt
выраженная
x a
F x 0,5 Ф
σ
через
4. Математическое ожидание и дисперсия
Для случайной величины , имеющей нормальноераспределение, параметры a и σ имеют простой
вероятностный смысл:
M ξ a
D ξ σ
2
σ ξ σ
где M( ) – математическое ожидание случайной
величины ;
D( ) – дисперсия случайной величины ;
σ( ) – среднее квадратическое отклонение случайной
величины .
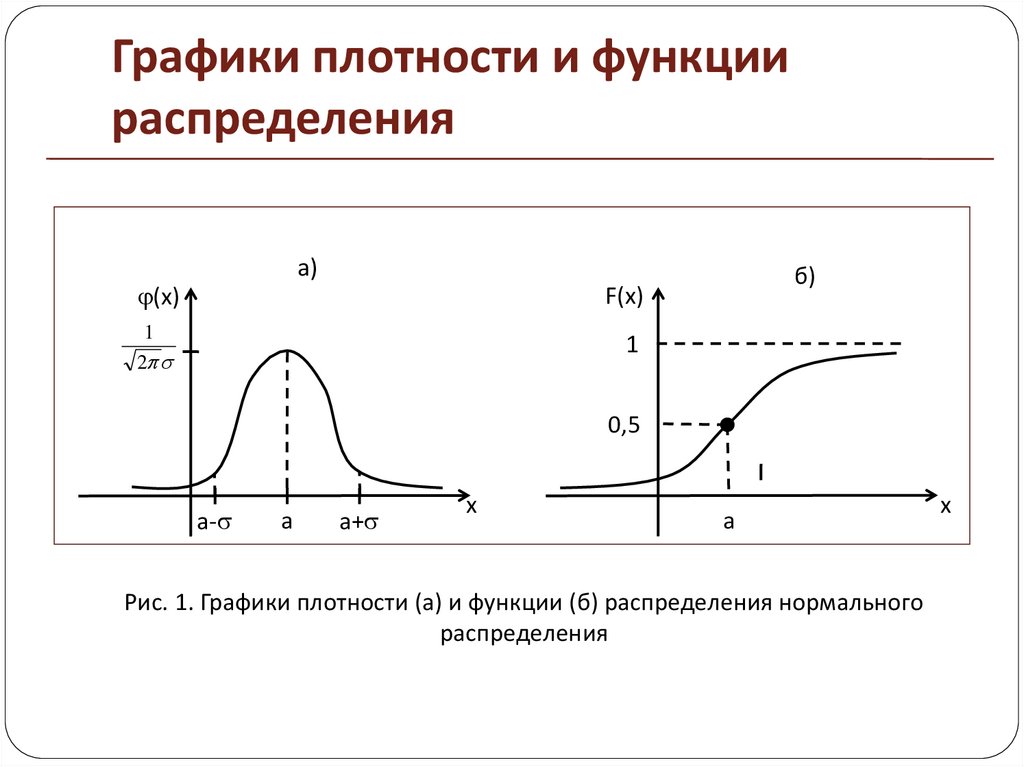
5. Графики плотности и функции распределения
а)(x)
б)
F(x)
1
2
1
0,5
a-
a
a+
x
a
Рис. 1. Графики плотности (а) и функции (б) распределения нормального
распределения
x
6. Вероятность попадания нормальной случайной величины в заданный интервал
Формула вероятности попадания нормальной случайнойвеличины в заданный интервал:
x a
x1 a
P x1 ξ x2 Ф 2
Ф
σ
σ
где - случайная величина;
x1и x2 – границы интервала.
Если интервал полубесконечный, то на основе свойств функции
Лапласа Ф 0,5;Ф 0,5 :
x2 a
P ξ x2 Ф
0,5
σ
x1 a
P x ξ 0 ,5 Ф
σ
7. Отклонение нормальной случайной величины
Вероятность заданного отклонения нормальнойслучайной величины от математического ожидания:
ε
P ξ a ε 2Ф
σ
8. «Правило трёх сигм»
Для нормально распределенной случайнойвеличины практически невозможно её отклонение
от математического ожидания по абсолютной
величине более трех σ.
9. Определение
Случайная величина, имеющая нормальноераспределение с параметрами a=0 и σ=1,
называется
стандартной
(нормированной)
нормальной
случайной
величиной,
а
её
распределение - стандартным (нормированным)
нормальным.
10. Теорема 8.1
Если N(a;σ), то ζ=k +b N(ka+b;|k|σ).11. Теорема 8.2
Если ζ N(a;σ), то ξ стξ a
N(0;1).
σ
12. Плотность и функция стандартного нормального распределения
1x
e
2π
Fст x
1
2π
e
t2
2
x2
2
dt 0,5 Ф x











 Математика
Математика








