Похожие презентации:
Определение и обозначение функции
1.
Определение функции.Обозначение функции.
у( х ) - функция
х - аргумент
зависимая переменная
независимая переменная
2. Область определения функции.
Область определения функции у(х)это все значения аргумента - Х
Обозначение
области определения - D(у)
3. Область значений функции.
Область значений функции у(х)это все значения -
У_
Обозначение области значений - Е(у)
4.
xy
-4
-8
-3
-6
-2
-4
-1
-2
0
0
1
2
2
4
3
6
5.
D(у)= [-3; 3]Е(у)= [-2; 3]
6. График функции
(х; у)- координаты точки в плоскостиу – ордината точки
(координата оси ОУ)
х – абсцисса точки
(координата оси ОХ)
у( х )- функция
х - аргумент
7. Область определения линейной функции y(х)= kx + b, k≠0
yk> 0
Iч.
y k< 0
IIч.
-∞ х< 0
IIIч.
+∞
О х>0
x -∞
О
х< 0
D(у) = (-∞; + ∞)
х Є (-∞; + ∞)
х > 0+ ∞
x
IVч.
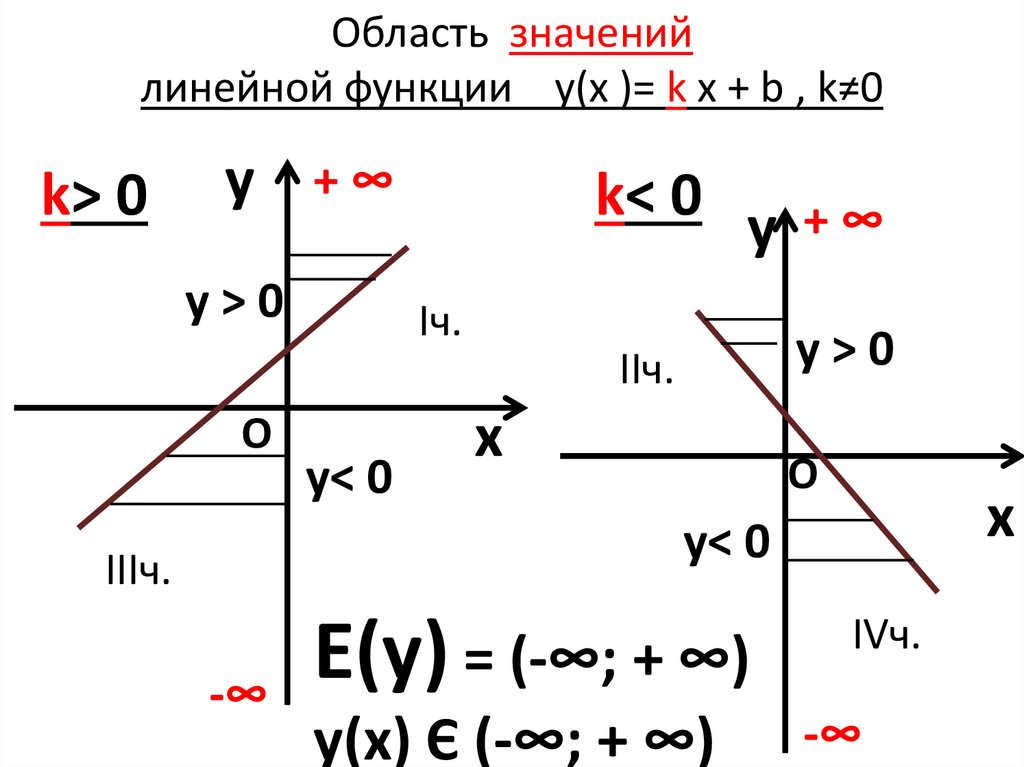
8. Область значений линейной функции y(х )= k x + b , k≠0
k> 0y +∞
у>0
k< 0
y +∞
Iч.
у>0
IIч.
О
IIIч.
у< 0
x
О
x
у< 0
Е(у)
= (-∞; + ∞)
-∞
у(х) Є (-∞; + ∞)
IVч.
-∞
9. Область определения линейной функции y(х)= kx + b, k= 0
yy(х)= b
IIч.
-∞
y y(х)= -b
Iч.
х< 0
+∞
х< 0
О х>0
x
D(у) = (-∞; + ∞)
х Є (-∞; + ∞)
О
-∞
IIIч.
x
х>0
+∞
IVч.
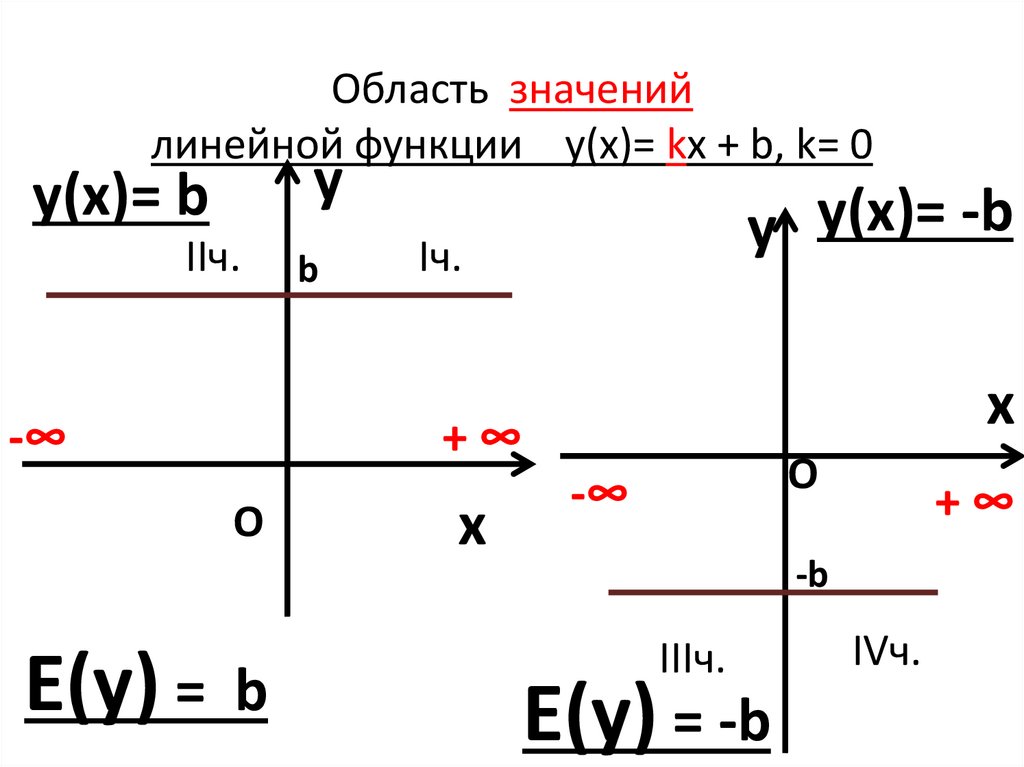
10. Область значений линейной функции y(х)= kx + b, k= 0
yy(х)= b
IIч.
-∞
b
y y(х)= -b
Iч.
x
+∞
О
Е(у) = b
x
О
-∞
+∞
-b
IIIч.
Е(у) = -b
IVч.
11. Область определения прямой пропорциональности y(х)= kx
k> 0-∞
Область определения прямой
пропорциональности
y(х)= kx
y
y
Iч.
х< 0
+∞
О х>0
IIIч.
k< 0
IIч.
x -∞
х > 0+ ∞
х< 0
D(у) = (-∞; + ∞)
х Є (-∞; + ∞)
О
x
IVч.
12. Область значений прамой пропорциональности y(х )= k x
+∞
k< 0
k> 0 y
y +∞
Iч.
у>0
IIч.
О
IIIч.
у< 0
у>0
x
О
x
у< 0
Е(у)
= (-∞; + ∞)
-∞
у(х) Є (-∞; + ∞)
IVч.
-∞
13. Область определения обратной пропорциональности , х≠0
k> 0y
y
Iч.
k< 0
IIч.
-∞
х< 0
IIIч.
+∞
О х>0
x
-∞ х< 0
D(у) = (-∞; 0) U (0; + ∞)
х Є (-∞; 0) U (0; + ∞)
О
х > 0+ ∞
x
IVч.
14. Область значений обратной пропорциональности, х≠0
k< 0k> 0 y + ∞
y +∞
Iч.
y> 0
IIч.
y>0
x
О
IIIч.
О
y< 0
-∞
Е(у) = (-∞; 0) U (0; + ∞)
у(х) Є (-∞; 0) U (0; + ∞)
y< 0
x
IVч.
-∞
15. Область определения квадратичной функции, а≠0
а> 0y
IIч.
y
Iч.
х< 0
О
а< 0
х>0
-∞
+∞
x
-∞
О
х< 0 х > 0
D(у) = (-∞; + ∞)
х Є (-∞; + ∞)
x
+∞
IIIч.
IVч.
16. Область значений квадратичной функции, а≠0
а> 0y
IIч.
y
Iч.
а< 0
О
+∞
-∞
IIIч.
у>0
y< 0
x
-∞
О
Е(у) = [о; + ∞)
у(х) Є [о; + ∞)
x
IVч.
+∞
Е(у) = (-∞;0]
у(х) Є (-∞;0]
17. Область определения функции , х ≥ 0
y Область определенияфункции
, х≥0
Iч.
x
О
D(у) = [0; + ∞);
х≥0
х Є [0; + ∞)
+∞
18. Область значений функции , х ≥ 0
Область значенийфункции
, х≥0
y
Iч.
у≥0
x
О
Е(у) = [0; + ∞);
+∞
у(х) Є [0; + ∞)
19. Область определения функции у = lхl_
yIIч.
Iч.
x
-∞
х<0
О
D(у) = (- ∞ ; + ∞);
х≥0
+∞
х Є (- ∞ ; + ∞)
20. Область значений функции у = lхl_
+∞y
Iч.
IIч.
у≥0
x
О
Е(у) = [0; + ∞);
у(х) Є [0; + ∞)
21. Область определения функции у = х³
yIч.
x
х<0 О
х≥0
-∞
+∞
IIIч.
D(у) = (-∞; + ∞);
х Є (-∞; + ∞)
22. Область значений функции у = х³
+∞y
Iч.
у≥0
О
x
у<0
IIIч.
-∞
D(у) = (-∞; + ∞);
у(х) Є (-∞; + ∞)
23. Найдите по графику область определения функции - D(у)
D(у)= [-5; 4,5]24. Найдите по графику область значений функции - Е(у)
Е(у)= [-2; 5]25. Найдите по графику область определения функции - D(у)
D(у)= [-6; 3,5]26. Найдите по графику область значений функции - Е(у)
Е(у)= [-2; 4]27. Найдите по графику область определения функции - D(у)
D(у)= [-5; 5]28. Найдите по графику область значений функции - Е(у)
Е(у)= [-2; 6]29. Найдите область определения и значений функции
а)3
б)
4
в)
г)
-4
д)
[ -4;4)
( -1;3]
30. Найдите область определения и значений функции
а)4
б)
в)
5
г)
д)
-3
( -1;5]
[ -3;4)
31. Найдите область определения и значений функции
а)4
б)
в)
-2
4
г)
д)
[ -2;4)
[ -1;4]
32. Найдите область определения и значений функции
а)б)
2
в)
г)
-4
2
д)
[ -4;2]
[ -1;2]
33.
34.
35.
36.
1)f(-3) =
2)
f(- 1) =
3)
f(x) = - 1,5 при x =
4)
f(x) = 2 при х =
х=
5)
D(f) =
6)
E(f) =
,x=
37.
x 2 3x 101) f ( x)
x 3
2) f ( x) 2 x 7
а) f(2) =?
б) D(f) = ?
а) f(16) =?
б) D(f) = ?
Решение:
Решение:



































 Математика
Математика








