Л.Плоскость

1.

«ПЛОСКОСТЬ»
Кафедра: Начертательная геометрия и
инженерная графика

2.

«ПЛОСКОСТЬ»
1.Способы задания плоскостей
2.Классификация плоскостей
ПЛОСКОСТЬ в линейной алгебре – поверхность первого
порядка:
в декартовой системе координат плоскость может быть
задана уравнением 1-ой степени.
Ax+By+Cz+D=0,
где А, В, С, и D - постоянные, одновременно не
равные нулю.

3.

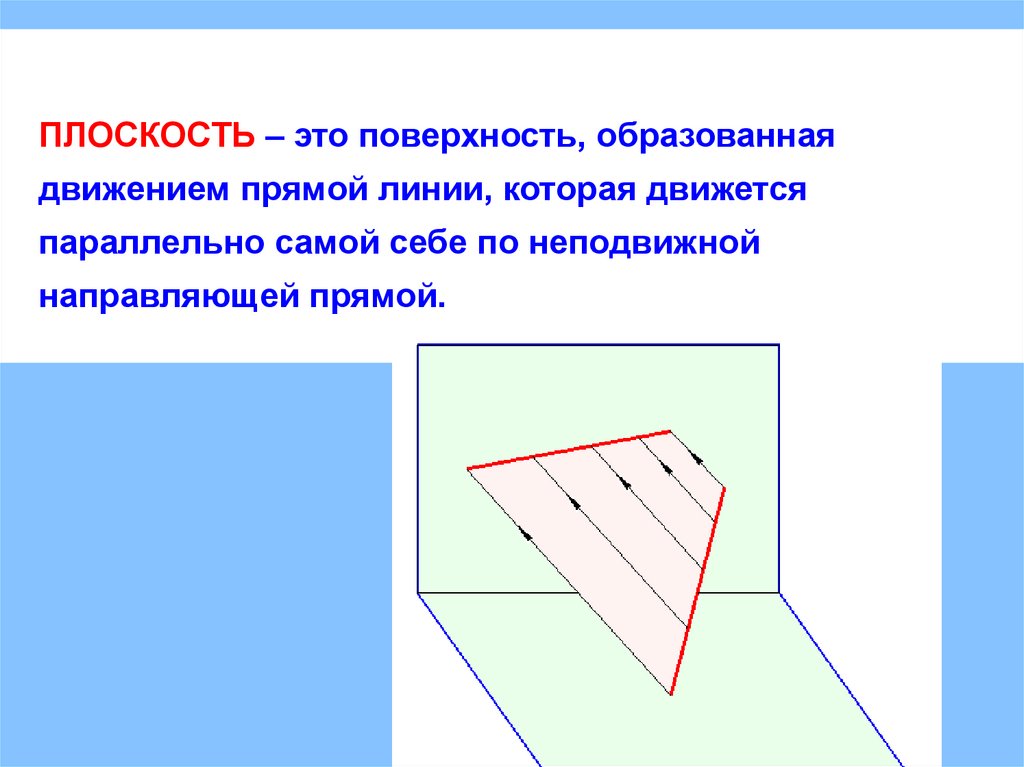
ПЛОСКОСТЬ – это поверхность, образованная
движением прямой линии, которая движется
параллельно самой себе по неподвижной
направляющей прямой.

4.

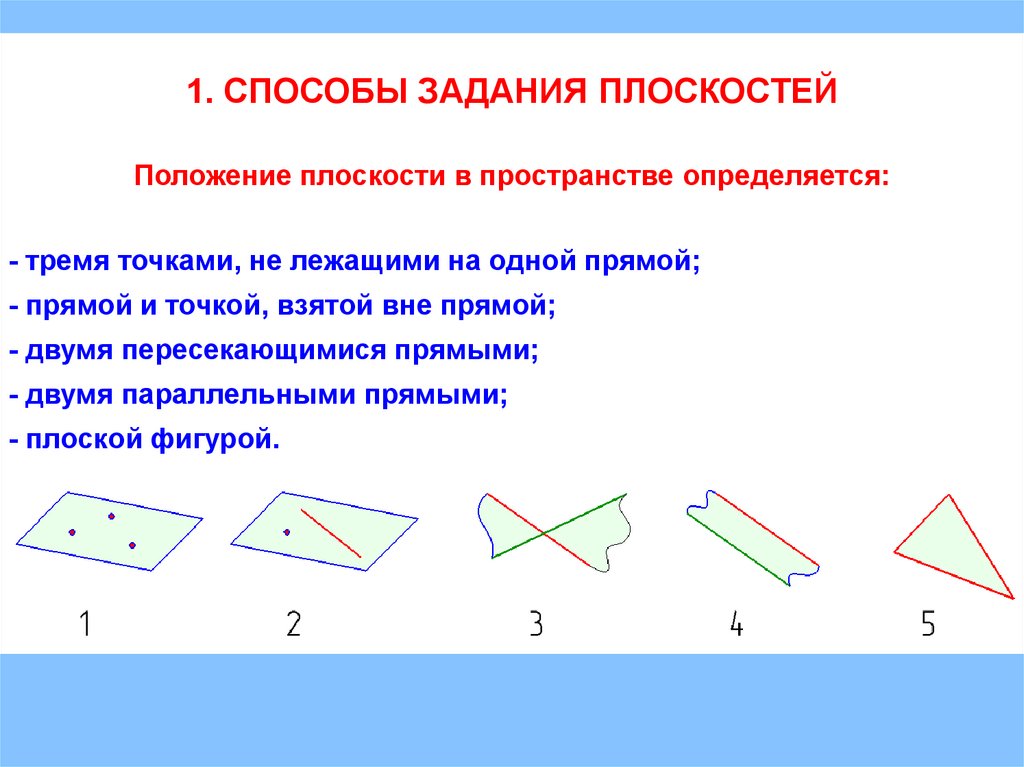
1. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.

5.

1.1. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ НА
КОМПЛЕКСНОМ ЧЕРТЕЖЕ:
1) проекциями трёх точек, не лежащих на одной прямой;

6.

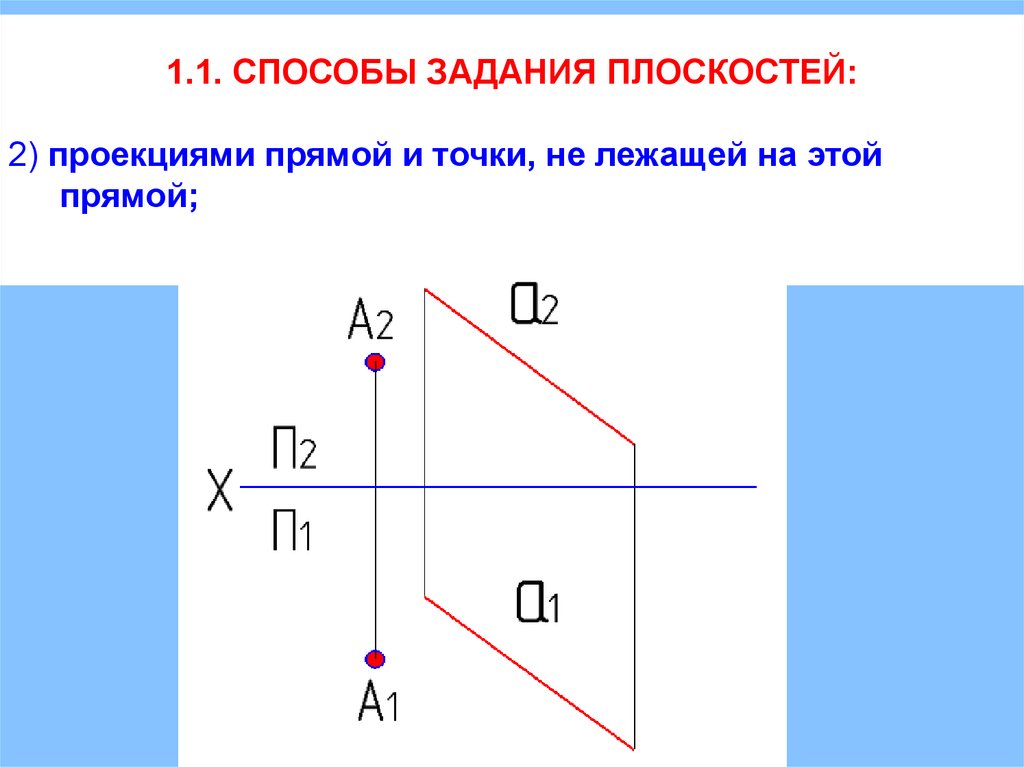
1.1. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ:
2) проекциями прямой и точки, не лежащей на этой
прямой;

7.

1.1. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ:
3) проекциями двух пересекающихся прямых;

8.

1.1. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ:
4) проекциями двух параллельных прямых;

9.

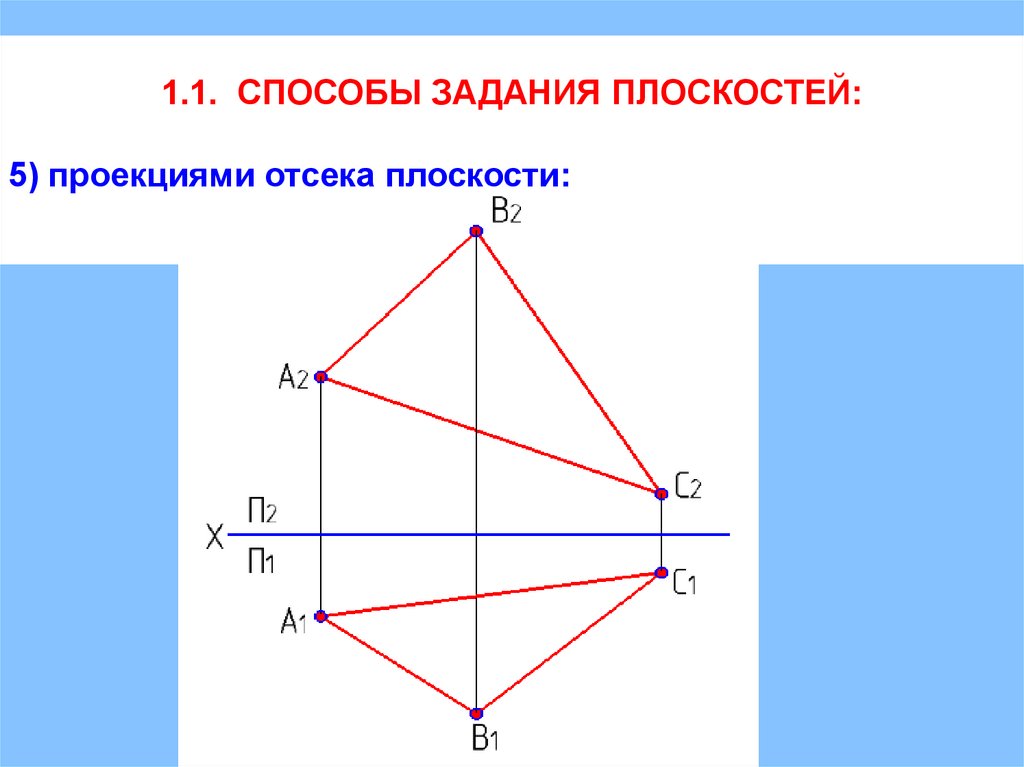
1.1. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ:
5) проекциями отсека плоскости;

10.

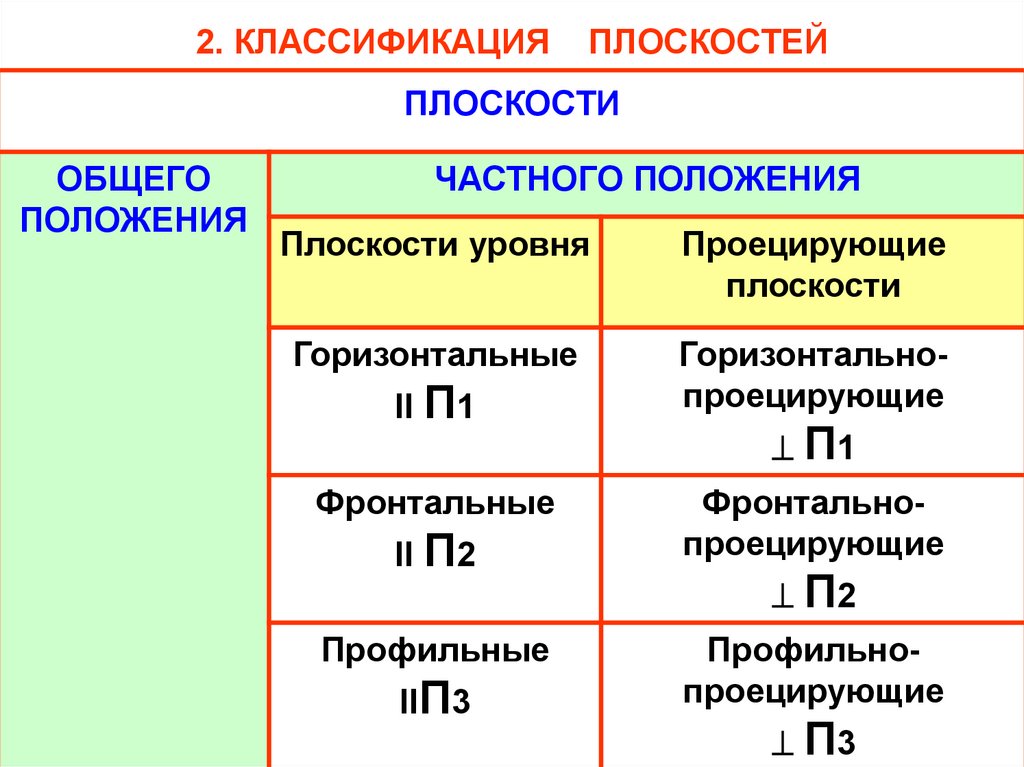
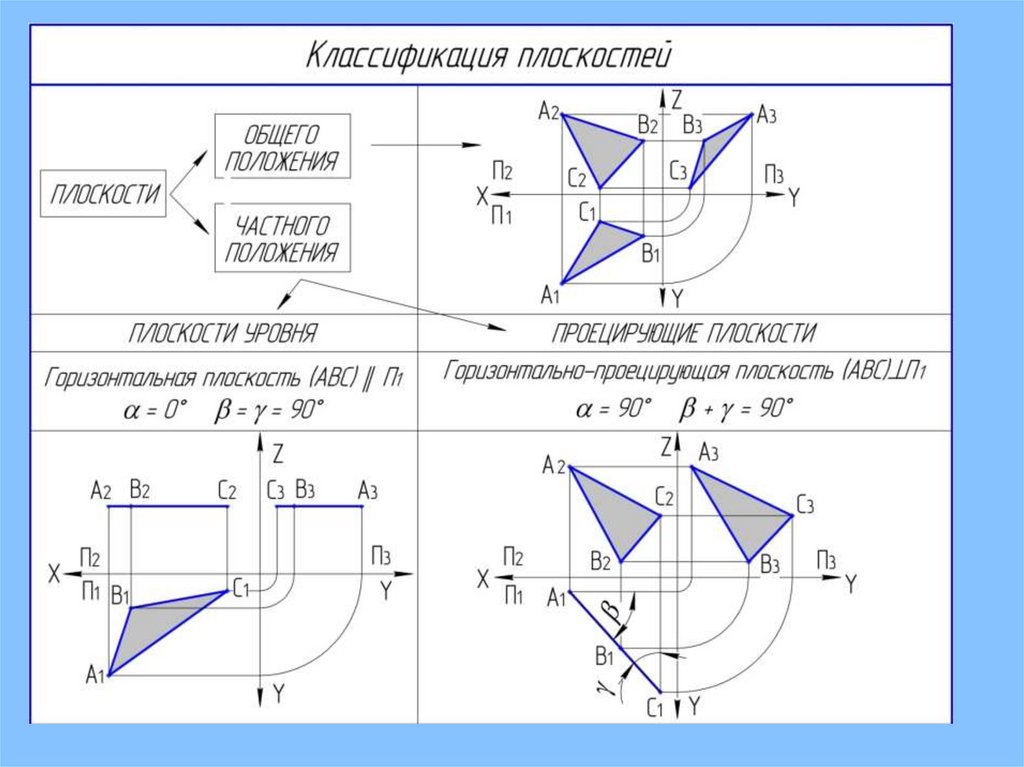
2. КЛАССИФИКАЦИЯ
ПЛОСКОСТЕЙ
ПЛОСКОСТИ
ОБЩЕГО
ПОЛОЖЕНИЯ
ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскости уровня
Проецирующие
плоскости
Горизонтальные
Горизонтальнопроецирующие
II П1
Фронтальные
II П2
Профильные
IIП3
П1
Фронтальнопроецирующие
П2
Профильнопроецирующие
П3

11.

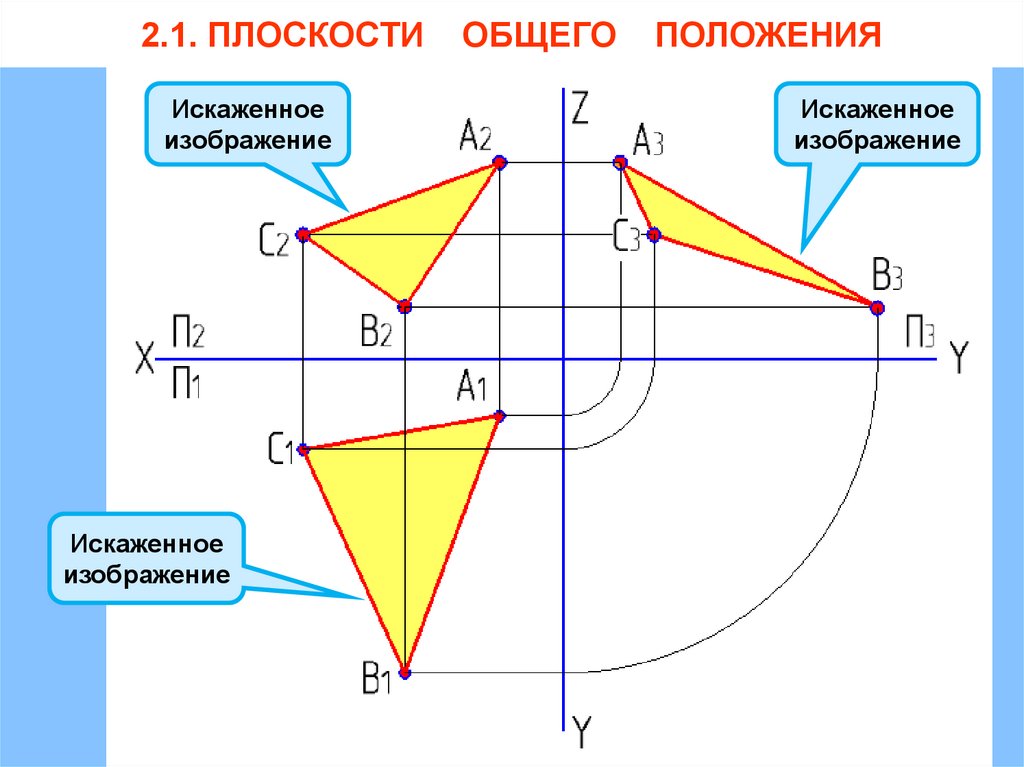
2.1. ПЛОСКОСТИ
ОБЩЕГО ПОЛОЖЕНИЯ
Свойства плоскостей общего положения (ОП):
1) не параллельны и не перпендикулярны
ни одной из плоскостей проекций;
2) проекции плоскостей ОП искажены;
3) углы наклона плоскостей ОП к плоскостям проекций
нельзя определить по комплексному чертежу
без дополнительных построений
- угол наклона к горизонтальной плоскости П
- угол наклона к фронтальной плоскости П
- угол наклона к профильной плоскости П
2
3
1

12.

2.1. ПЛОСКОСТИ
Искаженное
изображение
Искаженное
изображение
ОБЩЕГО
ПОЛОЖЕНИЯ
Искаженное
изображение

13.

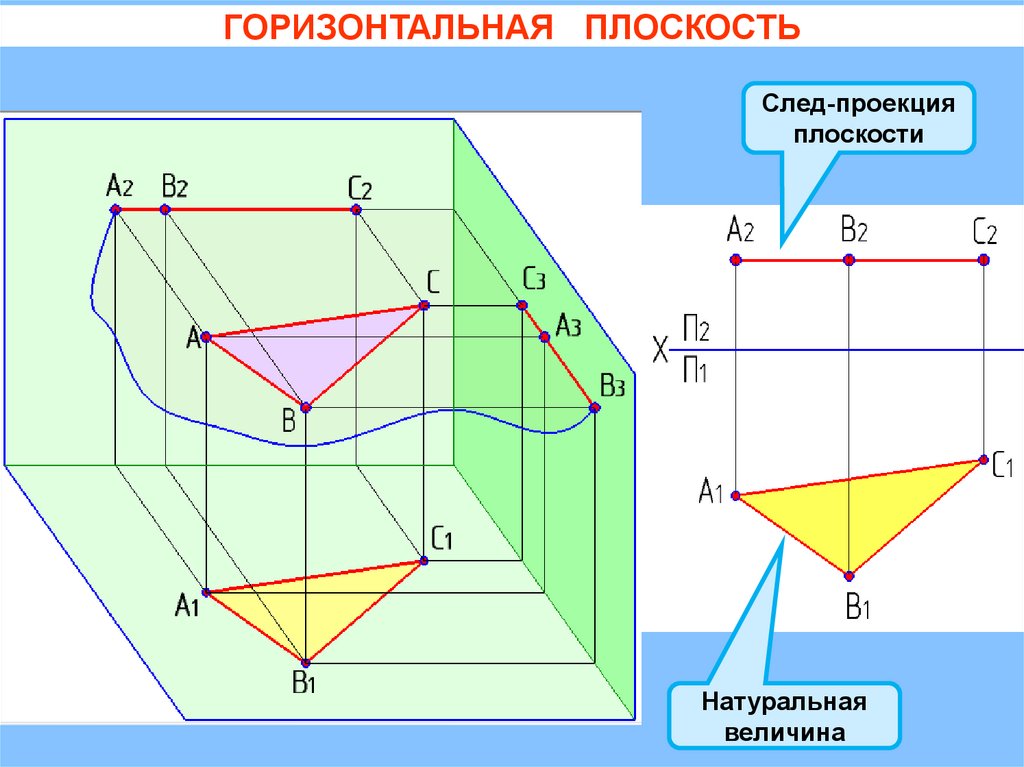
2.2. ПЛОСКОСТИ УРОВНЯ.
Свойства плоскостей уровня:
1) параллельны одной из плоскостей проекций;
2) на одной из плоскостей проекций проецируются в натуральную
величину,
на две другие плоскости – в виде отрезков (след-проекция),
параллельных осям;
3) след-проекция обладает собирательным свойством;
4) с одной из плоскостей проекций - угол 00,
два других угла равны по 900

14.

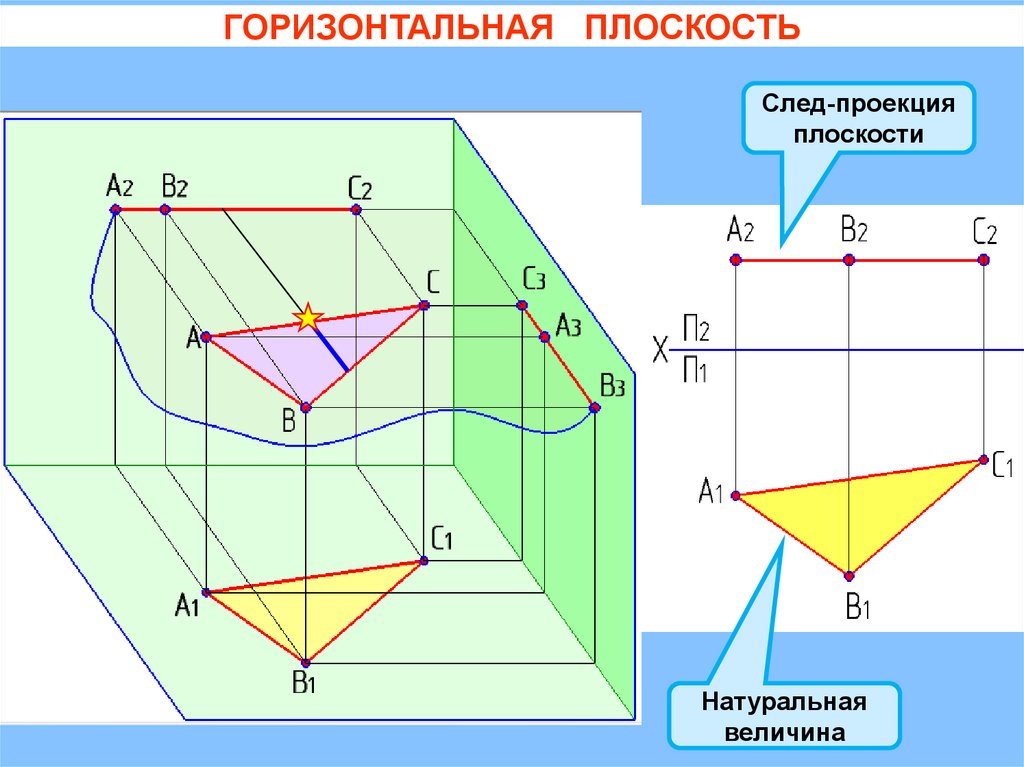
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
След-проекция
плоскости
Натуральная
величина

15.

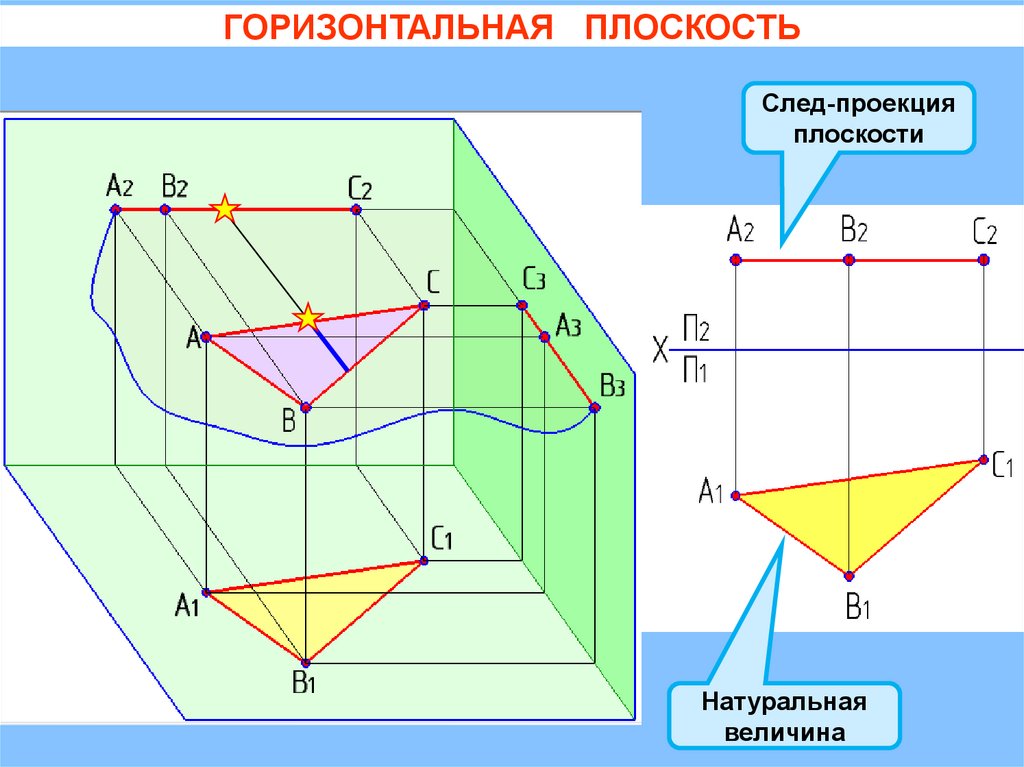
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
След-проекция
плоскости
Натуральная
величина

16.

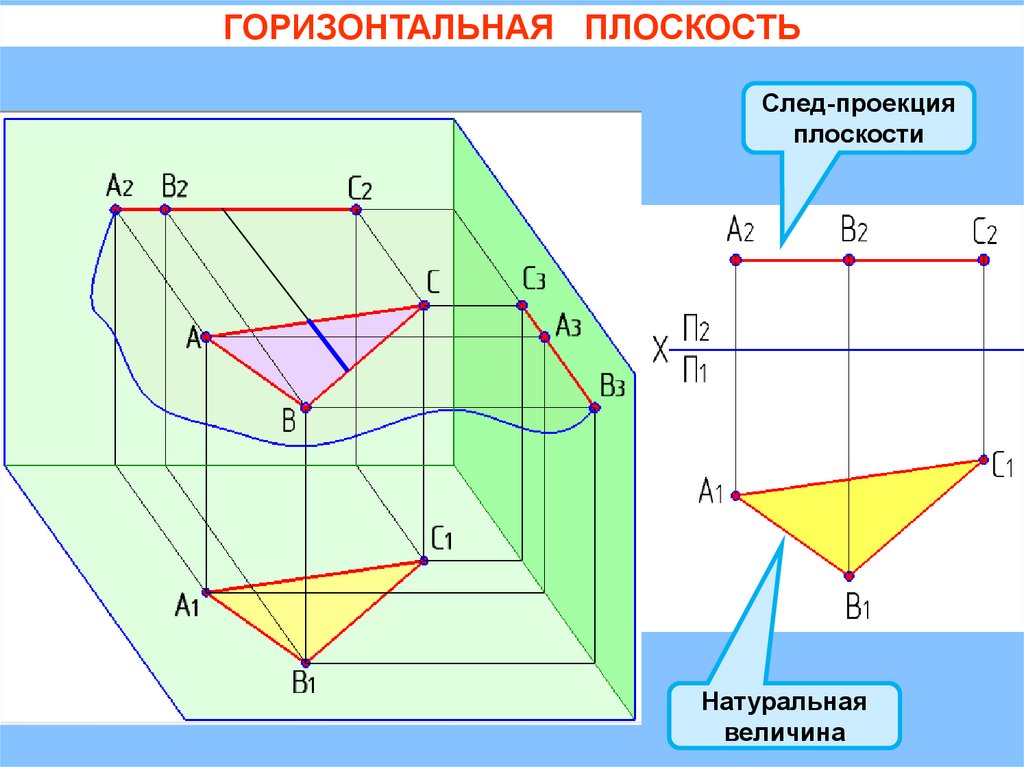
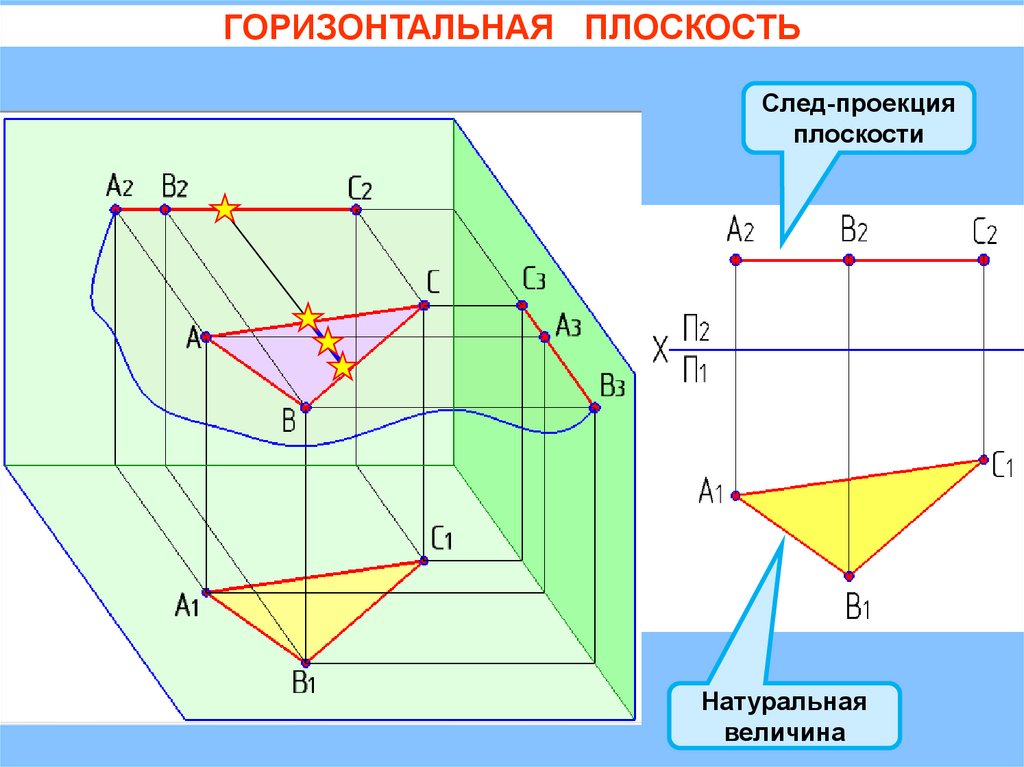
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
След-проекция
плоскости
Натуральная
величина

17.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
След-проекция
плоскости
Натуральная
величина

18.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
След-проекция
плоскости
Натуральная
величина

19.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
След-проекция
плоскости
Натуральная
величина

20.

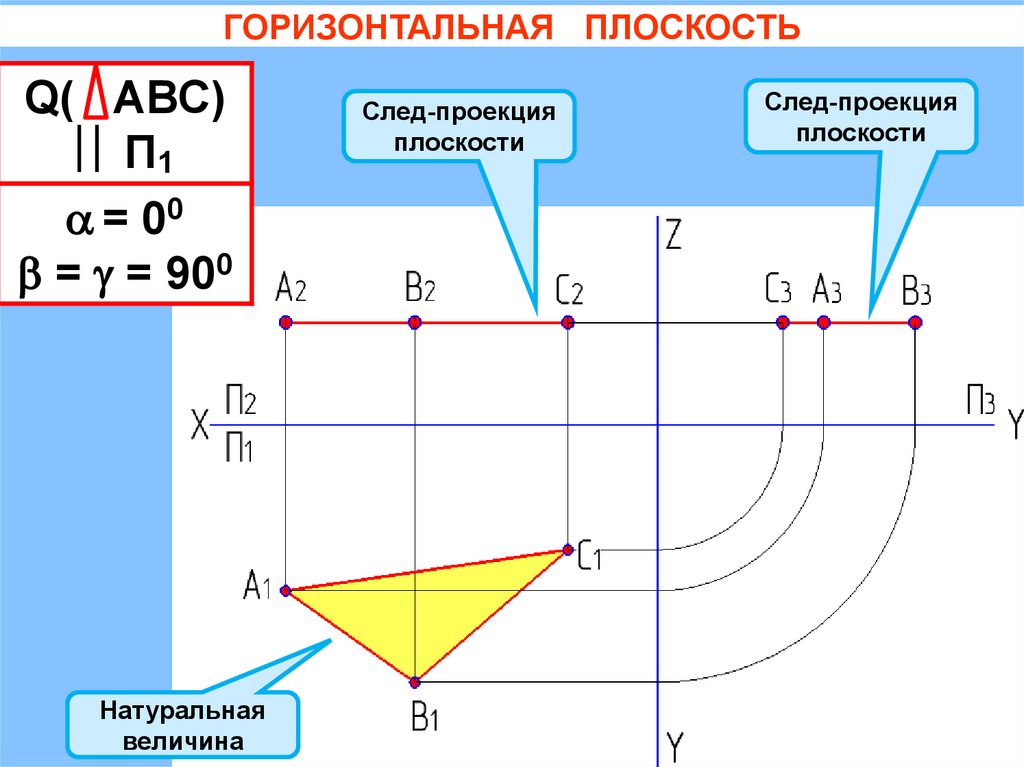
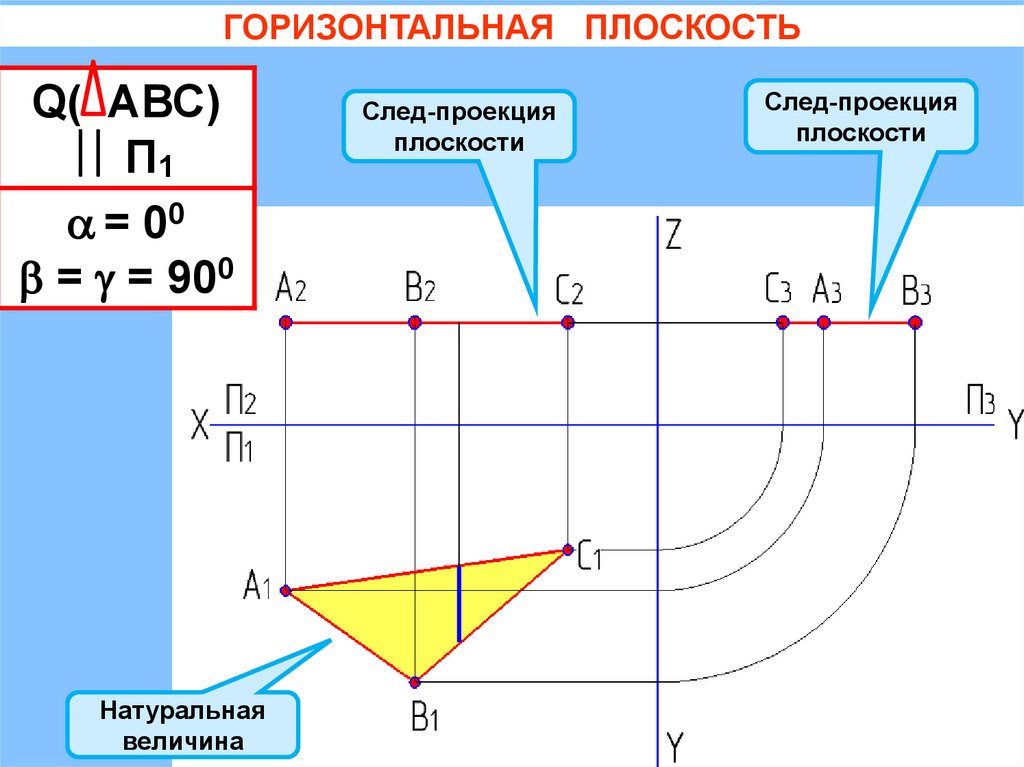
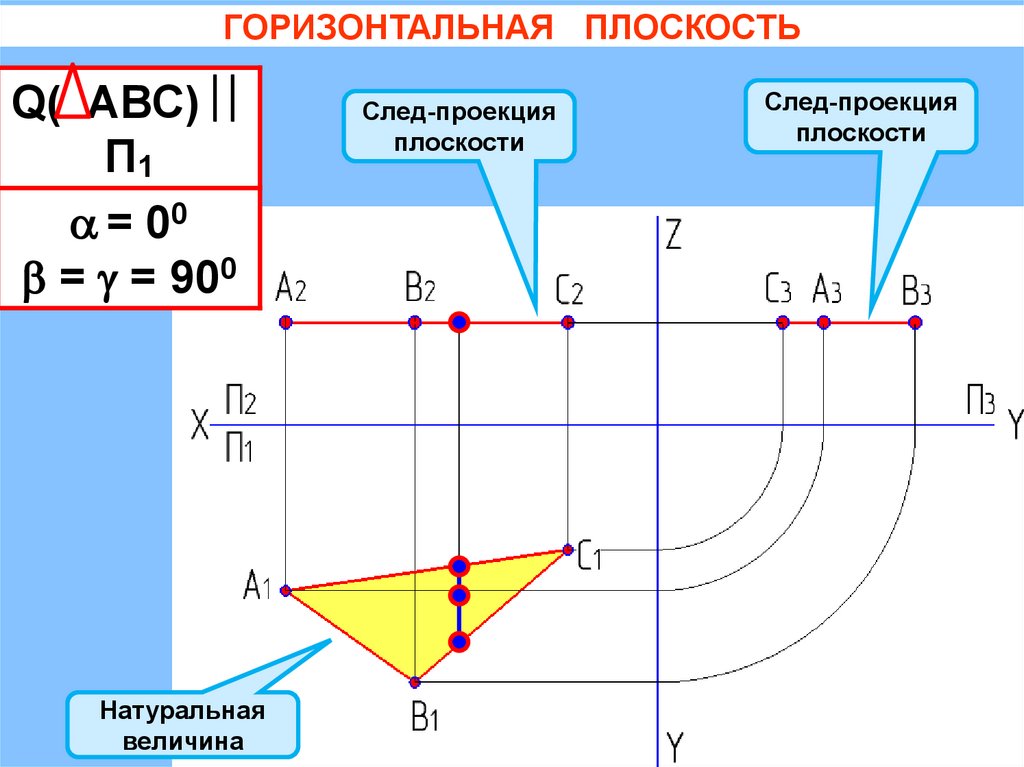
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

21.

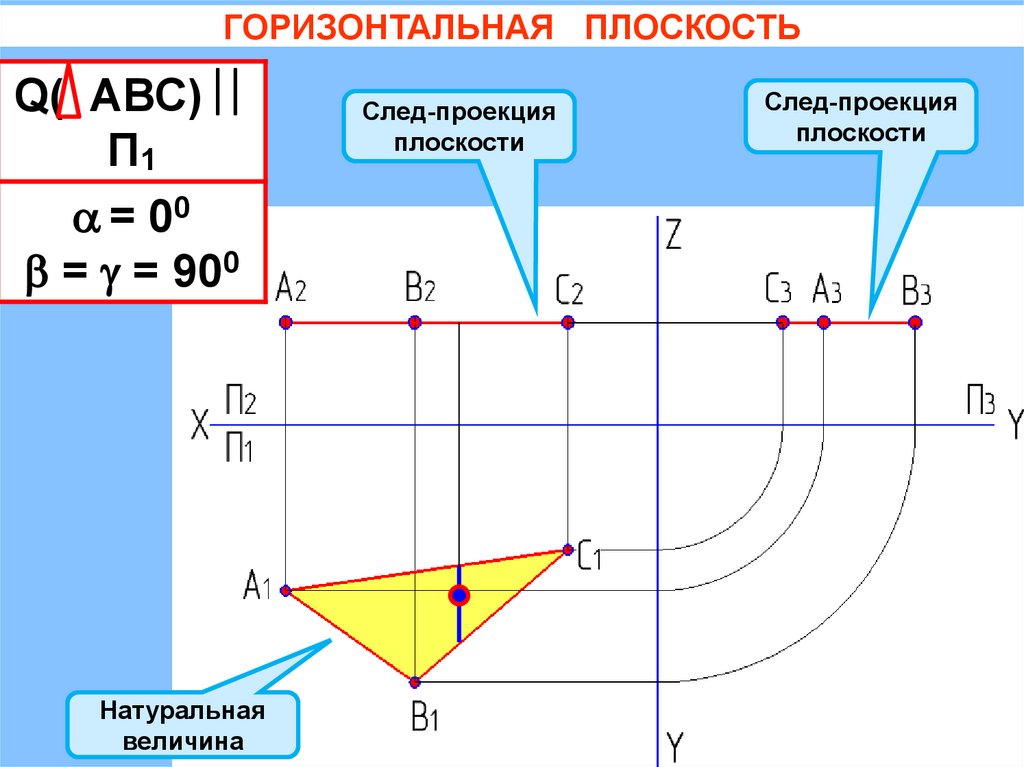
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

22.

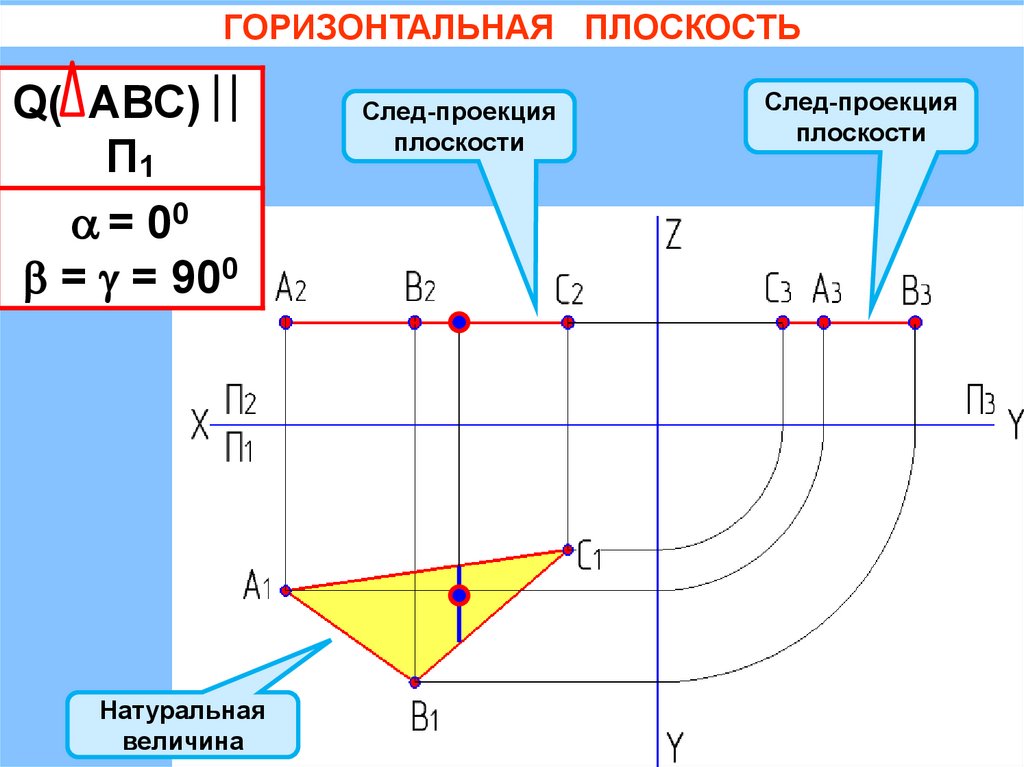
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

23.

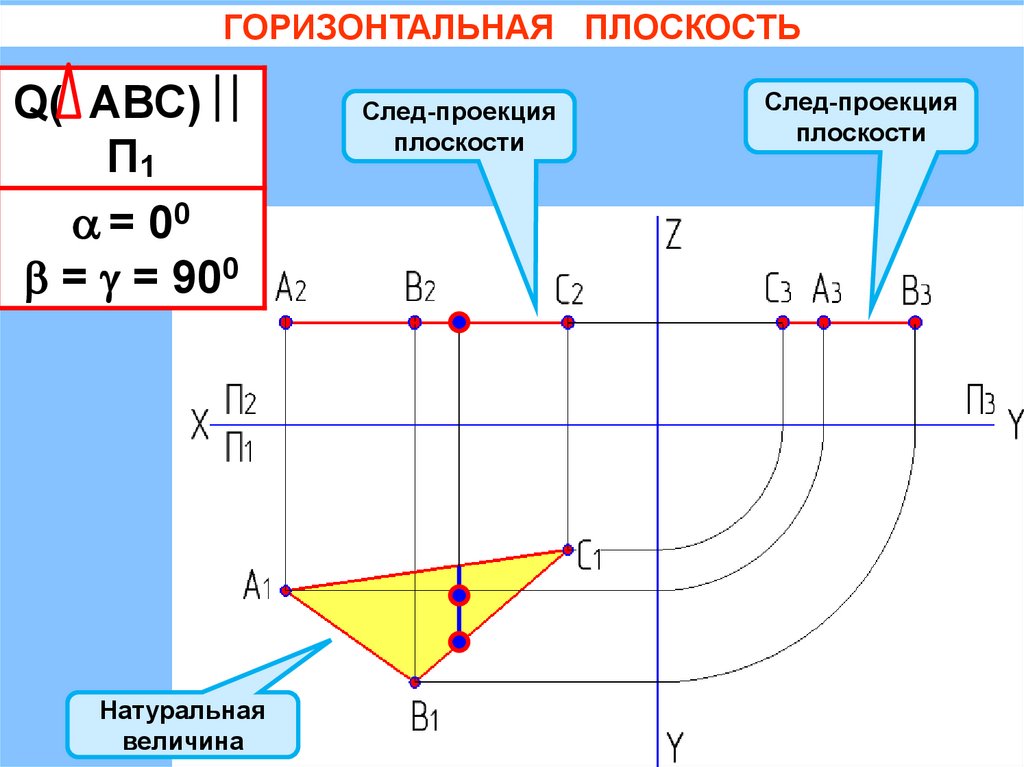
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

24.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

25.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

26.

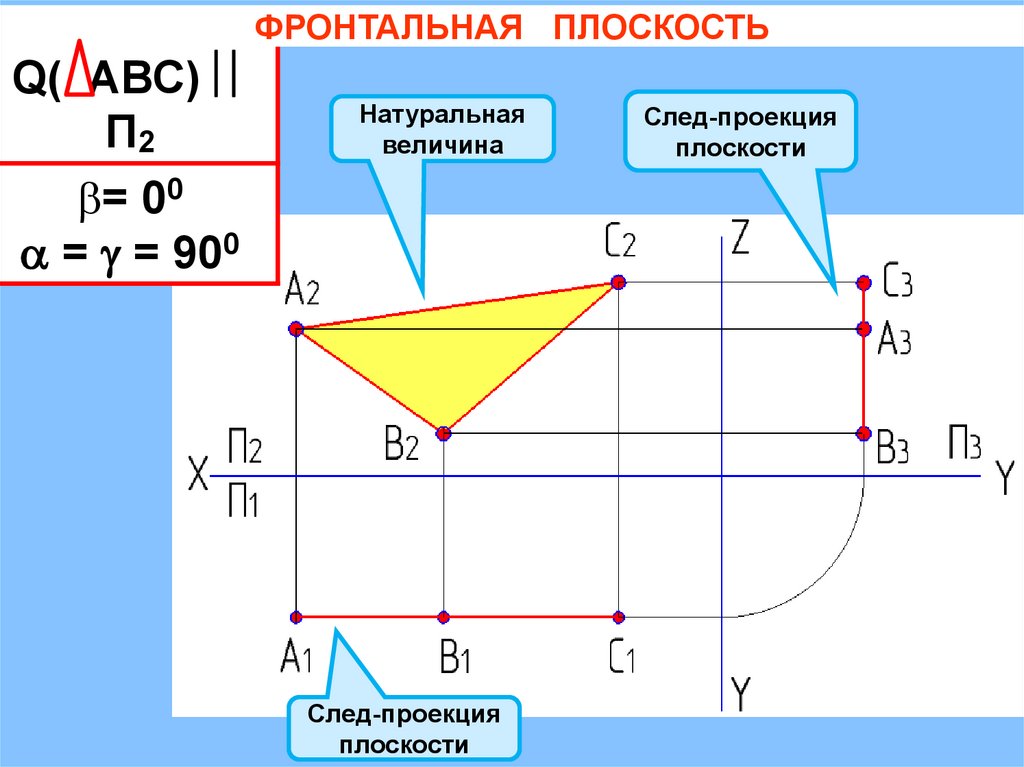
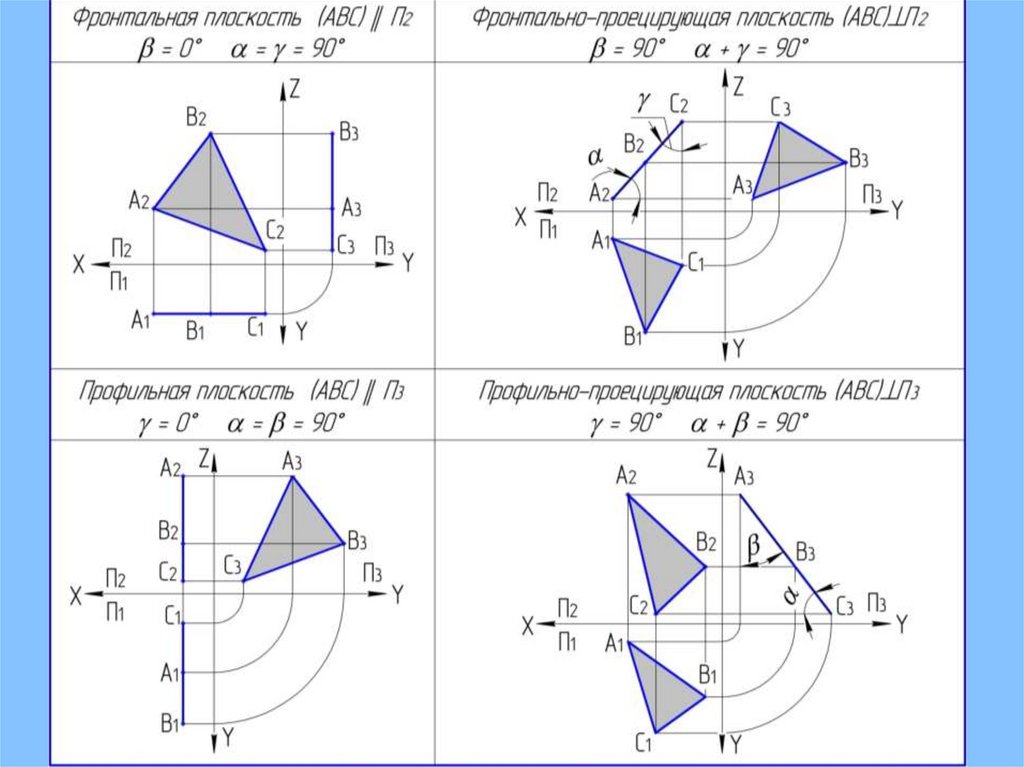
ФРОНТАЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П2
= 00
= = 900
Натуральная
величина
След-проекция
плоскости
След-проекция
плоскости

27.

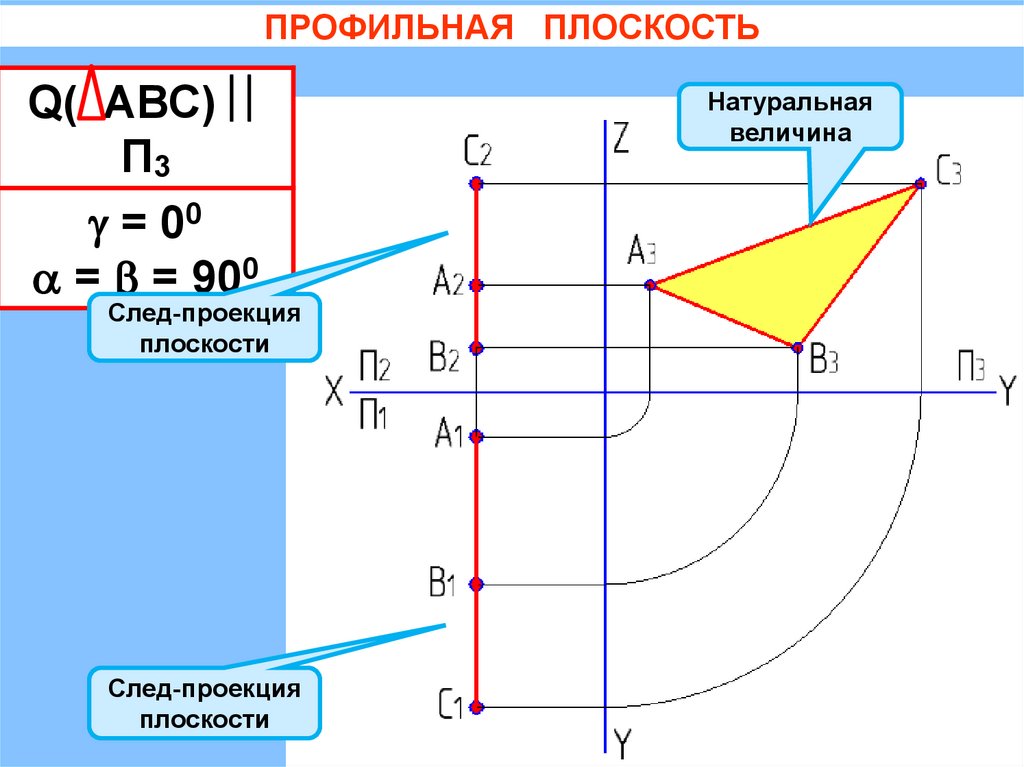
ПРОФИЛЬНАЯ ПЛОСКОСТЬ
Q( АВС)
П3
= 00
= = 900
След-проекция
плоскости
След-проекция
плоскости
Натуральная
величина

28.

2.3. ПРОЕЦИРУЮЩИЕ
ПЛОСКОСТИ, т.е.
ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТЯМ ПРОЕКЦИЙ
Свойства проецирующих плоскостей:
1) перпендикулярны одной из плоскостей проекций;
2) на одну из плоскостей проецируются в виде отрезка
прямой (след-проекция), а на две другие плоскости –
с искажением;
3) след-проекция обладает собирательным свойством;
4) по расположению следа-проекции определяются
углы наклона плоскости к плоскостям проекций

29.

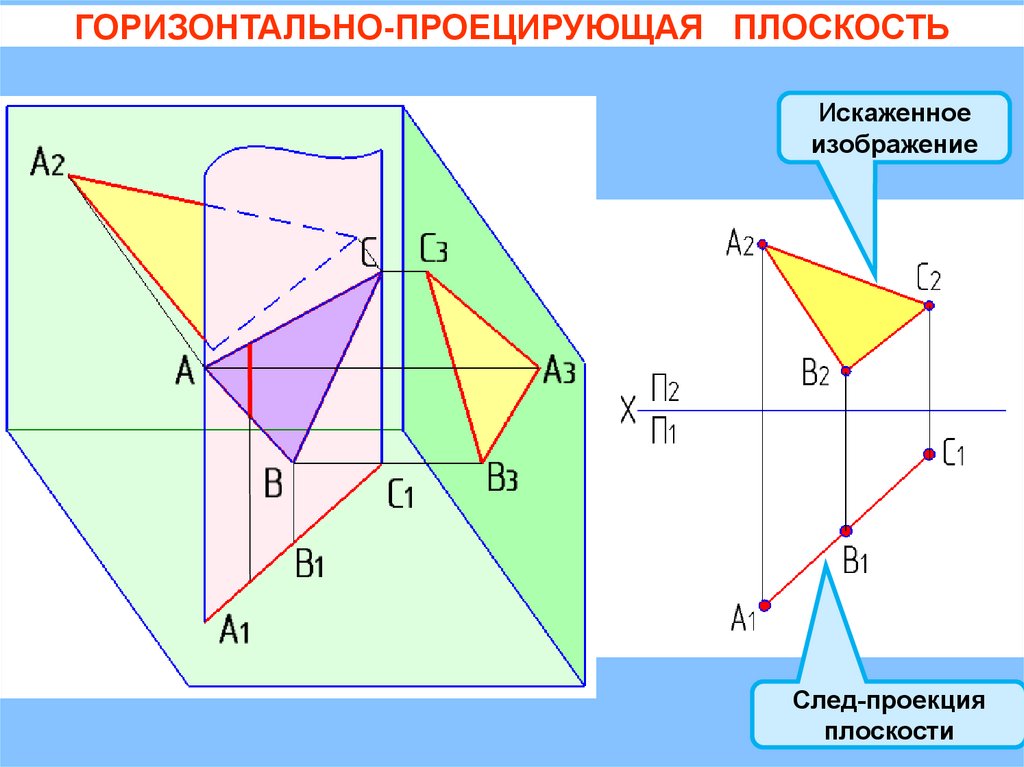
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

30.

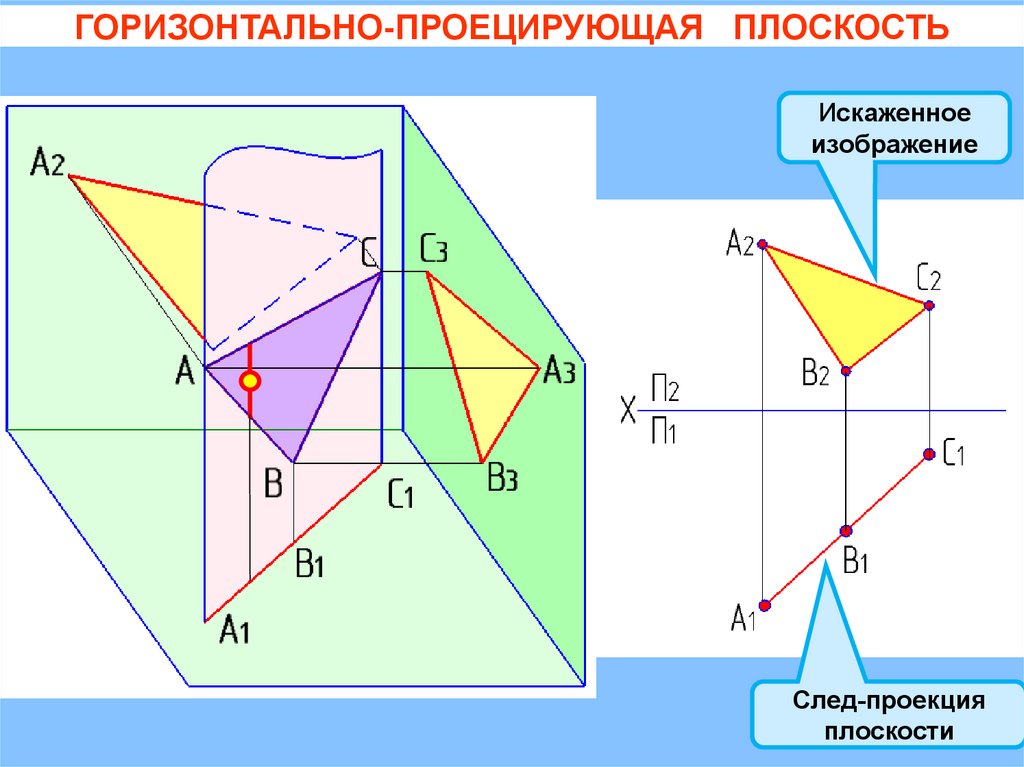
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

31.

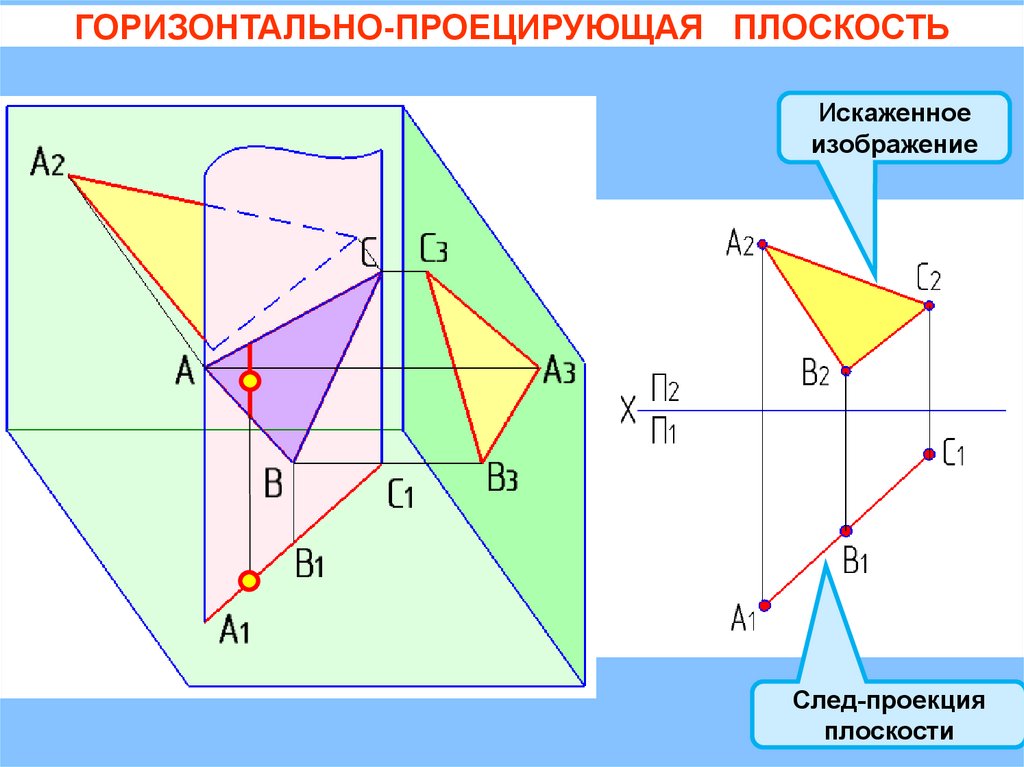
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

32.

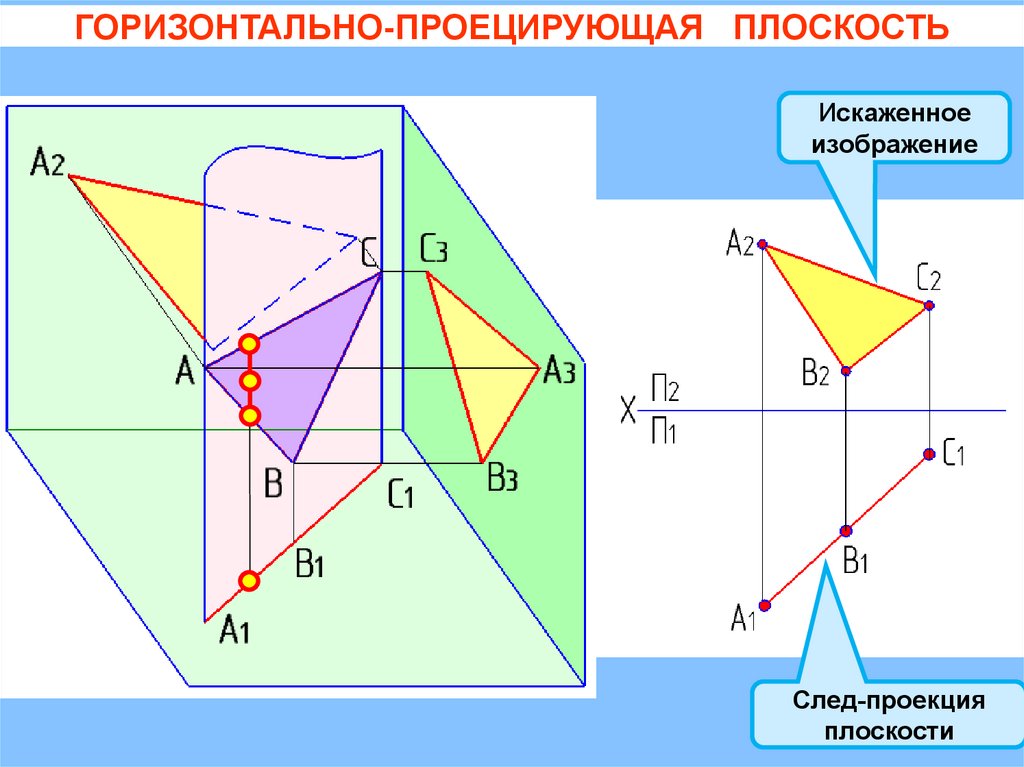
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

33.

ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

34.

ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

35.

ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Искаженное
изображение
След-проекция
плоскости

36.

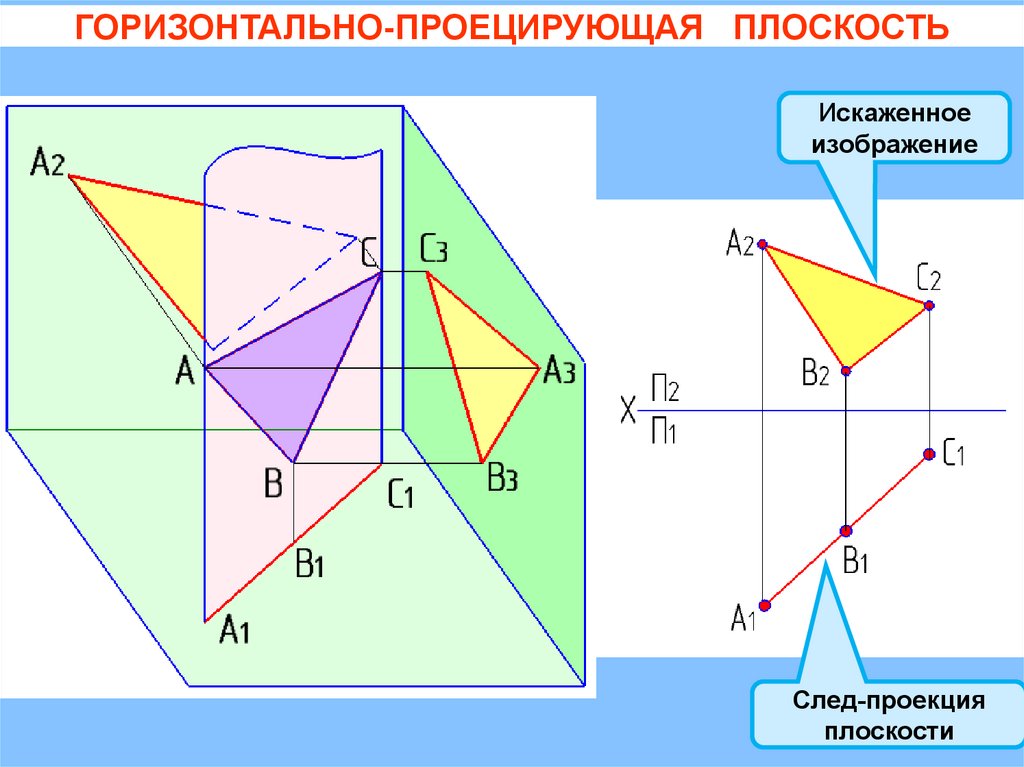
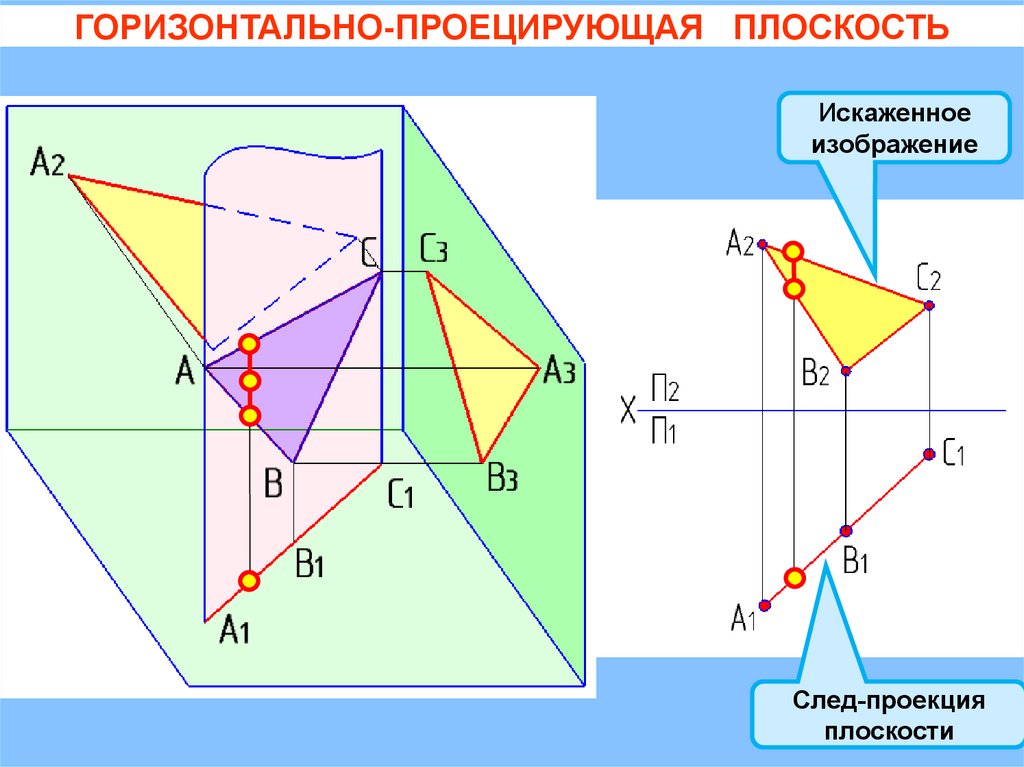
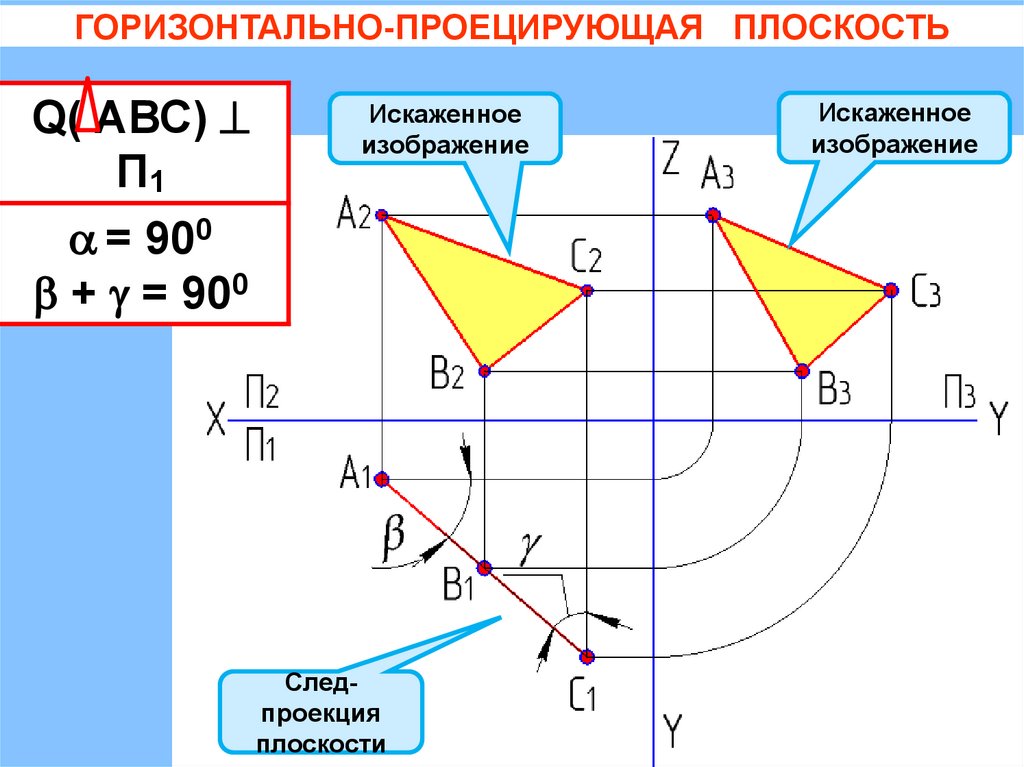
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Q( АВС)
П1
= 900
+ = 900
Искаженное
изображение
Следпроекция
плоскости
Искаженное
изображение

37.

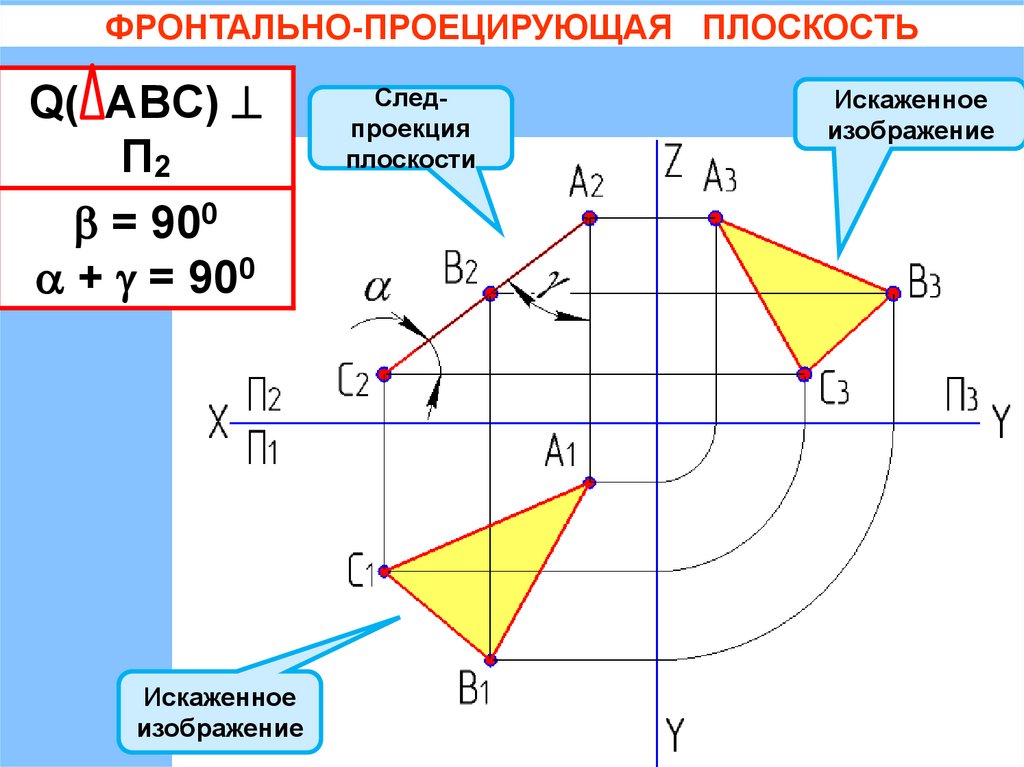
ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Q( АВC)
П2
= 900
+ = 900
Искаженное
изображение
Следпроекция
плоскости
Искаженное
изображение

38.

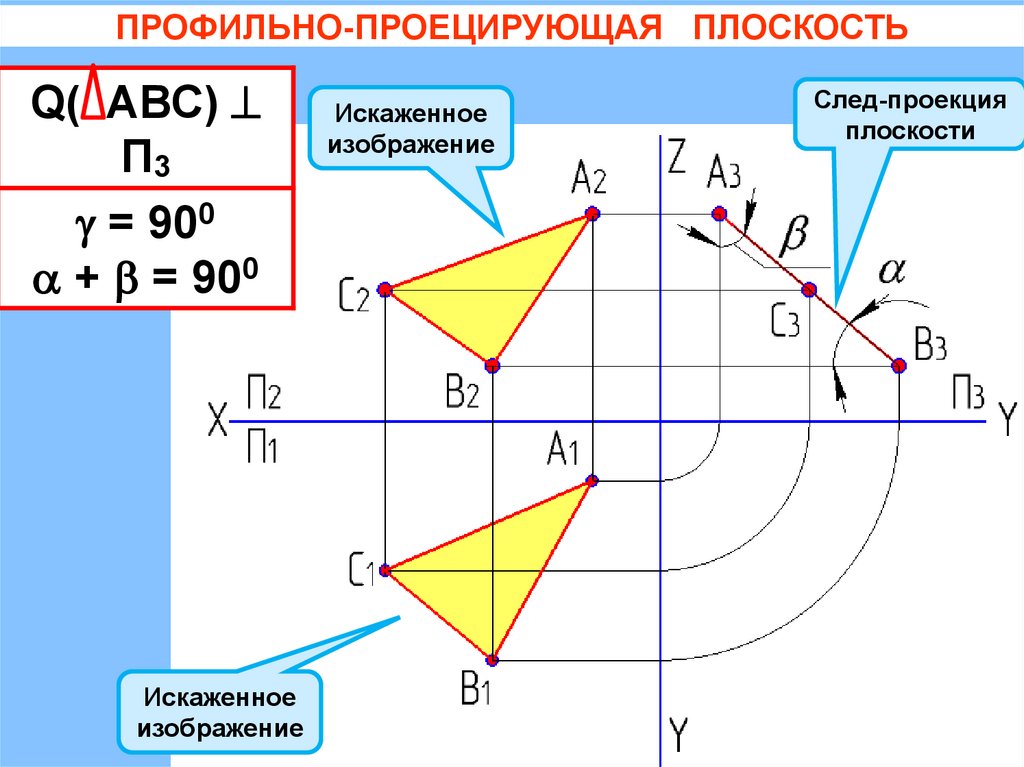
ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ
Q( АВС)
П3
= 900
+ = 900
Искаженное
изображение
Искаженное
изображение
След-проекция
плоскости

39.

40.

41. Контрольное задание

1. В КОНСПЕКТАХ ВЫПОЛНИТЬ ГРАФИЧЕСКИ С
ИСПОЛЬЗОВАНИЕМ ЛИНЕЙКИ, КАРАНДАША:
- ПРИМЕРЫ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ;
- ПРИМЕРЫ ПЛОСКОСТЕЙ ЧАСТНОГО
ПОЛОЖЕНИЯ: УРОВНЯ И ПРОЕЦИРУЮЩИХ.
2. Решить задачи.
Задача 2.1. В плоскости общего положения
(плоскость задать самостоятельно) построить
точку А, принадлежащую плоскости, отрезок ВС,
принадлежащий плоскости.
Задача 2.2. Через прямую общего положения (
прямую задать самостоятельно) провести
горизонтально-проецирующую плоскость.

42.

Список рекомендуемой литературы
1.
Фролов С.А. Начертательная геометрия: Учебник для вузов/С.А.
Фролов. - 3-е изд., перераб. и доп. - М.: ИНФРА, 2007. - 286 с.
2.
Чекмарев А. А. Инженерная графика: Учеб. для немаш. спец.
вузов/А.А. Чекмарев. - 10-е изд. стер. - М.: Высшая школа., 2008.-382
с.:ил.
3.
Вольхин К.А. Начертательная геометрия. Учебное пособие.
[Электронный ресурс] URL:
http://graph.power.nstu.ru/wolchin/umm/Graphbook/