Прямая линия. Способы графического задания прямой

1.

Прямая линия
Способы
графического
задания прямой

2.

Способы задания прямой на эпюре:
Проекциями двух
принадлежащих ей точек
Проекцией точки
и направлением
b2
В2
А2
А2
X
X
А1
А1
b1
В1
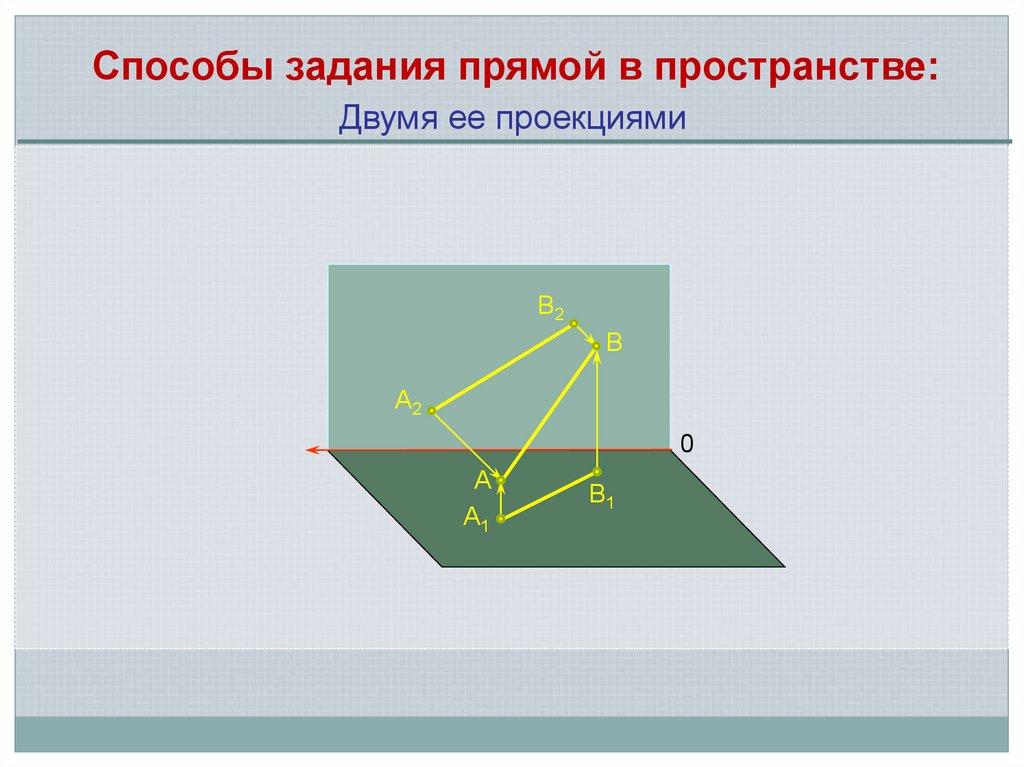
Эпюром прямой называется чертеж, состоящий из двух или
более ортогональных проекций, связанных между собой

3.

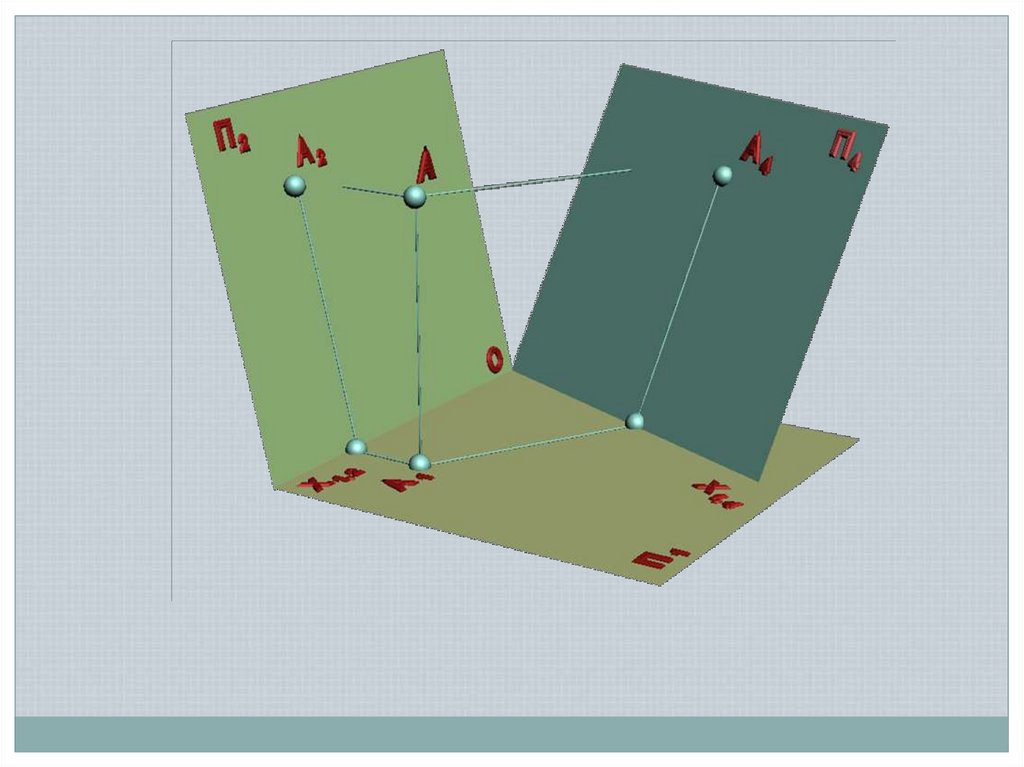
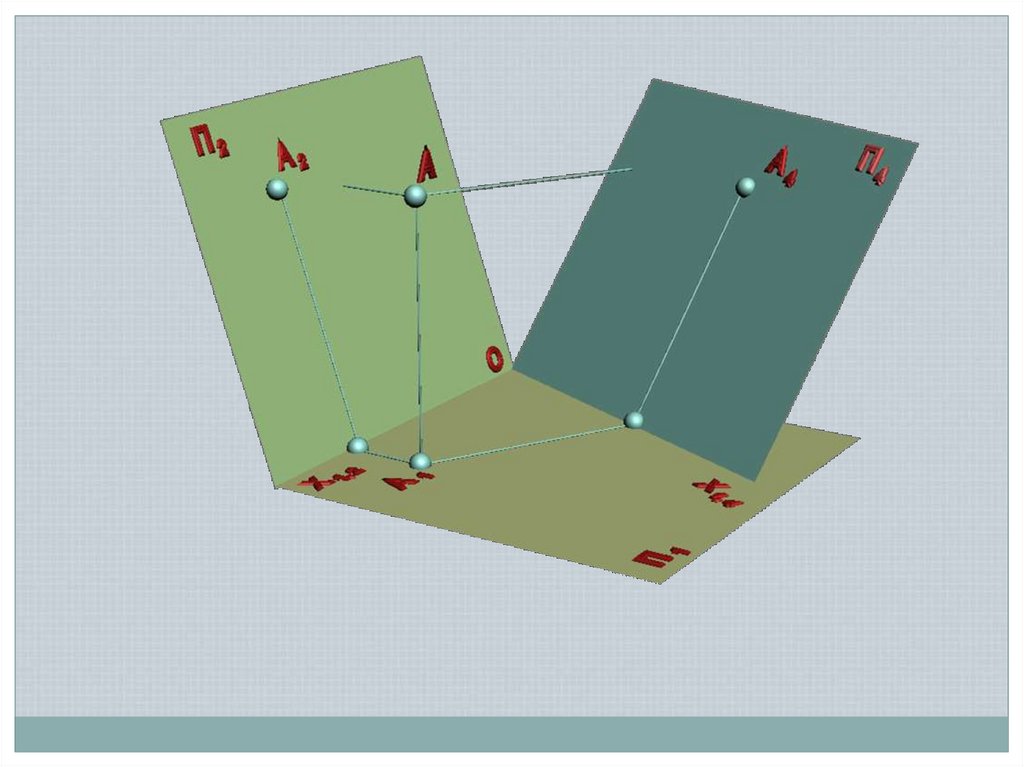
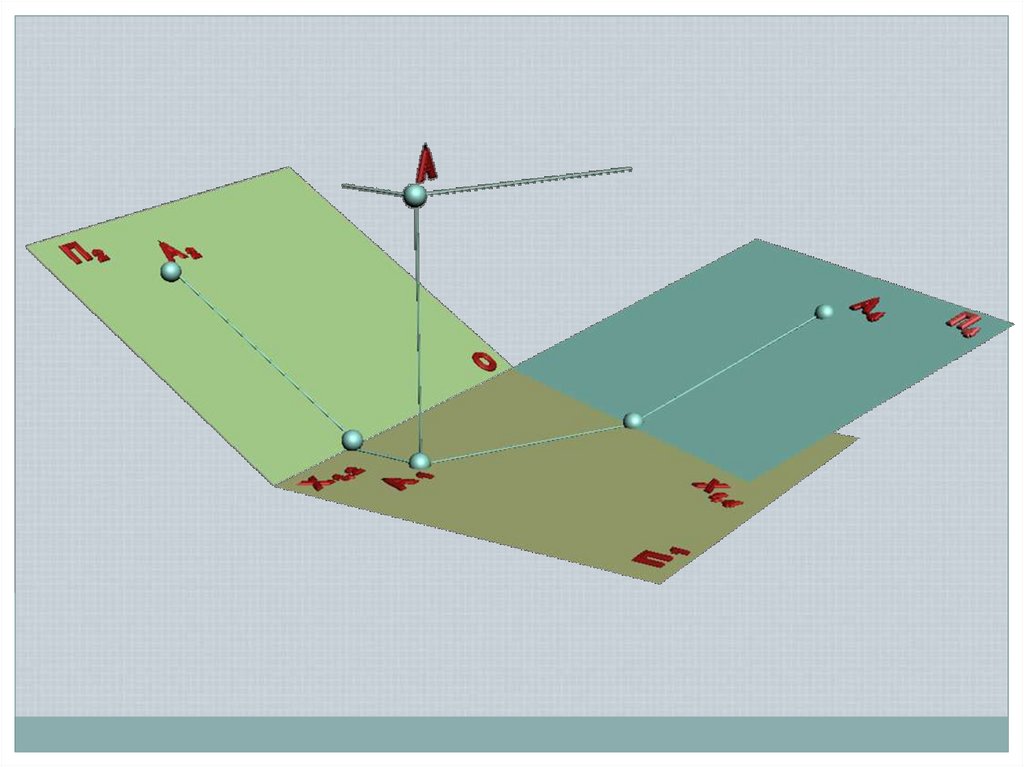
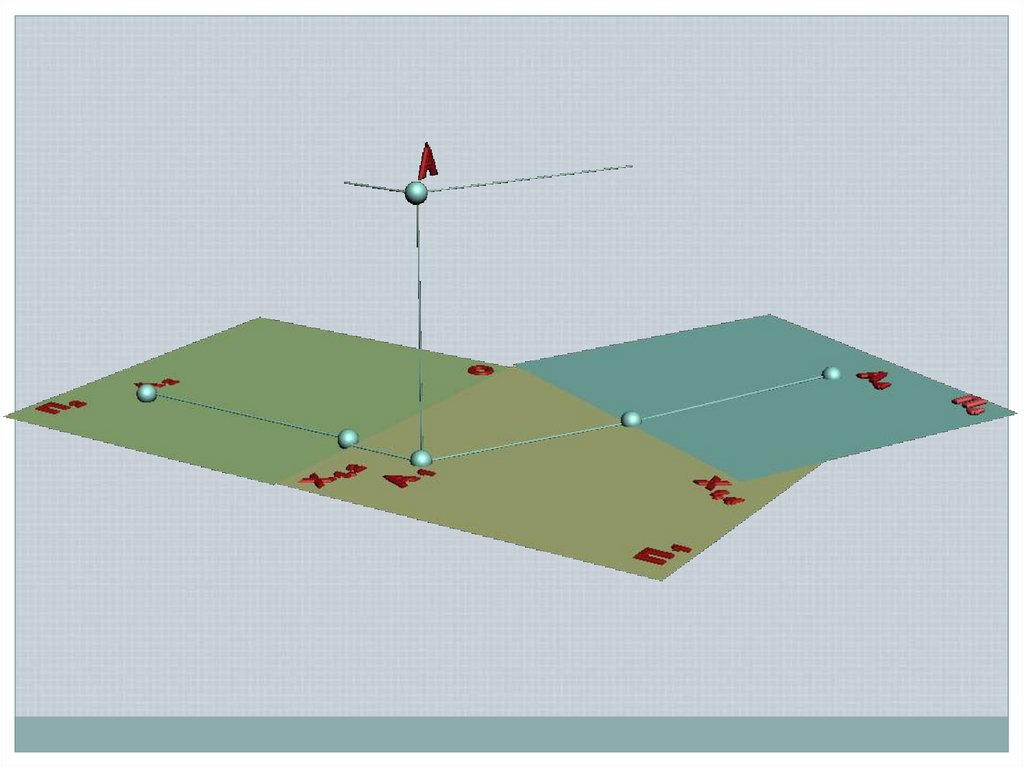
Способы задания прямой в пространстве:
Двумя ее проекциями
B2
B
A2
0
A
A1
B1

4.

Определение длины
отрезка прямой линии
и
углов наклона прямой
к плоскостям проекций

5.

Натуральная величина отрезка прямой
Пi
Способ прямоугольного треугольника
Дано:
[АВ] ; [АiBi]; [AjBj]
Теорема:
Натуральная величина отрезка
АВ равна гипотенузе
прямоугольного треугольника,
одним катетом которого является
любая проекция АiВi отрезка,
а другим катетом служит
разность k = kB – kA = Вj хi,j –
Aj xi,j расстояний концов другой
проекции AjВj до оси хi,j,
разделяющей эти две проекции.
Угол между проекцией АiВi
и гипотенузой (натуральной
величиной АВ ) равен углу оi
наклона отрезка АВ к плоскости
П i и к проекции АiВi

6.

Доказательство:
АВI ll AiBi; BBI АВI
[АВ] – натуральная величина
(гипотенуза)
АВI= AiBi (1катет)
kA = ВiВI kB = ВiВ
k = kB – kA = ВIВ
k = kB – kA = Вj хi,j – Aj хi,j
ВАВI = ВСBi
Пi

7.

[АВ] – натуральная
величина (гипотенуза)
B2
A0
zAB
A2
х
B1
A1
zAB
B0
α - угол наклона
отрезка АВ
к плоскости П1
и к проекции А1В1
β - угол наклона
отрезка АВ
к плоскости П2
и к проекции А2В2

8.

Следы прямой

9.

B2
N≡N2
A0
N – фронтальный след
прямой АВ
A2
х
C2
N1
B1
A1
С≡С1
С – горизонтальный след
прямой АВ
B0

10.

Положение прямой
относительно
плоскостей проекций

11.

Положение прямых в пространстве (относительно плоскостей проекций)
на комплексном чертеже
определяют их графические признаки
Прямые
общего положения
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
частного положения
Уровня
параллельны
одной из плоскостей
проекций
B2
B
A2
Ax
A
A1
Вx
B2
B
A2
A
B0
Ax
B1
А1В1 = АВ cosα
Вx
Проецирующие
перпендикулярны
одной из плоскостей
проекций
C2
C
D2
D
B1
A1
= 0; АВ||П1
0
C1≡D1
= 90o

12.

Линии уровня

13.

Линией уровня или
«уровенной» прямой
называется линия,
параллельная одной
из плоскостей проекций
Линия уровня и плоскость,
которой она параллельна,
имеют одинаковые названия
(имена)
Пi
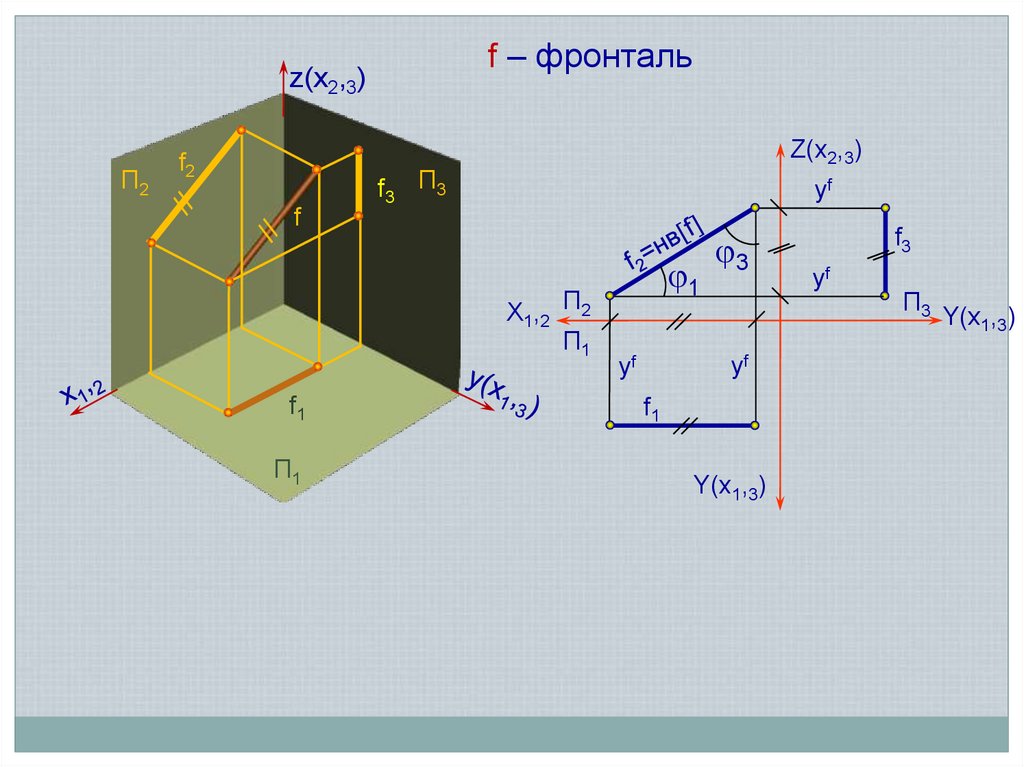
Метрические свойства:
Длина одноименной проекции отрезка прямой равна длине
самого отрезка [АВ] = [АiВi],
а угол оj наклона одноименной проекции отрезка [АiВi]
к оси хi,j равен углу о наклона самого отрезка [АВ]
к разноименной плоскости проекций j

14.

h – горизонталь
z(х2,3)
Z(х2,3)
h3
h2
h3
h2
h
h1
П2
Zh
П3
П1
Y(х1,3)
Zh
Х1,2
Zh
Zh
2 3
Y(х1,3)

15.

f – фронталь
z(х2,3)
П2
f2
Z(х2,3)
f 3 П3
yf
f
Х1,2 П2
П1
f1
П1
1
3
yf
yf
f1
Y(х1,3)
f3
yf
П3
Y(х1,3)

16.

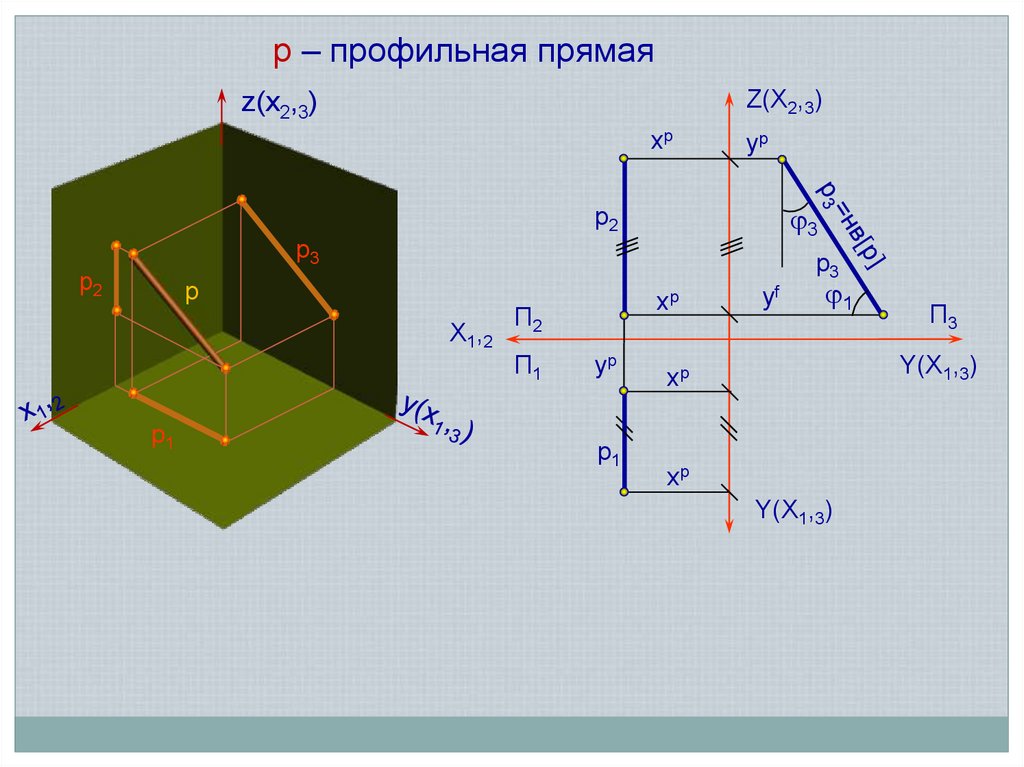
р – профильная прямая
Z(Х2,3)
z(х2,3)
хр
р3
р
Х1,2
р1
3
р2
р3
р2
yр
хр
П2
П1
yр
р1
yf
1
П3
Y(Х1,3)
хр
хр
Y(Х1,3)

17.

z(х2,3)
nj
ni
n
nq
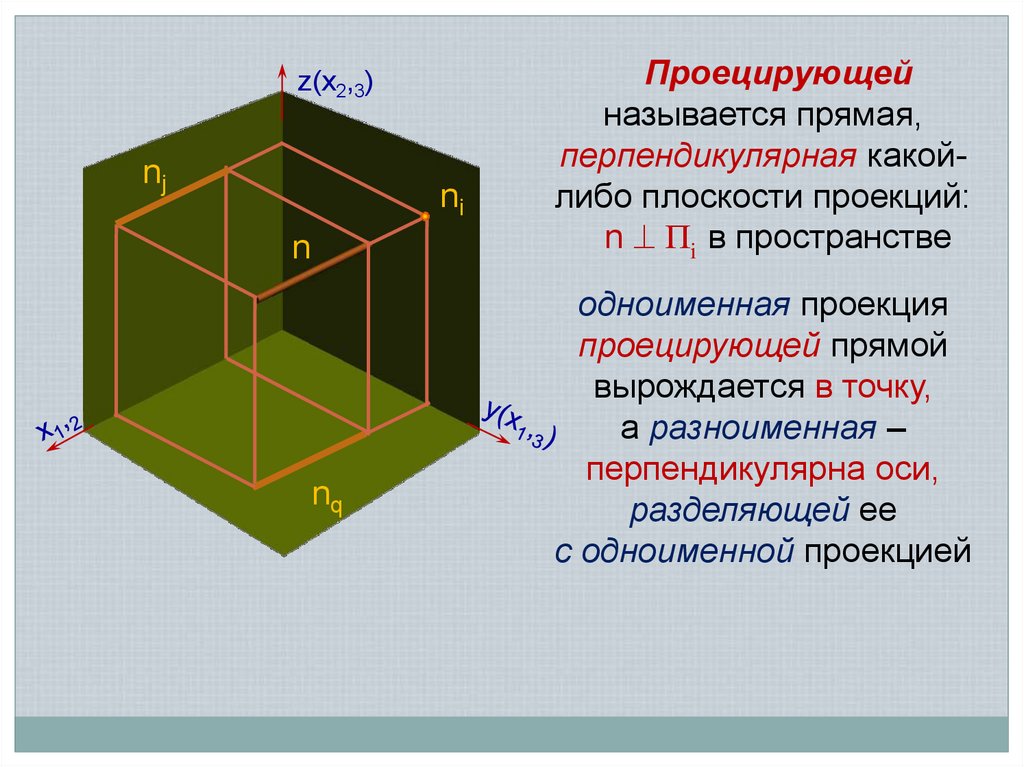
Проецирующей
называется прямая,
перпендикулярная какойлибо плоскости проекций:
n Пi в пространстве
одноименная проекция
проецирующей прямой
вырождается в точку,
а разноименная –
перпендикулярна оси,
разделяющей ее
с одноименной проекцией

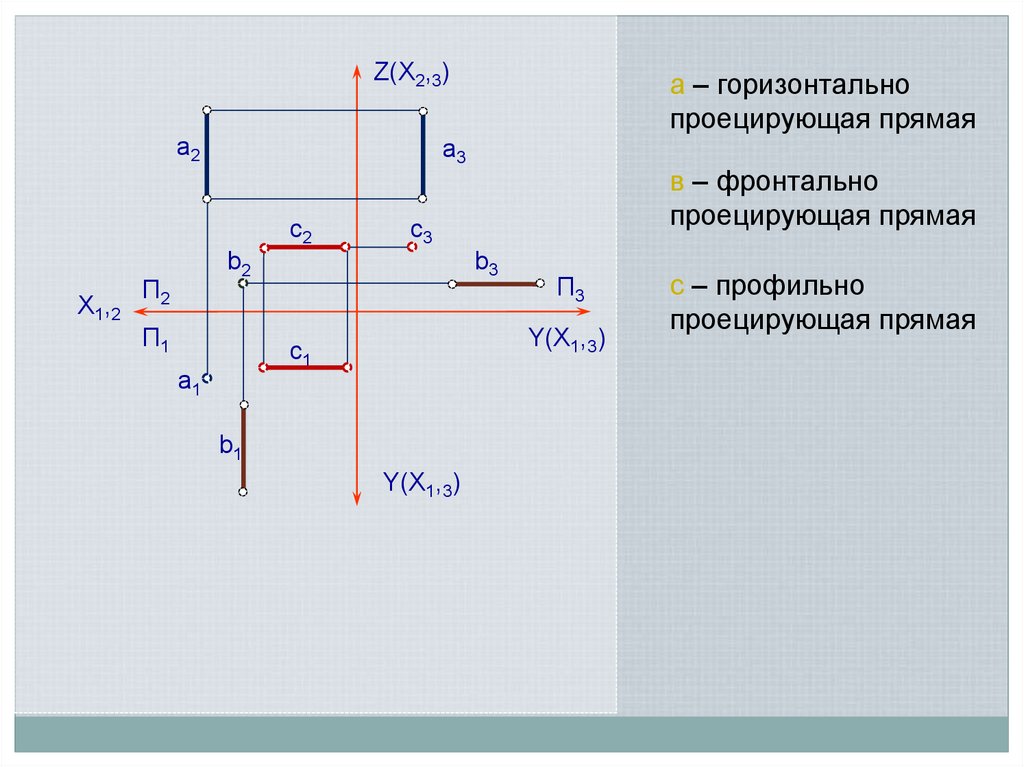
18.

Z(Х2,3)
а2
а3
c2
Х1,2
П1
b3
П3
Y(Х1,3)
c1
а1
в – фронтально
проецирующая прямая
c3
b2
П2
а – горизонтально
проецирующая прямая
b1
Y(Х1,3)
с – профильно
проецирующая прямая

19.

Взаимное расположение двух прямых

20.

Пересекающиеся прямые
Графический признак: (a ∩ b = K) (ai ∩ bi = Ki), (aj ∩ bj = Kj),
Ki Kj xi,j, т.е. если две прямые a и b пересекаются в точке K,
то проекции Ki и Kj этой точки принадлежат одноименным проекциям
пересекающихся прямых и, следовательно, лежат на линии
проекционной связи KiKj xi,j между этими проекциями

21.

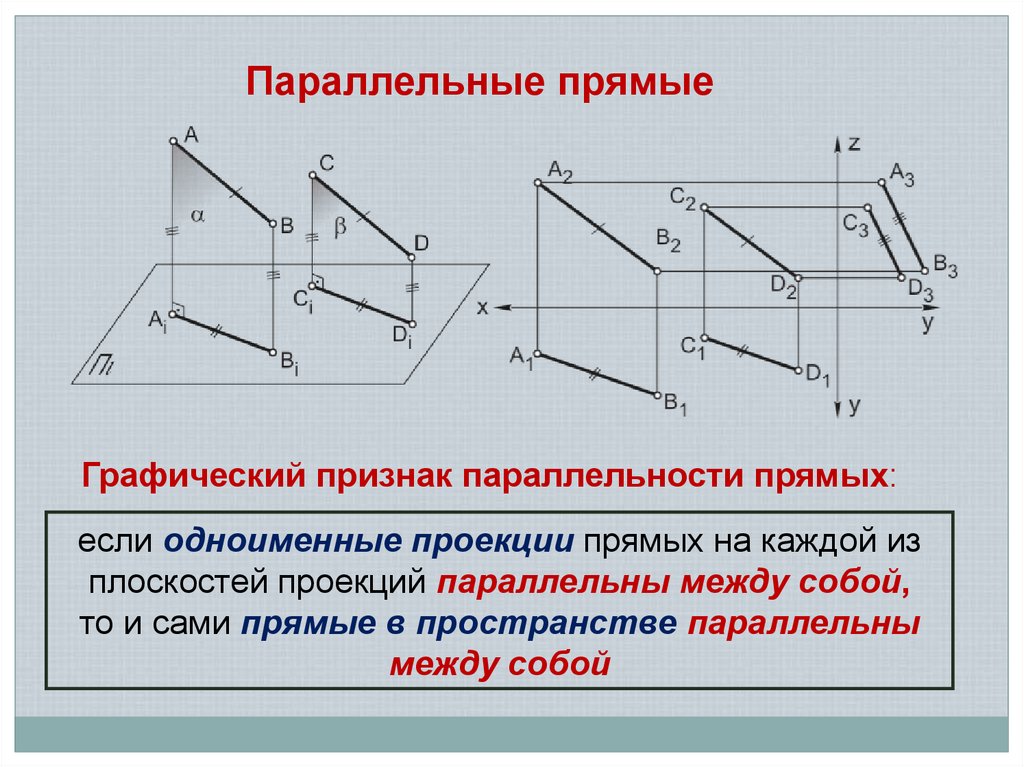
Параллельные прямые
Графический признак параллельности прямых:
если одноименные проекции прямых на каждой из
плоскостей проекций параллельны между собой,
то и сами прямые в пространстве параллельны
между собой

22.

Скрещивающиеся прямые
Графический признак скрещивающихся прямых:
признак основан на невыполнении признаков параллельности или
пересечения таких прямых.
Точки пересечения одноименных проекций на смежных
плоскостях не лежат на линии их проекционной связи, а
параллельность проекций может иметь место только на одной из
плоскостей проекций

23.

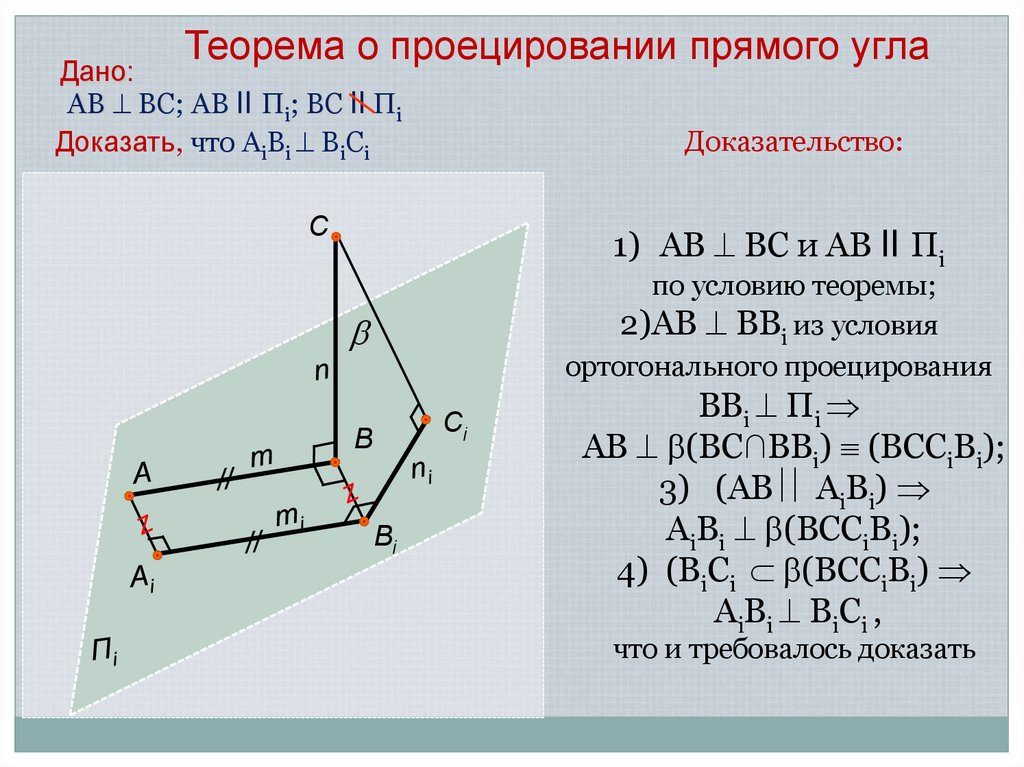
Теорема о проецировании прямого угла
Дано:
АВ ВС; АВ ll Пi; ВС ll Пi
Доказать, что АiВi ВiСi
Доказательство:
С
1) АВ ВС и АВ ll Пi
по условию теоремы;
2)АВ ВВi из условия
ортогонального проецирования
Сi
В
Вi
ВВi Пi
АВ (ВС∩ВВi) (ВССiВi);
3) (АВ АiВi)
АiВi (ВССiВi);
4) (ВiСi (ВССiВi)
АiВi ВiСi ,
что и требовалось доказать

24.

Способы задания плоскости

25.

Плоскость, произвольно расположенная
в пространстве, называется плоскостью
общего положения
Набор параметров,
выделяющих единственную плоскость,
называется ее
определителем (∆)

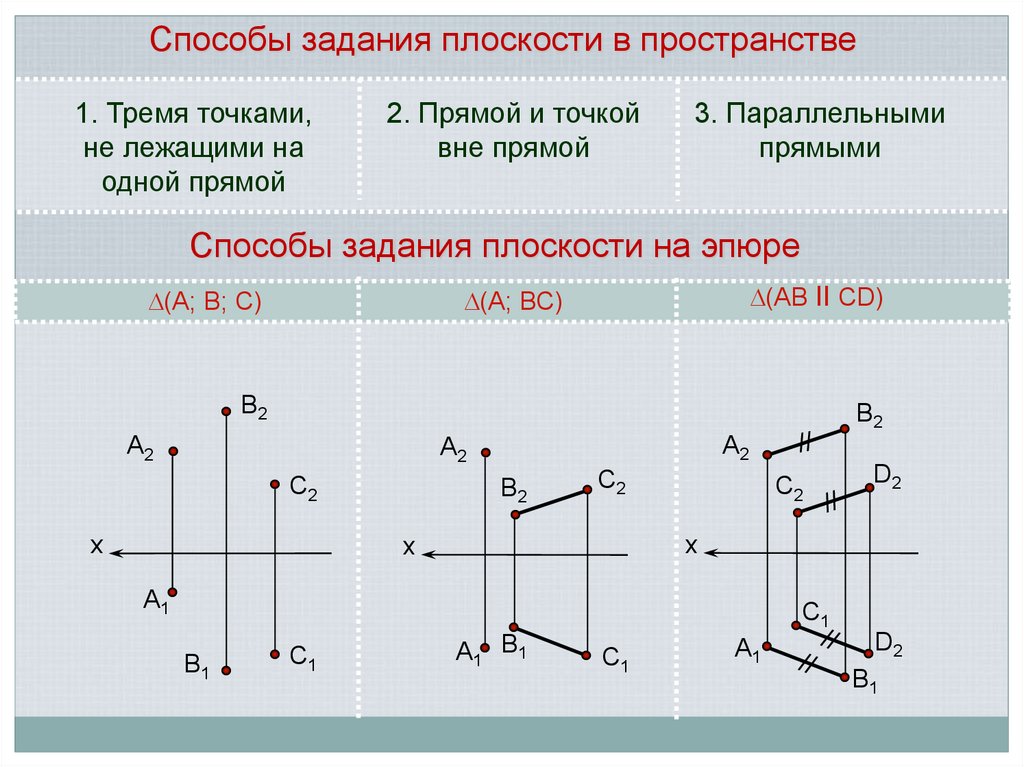
26.

Способы задания плоскости в пространстве
1. Тремя точками,
не лежащими на
одной прямой
2. Прямой и точкой
вне прямой
3. Параллельными
прямыми
Способы задания плоскости на эпюре
(АВ ll СD)
(А; ВС)
(А; В; С)
В2
А2
А2
А2
С2
х
В2
С2
С2
А1
В1
D2
х
х
С1
В2
А1 В1
С1
С1
А1
D2
В1

27.

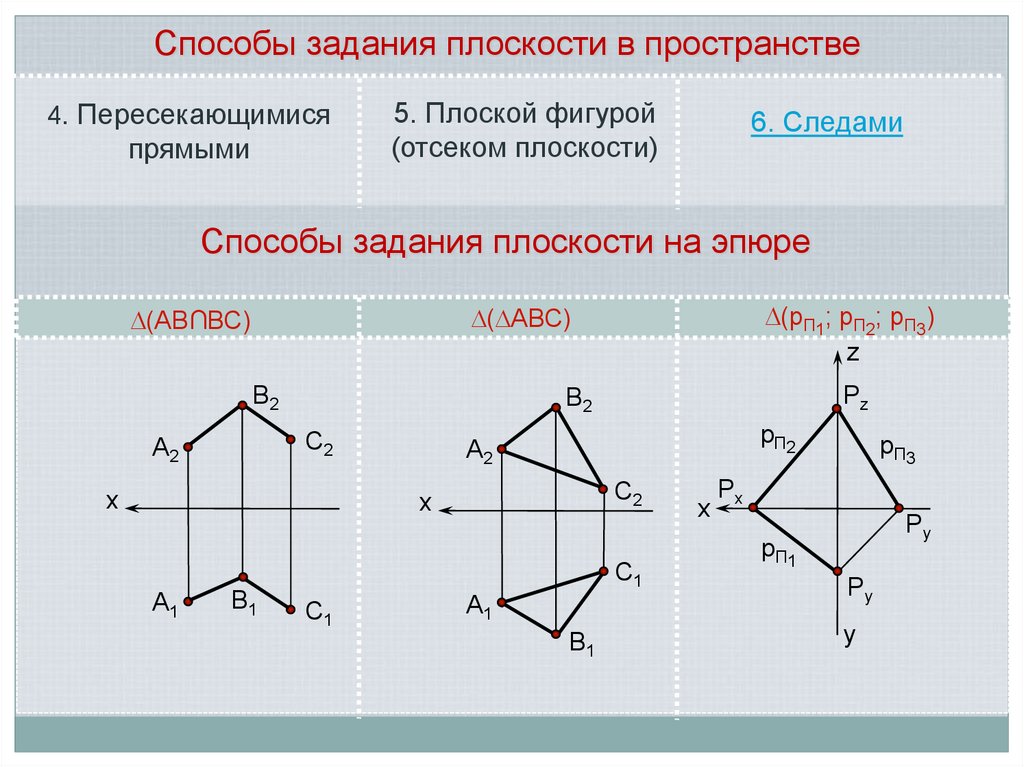
Способы задания плоскости в пространстве
4. Пересекающимися
прямыми
5. Плоской фигурой
(отсеком плоскости)
6. Следами
Способы задания плоскости на эпюре
В2
В2
С2
А2
х
В1
С1
Pz
pП2
А2
С2
х
А1
(рП1; рП2; рП3)
z
( АВС)
(
АВС)
(АВ∩ВС)
(АВ BС)
С1
А1
В1
х
pП3
Px
Py
pП1
Py
y

28.

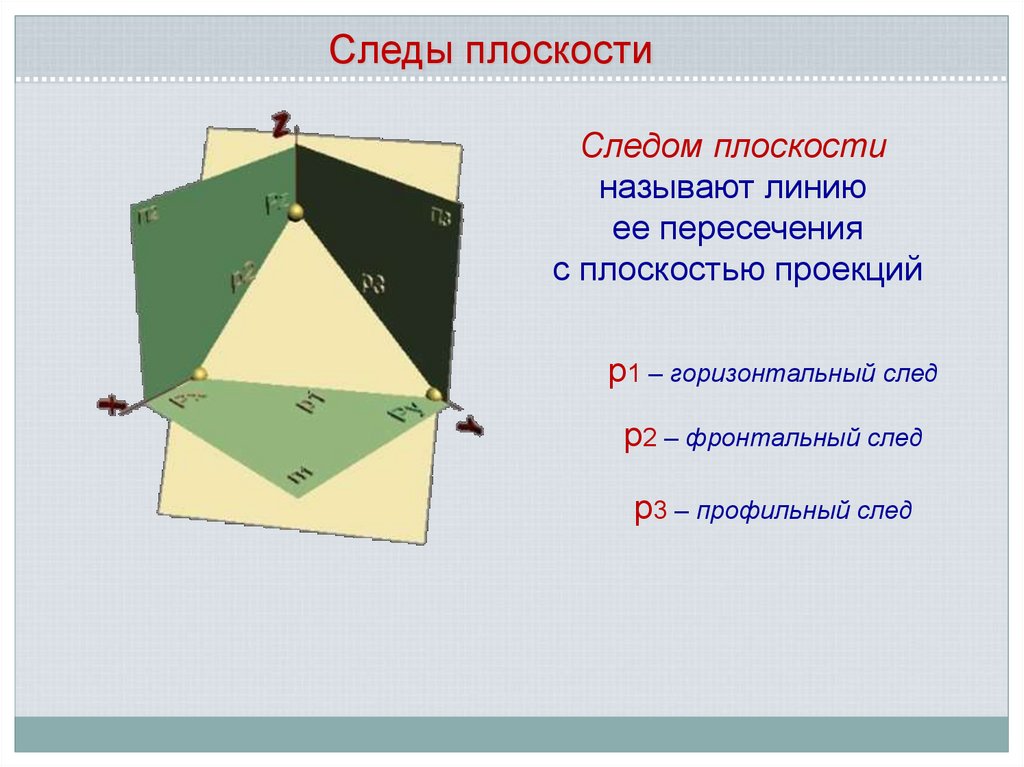
Следы плоскости
Следом плоскости
называют линию
ее пересечения
с плоскостью проекций
р1 – горизонтальный след
р2 – фронтальный след
р3 – профильный след

29.

Положение плоскости
относительно
плоскостей проекций

30.

Плоскости частного положения

31.

Проецирующие плоскости
Плоскость, перпендикулярная к плоскости
проекций, называется проецирующей
Особенности
проецирующих плоскостей:
– одна проекция любого элемента, расположенного
– в проецирующей плоскости, совпадает
с соответствующим следом этой плоскости
– угол наклона заданной плоскости к плоскости
проекций на эпюре проецируется в натуральную
величину

32.

Горизонтально – проецирующая плоскость
П1
( АВС)∈ ;
П1; 1≡ 1
Угол наклона к П2
П2
П2
B
A
П2
П1
x
( АВС) П1
В2
C
П1 A1 С1
x
x
0
А2
B1
С2
х
П1
С1
А1
В1

33.

Фронтально – проецирующая плоскость
П2
( АВС)∈ ;
П2; 2≡ 2
П2
A2
B2
Угол наклона к П1
П2
x
x
П1
A
( АВС) П2
С2
2
x
C
П2
С2
В2
0
А2
B
П1
х
П1
С1
А1
В1

34.

Профильно – проецирующая плоскость
П2
z
П3
П3; ( АВС) П3; П3≡ 3
x
П1
П2
П2
A3 П3
С1
0 3
B1
П
3
x
B
П1
П1
= П2
= П1
у
( АВС) П3
A
C
у
z
В2
А2
А3
С3
С2
х
В3
В1
А1
С1
y

35.

Плоскости уровня
Плоскость,
параллельная к плоскости проекций,
называется плоскостью уровня
Особенности
плоскостей уровня:
– любая плоская фигура,
расположенная в плоскости уровня,
проецируется на параллельную ей плоскость проекций
без искажения, – т.е. в натуральную величину

36.

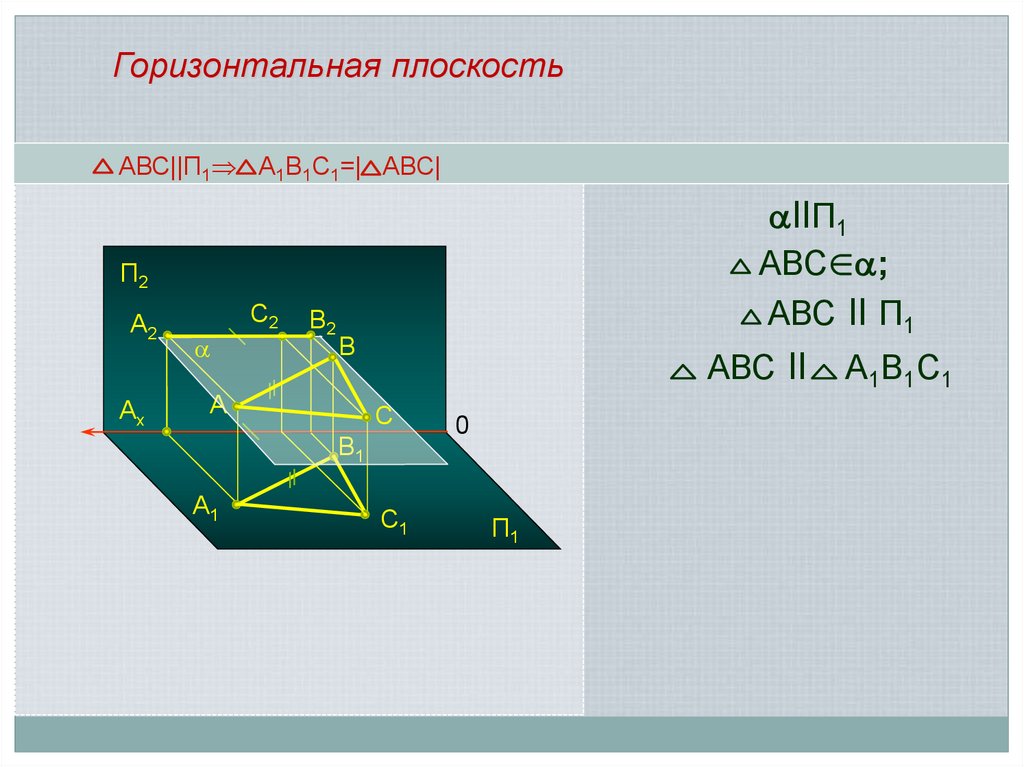
Горизонтальная плоскость
АВС||П1 А1В1С1=| АВС|
llП1
АВС∈ ;
АВС ll П1
П2
A2
Ax
С2
B2
B
A
АВС ll
С
B1
A1
С1
0
П1
А1В1С1

37.

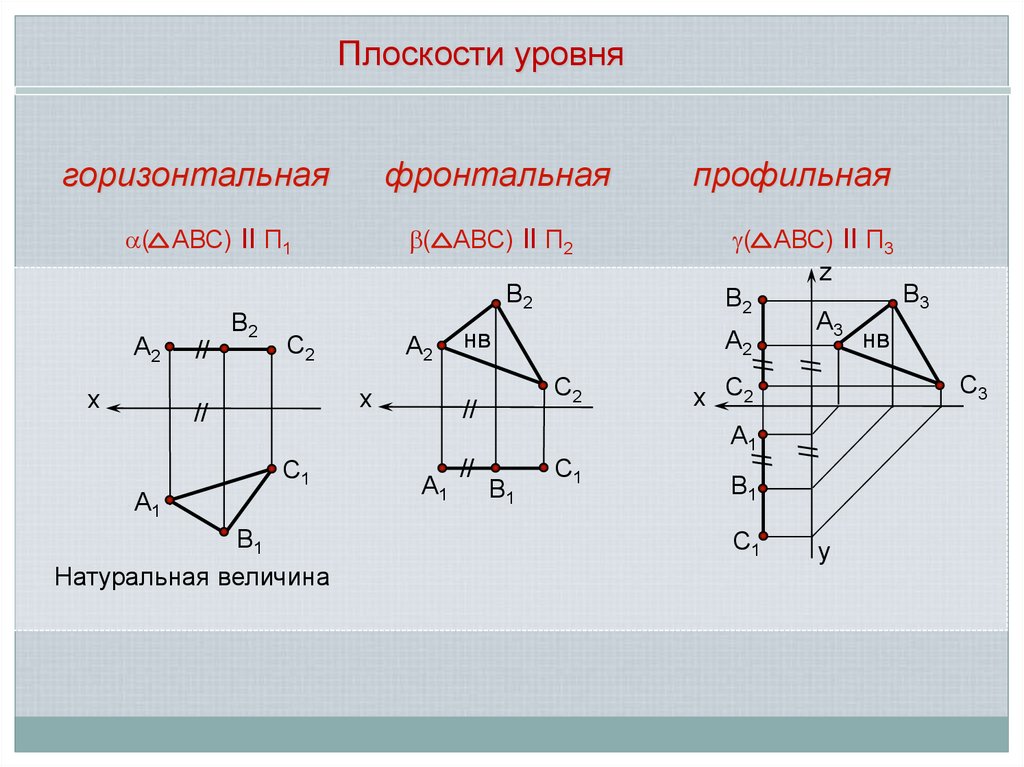
Плоскости уровня
горизонтальная
фронтальная
( АВС) ll П1
( АВС) ll П2
А2
х
//
В2
В2
С2
х
//
А1
А2
С1
В1
Натуральная величина
нв
С2
//
А1
//
В1
С1
профильная
( АВС) ll П3
z
В3
В2
А3
нв
А2
С3
х С2
А1
В1
С1
y

38.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ПРЯМЫХ И ПЛОСКОСТЕЙ,
ДВУХ ПЛОСКОСТЕЙ

39.

Прямая и точка в плоскости
В2
22
А2
12
D2
Прямая принадлежит плоскости,
если она проходит через две
точки, принадлежащие плоскости
l2
С2
х
С1
11
А1
D1
21
В1
l1
Точка лежит в плоскости, если
она лежит на прямой,
расположенной в данной
плоскости

40.

Главные линии плоскости
В2
22
А2
х
А1
2
//
//
//
f2
12 h
K2
С2
K1
С1
21
В1
11
f1
h1
h ll П1; h ABC
f ll П2; f ABC
f ll П2; BK f; f1 ll x;
В2К2 f2; ВК ABC
ВК – линия наибольшего наклона

41.

Прямая, параллельная плоскости
Прямая параллельна плоскости, если она параллельна какой-либо
прямой, принадлежащей плоскости
a2
α (m∩ n)
m
ℓ
a
12
n2
х
11
n
a1
n1
ℓ (m∩n) ; а ||ℓ, следовательно, ||а
m2
ℓ2
22
m1
ℓ1
21
а1|| ℓ1; а2|| ℓ2; а || (m ∩ n)

42.

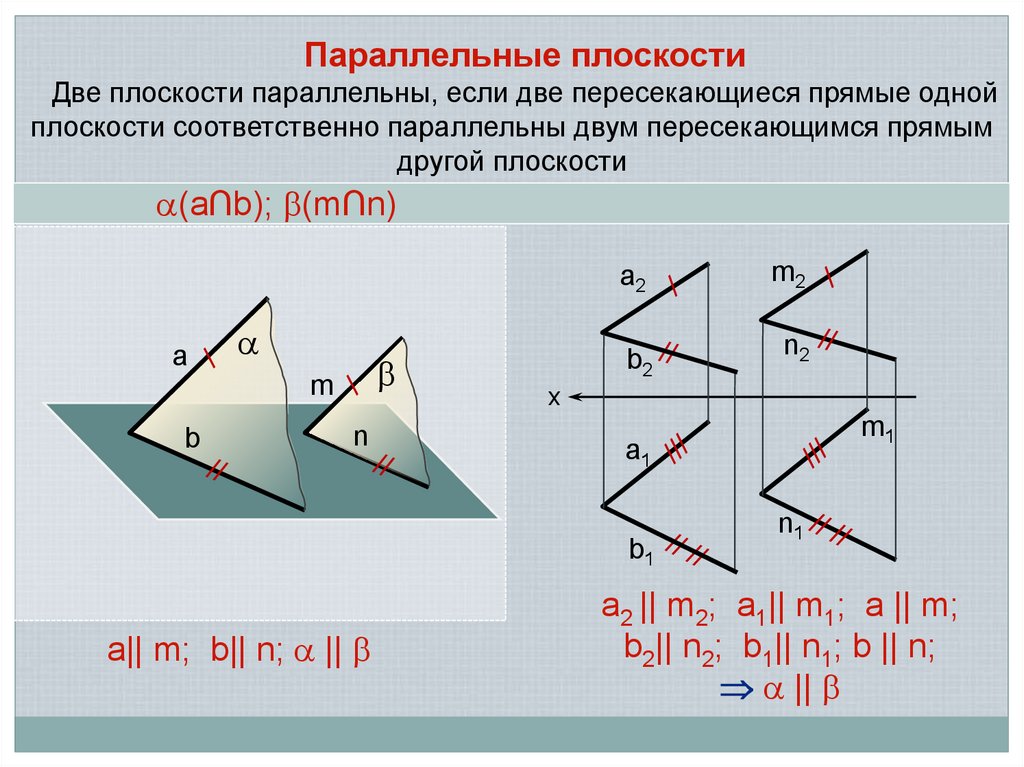
Параллельные плоскости
Две плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся прямым
другой плоскости
(а∩b); (m∩n)
a2
a
m
b
n
b2
n2
х
m1
a1
b1
а|| m; b|| n; ||
m2
n1
а2 || m2; a1|| m1; a || m;
b2|| n2; b1|| n1; b || n;
||

43.

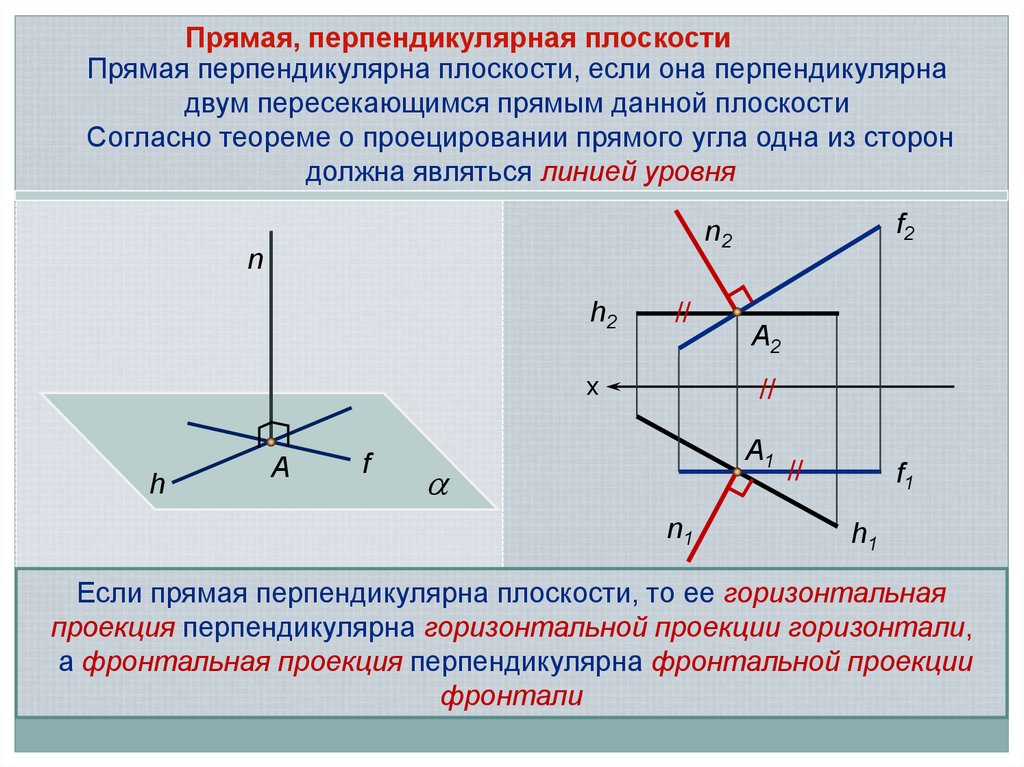
Прямая, перпендикулярная плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым данной плоскости
Cогласно теореме о проецировании прямого угла одна из сторон
должна являться линией уровня
n
h2
//
х
h
f2
n2
A
f
A2
//
A1
n1
//
f1
h1
Если прямая перпендикулярна плоскости, то ее горизонтальная
проекция перпендикулярна горизонтальной проекции горизонтали,
а фронтальная проекция перпендикулярна фронтальной проекции
фронтали

44.

Взаимно перпендикулярные плоскости
Построение взаимно перпендикулярных плоскостей основано
на одном из следующих положений:
K
П
h
L
f
; KL ; KL
1. Если прямая
перпендикулярна к какой-либо
плоскости, то всякая плоскость,
проведенная через эту прямую,
будет перпендикулярна первой
плоскости
2. Если плоскость
перпендикулярна к какой-либо
прямой другой плоскости,
эти плоскости взаимно
перпендикулярны

45.

Через прямую DЕ провести плоскость ,
перпендикулярную к плоскости ( АВС)
Задача
E2
n2
D2
х
D1
22
F2
А2
//
E1
n1
f2
12
//
F1
А1
( ABC);
В2
11
//
21 f1
В1
h2
С2
С1
h1
(DE EF);
h2 ll ox; h1 n1;
f1 ll ox; f2 n2

46. Преобразование комплексного чертежа

47.

Способ
замены плоскостей
проекций
Геометрический объект в
пространстве остается
неподвижным,
изменяет положение аппарат
проецирования
Способ
вращения
Геометрический объект
изменяет свое положение
в пространстве, аппарат
проецирования
остается неподвижным

48. Cпособ замены плоскостей проекций

Cпособ
замены плоскостей проекций
4 основные задачи

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61.

62.

63.

64.

65.

66.

67.

68.

69.

70.

71.

72.

А2
zA
s
s
s
Х1,2
П2
П1
А1
s
s
Заменяемая
плоскость
АХ1,2
Рабочая
плоскость
Новая
плоскость

73.

//
х
//
//
//
При переходе
к новой системе плоскостей
одну из плоскостей заменяют
так, чтобы геометрический
элемент занял частное
положение
Вновь вводимая плоскость
должна быть
перпендикулярна оставшейся
плоскости
Направление проецирования
к новой плоскости должно
быть ортогональным
Натуральная
величина

74.

75.

76.

77.

78.

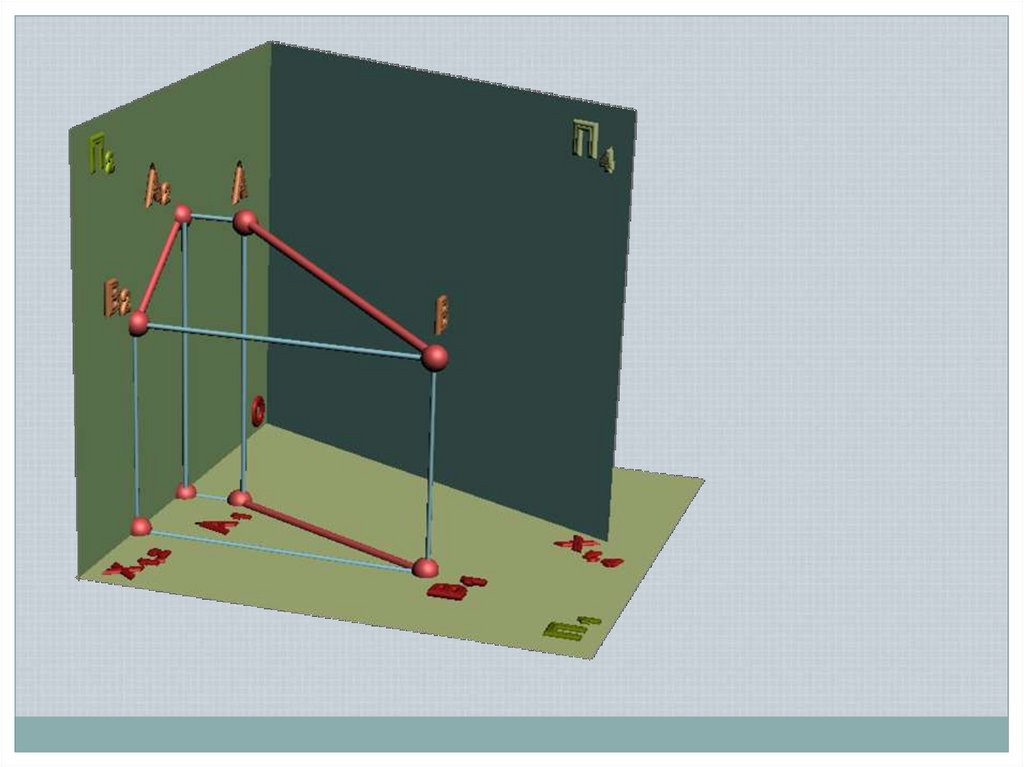
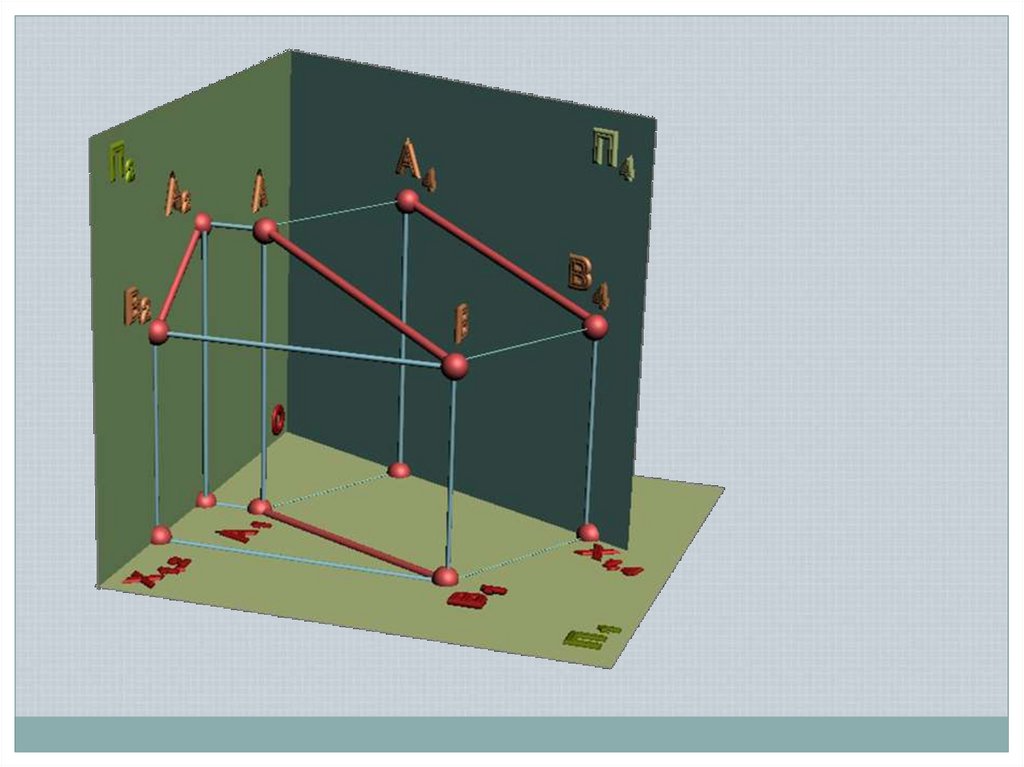
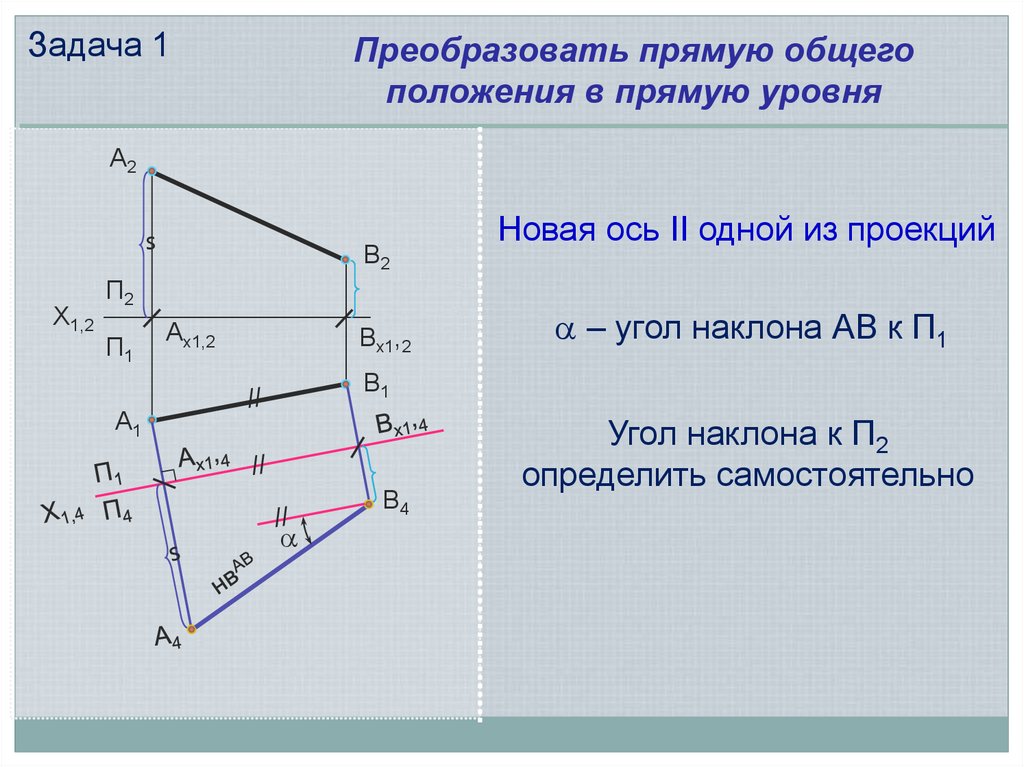
Задача 1
Преобразовать прямую общего
положения в прямую уровня
А2
s
Х1,2
В2
П2
П1
Ах1,2
Вх1,2
Новая ось ІІ одной из проекций
– угол наклона АВ к П1
В1
А1
В4
Угол наклона к П2
определить самостоятельно

79.

Задача 2
А2
Преобразовать прямую уровня
в проецирующую прямую
h2
Новая ось
одноименной проекции
линии уровня
В2
Х1,4 h1
П2
Х1,2
П1
А1
Х2,5 f2
h1
В1
П1 П
4
Х1,4
А4≡ В4

80.

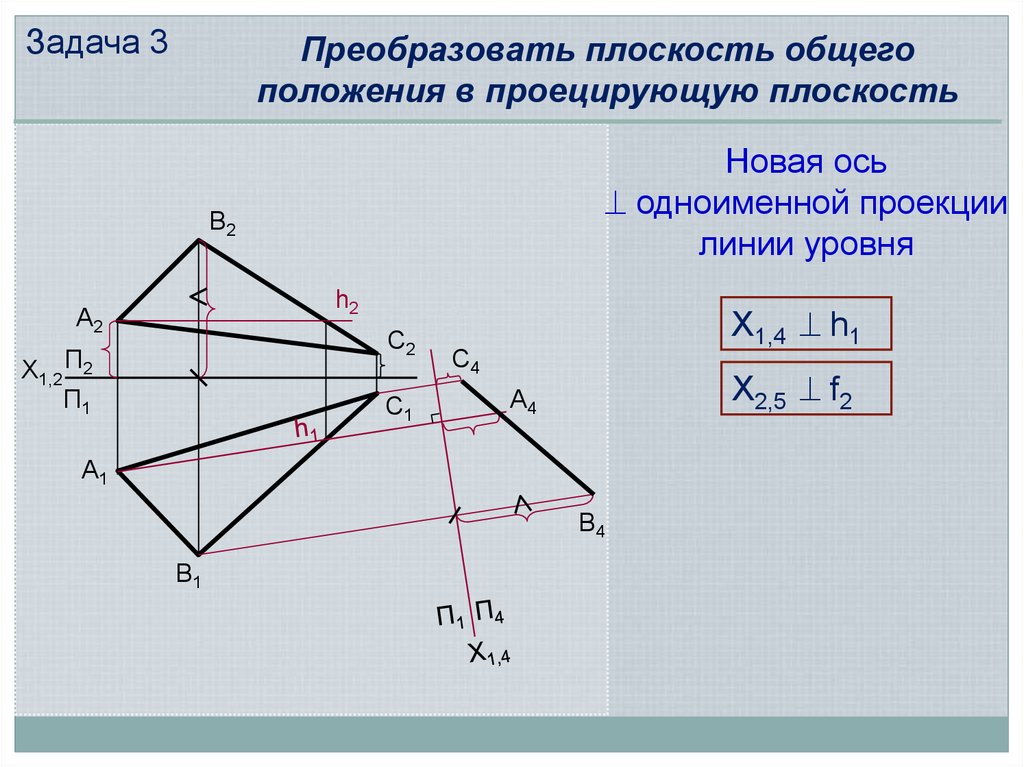
Задача 3
Преобразовать плоскость общего
положения в проецирующую плоскость
Новая ось
одноименной проекции
линии уровня
В2
h2
А2
С2
Х1,2 П2
П1
С1
Х1,4 h1
С4
Х2,5 f2
А4
А1
В4
В1

81.

Задача 4
Преобразовать проецирующую
плоскость в плоскость уровня
В5
А5
нв
С5
А2
Х2,1
В2
П2
П1
С2
А1
С1
В1
новая плоскость ll следу

82.

10 задач,
которые можно
решить методом
замены
плоскостей
проекций:

83.

1. Определение натуральной величины отрезка
(см. основную задачу 1)
2. Определение расстояния от точки до прямой
(прямую преобразовать в проецирующую)
3. Определение расстояния между
параллельными прямыми
(прямые преобразовать в проецирующие)
4. Определение величины двугранного угла
(общее ребро преобразовать в
проецирующую прямую)
5. Определение расстояния между скрещивающими
прямыми
(одну из прямых преобразовать в проецирующую)

84.

6. Определение расстояния от точки до плоскости
(плоскость преобразовать в след)
7. Определение расстояния между параллельными
плоскостями
(обе плоскости преобразовать в след)
8. Определение натуральной величины плоской
фигуры
(см. основную задачу 4 )
9. Определение угла наклона прямой к плоскости
(см. основную задачу 1 )
10. Определение угла наклона плоскости
к плоскостям проекций
(см. основную задачу 3 )

85.

Способ вращения вокруг оси,
перпендикулярной плоскости
проекций

86.

Вращение точки вокруг горизонтально
проецирующей оси
П2
A2
i2
k2
02
i
k2
A2
k
A
i1
A1
01
x
A
0
x
i2 A
2
i П1
A1
0
i1
A1
01
k1
П1
k1
При вращении точки вокруг горизонтально проецирующей оси ее
горизонтальная проекция перемещается по окружности с центром в
точке, являющейся проекцией оси вращения, а ее фронтальная
проекция перемещается по прямой, перпендикулярной фронтальной
проекции оси вращения

87.

Вращения точки вокруг фронтально
проецирующей оси
Определить натуральную
величину отрезка прямой АВ
i П2
i П2
A2
k2
02
В2
А2
i2
i2
А2
x
x
В1
01
A1 i
1
k1
А1
А1
i1

88.

Задача
A2
12
A2
натуральную величину
плоскости общего
положения
f2
C2
12
f2
i2
B2
C2
//
A1
A1
f1
//
11
B1
i1
C1
C1
Определить

89.

A2
12
C2
нвАВС
f2
A2
12
f2
C2
j2
i
B2 2
//
B2
A1 ≡j1
A1
f1
//
11
В1
B1
i1
C1
C1
C2
C1