Математическая логика-1

1. Математическая логика

1
Математическая
логика
Урок 1. Логические высказывания. Логические
операции. Приоритет логических операций

2.

Логика
Аристотель (384-322 до н.э.).
Основоположник формальной логики (понятие,
суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую
область науки - Математическую логику
(Булеву алгебру или Алгебру высказываний).
Клод Шеннон (1916-2001). Его
исследования позволили применить алгебру
логики в вычислительной технике

3.

Логическое высказывание
Логическое высказывание – это повествовательное
предложение, относительно которого можно однозначно
сказать, истинно оно или ложно.
В
русском
языке
высказывания
выражаются
повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Но не всякое повествовательное предложение является
высказыванием.
Побудительные
и
вопросительные
предложения
высказываниями не являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?

4.

Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У треугольника 5 сторон.
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание

5. Логика и компьютер

5
Логика и компьютер
двоичная логика
! Любое высказывание может быть ложно (0)
или истинно (1).
Логика изучает операции между 0 и 1!
! Связь с двоичным кодированием!
Алгебра логики — это математический
аппарат, с помощью которого
записывают, упрощают и преобразуют
логические высказывания, вычисляют
их значения.
Алгебра высказываний,
булева алгебра

6. Простые и составные высказывания

6
Простые и составные высказывания
A – Сейчас идет дождь.
B – Форточка открыта.
}
простые
высказывания
(элементарные)
Составные высказывания строятся из простых с
помощью логических связок (операций) «и», «или»,
«не», «если…то….», «тогда и только тогда»
AиB
A или не B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
А В
Если идет дождь, то форточка открыта.
А В
Дождь идет тогда и только тогда, когда
форточка открыта.

7. Операция НЕ (инверсия)

7
Логические операции
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
А
не А
0
1
1
0
Обозначения: НЕ, ¬ , ¯

8. Операция И (логическое умножение, конъюнкция)

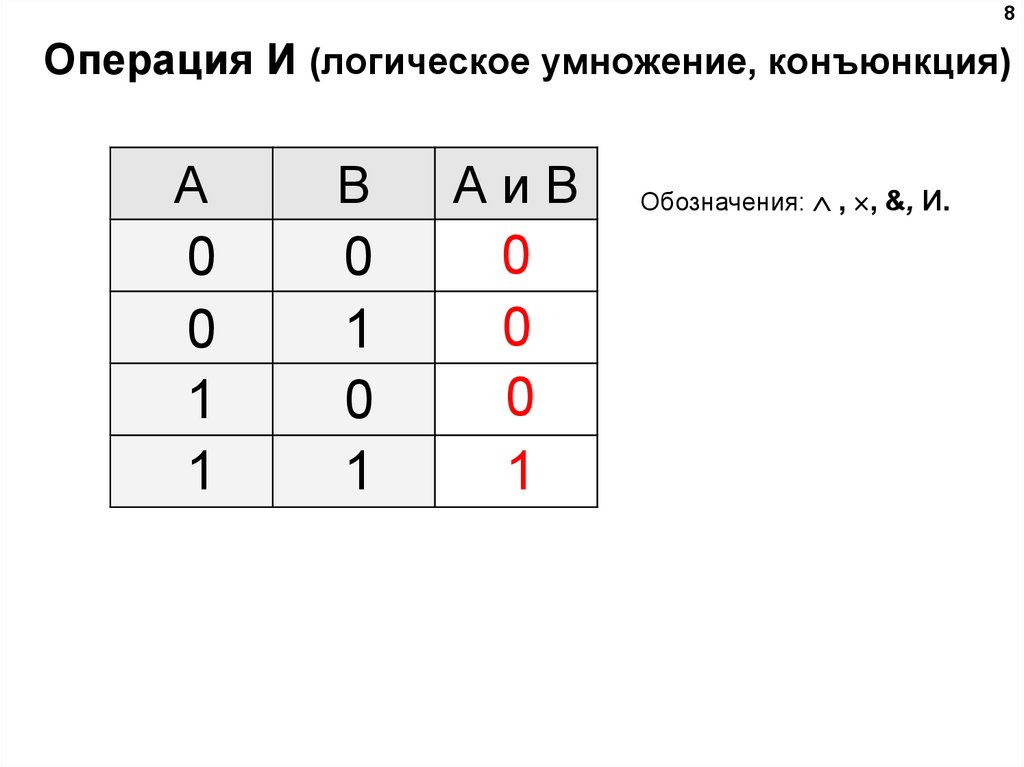
8
Операция И (логическое умножение, конъюнкция)
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
Обозначения: , , &, И.

9. Операция ИЛИ (логическое сложение, дизъюнкция)

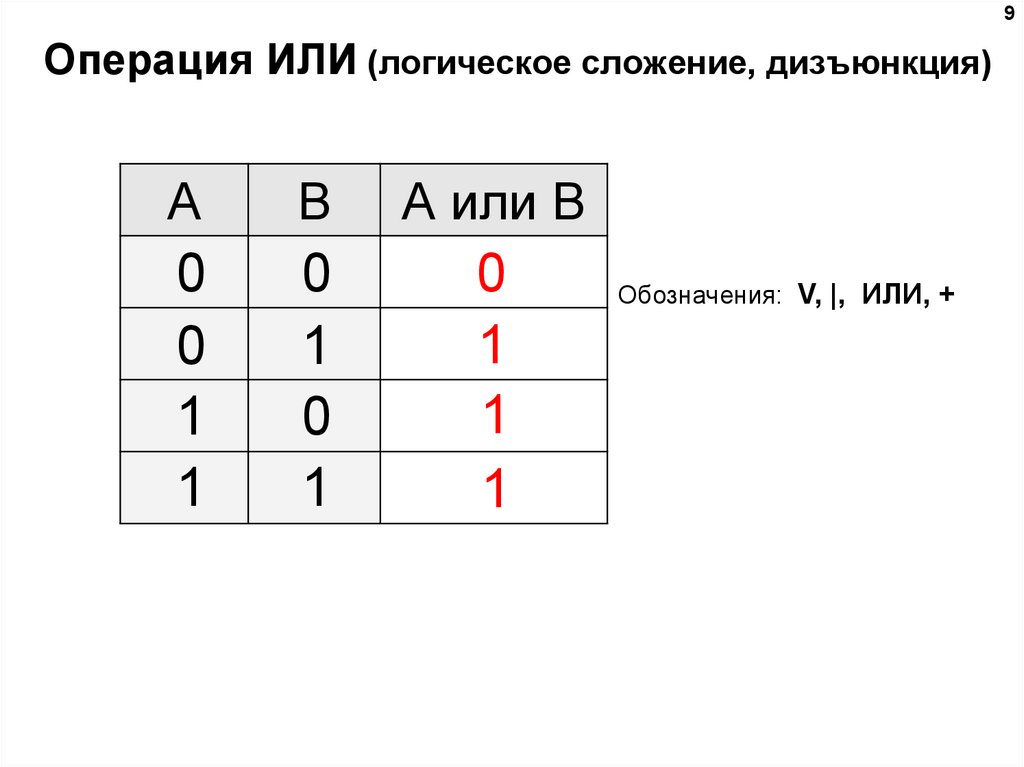
9
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
Обозначения: V, |, ИЛИ, +

10. Импликация (если…., то……)

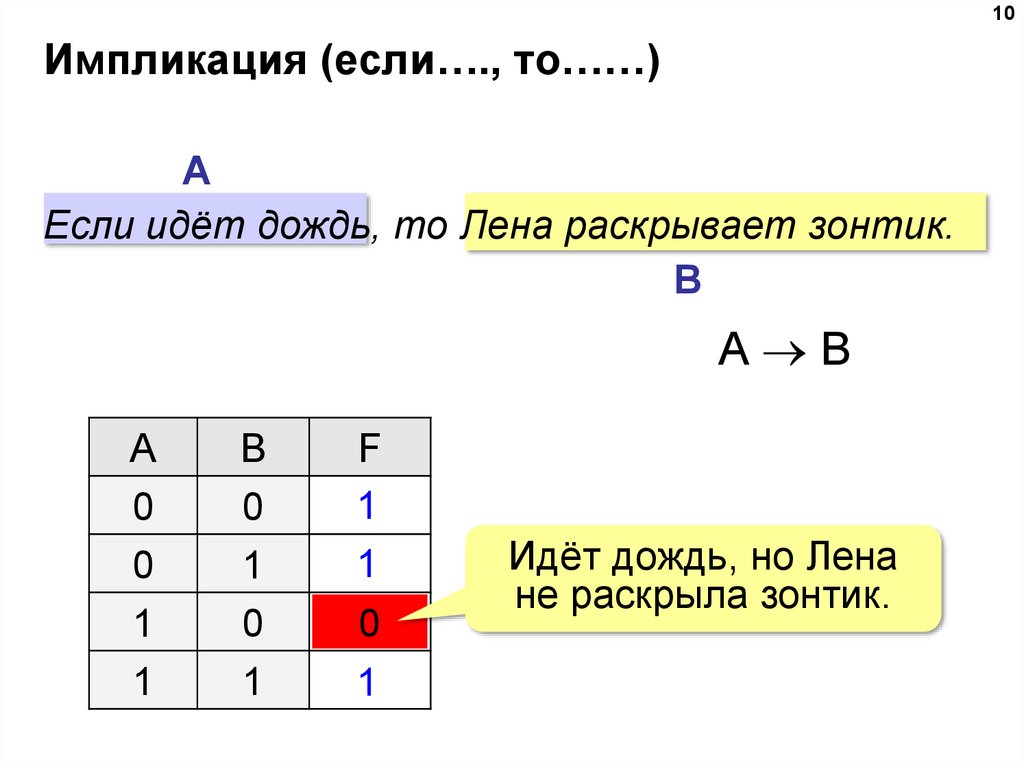
10
Импликация (если…., то……)
A
Если идёт дождь, то Лена раскрывает зонтик.
B
A B
A
0
0
1
1
B
0
1
0
1
F
1
1
0
1
Идёт дождь, но Лена
не раскрыла зонтик.

11. Эквиваленция (тогда и только тогда)

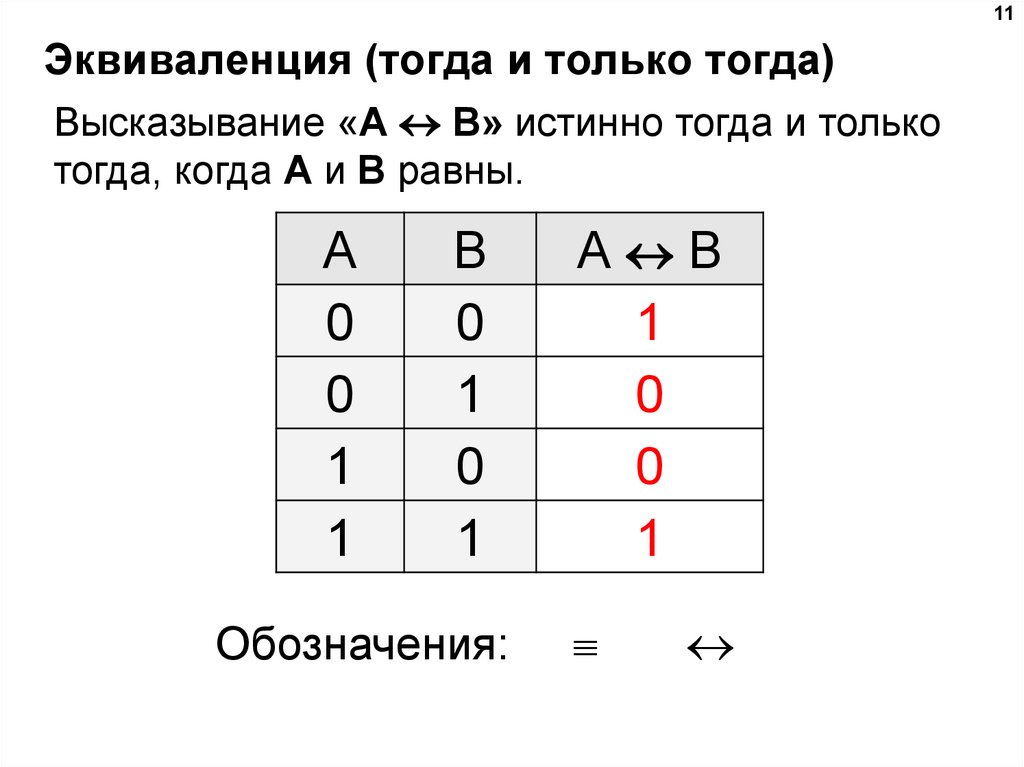
11
Эквиваленция (тогда и только тогда)
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
Обозначения:
А B
1
0
0
1

12. Порядок вычисления

Математическая логика, 9 класс
12
Логические выражения
Логические выражения – выражения, содержащие
логические переменные, скобки и знаки логических
операций
Порядок вычисления
• скобки
• НЕ
•И
• ИЛИ
• импликация
• эквиваленция
5
6
1 3
4 2
X A B (A B B )
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru