Лекция

1.

Галактионова Арина Владимировна
Ст. преподаватель каф. МиФМ
1

2.

Зачет: конспект лекций + задачи по
индивидуальным заданиям (не менее 7
задач по каждой теме)
Задачник:
Контрольно-измерительные материалы
по физике (КИМ) // Хатмуллина М.Т.,
Рабчук Л.В., Уфа, 2015 г.
С. 108-112.
2

3.

Механика
Кинематика:
описание движения в пространстве и времени
без учета причин, вызвавших это движение.
3

4.

Материальная точка – тело,
размерами которого в условиях данной задачи
можно пренебречь.
Система отсчета – совокупность неподвижных
относительно друг друга тел, по отношению к
которым рассматривается движение и
отсчитывается время.
Механическая система – совокупность тел,
выделенная для рассмотрения.
4

5.

Три типа механического движения:
1) поступательное,
2) вращательное,
3) колебательное.
5

6.

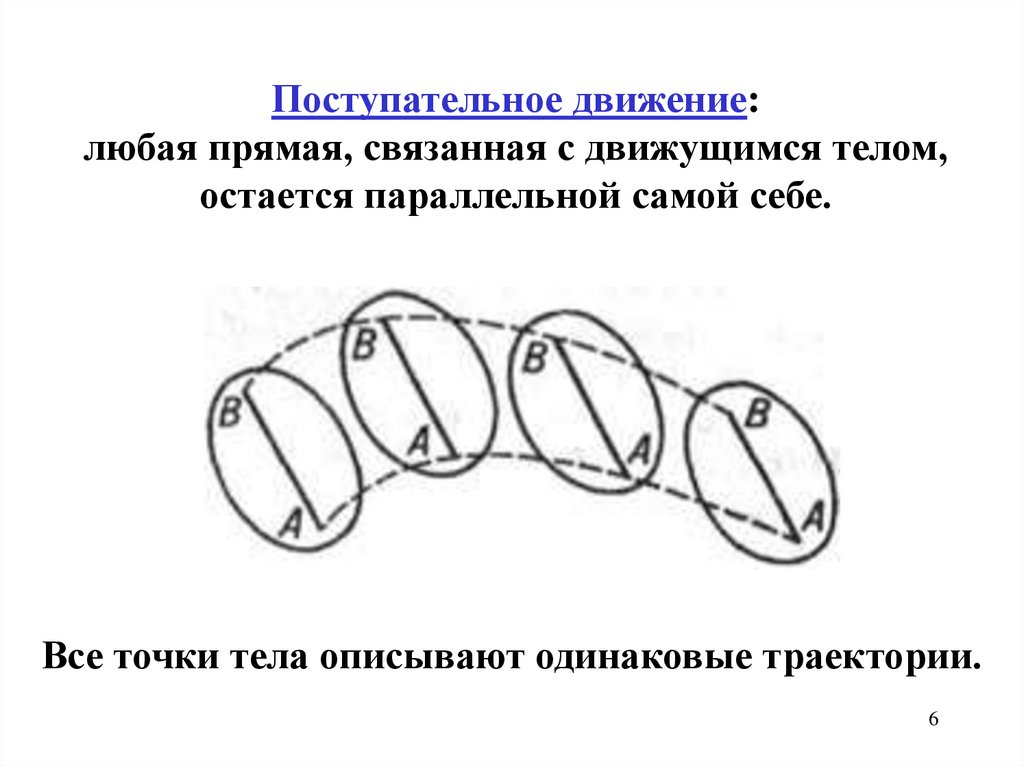
Поступательное движение:
любая прямая, связанная с движущимся телом,
остается параллельной самой себе.
Все точки тела описывают одинаковые траектории.
6

7.

Траектория - линия, описываемая частицей
при своем движении.
Перемещение – векторная величина,
характеризующая изменение положения тела
за заданный промежуток времени.
Путь – длина траектории.
7

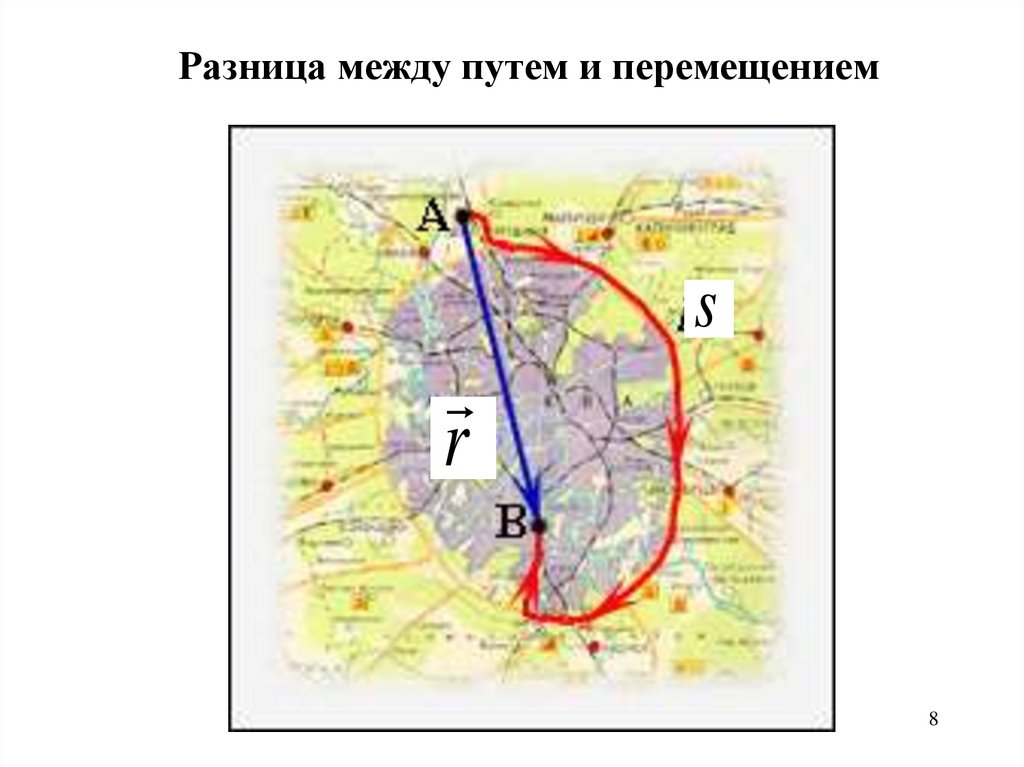
8.

Разница между путем и перемещением
s
r
8

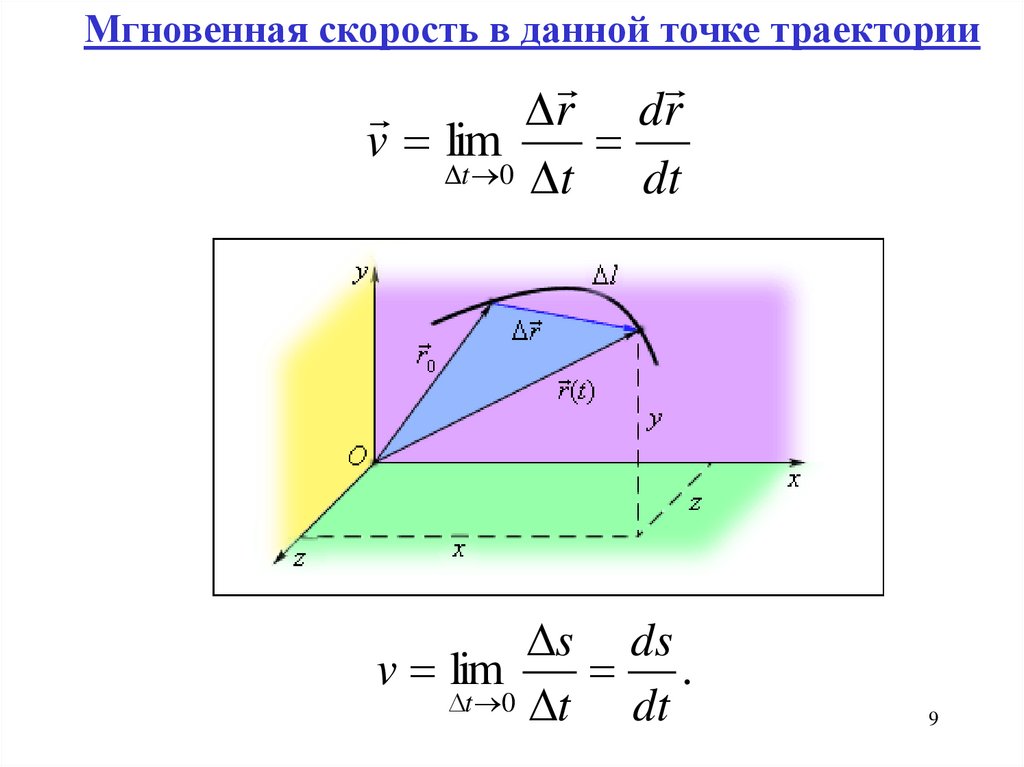
9.

Мгновенная скорость в данной точке траектории
r dr
v lim
t 0 t
dt
s ds
v lim
.
t 0 t
dt
9

10.

Среднее значение модуля скорости
Весь пройденный путь
Средняя скорость
Суммарное время в пути
s
v
t2 t1
10

11.

Ускорение
v dv
a lim
t 0 t
dt
11

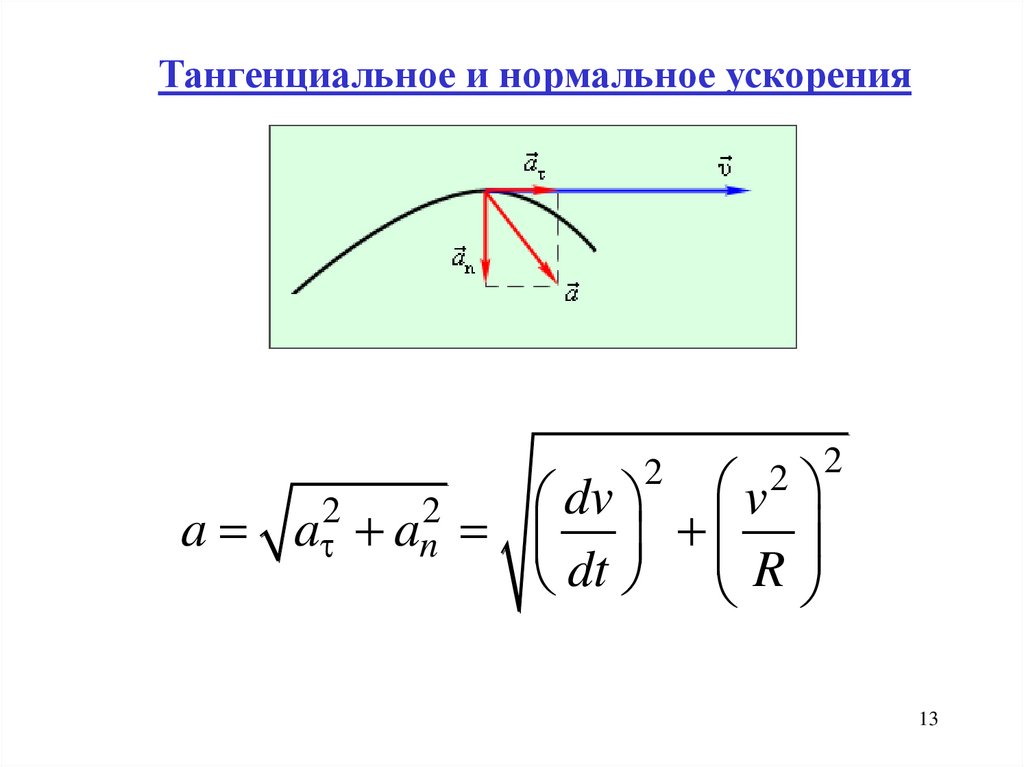
12.

Тангенциальное и нормальное ускорения
dv
a -
dt
2
v
an n
R
тангенциальное (касательное) ускорение
нормальное ускорение
a a an
12

13.

Тангенциальное и нормальное ускорения
a
2
2
a an
2 2
dv v
dt R
2
13

14.

Динамика поступательного движения
Динамика – изучение движения тел с учетом причин,
вызвавших это движение.
Причины, вызвавшие движение взаимодействие между телами.
14

15.

Инерциальные системы отсчета
Инерциальные системы отсчета –
системы отсчета, относительно которых тела,
не подверженные воздействию других тел,
движутся без ускорения, т.е. прямолинейно и равномерно.
15

16.

Первый закон Ньютона
(закон инерции)
Всякое тело находится в состоянии покоя или
равномерного и прямолинейного движения,
пока воздействие со стороны других тел
не заставит его изменить это состояние.
Закон утверждает о существовании инерциальных
систем отсчета.
16

17.

Ускорение тела –
результат его взаимодействия с другими телами.
Масса тела – мера инертности тела.
Импульс тела – произведение массы тела на его
скорость.
p mv
17

18.

Ньютоновская (классическая) механика:
скорость тела много меньше скорости света
v << c
Масса тела - постоянная физическая величина,
не зависящая от скорости тела.
18

19.

Второй закон Ньютона
dp
F
dt
Скорость изменения импульса тела равна
действующей на него силе.
Или
F ma
Произведение массы тела на его ускорение равно
действующей на тело силе.
Второй закон Ньютона - это уравнение движения тела.
19

20.

Второй закон Ньютона
F ma
Если F 0, то a 0.
Первый закон Ньютона – следствие второго закона Ньютона.
20

21.

Третий закон Ньютона
Если тело 1 действует на тело 2 с силой F21 ,
то тело 2 действует на тело 1 с силой F12 ,
F12 F21.
21

22.

Закон сохранения импульса
Полный импульс замкнутой системы взаимодействующих тел
остается постоянным.
p const
Или
p 0
22

23.

Энергия
общая количественная мера движения и взаимодействия
всех видов материи.
Невозможность
исчезновения и возникновения энергии из ничего.
23

24.

Различные виды энергии:
-
механическая,
внутренняя,
электромагнитная,
ядерная
и др.
Возможность перехода энергии из одной формы в другую.
Связь воедино всех явлений природы
посредством понятия «энергия».
24

25.

Виды механической энергии –
потенциальная и кинетическая.
25

26.

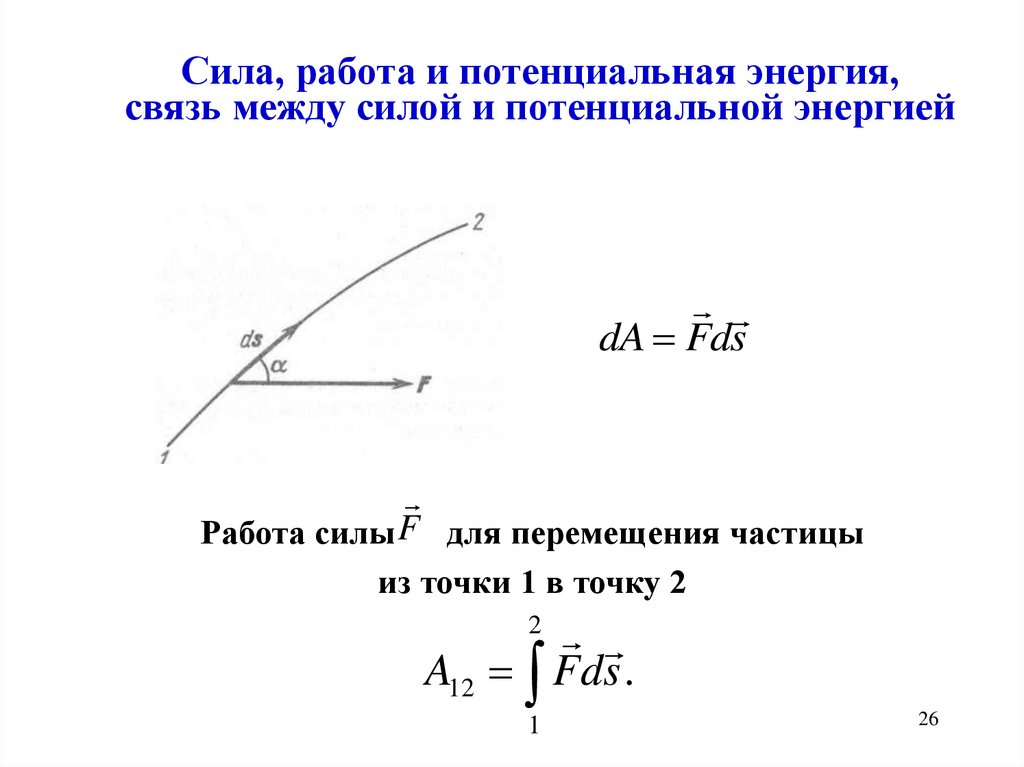
Сила, работа и потенциальная энергия,
связь между силой и потенциальной энергией
dA Fds
Работа силы F для перемещения частицы
из точки 1 в точку 2
A12 Fds .
2
1
26

27.

t2
A12 Fds Fv dt.
2
1
t1
1 Дж (джоуль) = 1 Н·1 м
Мощность
dA
P
Fv
dt
1 Вт (ватт) = 1 Дж / 1 сек
27

28.

Закон сохранения полной механической энергии
в поле консервативных сил
Полная механическая энергия
системы невзаимодействующих частиц,
на которые действуют только консервативные силы,
сохраняется
28

29.

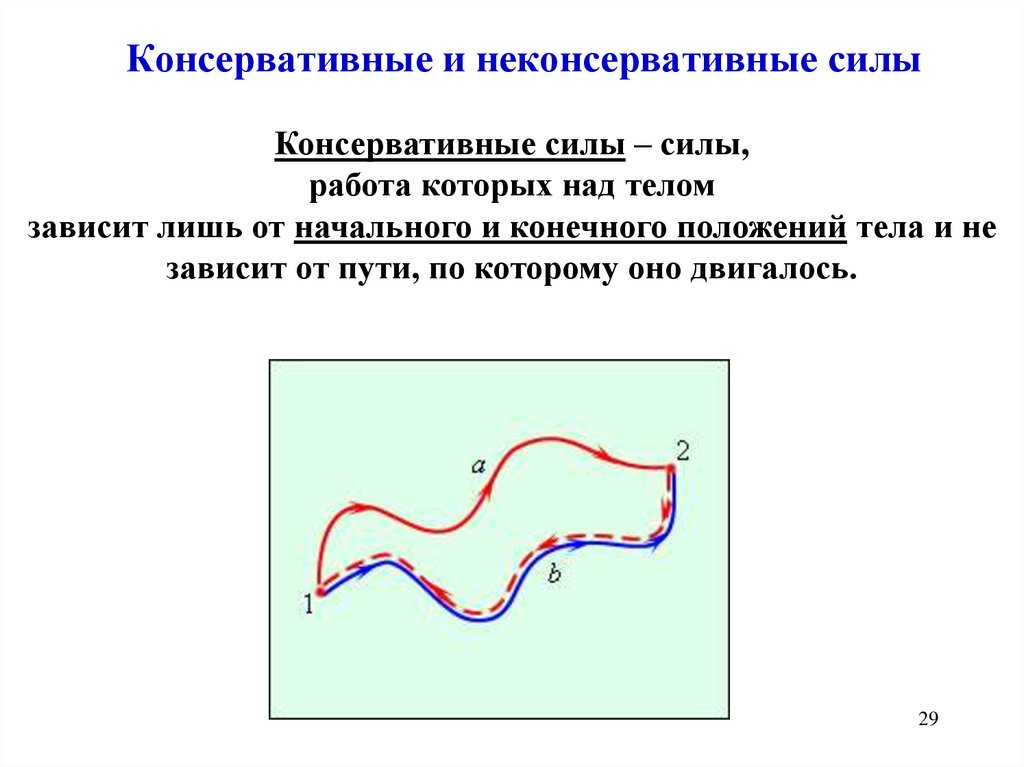
Консервативные и неконсервативные силы
Консервативные силы – силы,
работа которых над телом
зависит лишь от начального и конечного положений тела и не
зависит от пути, по которому оно двигалось.
29

30.

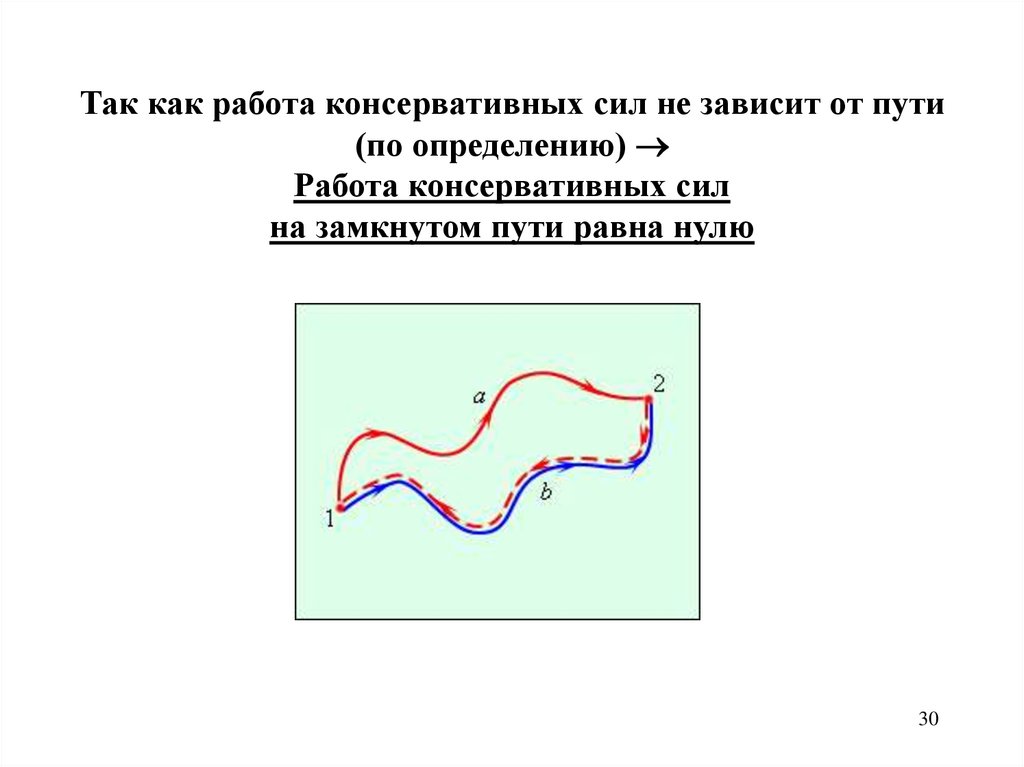
Так как работа консервативных сил не зависит от пути
(по определению)
Работа консервативных сил
на замкнутом пути равна нулю
30

31.

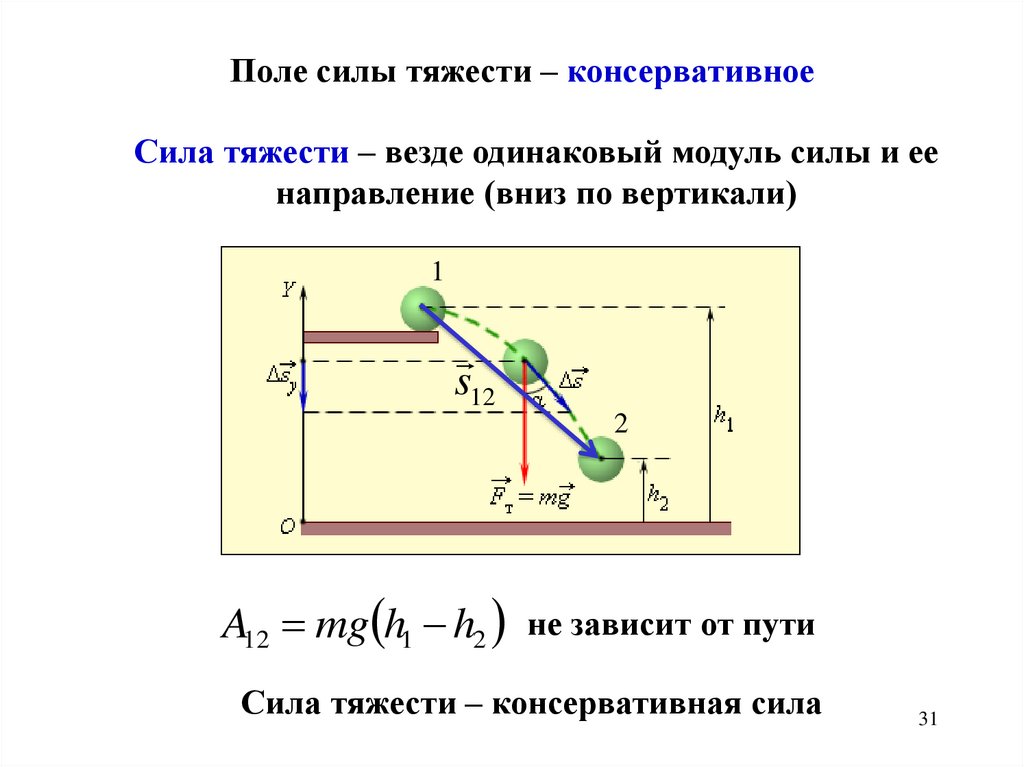
Поле силы тяжести – консервативное
Сила тяжести – везде одинаковый модуль силы и ее
направление (вниз по вертикали)
1
s12
2
A12 mg h1 h2 не зависит от пути
Сила тяжести – консервативная сила
31

32.

Закон сохранения полной механической энергии
в поле консервативных сил
Полная механическая энергия тела, на которое
действуют только консервативные силы, остается
постоянной
E T U const
32

33.

Неконсервативные силы
Силы трения
Fтр
Противоположные
направления
силы трения и
скорости частицы
dA Fds Fvdt Fvdt Fds
Отрицательная работа сил трения на любом замкнутом пути
Силы трения не консервативны
33

34.

Кинетическая энергия
Замкнутая система:
2
mv
Т
const
2
2
p
Т
2m
Кинетическая энергия (энергия движения) зависит от
массы и скорости рассматриваемого тела
34

35.

Работа кинетической энергии
Работа результирующей всех сил, действующих на тело,
равна приращению кинетической энергии тела
A12 Т 2 T1.
35

36.

Столкновение тел
Соударения тел:
абсолютно упругий и абсолютно неупругий удары
36

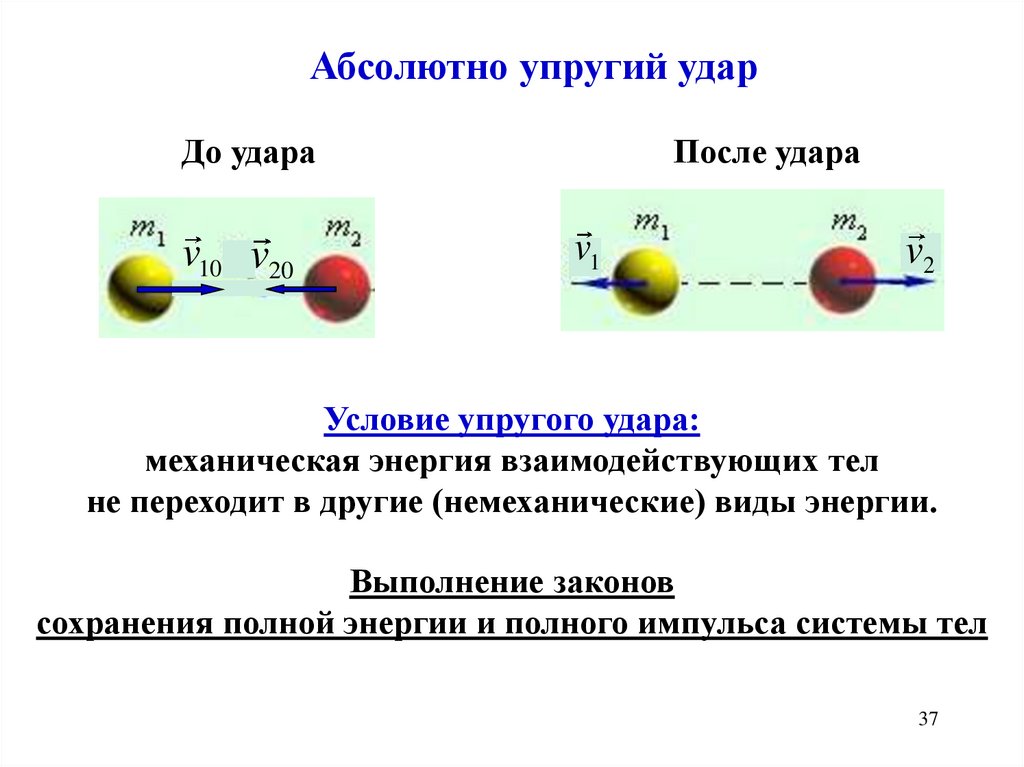
37.

Абсолютно упругий удар
До удара
v10 v20
После удара
v1
v2
Условие упругого удара:
механическая энергия взаимодействующих тел
не переходит в другие (немеханические) виды энергии.
Выполнение законов
сохранения полной энергии и полного импульса системы тел
37

38.

Отсутствие вращения частиц (только поступательное
движение)
Выполнение закона сохранения механической энергии:
2
2
2
2
m1v10 m2 v20 m1v1 m2 v2
.
2
2
2
2
Выполнение закона сохранения суммарного импульса частиц:
m1v10 m2v20 m1v1 m2v2 .
38

39.

Абсолютно неупругий удар
Полное или частичное превращение
кинетической энергии во внутреннюю энергию
После удара:
движение тел с одинаковой скоростью
или их нахождение в состоянии покоя.
39

40.

Абсолютно неупругий удар
Выполнение закона сохранения импульса
Выполнение закона сохранения суммарной энергии
различных видов - механической и внутренней
Невыполнение закона сохранения механической энергии
40

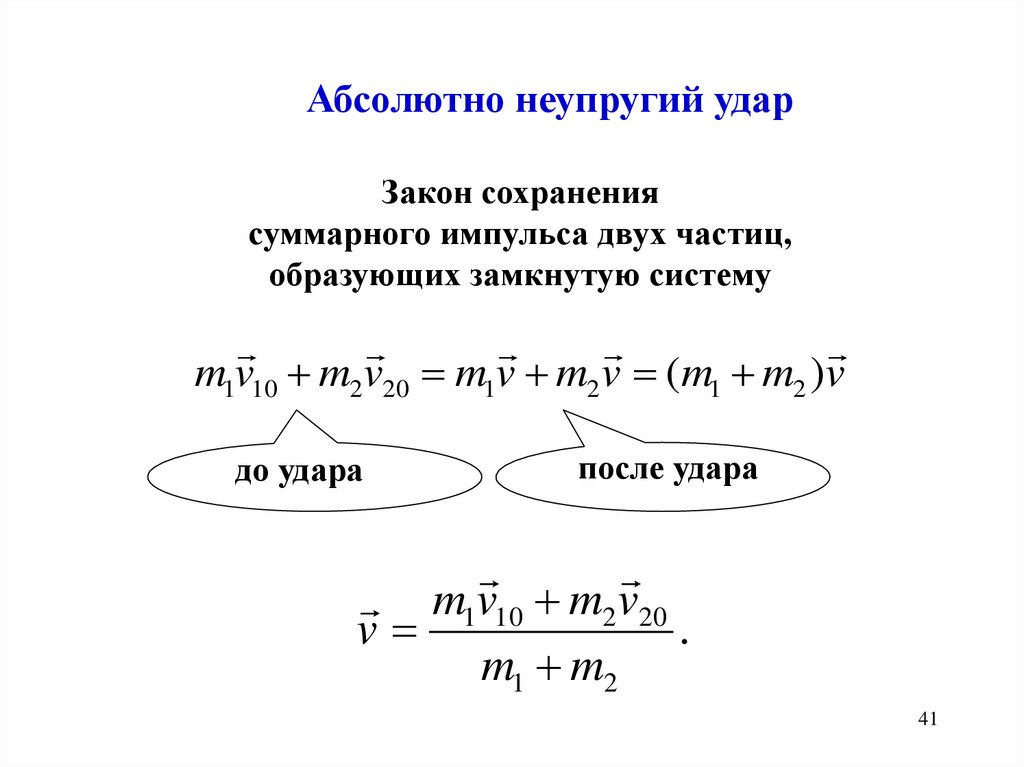
41.

Абсолютно неупругий удар
Закон сохранения
суммарного импульса двух частиц,
образующих замкнутую систему
m1v10 m2v20 m1v m2v (m1 m2 )v
до удара
после удара
m1v10 m2 v20
v
.
m1 m2
41

42.

Вращательное движение твердых тел:
движение по окружности
Вращательным движением называется движение, при
котором все точки тела движутся по окружностям, центры
которых лежат на одной прямой – оси вращения.
Центральная ось – ось вращения
твердого тела, которая проходит через
его центр масс.
42

43.

Вращательное движение твердых тел:
движение по окружности
Все точки тела в данный момент времени при
вращательном движении имеют одинаковую угловую
скорость ω и одинаковое угловое ускорение ε
относительно оси вращения.
При вращательном движении
положение тела в любой момент
времени определяется углом
поворота φ.
43

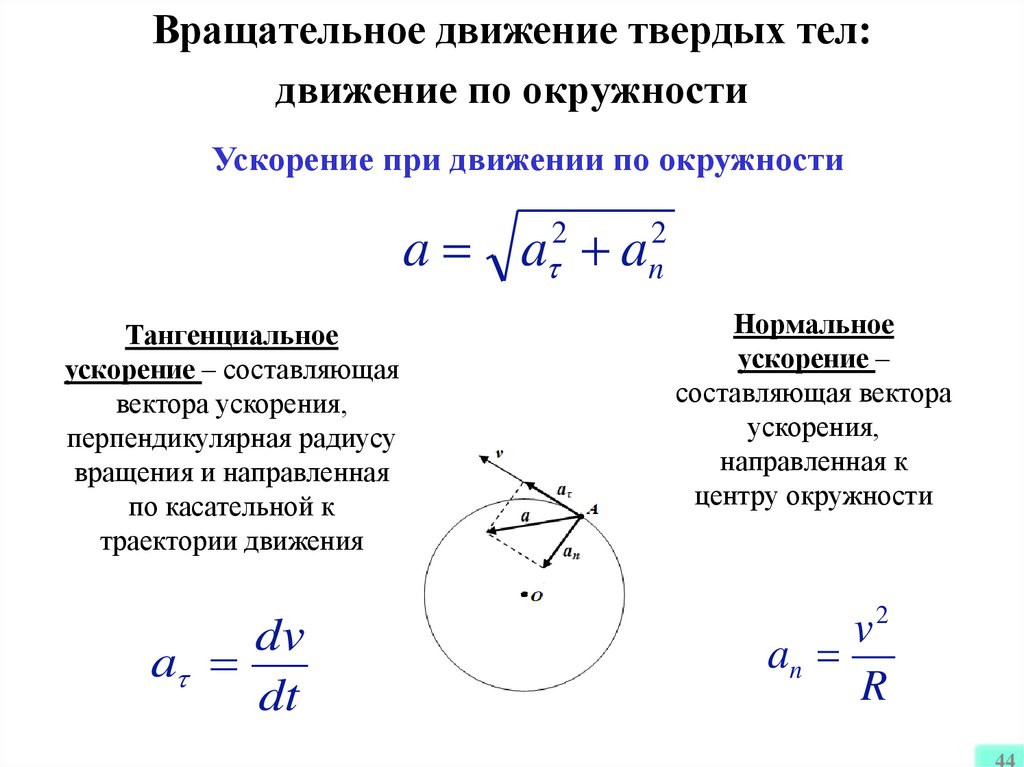
44.

Вращательное движение твердых тел:
движение по окружности
Ускорение при движении по окружности
a a a
2
2
n
Тангенциальное
ускорение – составляющая
вектора ускорения,
перпендикулярная радиусу
вращения и направленная
по касательной к
траектории движения
Нормальное
ускорение –
составляющая вектора
ускорения,
направленная к
центру окружности
dv
a
dt
v2
an
R
44

45.

Угловая скорость и угловое ускорение
Угловая скорость ω – векторная физическая
величина, равная первой производной угла
поворота тела по времени.
d
lim
t 0 t
dt
Единица измерения угловой скорости – радиан в секунду (рад/с).
45

46.

Угловая скорость и угловое ускорение
Период вращения T – время, за которое точка
совершает один полный оборот, т.е. поворачивается
на угол 2π.
t 2
T
N
t – время, N – число оборотов
Единица измерения периода вращения – секунда (с).
46

47.

Угловая скорость и угловое ускорение
Частота вращения – это
число полных оборотов,
совершаемых телом при его
равномерном движении по
окружности, в единицу
времени.
Циклическая (круговая)
частота вращения – это число
полных оборотов, совершаемых
телом при его равномерном
движении по окружности, за
время 2π.
N 1
t T 2
2
2
T
Единица измерения частоты вращения – с-1 или герц (Гц).
47

48.

Угловая скорость и угловое ускорение
Угловое ускорение ε – векторная
физическая величина, равная
первой производной угловой
скорости по времени.
d
lim
t 0 t
dt
48

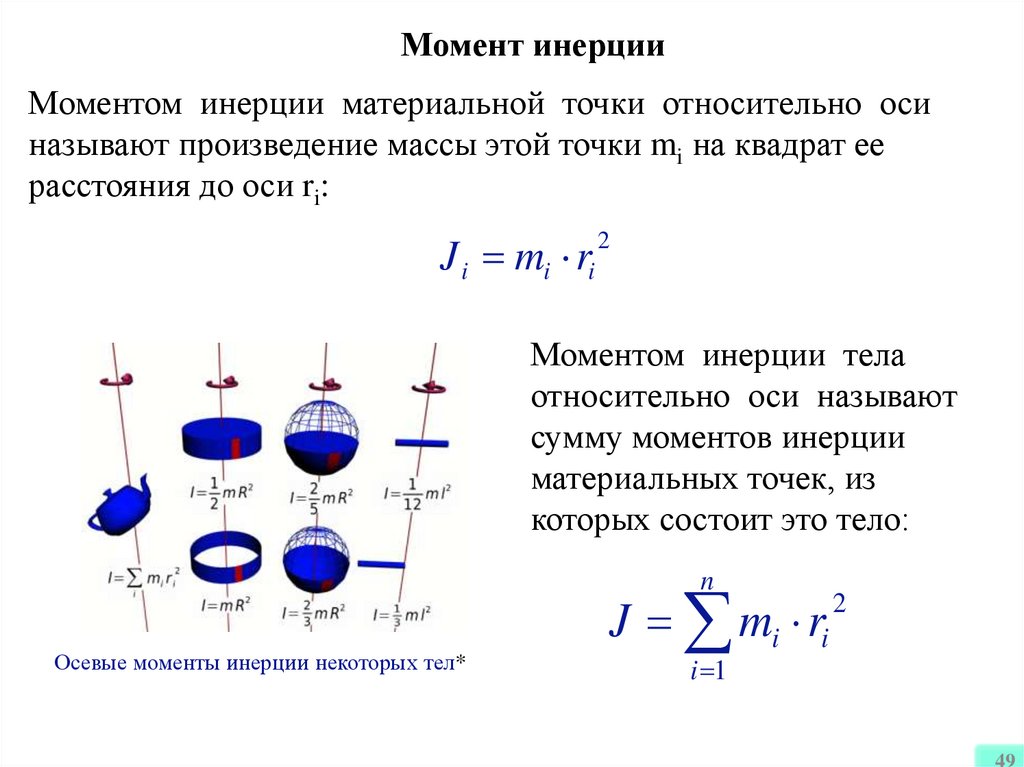
49.

Момент инерции
Моментом инерции материальной точки относительно оси
называют произведение массы этой точки mi на квадрат ее
расстояния до оси ri:
J i mi ri
2
Моментом инерции тела
относительно оси называют
сумму моментов инерции
материальных точек, из
которых состоит это тело:
n
Осевые моменты инерции некоторых тел*
J mi ri
2
i 1
49

50.

Момент инерции
Физический смысл момента инерции
Любое тело не может мгновенно изменить свою
скорость. Это свойство тел называется инертностью.
Для
поступательно
движущегося
тела мерой
инертности
является масса.
При вращательном
движении мерой
инертности тела является
момент инерции тела
относительно оси
50

51.

Момент инерции тела относительно оси зависит от:
Массы тела;
Формы и размеров тела;
Распределения массы в пространстве
относительно оси, вокруг которой движется тело;
Положения оси вращения.
Таким образом, для определения момента инерции
нет единой формулы.
51

52.

Момент инерции
Значения моментов инерции для некоторых тел
(тела считаются однородными, т – масса тела)*
*Трофимова Т. И. Курс физики. – М.: Academia, 2014, 560 с.
52

53.

Теорема Штейнера
Для нахождения момента инерции относительно любой
произвольной оси вращения применяется теорема
Штейнера, согласно которой момент инерции тела J
относительно произвольной оси вращения равен сумме
момента инерции этого тела JC относительно оси,
параллельной данной и проходящей через центр масс C
данного тела, и произведения массы тела m на квадрат
расстояния a между осями.
J J C ma
2
53

54.

Теорема Штейнера
Таким образом, чтобы определить момент инерции тела относительно
произвольной оси вращения необходимо:
1) Найти центр масс данного тела и провести через него ось,
параллельную данной оси;
2) Определить момент инерции тела JC относительно проведенной
центральной оси;
3) Найти расстояние a между двумя осями и определить момент инерции J
по теореме Штейнера.
Например, момент инерции стержня длиной l относительно оси, проходящей через конец
стержня, равен:
2
1
l 1
J J C ma ml 2 m ml 2
12
2 3
2
54

55.

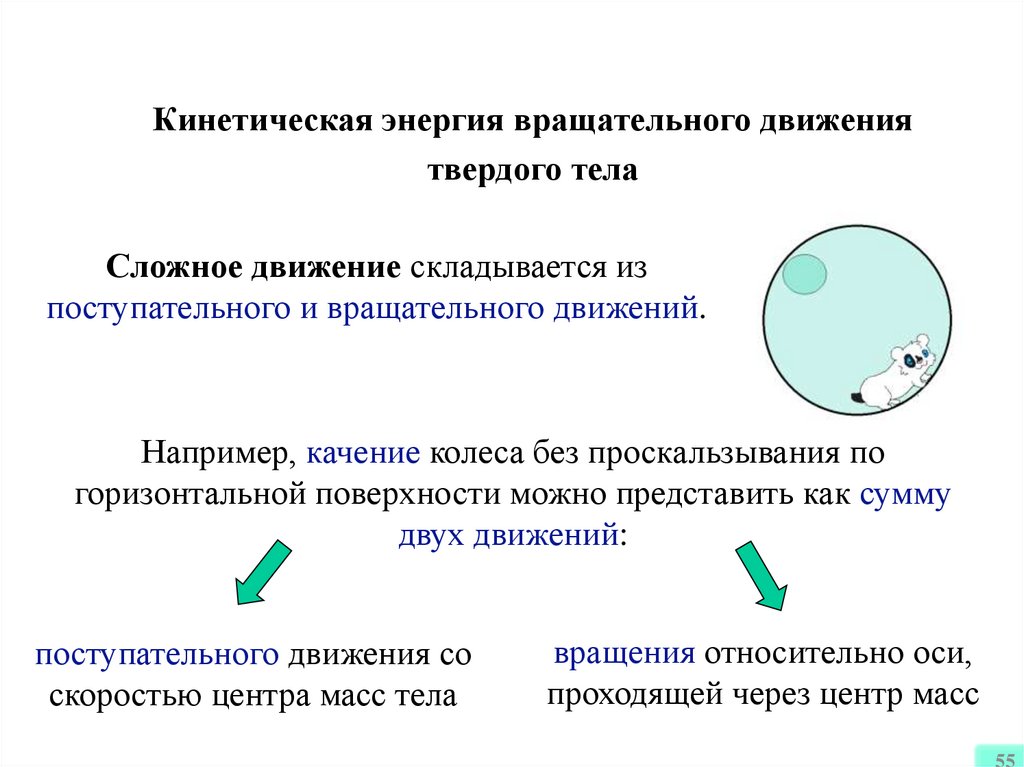
Кинетическая энергия вращательного движения
твердого тела
Сложное движение складывается из
поступательного и вращательного движений.
Например, качение колеса без проскальзывания по
горизонтальной поверхности можно представить как сумму
двух движений:
поступательного движения со
скоростью центра масс тела
вращения относительно оси,
проходящей через центр масс
55

56.

Кинетическая энергия вращательного движения
твердого тела
Кинетическая энергия
поступательно движущегося
тела:
Кинетическая энергия
вращающегося тела:
J 2
EK
2
mv 2
EK
2
Если тело совершает поступательное и вращательное движения
одновременно, то его полная кинетическая энергия равна
mv J
EK
2
2
2
2
где m – масса катящегося тела; v – скорость центра масс
тела; J – момент инерции тела относительно оси,
проходящей через его центр масс; ω – угловая скорость тела.
56

57.

Основное уравнение вращательного движения
твердого тела
Основное уравнение динамики
вращательного движения:
M J
При вращательном движении роль силы F выполняет
момент силы М,
роль массы m – момент инерции J.
57

58.

Момент импульса твердого тела
Момент импульса вращательного
движения:
L J
При вращательном движении
роль импульса p выполняет момент импульса L,
роль массы m – момент инерции J,
линейной скорости v – угловая скорость ω.
58

59.

Закон сохранения момента импульса
Закон сохранения момента импульса: момент импульса
замкнутой системы сохраняется, т. е. не изменяется с
течением времени.
L const
59

60.

Закон сохранения момента импульса
Продемонстрировать закон сохранения
момента импульса можно с помощью
скамьи Жуковского.
Человек, сидящий на скамье, которая без
трения вращается вокруг вертикальной
оси, держит в вытянутых руках гантели.
Он приведен во вращение с угловой
скоростью ω1.
Если человек прижмет гантели к себе, то
момент инерции системы уменьшится.
Скамья Жуковского*
Так как момент внешних сил равен нулю,
то момент импульса системы сохраняется
и угловая скорость вращения ω2
возрастает.
*Трофимова Т. И. Курс физики. – М.: Academia, 2014, 560 с.
60

61.

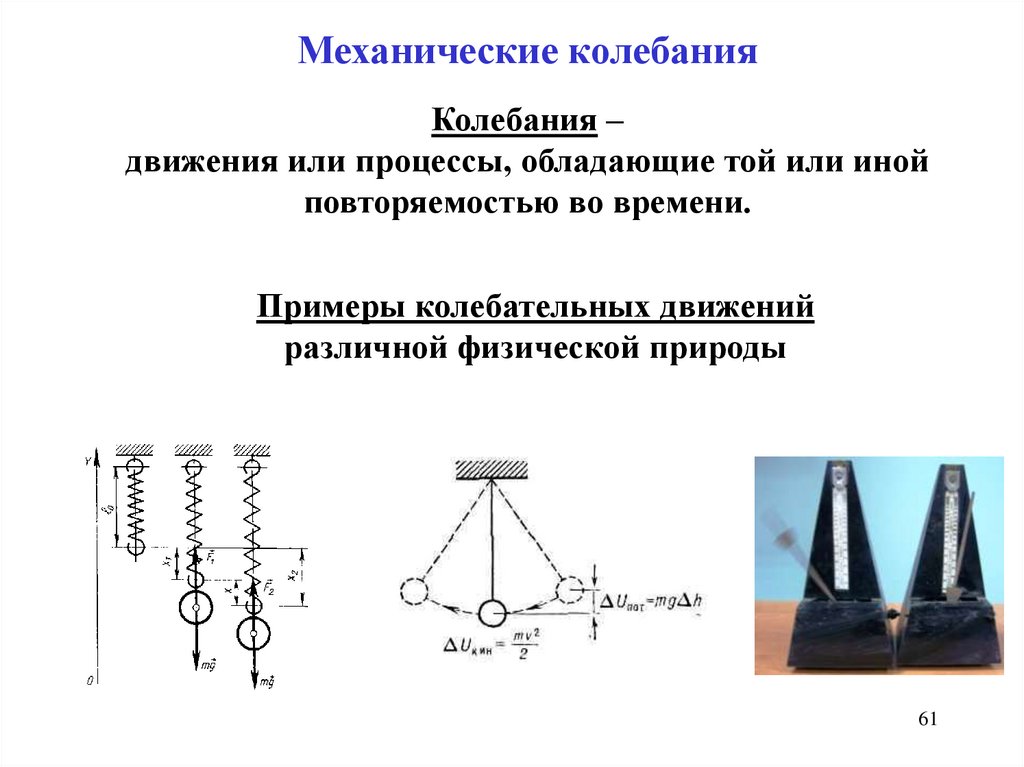
Механические колебания
Колебания –
движения или процессы, обладающие той или иной
повторяемостью во времени.
Примеры колебательных движений
различной физической природы
61

62.

Механические колебания
Гармонические колебания –
колебания, при которых колеблющаяся величина
изменяется со временем по закону синуса или косинуса.
Периодические процессы иной формы
(с другой зависимостью от времени) –
результат наложения нескольких гармонических колебаний.
62

63.

Гармонические колебания
x(t ) A cos t
А, , - параметры колебательного движения
А – амплитуда или максимальное отклонение от
положения равновесия
- циклическая или круговая частота
- начальная фаза
t - фаза колебательного движения
63

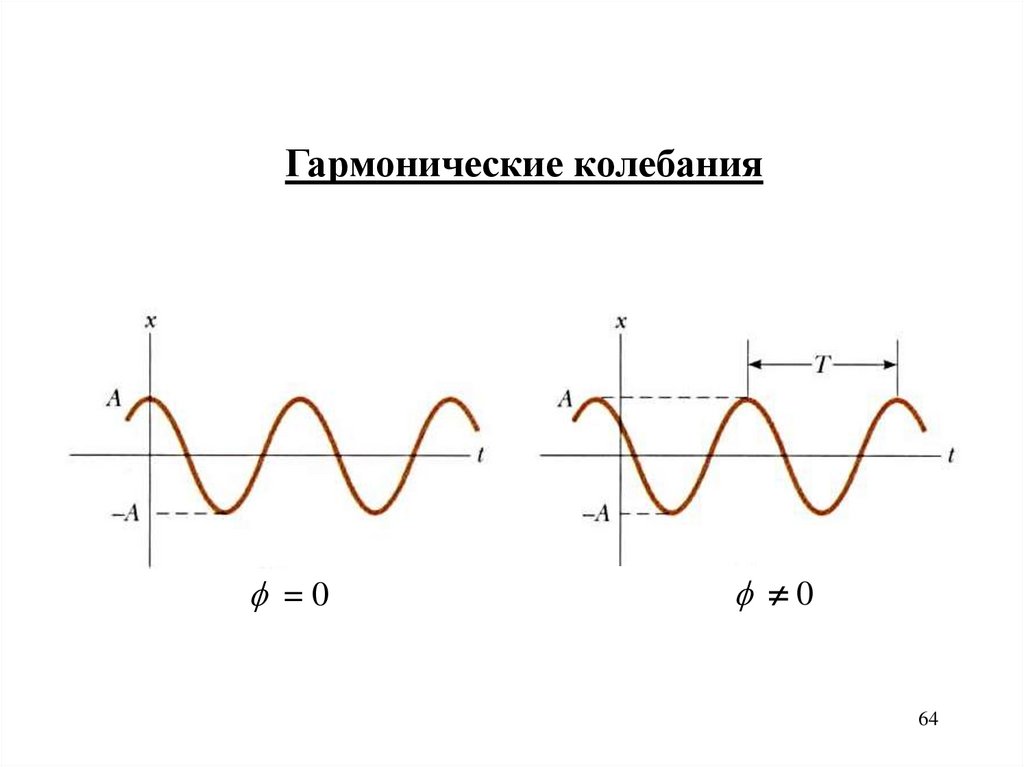
64.

Гармонические колебания
=0
0
64

65.

Гармонические колебания
Период Т – время, необходимое для совершения телом
одного полного колебательного движения
T
2
Частота колебаний – число колебаний в единицу времени
1
T 2
2
2 f
T
65

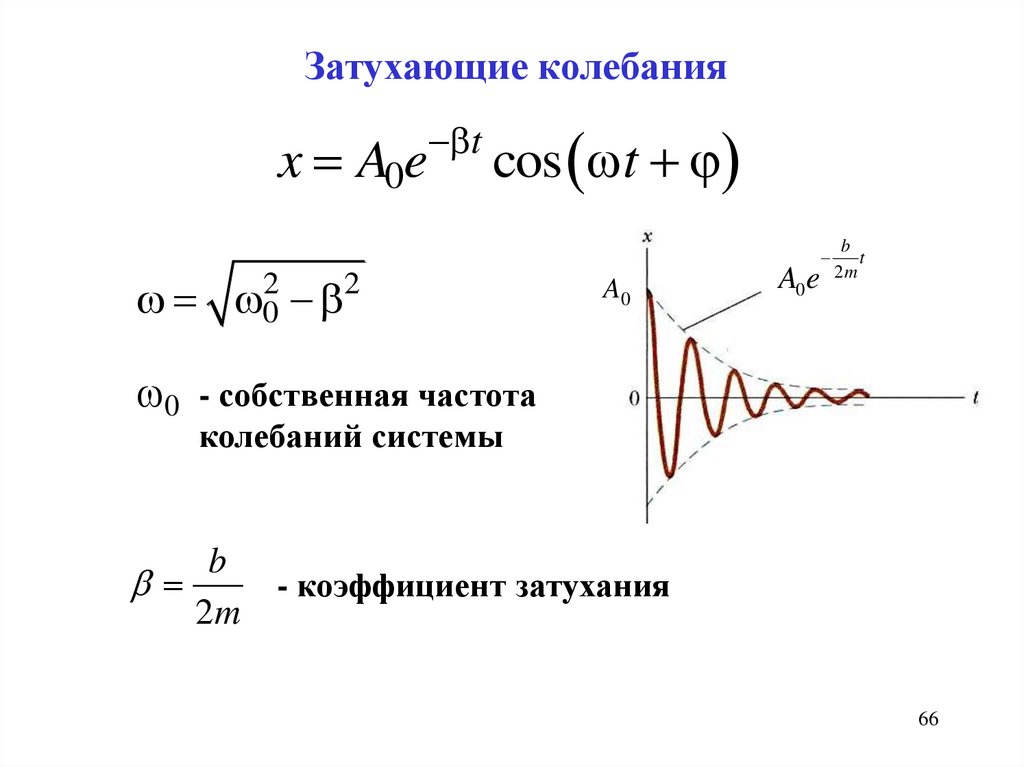
66.

Затухающие колебания
x A0e
t
cos t
2
2
0
A0
A0 e
b
t
2m
0 - собственная частота
колебаний системы
b
- коэффициент затухания
2m
66

67.

Затухающие колебания
x A0 e
t
cos t
1. Характеристика колебательной системы декремент затухания
A(t )
T
e
A(t T )
2. Характеристика колебательной системы логарифмический декремент затухания
A(t )
ln
T
A(t T )
67

68.

Логарифмический декремент затухания –
величина, обратная числу колебаний,
совершаемых за время уменьшения амплитуды в е раз
= 1 / Ne
3. Характеристика колебательной системы добротность
Q = / = Ne
68

69.

Затухающие колебания
x A0 e
t
cos t
t
t
T
A A0e A0e
69

70.

Вынужденные колебания
Возможность компенсации потерь энергии колебаний
при затухающих колебаниях за счет внешней силы,
совершающей положительную работу над системой.
F (t ) F0 sin t
70

71.

Вынужденные колебания
x A cos t
A
F0 / m
2
2 2
0
b
m
2
71

72.

Резонанс – резкое возрастание амплитуды
колебаний при совпадении частоты колебаний с
собственной частотой колебаний системы
Разрушение моста в результате резонанса
72

73.

Сложение колебаний одного направления
и одинаковой частоты
x1 A1 cos 0t 1 x2 A2 cos 0t 2
2
A
x x1 x2
2
2
A1 A2 2 A1 A2 cos( 2 1 )
73

74.

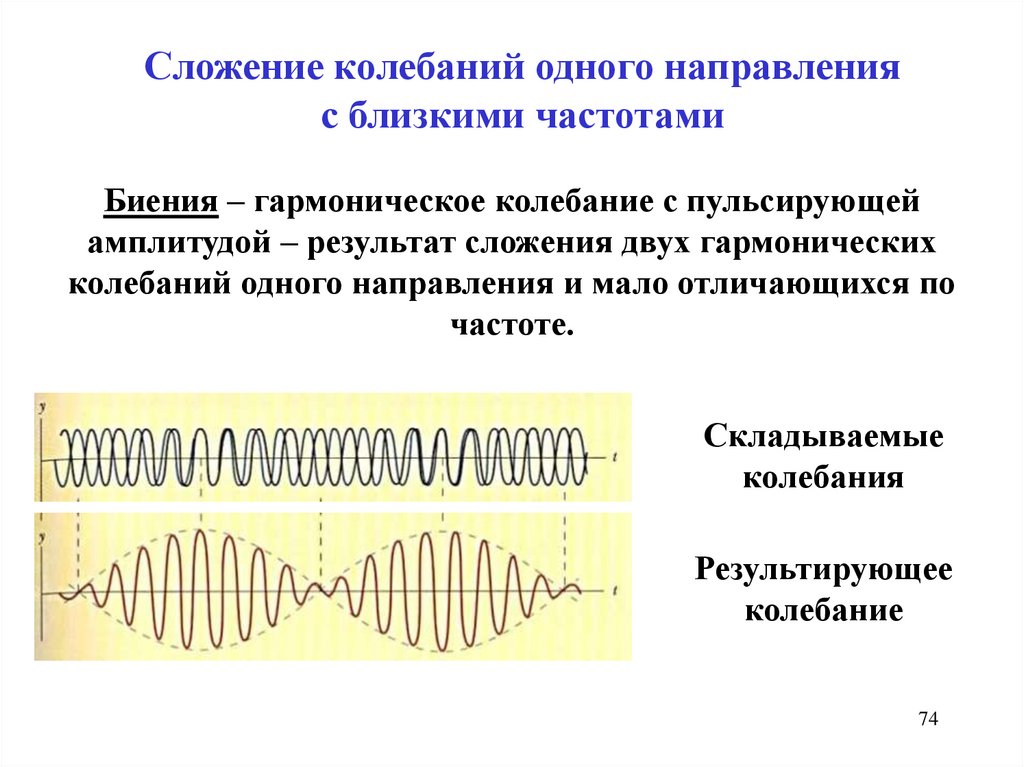
Сложение колебаний одного направления
с близкими частотами
Биения – гармоническое колебание с пульсирующей
амплитудой – результат сложения двух гармонических
колебаний одного направления и мало отличающихся по
частоте.
Складываемые
колебания
Результирующее
колебание
74

75.

Сложение колебаний одного направления
с близкими частотами
x1 A cos t,
x2 A cos t
x x1 x2 2 A cos
t cos t
2
Медленно
изменяющаяся во
времени
амплитуда
-
частота биений (пульсаций амплитуды), равная
разности частот складываемых колебаний.
75

76.

Волновое движение
Волновое движение - результат колебательного процесса
76

77.

Две разновидности волн –
механические и электромагнитные волны
Распространение механических волн в какой-либо среде:
звуковые волны в воздухе, волны на поверхности воды,
упругие волны в твердом теле
Распространение электромагнитных волн: видимый свет,
радиоволны, телевизионный сигнал, рентгеновские лучи
77

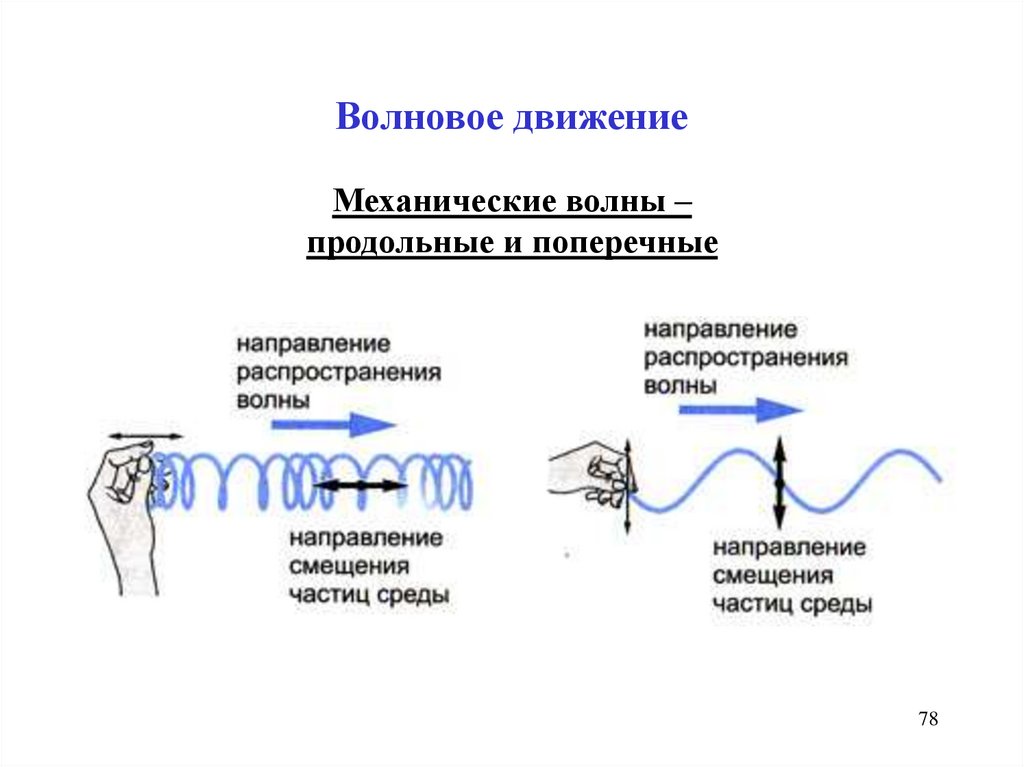
78.

Волновое движение
Механические волны –
продольные и поперечные
78

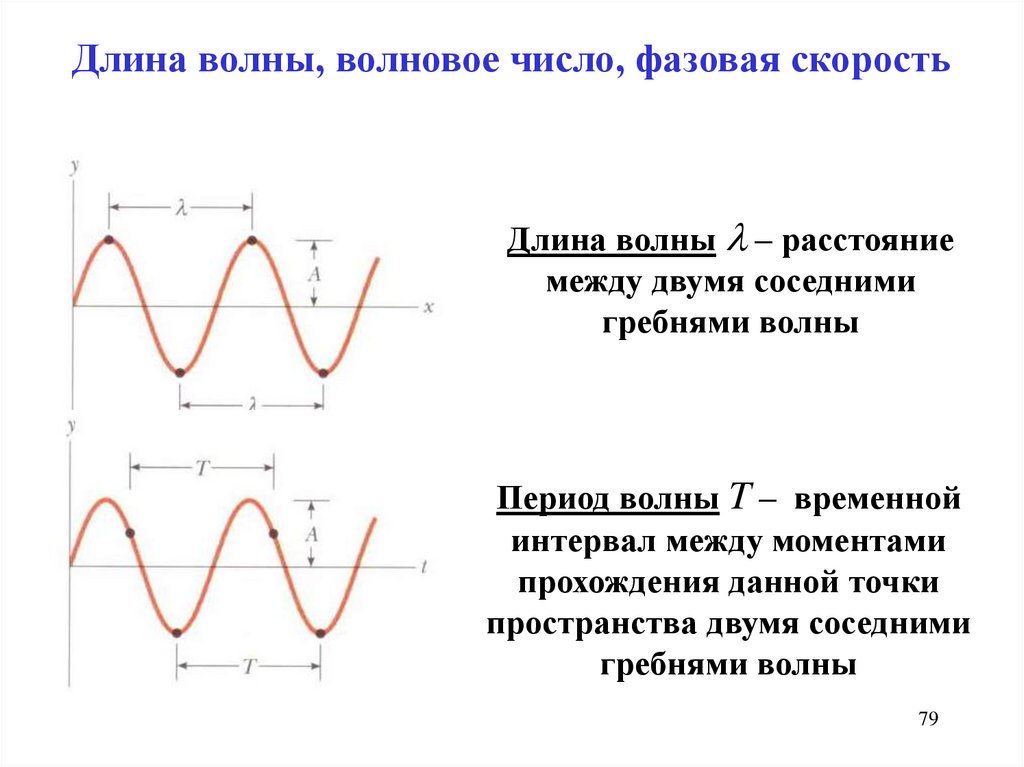
79.

Длина волны, волновое число, фазовая скорость
Длина волны – расстояние
между двумя соседними
гребнями волны
Период волны T – временной
интервал между моментами
прохождения данной точки
пространства двумя соседними
гребнями волны
79

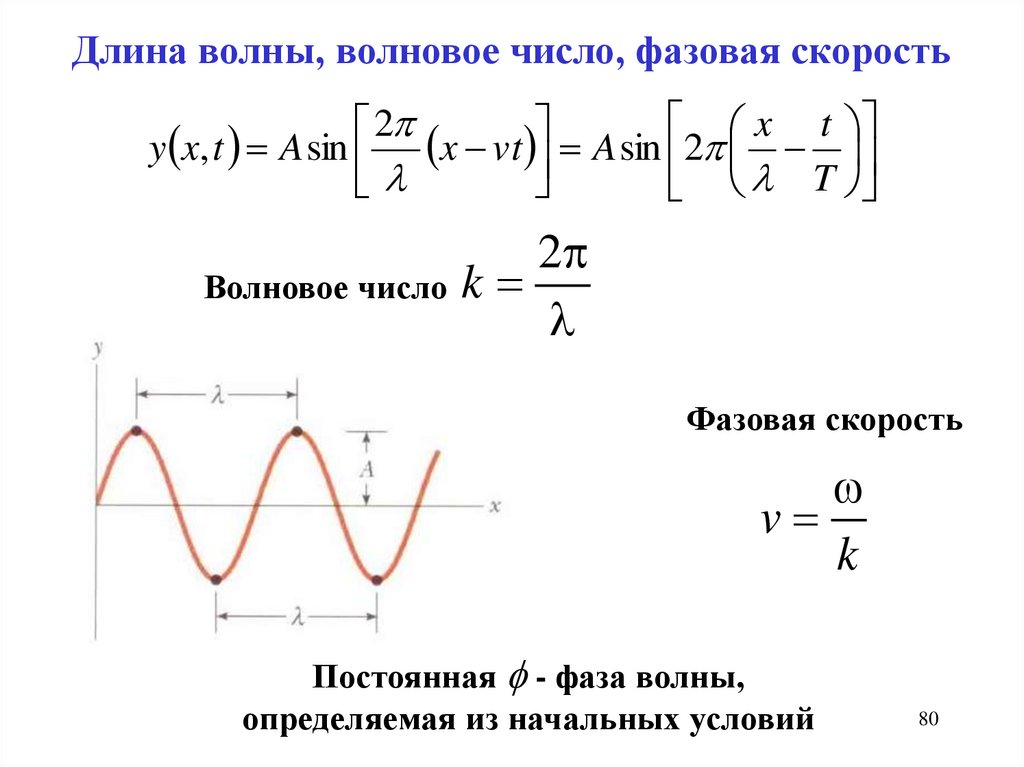
80.

Длина волны, волновое число, фазовая скорость
x t
2
y x, t A sin x vt A sin 2
T
2
Волновое число k
Фазовая скорость
Общий случай:
v
k
Постоянная - фаза волны,
определяемая из начальных условий
80

81.

Молекулярная физика
Молекулярная физика –
раздел физики, изучающий строение и свойства вещества
на основе молекулярно-кинетических представлений.
81

82.

Броуновское движение - беспорядочное, хаотическое
движение взвешенных частичек –
доказательство существования молекул.
82

83.

Идеальный газ
• число молекул в газе велико, среднее расстояние между
ними велико по сравнению с их размерами,
• хаотичное движение молекул, подчиняющееся законам
Ньютона,
• взаимодействие молекул между собой посредством упругих
короткодействующих сил,
• все молекулы газа одинаковы (простое вещество)
83

84.

Модель идеального газа
Соответствует поведению газа,
состоящего из отдельных атомов при низких давлениях.
Исключение из рассмотрения вращения и колебания
молекул.
84

85.

Термодинамика
Термодинамика рассматривает не отдельные молекулы,
а макроскопические тела,
состоящие из огромного числа частиц.
85

86.

Термодинамика
Температура, давление, объем, плотность и т.д. –
параметры состояния термодинамической системы
86

87.

Уравнение состояния идеального газа
связывает параметры состояния идеального газа
(давление p, объем V, температура Т)
между собой соотношением
m
pV RT
M
Дж
R 8,31
моль К
- универсальная газовая постоянная
Молярная масса M - масса 1 моля вещества
87

88.

Давление газа с точки зрения МКТ
p nkT
Давление газа
прямо пропорционально
концентрации молекул в газе и температуре
88

89.

Cреднеквадратическая скорость молекул
3kT
3RT
vср.-кв. v
m
M
2
M – молярная масса, равная mNA.
89

90.

Явления переноса
Диффузия – обусловленное тепловым движением молекул
самопроизвольное выравнивание концентраций
в смеси нескольких различных веществ.
Диффузия может наблюдаться в твердых, жидких и
газообразных средах.
90

91.

Теплопроводность
Уравнение Фурье:
dT
q S
dz
q - поток теплоты (количество теплоты в единицу времени)
через поверхность S, расположенную перпендикулярно к оси z,
dT/dz – градиент температуры (проекция градиента температуры на ось z),
χ – коэффициент теплопроводности, зависящий от свойств среды
[Вт/(м К)].
Знак «-» - поток теплоты направлен в сторону убывания температуры.
91

92.

Внутреннее трение
Вязкость (внутреннее трение) - одно из явлений
переноса, свойство текучих тел (жидкостей и газов)
оказывать сопротивление перемещению одной их
части относительно другой.
Механизм внутреннего трения в жидкостях и газах –
перенос импульса хаотически движущимися
молекулами из одного слоя в другой.
92

93.

Температура
Температура – параметр, позволяющий определить
находится ли тело в тепловом равновесии с другими телами.
Одинаковая температура – тела находятся в тепловом
равновесии
93

94.

Температура
Кельвин – единица термодинамической температуры.
Соответствие 0 К по термодинамической шкале - 273,15 С.
Термодинамическая температура
T = t + 273,15
94

95.

Теплоемкость
Теплоемкость тела – величина, равная количеству теплоты, которое
нужно сообщить телу, чтобы повысить его температуру на один
кельвин.
dQ
Cтела
dT
dQ - количество теплоты, повышающей температуру
тела на dT.
Дж
Cтела .
К
95

96.

Теплоемкость
Удельная теплоемкость тела с – теплоемкость единицы массы вещества.
Дж
c
.
кг К
Молярная теплоемкость тела С – теплоемкость 1 моля вещества.
Дж
C
.
моль К
96

97.

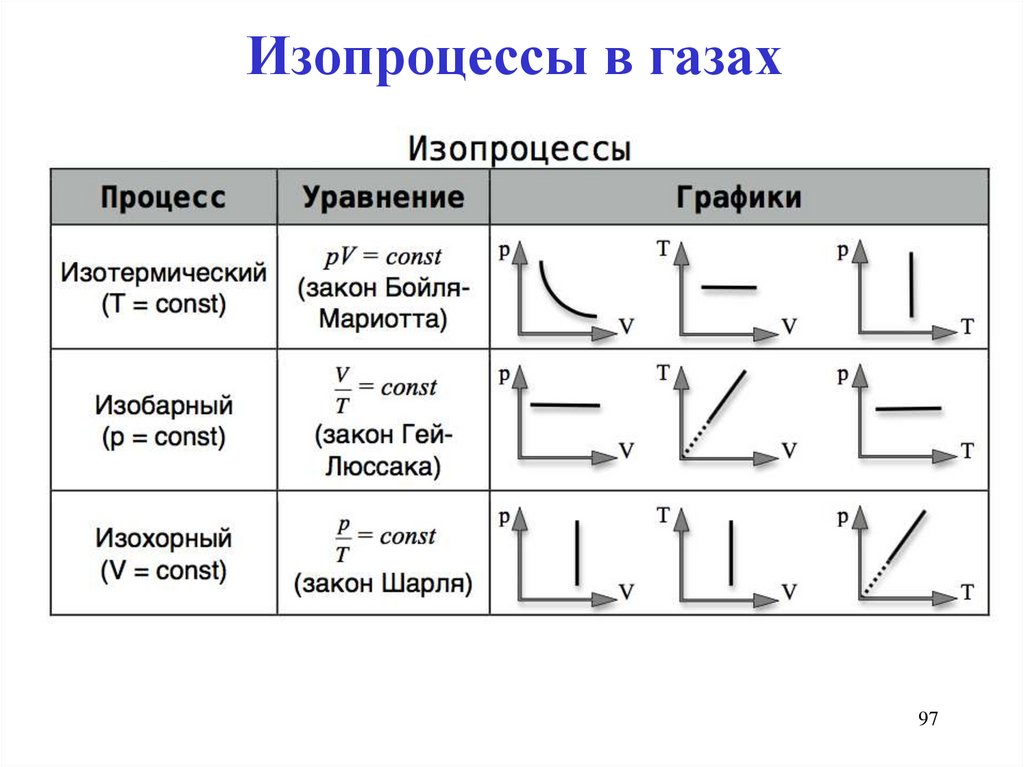
Изопроцессы в газах
97

98.

Теплоемкость
Коэффициент Пуассона - характерная для каждого газа величина,
определяемая числом и характером степеней свободы молекул.
Cp i 2
γ
CV
i
i = 3 – для одноатомной молекулы,
i = 5 – для двухатомной молекулы,
i = 6 – для многоатомной молекулы
98

99.

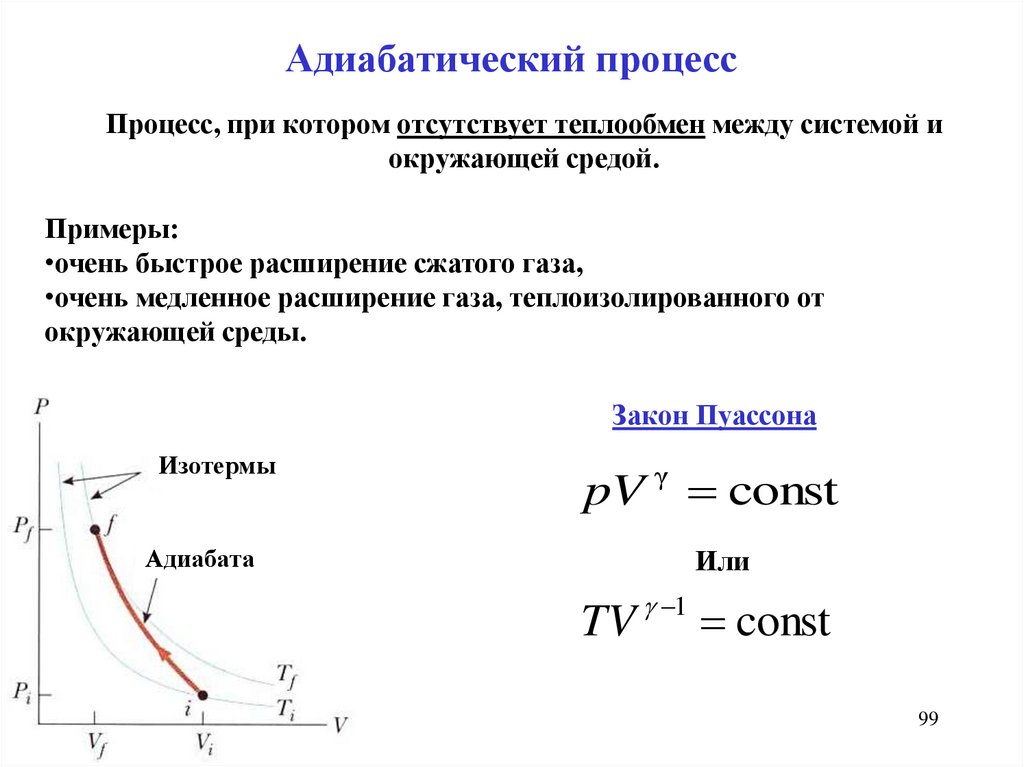
Адиабатический процесс
Процесс, при котором отсутствует теплообмен между системой и
окружающей средой.
Примеры:
•очень быстрое расширение сжатого газа,
•очень медленное расширение газа, теплоизолированного от
окружающей среды.
Закон Пуассона
Изотермы
pV γ const
Адиабата
Или
TV 1 const
99

100.

Первый закон термодинамики
Q = U2 – U1 + A,
U1 и U2 – начальное и конечное значения внутренней энергии тела
(или системы тел),
A – работа, совершенная телом (или системой тел),
Q – количество теплоты, сообщенной телу (системе тел).
Количество теплоты, сообщенное системе,
идет на приращение внутренней энергии системы и
на совершение системой работы над внешними телами.
100

101.

Энтропия и ее статистический смысл
Стремление изолированной системы перейти
в состояние с минимумом энергии,
состояние хаоса, беспорядка.
Направленность всех процессов во Вселенной к беспорядку.
101

102.

Энтропия как количественная мера хаотичности
Второй закон термодинамики (закон возрастания энтропии):
энтропия изолированной системы
не может убывать.
102

103.

Теорема Нернста
(третий закон термодинамики)
Энтропия – мера степени беспорядка в системе.
Теорема Нернста: энтропия любого тела стремится
к нулю при стремлении температуры к нулю:
lim S 0.
T 0
103

104.

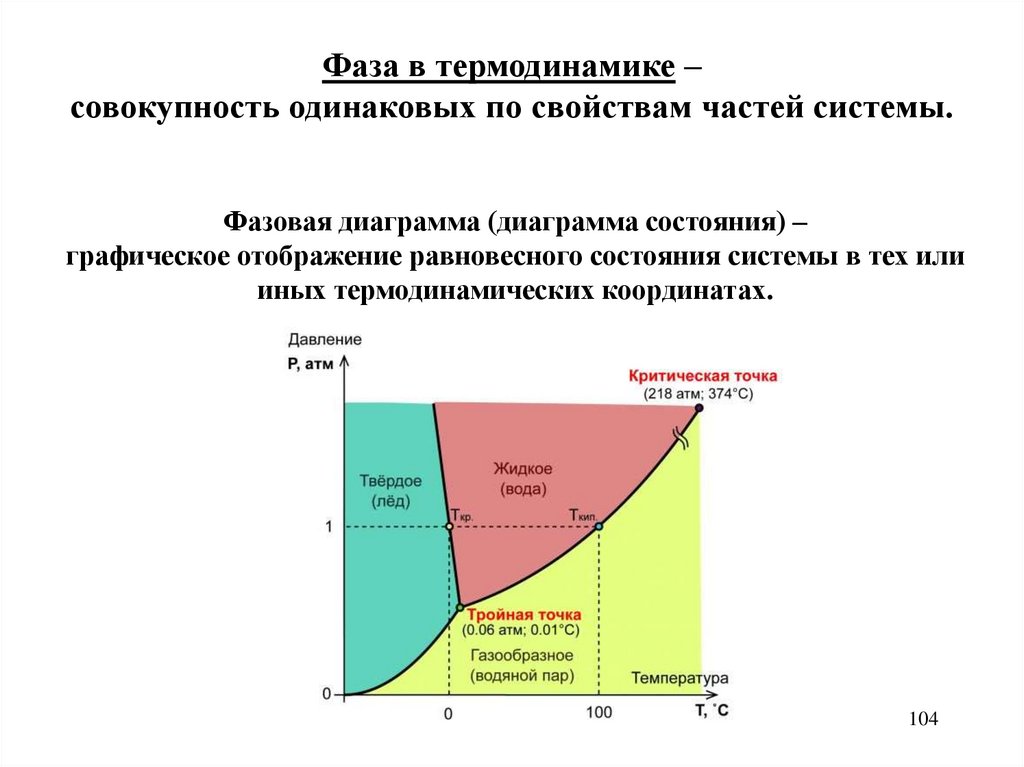
Фаза в термодинамике –
совокупность одинаковых по свойствам частей системы.
Фазовая диаграмма (диаграмма состояния) –
графическое отображение равновесного состояния системы в тех или
иных термодинамических координатах.
104