Похожие презентации:
Кинематика поступательного движения
1.
ШабунинаНаталья Владимировна
к.п.н., доцент кафедры
фундаментальной и прикладной физики
высшей школы естественных наук и
технологий САФУ
2.
МЕХАНИКАКинематика
поступательного
движения
3.
Механическое движение – изменение положениятела (частей тела) в пространстве с течением
времени
Объекты изучаемые механикой:
1) Материальная точка – тело, размерами которого по сравнению с масштабом движения, в
условии данной задачи можно пренебречь
2) Абсолютно твёрдое тело – тело, деформацией которого в условии данной задачи можно
пренебречь
4.
Поступательным движением абсолютно твёрдоготела называют
В
А
Система отсчёта включает:
1) тело отсчёта;
2) систему координат, связанную с телом отсчёта;
3) часы для временного описания движения.
5.
zА
r (t )
k
i
j
x
y
Радиус-вектор r (t ) -
а) векторная форма:
r (t ) x(t ) i y (t ) j z (t ) k
б) скалярная форма:
| r | r x y z
2
2
2
6.
Основныекинематические
характеристики
7.
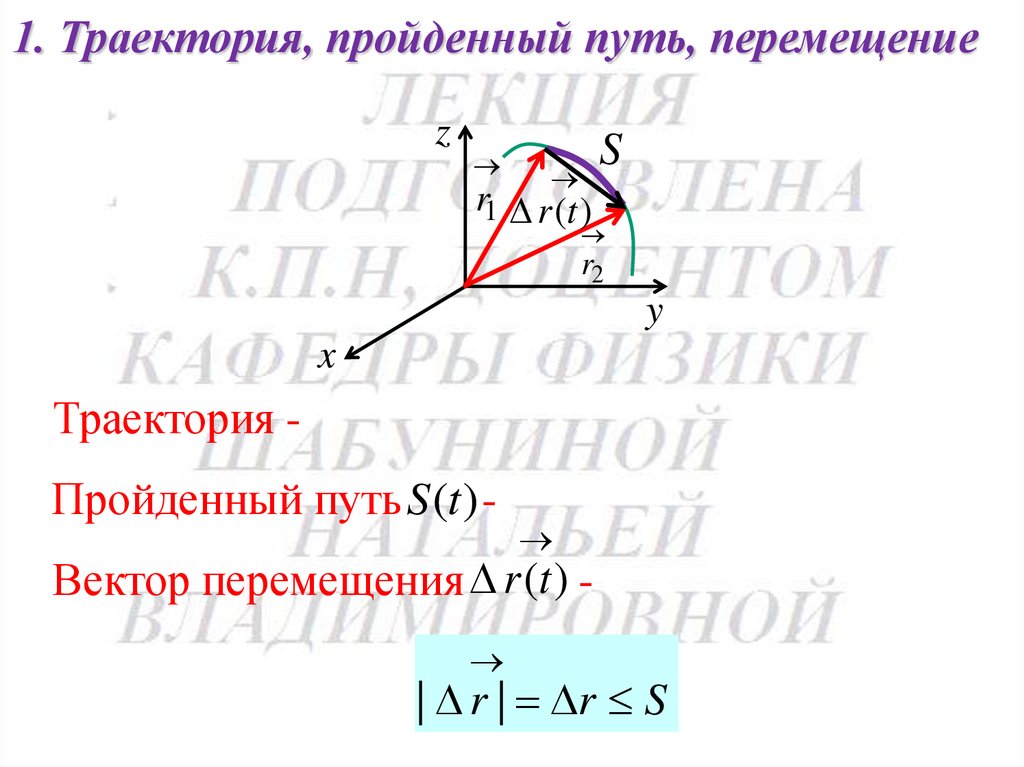
1. Траектория, пройденный путь, перемещениеz
S
r1 r (t )
r2
y
x
Траектория Пройденный путь S (t ) -
Вектор перемещения r (t )
| r | r S
8.
2. Скорость произвольного движенияа) Вектор средней скорости υ
r
υ
t
Модуль вектора средней скорости:
r
υ
t
м
υ 1
с
Вектор средней скорости направлен по вектору
перемещения
9.
б) Вектор мгновенной скорости υdr
υ
r
dt
Вектор мгновенной скорости в проекции на координатные оси:
υ υx i υ y j υz k
dx
dy
dz
υx
x ; υ y
y ; υz z
dt
dt
dt
Вектор мгновенной скорости направлен по касательной к траектории
10.
с) Средняя путевая скорость υS
υ
t
υ υ
11.
3. Ускорение произвольного движенияа) Вектор среднего ускорения a
υ
a
t
Модуль вектора среднего ускорения:
υ
a
t
a 1
м
с
2
Вектор среднего ускорения направлен по векторному изменению скорости
12.
б) Вектор мгновенного ускорения a2
dυ
d r
a
υ 2 r
dt
dt
Вектор мгновенного ускорения в проекции на координатные оси:
a ax i a y j az k
2
dυ y
2
2
dυx d x
d y
dυz d z
ax
2 ; ay
2 ; az
2
dt dt
dt
dt dt
dt
13.
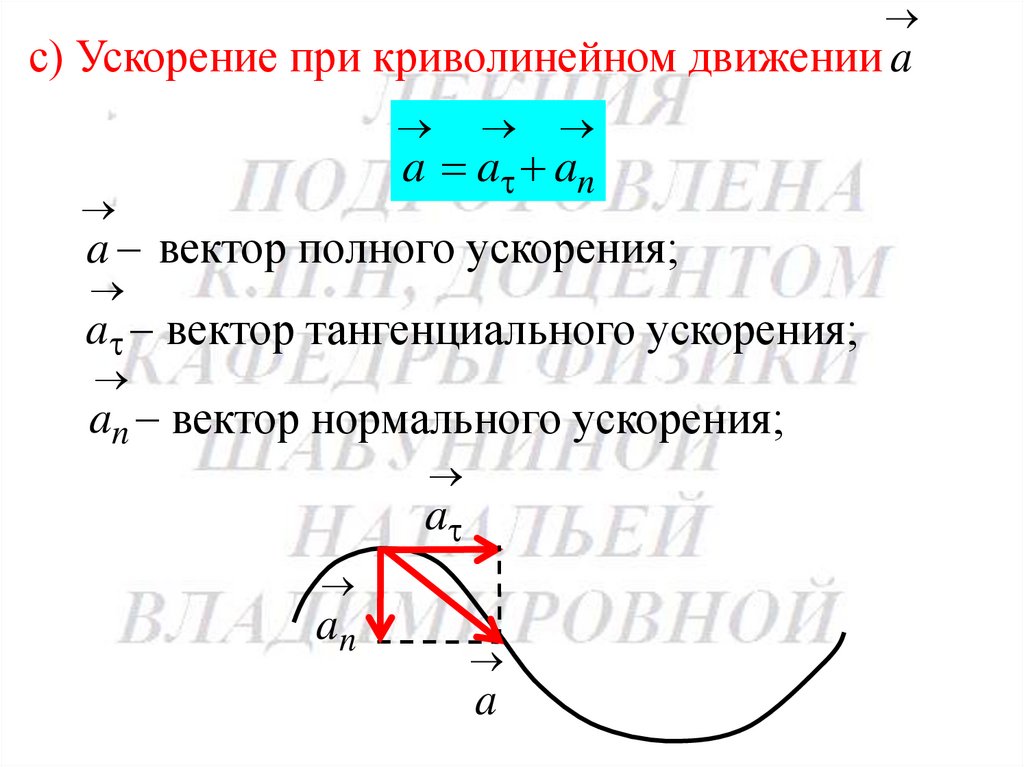
с) Ускорение при криволинейном движении aa a an
a вектор полного ускорения;
a вектор тангенциального ускорения;
an вектор нормального ускорения;
a
an
a
14.
Модуль полного ускорения:a a an
2
2
Модуль нормальной составляющей ускорения:
υ2
an
R
Модуль тангенциальной составляющей ускорения:
d|υ|
a
dt
15.
Кинематикавращательного
движения
16.
Вращательным движением абсолютно твёрдоготела называют
17.
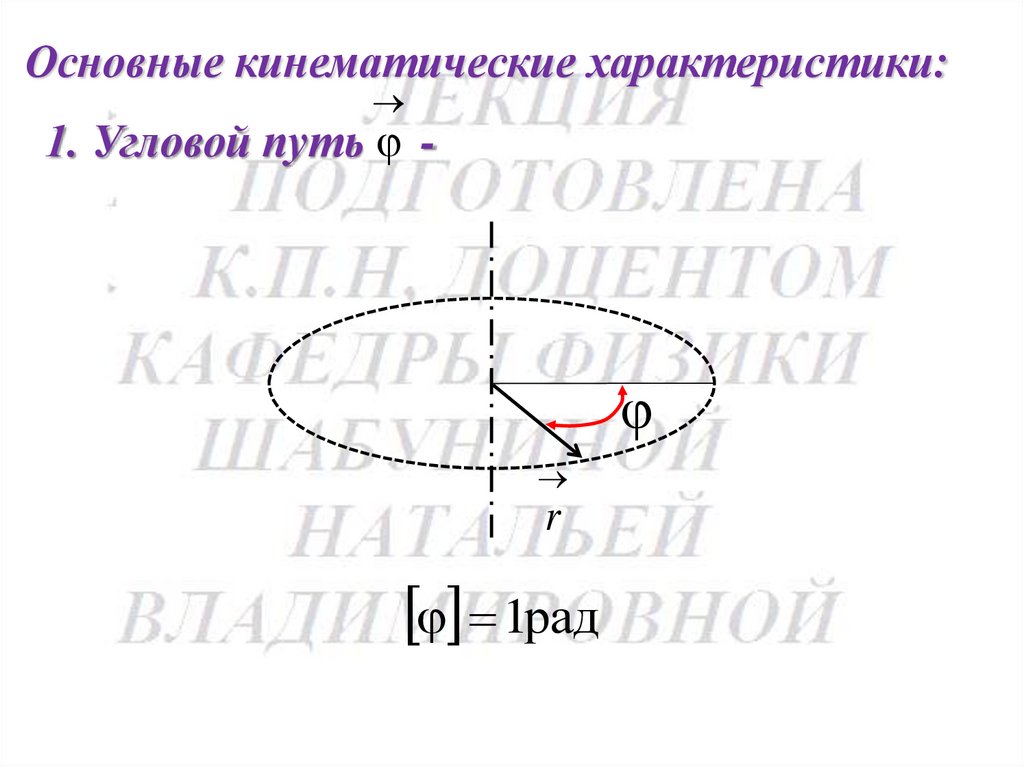
Основные кинематические характеристики:1. Угловой путь -
r
1рад
18.
2. Угловая скоростьа) Вектор средней угловой скорости
t
Модуль вектора средней угловой скорости:
t
рад
1
с
б) Вектор мгновенной угловой скорости
d
dt
19.
3. Угловое ускорениеа) Вектор среднего углового ускорения
t
Модуль вектора среднего углового ускорения:
рад
1 2
t
с
б) Вектор мгновенного углового ускорения
2
d
d
2
dt
dt
20.
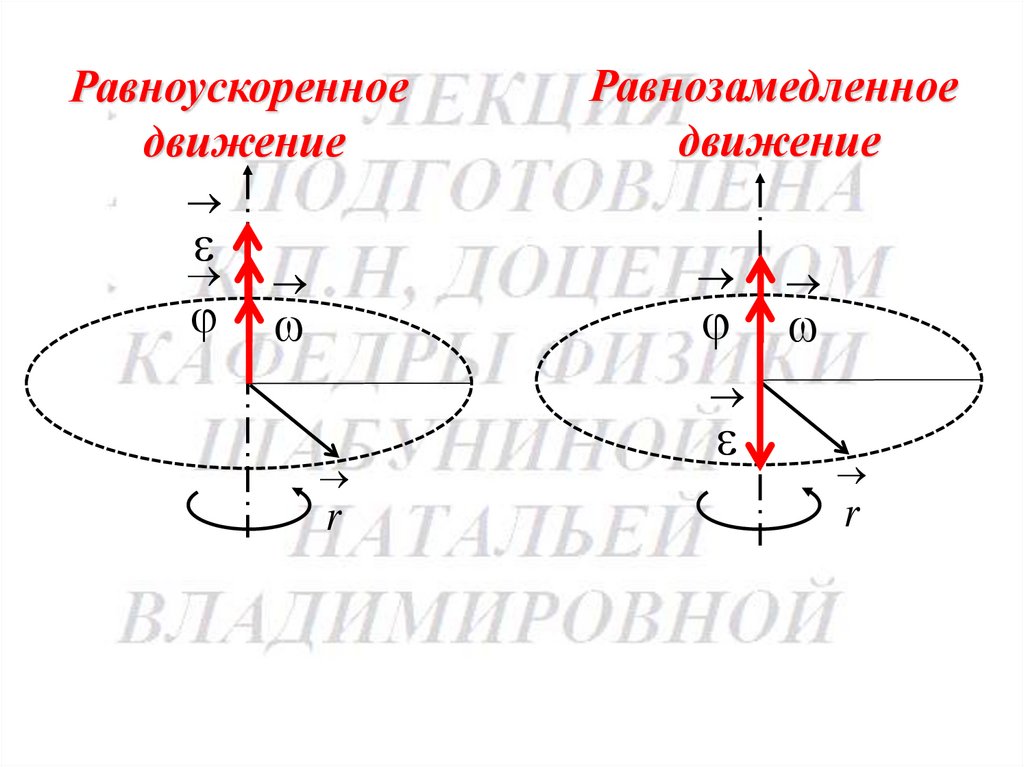
Равноускоренноедвижение
Равнозамедленное
движение
r
r
21.
Связь междуугловыми и линейными
характеристиками
22.
1. Связь между линейным и угловым путями:S R
2. Связь между линейной и угловой скоростями:
υ R
3. Связь между тангенциальным и угловым ускорениями:
a R
4. Связь между нормальным ускорением и угловой скоростью:
an R
2
23.
5. Полное линейное ускорение через угловые характеристики:a
2
an
2
a
a R
an R
2
a R
4
2
24.
Динамикапоступательного
движения
25.
ЗаконыНьютона
26.
1 закон НьютонаФормулировка:
Существуют такие инерциальные системы отсчета в
которых тело покоится или движется прямолинейно
равномерно до тех пор, пока воздействие со стороны
других тел не вызовут изменение этого состояния
Любая другая система отсчета, движущаяся
относительно инерциальной равномерно прямолинейно
также является инерциальной, то есть ИСО
существует бесконечно много
27.
2закон
Ньютона
Импульс тела p - векторная физическая величина,
численно равная произведению
массы тела на скорость его движения
p m υ
кг м
p 1
с
Результирующая сила F рез - векторная сумма всех
сил, действующих на тело
N
Fрез Fi
i 1
28.
Формулировка:Производная импульса тела по времени равна
результирующей всех сил, действующих на тело
Fрез
d p - 2 закон Ньютона в диф
dt ференциальной форме
Формулировка (в классической механике):
Результирующая сила, действующая на тело равна
произведению массы тела на ускорение, сообщенное
этой силой
Fрез m a - основной закон динамики поступательного движения (2 закон
Ньютона в классической механике)
29.
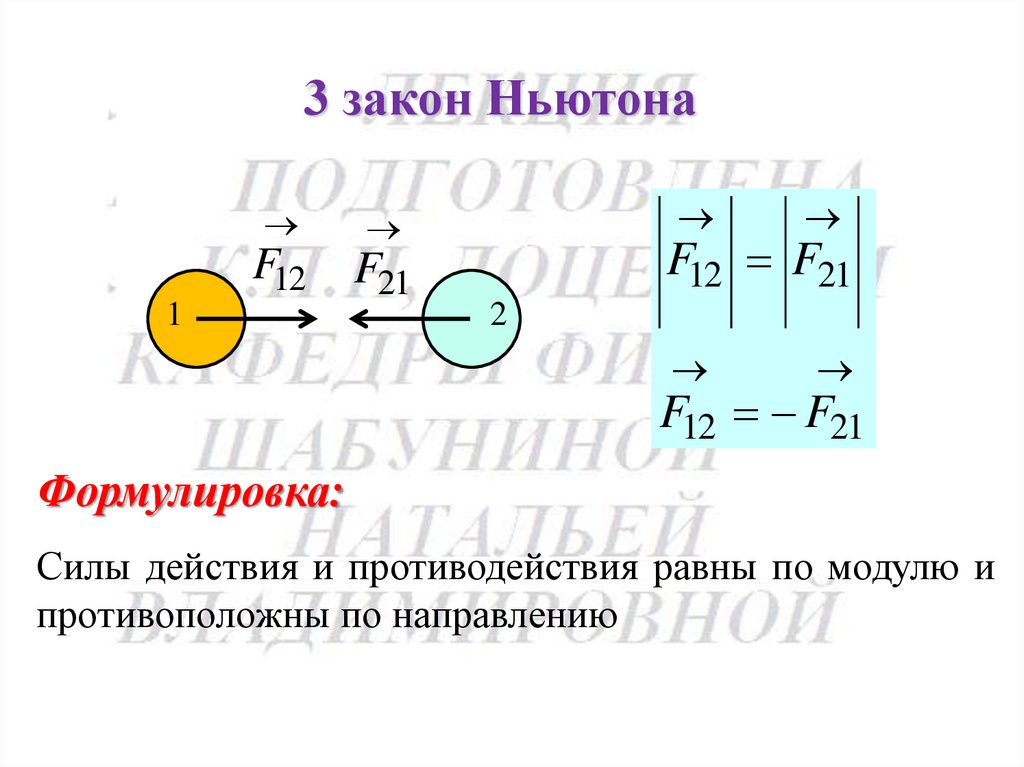
3 закон НьютонаF12
F21
1
F12 F21
2
F12 F21
Формулировка:
Силы действия и противодействия равны по модулю и
противоположны по направлению
30.
Законсохранения импульса
31.
Механическая система– совокупность тел, вы-
деленных для рассмотрения
Силы
внешние
Замкнутая система
внутренние
– система в которой не
действуют внешние силы
Все законы сохранения выполняются только в замкнутых системах
32.
Формулировка:Суммарный импульс замкнутой системы тел есть
величина постоянная
p const
Замечание:
Если система тел не замкнутая, то для применения
закона сохранения импульса необходимо выбрать
направление на которое проекция всех внешних сил
равна нулю
33.
Динамикавращательного
движения
34.
Момент силы имомент импульса
35.
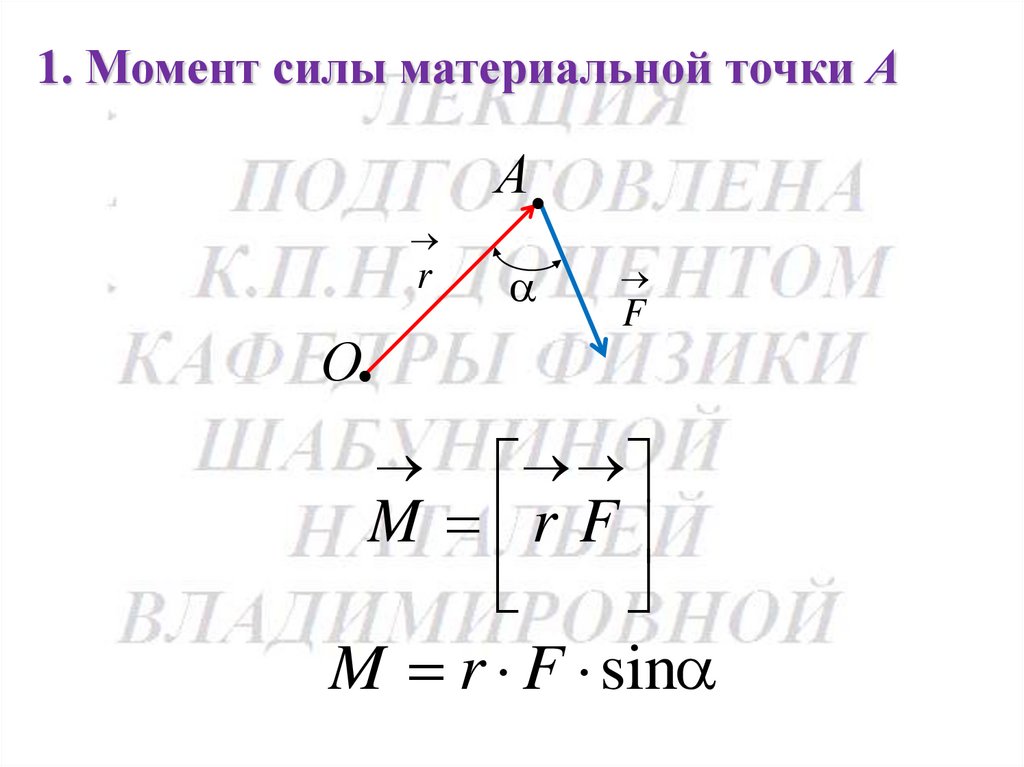
1. Момент силы материальной точки АА
r
О
F
M r F
M r F sin
36.
M r F sin F d Fd F r sin
А
r
О
dF
F
M F dF
M 1Н м
M
Направление вектора момента силы определяют по правилу правого винта
37.
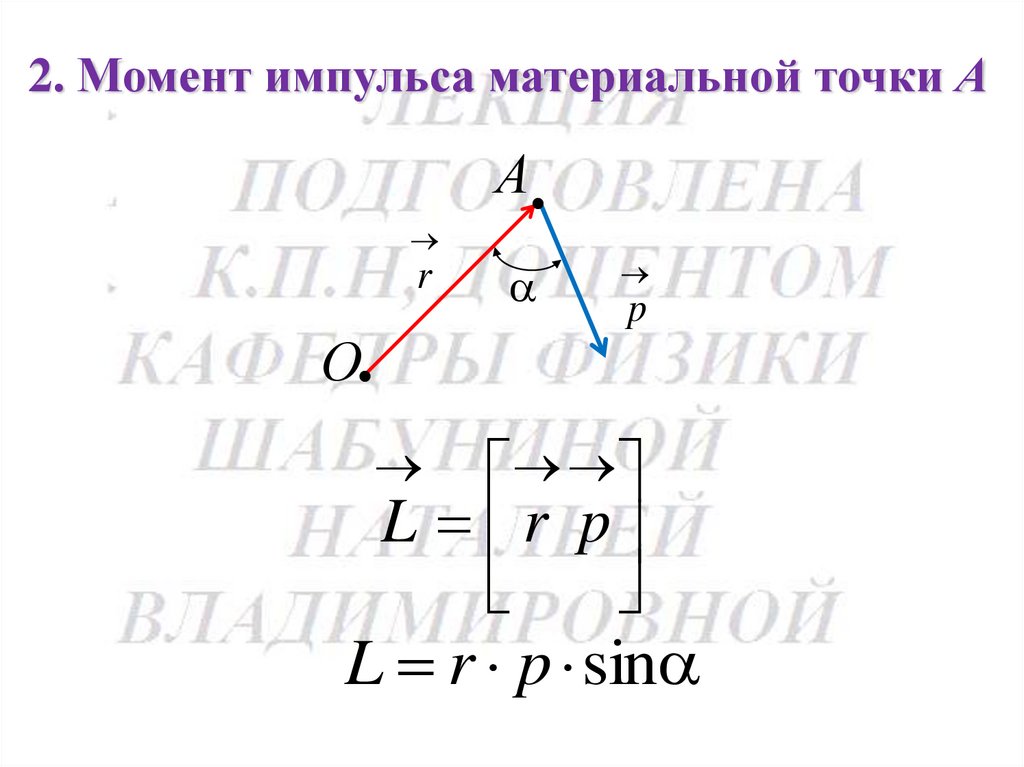
2. Момент импульса материальной точки АА
r
О
p
L r p
L r p sin
38.
L r p sin p d pd p r sin
А
r
О
L
dp
p
L p dp
кг м
L 1
с
2
Направление вектора момента импульса определяют по правилу правого винта
39.
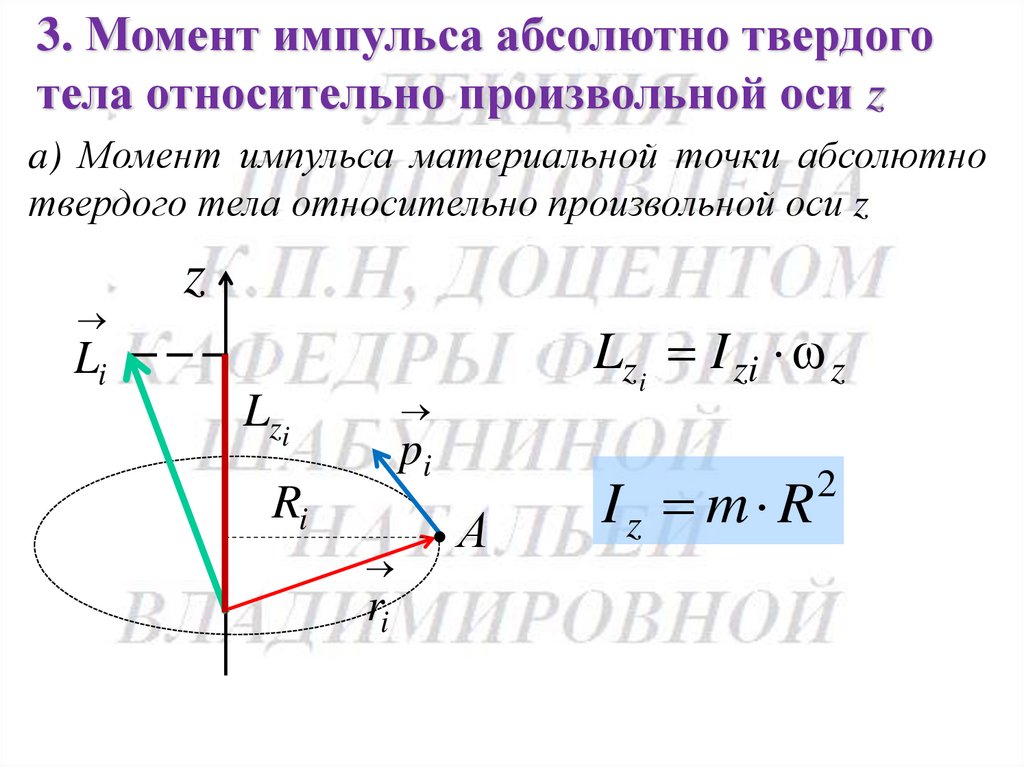
3. Момент импульса абсолютно твердоготела относительно произвольной оси z
a) Момент импульса материальной точки абсолютно
твердого тела относительно произвольной оси z
z
Li
Lzi I zi z
Lzi
pi
Ri
ri
А
Iz m R
2
40.
Iz m R2
Момент инерции материальной
точки относительно оси I z- скалярная физическая величина, численно равная произведению
массы материальной точки на квадрат
расстояния от неё до оси вращения
I 1 кг м
2
41.
б) Пусть абсолютно твердое тело - это совокупностьматериальных точек, тогда
N
Lz Lz i
i 1
Момент импульса абсолютно твердого тела
относительно произвольной оси равен алгебраической сумме моментов импульса каждой
точки тела относительно той же оси
42.
NLz Lz i
i 1
N
N
i 1
i 1
Lz Lz i I z i z I z z
Lzi N I z i z
I z I zi - свойство аддитивности момента
i 1
инерции абсолютно твердого тела
Момент инерции абсолютно твердого тела относительно произвольной оси равен сумме моментов
инерции материальных точек тела относительно той же
оси
43.
NN
i 1
i 1
I z I zi
2
mi Ri
2
I zi N mi Ri 2
I z mi Ri
i 1
Момент инерции абослютно твердого тела относительно оси I z - скалярная физическая
величина, численно равная сумме произведений масс материальных точек на
квадрат их расстояния до оси вращения
44.
Вывод:Lz I z z
Момент импульса абсолютно твердого тела
относительно произвольной оси равен произведению момента инерции твердого тела на
угловую скорость относительно той же оси
45.
Основной закондинамики
вращательного
движения
46.
Формулировка:Производная момента импульса тела по времени равна
результирующему моменту всех внешних сил, действующих на тело
внеш
M рез
M
внеш
резz
dL
dt
Iz εz
- основной закон динамики
вращательного движения
- основной закон динамики
вращательного движения в
проекции на ось
47.
Сравним основные законы динамики для поступательного и вращательного движенийFрезx m ax
M
внеш
резz
Iz εz
Вывод:
Момент инерции «играет» роль массы во вращательном движении.
Момент инерции является мерой инертности
во вращательном движении.
48.
Момент инерциии способы его
вычисления
49.
Момент инерции материальной точки относительно осиIz m R
2
Момент инерции абсолютно твердого тела
относительно оси
N
N
i 1
i 1
I z I zi
2
mi Ri
50.
Момент инерции однородного твердого тела,масса которого равномерно распределена по
всему объёму
I z dm R
V
2
51.
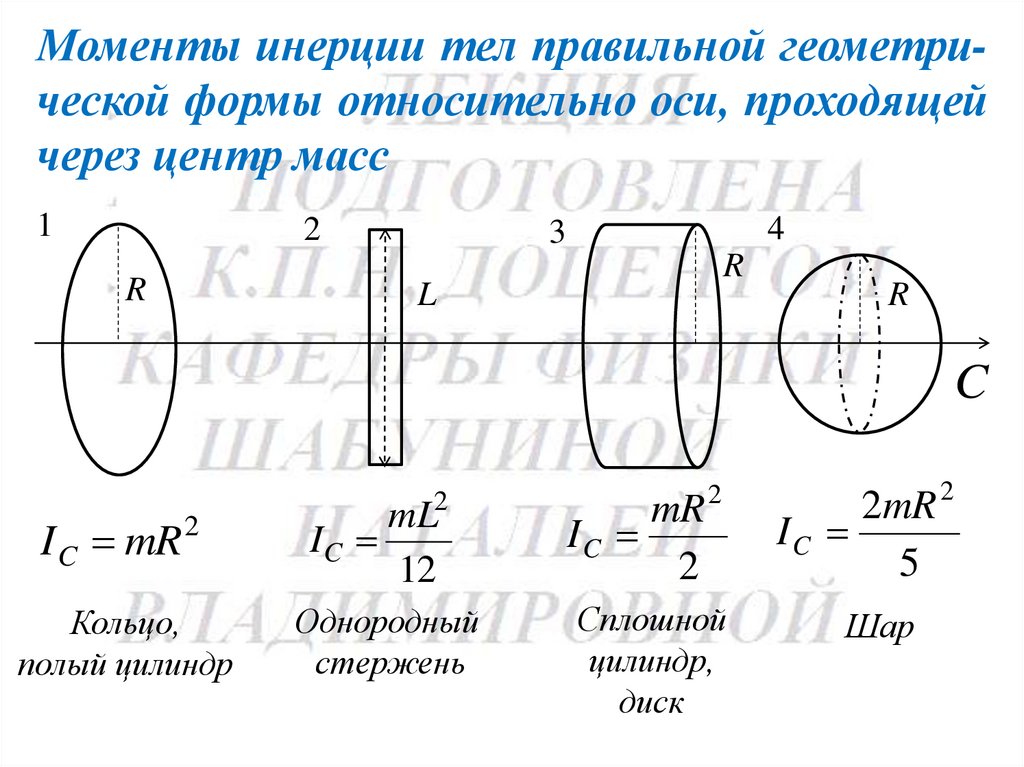
Моменты инерции тел правильной геометрической формы относительно оси, проходящейчерез центр масс
1
2
R
4
3
R
L
R
C
I C mR
2
Кольцо,
полый цилиндр
2
mL
IC
12
Однородный
стержень
mR
IC
2
2
Сплошной
цилиндр,
диск
2mR
IC
5
Шар
2
52.
Теорема Штейнера (позволяет определитьмомент инерции твердого тела относительно
произвольной оси)
Формулировка:
Момент инерции твердого тела относительно произвольной оси равен сумме момента инерции тела
относительно оси, проходящей через центр масс тела
параллельно произвольной и произведения массы тела
на квадрат расстояния между осями
I Z I C md
2
53.
Закон сохранениямомента импульса
54.
Формулировка:В замкнутой системе векторная сумма моментов импульса всех тел системы есть величина постоянная
n
Li const
i 1
Закон сохранения момента импульса в проекции на ось
z имеет вид
Lz const
I z z const
Lz I z z
55.
РАБОТА, МОЩНОСТЬИ МЕХАНИЧЕСКАЯ
ЭНЕРГИЯ
56.
Физическое понятиеработы. Мощность
57.
1) Работа переменной силыПолная работа переменной силы F на всём
пути
2
A12 dA
1
2
2
2
1
1
1
A12 F dr Fdrcos FdScos
A 1 Дж
58.
2) Работа постоянной силыF const; const
A12 FS12cos
3) Мощность
а) мгновенная мощность
dA
Дж
N 1 1Вт
N
c
dt
N Fυcos
59.
б) средняя мощностьA
N
t
60.
Механическаяэнергия
61.
1) Кинетическая энергия поступательногодвижения. Теорема об изменении кинетической энергии
Кинетическая энергия Eк , T - энергия движения, определяемая массой и скоростью рассматриваемого тела
mυ
Eк
2
2
- кинетическая энергия поступательного движения
A12 Eк2 Eк1 Eк
- теорема об изменении
кинетической энергии
62.
2) Кинетическая энергия вращающегося тела.Работа и мощность во вращательном движении
Eквр
2
I z z
2
- кинетическая энергия во
вращательном движении
A
внеш .
M Z Z
N
внеш .
M Z Z - мощность во вращательном
движении
- работа во вращательном
движении
63.
3) Кинетическая энергия плоского движенияПлоское движение – движение при котором все точки
тела движутся в параллельных плоскостях
Eк Eк пост Eк вращ
2
mυc
2
2
I c c
2
64.
4) Потенциальная энергияСилы
потенциальные
(консервативные)
непотенциальные
(диссипативные)
Работа потенциальных сил не зависит от формы траектории по которой движется тело, а зависит от характеристик начального и конечного положений тела
Работа потенциальных сил по замкнутой траектории
равна нулю
65.
a) работа силы тяжестиA12 mgh1 mgh2
б) работа силы упругости
A12
2
kx1
2
2
kx2
2
Сила тяжести и сила упругости – это потенциальные
силы
66.
Потенциальная энергия E p , П - энергия положения;энергия взаимодействия тел или частей тела
Работа потенциальных сил совершается за счёт убыли
потенциальной энергии
пот
A12
E p E p1 E p 2
E p mgh
kx
Ep
2
- потенциальная энергия в
поле силы тяжести
2
- потенциальная энергия в
поле силы упругости
67.
Закон сохраненияэнергии
68.
1. Закон сохранения полной механической энергииEк1 E p1 Eк 2 E p 2
E Eк E p
- полная механическая энергия
E1 E2
E const
- закон сохранения полной механической энергии
Формулировка:
Только в поле потенциальных сил полная механическая
энергия замкнутой системы тел есть величина
постоянная
69.
2. Если в системе действуют и потенциальные, и непотенциальные силы, тодис
A12
E2 E1
дис
A12
E
Формулировка:
Работа диссипативной силы равна изменению полной
механической энергии системы тел
70.
3. Закон сохранения энергииФормулировка:
Полная энергия замкнутой системы тел есть величина
постоянная, то есть энергия не исчезает в никуда и не
возникает ни из чего, она превращается из одного вида
в другой или передаётся от одного тела к другому
71.
ЭЛЕКТРОСТАТИКАЗакон Кулона.
Напряженность
электрического поля
72.
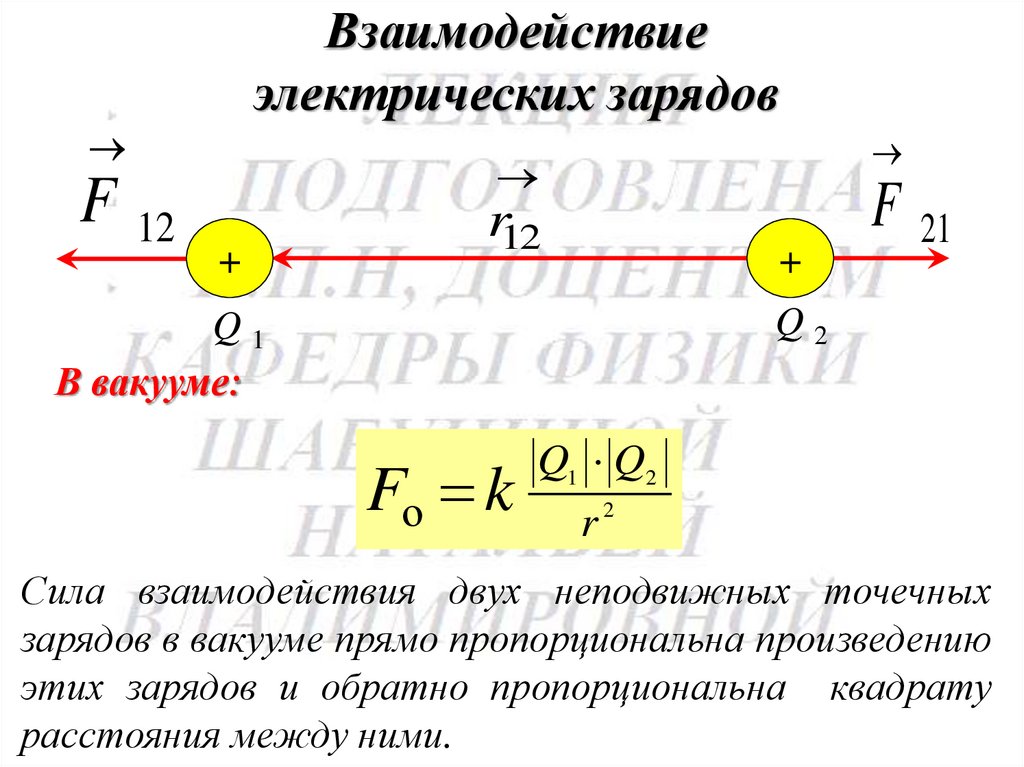
Взаимодействиеэлектрических зарядов
F 12
+
r12
F
+
21
Q2
Q1
В вакууме:
Fо k
Q1 Q2
2
r
Сила взаимодействия двух неподвижных точечных
зарядов в вакууме прямо пропорциональна произведению
этих зарядов и обратно пропорциональна квадрату
расстояния между ними.
73.
k = 9 109 (Н м2 )/Кл21
k
4 0
0 = 8,85 10 -12 Ф/м
В среде:
F0
F
F k
F0
F
Q1 Q2
r
2
74.
Электрическое полесоздаёт
ЗАРЯД
действует
ЭЛЕКТРИЧЕСКОЕ
ПОЛЕ
действует
создаёт
ЗАРЯД
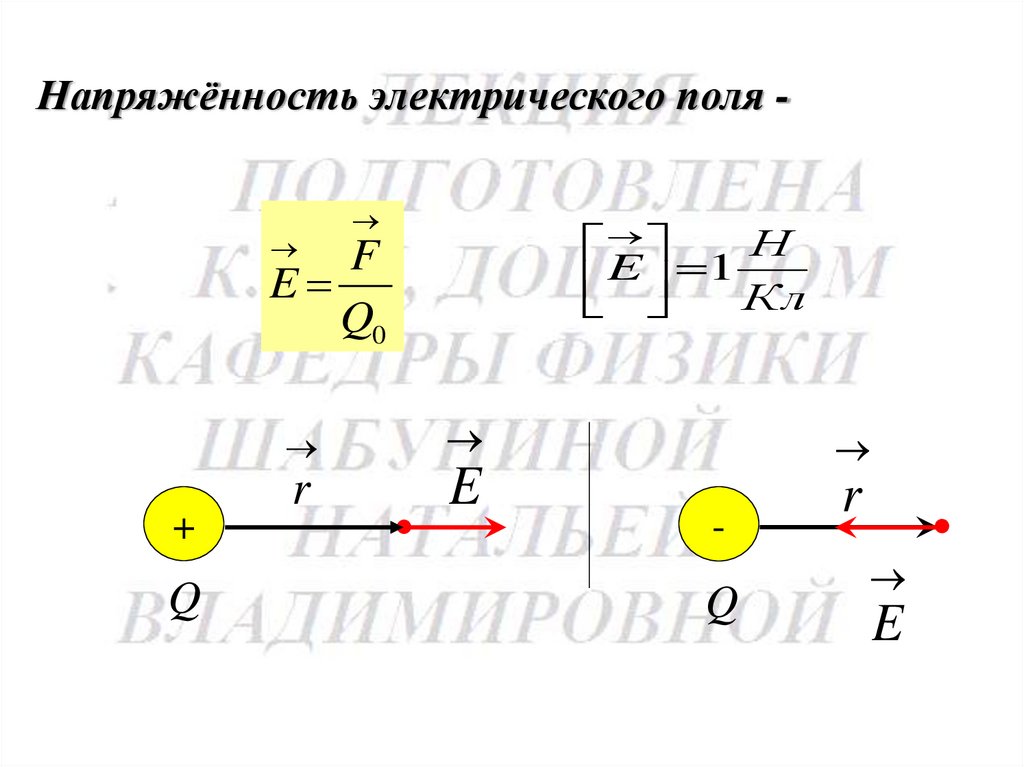
75.
Напряжённость электрического поля -Н
E 1 Кл
F
E
Q0
+
Q
r
E
-
Q
r
E
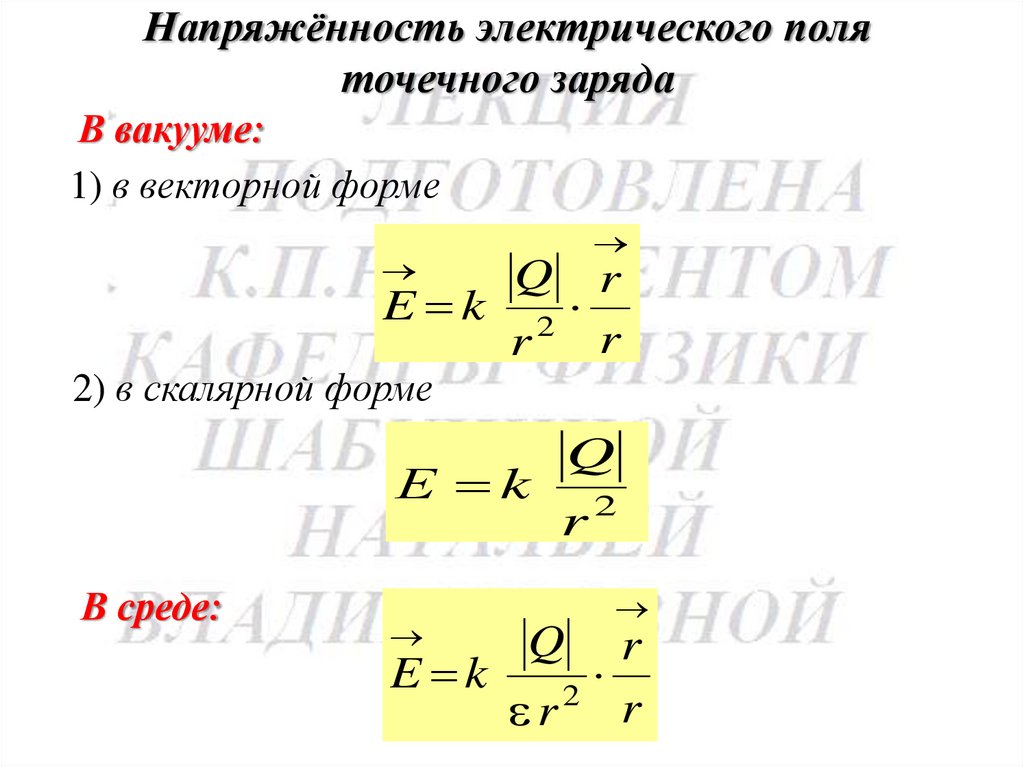
76.
Напряжённость электрического поляточечного заряда
В вакууме:
1) в векторной форме
Q
r
E k 2
r
r
2) в скалярной форме
Е k
В среде:
Q
r
2
Q
r
E k
2
r r
77.
Силовые линии электрического поляE
E
+
А
EA
В •
EB
78.
Работа электрическогополя. Потенциал.
Связь между
напряженностью и
потенциалом
79.
Работа электростатического поля при перемещениизаряда Q0 из точки 1 в точку 2 определяется:
1 1
A12 k Q Q0
r1 r2
Вывод: ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ЯВЛЯЕТСЯ
ПОТЕНЦИАЛЬНЫМ.
Потенциал электростатического поля -
Ер
q0
Дж
1 1В
Кл
80.
Тогда потенциальная энергия заряда Q0 в электрическомполе:
Е р Q0
Работа электростатического поля при перемещении
заряда Q0:
А12 Q0 ( 1 2 )
Потенциал поля точечного заряда:
1 Q
4 0 r
или
Q
k
r
81.
Связь между напряжённостью электрического поля ипотенциалом
d
Е
d
В проекции на координатные оси выражение имеет вид:
Е
x i y j z k
grad
i
j
k
y
z
x
Е grad
82.
Теорема Гаусса дляэлектростатического поля в
вакууме
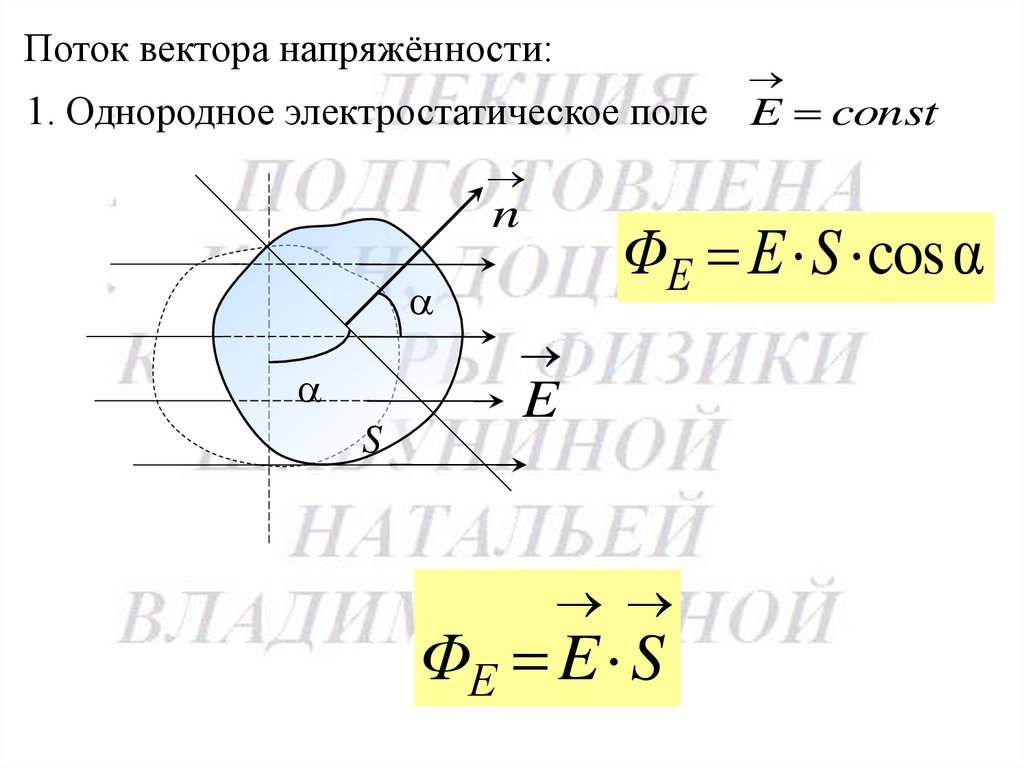
83.
Поток вектора напряжённости:1. Однородное электростатическое поле
E const
n
ΦЕ Е S cos α
S
E
ΦЕ E S
84.
2. Неоднородное электростатическое поле и не плоскаяповерхность
ФE E dS
S
ФE E dS
S
85.
Теорема Гаусса для электростатического поля ввакууме.
Q
E dS
S
0
Поток вектора напряжённости электрического поля
через произвольную замкнутую поверхность в вакууме
равен алгебраической сумме зарядов, заключённых
внутри поверхности, делённой на электрическую
постоянную
86.
Электроёмкость уединённого проводникаQ E
Q
Q C
Кл
C 1 1Ф
В
Ёмкость заряженного шара радиусом R:
С 4 0 R
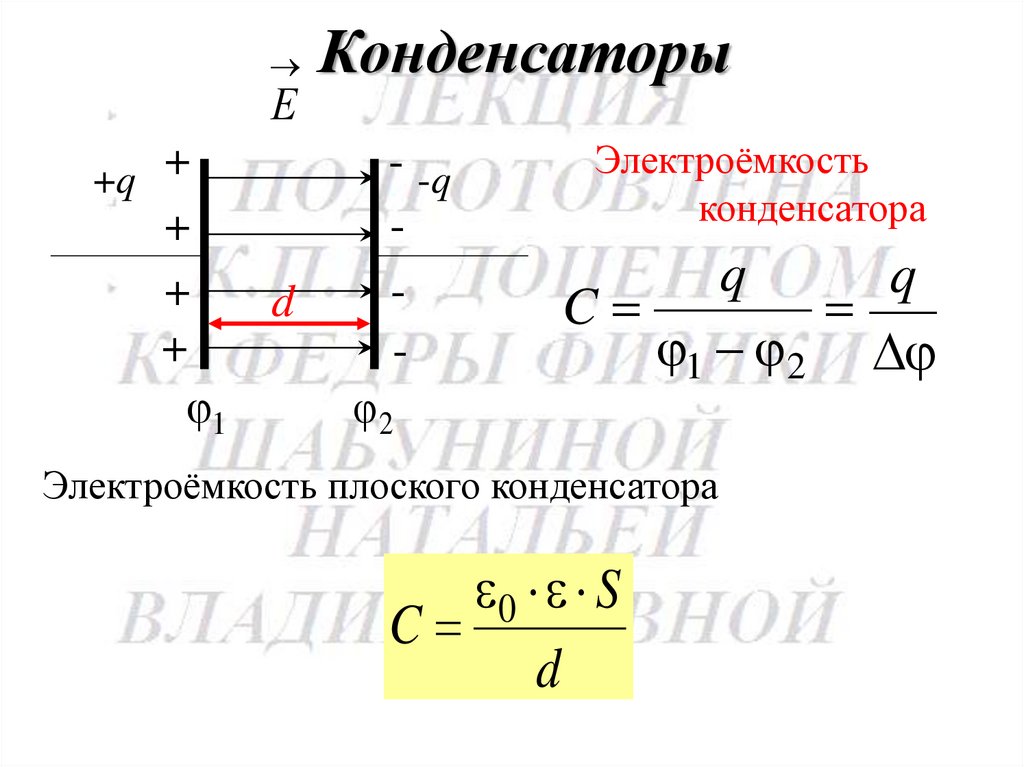
87.
Е+
+q
+
+
d
+
1
Конденсаторы
- -q
2
Электроёмкость
конденсатора
q
q
C
1 2
Электроёмкость плоского конденсатора
0 S
C
d
88.
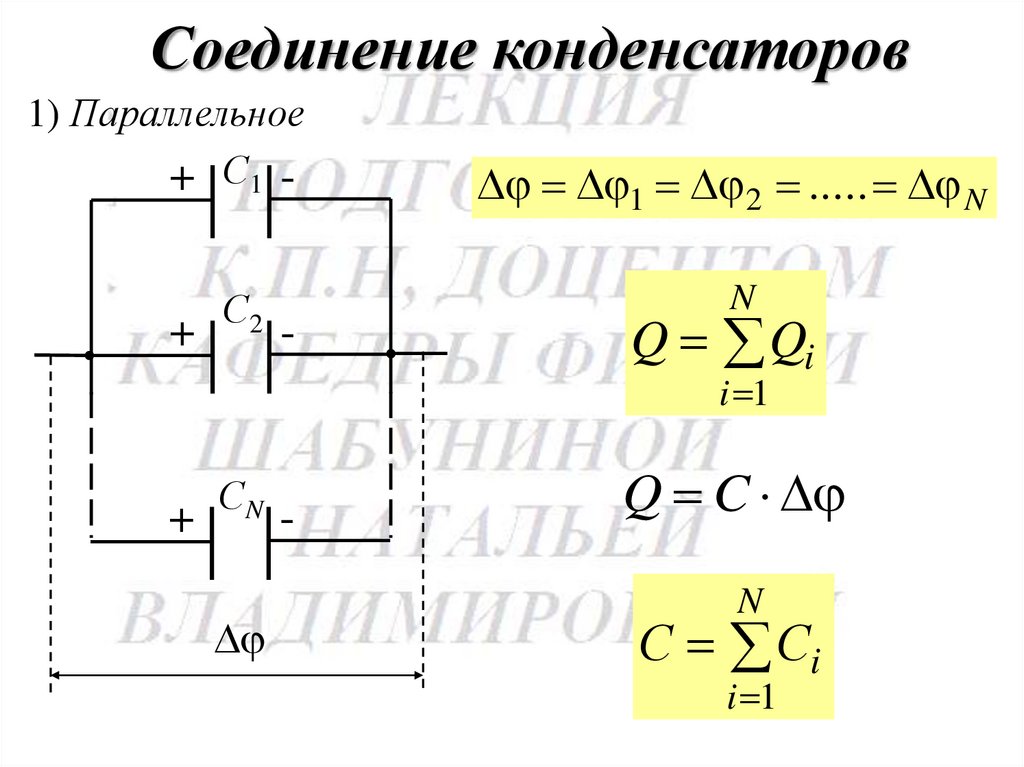
Соединение конденсаторов1) Параллельное
+ С1 -
+
С2
-
1 2 ..... N
N
Q Qi
i 1
+
СN
-
Q C
N
С Сi
i 1
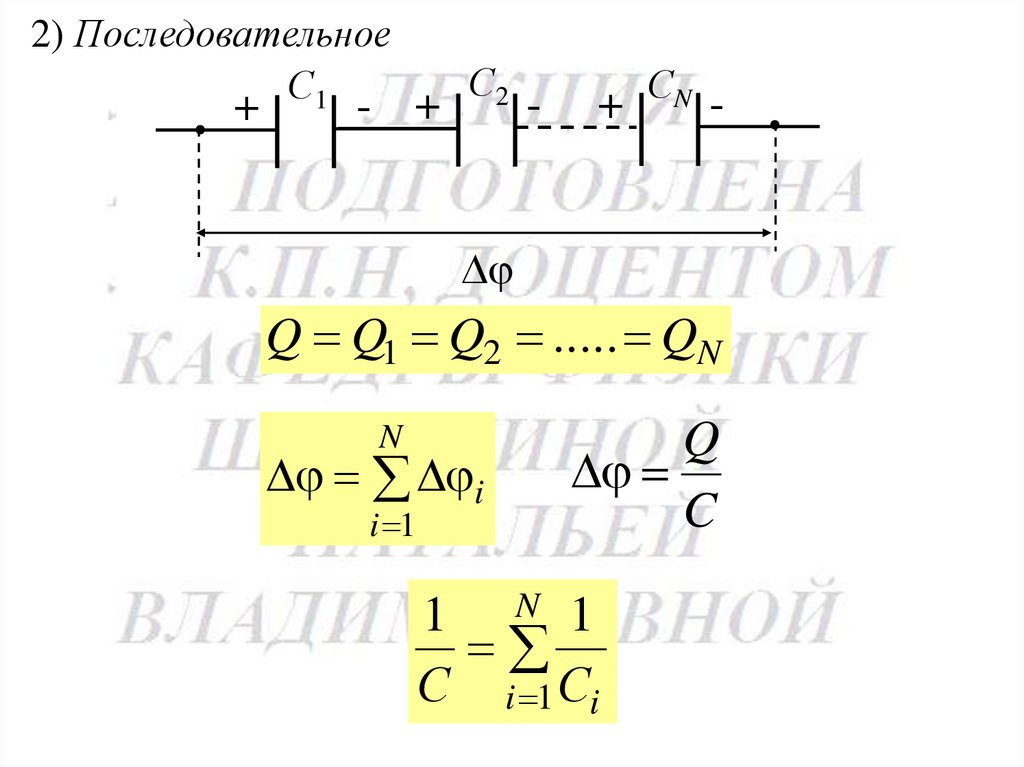
89.
2) ПоследовательноеС1
+
- +
С2
-
+ СN -
Q Q1 Q2 ..... QN
N
i
i 1
Q
C
1 N 1
С i 1 Сi
90.
Энергия заряженного конденсатораq
q C
W
2
2
2C
2
2
q
C
Энергия электростатического поля
1
2
W 0 E V
2
W 0 E 2
V
2
91.
ПОСТОЯННЫЙЭЛЕКТРИЧЕСКИЙ
ТОК
Электрический ток и
его характеристики
92.
Электрический ток- упорядоченное движение заряженныхчастиц
Сила тока ( I ) -
Кл
I 1 1А
с
dq
I
dt
ЭДС ( ) -
Астор
q
Дж
1 1В
Кл
Напряжение на участке цепи ( U ) -
U12
Aстор.12 Аэл.12
q
93.
A12 q ε12 q ( 1 2 ) qU12U12 12 ( 1 2 )
U12 1 2
94.
Законы Ома. Закон Джоуля–Ленца.Правила Кирхгофа
U12
I
R
1 2
I
R
12 ( 1 2 )
I
R12
R ρ
S
-закон Ома для однородного
участка цепи
-закон Ома для неоднородного
участка цепи
95.
IR r
-закон Ома для полной
цепи
2
U
t IU t -закон Джоуля-Ленца для
Q I 2 R t
R
постоянного тока
96.
Для разветвлённых цепей расчёты значительно упрощаются,если использовать правила Кирхгофа
n
Ii 0
1.
i 1
I1 I 2
I5
I4
I3
I1 I 2 I 3 I 4 I 5 0
2.
n
n
i 1
i 1
Ii Ri i
А
K
ABCDA
I1 r1 I R 1
ABFKA
D
I1 r1 I 2 r2 1 2
1 r1
2
r2
I2
R
В
I1
F
I
С
97.
Мощность постоянного тока.КПД источника тока
Полная мощность:
2
P I
R r
Полезная мощность:
2
2
R
U
2
PR IU
I R
2
(
R
r
)
R
Мощность, выделяющаяся на внутреннем сопротивлении:
Pr I U r I 2 r
98.
PR P PrPR
PR I I r
2
dPR
0
dI
0
I’
IКЗ
КПД источника питания:
2
R R r
PR
2
2
P
(R r)
I
I КЗ
I
2r
2
'
R
R
R r
R r
При R = r или при I’ КПД источника тока равен 50%.
99.
МАГНИТНОЕ ПОЛЕТОКА
Магнитное поле
Магнитная индукция
Линии магнитной индукции
100.
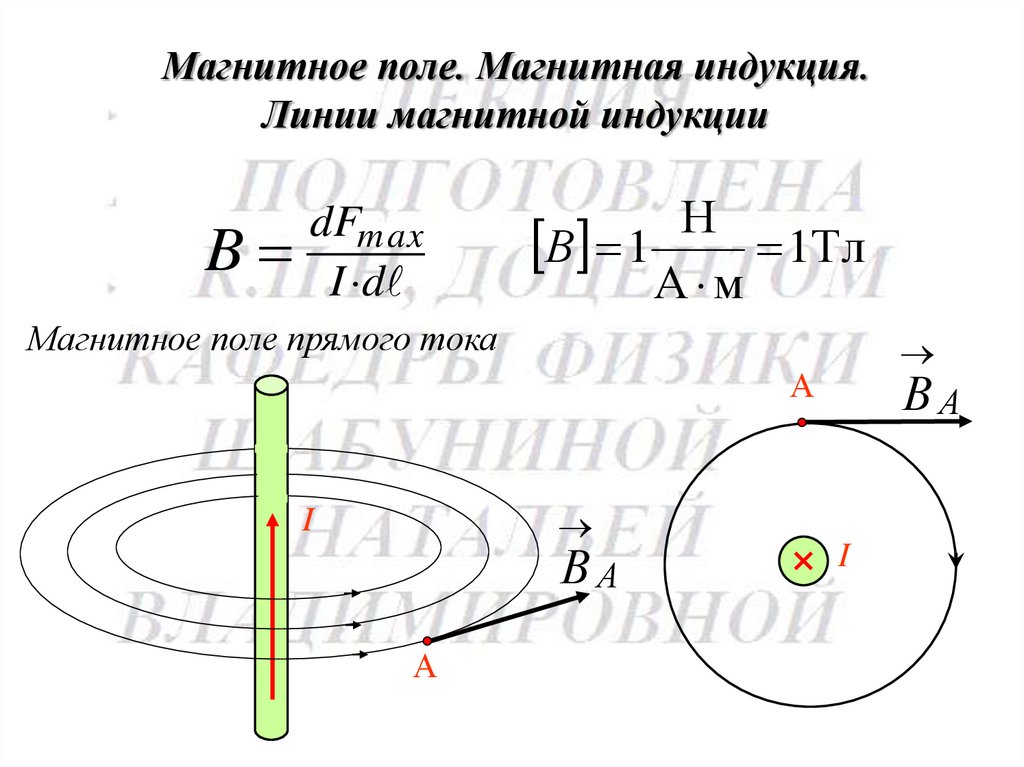
Магнитное поле. Магнитная индукция.Линии магнитной индукции
B
dFmax
I d
Н
В 1
1Тл
А м
Магнитное поле прямого тока
ВА
А
I
ВА
А
I
101.
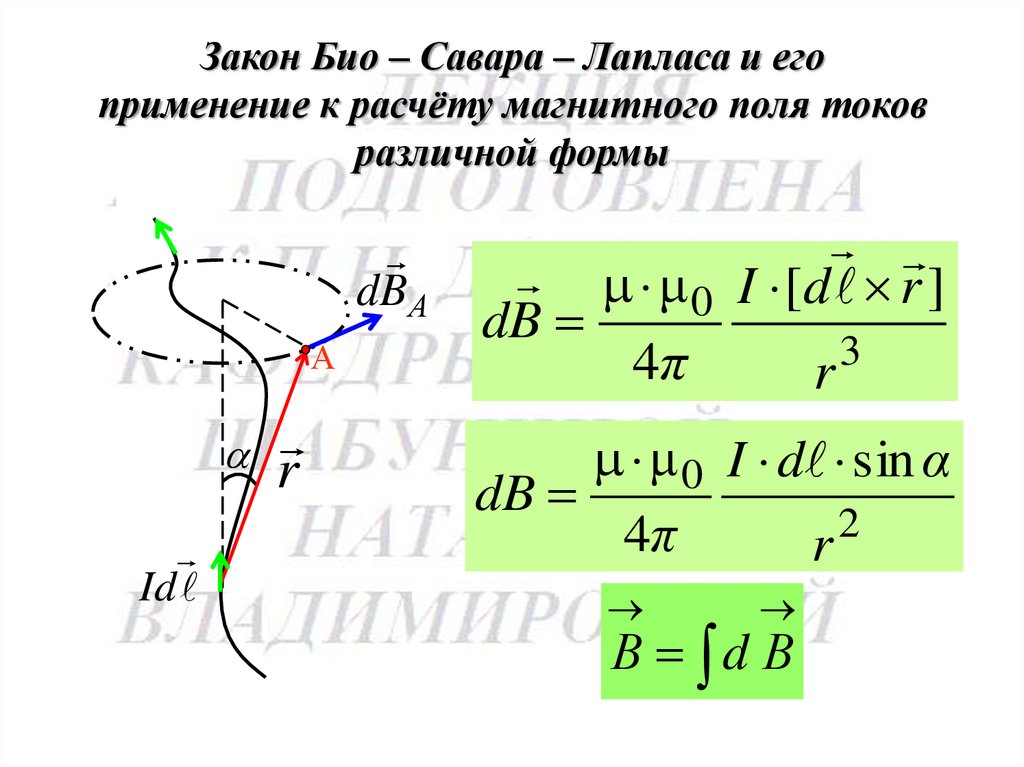
Закон Био – Савара – Лапласа и егоприменение к расчёту магнитного поля токов
различной формы
dB А
А
Id
r
μ 0 I [d r ]
dB
3
4π
r
μ 0 I d sin α
dB
2
4π
r
В d В
102.
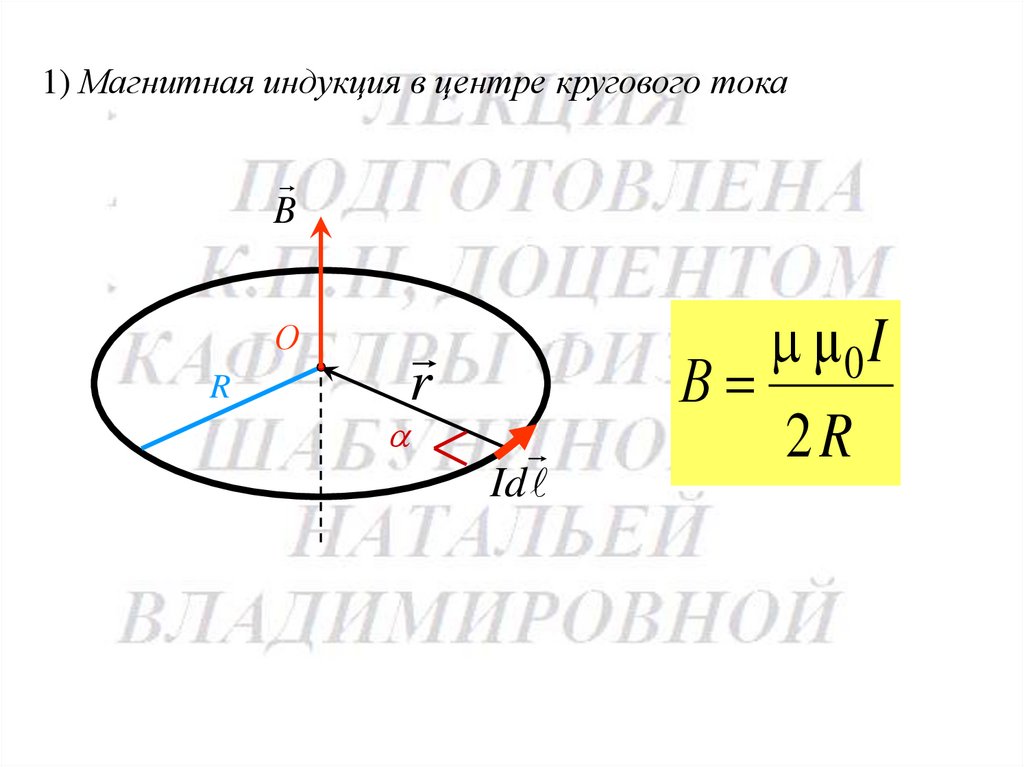
1) Магнитная индукция в центре кругового токаB
О
R
r
Id
μ0I
В
2R
103.
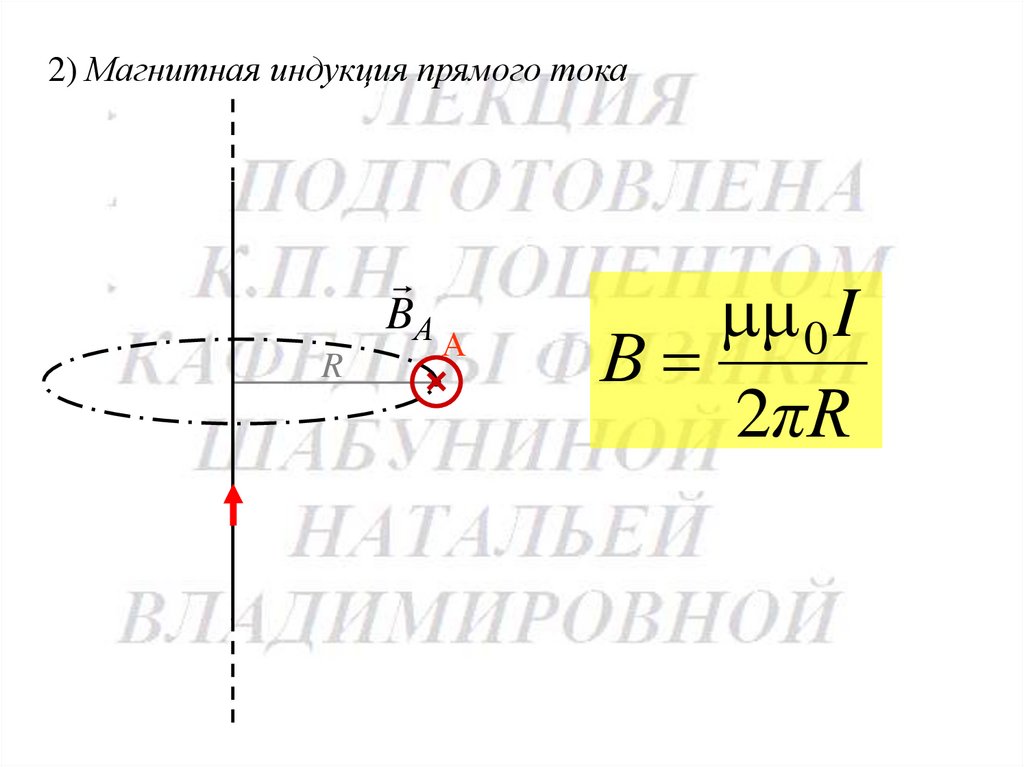
2) Магнитная индукция прямого токаBА
R
А
μ 0 I
В
2πR
104.
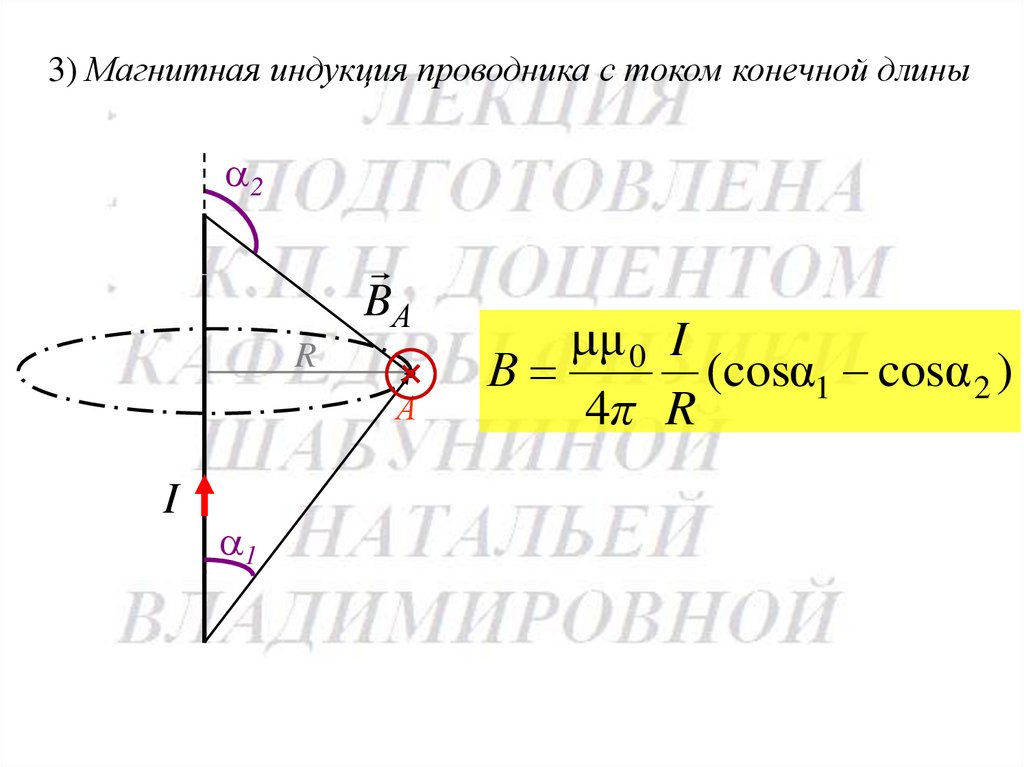
3) Магнитная индукция проводника с током конечной длины2
BА
R
А
I
1
μ 0 I
В
(cosα1 cosα 2 )
4π R
105.
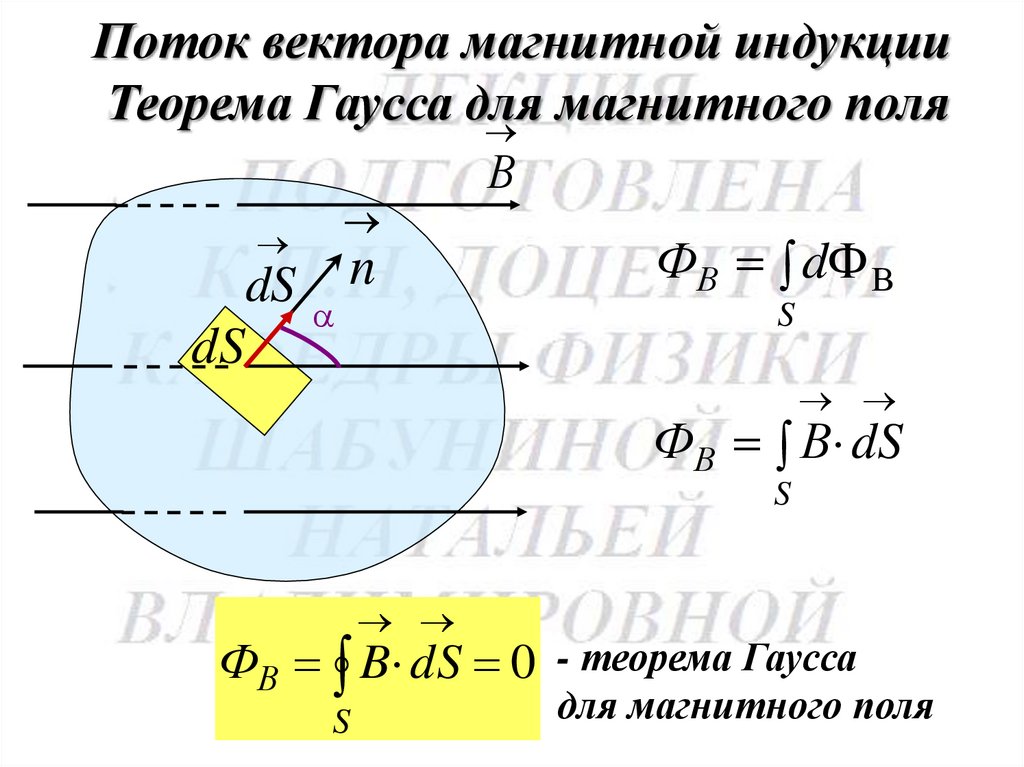
Поток вектора магнитной индукцииТеорема Гаусса для
магнитного
поля
n
dS
dS
В
ФВ dФ В
S
ФВ В dS
S
ФВ B dS 0 - теорема Гаусса
S
для магнитного поля
106.
Сила Ампера. Взаимодействие двухпараллельных токов
dFА I d B
dFА I d B sin
В
I d
dF A
107.
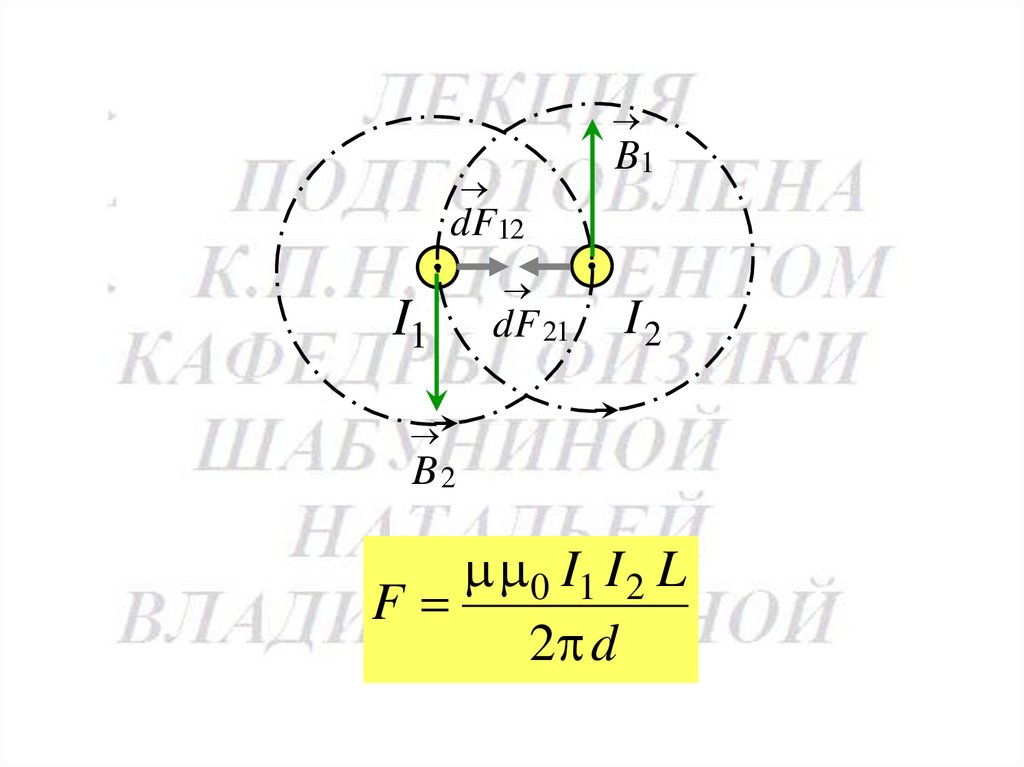
B1dF12
I1
dF 21
I2
B2
0 I1 I 2 L
F
2 d
108.
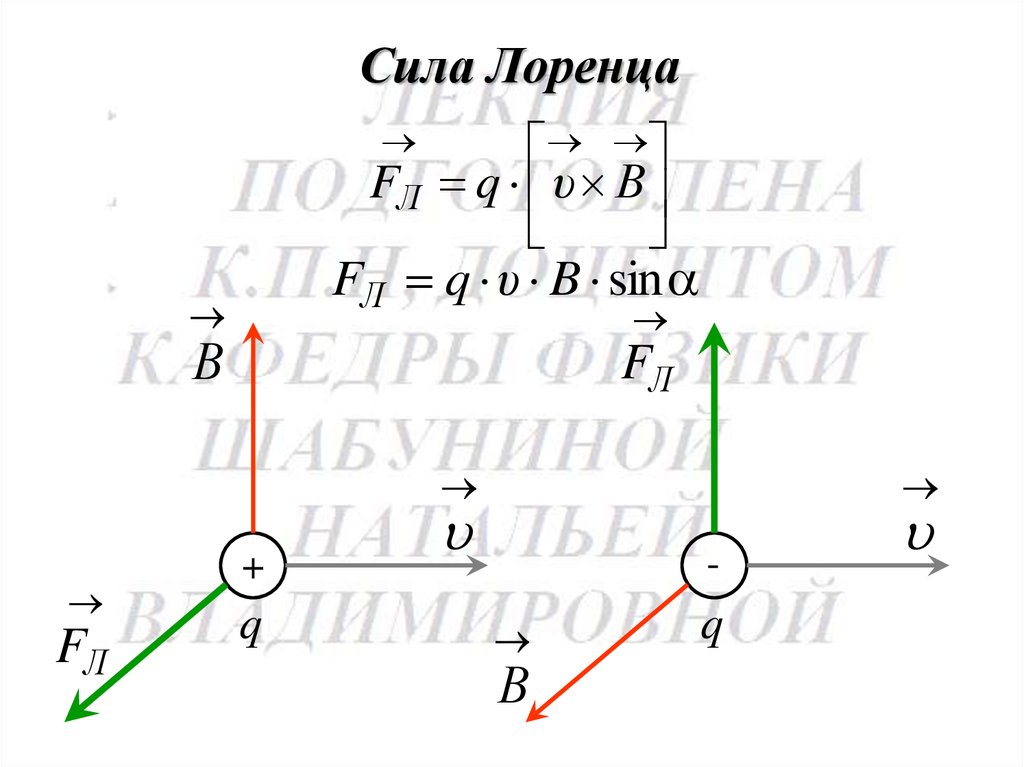
Сила ЛоренцаFЛ q υ В
FЛ q υ B sin
В
FЛ
FЛ
+
q
В
q
109.
Движение заряженных частицв однородном магнитном поле
1. υ В; ( 0)
FЛ 0
const
+
q
В
Траектория – прямая, параллельная линиям магнитной
индукции поля
Вид движения – равномерное
110.
2. υ В; ( 90 )В
F л аn
+
q
R
FЛ const
FЛ q B
FЛ m an
q B m
2
2 R 2 Rm
T
υ
m
qB
R υ
q B
Траектория – окружность, вокруг линий магнитной
индукции поля
Вид движения – равномерное по окружности с нормальным
ускорением
111.
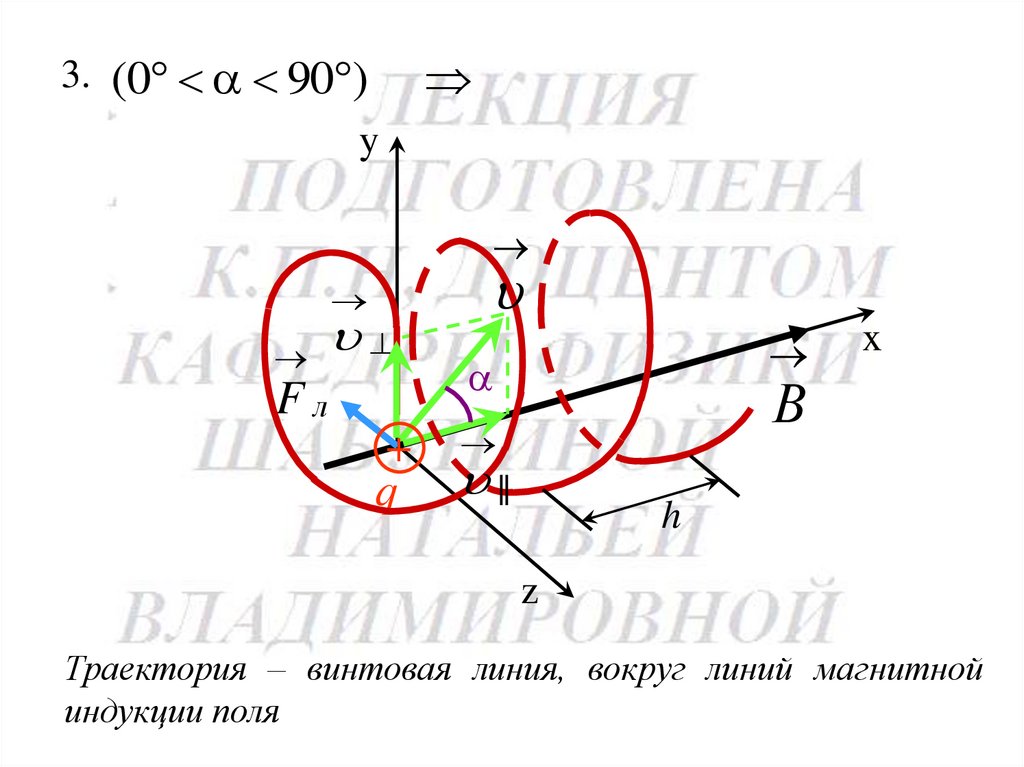
3. (0 90 )y
Fл
+
q
x
В
||
h
z
Траектория – винтовая линия, вокруг линий магнитной
индукции поля
112.
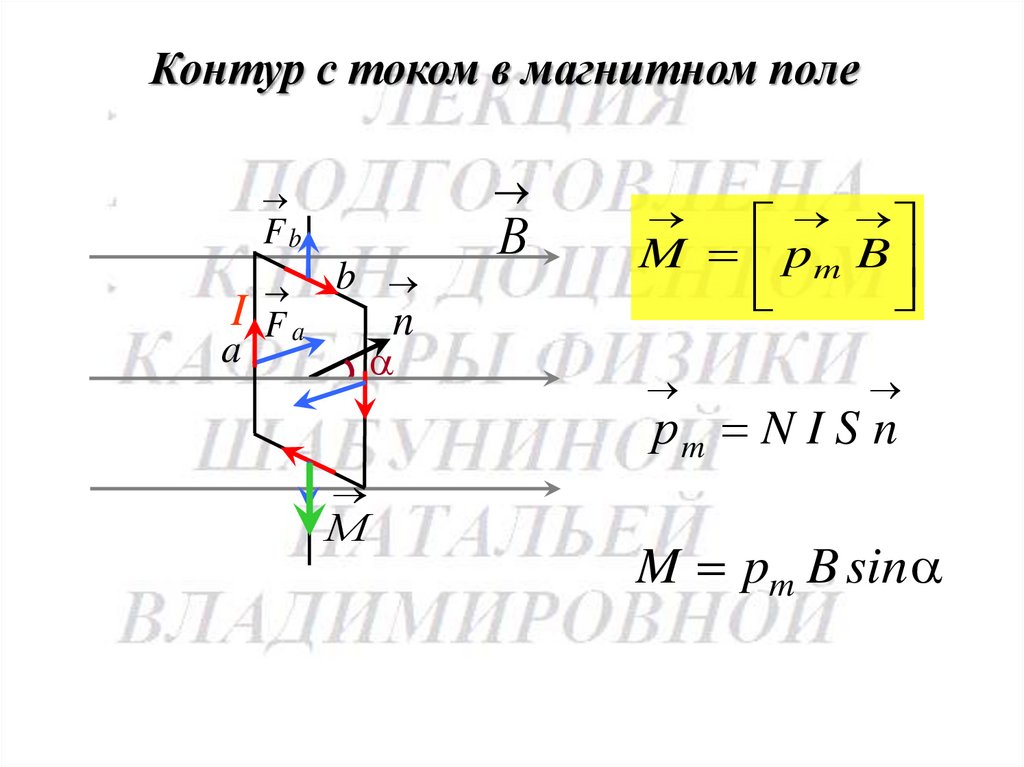
Контур с током в магнитном полеFb
I Fa
b
n
a
В
M pm B
рm N I S n
М
M pm B sin
113.
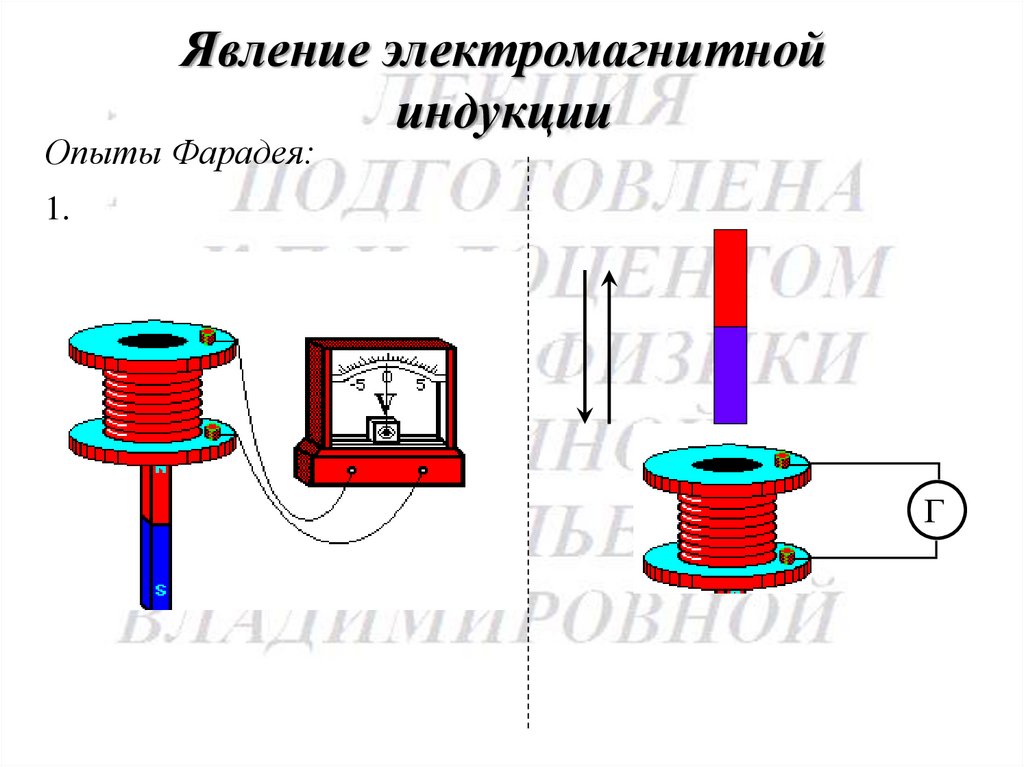
Явление электромагнитнойиндукции
Опыты Фарадея:
1.
Г
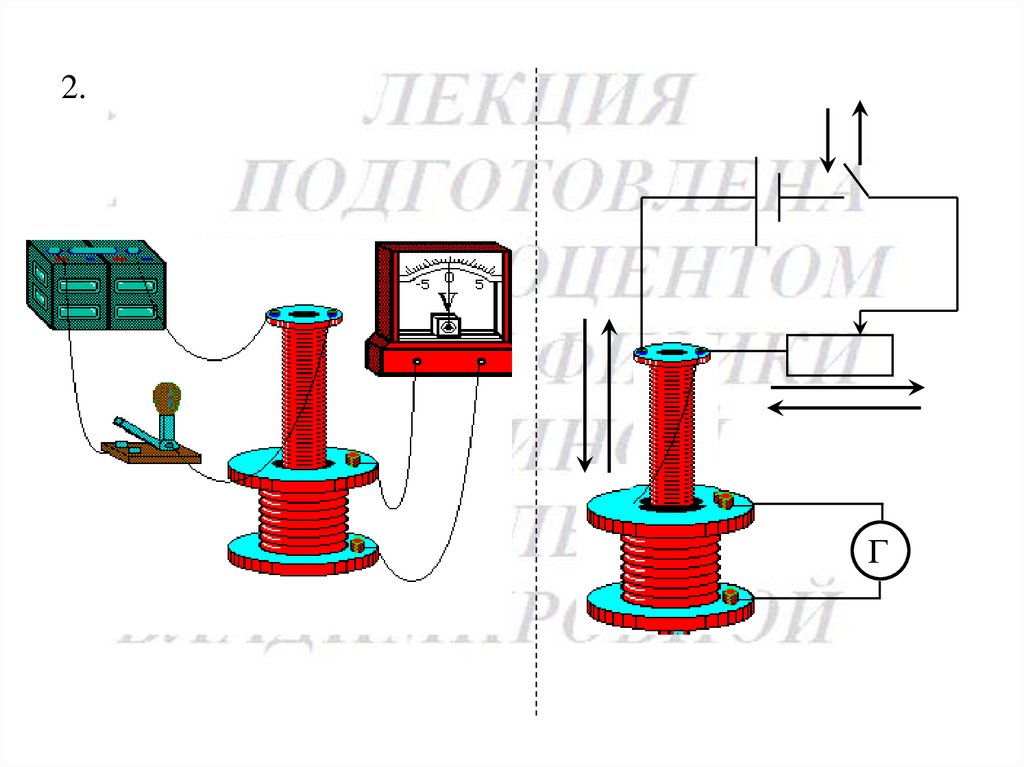
114.
2.Г
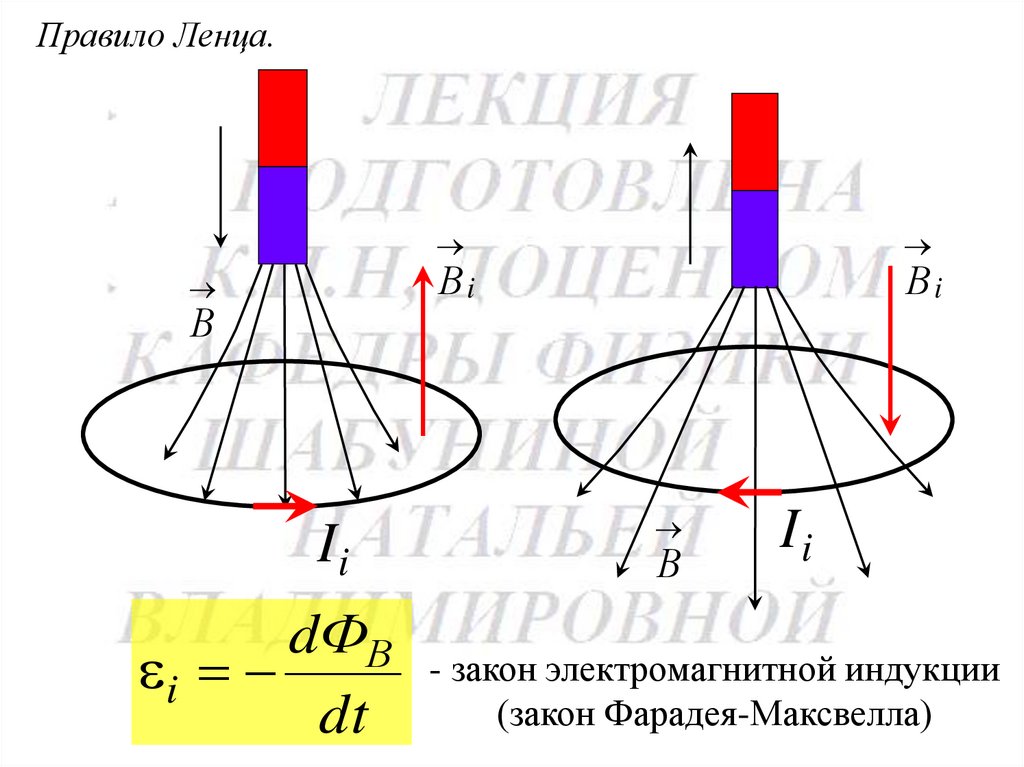
115.
Правило Ленца.Вi
В
Ii
dФВ
i
dt
Вi
В
Ii
- закон электромагнитной индукции
(закон Фарадея-Максвелла)
116.
Если изменяющийся магнитный поток пронизываетнесколько контуров, то
d
i
dt
Если Ф=const, то =N Ф
dФ
i N
dt
117.
Явление самоиндукции. ЭДС самоиндукции.Индуктивность соленоида. Энергия магнитного
поля
I
L I
ЭДС самоиндукции:
Si
dI
L
dt
Знак “-”обусловленный правилом Ленца, показывает, что наличие индуктивности L в контуре приводит к замедлению изменения тока в нём
118.
Индуктивность соленоида:0 N S
L
2
Энергия магнитного поля:
I
LI
W
2L
2
2
2
2
L I
119.
Электромагнитная картина мираФизический смысл уравнений Максвелла:
Q
E d S
0
S
(1)
B d S 0
(2)
S
dФВ
E вих . d
S
dt
d ФE
В d 0 I 0 0 d t
(3)
(4)
120.
МЕХАНИЧЕСКИЕКОЛЕБАНИЯ
Свободные
незатухающие
колебания
121.
F кв k xа
F кв
О
m
X
x
(1)
(2)
2
x ω0 x 0
x(t ) А cos( 0t 0 )
2
0
k
m
122.
Кинематический иэнергетический анализ
свободных незатухающих
колебаний
123.
x(t ) А cos( 0t 0 )1. Скорость колебательной системы
dx
x x А 0 sin( 0t 0 )
dt
υx max А 0
sin( 0t 0 ) 1
2. Ускорение колебательной системы
2
d d x
2
аx
2 x А 0 cos( 0t 0 )
dt dt
a x max А 0
2
cos( 0t 0 ) 1
124.
3. Кинетическая энергия колебательной системы2
2 2
2
m x m A 0 sin ( 0t 0 )
Ек
2
2
4. Потенциальная энергия колебательной системы
2
2
2
kx
k
A
cos
(
t
)
0
0
Ep
2
2
5. Полная энергия колебательной системы
Е Ек Е р
Е
2 2
m A 0
2
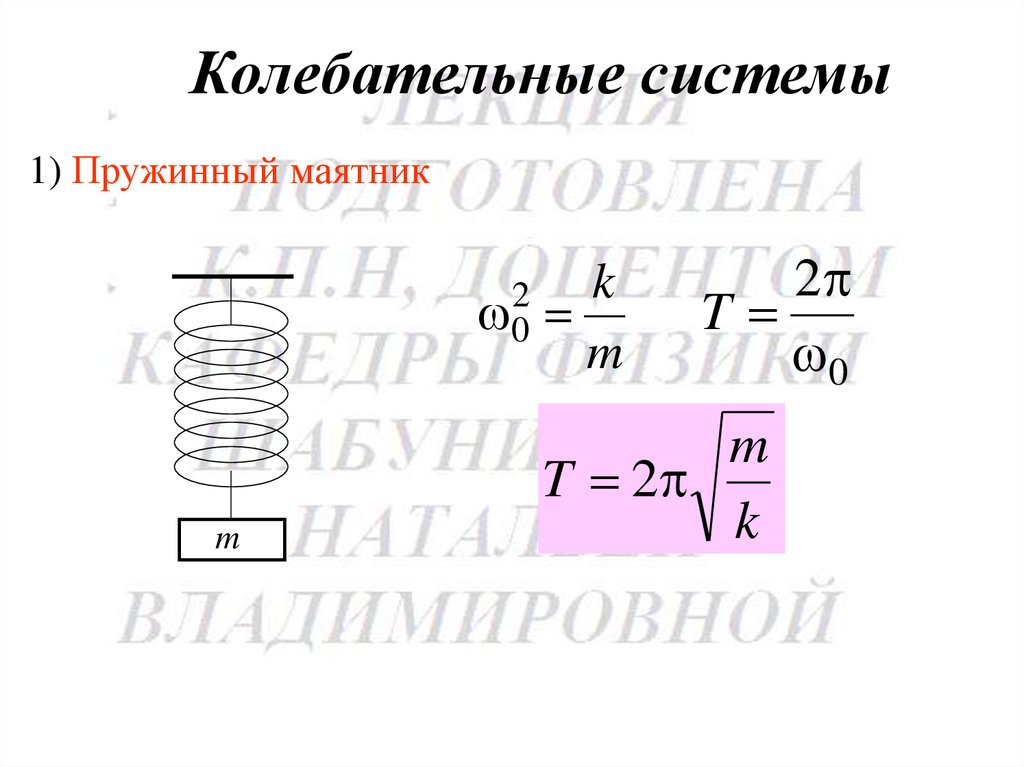
125.
Колебательные системы1) Пружинный маятник
2
0
m
k
m
2
T
0
m
T 2
k
126.
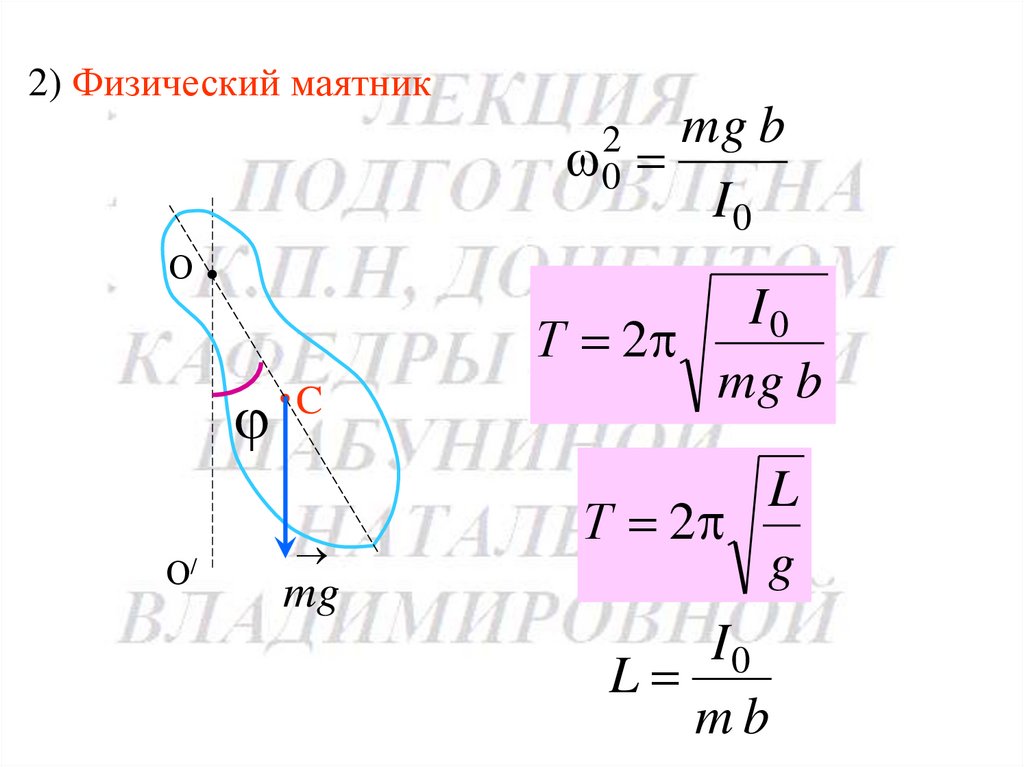
2) Физический маятник2
0
mg b
I0
О
О/
C
mg
I0
Т 2
mg b
L
Т 2
g
I0
L
mb
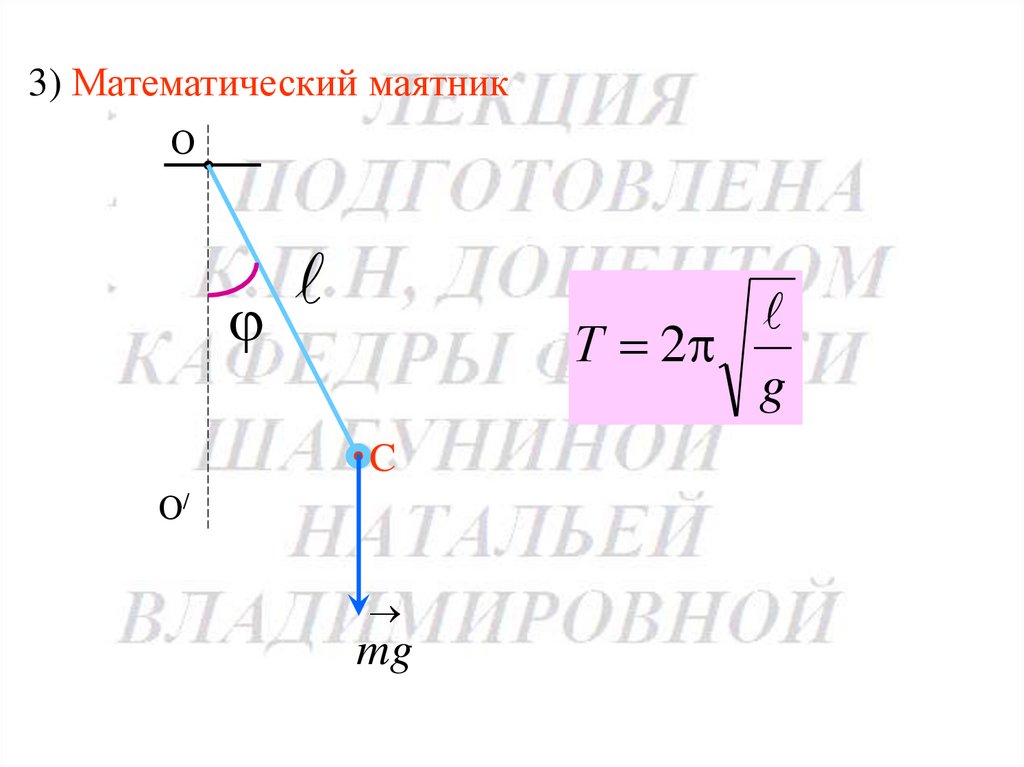
127.
3) Математический маятникО
Т 2
g
C
О/
mg
128.
Свободныезатухающие
колебания
129.
F с r υF кв k x
а
F кв
О
Fс
m
X
x
(1)
(2)
2
x 2 δ x 0
x A e
2
00
k t
m
x 0
r
2 t
cos(
m
0 )
130.
x A0 et
cos( t 0 )
А(t ) A0 e
Т
2
0
t
2
2
2
0
2
131.
Вынужденныеколебания
132.
F кв k xF с r
F кв
О
Fс
F F0 cos t
а
m
F
X
x
2
x 2 x 0
r
2
m
2
0
x f 0cos t
k
m
F0
f0
m
133.
Общее решение:x(t ) x1 (t ) x2 (t )
x1 (t ) A0 e
'
t
cos( t 0 )
2
0
'
2
x2 (t ) A cos( t )
А
f0
2
( 0
- ) 4
2 2
2 2
2
arctg 2
2
0
134.
ВОЛНОВАЯ ОПТИКАВолновое движение.
Виды волн
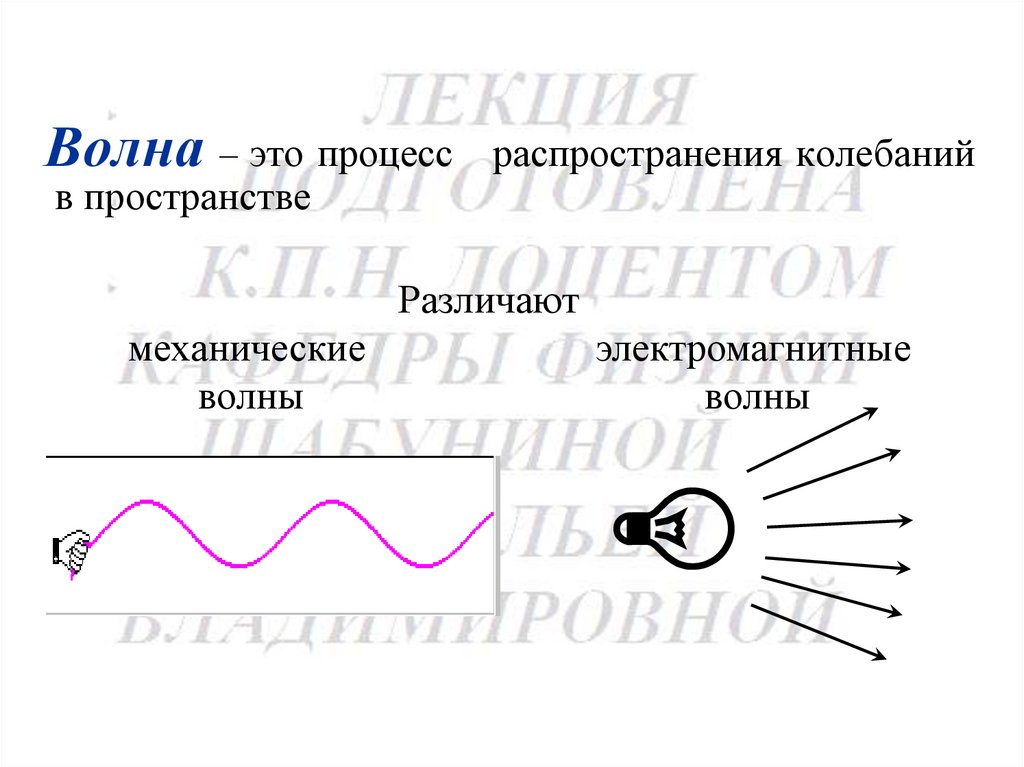
135.
Волна – это процессв пространстве
распространения колебаний
Различают
механические
волны
электромагнитные
волны
136.
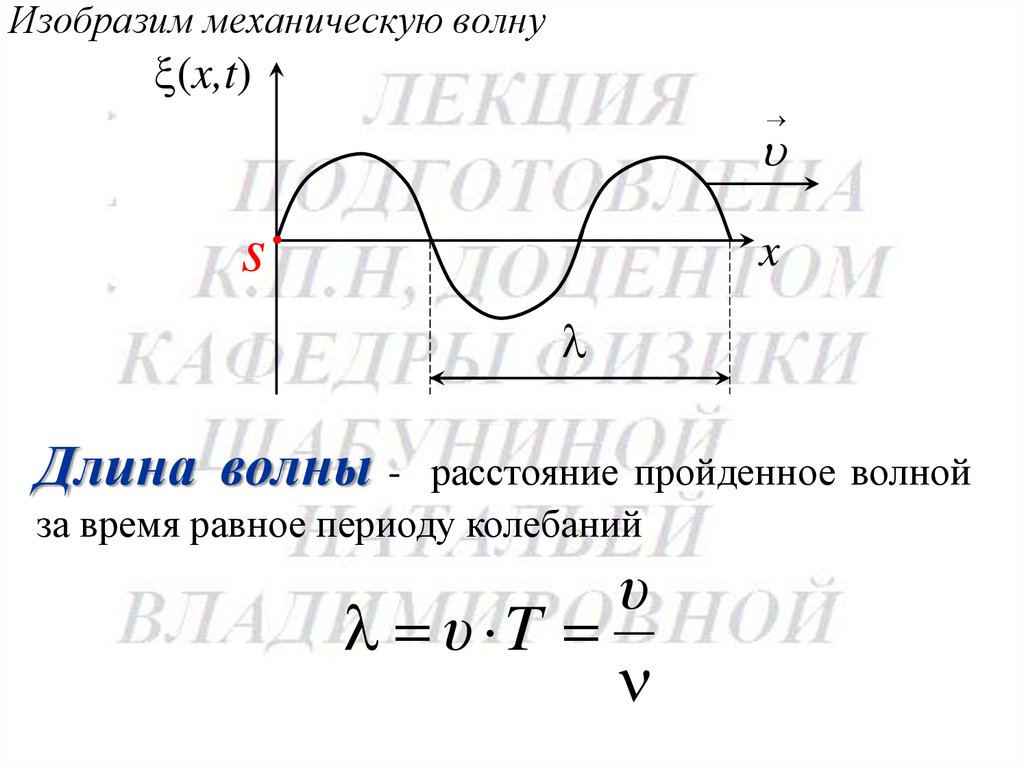
Изобразим механическую волну(x,t)
s
x
Длина волны -
расстояние пройденное волной
за время равное периоду колебаний
υ
υ T
137.
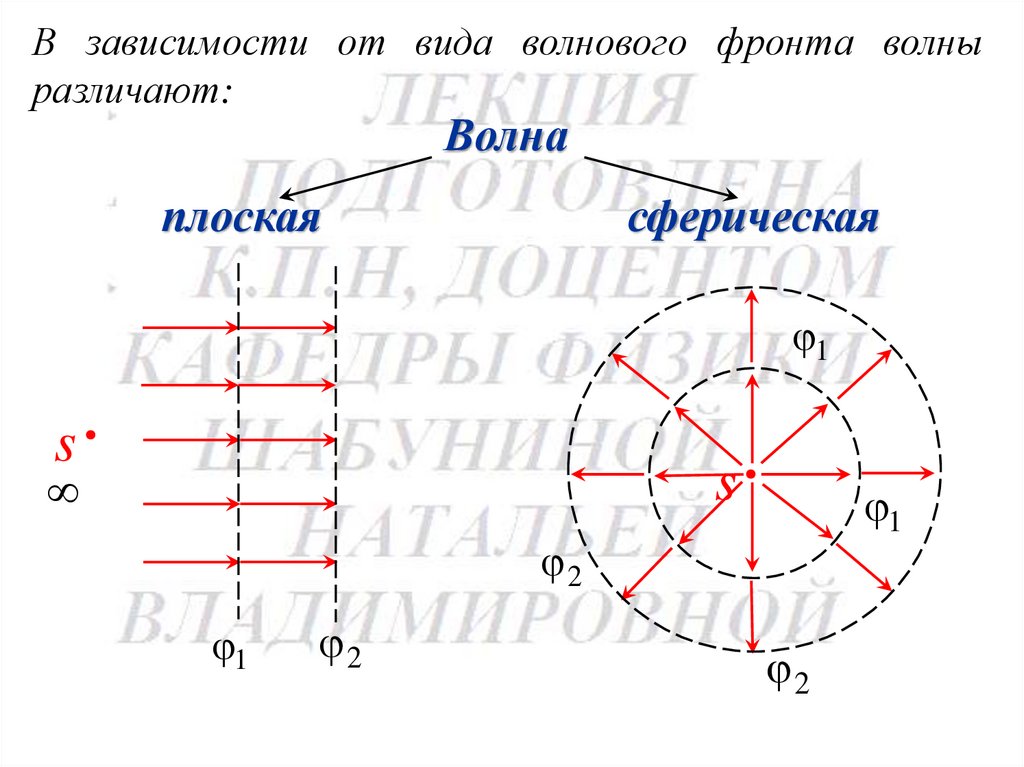
В зависимости от вида волнового фронта волныразличают:
Волна
плоская
сферическая
1
s
s
1
2
1
2
2
138.
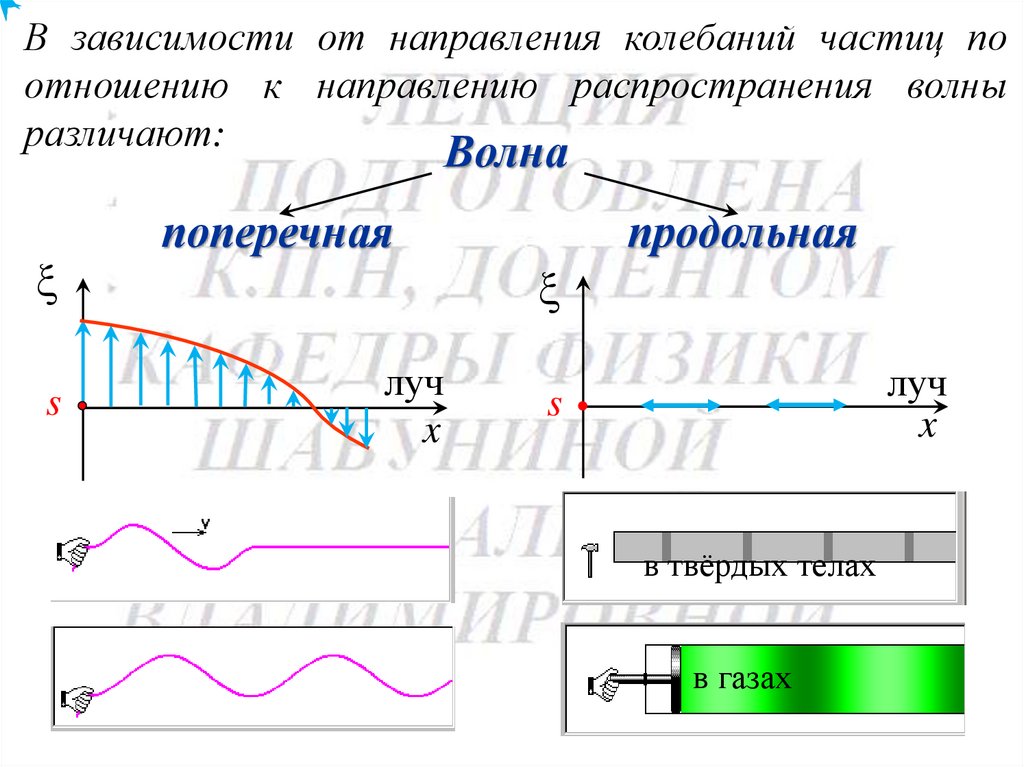
В зависимости от направления колебаний частиц поотношению к направлению распространения волны
различают:
Волна
s
поперечная
продольная
луч
x
луч
x
s
в твёрдых телах
в газах
139.
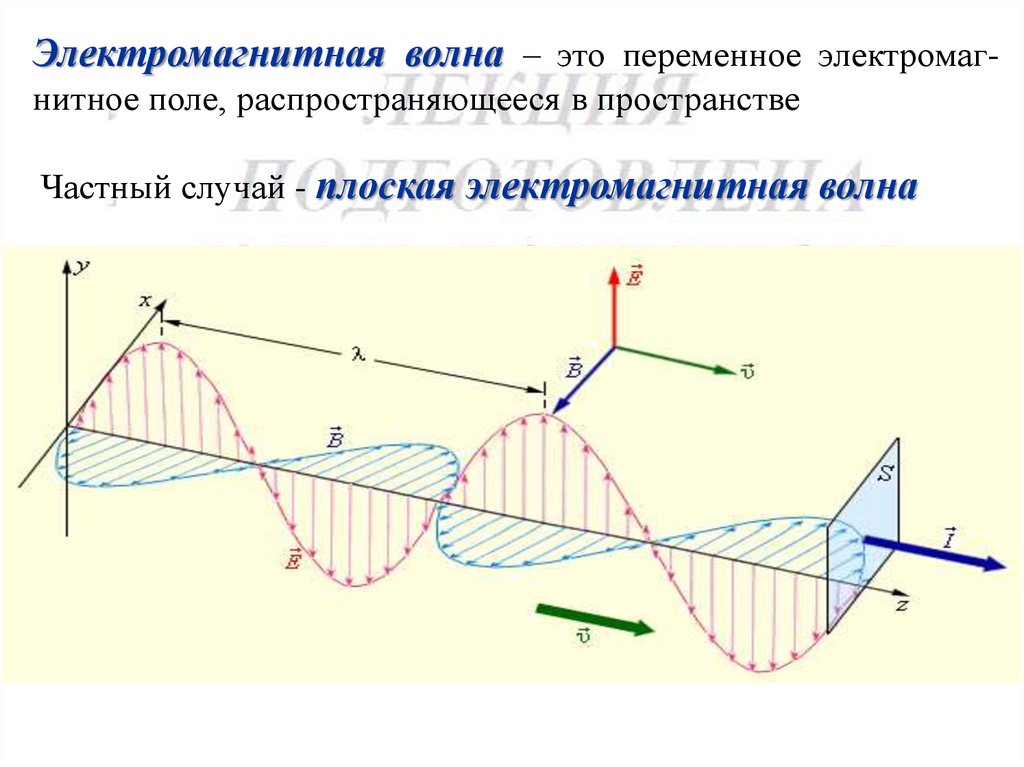
Электромагнитная волна – это переменное электромагнитное поле, распространяющееся в пространствеЧастный случай - плоская электромагнитная волна
140.
СВЕТ – это электромагнитная волна1
υ
0 0
с
1
0 0
1
1
0 0
с
3 108 м/с - скорость электромагнитной волны
(света) в вакууме
Длина волны в вакууме: 0 с T
Длина волны в среде:
υ T
0 с
n
υ
где n - абсолютный показатель преломления -
141.
Для однородной среды оптическая длина пути равнаL nS
где S – геометрическая длина пути.
Оптическая разность хода – это величина равная разности
оптических длин путей, проходимых волнами
L2 L1
142.
Интерференция света.Способы наблюдения
интерференционных
картин
143.
Условия интерференционных максимумов и минимумовчерез оптическую разность хода:
1) Условие интерференционного максимума:
0
2m
2
Оптическая разность хода равна чётному числу длин полуволн
в вакууме.
2) Условие интерференционного минимума:
0
(2 m 1)
2
Оптическая разность хода равна нечётному числу длин
полуволн в вакууме.
144.
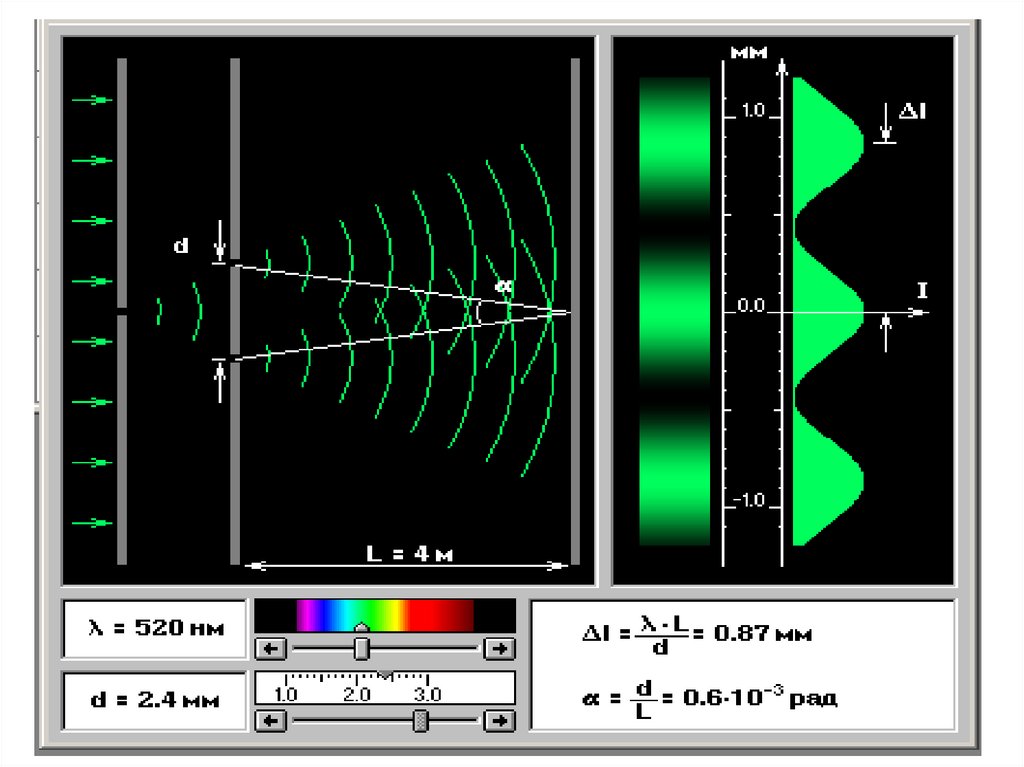
1. Опыт ЮнгаS1
S2
экран
В области перекрывания когерентных волн на экране
будет видна интерференционная картина в виде полос
равной толщины.
145.
146.
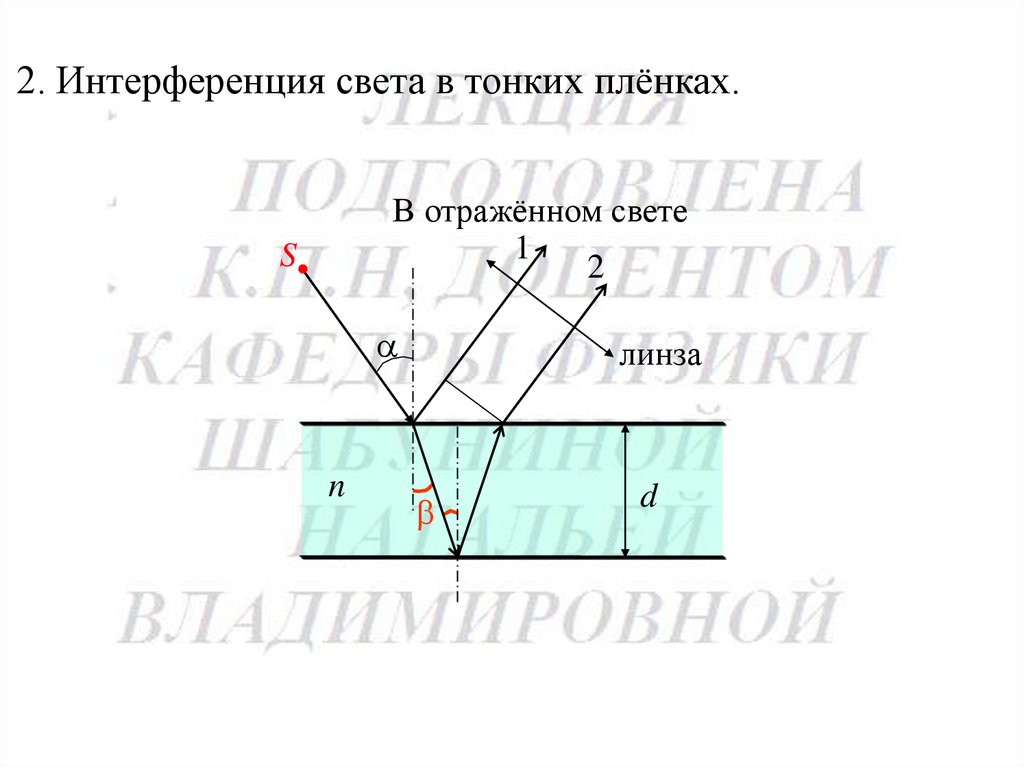
2. Интерференция света в тонких плёнках.В отражённом свете
1
2
S
n
линза
d
147.
В общем случае оптическая разность хода в тонкойплёнке определяется:
0
2 d ncos
2
или
0
2 d n sin
2
2
2
1) Условие максимума:
0
0
2 d n sin
2m
2
2
2
2
2) Условие минимума:
0
0
2 d n sin
(2 m 1)
2
2
2
2
148.
Дифракция светаПринцип Гюйгенса-Френеля
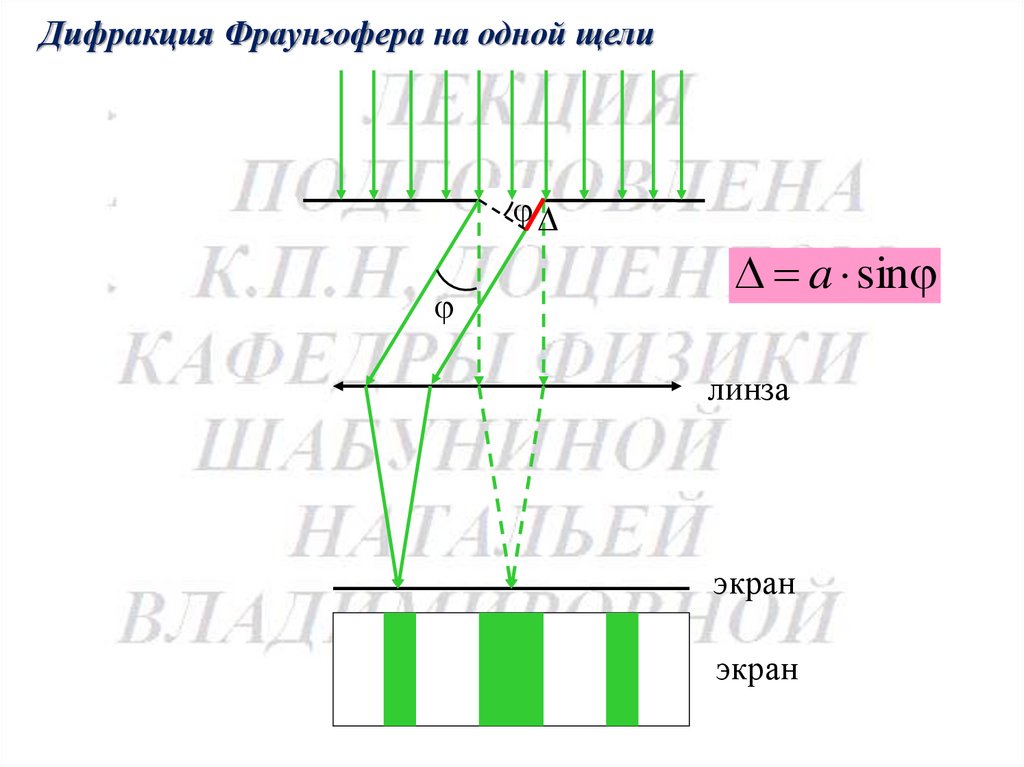
Дифракция Фраунгофера
на одной щели
Дифракционная решётка
149.
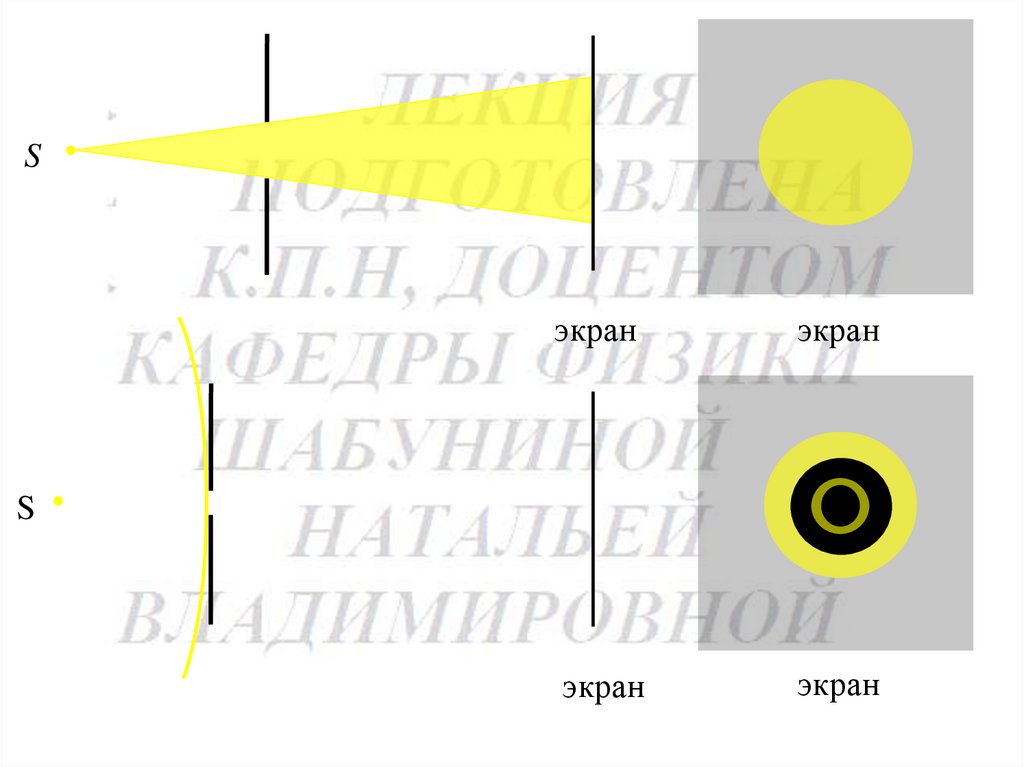
Sэкран
экран
экран
экран
S
150.
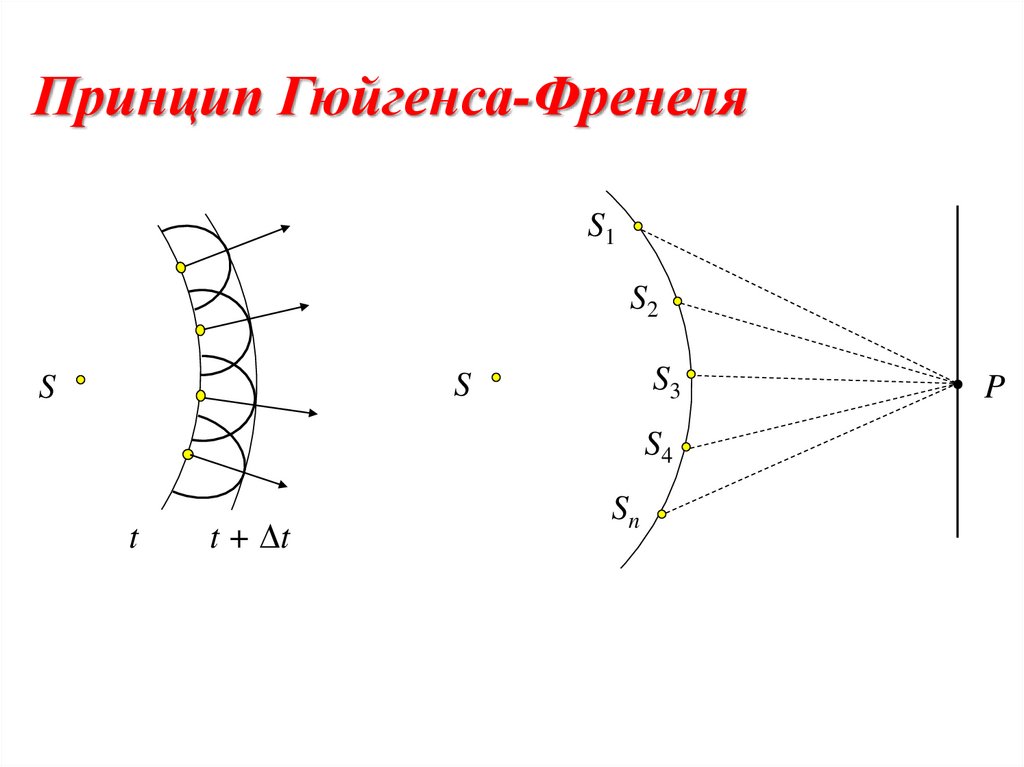
Принцип Гюйгенса-ФренеляS1
S2
S3
S
S
S4
t
t + t
Sn
P
151.
Дифракция Фраунгофера на одной щелиa sin
линза
экран
экран
152.
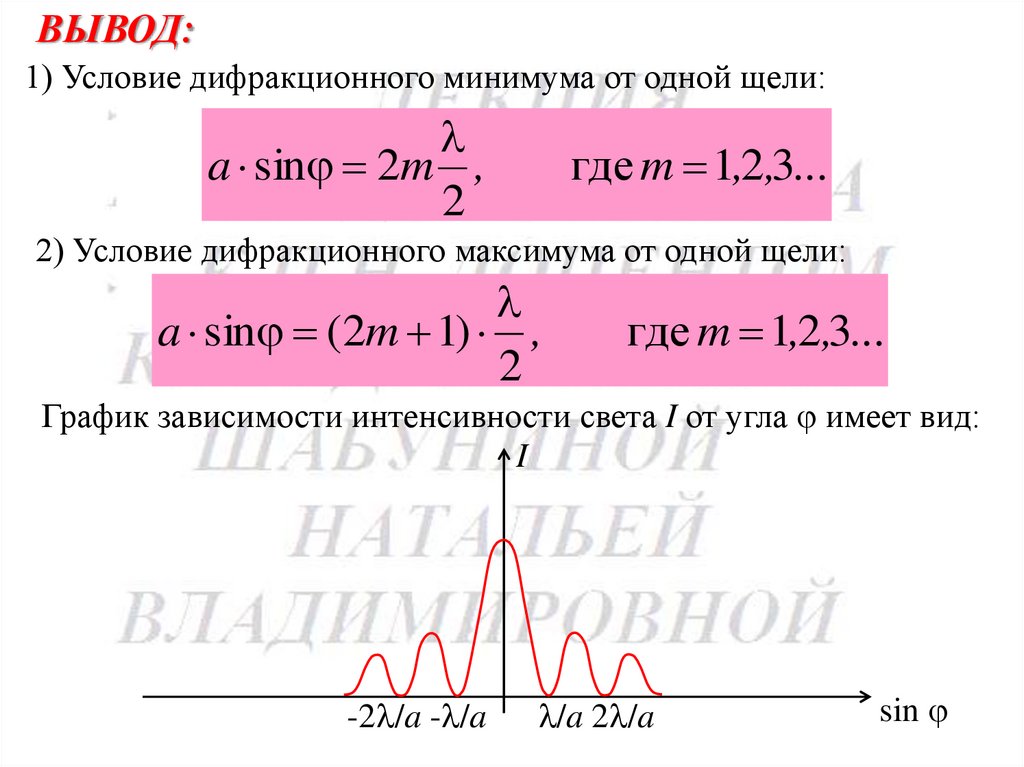
ВЫВОД:1) Условие дифракционного минимума от одной щели:
a sin 2m ,
2
где m 1,2,3...
2) Условие дифракционного максимума от одной щели:
a sin (2m 1) ,
2
где m 1,2,3...
График зависимости интенсивности света I от угла имеет вид:
I
-2 /a - /a
/a 2 /a
sin
153.
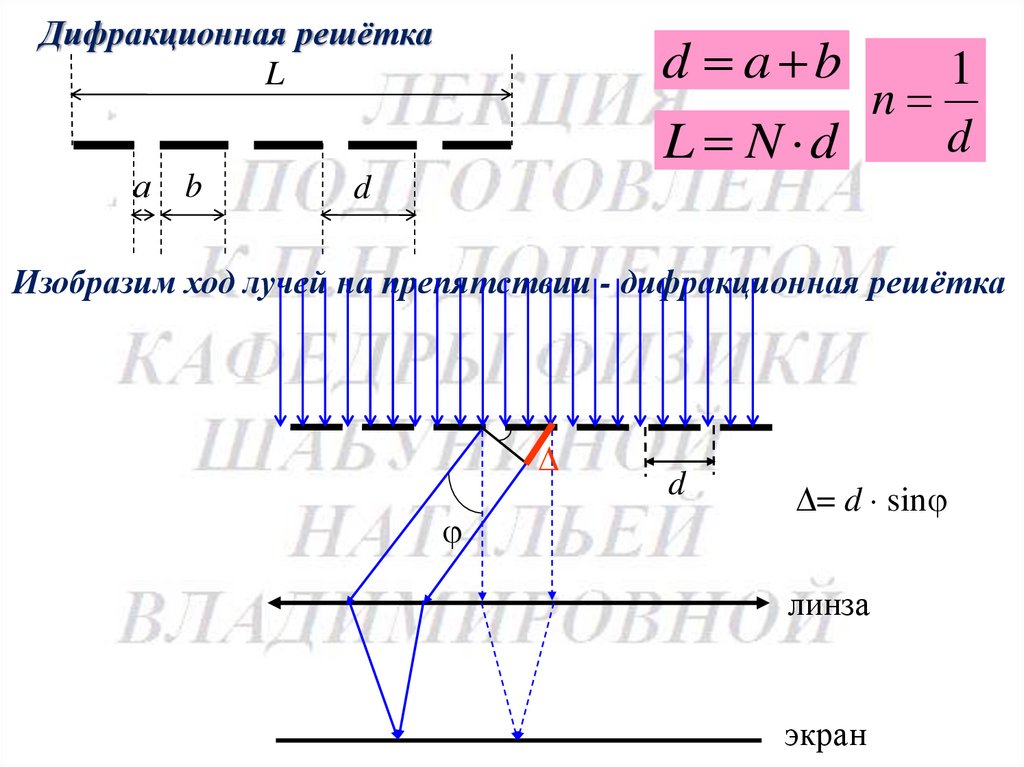
Дифракционная решёткаL
а b
d a b
1
n
d
L N d
d
Изобразим ход лучей на препятствии - дифракционная решётка
d
= d sin
линза
экран
154.
Условие минимумов для дифракционной решёткиa sin 2m , где m 1,2,3...
2
Условие дополнительных минимумов
d sin (2m 1) , где m 0,1,2,3...
2
Условие главных максимумов для дифракционной решётки
d sin 2m , где m 0,1,2,3...
2
155.
Поляризация светаСпособы получения
поляризованного света
Закон Малюса
Закон Брюстера
156.
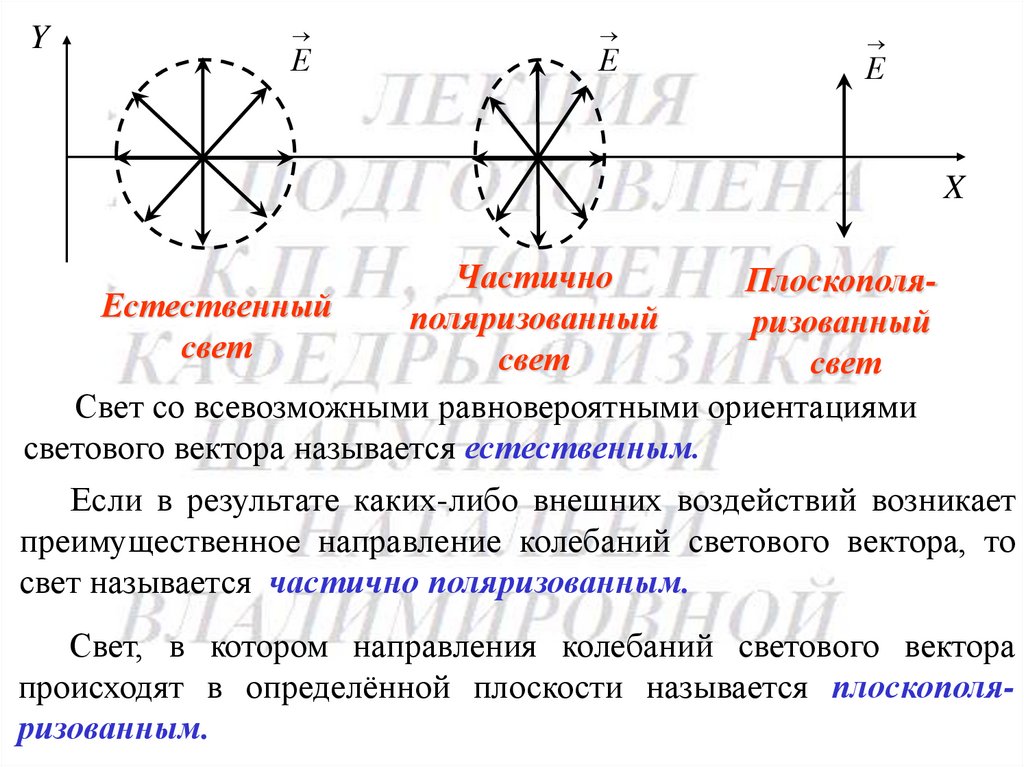
YЕ
Е
Е
X
Частично
ПлоскополяЕстественный
поляризованный
ризованный
свет
свет
свет
Свет со всевозможными равновероятными ориентациями
светового вектора называется естественным.
Если в результате каких-либо внешних воздействий возникает
преимущественное направление колебаний светового вектора, то
свет называется частично поляризованным.
Свет, в котором направления колебаний светового вектора
происходят в определённой плоскости называется плоскополяризованным.
157.
За меру степени поляризации принимают величину:I max I min
Р
I max I min
Для естественного света Imax= Imin. Следовательно Р = 0.
Для плоскополяризованного света Imin= 0. Следовательно Р=1.
Для частично поляризованного света 0 < Р < 1.
158.
1.ПолучениеПОЛУЧЕНИЯ
поляризованного
света с помощью поляризатора
СПОСОБЫ
ПОЛЯРИЗОВАННОГО
СВЕТА:
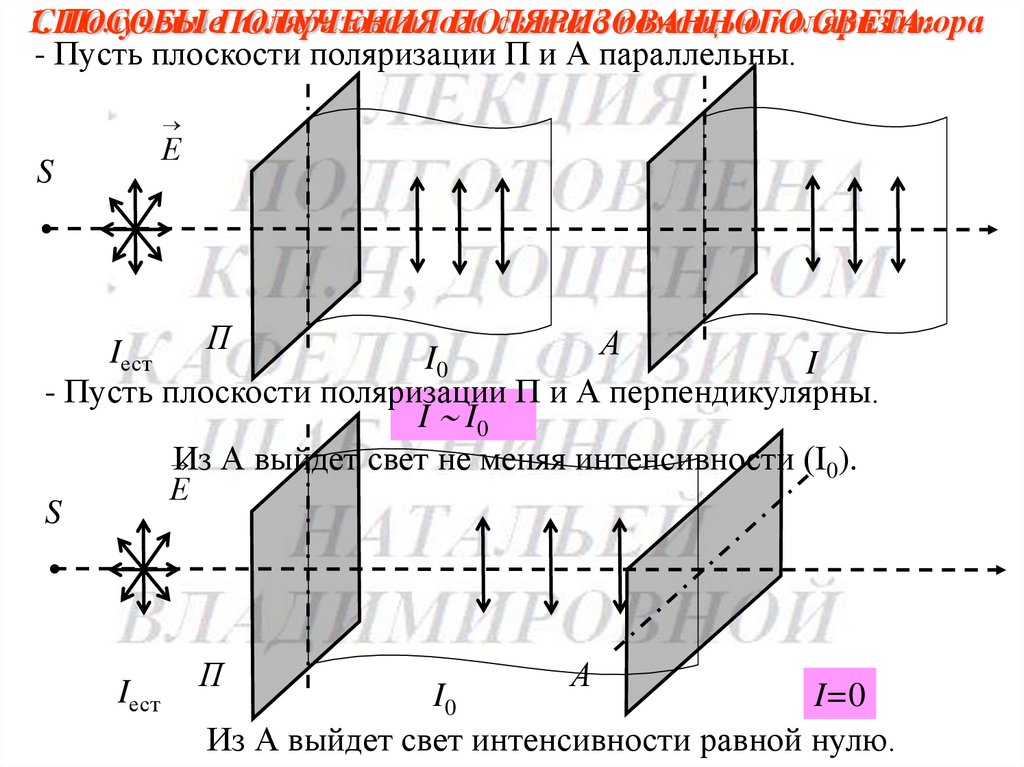
- Пусть плоскости поляризации П и А параллельны.
Е
S
П
А
Iест
I0
I
- Пусть плоскости поляризации П и А перпендикулярны.
I I0
Из А выйдет свет не меняя интенсивности (I0).
Е
S
Iест
П
А
I0
I=0
Из А выйдет свет интенсивности равной нулю.
159.
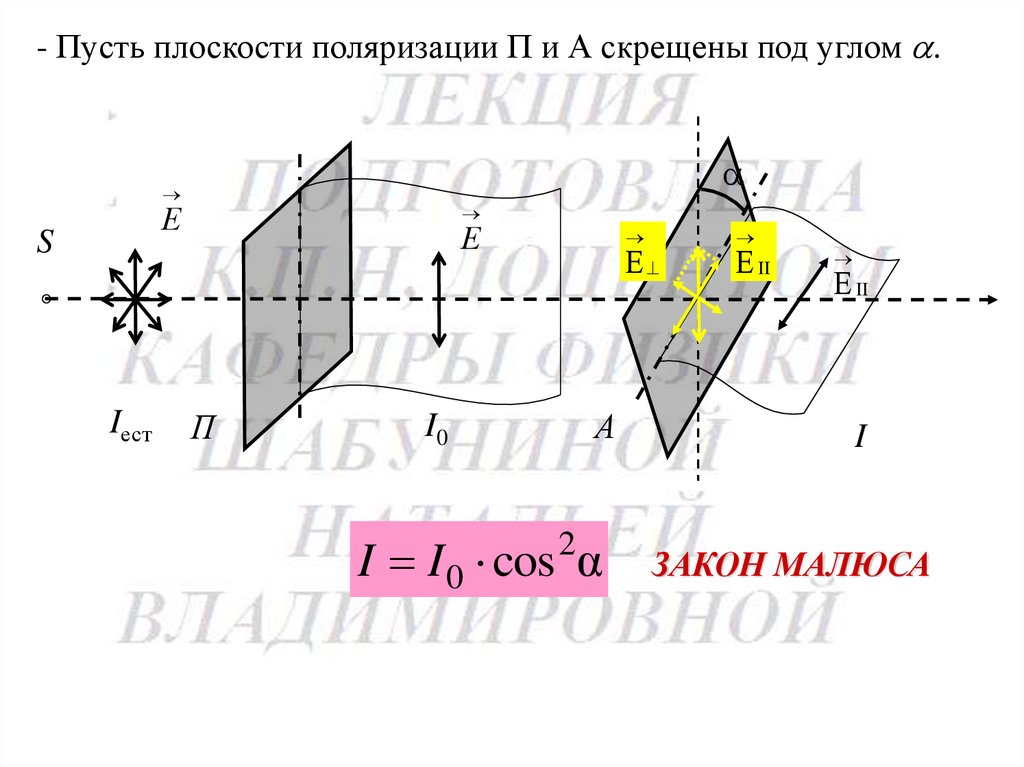
- Пусть плоскости поляризации П и А скрещены под углом .Е
S
Iест
Е
П
Е
А
I0
I I 0 cos α
2
Е II
Е II
I
ЗАКОН МАЛЮСА
160.
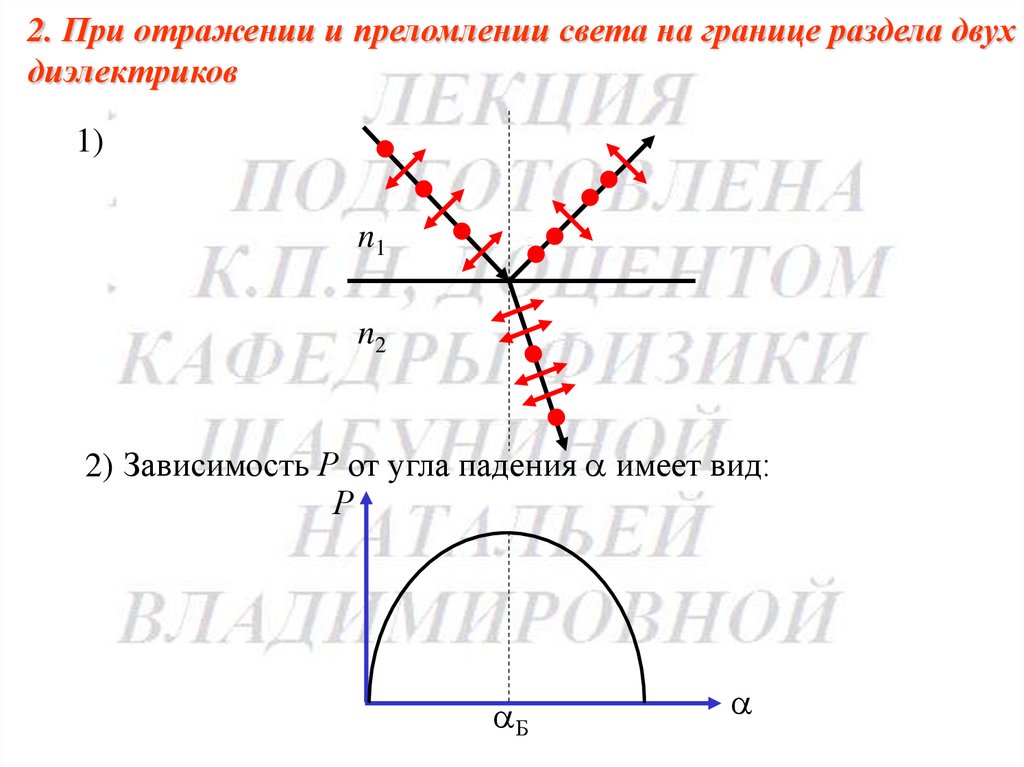
2. При отражении и преломлении света на границе раздела двухдиэлектриков
1)
n1
n2
2) Зависимость Р от угла падения имеет вид:
Р
Б
161.
Бn1
n2
n2
tg Б n21
n1
ЗАКОН БРЮСТЕРА
При угле падения Б отражённый и преломлённый лучи взаимно
перпендикулярны.
Б
2
162.
КВАНТОВАЯ ОПТИКАТепловое излучение. Законы
теплового излучения.
Формула Планка
163.
Тепловое излучение - электромагнитное излучение,возникающее за счёт внутренней энергии излучающего
тела, и зависящее только от температуры и оптических
свойств этого тела
Тепловое излучение – единственное излучение способное находиться в термодинамическом равновесии с
излучающим телом
Характеристики теплового излучения:
1) Излучательность (энергетическая светимость) Rэ
dW
RЭ
Дж Вт
d S dt
RЭ 2 2
м с м
W
RЭ
S t
164.
2) Спектральная излучательная способность(спектральная плотность энергетической светимости) r ,T
dRЭ1
1
dRЭ2
2
d
r ,T
d
dRЭ
d
3) Спектральная поглощательная и отражающая
способность
а ,Т
dWпогл
dW
ρ λ,Т
dWотр
dW
165.
Окраска тела:1) ,Т 1, а ,Т 0
2) ,Т 0, а ,Т 1
3) а ,Т аТ 1
- абсолютно белое
тело
- абсолютно чёрное
тело
- серое тело
166.
ЗАКОНЫИЗЛУЧЕНИЯ.
1. Закон ТЕПЛОВОГО
Кирхгофа
Отношение спектральной излучательной способности
к спектральной поглощательной способности не зависит
от природы тела и является универсальной функцией от
длины волны (частоты) и температуры.
r ,T
f ( ,T )
a ,T
Так как для абсолютно чёрного тела а ,Т 1, то
0
r ,T
f ( ,T )
Вывод: Универсальная функция Кирхгофа есть
спектральная излучательная способность абсолютно
чёрного тела.
167.
2. Закон Стефана-БольцманаRЭ
4 - закон Стефана-Больцмана
Т
5,67 10
8
Вт
м 2К 4
ФОРМУЛИРОВКА:
Излучательность абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической
температуры
168.
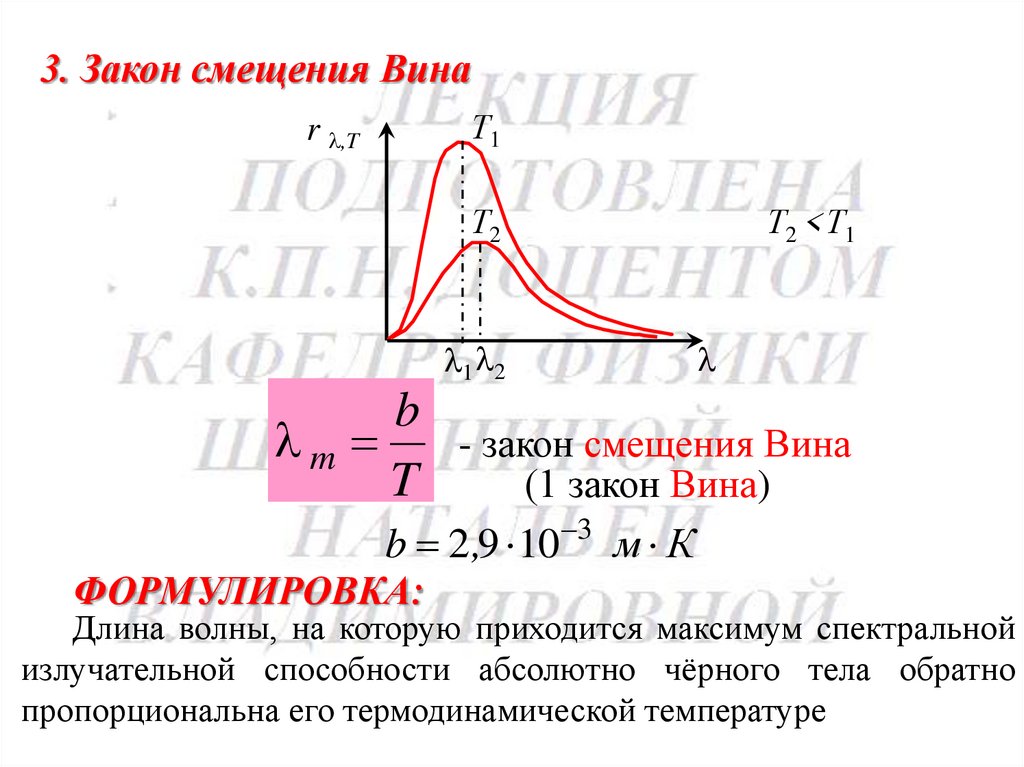
3. Закон смещения ВинаТ1
r ,T
Т2
1 2
m
Т2 <Т1
b
- закон смещения Вина
T
(1 закон Вина)
b 2,9 10 3 м К
ФОРМУЛИРОВКА:
Длина волны, на которую приходится максимум спектральной
излучательной способности абсолютно чёрного тела обратно
пропорциональна его термодинамической температуре
169.
4. Второй закон Вина(r ,T )max c T
с 1,29 10
5
5
- 2 закон Вина
Вт
м 3К 5
ФОРМУЛИРОВКА:
Максимальная спектральная излучательная способность абсолютно чёрного тела пропорциональна пятой
степени его термодинамической температуре
Энергия кванта:
c
h h
170.
h 6,63 10 34 Дж сh
1,05 10 34 Дж с
2
2 c
2
W N , N 0,1,2,3...
Формула Планка:
f ( , T ) r ,T
2 2
2
с
h
e
h
kT
1
171.
Внешний фотоэффект.Фотоны. Уравнение
Эйнштейна для внешнего
фотоэффекта
172.
Фотоэлектрический эффект – явление измененияэлектрических свойств веществ под действием
электромагнитного излучения.
Фотоэффекты различают:
1. Внешний фотоэффект;
2. Внутренний фотоэффект;
3. Вентильный фотоэффект.
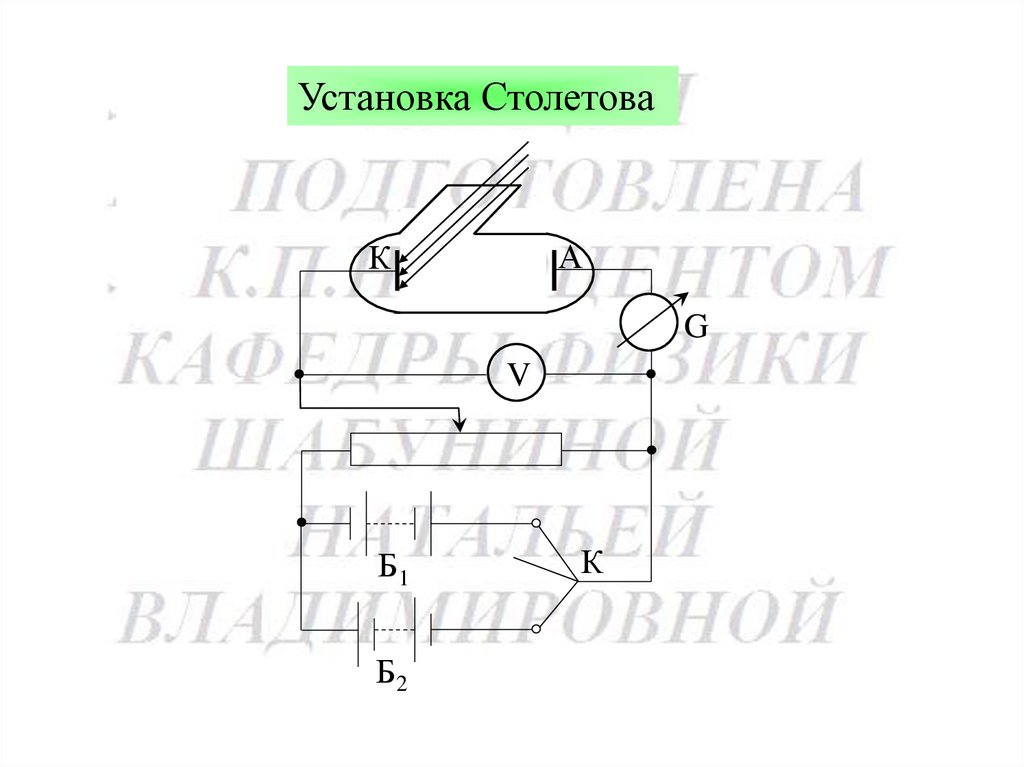
173.
Установка СтолетоваА
К
G
V
Б1
Б2
К
174.
ВАХ для внешнего фотоэффекта.= const;
Iф
I1>I2
Iф нас 1
Е1
Iф нас 2
Е2
Uз
0
U
Eкmax eU з
175.
Энергия фотонаhc
h
Масса фотона
mф с
hc
2
hc
mф с
h h
mф
2
с c
2
Фотон существует только в движении, т.е. масса
покоя фотона m0 равна нулю.
176.
Импульс фотонаh hc h
рф mф с 2 с
с
с
с
с
Согласно теории Эйнштейна квант
поглощается только одним электроном.
A вых Ек max
Eк max eU з
излучения
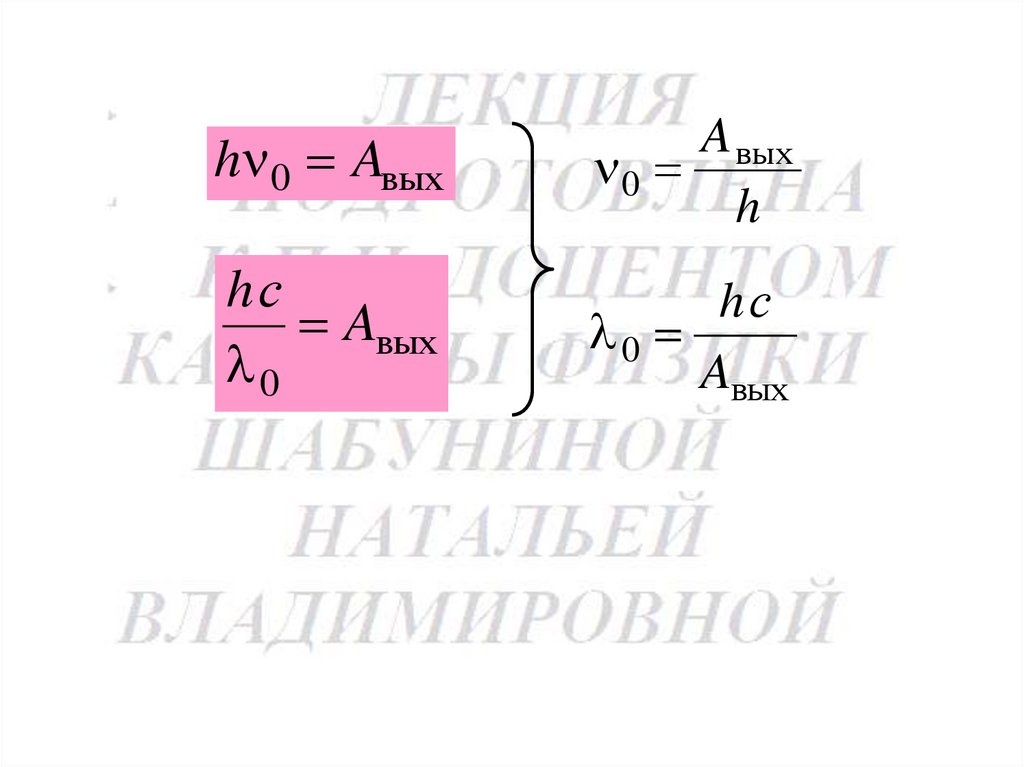
177.
h 0 AвыхA вых
0
h
hс
Aвых
0
hс
0
Aвых
178.
Световое давление.Эффект Комптона
179.
Давление, производимое светом при нормальномпадении на поверхность:
Еe
р
(1 ) (1 )
с
Энергетическая освещённость - это физическая
величина, равная количеству энергии попадаемой на
единицу освещаемой поверхности, перпендикулярной к
направлению потока в единицу времени
W
Ее
S t
- объёмная плотность энергии
Вт
Ее 1 2
м
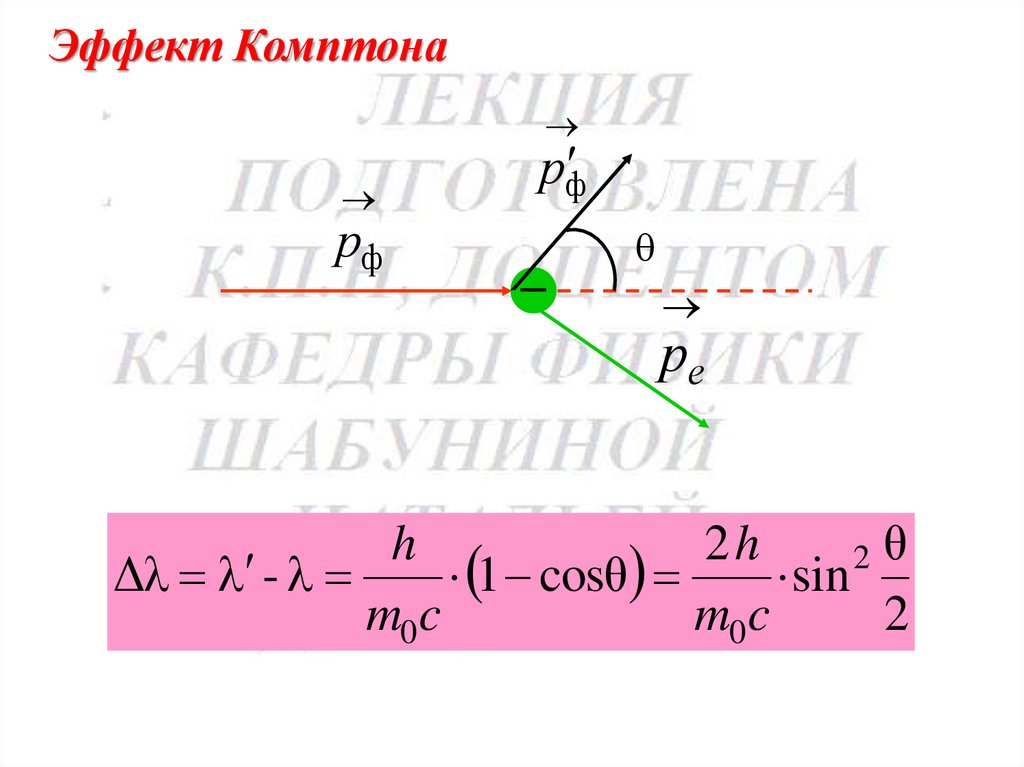
180.
Эффект Комптонарф
рф
ре
h
2h
2θ
Δλ -
1 cosθ
sin
m0c
m0c
2
181.
hm0c
h
6,63 10 34
2,426 пм.
31
8
m0c 9,1 10 3 10
θ
1 cosθ 2 sin
2
2
182.
ЭЛЕМЕНТЫКВАНТОВОЙ МЕХАНИКИ
Гипотеза де Бройля.
Соотношение
неопределённостей
Гейзенберга
183.
Для фотона:hc
ф h
h
рф
Для частицы:
дб
h 2
E
p
p
h
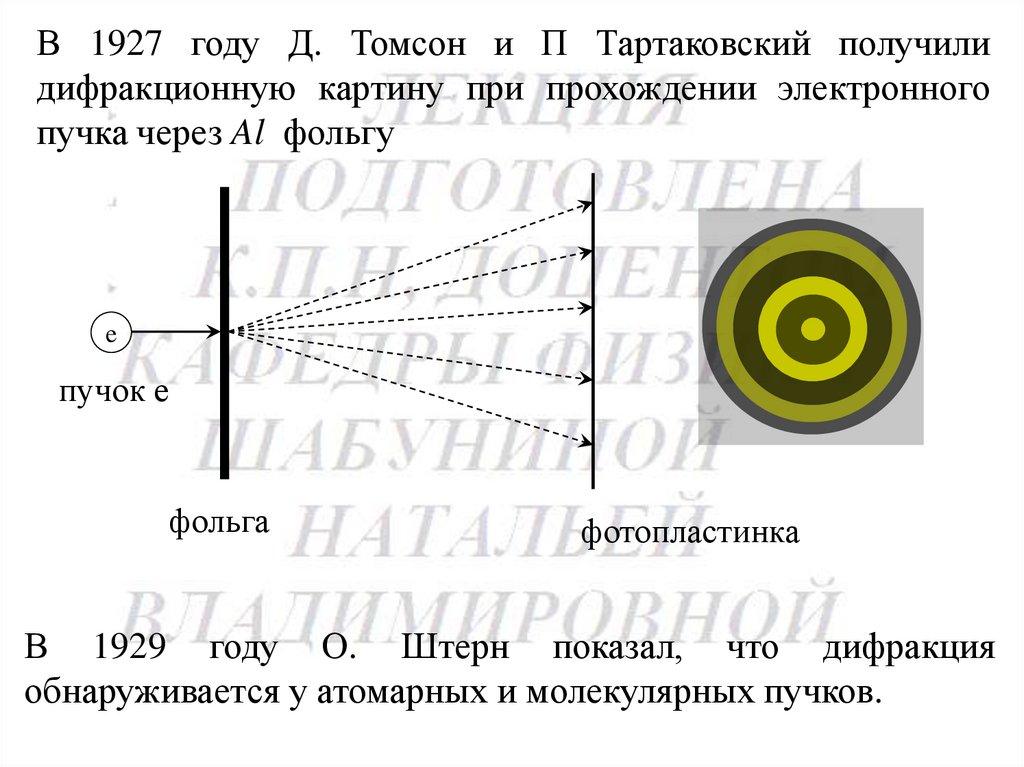
184.
В 1927 году Д. Томсон и П Тартаковский получилидифракционную картину при прохождении электронного
пучка через Al фольгу
e
пучок е
фольга
фотопластинка
В 1929 году О. Штерн показал, что дифракция
обнаруживается у атомарных и молекулярных пучков.
185.
Гейзенберг сделал вывод, что одновременно точноеопределение координаты и импульса частицы невозможно.
x px
- соотношения
неопределённостей
y
для координаты и
импульса
y p
z pz
x, y, z
- неопределённость координаты;
px , p y , pz - неопределённость в определении
соответствующей проекции импульса.
186.
ФОРМУЛИРОВКА:Произведение неопределённости координаты и соответствующей ей неопределённости проекции импульса не может
быть меньше .
187.
АТОМНАЯ ФИЗИКАМодели строения
атома. Постулаты
Бора. Атом водорода по
Бору
188.
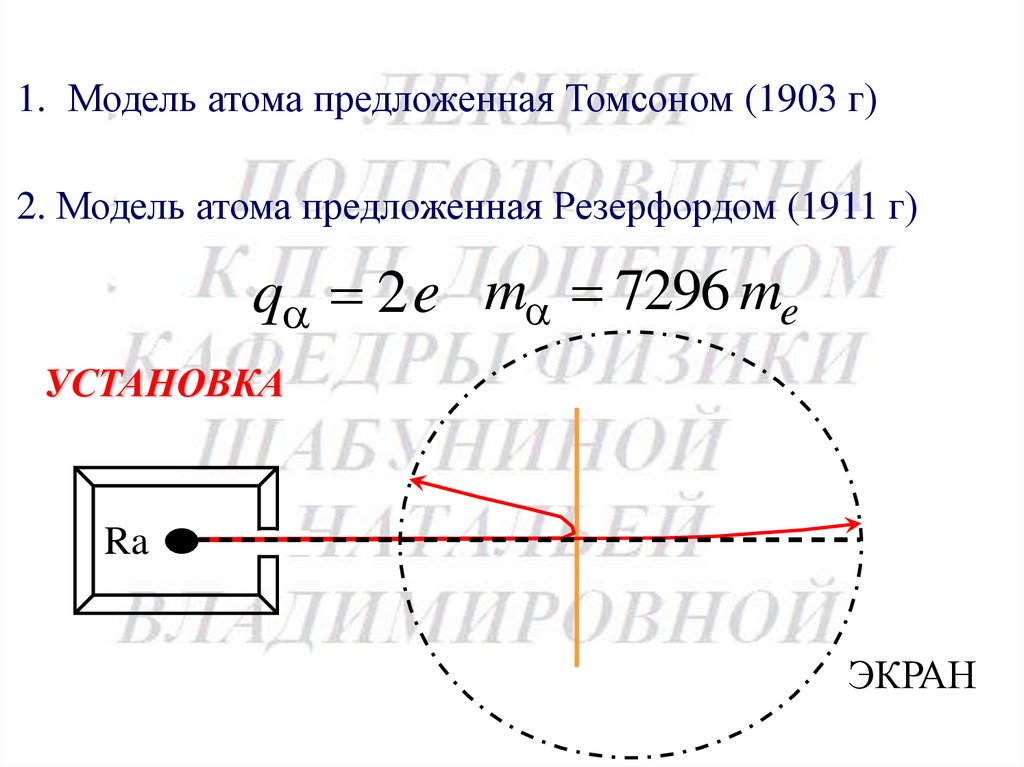
1. Модель атома предложенная Томсоном (1903 г)2. Модель атома предложенная Резерфордом (1911 г)
q 2 e m 7296 me
УСТАНОВКА
Ra
ЭКРАН
189.
Результаты исследования:+
Qя
+
Qя
Qя = Z e
Rя ~10 -10 м
190.
191.
Постулаты Бора.1 постулат (правило квантования):
В атоме существуют стационарные не изменяющиеся
со временем состояния, в которых он не излучает.
Движение электронов по стационарным орбитам не
сопровождается излучением.
В стационарном состоянии электрон двигаясь по
круговой орбите должен иметь квантованное значение
момента импульса.
m r n , n 1,2,3,4...
192.
2 постулат (правило частот):При переходе электрона с одной стационарной орбиты
на другую излучается (поглощается) квант излучения
с энергией равной .
En 2 En1
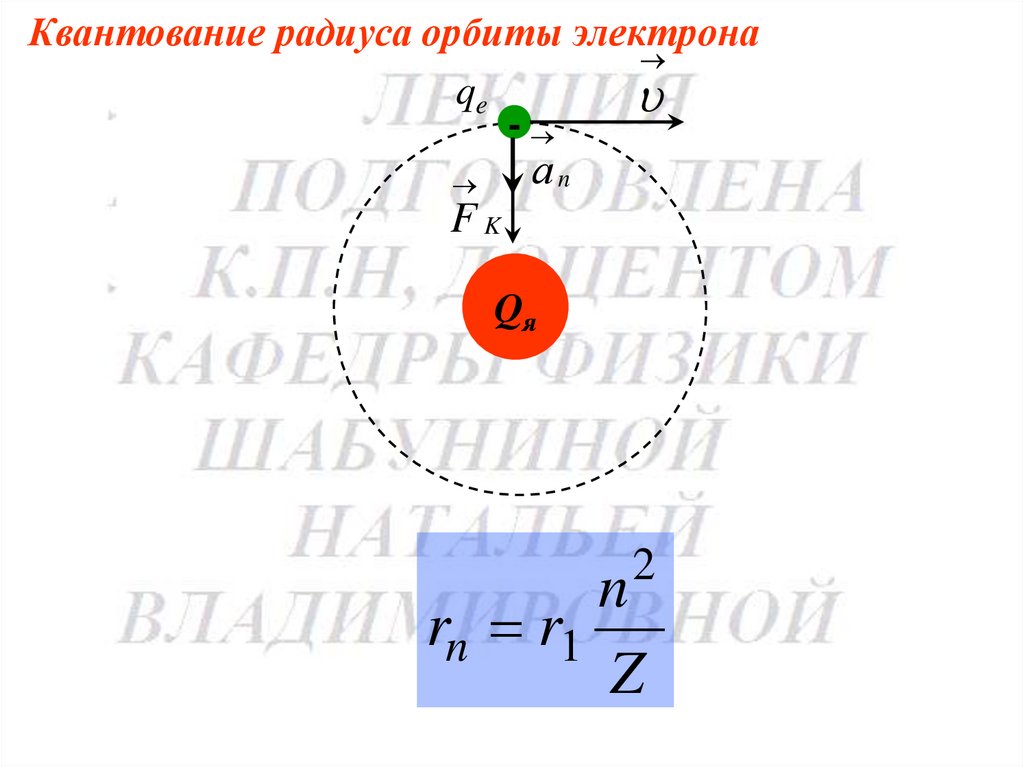
193.
Квантование радиуса орбиты электронаqe
-
аn
FK
Qя
2
n
rn r1
Z
194.
r1 0,529 1010
м 0,529 А
- первый боровский
радиус
Квантование энергии электрона в атоме
Еn Е1
Z
2
n
2
Е1 13,6 эВ
1эВ 1,6 10-19 Дж
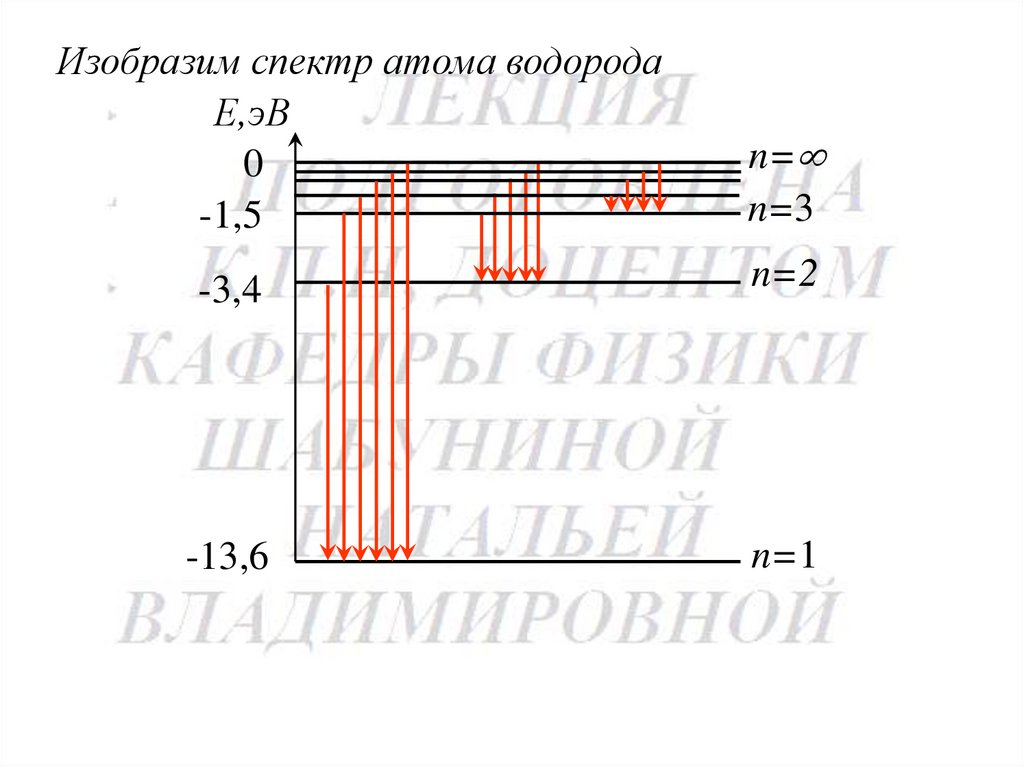
195.
Изобразим спектр атома водородаЕ,эВ
0
-1,5
n=
n=3
-3,4
n=2
-13,6
n=1
196.
11
1
2
R Z 2 2
n1 n2
R 1,097 10 м
7
1
1
R Z 2 2
n1 n2
'
2
-1
- сериальная
формула
R 3,29 10 с
'
15 -1
197.
1. Если n1=1 и n2=2,3,4,5…, то серия Лаймана2. Если n1=2 и n2=3,4,5,6…, то серия Бальмера
3. Если n1=3 и n2=4,5,6,7…, то серия Пашена
4. Если n1=4 и n2=5,6,7,8…, то серия Брэкета
5. Если n1=5 и n2=6,7,8,9…, то серия Пфунда
6. Если n1=6 и n2=7,8,9…, то серия Хэмфри
Перевод
электрона с
первой
соответствует ионизации атома.
орбиты
в
Ei E E1 0 13,6 эВ 13,6 эВ
Е е
198.
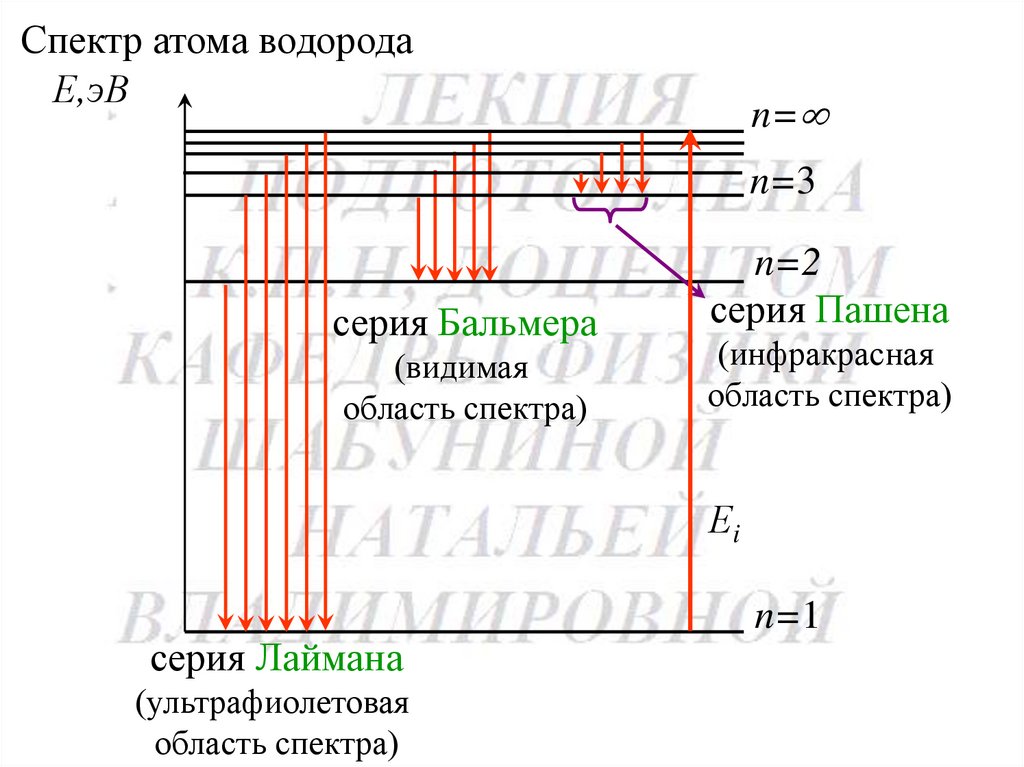
Спектр атома водородаЕ,эВ
n=
n=3
серия Бальмера
(видимая
область спектра)
n=2
серия Пашена
(инфракрасная
область спектра)
Еi
серия Лаймана
(ультрафиолетовая
область спектра)
n=1
199.
АТОМНОЕ ЯДРОСтроение атомного ядра.
Энергия связи и дефект
массы ядра
200.
Протон (p):q p 1,6 10
19
Кл
27
кг
27
кг
m p 1,6728 10
Нейтрон (n):
mn 1,6749 10
Ядро обозначается тем же символом, что и нейтральный
атом.
A
ZX
X – символ химического элемента; A – массовое число;
Z – зарядовое число.
Массы атомныхИзотопы:
ядер принято
1 измерять
2
3 в атомных
H;
H;
H
1
1
1
единицах массы.
3
3
Изобары: 2 He; 1H 27
1 а.е. м. 1,6606 10
кг
201.
Есв m c2
m Z m p ( A Z ) mn mя
Есв ( Z m1 Н ( A Z ) mn mа ) с
2
1
если
m 1 кг
с (3 10 ) м /с
2
8 2
2
2
МэВ
если m 1 а.е.м. с 931,5
а.е.м.
2
Есв
А
202.
Радиоактивность. Законрадиоактивного распада
203.
1. Радиоактивный распадN N0
- t -закон радиоактивного
е
распада:
Число распавшихся ядер:
N N0 N
N N 0 N N 0 (1 е
- t
)
204.
Радиоактивный распад характеризуют:1. Период полураспада
ln 2
Т21
/ 2е Т1 / 2
2. Среднее время жизни радиоактивного ядра
1
205.
3. Активность ядраdN
A
N
dt
Закон изменения активности ядра с течением времени:
A A0 e
t
A 1 Бк
206.
Правила смещения:1. - распад:
A
ZX
A 4
Z 2 Y
4
2 He
2. - - распад:
A
ZX
A
Z 1 Y
0
1e
207.
Ядерные реакции208.
Ядерные реакции – это превращение атомных ядер привзаимодействии с элементарными частицами (в том
числе и с -квантами) или друг с другом.
Символическая запись ядерной реакции:
A3
A1
A2
A4
X
a
Y
b
Z1
Z2
Z3
Z4
X (a,b)Y
В любой ядерной реакции выполняются:
1. Закон сохранения зарядового числа
Z const
209.
2. Закон сохранения массового числаA1 A2 A3 A4
3. Законы сохранения полной энергии (Е=Е0+Т),
импульса и момента импульса.
Энергетический выход ядерной реакции тождественен
тепловому эффекту и определяется:
Q m c [(m1 m2 ) (m3 m4 )] c
2
Q (T1 T2 ) (T3 T4 )
Если Q>0, ядерная реакция экзотермическая.
Если Q<0, ядерная реакция эндотермическая.
2
210.
Элементарные частицы и ихклассификация
211.
Элементарные частицы различают:1) Мюоны ( )
Мюоны нестабильные частицы и распадаются по схемам
(время жизни 2 10-6 с):
0
0
0~
1e 0 e 0
0
0~
0
1e 0 e 0
2) Мезоны
а) - мезоны (пионы)
Пионы нестабильные частицы и распадаются по схемам:
а)
0
0
( t 2,6 10 c)
-8
212.
б)0~
0
( t 2,6 10 c)
в) 2 (t 0,8 10
0
-8
-16
c)
б) k - мезоны (каоны).
Классификация элементарных частиц:
1 ГРУППА: фотон.
2 ГРУППА: лептоны (лёгкие)
Электрон (е-), мюон ( -), таон ( -), соответствующие им
нейтрино ( е, , ) и их античастицы (е+, +, +,
~
e , ~
, ~
).
3 ГРУППА: адроны (крупные)
Мезоны(пионы, каоны, эта-мезоны), нуклоны (протон,
нейтрон), гипероны и их античастицы.






























































































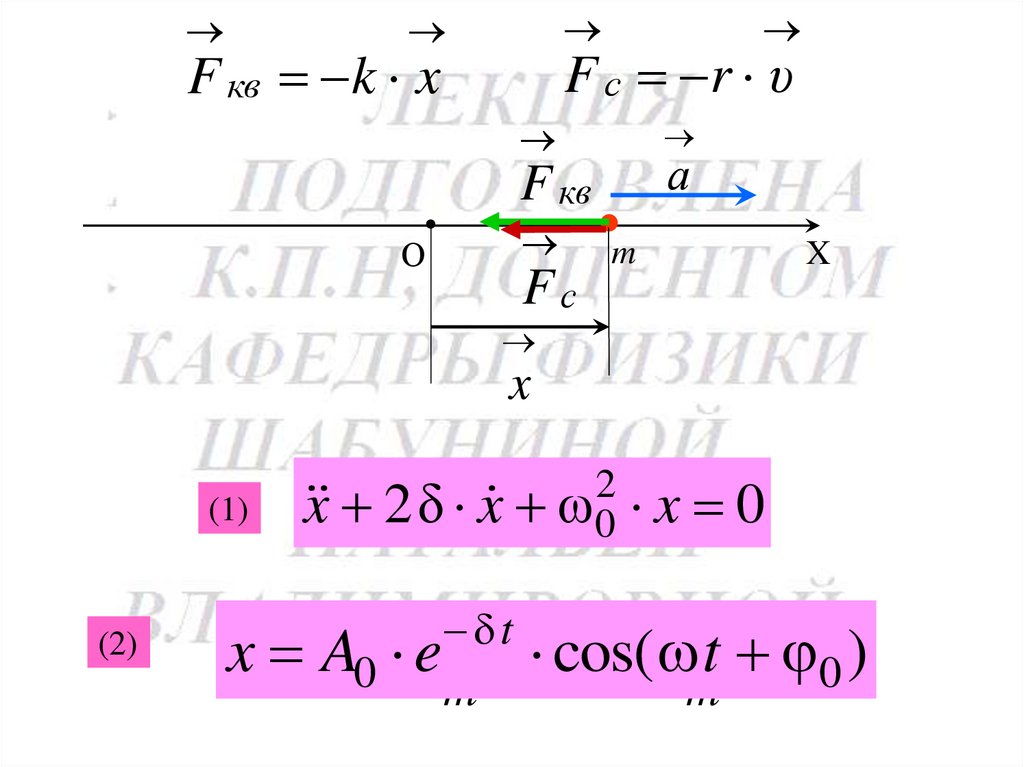













































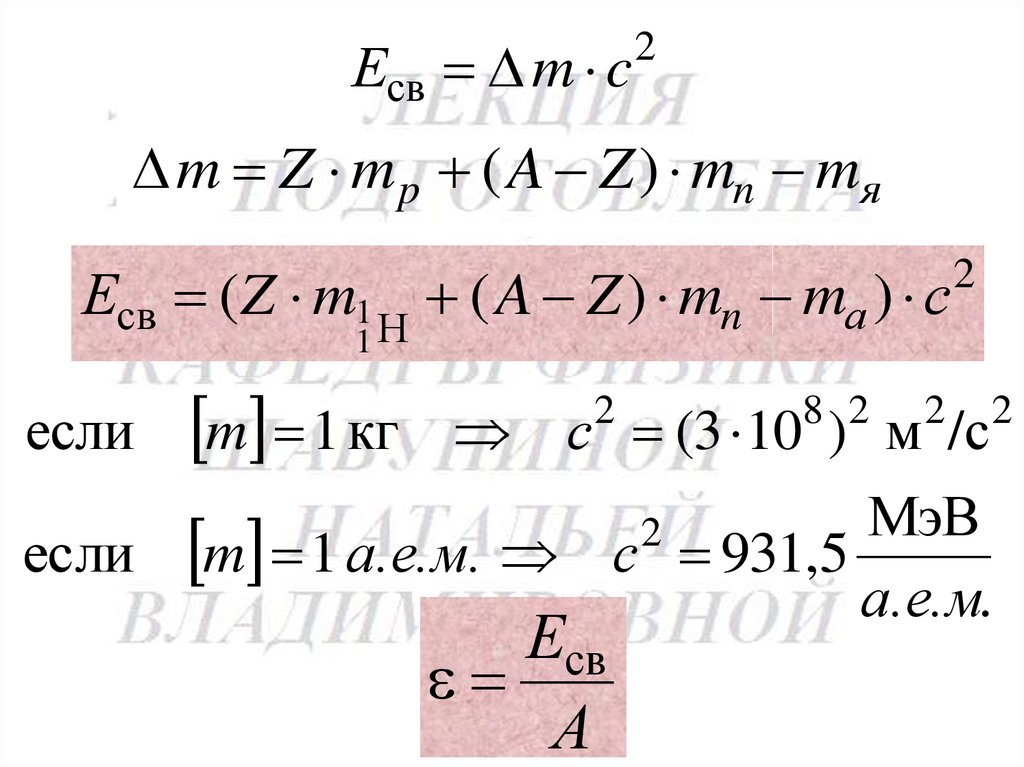











 Физика
Физика








