Похожие презентации:
Решение простейших тригонометрических уравнений
1.
Решение простейшихтригонометрических уравнений.
1
2.
1) уметь отмечать точки на числовойокружности;
2) уметь определять значения синуса, косинуса,
тангенса и котангенса для точек числовой
окружности;
3) знать свойства основных
тригонометрических функций;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
05.11.2024
2
3.
уАрксинусом числа
а называют такое
число из отрезка
[- П/2; П/2], синус
которого равен а.
1
П/2
а
arcsin а
х
0
-arcsin а
-а
-1
- П/2
arcsin (-a)= - arcsin a
3
4.
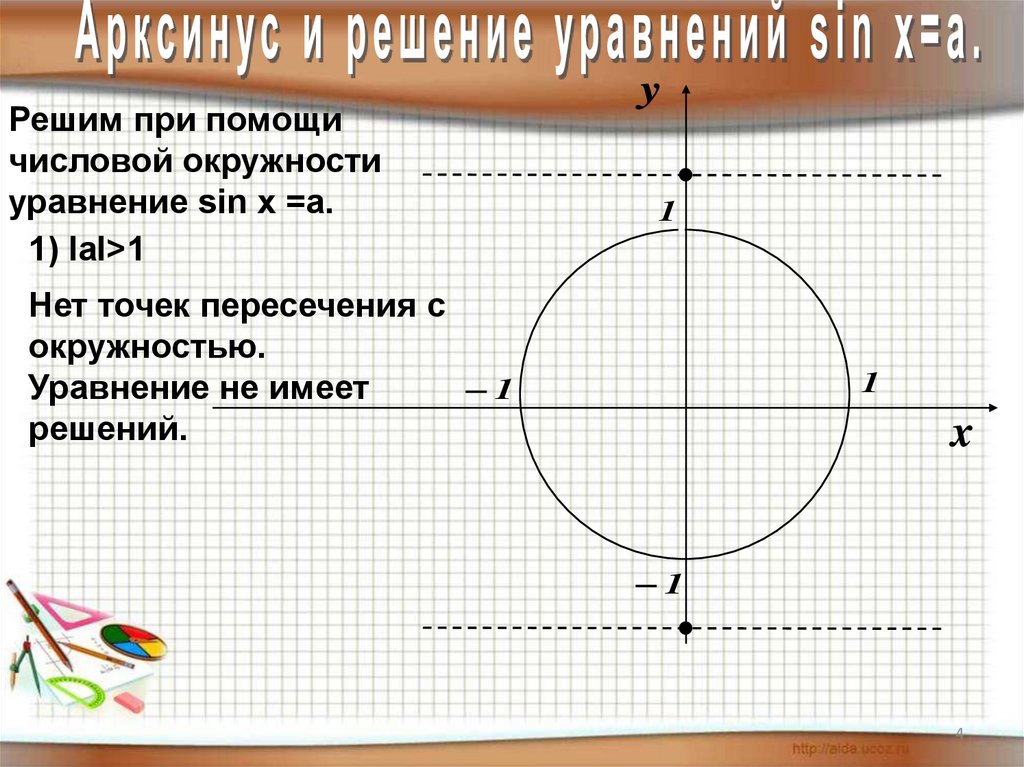
Решим при помощичисловой окружности
уравнение sin х =a.
1) IаI>1
y
1
Нет точек пересечения с
окружностью.
Уравнение не имеет
1
решений.
1
x
1
4
5.
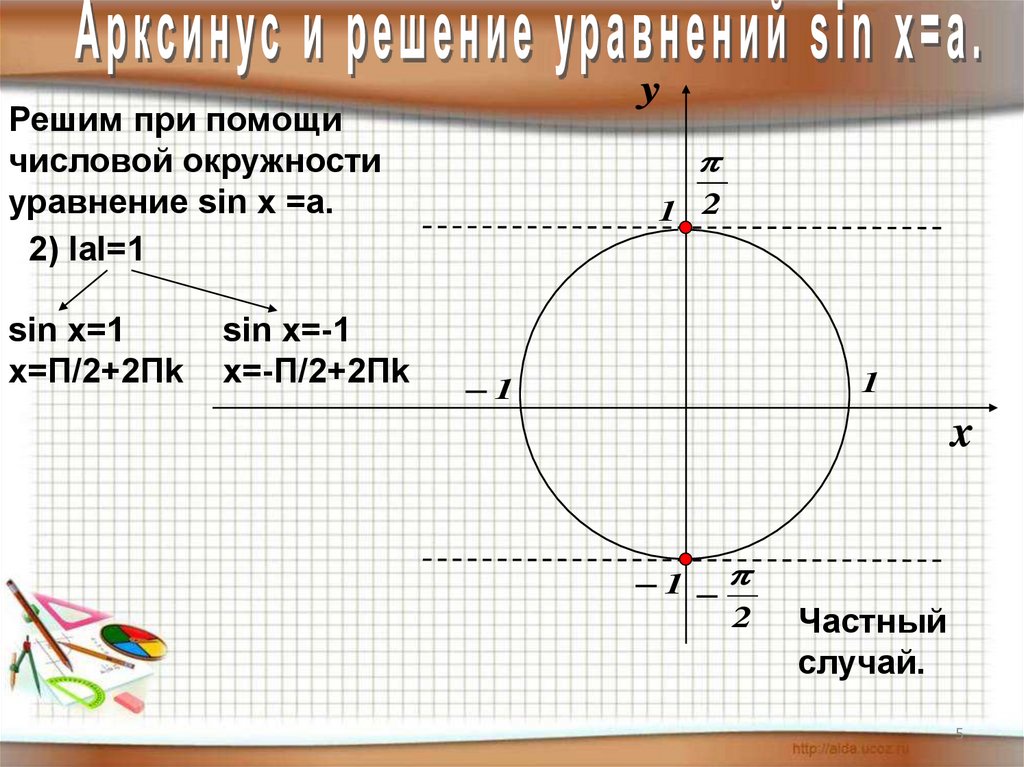
yРешим при помощи
числовой окружности
уравнение sin х =a.
2) IаI=1
sin х=1
х=П/2+2Пk
sin х=-1
х=-П/2+2Пk
1 2
1
1
x
1
2
Частный
случай.
5
6.
yРешим при помощи
числовой окружности
уравнение sin х=a.
1
3) а=0
1
1
0
x
1
Частный
случай.
6
7.
Решим при помощичисловой окружности
уравнение sin х=a.
4) IаI<1
y
1
П-arcsin а
Корни, симметричные
относительно Оу
могут быть записаны:
а
1
arcsin а
1
x
arcsin a 2 k
х
arcsin a 2 k
или
х 1 arcsin a k ,
k
1
k Z
Общий
случай.
8.
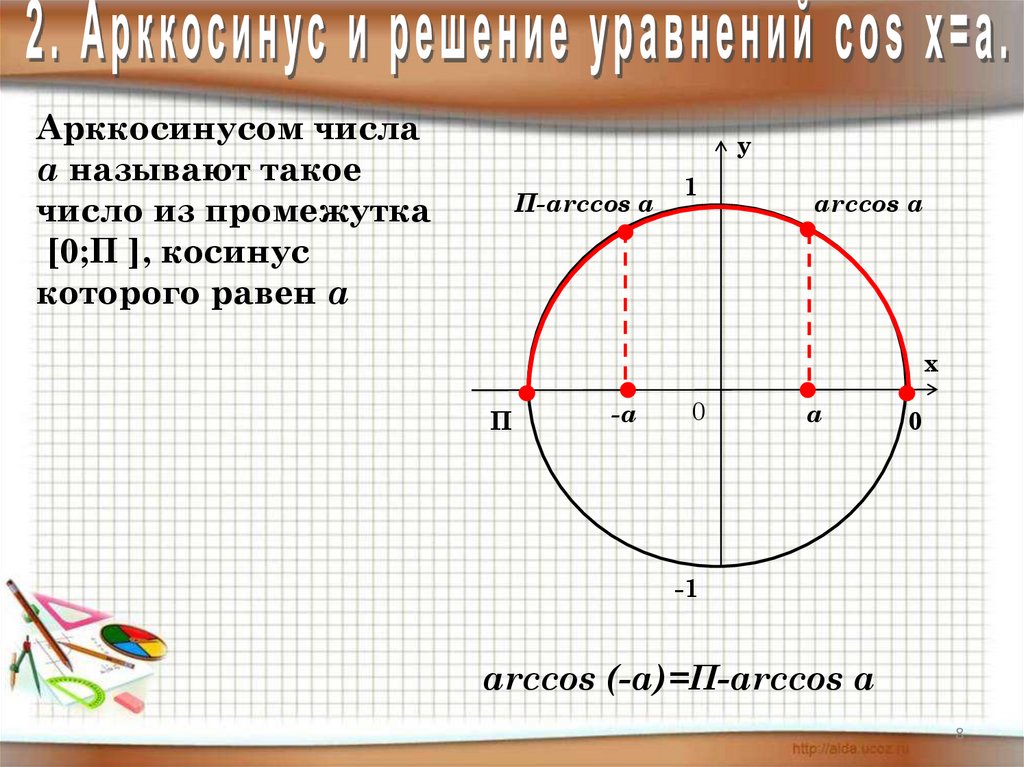
Арккосинусом числаа называют такое
число из промежутка
[0;П ], косинус
которого равен а
у
П-arccos a
1
arccos а
х
П
-а
0
а
0
-1
arccos (-a)=П-arccos a
8
9.
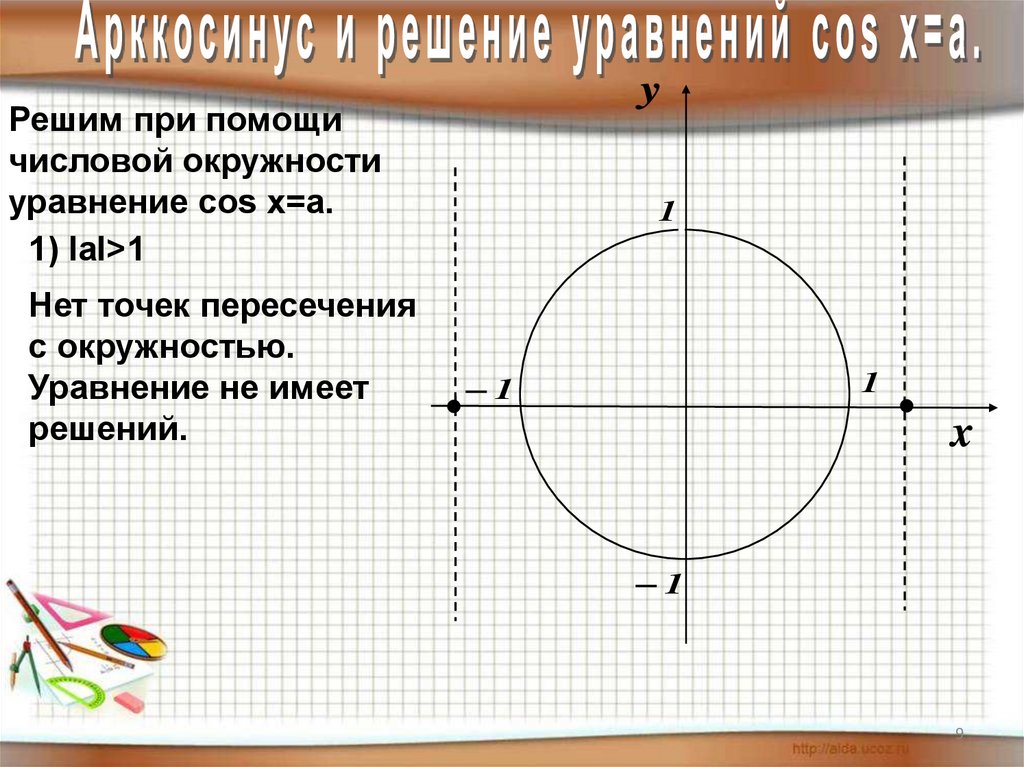
yРешим при помощи
числовой окружности
уравнение cos х=a.
1) IаI>1
Нет точек пересечения
с окружностью.
Уравнение не имеет
решений.
1
1
1
x
1
9
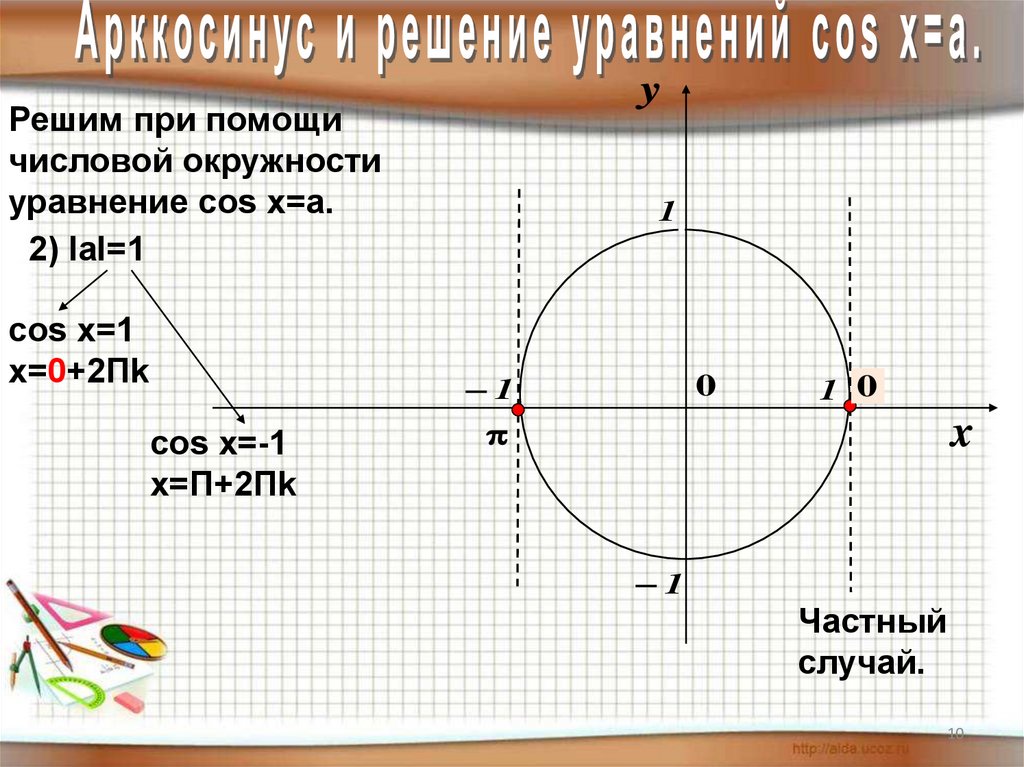
10.
yРешим при помощи
числовой окружности
уравнение cos х=a.
2) IаI=1
cos х=1
х=0+2Пk
1
1
cos х=-1
х=П+2Пk
0
1 0
x
1
Частный
случай.
10
11.
yРешим при помощи
числовой окружности
уравнение cos х =a.
1 2
1
1
0
x
2
Частный
случай.
11
12.
y1
4) IаI<1
Корни, симметричные
относительно Оx
могут быть записаны:
arccos а
1
а
x
arccos a 2 k
х
arccos a 2 k
-arccos а
или
x arccos a 2 k ,
1
k Z
1
Общий
случай.
12
13.
Арктангенсом числа аназывают такое число
из интервала
(-П/2; П/2), тангенс
которого равен а
у
1
П/2
а
arctg a
х
0
-arctg a
-1
-а
- П/2
arctg (- a)= - arctg a
13
14.
yРешим при помощи
числовой окружности
уравнение tg х=a.
а
2 arctg a
a – любое число.
0
x
05.11.2024
2
Частных
случаев нет.
14
15.
Арккотангенсом числа аназывают такое число
из интервала (0;П),
котангенс которого -а
равен а
у
а
1
ось ctg
П-arcctg a
arcctg a
П
0
х
0
arcctg (-a)=П-arcсtg a
15
16.
yРешим при помощи
числовой окружности
уравнение сtg х=a.
a – любое число.
х=arcctg a+Пk.
а
arcctg a
0
x
Частных
случаев
нет.
05.11.2024
16
17.
1718.
Примеры.Пример 1.





















 Математика
Математика








