Похожие презентации:
Digital Logic Design Lecture – 8: Arithmetic circuits: binary addition, half adders, full adders, binary subtraction…
1.
Digital Logic DesignLecture – 8:
Arithmetic circuits: binary addition, half
adders, full adders, binary subtraction…
Konakbayev Olzhas, senior-lecturer,
2.
Lecture baseDigital Electronics: Principles & Applications, 9th edition by Roger
Tokheim & Patrick E. Hoppe:
• Chapter 10
2
3.
Introduction 1• Binary Addition
• Half & Full Adders
• 3-Bit Adders
• Binary Subtraction
• Parallel Subtractors
3
4.
Introduction 2• IC Adders
• Binary Multiplication
• 2s Complement Notation
• 2s Complement Adding/Subtracting
4
5.
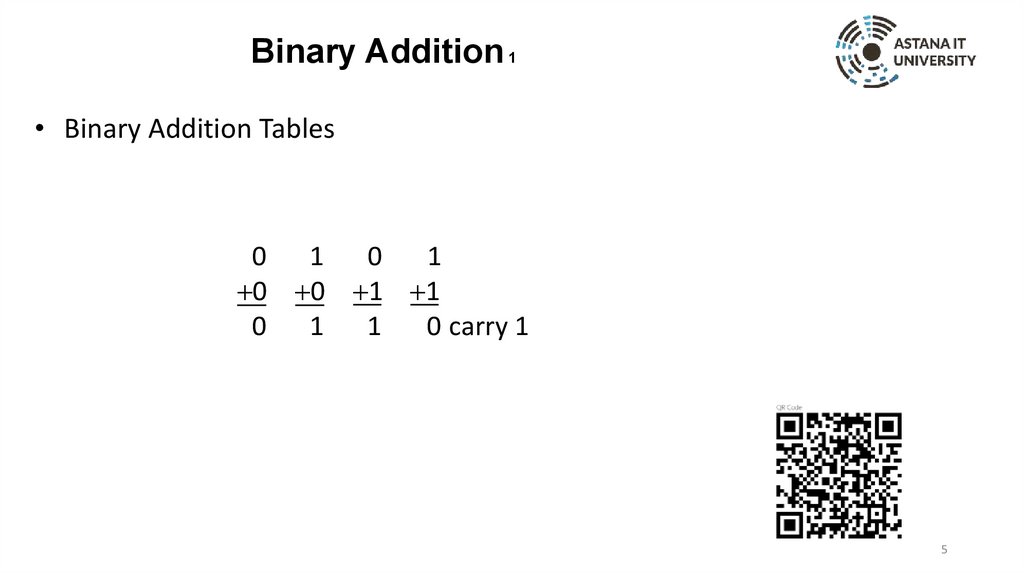
Binary Addition 1• Binary Addition Tables
0 1 0
1
0 0 1 1
0 1 1
0 carry 1
5
6.
Binary Addition 2• Binary Addition Examples
6
7.
Binary Addition 3• Binary Addition Practice
1 0 1 0
0 1 0 1
7
8.
Binary Addition 4• Binary Addition Practice
1 0 1 0
0 1 0 1
1 1 1 1
check
10
5
15
8
9.
Binary Addition 5• Binary Addition Practice
1 0 1 1
0 1 0 1
9
10.
Binary Addition 6• Binary Addition Practice
carry bits 1 1 1 1
1 0 1 1
0 1 0 1
1 0 0 0 0
check
11
5
16
10
11.
Binary Addition 7• Binary Addition Practice
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
1 0 0 0 1 0 0 1 1
11
12.
Binary Addition 8• Binary Addition Practice
carry bits 1 1 1 1 1 1
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
1 0 0 0 1 0 0 1 1
check
183
92
275
12
13.
Half & Full Adders 1• Half Adder
• Two input bits
• Sum bit out
• Carry bit out
• Full Adder
• Two input bits plus a
carry bit in
• Sum bit out
• Carry bit out
13
14.
Half & Full Adders 2• Half Adder
14
15.
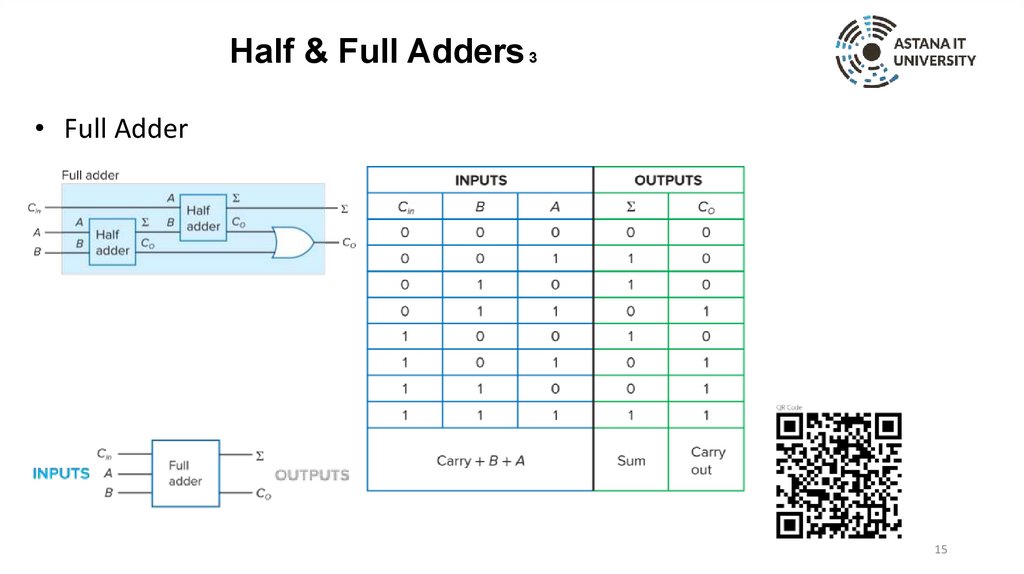
Half & Full Adders 3• Full Adder
15
16.
Half & Full Adders 4• Full Adder
16
17.
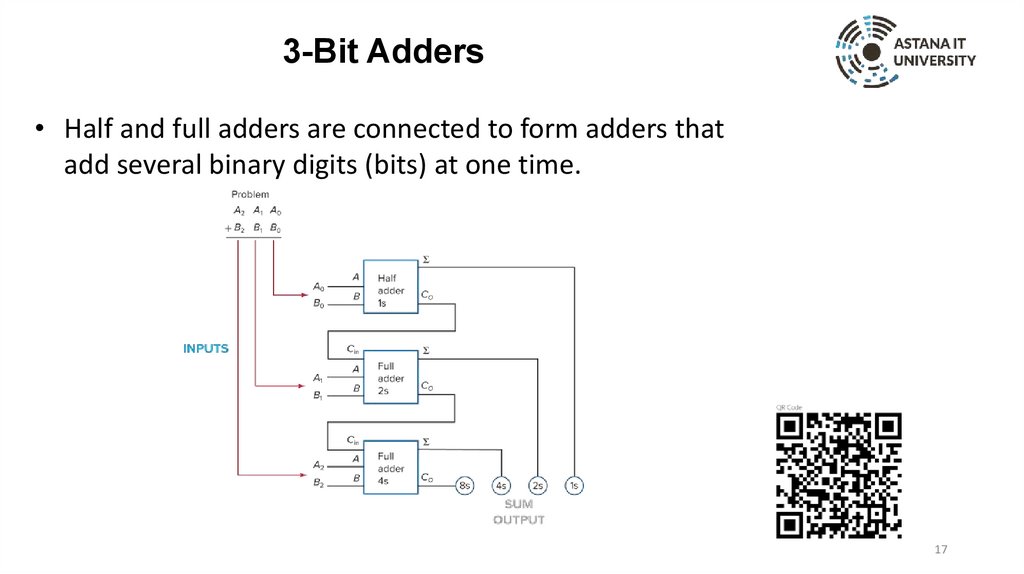
3-Bit Adders• Half and full adders are connected to form adders that
add several binary digits (bits) at one time.
17
18.
Binary Subtraction 1• Binary subtractors are very similar to binary adders.
• Instead of a carry out, there is a borrow.
18
19.
Binary Subtraction 2• Half subtractor
19
20.
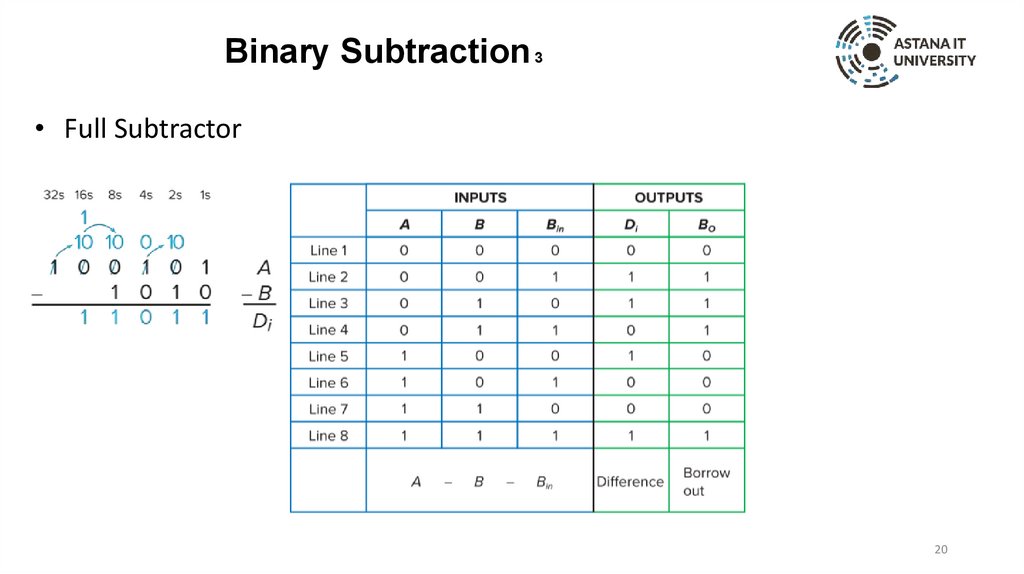
Binary Subtraction 3• Full Subtractor
20
21.
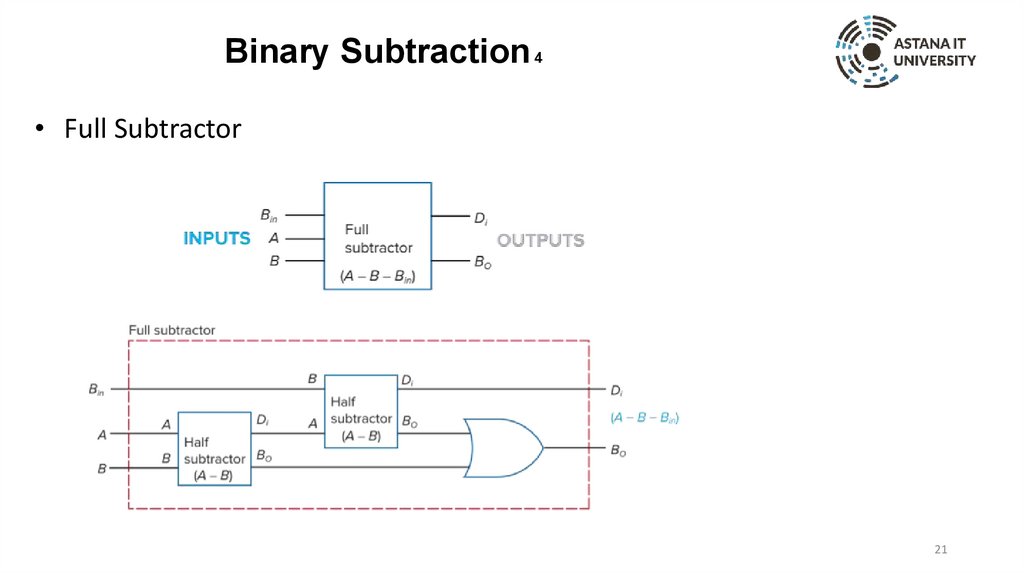
Binary Subtraction 4• Full Subtractor
21
22.
Binary Subtraction 5• Binary Subtraction Practice
1 0 1 1
0 1 0 1
22
23.
Binary Subtraction 6• Binary Subtraction Practice
borrow bits
10
1 0 1 1
0 1 0 1
0 1 1 0
check
11
5
6
23
24.
Binary Subtraction 7• Binary Subtraction Practice
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
24
25.
Binary Subtraction 8• Binary Subtraction Practice
borrow bits
10 10 10
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
0 1 0 1 1 0 1 1
check
183
92
91
25
26.
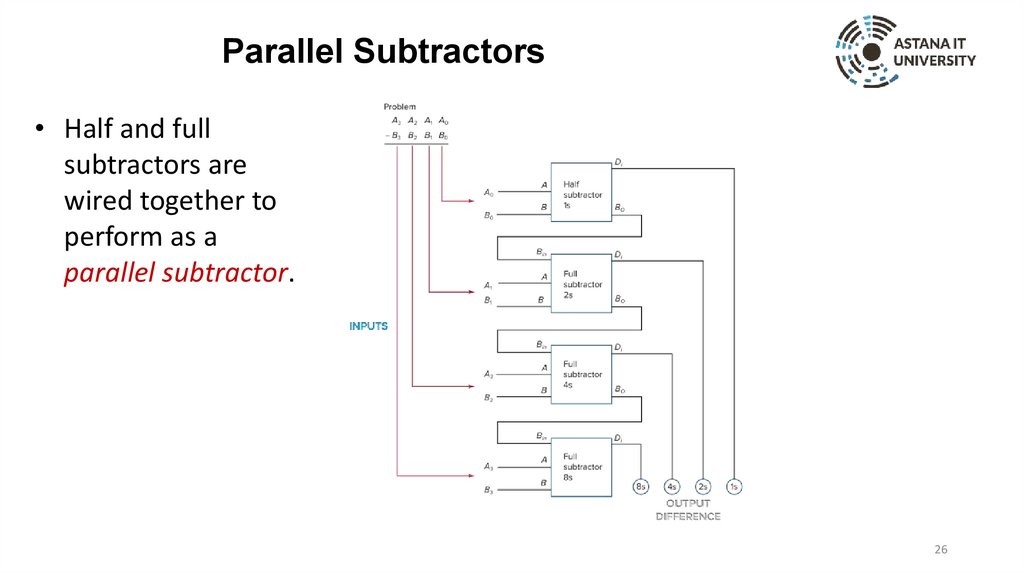
Parallel Subtractors• Half and full
subtractors are
wired together to
perform as a
parallel subtractor.
26
27.
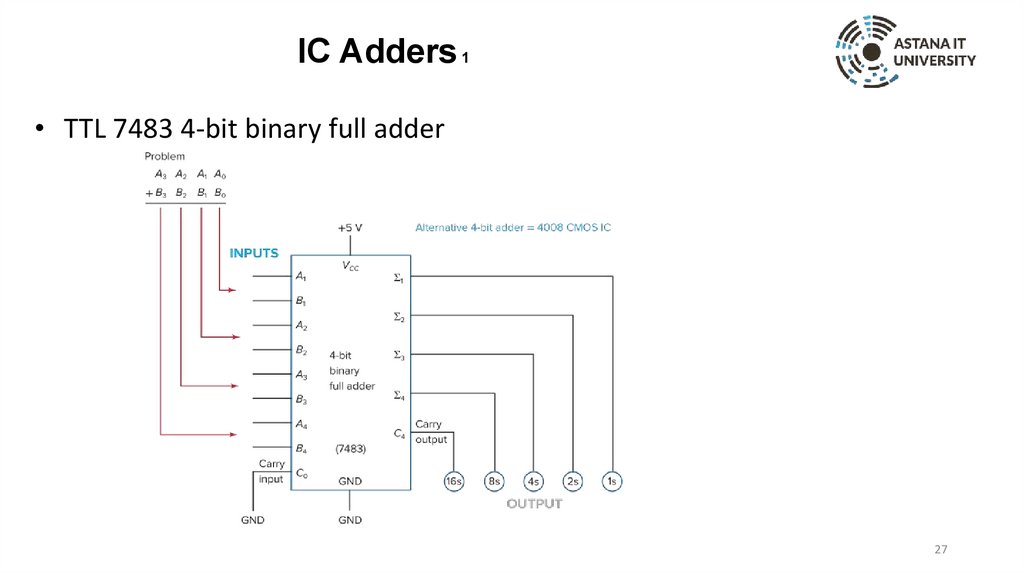
IC Adders 1• TTL 7483 4-bit binary full adder
27
28.
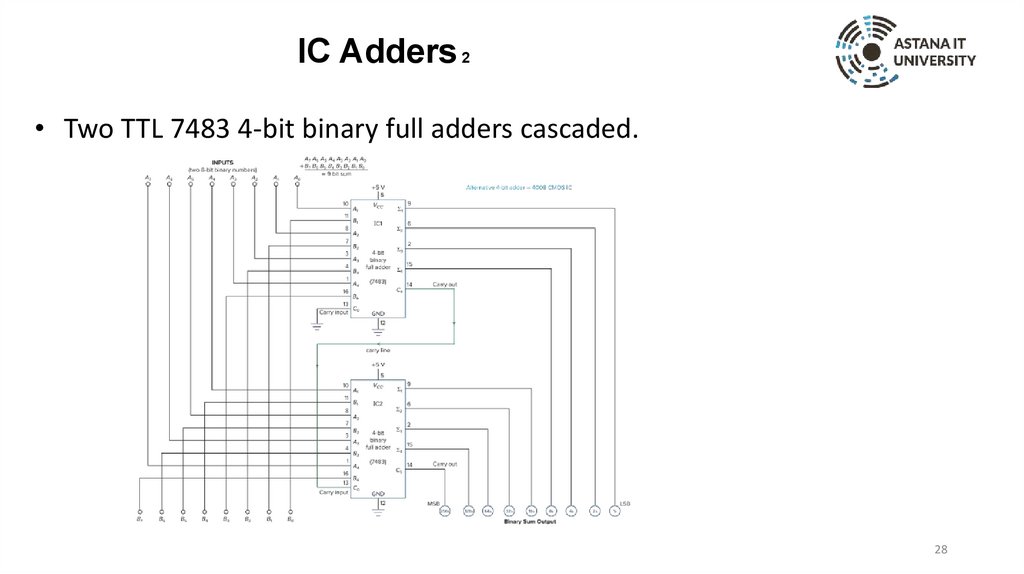
IC Adders 2• Two TTL 7483 4-bit binary full adders cascaded.
28
29.
Binary Multiplication 1• Multiplication can be thought of as repeated addition.
29
30.
Binary Multiplication 2• Multiplication is the sum of partial products.
216
540
756
30
31.
Binary Multiplication 3• Rules for Multiplication
• Example
31
32.
Binary Multiplication 4• Example
32
33.
2s Complement Notation 1• Sign Bit
• Positive number, sign bit = 0
• Negative number, sign bit = 1
• The 2s complement of a positive number is the same
as binary: +7 (decimal) = 0111 (2s complement) = 0111
(binary).
33
34.
2s Complement Notation 2• The 2s complement of a negative number is found by
first taking the 1s complement and then adding 1.
• Convert the decimal number to its binary equivalent.
• Convert the binary number to its 1s complement by
changing all 1s to 0s and all 0s to 1s.
• Add 1 to the 1s complement number, using regular binary
addition.
34
35.
2s Complement Notation 335
36.
2s Complement Notation 4• Example: Convert 410 to its 2s complement.
36
37.
2s Complement Notation 5• Converting from 2s complement to binary.
37
38.
2s Complement Adding/Subtracting 1• The 2s complement is useful in the addition of signed
numbers.
( 4)
( 3)
710
0100
0011
0111 (2s complement SUM)
38
39.
2s Complement Adding/Subtracting 2• The 2s complement is useful in the addition of signed
numbers.
( 1)
( 2)
310
1111
1110
11101 (2s complement SUM)
Discard
39
40.
2s Complement Adding/Subtracting 3• The 2s complement is useful in the addition of signed
numbers.
( 1)
( 3)
210
0001
1101
1110 (2s complement SUM)
40
41.
2s Complement Adding/Subtracting 4• The 2s complement is useful in the addition of signed
numbers.
( 5)
( 4)
110
0101
1100
10001 (2s complement SUM)
Discard
41
42.
2s Complement Adding/Subtracting 5• The 2s complement is useful in the addition of signed
numbers.
( 50)
( 30)
8010
1 1 0 0 1 1 1 0 2s
1 1 1 0 0 0 1 0 2s
11011 0 0 0 0
Negative
sign
0 1 0 0 1 1 1 1 1s
1
0 1 0 1 0 0 0 0 2s
8010
42
43.
2s Complement Adding/Subtracting 6• The 2s complement is useful in the subtraction of
signed numbers.
( 7) Form 2s comp. 0111
( 3)
1101
410 and ADD 1 0100 (2s comp. Difference)
Discard
43
44.
2s Complement Adding/Subtracting 7• The 2s complement is useful in the subtraction of
signed numbers.
( 8) Form 2s comp. 1000
( 3)
0011
510 and ADD
1011 (2s comp. Difference)
44
45.
2s Complement Adding/Subtracting 8• The 2s complement is useful in the subtraction of
signed numbers.
( 3) Form 2s comp.
0011
( 3)
0011
610 and ADD
0110 (2s comp. Difference)
45
46.
2s Complement Adding/Subtracting 9• The 2s complement is useful in the subtraction of
signed numbers.
( 4) Form 2s comp. 1100
( 2)
1110
610 and ADD 1 1010 (2s comp. Difference)
Discard
46
47.
Review 1• Add the following binary numbers.
1011
0111
47
48.
Review 2• Add the following binary numbers.
1011
0111
10010
48
49.
Review 3• Add the following binary numbers.
10111101
01110 011
49
50.
Review 4• Add the following binary numbers.
10111101
01110 011
10 0110 0 0 0
50
51.
Review 5• Draw a block diagram of a half adder.
• Draw a block diagram of a full adder.
51
52.
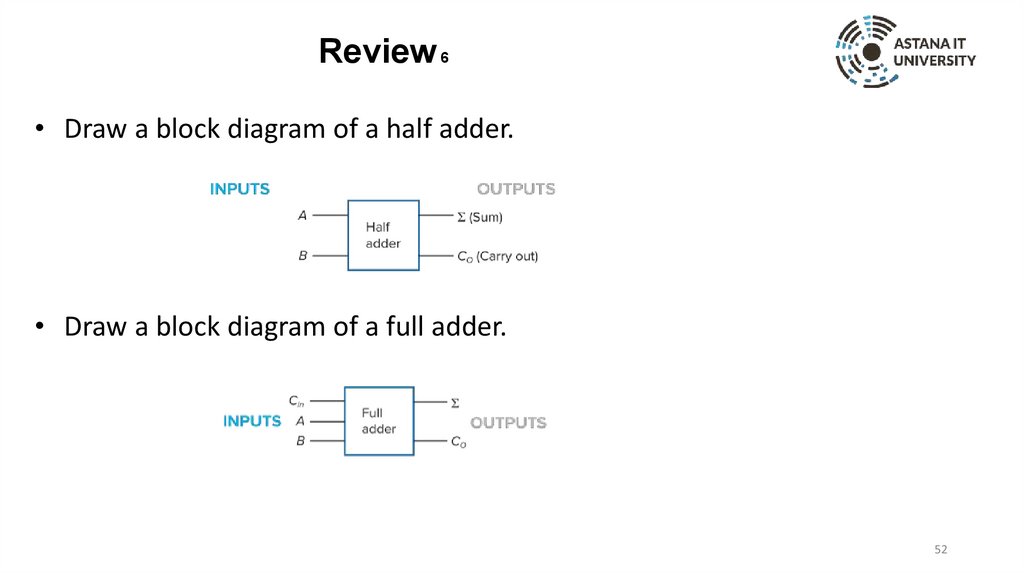
Review 6• Draw a block diagram of a half adder.
• Draw a block diagram of a full adder.
52
53.
Review 9• Complete the following binary subtraction.
10101010
01010110
53
54.
Review 10• Complete the following binary subtraction.
Borrow
10 10 10
10101010
01010110
01010100
54
55.
Review 17• Complete the following binary multiplication.
111
101
55
56.
Review 18• Complete the following binary multiplication.
111
101
111
000
111
10 0 011
56
57.
Review 13• Draw a block diagram of a half subtractor.
• Draw a block diagram of a full subtractor.
57
57
58.
Review 14• Draw a block diagram of a half subtractor.
• Draw a block diagram of a full subtractor.
58
59.
Thank you!59


















































 Электроника
Электроника








