Тема_5

1. Тема 5 Решение систем нелинейных уравнений

«Вычислительная математика»
Тема 5
Решение систем
нелинейных уравнений
5.1. Отделение решений.
5.2. Методы уточнения решений СНУ (Метод простых итераций. Метод
Ньютона–Рафсона.)

2.

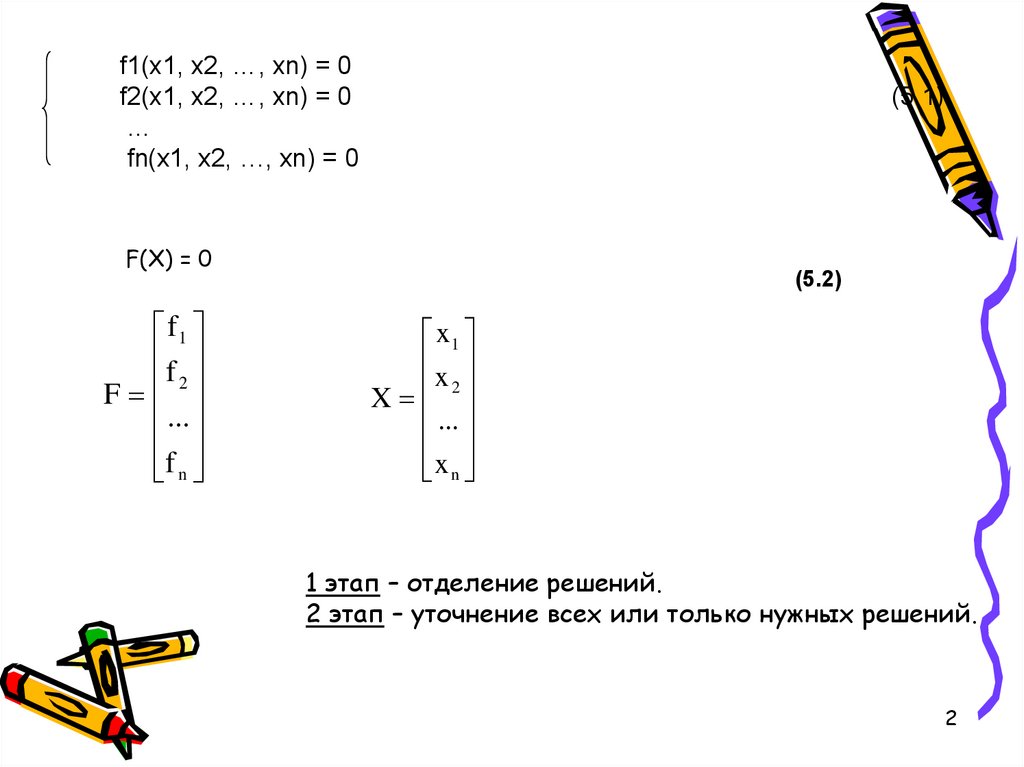
f1(x1, x2, …, xn) = 0
f2(x1, x2, …, xn) = 0
…
fn(x1, x2, …, xn) = 0
(5.1)
F(X) = 0
f1
f
F 2
...
f n
(5.2)
x1
x
X 2
...
x n
1 этап – отделение решений.
2 этап – уточнение всех или только нужных решений.
2

3.

5.1. Отделение решений.
f1(x1, x2) = 0
f2(x1, x2) = 0
Графическое отделение решений СНУ.
f2(x1,х2)=0
x2
Имеется два решения.
D1 – область существования
первого решения.
D1
b2
x2*
D1 = {a1 < x 1< b1 , a2 < x 2< b2}.
f1(x1,х2)=0
a2
0
a1 x1* b1
x1
Отделение решений позволяет:
1) Выявить число решений и область
существования каждого из них.
2) Проанализировать возможность
применения выбранного метода
решения СНУ в каждой области.
3) Выбрать начальное приближение
решения X(0) из области его
существования, так что X(0) D.
3

4.

5.2. Методы уточнения решений СНУ.
5.2.1. Метод простых итераций.
X=Φ(X)
X(k) = Φ(X(k-1)) , где k=1,2,3,… - номер итерации
1
2
...
n
X(0) D
xi.(k) = φi(x1(k-1), x2(k-1), … , xn(k-1)), i 1, n
.
Условие окончания расчета:
δ≤ε
(k )
( k 1)
max
|
x
x
|
δ=
i
i
i 1, n
δ=
Условия сходимости:
i
1, i 1, n
j 1 x j
n
i
1,
x
i 1
j
n
или
1 n
| xi( k ) xi( k 1) |
n i 1
j 1, n
4

5.

Получение эквивалентной системы:
x i x i f i (x1 , x 2 ,..., x n ) i (x1 , x 2 ,..., x n )
i 1, n
x i i (x1 , x 2 ,..., x n ) f i (x1 , x 2 ,..., x n ) 0
i ≠ 0,
f i ( x) 0 i f i ( x) 0 xi xi i f i ( x),
Улучшение сходимости метода простых итераций:
x
(K)
i
i (x
,
(K)
1
,x
(K)
2
,..., x
(K)
i 1
1)
, x i(K 1) ,..., x (K
)
n
xi i (x1, x 2 ,..., x n )
или
или
x
или
(k)
i
x i(k 1) x i(k 2)
2
x
(k)
i
x
(k 1)
i
(x i(k 1) x i(k 2) ) 2
2x i(k 2) x i(k 1) x i(k 2)
5

6.

5.2.2. Метод Ньютона–Рафсона.
x i x *i x i(k) x *i x i(k) x i
i 1, n
(k)
f1 (x 1(k) Δx 1 , x (k)
2 Δ x 2 , ... , x n Δ x n ) 0
(k)
f 2 (x 1(k) Δx1 , x (k)
2 Δ x 2 , ... , x n Δ x n ) 0
…
(k)
f n (x 1(k) Δx1 , x (k)
2 Δ x 2 , ... , x n Δ x n ) 0
x i(k 1) x i(k) x i(k)
i 1, n
(k)
f i (x 1(k) , x (k)
(k)
2 ,..., x n )
x i(k) f j (x 1(k) , x (k)
2 ,..., x n )
x i
i 1
n
max x
i 1,n
(k)
i
ε
j 1, n
1 n
| xi |
n i 1
6

7.

W(X (k) ) X (k) F(X (k) )
f 1
x 1
f j
...
W(X)
x
i n ,n f n
x
1
f 1
x 2
...
f n
x 2
f 1
x n
... ...
f n
...
x n
...
x 1(k)
(k)
x
(k)
X 2
...
(k)
x n
X (k) W 1 (X (k) ) F(X (k) )
X (k 1) X (k) W 1 (X (k) ) F(X (k) )
Пример 5.3.
ε=0,001
x12+x22=1
ln x1+2x2= –1
D2 {0,8 x1 1; 0,5 x2 0,3}
f1 (x 1 , x 2 ) x12 x22 1 0
f 2 (x 1 , x 2 ) ln(x 1 ) 2 x2 1 0
Х(0)=(0,9;-0,4).
7

8.

w1,1=
f1
2 x1 2 0,9 1,8;
x1
w1,2=
f1
2 x 2 2 ( 0,4) 0,8;
x 2
f 2
1
1/0,9 1,1111;
w2,1= x
x
1
1
w2,2=
f 2
2;
x 2
f1(0,9;-0,4) = 0,9 0,9 + 0,4 0,4 – 1 = 0,81+ 0,16 – 1 = -0,03
f2(0,9;-0,4) = ln(0,9) + 2*(-0,4) + 1 = -0,1054 – 0,8 + 1 = 0,0946
1,8 ∆x1 - 0,8 x2= -(-0,03)
1,1111 ∆x1 + 2 ∆x2= –0,0946
По формулам Крамера:
det W
1,8
0,8
1,8 2 0,8 1,1111 3,6 0,88888 4,4889
1,1111
2
detW≠0 – система обусловлена.
8

9.

0,03
0,8
det W1
0,03 2 0,8 0,0946 0,0157
0,0946 2
1,8
0,03
det W2
1,8 0,0946 0,03 1,1111 0,2036
1,1111 0,0946
x1
x 2
det W1 0,0157
0,0035
det W
4,4889
det W2 0,2036
0,0454
det W
4,4889
х1 = х1 + ∆х1 = 0,9+(-0,0035) = 0,8965
х2 = х2 + ∆х2 = -0,4 + (-0,0454) = -0,4454
max x i max(| x1 |, | x2 |) 0,0454
i 1,2
х1=0,8995 х2=-0,4449, 0,001.
9