Лекция 1

1.

Лекция №1
Функции, свойства функций
Доцент кафедры математики и теории игр
Перькова Н.В.
2020

2.

План лекции
• 1. Определение функции (основные понятия)
• 2. Тождественно равные функции
• 3.Действия над функциями
• 4.Элементарные свойства функции
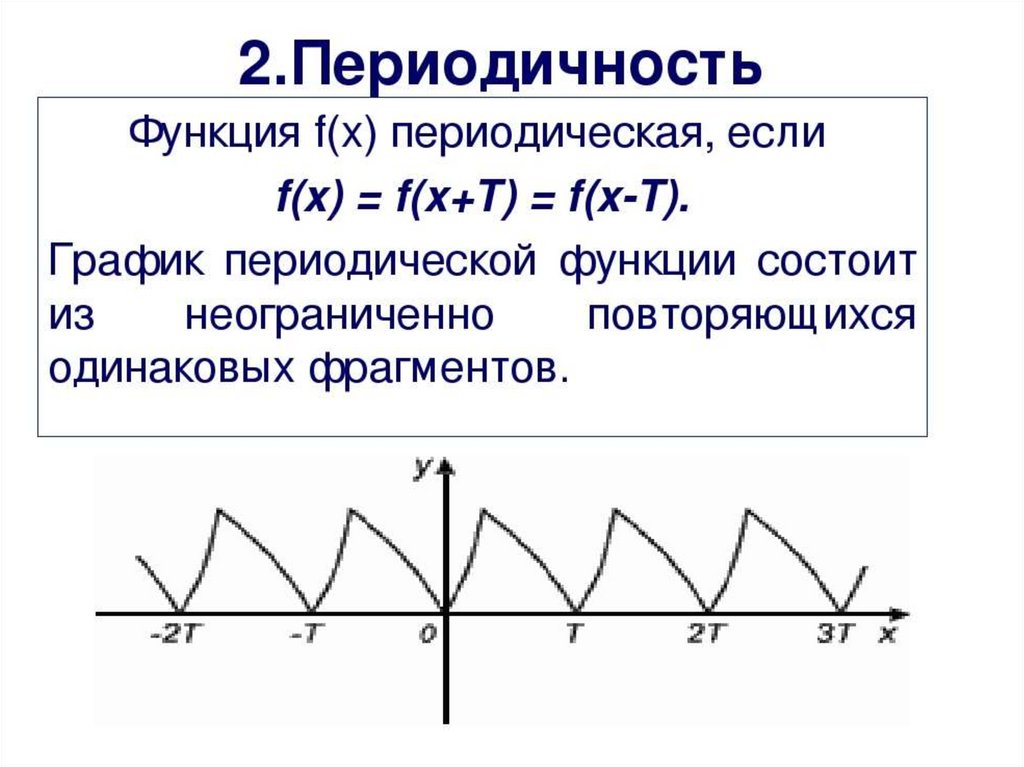
(монотонность, ограниченность, четность и
нечетность, периодичность)
• 5 Обратная функция.

3.

4.

5.

6.

Задачи
1. Пусть Т-множество равнобедренных треугольников плоскости α, Pмножество прямых плоскости α. Задано соответствие F: каждому
равнобедренному треугольнику множества Т ставится в соответствие
прямая
множества
P,
являющаяся
осью симметрии данного
треугольника.
Будет ли это соответствие функциональным? Опишите соответствие,
обратное данному. Будет ли оно функцией?
х 4 , если 2 х 0
2. Является ли соответствие f 1, если х 0
2 х 1, если 0 x 2
f функциональным? Постройте график.

7.

Тождественно равные функции
• Функции f(x) и g(x) называются
тождественно равными на промежутке,
если выполняются два условия:
• 1. Области определения функций f(x) и
g(x) равны
• 2. f(x)= g(x)

8.

9.

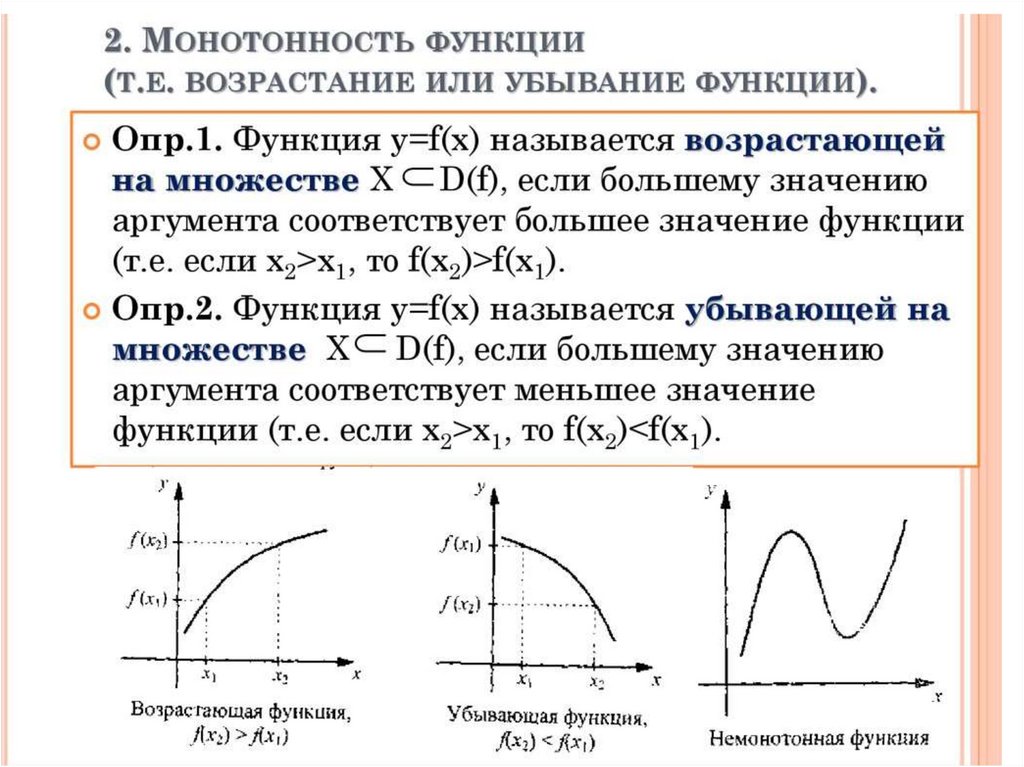
Утверждения
Если функции f (x) и g(x) возрастают (убывают) на D, то f(x)+g(x) является
возрастающей функцией (убывающей) на D.
Если функции f (x) и g(x) возрастают (убывают) на D и f ( x) 0; g ( x) 0 ,
то f ( x) g ( x) есть возрастающая (убывающая ) функция .
Если функция f (x) возрастает, то функция -f(x) убывает
Если функция f (x) возрастает, то c f (c > 0) и f + c также возрастают, а
функция c f (c < 0) убывает (c – некоторая константа).
Если функция f(x) возрастает (убывает) на D и сохраняет знак, то функция
убывает (возрастает) на D.
Если функция f(x) возрастает и неотрицательна, то f n (x) где n є N, также
возрастает.
Если функция f(x) возрастает и n – нечетное число, то f n (x) также
возрастает.
Композиция g (f (x)) возрастающих функций f(x) и g (x) также возрастает.

10.

11.

12.

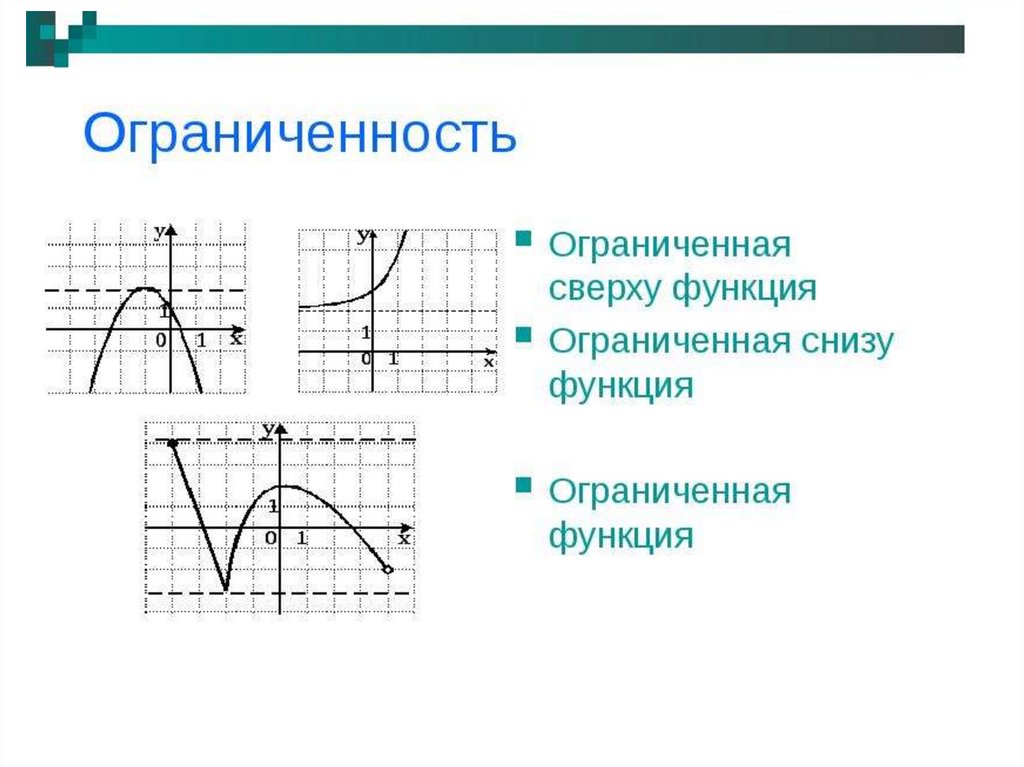
Утверждения
Если функции f (x) и g(x) ограничены на D, то f(x)+g(x)
и f ( x) g ( x) является ограниченной функцией на D.
.Если функция f (x) ограничена сверху на D, то функция
-f(x) ограничена на D снизу
Если функции f(x) ограничена на множествах М и N, то
f(x) ограничена на объединении множеств М и N.
Если f(x) >0 на D и ограничена снизу положительным
числом, то ог ограничена на D

13.

14.

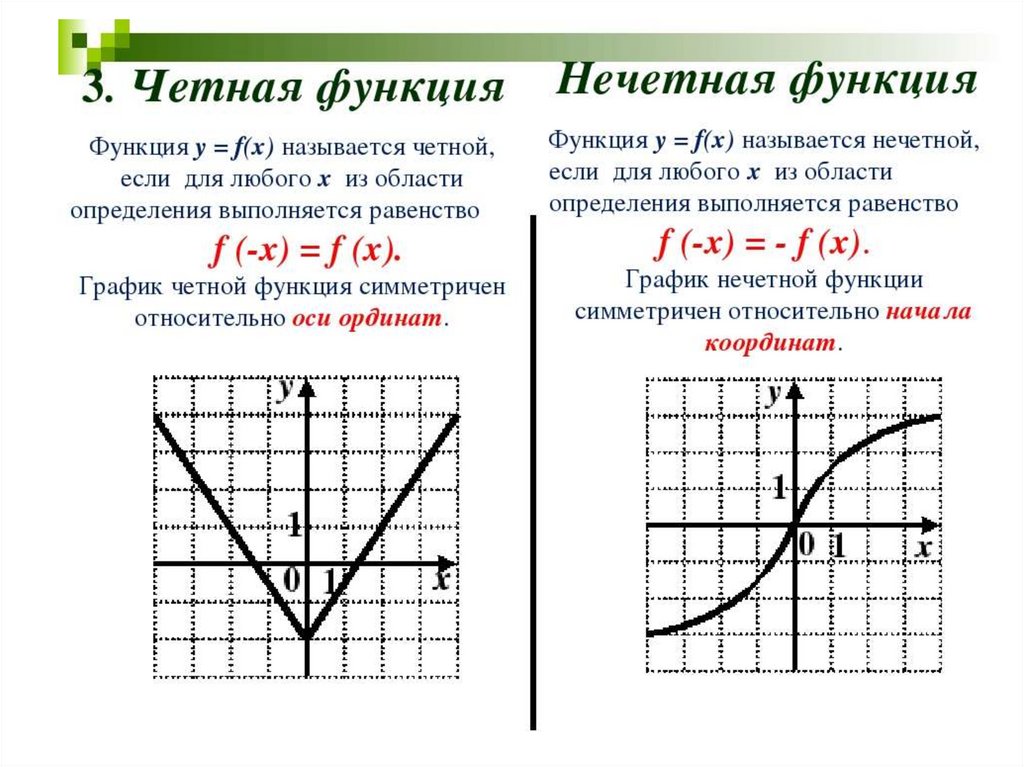
Утверждения
1. Сумма двух четных (нечетных) функций есть
функция четная (нечетная)
2. Произведение двух четных или нечетных
функций есть функция четная
3. Произведение четной и нечетной функции есть
нечетная функция
4. Композиция двух четных функций g (f (x)) есть
четная функция

15.

16.

17.

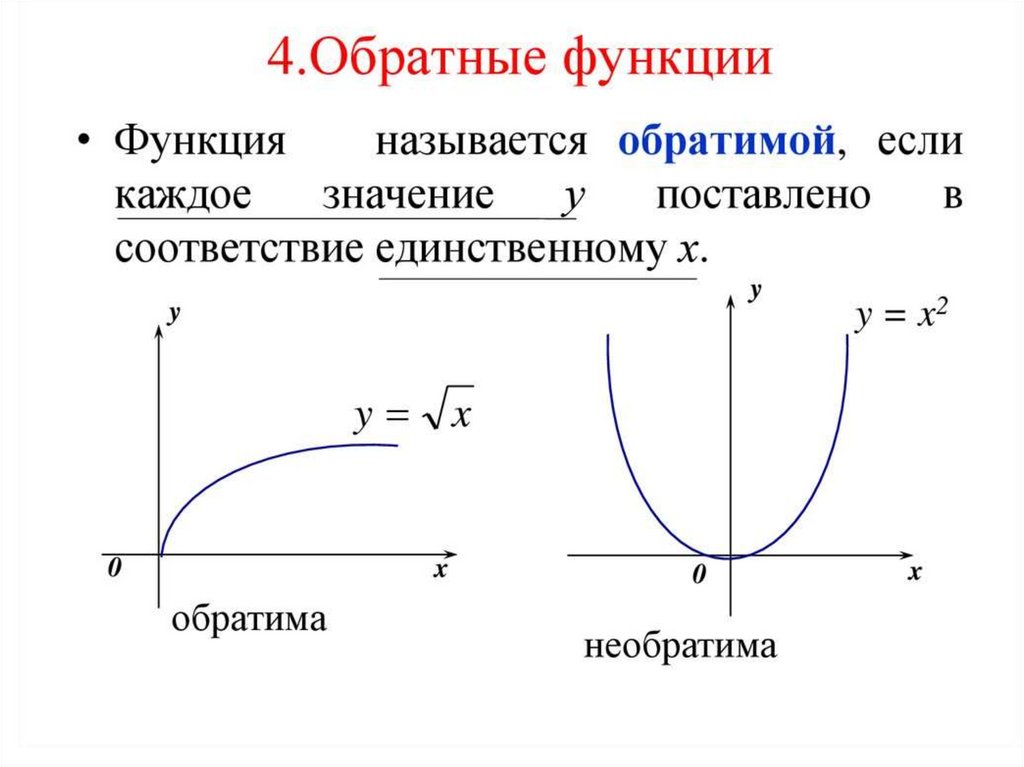
Условие обратимости функции
Теорема (достаточное условие обратимости функции).
Если функция монотонная на своей области
определения D, то она обратима на этой области.
Теорема.
Если функция f(x) возрастает (убывает) на своей
области определения D, то существует обратная
функция и она возрастает (убывает) на области
значений функции f(x).
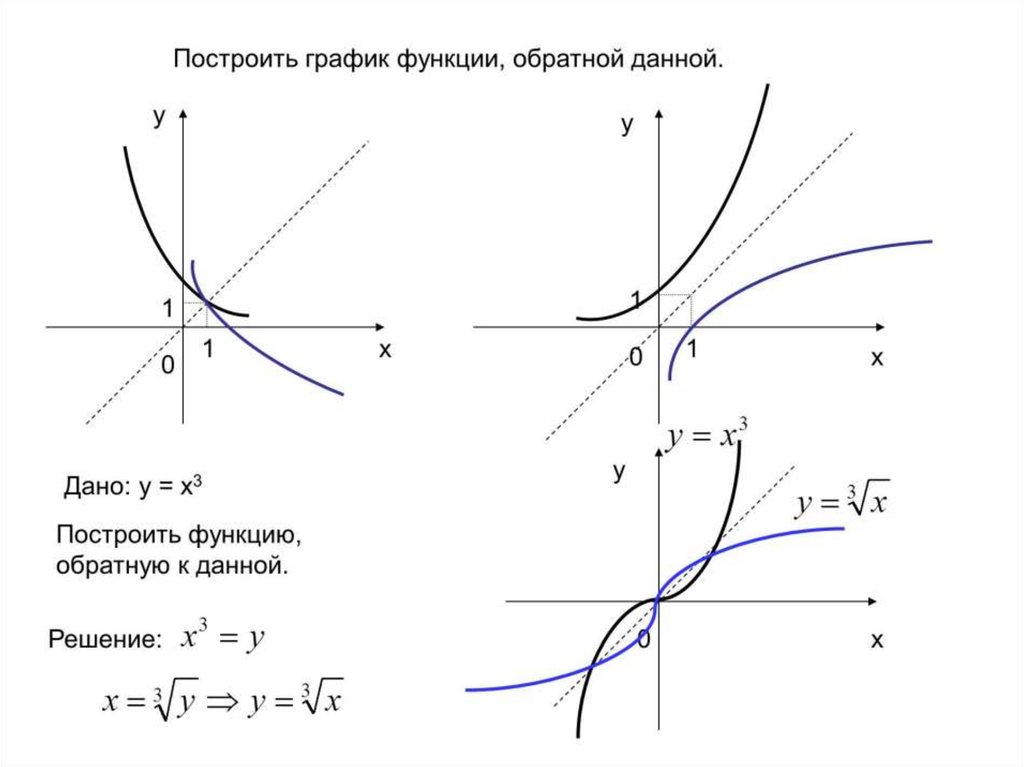
Графики прямой и обратной функций симметричны
относительно биссектрисы 1-го и 3-го координатных
углов.