Похожие презентации:
Комбинаторика. Принцип включения-исключения
1.
КомбинаторикаПринцип
включения-исключения
2.
Принцип включения-исключенияЯвляется обобщением принципа сложения
Принцип сложения
Если все множество комбинаторных объектов C можно
разбить на два непересекающихся подмножества A и
B (иными словами, есть два разных способа
(алгоритма) построения объекта c C), то |C| = |A| + |B|
Но что если множества A и B пересекаются?
3.
Принцип включения-исключенияНо что если множества A и B пересекаются?
|A B| = |A| + |B| - |A B|
4.
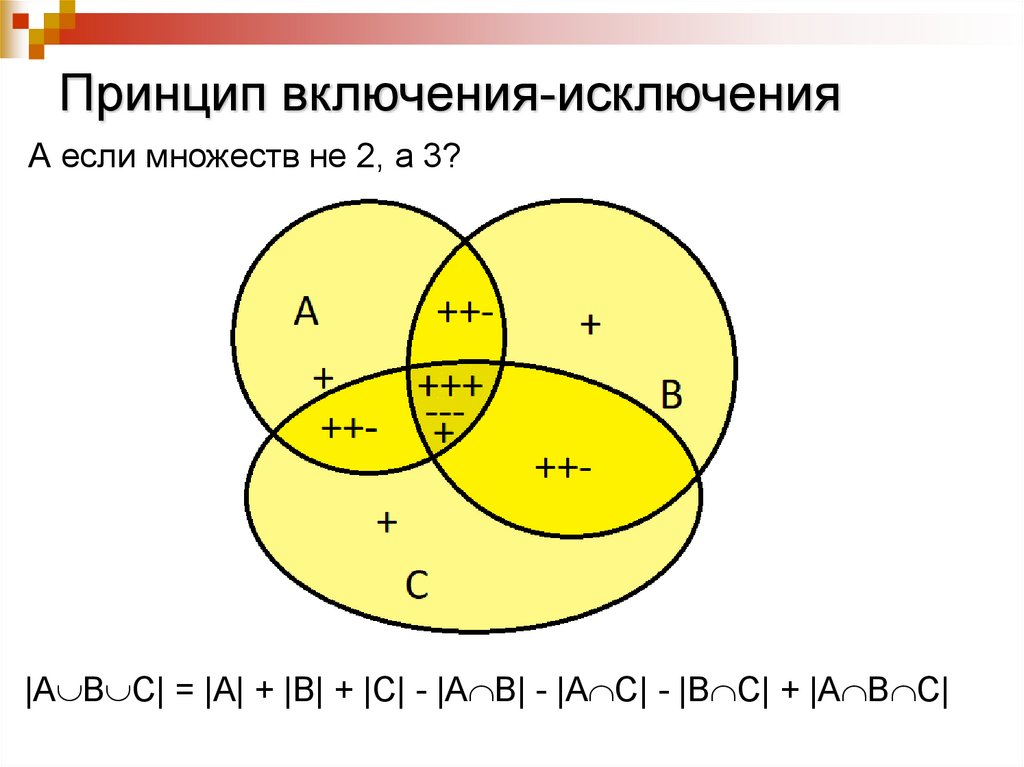
Принцип включения-исключенияА если множеств не 2, а 3?
|A B C| = |A| + |B| + |C| - |A B| - |A C| - |B C| + |A B C|
5.
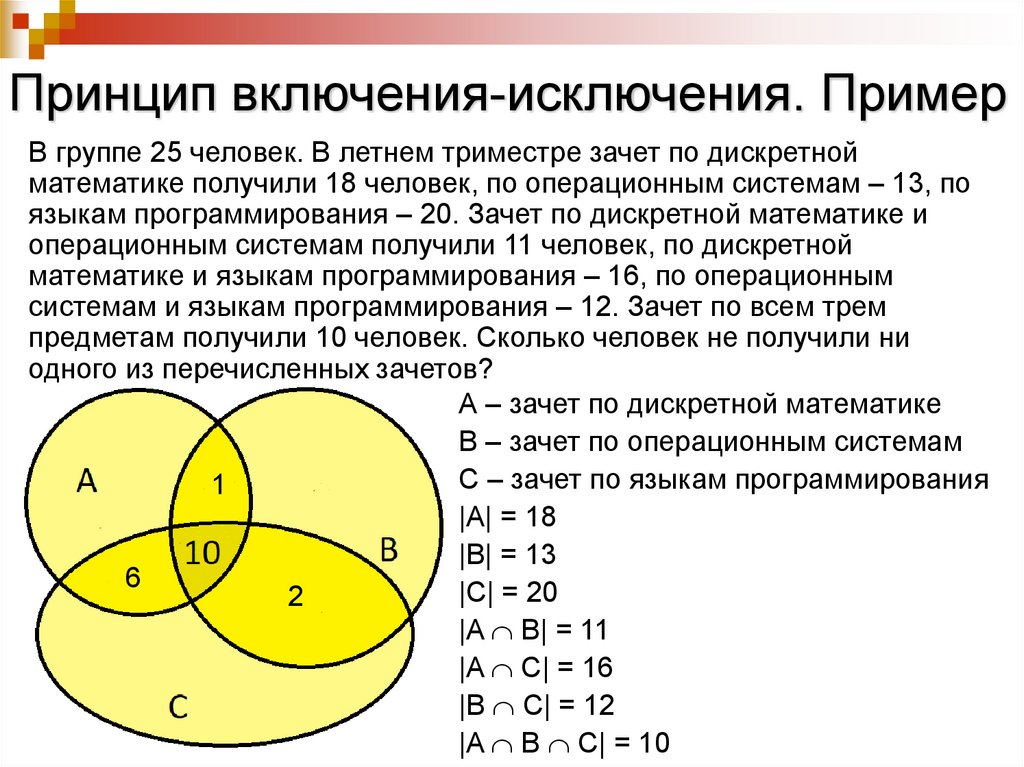
Принцип включения-исключения. ПримерВ группе 25 человек. В летнем триместре зачет по дискретной
математике получили 18 человек, по операционным системам – 13, по
языкам программирования – 20. Зачет по дискретной математике и
операционным системам получили 11 человек, по дискретной
математике и языкам программирования – 16, по операционным
системам и языкам программирования – 12. Зачет по всем трем
предметам получили 10 человек. Сколько человек не получили ни
одного из перечисленных зачетов?
А – зачет по дискретной математике
B – зачет по операционным системам
C – зачет по языкам программирования
|A| = 18
|B| = 13
|C| = 20
|A B| = 11
|A C| = 16
|B C| = 12
|A B C| = 10
6.
Принцип включения-исключения. ПримерВ группе 25 человек. В летнем триместре зачет по дискретной
математике получили 18 человек, по операционным системам – 13, по
языкам программирования – 20. Зачет по дискретной математике и
операционным системам получили 11 человек, по дискретной
математике и языкам программирования – 16, по операционным
системам и языкам программирования – 12. Зачет по всем трем
предметам получили 10 человек. Сколько человек не получили ни
одного из перечисленных зачетов?
А – зачет по дискретной математике
B – зачет по операционным системам
C – зачет по языкам программирования
1
|A| = 18
|B| = 13
6
|C| = 20
2
|A B| = 11
|A C| = 16
|B C| = 12
|A B C| = 10
7.
Принцип включения-исключения. ПримерВ группе 25 человек. В летнем триместре зачет по дискретной
математике получили 18 человек, по операционным системам – 13, по
языкам программирования – 20. Зачет по дискретной математике и
операционным системам получили 11 человек, по дискретной
математике и языкам программирования – 16, по операционным
системам и языкам программирования – 12. Зачет по всем трем
предметам получили 10 человек. Сколько человек не получили ни
одного из перечисленных зачетов?
А – зачет по дискретной математике
B – зачет по операционным системам
1
0
C – зачет по языкам программирования
1
|A| = 18
|B| = 13
6
|C| = 20
2
|A B| = 11
2
|A C| = 16
|B C| = 12
|A B C| = 10
8.
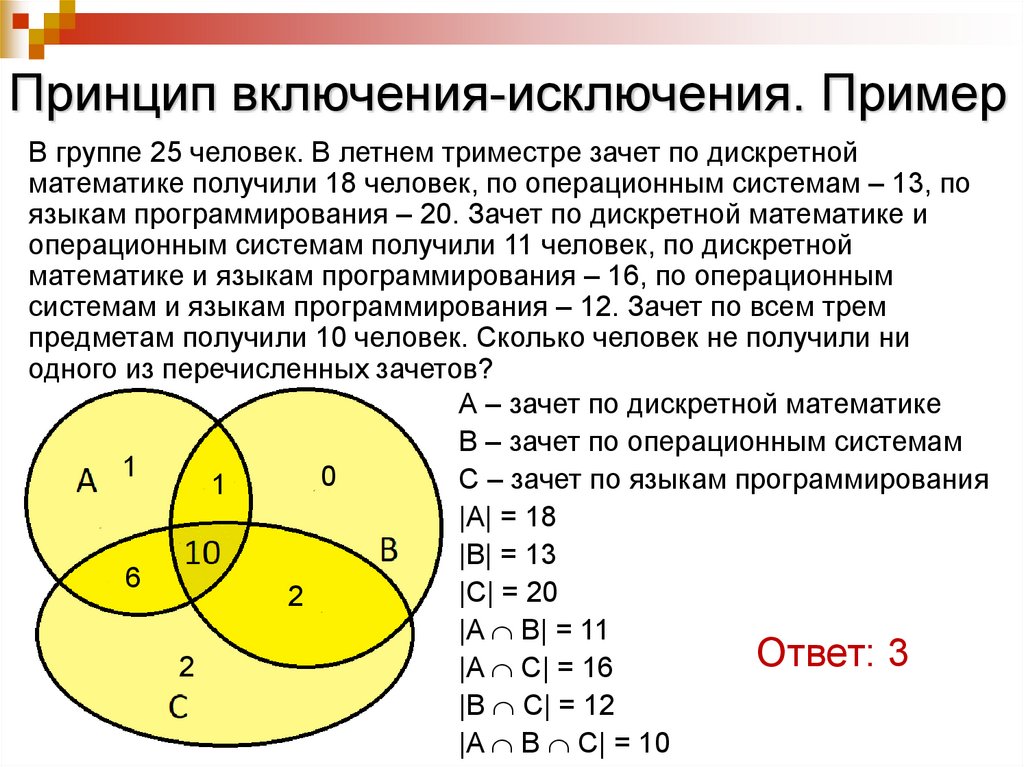
Принцип включения-исключения. ПримерВ группе 25 человек. В летнем триместре зачет по дискретной
математике получили 18 человек, по операционным системам – 13, по
языкам программирования – 20. Зачет по дискретной математике и
операционным системам получили 11 человек, по дискретной
математике и языкам программирования – 16, по операционным
системам и языкам программирования – 12. Зачет по всем трем
предметам получили 10 человек. Сколько человек не получили ни
одного из перечисленных зачетов?
А – зачет по дискретной математике
B – зачет по операционным системам
1
0
C – зачет по языкам программирования
1
|A| = 18
|B| = 13
6
|C| = 20
2
|A B| = 11
Ответ: 3
2
|A C| = 16
|B C| = 12
|A B C| = 10
9.
КомбинаторикаБиномиальные
коэффициенты














 Математика
Математика








