Урок № 19 Построение четвертого пропорционального отрезка.. (1)

1.

18.11.2024
Тема урока:
Построение четвертого
пропорционального
отрезка.
Урок геометрии
в 8 классе.

2.

Посмотрите видео по ссылке
https://urokimatematiki.ru/urok-proporcionalnie-otrezki-593.html

3.

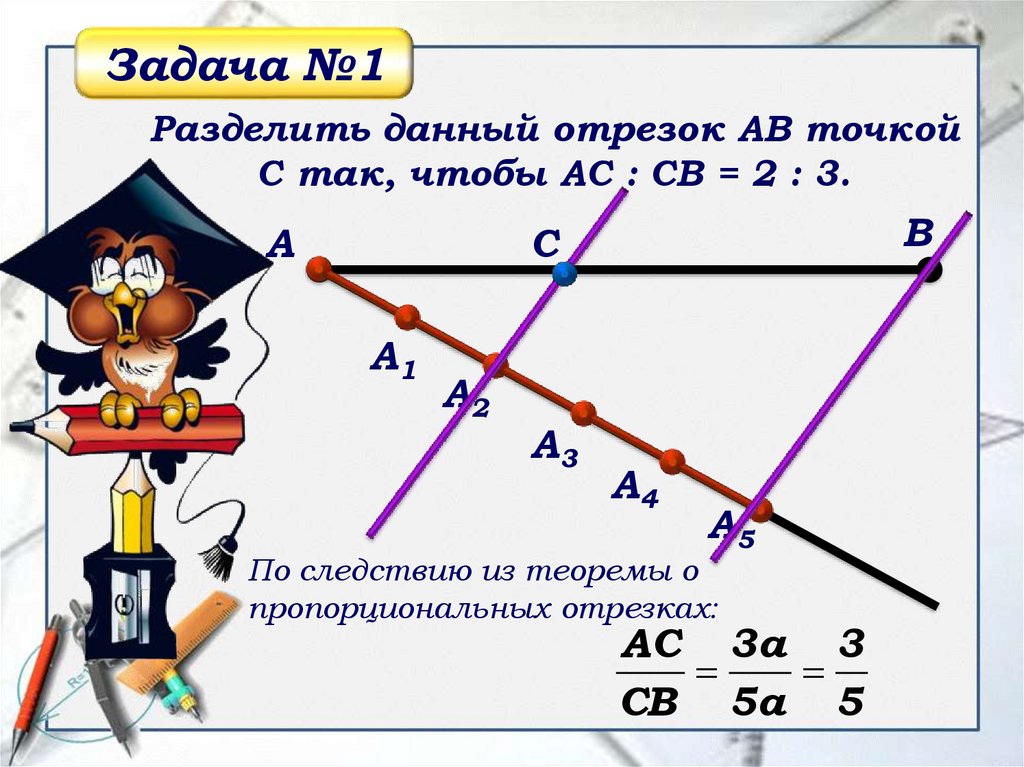
Задача №1
Разделить данный отрезок АВ точкой
С так, чтобы АС : СВ = 2 : 3.
А
В
С
А1
А2
А3
А4
А5
По следствию из теоремы о
пропорциональных отрезках:
АС 3а 3
СВ 5а 5

4.

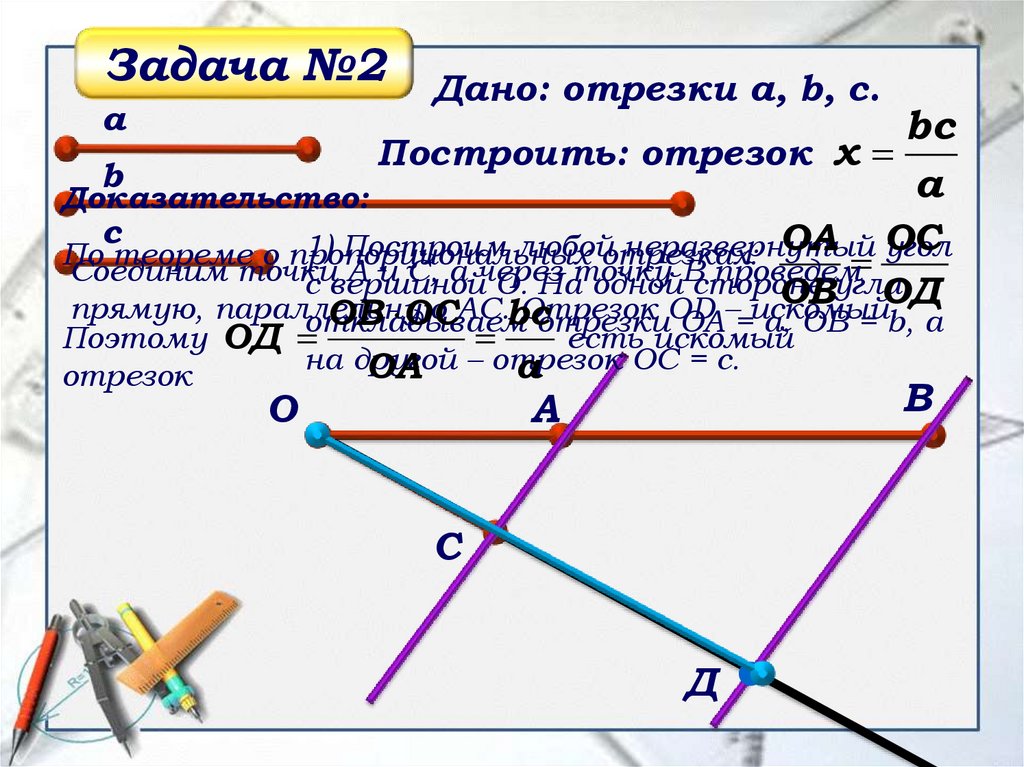
Задача №2
а
Дано: отрезки а, b, с.
bc
Построить: отрезок х
b
а
Доказательство:
с
ОА ОС
1) Построим любойотрезках:
неразвернутый
угол
По теореме о пропорциональных
Соединим точки
A и C, а через
проведем
с вершиной
O. Наточку
однойBстороне
угла
ОВ
ОД
прямую, параллельную
AC.
Отрезок
OD
–
искомый.
ОВ ОС bсотрезки OA = a, OB = b, а
откладываем
Поэтому ОД
есть искомый
на другой
OC = c.
ОА – отрезок
а
отрезок
О
В
А
С
Д

5.

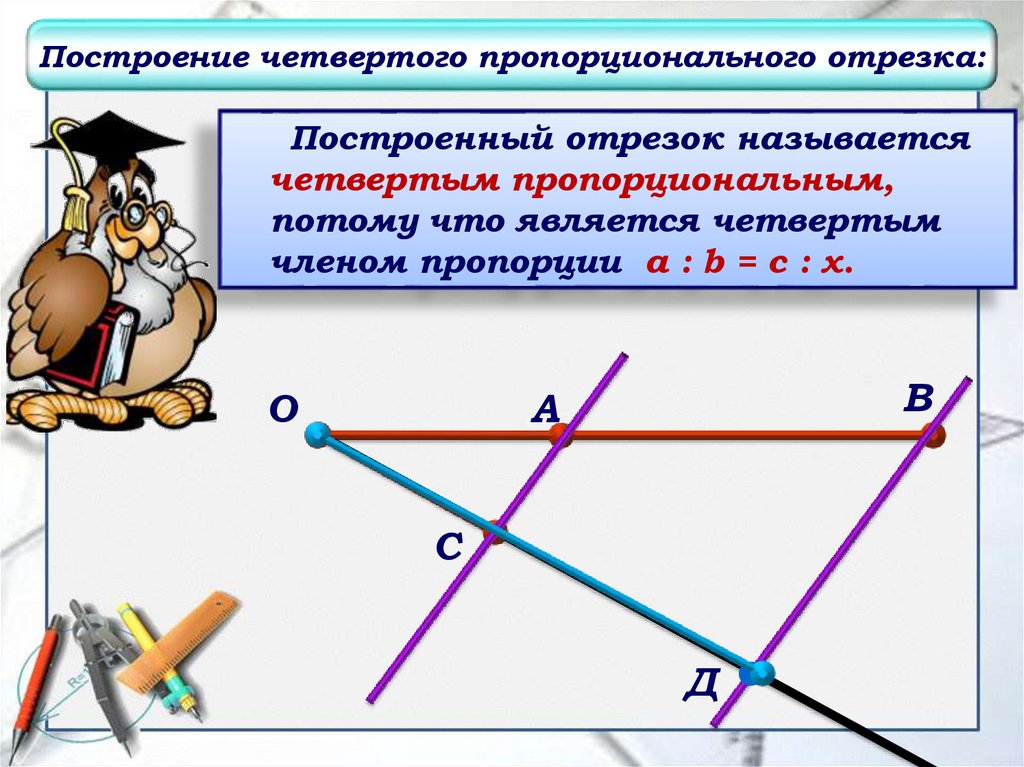
Построение четвертого пропорционального отрезка:
Построенный отрезок называется
четвертым пропорциональным,
потому что является четвертым
членом пропорции a : b = с : x.
О
В
А
С
Д

6.

Задача №1
Отрезок МК параллелен стороне
АС треугольника АВС (М АВ, К ВС),
Найдите длину отрезка СК, если
АМ=6см, а отрезок ВМ в 1,5 раза
больше отрезка ВК.

7.

Задача №1

8.

Задача №2
Точка А делит боковую сторону
трапеции на отрезки, один из
которых в 3 раза больше другого.
Ч/з точку А проходит прямая,
параллельная основаниям трапеции.
Она пересекает вторую боковую
сторону, равную 20 см, в точке В.
Найдите длины отрезков, на
которые точка В делит боковую
сторону.
Ответ: 5 см и 15 см.

9.

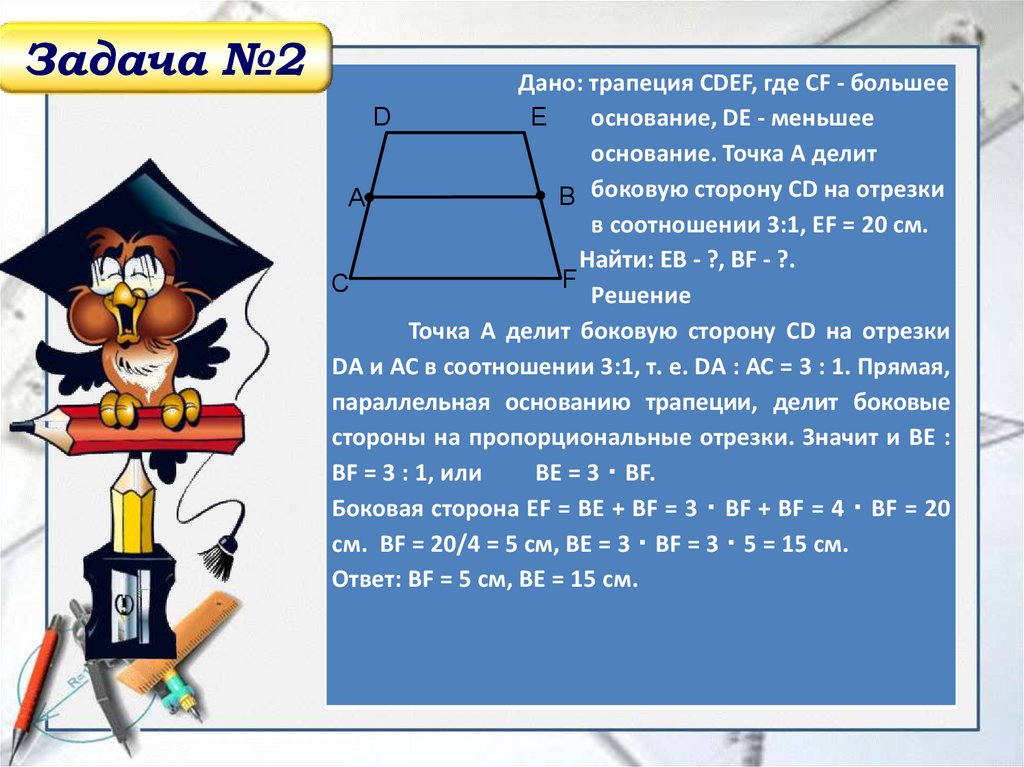
Задача №2
Дано: трапеция СDЕF, где СF - большее
D
E
основание, DЕ - меньшее
основание. Точка А делит
В боковую сторону СD на отрезки
А
в соотношении 3:1, ЕF = 20 см.
Найти: ЕB - ?, BF - ?.
F
С
Решение
Точка А делит боковую сторону СD на отрезки
DА и АС в соотношении 3:1, т. е. DА : АС = 3 : 1. Прямая,
параллельная основанию трапеции, делит боковые
стороны на пропорциональные отрезки. Значит и ВЕ :
ВF = 3 : 1, или
ВЕ = 3 ‧ ВF.
Боковая сторона ЕF = ВЕ + ВF = 3 ‧ ВF + ВF = 4 ‧ ВF = 20
см. ВF = 20/4 = 5 см, ВЕ = 3 ‧ ВF = 3 ‧ 5 = 15 см.
Ответ: ВF = 5 см, ВЕ = 15 см.

10.

Задача №3
В прямоугольнике АВСД: АВ = 6см, АД
= 10 см, АК – биссектриса угла А
(К ВС). Определите среднюю линию
трапеции АКСД.

11.

Задача №4
АВСД – равнобокая трапеция. АД –
большее основание. Разность между
периметрами треугольников АСД и
ВАС равна 6 см, средняя линия – 12
см. Вычислить основания.

12.

Задача №5
В равнобокой трапеции диагональ
делит острый угол пополам,
периметр ее равен 54 дм, большее
основание ее – 1,8 м. Вычислить
меньшее основание трапеции.
Ответ: 12 дм.

13.

Задача №6
В равнобокой трапеции высота,
проведенная из вершины тупого угла,
делит большее основание на отрезки
6,5 см и 29,5 см. Вычислите среднюю
линию трапеции.
Ответ: 29,5 см.